Дифракция формулы: Дифракция света. Дифракционная решетка. | Объединение учителей Санкт-Петербурга

Дифракция света. Дифракционная решетка. | Объединение учителей Санкт-Петербурга

Основные ссылки

CSS adjustments for Marinelli theme

Объединение учителей Санкт-Петербурга

Форма поиска

Поиск

Вы здесь

Главная » Дифракция света. Дифракционная решетка.

Дифракция света
Характерным проявлением волновых свойств света является дифракция света — отклонение света от прямолинейного рас­пространения на резких неоднородностях среды. Дифракция была открыта Ф.Гримальди в конце XVII в. Объяснение яв­ления дифракции света дано Т. Юнгом и О. Френелем, которые не только дали описание экспериментов по наблюдению явлений интерференции и дифракции света, но и объяснили свойство пря­молинейности распространения света с позиций волновой теории.
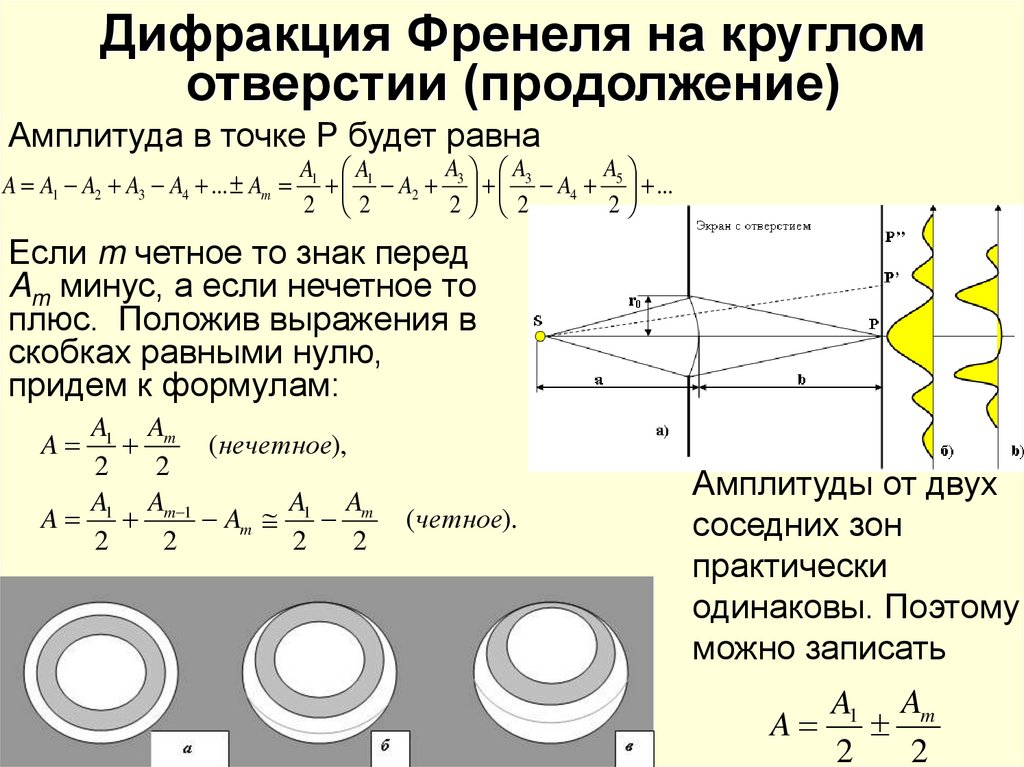
Зоны Френеля Принцип Гюйгенса — Френеля: волновая поверх­ность в любой момент времени представляет собой не просто огибающую вторичных волн, а результат их интерференции. Для того чтобы найти амплитуду световой волны от точечного моно­хроматического источника света А в произвольной точке О изо­тропной среды, надо источник света окружить сферой радиусом r=ct. Интерференция волны от вторичных источников, располо­женных на этой поверхности, определяет амплитуду в рассмат­риваемой точке О, т. е. необходимо произвести сложение коге­рентных колебаний от всех вторичных источников на волновой поверхности. Так как расстояния от них до точки О различны, то колебания будут приходить в различных фазах. Наименьшее расстояние от точки О до волновой поверхности В равно r0. Первая зона Френеля ограничивается точками волновой поверхности, рассто­яния от которых до точки О равны: , где λ — длина световой волны. Вторая зона . Аналогично определяются границы других зон. Если разность хода  от двух соседних зон равна половине длины волны, то коле­бания от них приходят в точку О в противоположных фазах и на­блюдается интерференционный минимум, если разность хода равна длине волны, то наблю­дается интерференционный максимум. Таким образом, если на препятствии укладывается целое число длин волн, то они гасят друг друга и в данной точке наблюдается минимум (темное пятно). Если нечетное число полуволн, то наблюдается максимум (светлое пятно). Расчеты позволили понять, каким образом свет от точечного источника, испускающего сферические волны, достигает про­извольной точки О пространства.
Дифракция от различных препятствий: от тонкой прово­лочки; от круглого отверстия; от круглого непрозрачного экрана.
Дифракция происходит на предметах любых размеров, а не только соизмеримых с длиной волны λ. Трудности наблюдения заключаются в том, что вследствие малости длины световой волны интерференционные максиму­мы располагаются очень близко друг к другу, а их интенсив­ность быстро убывает.
Дифракция наблюдается хорошо на расстоянии . Если , то дифракция невидна и получается резкая тень (d — диаметр экрана). Эти соотношения определяют границы применимости геометрической оптики. Если наблюдение ведется на расстоянии , где d—размер предмета, то начинают проявляться волновые свойства света. На рис. показана примерная зависимость результатов опыта по распространению волн в зависимости от соотношения размеров препятствия и длины волны.
Интерференционные картины от разных точек предмета пе­рекрываются, и изображение смазывается, поэтому прибор не выделяет отдельные детали предмета. Дифракция устанавлива­ет предел разрешающей способности любого оптического при­бора. Разрешающая способность человеческого глаза приблизите­льно равна одной угловой минуте: , где D — диаметр зрач­ка; телескопа α=0,02» микроскопа: увеличение не более 2-103 раз. Можно видеть предметы, размеры которых соизмеримы с длиной световой волны.
Дифракционная решетка
Дифракционная решетка — система препятствий (параллельных штрихов), сравнимых по размерам с длиной волны. Величина  d = a + b называется постоянной (периодом) дифракционной решетки, где а — ширина щели; b — ширина непрозрачной части. Угол φ — угол отклонения световых волн вследствие дифракции. Наша задача — определить, что будет наблюдаться в произвольном направлении φ — максимум или минимум. Оптическая разность хода  Из условия максимума интерференции получим: . Следовательно:  — формула дифракционной решетки. Величина k — порядок дифракцион­ного максимума ( равен 0, ± 1, ± 2 и т.д.).
Определение λ с помощью дифракционной решетки

Теги: 

конспект

§20.

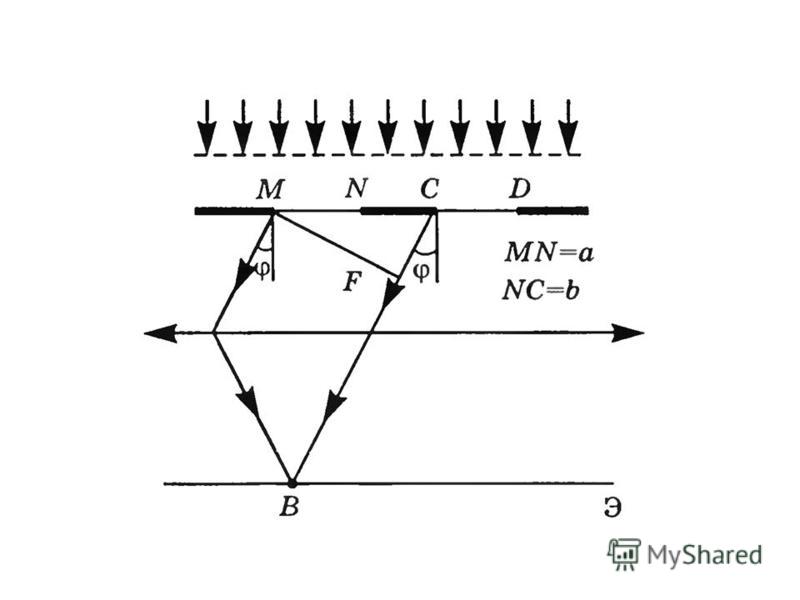
Дифракция света Основные формулы

Угол отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели, определяется из условия

,

где а – ширина щели; k – порядковый номер максимума (k = 1,2,3,…).

Угол отклонения лучей, соответствующий минимуму (темная полоса) при дифракции на одной щели, определяется из условия

.

Угол отклонения лучей, соответствующий максимуму при дифракции света на дифракционной решетке, определяется из условия

,

где k = 0,1,2,3,…; d – период дифракционной решетки.

Разрешающая способность дифракционной решетки равна

где – наименьшая разность длин волн двух соседних спектральных линий ( и ), при которой эти линии могут быть видны раздельно в спектре, полученном посредством данной решет­ки;

N – полное число щелей решетки; k – порядковый номер дифракционного максимума.

Формула Вульфа – Брэггов имеет вид

,

где – угол скольжения, то есть угол между направлением пучка парал­лельных рентгеновских лучей, падающих на кристалл, и гранью кристалла; d – расстояние между атомными плоскостями кри­сталла. Формула Вульфа – Брэггов определяет направление лучей, при которых возникает дифракционный максимум.

Задачи

20.1. На щель шириной а = 0,05 мм падает нормально монохро­матический свет (λ= 0,6 мкм). Определить угол φ между первоначаль­ным направлением пучка света и направлением на четвертую тем­ную дифракционную полосу.

20.2 Точечный источник света с длиной волны λ =0,5мкм расположен на расстоянии а = 100 см перед диафрагмой с круглым отверстием радиуса r = 1,0 мм. Найти расстояние b от диафрагмы до точки наблюдения, для которой число зон Френеля в отверстии составляет к = 3.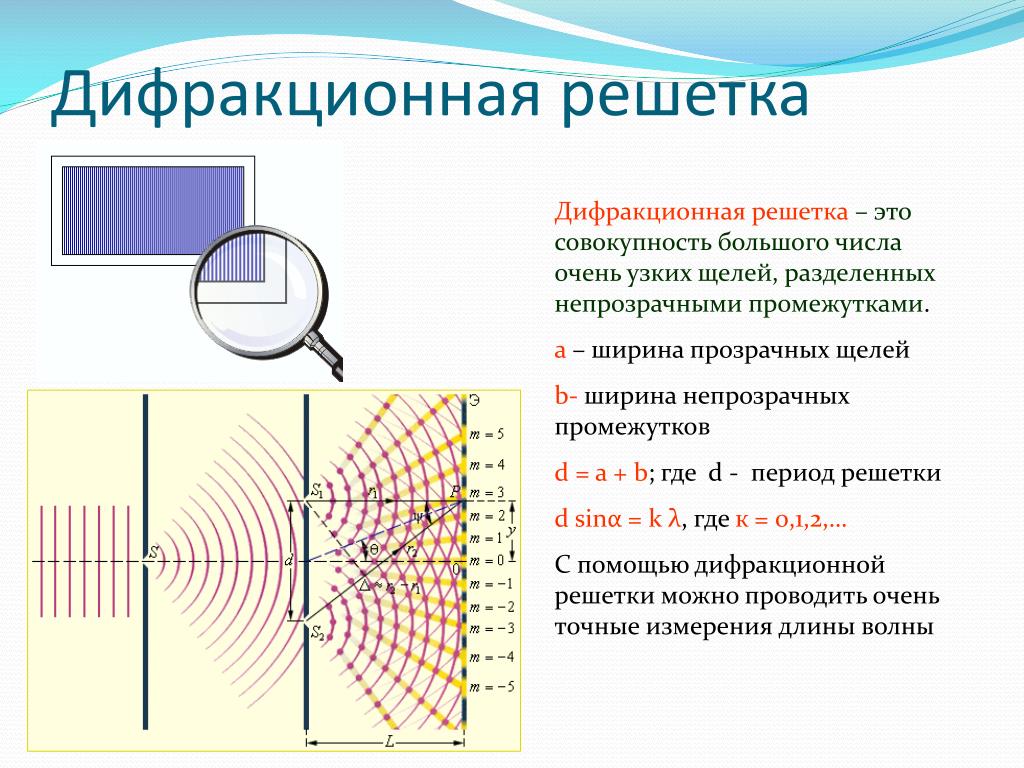

20.3. Между точечным источником света и экраном поместили диафрагму с круглым отверстием, радиус которого r можно менять. Расстояние от диафрагмы до источника и экрана равны а = 100 см и b = 125 см. Определить длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при r₁ = 1,00 мм и следующий максимум — при r₂ = 1,29 мм.

20.4. На узкую щель падает нормально монохроматический свет. Угол φ отклонения пучков света, соответствующих второй светлой дифракционной полосе, равен 1

0. Скольким длинам волн падающего света равна ширина щели?

20.5. На щель шириной а = 0,1 мм падает нормально монохрома­тический свет (λ= 0,5 мкм). За щелью помещена собирающая лин­за, в фокальной плоскости которой находится экран. Что будет на­блюдаться на экране, если угол φ дифракции равен: 1) 17^/; 2) 43^/?

20. 6. Сколько штрихов на каждый миллиметр содержит дифракционная решетка, если при наблюдении в монохроматическом свете (λ= 0,6 мкм) максимум пятого порядка отклонен на угол φ = 18⁰?

20.7. На дифракционную решетку, содержащую n = 100 штри­хов на 1 мм, падает нормально монохроматический свет. Зритель­ная труба спектрометра наведена на максимум третьего порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол = 20°. Определить длину волны света.

20.8. Дифракционная решетка освещена нормально падающим монохроматическим светом. В дифракционной картине максимум второго порядка отклонен на угол φ₁ = 14⁰. На какой угол φ₂ откло­нен максимум третьего порядка?

20.9. Дифракционная решетка содержит n = 200 штрихов на 1 мм. На решетку падает нормально монохроматический свет (λ= 0,6 мкм). Максимум какого наибольшего порядка дает эта решетка?

20. 10. На дифракционную решетку, содержащую n = 400 штри­хов на 1 мм, падает нормально монохроматический свет (λ= 0,6мкм). Найти общее число дифракционных максимумов, которые дает эта решетка. Определить угол φ дифракции, соответствующий послед­нему максимуму.

20.11. При освещении дифракционной решетки белым светом спектры второго и третьего порядков отчасти перекрывают друг друга. На какую длину волны в спектре второго порядка накладывается фиолетовая граница (λ= 0,4 мкм) спектра третьего порядка?

20.12. На дифракционную решетку, содержащую n = 500 штри­хов на 1 мм, падает в направлении нормали к ее поверхности белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить ширину b спектра первого порядка на экране, если расстояние L от линзы до экрана равно 3 м. Границы видимого спектра = 780 нм, = 400 нм.

20.13. Дифракционная картина получена с помощью дифракционной решетки длиной l = 1,5 см и периодом d = 5 мкм. Определить, в спектре какого наименьшего порядка этой картины получатся раздельные изображения двух спектральных линий с разностью длин волн = 0,1 нм, если линии лежат в крайней красной части спектра ( ≈ 760 нм).

20.14. Какой наименьшей разрешающей силой R должна обла­дать дифракционная решетка, чтобы с ее помощью можно было раз­решить две спектральные линии калия ( = 578 нм и = 580 нм)? Какое наименьшее число N штрихов должна иметь эта решетка, чтобы разрешение было возможно в спектре второго порядка?

20.15. С помощью дифракционной решетки с периодом d = 20 мкм требуется разрешить дублет натрия ( = 589,0 нм и = 589,6 нм) в спектре второго порядка. При какой наименьшей длине l решетки это возможно?

20.16. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения (λ= 147 пм). Определить расстоя­ние d между атомными плоскостями кристалла, если дифракционный максимум второго порядка наблюдается, когда излучение надает под углом θ = 31⁰30^/ к поверхности кристалла.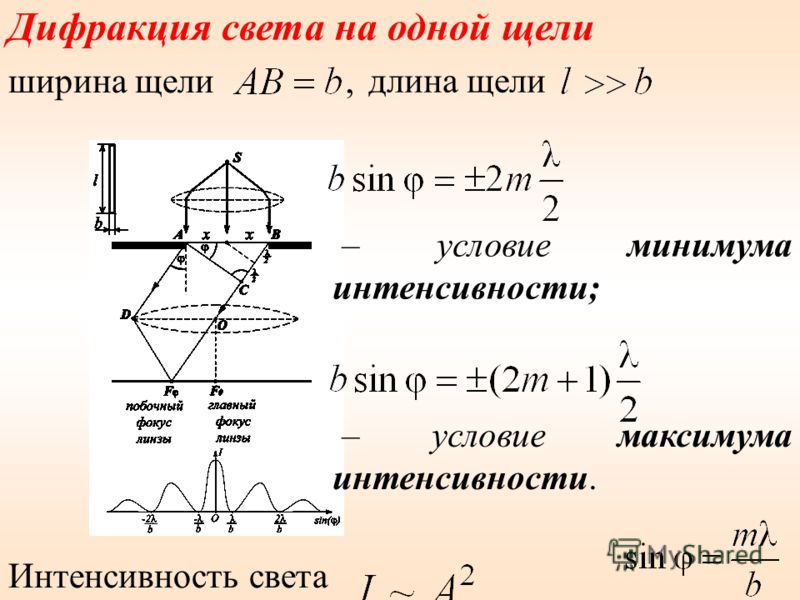

20.17. Какова длина волны λ монохроматического рентгеновского излучения, падающего на кристалл кальцита, если дифракционный максимум первого порядка наблюдается, когда угол θ между на­правлением падающего излучения и гранью кристалла равен 3⁰? Расстояние d между атомными плоскостями кристалла принять рав­ным 0,3 нм.

20.18. Параллельный пучок рентгеновского излучения падает на грань кристалла. Под углом θ = 65⁰ к плоскости грани наблю­дается максимум первого порядка. Расстояние d между атомными плоскостями кристалла 280 пм. Определить длину волны рентге­новского излучения.

4.3 Двухщелевая дифракция — University Physics Volume 3

Цели обучения

К концу этого раздела вы сможете:

• Описать комбинированный эффект интерференции и дифракции с двумя щелями, каждая из которых имеет конечную ширину
• Определение относительной интенсивности интерференционных полос на дифракционной картине
• Определите пропущенные порядки, если таковые имеются

Когда мы изучали интерференцию в эксперименте Юнга с двумя щелями, мы игнорировали эффект дифракции в каждой щели. Мы предполагали, что щели настолько узкие, что на экране вы видите только интерференцию света всего от двух точечных источников. Если щель меньше длины волны, то на рис. 4.10 (а) видно, что на экране наблюдается только распространение света, а не пики и провалы. Поэтому было разумно исключить в этой главе эффект дифракции. Однако, если вы сделаете щель шире, рис. 4.10 (b) и (c) показывают, что вы не можете игнорировать дифракцию. В этом разделе мы изучаем сложности эксперимента с двумя щелями, которые возникают, когда вам также необходимо учитывать дифракционный эффект каждой щели.

Чтобы рассчитать дифракционную картину для двух (или любого количества) щелей, нам нужно обобщить метод, который мы только что использовали, для одной щели. То есть поперек каждой щели мы размещаем равномерное распределение точечных источников, излучающих вейвлеты Гюйгенса, а затем суммируем вейвлеты от всех щелей. Это дает интенсивность в любой точке экрана. Хотя детали этого вычисления могут быть сложными, окончательный результат довольно прост:

.

Двухщелевая дифракционная картина

Дифракционная картина двух щелей шириной a , разделенных расстоянием d , представляет собой интерференционную картину двух точечных источников, разделенных d , умноженную на дифракционную картину щели шириной a .

Другими словами, местоположений интерференционных полос задаются уравнением дифракционные эффекты согласно уравнению 4.4. [Обратите внимание, что в главе об интерференции мы написали dsinθ=mλdsinθ=mλ и использовали целое число m для обозначения интерференционных полос. В уравнении 4.1 также используется м , но на этот раз для обозначения дифракционных минимумов. Если оба уравнения используются одновременно, рекомендуется использовать другую переменную (например, n ) для одного из этих целых чисел, чтобы они были различны. ]

Эффекты интерференции и дифракции действуют одновременно и обычно дают минимумы при разных углы. Это приводит к сложной картине на экране, в которой отсутствуют некоторые максимумы интерференции от двух щелей, если максимум интерференции находится в том же направлении, что и минимум дифракции. Такой отсутствующий пик мы называем отсутствующим порядком. Один из примеров дифракционной картины на экране показан на рис. 4.11. Сплошная линия с несколькими пиками разной высоты — интенсивность, наблюдаемая на экране. Это результат интерференции волн от отдельных щелей и дифракции волн внутри одной щели.

Рисунок 4.11 Дифракция от двойной щели. Фиолетовая линия с пиками одинаковой высоты — результат интерференции волн от двух щелей; синяя линия с одним большим горбом посередине — дифракция волн внутри одной щели; а толстая красная линия — это произведение двух, то есть картина, наблюдаемая на экране. График показывает ожидаемый результат для ширины щели a=2λa=2λ и расстояния между щелями d=6λd=6λ. Максимум порядка m=±3m=±3 для интерференции отсутствует, поскольку минимум дифракции происходит в том же направлении.

Пример 4.3

Интенсивность полос

На рис. 4.11 показано, что интенсивность полос при m=3m=3 равна нулю, но как насчет других полос? Рассчитайте интенсивность полосы при m=1m=1 относительно I0,I0, интенсивности центрального пика.

Стратегия

Определите угол интерференционной полосы с двумя щелями, используя уравнение из Interference, затем определите относительную интенсивность в этом направлении из-за дифракции, используя уравнение 4.4.

Решение

Из главы об интерференции мы знаем, что яркие интерференционные полосы возникают при dsinθ=mλdsinθ=mλ, или

sinθ=mλd.sinθ=mλd.

Из уравнения 4.4,

I=I0(sinββ)2, где β=ϕ2=πasinθλ.I=I0(sinββ)2, гдеβ=ϕ2=πasinθλ.

Подстановка сверху,

β=πasinθλ=πaλ·mλd=mπad.β=πasinθλ=πaλ·mλd=mπad.

Для a=2λa=2λ, d=6λd=6λ и m=1m=1,

β=(1)π(2λ)(6λ)=π3.β=(1)π(2λ)(6λ )=π3.

Тогда интенсивность равна

I=I0(sinββ)2=I0(sin(π/3)π/3)2=0,684I0.I=I0(sinββ)2=I0(sin(π/3)π/3)2=0,684 I0.

Значение

Обратите внимание, что этот подход относительно прост и дает результат, почти такой же, как и более сложный анализ с использованием векторов для определения значений интенсивности двухщелевой интерференции (тонкая линия на рис. 4.11). Метод фазора учитывает нисходящий наклон интенсивности дифракции (синяя линия), так что пик около м=1м=1 возникает при значении θθ немного меньшем, чем мы показали здесь.

Пример 4.4

Двухщелевая дифракция

Предположим, что в эксперименте Юнга щели шириной 0,020 мм разнесены на 0,20 мм.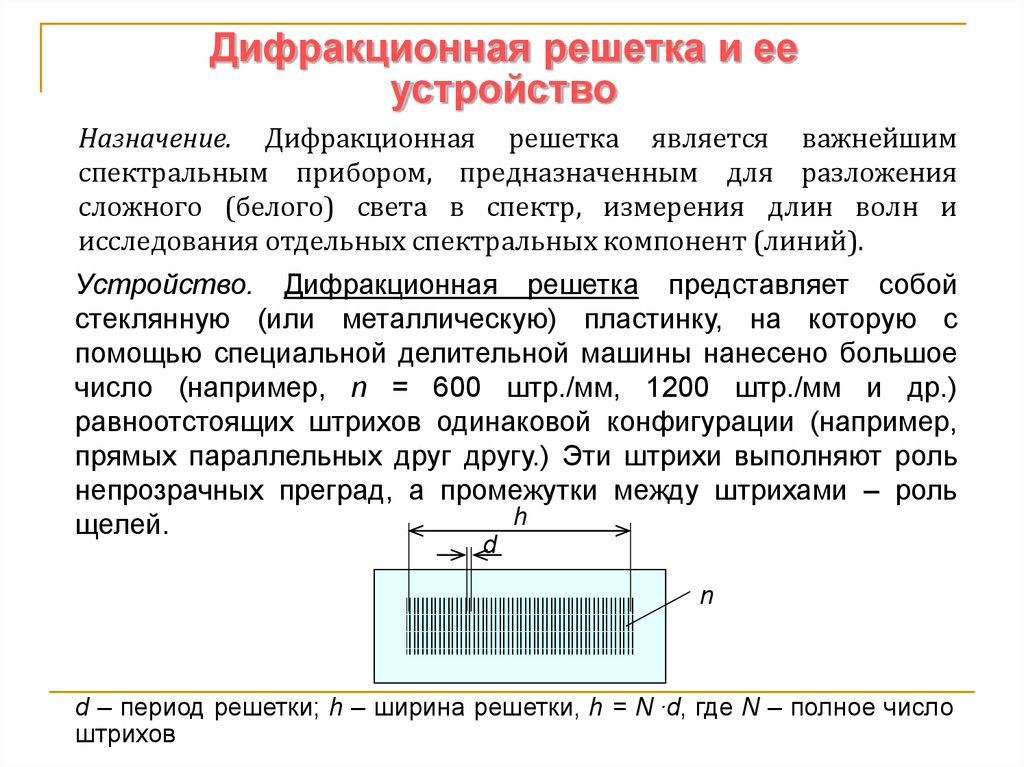 Если щели освещаются монохроматическим светом с длиной волны 500 нм, сколько ярких полос наблюдается в центральном пике дифракционной картины?

Раствор

Из уравнения 4.1 угловое положение первого дифракционного минимума равно ×10−5м=2,5×10−2рад.

Используя dsinθ=mλdsinθ=mλ для θ=2,5×10−2радθ=2,5×10−2рад, находим

m=dsinθλ=(0,20 мм)(2,5×10−2рад)(5,0×10−7м)= 10,m=dsinθλ=(0,20 мм)(2,5×10-2рад)(5,0×10-7м)=10,

, что является максимальным порядком интерференции, который находится внутри центрального пика. Заметим, что m=±10m=±10 — недостающие порядки, так как θθ точно совпадает. Соответственно, мы наблюдаем яркие полосы для

m=−9,−8,−7,−6,−5,−4,−3,−2,−1,0,+1,+2,+3,+ 4,+5,+6,+7,+8 и+9m=-9,-8,-7,-6,-5,-4,-3,-2,-1,0,+1, +2,+3,+4,+5,+6,+7,+8 и+9

всего 19 ярких полос.

Проверьте свое понимание 4.3

Для эксперимента в примере 4.4 покажите, что m=20m=20 также является отсутствующим порядком.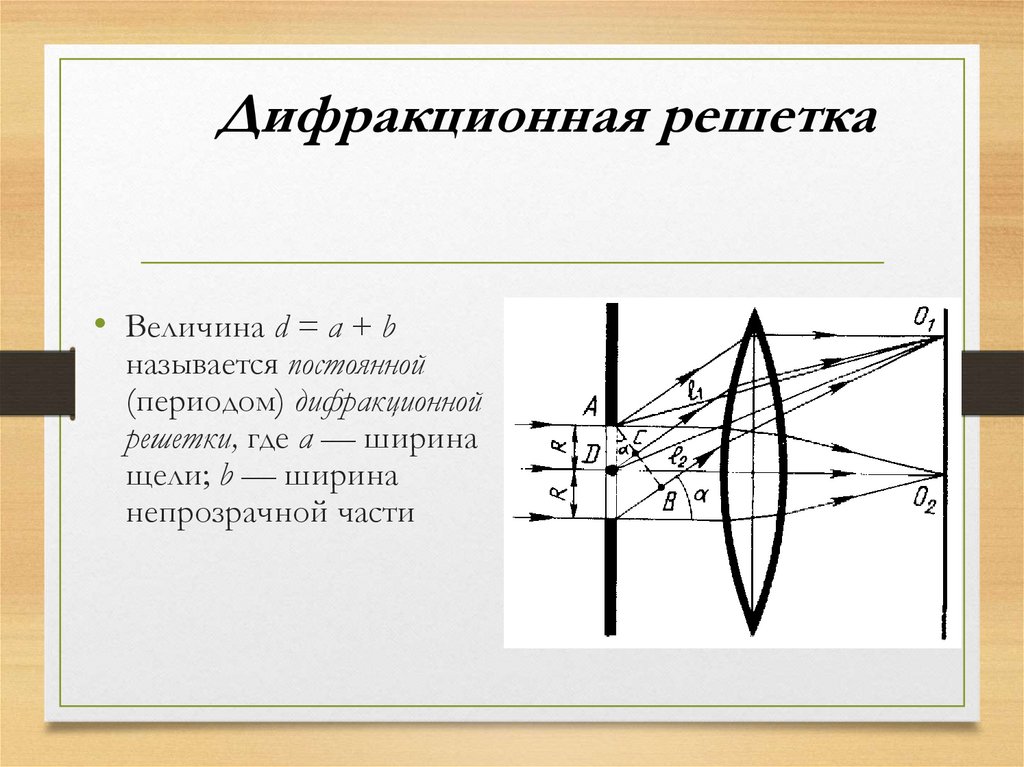

Интерактивный

Исследуйте эффекты двухщелевой дифракции. В этой симуляции, написанной Фу-Квун Хвангом, выберите N=2N=2 с помощью ползунка и посмотрите, что произойдет, если вы зададите ширину щели, расстояние между щелями и длину волны. Можете ли вы сделать заказ «пропавшим без вести»?

17.1 Понимание дифракции и интерференции — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

• Объяснять волновое поведение света, включая дифракцию и интерференцию, включая роль конструктивной и деструктивной интерференции в экспериментах Юнга с одной и двумя щелями
• Выполнение расчетов с учетом дифракции и интерференции, в частности длины волны света с использованием данных двухщелевой интерференционной картины

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:

• (7) Научные концепции. Учащийся знает характеристики и поведение волн. Ожидается, что студент:
  • (Д) исследовать поведение волн, включая отражение, преломление, дифракцию, интерференцию, резонанс и эффект Доплера

Основные термины раздела

дифракция

Принцип Гюйгенса

однотонный

волновой фронт

Дифракция и интерференция

Поддержка учителей

Поддержка учителей

[BL]Объясните конструктивное и деструктивное вмешательство графически на доске.

[OL]Попросите учащихся внимательно посмотреть на тень. Спросите, почему края не являются четкими линиями. Объясните, что это вызвано дифракцией, одним из волновых свойств электромагнитного излучения. Определите нанометр по отношению к другим метрическим измерениям длины.

[AL]Спросите учащихся, какие скорости, частоты и длины волн остаются неизменными, а какие изменяются при переходе луча света из одной среды в другую. Обсудите эти величины с точки зрения цветов (длин волн) видимого света.

Мы знаем, что видимый свет — это электромагнитная волна, на которую реагируют наши глаза. Как мы видели ранее, свет подчиняется уравнению

с=fλ,с=fλ,

, где c=3,00×108c=3,00×108 м/с — скорость света в вакууме, f – частота электромагнитной волны в Гц (или s ^–1 ), λλ – ее длина волны в м. Диапазон видимых длин волн составляет приблизительно от 380 до 750 нм. Как и для всех волн, свет распространяется прямолинейно и действует как луч, когда взаимодействует с объектами, в несколько раз превышающими его длину волны. Однако, когда он взаимодействует с более мелкими объектами, он заметно проявляет свои волновые характеристики. Интерференция — это идентифицирующее поведение волны.

На рис. 17.2 можно увидеть как лучевые, так и волновые характеристики света. Лазерный луч, испускаемый обсерваторией, отражает поведение луча, поскольку он движется по прямой линии. Пропускание чистого одноволнового луча через вертикальные щели шириной, близкой к длине волны луча, обнаруживает волновой характер света. Здесь мы видим, как луч распространяется горизонтально в виде узора из ярких и темных областей, которые вызваны систематической конструктивной и деструктивной интерференцией. Поскольку это характерно для волнового поведения, интерференция наблюдается для водяных, звуковых и световых волн.

Рисунок 17.2 (а) Луч света, испускаемый лазером в обсерватории Параналь (часть Европейской южной обсерватории в Чили), действует как луч, движущийся по прямой линии. (кредит: Юрий Белецкий, Европейская южная обсерватория) (б) Лазерный луч, проходящий через сетку вертикальных щелей, создает интерференционную картину, характерную для волны. (кредит: Шимон и Слава Рыбка, Wikimedia Commons)

То, что интерференция является характеристикой распространения энергии волнами, более убедительно демонстрируется волнами на воде. На рис. 17.3 показаны водные волны, проходящие через щели между некоторыми камнями. Вы можете легко увидеть, что ширина зазоров аналогична длине волны, и это вызывает интерференционную картину, когда волны проходят за зазоры. Поперечное сечение волн на переднем плане показало бы гребни и впадины, характерные для интерференционной картины.

Рисунок 17,3 Набегающие волны (вверху рисунка) проходят через щели в скалах и создают интерференционную картину (на переднем плане).

Свет имеет волновые характеристики в различных средах, а также в вакууме. Когда свет переходит из вакуума в какую-либо среду, например воду, его скорость и длина волны меняются, но его частота f остается неизменной. Скорость света в среде v=c/nv=c/n, где n — его показатель преломления. Если вы разделите обе части уравнения c=fλc=fλ на n , вы получаете c/n=v=fλ/nc/n=v=fλ/n . Следовательно, v=fλnv=fλn, где λnλn — длина волны в среде, а

λn=λn,λn=λn,

, где λλ — длина волны в вакууме, а n — показатель преломления среды.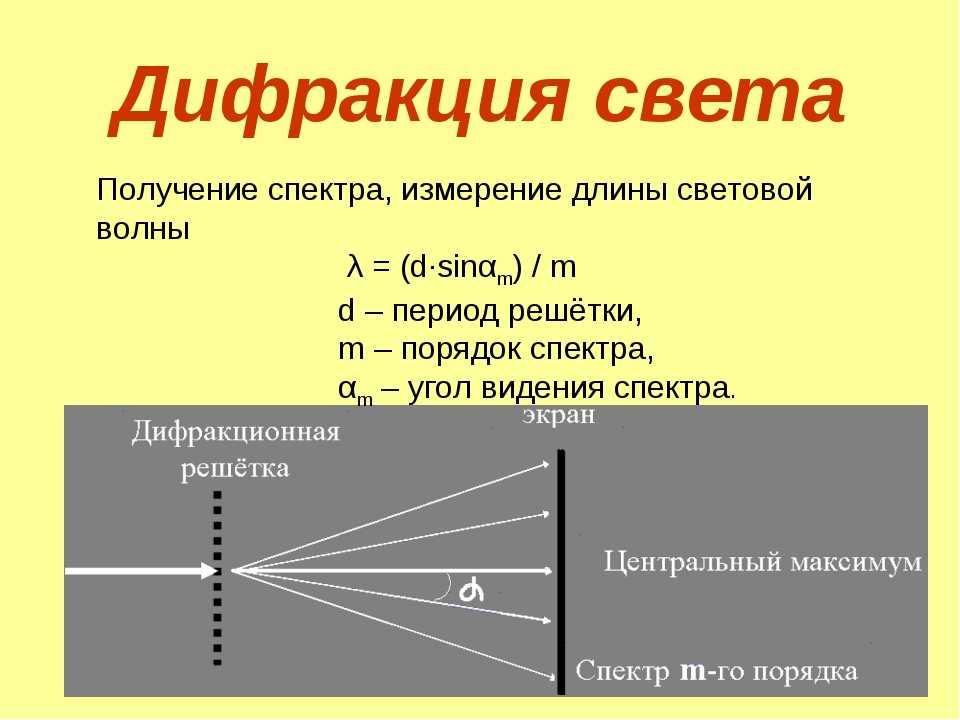 Отсюда следует, что длина волны света в любой среде меньше, чем в вакууме. Например, в воде, имеющей n = 1,333, диапазон видимых длин волн составляет от (380 нм)/1,333 до (760 нм)/1,333, или λn=λn= 285–570 нм. Хотя длины волн меняются при перемещении из одной среды в другую, цвета не меняются, поскольку цвета связаны с частотой.

Голландский ученый Христиан Гюйгенс (1629–1695) разработал полезную технику для детального определения того, как и где распространяются волны. Он использовал волновые фронты, которые представляют собой точки на поверхности волны, имеющие одну и ту же постоянную фазу (например, все точки, составляющие гребень водной волны). Принцип Гюйгенса гласит: «Каждая точка на фронте волны является источником вейвлетов, которые распространяются в прямом направлении с той же скоростью, что и сама волна. Новый волновой фронт — это линия, касательная ко всем вейвлетам».

На рис. 17.4 показано, как применяется принцип Гюйгенса. Фронт волны — это длинный фронт, который движется; например, гребень или корыто. Каждая точка волнового фронта излучает полукруглую волну, которая движется со скоростью v . Они рисуются позже в момент времени t , так что они переместились на расстояние s=vts=vt . Новый волновой фронт представляет собой линию, касательную к вейвлетам, и находится там, где волна находится в момент времени t . Принцип Гюйгенса работает для всех типов волн, включая волны воды, звуковые волны и световые волны. Это будет полезно не только при описании того, как распространяются световые волны, но и как они интерферируют.

Рисунок 17,4 Принцип Гюйгенса применим к прямолинейному волновому фронту. Каждая точка на фронте волны излучает полукруглый вейвлет, который перемещается на расстояние s=vts=vt. Новый волновой фронт представляет собой линию, касательную к вейвлетам.

Что происходит, когда волна проходит через отверстие, например свет проникает через открытую дверь в темную комнату? Что касается света, вы ожидаете увидеть резкую тень от дверного проема на полу комнаты, и вы ожидаете, что свет не будет огибать углы в другие части комнаты.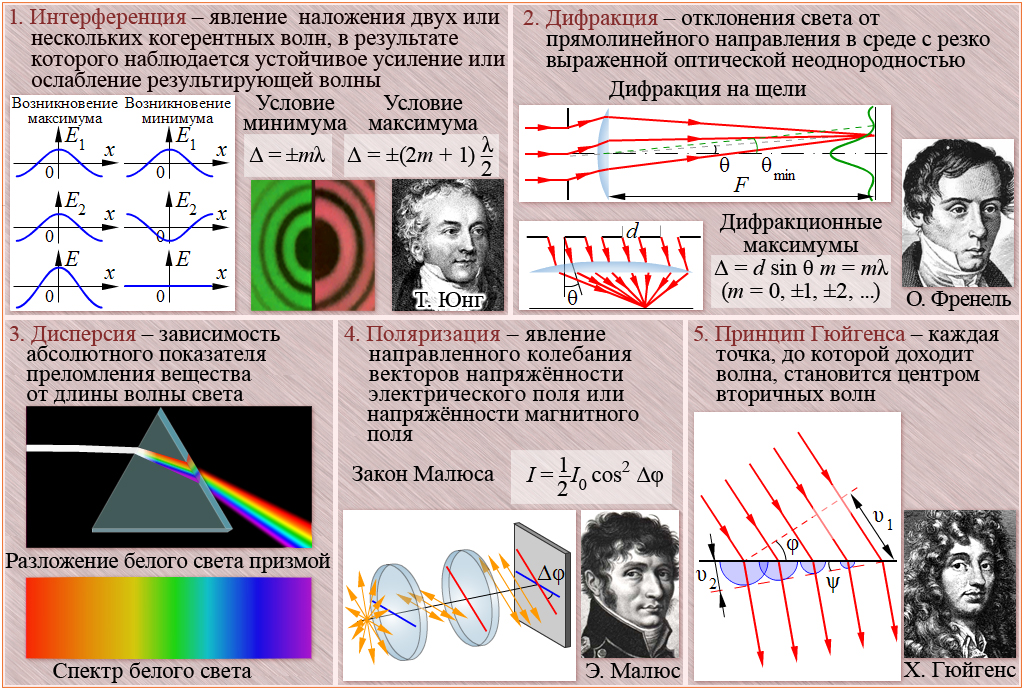 Когда звук проходит через дверь, вы слышите его повсюду в комнате и, таким образом, понимаете, что звук распространяется при прохождении через такой проем. Чем отличается поведение звуковых волн от световых в этом случае? Ответ заключается в том, что длины волн, из которых состоит свет, очень короткие, поэтому свет действует как луч. Звук имеет длину волны порядка размера двери, поэтому он огибает углы.

Поддержка учителей

Поддержка учителей

[OL]Обсудите тот факт, что для того, чтобы дифракционная картина была видимой, ширина щели должна примерно равняться длине волны света. Попытайтесь дать учащимся представление о длине волны видимого света, отметив, что человеческий волос примерно в 100 раз шире.

Если свет проходит через меньшие отверстия, часто называемые щелями, вы можете использовать принцип Гюйгенса, чтобы показать, что свет изгибается так же, как и звук (см. рис. 17.5). Огибание волной краев отверстия или препятствия называется дифракцией. Дифракция — это волновая характеристика, которая имеет место для всех типов волн. Если для явления наблюдается дифракция, это свидетельствует о том, что явление вызвано волнами. Таким образом, горизонтальная дифракция лазерного луча после прохождения через щели на рис. 17.2 свидетельствует о том, что свет обладает свойствами волны.

Рисунок 17,5 Принцип Гюйгенса применялся к прямому фронту волны, падающему на отверстие. Края волнового фронта изгибаются после прохождения через отверстие, этот процесс называется дифракцией. Величина изгиба является более экстремальной для небольшого отверстия, что согласуется с тем фактом, что волновые характеристики наиболее заметны при взаимодействии с объектами примерно того же размера, что и длина волны.

И снова волны на воде представляют собой знакомый пример волнового явления, которое легко наблюдать и понимать, как показано на рис. 17.6.

Рисунок 17,6 Океанские волны проходят через отверстие в рифе, образуя дифракционную картину. Дифракция возникает из-за того, что ширина отверстия аналогична длине волны.

Смотреть физику

Однощелевая интерференция

В этом видео используются математические расчеты, необходимые для прогнозирования дифракционных картин, вызванных однощелевой интерференцией.

Какие значения м обозначают место деструктивной интерференции на однощелевой дифракционной картине?

1. целые числа, кроме нуля
2. целых чисел
3. вещественных чисел без нуля
4. действительные числа

Тот факт, что принцип Гюйгенса работал, не считался достаточным доказательством того, что свет является волной. Люди также не хотели принимать волновую природу света, потому что это противоречило идеям Исаака Ньютона, который все еще пользовался большим уважением. Признание волнового характера света пришло после 1801 г., когда английский физик и врач Томас Юнг (1773–1829 гг.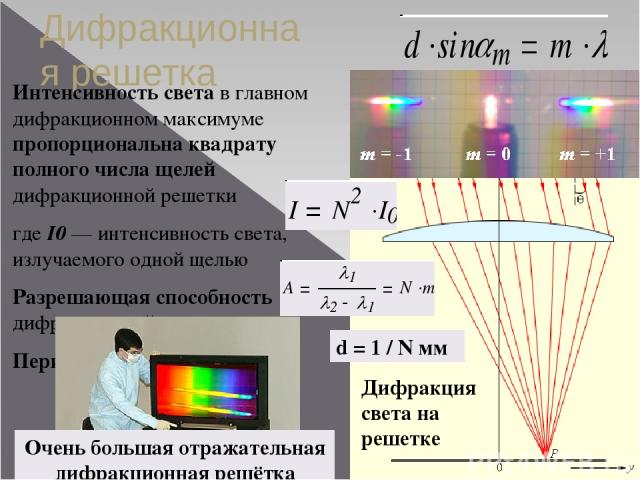 ) провел ставший уже классическим эксперимент с двумя щелями (см. рис. 17.7).

Рисунок 17,7 Эксперимент Юнга с двумя щелями. Здесь свет одной длины волны проходит через пару вертикальных щелей и создает на экране дифракционную картину — многочисленные вертикальные светлые и темные линии, разбросанные по горизонтали. Без дифракции и интерференции свет просто образовал бы две линии на экране.

Когда свет проходит через узкие щели, он преломляется в полукруглые волны, как показано на рис. 17.8 (а). Чистая конструктивная интерференция возникает там, где волны выстраиваются в линию гребень к гребню или впадина к впадине. Чисто деструктивное вмешательство происходит там, где они выстраиваются от гребня к впадине. Свет должен падать на экран и рассеиваться в наших глазах, чтобы рисунок был виден. Аналогичная картина для волн на воде показана на рис. 17.8 (b). Обратите внимание, что области конструктивной и деструктивной интерференции выходят из щелей под определенными углами к исходному лучу.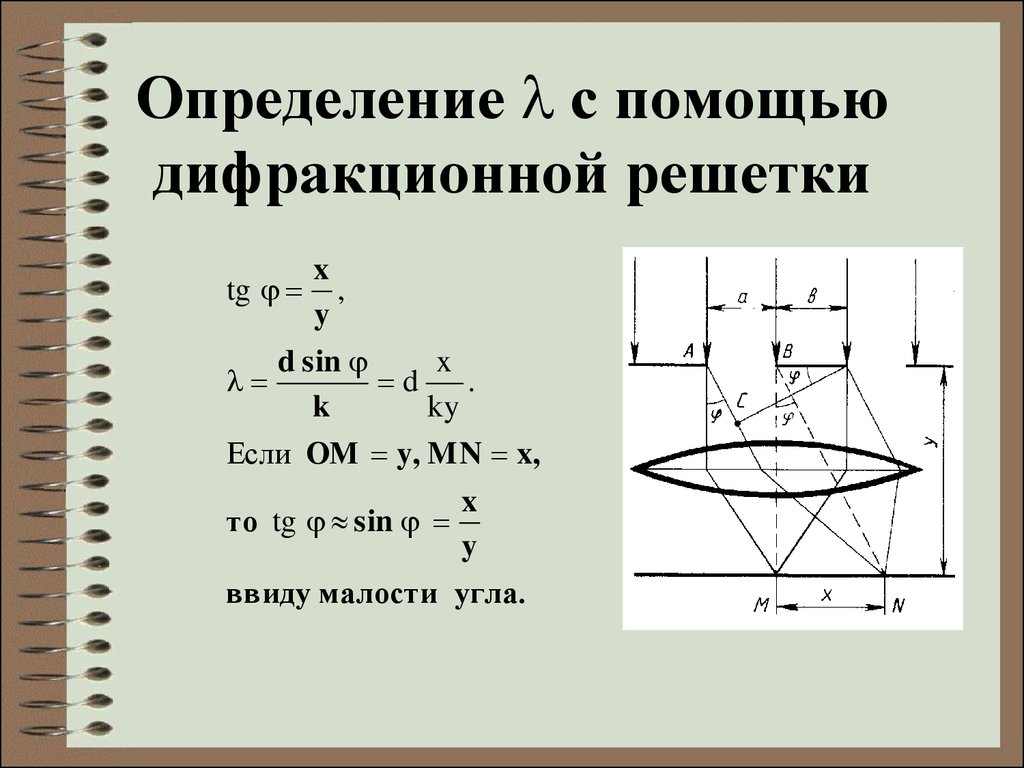 Эти углы зависят от длины волны и расстояния между щелями, как вы увидите ниже.

Рисунок 17,8 Двойные щели создают два интерферирующих источника волн. (а) Свет распространяется (дифрагирует) от каждой щели, потому что щели узкие. Волны перекрываются и интерферируют конструктивно (светлые линии) и деструктивно (темные области). Вы можете увидеть эффект, только если свет падает на экран и рассеивается в ваших глазах. (b) Двухщелевая интерференционная картина волн на воде почти идентична таковой для света. Волновое воздействие больше всего в областях конструктивной интерференции и наименьшее в областях деструктивной интерференции. в) Когда свет, прошедший через двойные щели, падает на экран, мы видим такую ​​картину.

Виртуальная физика

Интерференция волн

Это моделирование демонстрирует большинство волновых явлений, обсуждаемых в этом разделе. Во-первых, наблюдайте интерференцию между двумя источниками электромагнитного излучения без добавления щелей. Посмотрите, как волны воды, звук и свет демонстрируют интерференционные картины. Оставайтесь со световыми волнами и используйте только один источник. Создайте дифракционные картины с одной щелью, а затем с двумя. Возможно, вам придется отрегулировать ширину щели, чтобы увидеть рисунок.

Визуально сравните ширину щели с длиной волны. Когда вы получаете наиболее четкую дифракционную картину?

1. когда ширина щели больше длины волны
2. , когда ширина щели меньше длины волны
3. , когда ширина щели сравнима с длиной волны
4. , когда ширина щели бесконечна

Расчеты с учетом дифракции и интерференции

Поддержка учителей

Поддержка учителей

[BL] Греческая буква θθ пишется как тета . Греческая буква λλ пишется как лямда . Оба произносятся так, как вы ожидаете от правописания.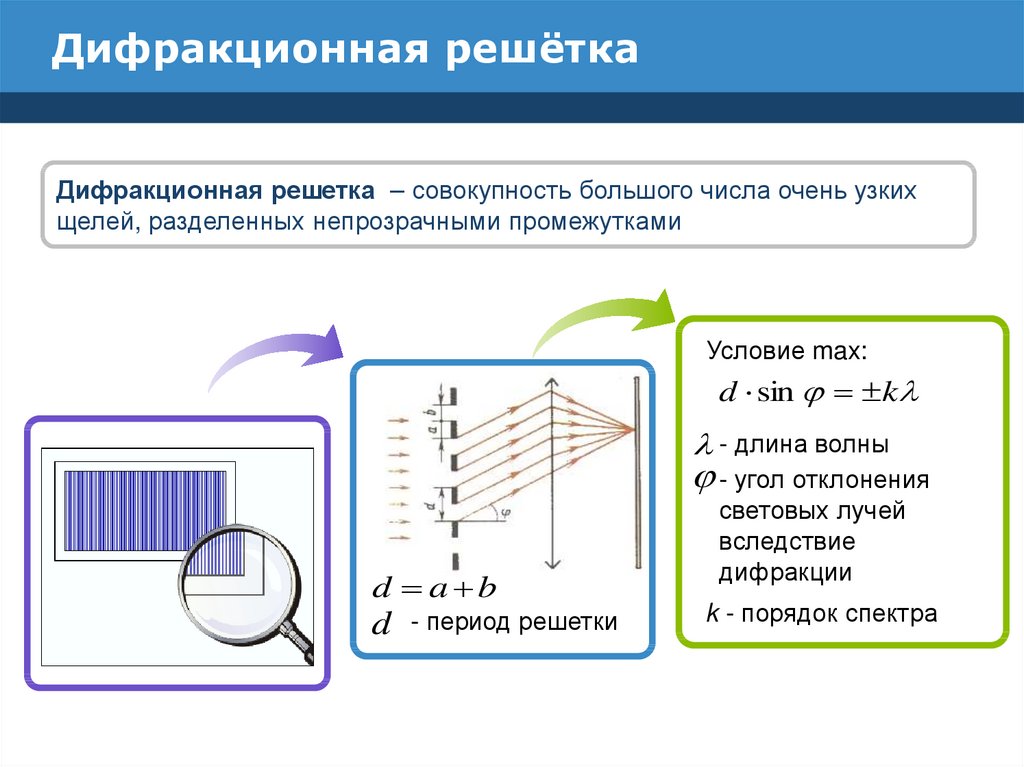 Множественное число от максимальное и минимальное равно максимальное и минимальное соответственно.

[OL]Объясните, что монохромный означает одноцветный. Монохроматический также означает одну частоту . Синус угла — это противолежащая сторона прямоугольного треугольника, деленная на гипотенузу. Противоположный означает противоположный данному острому углу. Обратите внимание, что знак угла всегда ≥ 1,

Тот факт, что длина волны света одного цвета или монохроматического света может быть рассчитана по его двухщелевой дифракционной картине в экспериментах Юнга, подтверждает вывод о том, что свет обладает волновыми свойствами. Чтобы понять основу таких расчетов, рассмотрим, как две волны проходят от щелей к экрану. Каждая щель находится на разном расстоянии от заданной точки на экране. Таким образом, на каждый путь укладывается разное количество длин волн. Волны начинаются от щелей в фазе (гребень к гребню), но заканчиваются в противофазе (гребень к впадине) на экране, если пути различаются по длине на половину длины волны, создавая деструктивные помехи. Если пути различаются на целую длину волны, то волны приходят на экран синфазно (гребень к гребню), конструктивно интерферируя. В более общем случае, если пути, по которым проходят две волны, отличаются на любое полуцелое число длин волн (12λ, 32λ, 52λ и т. д.) (12λ, 32λ, 52λ и т. д.), то возникает деструктивная интерференция. Точно так же, если пути, по которым проходят две волны, отличаются на любое целое число длин волн (λ, 2λ, 3λ и т. д.) (λ, 2λ, 3λ и т. д.), возникает конструктивная интерференция.

На рис. 17.9 показано, как определить разность длин пути для волн, идущих от двух щелей к общей точке экрана. Если экран находится на большом расстоянии по сравнению с расстоянием между щелями, то угол θθ между траекторией и линией от щелей, перпендикулярной экрану (см. рисунок), для каждой траектории примерно одинаков. Это приближение и простая тригонометрия показывают, что разность длин ΔLΔL равна dsinθdsinθ, где d — расстояние между щелями,

ΔL=dsinθ. ΔL=dsinθ.

Чтобы получить конструктивную интерференцию для двойной щели, разность длин пути должна быть целым числом, кратным длине волны, или

dsinθ=mλ, для m=0,1,−1,2,−2,… (конструктивный).dsinθ=mλ, для m=0,1,−1,2,−2,…(конструктивный).

Точно так же, чтобы получить деструктивную интерференцию для двойной щели, разность длин пути должна быть кратной половине длины волны, или

dsinθ=(m+½)λ, для m=0,1,−1,2,−2,… (разрушающий).dsinθ=(m+½)λ, для m=0,1,−1,2 ,−2,…(деструктивный).

Число м порядок помех. Например, м = 4 — это помехи четвертого порядка.

Рисунок 17,9 Пути от каждой щели до общей точки на экране различаются на величину d sin θd sin θ, если предположить, что расстояние до экрана много больше, чем расстояние между щелями (здесь не в масштабе).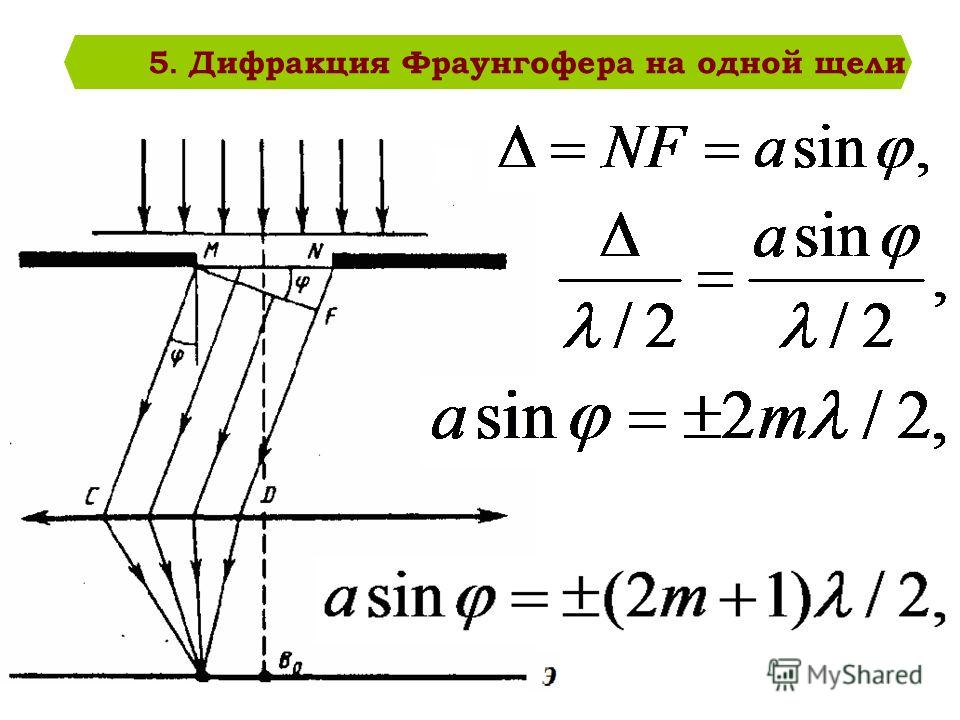

На рис. 17.10 показано, как уменьшается интенсивность полос конструктивной интерференции с увеличением угла.

Рисунок 17.10 Интерференционная картина для двойной щели имеет интенсивность, которая падает с углом. На фотографии видно множество ярких и темных линий или полос, образованных светом, проходящим через двойную щель.

Свет, проходящий через одиночную щель, образует дифракционную картину, несколько отличную от той, что образуется от двойных щелей. На рис. 17.11 показана картина дифракции от одной щели. Обратите внимание, что центральный максимум больше, чем с обеих сторон, и что интенсивность быстро уменьшается с обеих сторон.

Рисунок 17.11 (а) Однощелевая дифракционная картина. Монохроматический свет, проходящий через одну щель, дает центральный максимум и множество меньших и более тусклых максимумов по обеим сторонам. Центральный максимум в шесть раз выше показанного. (b) На рисунке показан яркий центральный максимум и более тусклые и тонкие максимумы по бокам.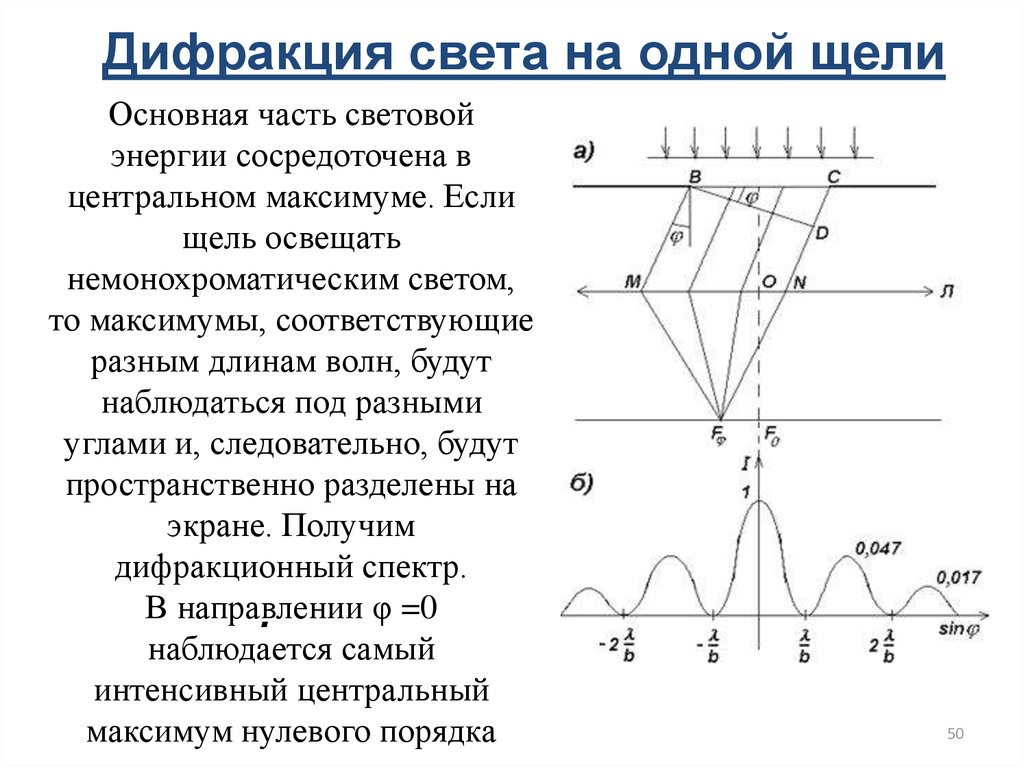 (c) Расположение минимумов показано через λλ и D .

Анализ однощелевой дифракции показан на рис. 17.12. Если предположить, что экран находится очень далеко по сравнению с размером щели, лучи, направляющиеся к общей цели, почти параллельны. Это приближение допускает ряд тригонометрических операций, которые приводят к уравнениям для минимумов, создаваемых деструктивной интерференцией.

Dsinθ=mλDsinθ=mλ

или

DyL=mλDyL=mλ

Когда лучи движутся прямо вперед, они остаются в фазе, и получается центральный максимум. Однако, когда лучи проходят под углом θθ относительно первоначального направления луча, каждый луч проходит разное расстояние до экрана, и они могут приходиться в фазе или в противофазе. Таким образом, луч из центра проходит на расстояние λ/2λ/2 дальше, чем луч от верхнего края щели, приходят в противофазе и деструктивно интерферируют. Точно так же для каждого луча между вершиной и центром щели существует луч между центром и низом щели, который проходит расстояние λ/2λ/2 дальше от общей точки на экране и, таким образом, деструктивно интерферирует.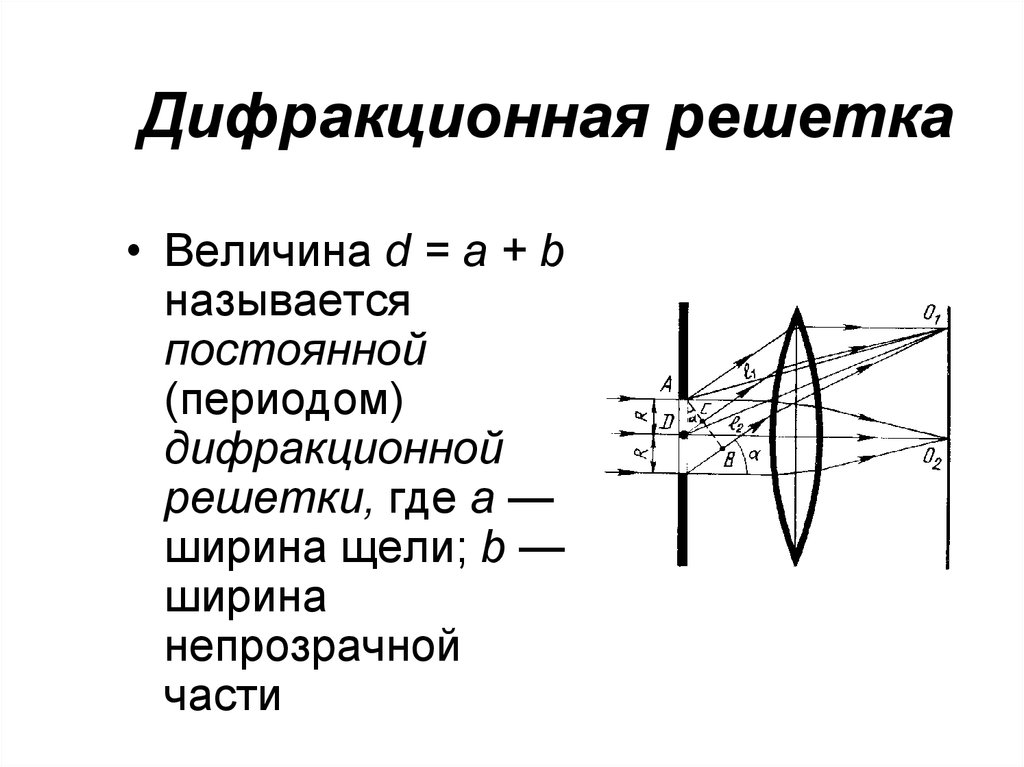 . Симметрично ниже прямого луча будет еще один минимум под тем же углом.

Рисунок 17.12 Уравнения для однощелевой дифракционной картины, где λ — длина волны света, D — ширина щели, θθ — угол между линией от щели до минимума и линией, перпендикулярной экрану, L — расстояние от щели до экрана, y — расстояние от центра узора до минимума, а м — ненулевое целое число, указывающее порядок минимума.

Ниже мы суммируем уравнения, необходимые для последующих расчетов.

Скорость света в вакууме c , длина волны света λλ и его частота f связаны следующим образом.

с=fλc=fλ

Длина волны света в среде, λnλn, по сравнению с его длиной волны в вакууме, λλ, равна

λn=λn.λn=λn.

17,1

Чтобы рассчитать положение конструктивной интерференции для двойной щели, разность длин пути должна быть целым числом, м , кратным длине волны.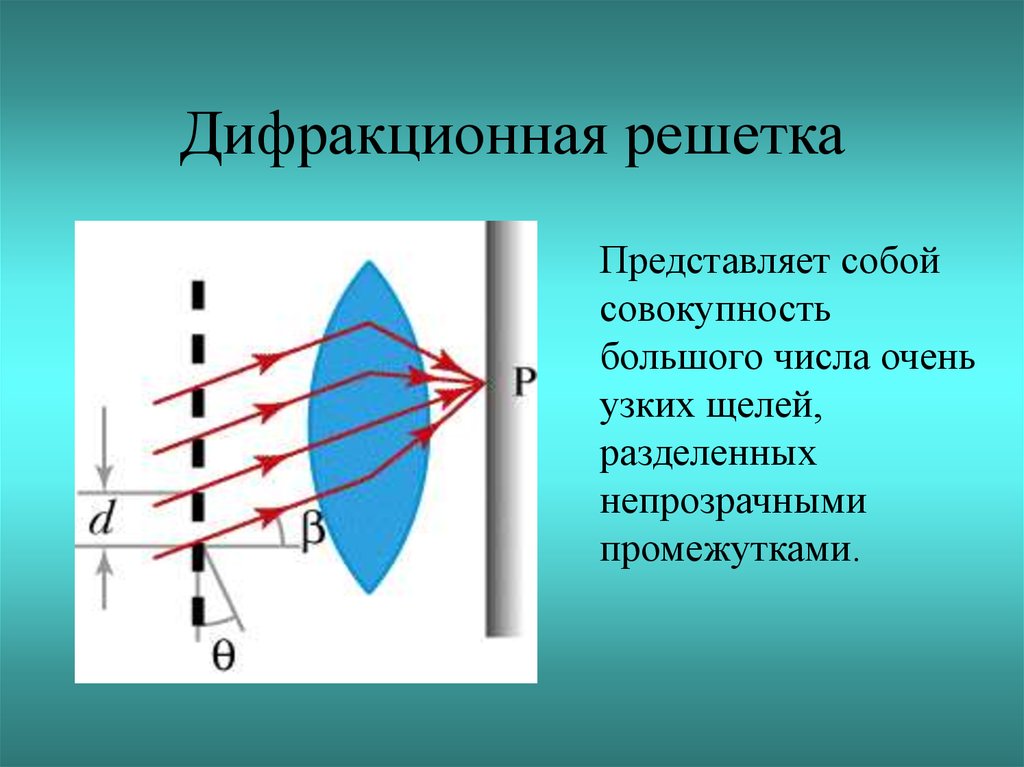 λλ

dsinθ=mλ, для m=0,1,−1,2,−2,… (конструктивное), dsinθ=mλ, для m=0,1,−1,2,−2,…(конструктивное),

, где d — расстояние между щелями, а θθ — угол между линией от щелей до максимума и линией, перпендикулярной преграде, в которой расположены щели. Чтобы рассчитать положение деструктивной интерференции для двойной щели, разность длин пути должна быть кратной половине длины волны:

dsinθ=(m+½)λ, для m=0,1,−1,2,−2,… (разрушающий).dsinθ=(m+½)λ, для m=0,1,−1,2 ,−2,…(деструктивный).

Для однощелевой дифрактограммы ширина щели, D , расстояние до первого ( м = 1) минимума деструктивной интерференции, y , расстояние от щели до экрана, L , а длина волны λλ определяется как

DyL=λ.DyL=λ.

Также для однощелевой дифракции

Dsinθ=mλ,Dsinθ=mλ,

, где θθ — угол между линией от щели до минимума и линией, перпендикулярной экрану, а м это порядок минимума.

Рабочий пример

Двухщелевая интерференция

Предположим, вы пропускаете свет гелий-неонового лазера через две щели, разделенные расстоянием 0,0100 мм, и обнаруживаете, что третья яркая линия на экране формируется под углом 10,95º по отношению к падающему лучу. Какова длина волны света?

Стратегия

Третья светлая линия обусловлена ​​конструктивной интерференцией третьего порядка, что означает, что м = 3. Вам дано d = 0,0100 мм и θθ = 10,95º. Таким образом, длину волны можно найти, используя уравнение dsinθ=mλdsinθ=mλ для конструктивной интерференции.

Решение

Уравнение dsinθ=mλdsinθ=mλ . Решение для длины волны λλ дает

λ=dsinθm.λ=dsinθm.

17,2

Подстановка известных значений дает

×10 −4 мм = 633 нм.

17,3

Обсуждение

В трехзначном выражении 633 нм — это длина волны света, излучаемого обычным гелий-неоновым лазером.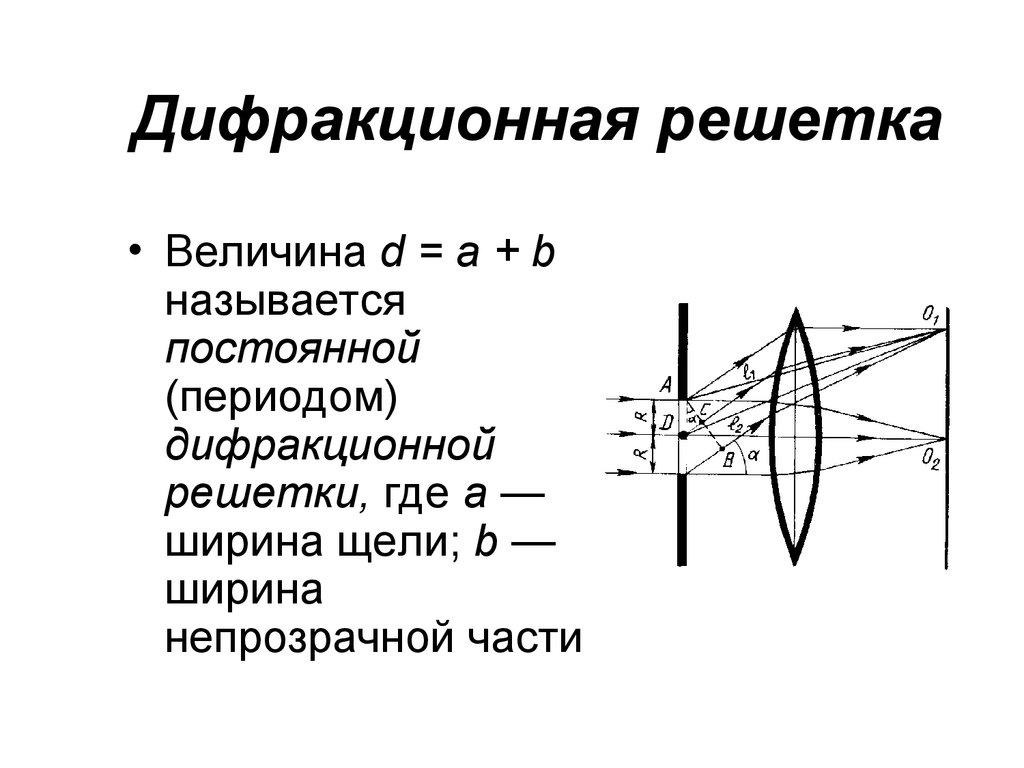 Не случайно этот красный цвет похож на тот, который излучают неоновые огни. Однако более важным является тот факт, что интерференционные картины можно использовать для измерения длины волны. Янг сделал это для видимых длин волн. Его аналитический метод до сих пор широко используется для измерения электромагнитных спектров. Для данного порядка угол конструктивной интерференции увеличивается с увеличением λλ, поэтому можно получить спектры (измерения интенсивности в зависимости от длины волны).

Рабочий пример

Однощелевая дифракция

Видимый свет с длиной волны 550 нм падает на одну щель и дает второй минимум дифракции под углом 45,0° к направлению падения света. Какова ширина щели?

Стратегия

Исходя из данной информации и предполагая, что экран находится далеко от щели, вы можете использовать уравнение Dsinθ=mλDsinθ=mλ, чтобы найти D .

Раствор

Приведены следующие величины: λλ = 550 нм, м = 2 и θ2θ2 = 45,0°.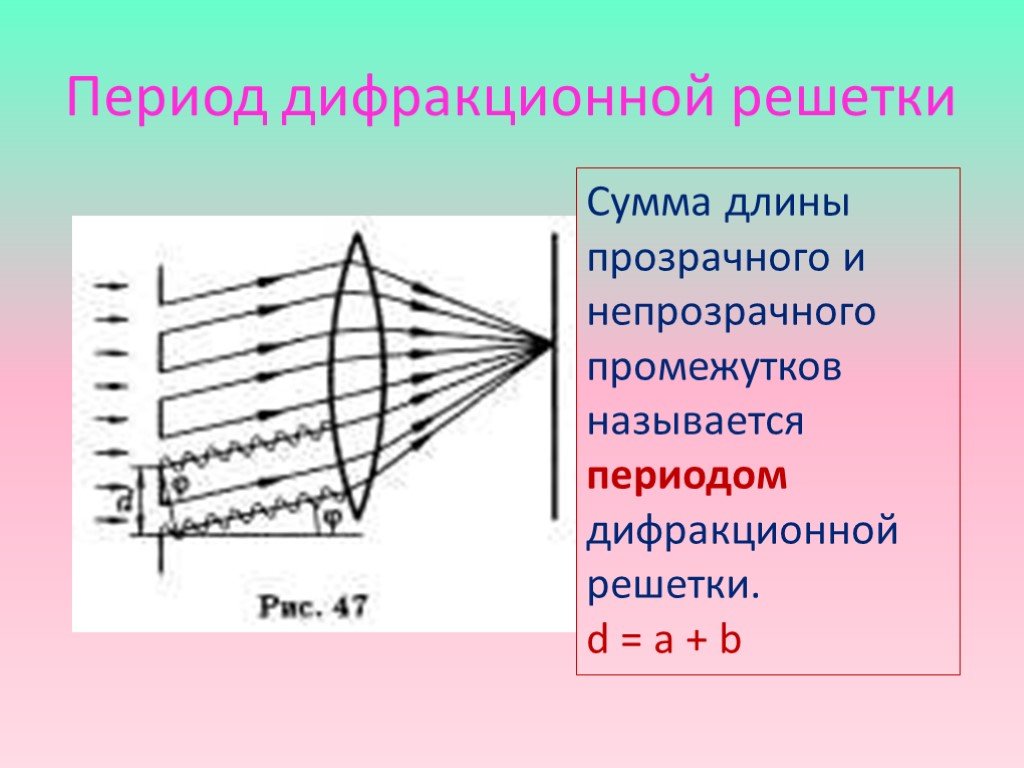 Решение уравнения Dsinθ=mλDsinθ=mλ для D и подстановка известных значений дает

D=mλsinθ=2(550 нм)sin45,0°=1,56 × 10–6 м.D=mλsinθ=2(550 нм)sin45,0 °=1,56×10-6 м.

17.4

Обсуждение

Вы видите, что щель узкая (всего в несколько раз больше длины волны света). Это согласуется с тем фактом, что свет должен взаимодействовать с объектом, сравнимым по размеру с его длиной волны, чтобы проявлять значительные волновые эффекты, такие как эта дифракционная картина с одной щелью. 9{\circ} относительно падающего луча. Какова длина волны света?

1. 51,5\,\текст{нм}

2. 77,3\,\текст{нм}

3. 515\,\текст{нм}

4. 773\,\text{nm}

2.

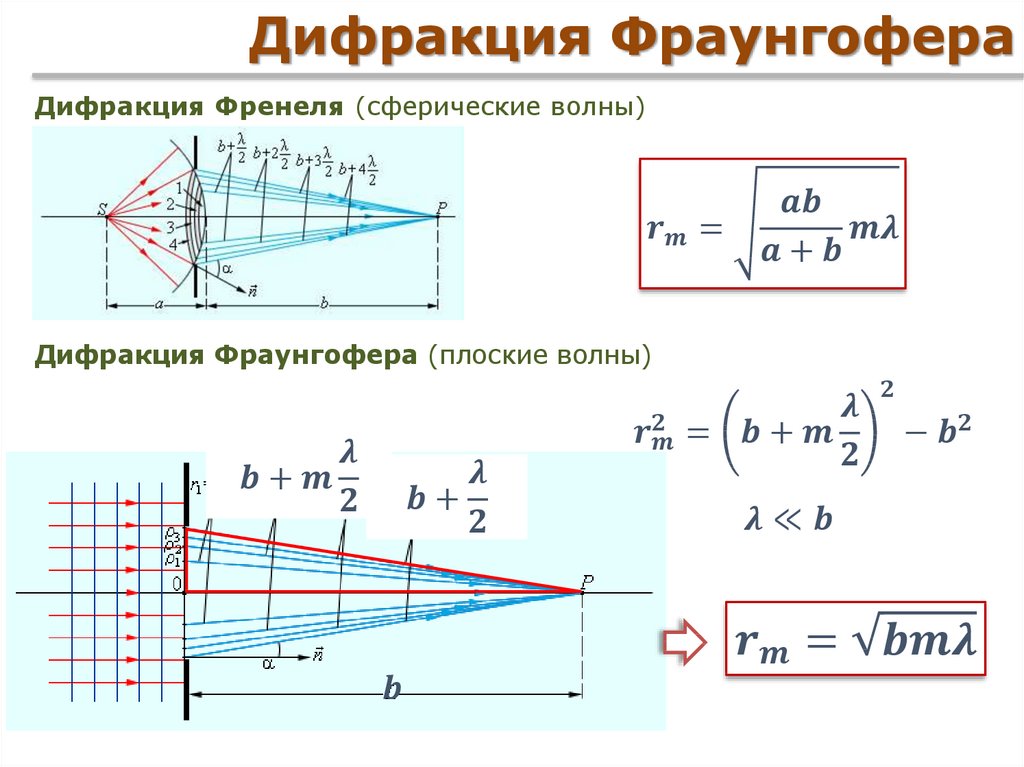
Какова ширина одиночной щели, через которую проходит оранжевый свет с длиной волны 610 нм, образуя первый дифракционный минимум под углом 30,0°?

1. 0,863 мкм
2. 0,704 мкм
3. 0,610 мкм
4. 1,22 мкм

Проверьте свое понимание

Поддержка учителей

Поддержка учителей

Используйте эти задачи, чтобы оценить достижение учащимися целей обучения раздела. Если учащиеся борются с определенной целью, эти проблемы помогут определить, какие и направят учащихся к соответствующим темам.

3.

Какой аспект луча монохроматического света изменяется, когда он попадает из вакуума в воду, и как он изменяется?

1. Длина волны сначала уменьшается, а затем увеличивается.

2. Длина волны сначала увеличивается, а затем уменьшается.

3. Длина волны увеличивается.

4. Длина волны уменьшается.

4.

Выйдите на улицу на солнечный свет и понаблюдайте за своей тенью. У него нечеткие края, даже если у вас их нет. Это дифракционный эффект? Объяснять.

1. Это эффект дифракции. Все ваше тело действует как источник нового волнового фронта.

2. Это эффект дифракции. Каждая точка на краю вашей тени действует как источник нового волнового фронта.

3. Это эффект преломления. Все ваше тело действует как источник нового волнового фронта.

4. Это эффект преломления. Каждая точка на краю вашей тени действует как источник нового волнового фронта.

5.

Какой аспект монохроматического зеленого света меняется, когда он переходит из вакуума в алмаз, и как он меняется?

1. Длина волны сначала уменьшается, а затем увеличивается.

   Дифракция формулы: Дифракция света. Дифракционная решетка. | Объединение учителей Санкт-Петербурга