§20. Дифракция света Основные формулы
Угол отклонения лучей, соответствующий максимуму (светлая полоса) при дифракции на одной щели, определяется из условия
,
где а – ширина щели; k – порядковый номер максимума (k = 1,2,3,…).
Угол отклонения лучей, соответствующий минимуму (темная полоса) при дифракции на одной щели, определяется из условия
.
Угол отклонения лучей, соответствующий максимуму при дифракции света на дифракционной решетке, определяется из условия
,
где k = 0,1,2,3,…; d – период дифракционной решетки.
Разрешающая способность дифракционной решетки равна

Формула Вульфа – Брэггов имеет вид
,
где – угол скольжения, то есть угол между направлением пучка параллельных рентгеновских лучей, падающих на кристалл, и гранью кристалла; d – расстояние между атомными плоскостями кристалла. Формула Вульфа – Брэггов определяет направление лучей, при которых возникает дифракционный максимум.
Задачи
20.1. На щель шириной а = 0,05 мм падает нормально монохроматический свет (λ= 0,6 мкм). Определить угол φ между первоначальным направлением пучка света и направлением на четвертую темную дифракционную полосу.
20.2
Точечный источник света с длиной волны
λ =0,5мкм расположен на расстоянии а
=
100 см перед диафрагмой с
круглым
отверстием радиуса r
= 1,0
мм. Найти расстояние b
от
диафрагмы
до точки наблюдения, для которой
число зон
Френеля
в отверстии составляет к
= 3.
20.3. Между точечным источником света и экраном поместили диафрагму с круглым отверстием, радиус которого r можно менять. Расстояние от диафрагмы до источника и экрана равны а = 100 см и b = 125 см. Определить длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при r1 = 1,00 мм и следующий максимум — при r2 = 1,29 мм.
20.4. На
узкую щель падает нормально монохроматический
свет. Угол φ отклонения пучков света,
соответствующих второй светлой
дифракционной полосе, равен 1
20.5. На щель шириной а = 0,1 мм падает нормально монохроматический свет (λ= 0,5 мкм). За щелью помещена собирающая линза, в фокальной плоскости которой находится экран. Что будет наблюдаться на экране, если угол φ дифракции равен: 1) 17/; 2) 43/?
20. 6. Сколько штрихов
на каждый миллиметр содержит дифракционная
решетка, если при наблюдении в
монохроматическом свете (λ= 0,6 мкм)
максимум пятого порядка отклонен на
угол φ = 180?
6. Сколько штрихов
на каждый миллиметр содержит дифракционная
решетка, если при наблюдении в
монохроматическом свете (λ= 0,6 мкм)
максимум пятого порядка отклонен на
угол φ = 180?
20.7. На дифракционную решетку, содержащую n = 100 штрихов на 1 мм, падает нормально монохроматический свет. Зрительная труба спектрометра наведена на максимум третьего порядка. Чтобы навести трубу на другой максимум того же порядка, ее нужно повернуть на угол = 20°. Определить длину волны света.
20.8. Дифракционная решетка освещена нормально падающим монохроматическим светом. В дифракционной картине максимум второго порядка отклонен на угол φ1 = 140. На какой угол φ2 отклонен максимум третьего порядка?
20.9. Дифракционная решетка содержит n = 200 штрихов на 1 мм. На решетку падает нормально монохроматический свет (λ= 0,6 мкм). Максимум какого наибольшего порядка дает эта решетка?
20. 10. На дифракционную
решетку, содержащую n
= 400 штрихов на 1 мм, падает нормально
монохроматический свет (λ= 0,6мкм).
Найти общее число дифракционных
максимумов, которые дает эта решетка.
Определить угол φ дифракции, соответствующий
последнему максимуму.
10. На дифракционную
решетку, содержащую n
= 400 штрихов на 1 мм, падает нормально
монохроматический свет (λ= 0,6мкм).
Найти общее число дифракционных
максимумов, которые дает эта решетка.
Определить угол φ дифракции, соответствующий
последнему максимуму.
20.11. При освещении дифракционной решетки белым светом спектры второго и третьего порядков отчасти перекрывают друг друга. На какую длину волны в спектре второго порядка накладывается фиолетовая граница (λ= 0,4 мкм) спектра третьего порядка?
20.12. На дифракционную решетку, содержащую n = 500 штрихов на 1 мм, падает в направлении нормали к ее поверхности белый свет. Спектр проецируется помещенной вблизи решетки линзой на экран. Определить ширину b спектра первого порядка на экране, если расстояние L от линзы до экрана равно 3 м. Границы видимого спектра = 780 нм, = 400 нм.
20.13.
Дифракционная картина получена с помощью
дифракционной решетки длиной l
= 1,5 см и периодом d
= 5 мкм.
20.14. Какой наименьшей разрешающей силой R должна обладать дифракционная решетка, чтобы с ее помощью можно было разрешить две спектральные линии калия ( = 578 нм и = 580 нм)? Какое наименьшее число N штрихов должна иметь эта решетка, чтобы разрешение было возможно в спектре второго порядка?
20.15. С помощью дифракционной решетки с периодом d = 20 мкм требуется разрешить дублет натрия ( = 589,0 нм и = 589,6 нм) в спектре второго порядка. При какой наименьшей длине l решетки это возможно?
20.16. На грань кристалла каменной соли падает параллельный пучок рентгеновского излучения (λ= 147 пм). Определить расстояние
20.17. Какова длина волны λ монохроматического рентгеновского излучения, падающего на кристалл кальцита, если дифракционный максимум первого порядка наблюдается, когда угол θ между направлением падающего излучения и гранью кристалла равен 30? Расстояние d между атомными плоскостями кристалла принять равным 0,3 нм.
20.18. Параллельный пучок рентгеновского излучения падает на грань кристалла. Под углом θ = 650 к плоскости грани наблюдается максимум первого порядка. Расстояние d между атомными плоскостями кристалла 280 пм. Определить длину волны рентгеновского излучения.
Оптика и волны
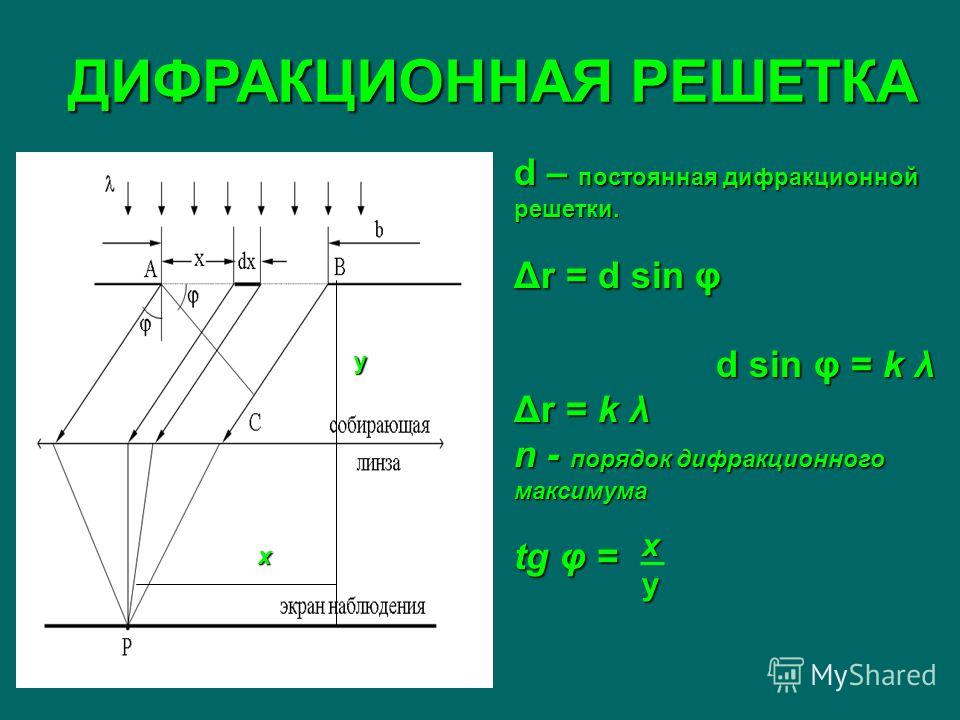
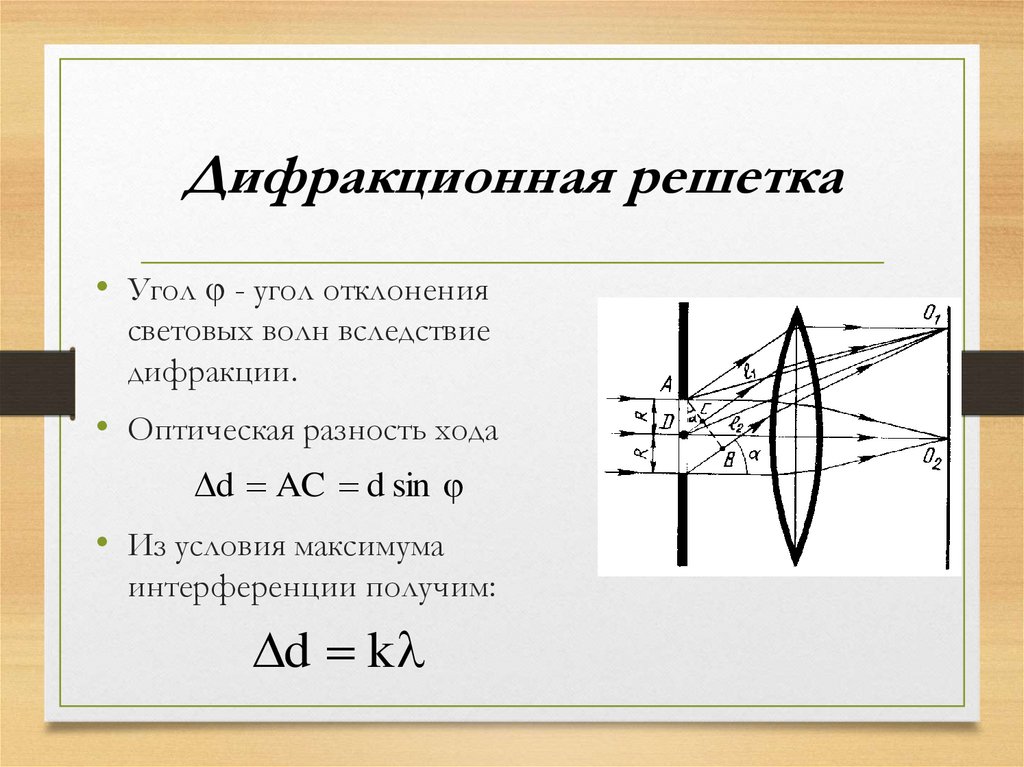
Широкое распространение в научном эксперименте и технике получили дифракционные решетки, которые представляют собой множество параллельных, расположенных на равных расстояниях одинаковых щелей, разделенных равными по ширине непрозрачными промежутками. Дифракционные решетки изготавливаются с помощью делительной машины, наносящей штрихи (царапины) на стекле или другом прозрачном материале. Там, где проведена царапина, материал становится непрозрачным, а промежутки между ними остаются прозрачными и фактически играют роль щелей.
Там, где проведена царапина, материал становится непрозрачным, а промежутки между ними остаются прозрачными и фактически играют роль щелей.
Рассмотрим сначала дифракцию света от решетки на примере двух щелей. (При увеличении числа щелей дифракционные максимумы становятся лишь более узкими, более яркими и отчетливыми.)
Пусть а — ширина щели, a b — ширина непрозрачного промежутка (рис. 5.6).
Рис. 5.6. Дифракция от двух щелей
|
Период дифракционной решетки — это расстояние между серединами соседних щелей:
|
Разность хода двух крайних лучей равна
|
|
(5.36) |
Если разность хода равна нечетному числу полуволн
|
|
(5. |
то свет, посылаемый двумя щелями, вследствие интерференции волн будет взаимно гаситься. Условие минимумов имеет вид
|
|
(5.38) |
Эти минимумы называются дополнительными.
Если разность хода равна четному числу полуволн
|
|
(5.39) |
то волны, посылаемые каждой щелью, будет взаимно усиливать друг друга. Условие интерференционных максимумов с учетом (5.36) имеет вид
Условие интерференционных максимумов с учетом (5.36) имеет вид
|
|
(5.40) |
Это формула для главных максимумов дифракционной решетки.
Видео 5.14 Дифракционные решетки с разными периодами.
Видео 5.15 Двумерные дифракционные решетки с разными периодами.
Кроме того, в тех направлениях, в которых ни одна из щелей не распространяет свет, он не будет распространяться и при двух щелях, то есть главные минимумы решетки будут наблюдаться в направлениях, определяемых условием (5.21) для одной щели:
|
|
(5. |
Если дифракционная решетка состоит из N щелей (современные решетки, применяемые в приборах для спектрального анализа, имеют до 200 000 штрихов, и период d = 0.8 мкм, то есть порядка 12 000 штрихов на 1 см), то условием главных минимумов является, как и в случае двух щелей, соотношение (5.41), условием главных максимумов — соотношение (5.40), а условие дополнительных минимумов имеет вид
|
|
(5.42) |
Здесь k’ может принимать все целочисленные значения, кроме 0, N, 2N, … . Следовательно, в случае N щелей между двумя главными максимумами располагается (N–1) дополнительных минимумов, разделенных вторичными максимумами, создающими относительно слабый фон.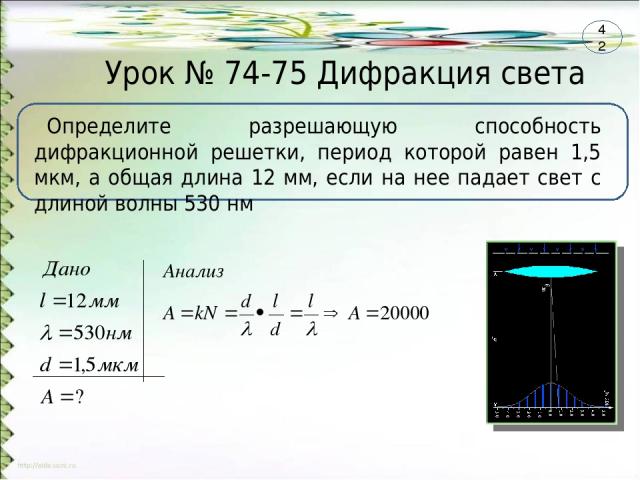
Положение главных максимумов зависит от длины волны l. Поэтому при пропускании через решетку белого света все максимумы, кроме центрального, разлагаются в спектр, фиолетовый конец которого обращен к центру дифракционной картины, а красный — наружу. Таким образом, дифракционная решетка представляет собой спектральный прибор. Заметим, что в то время как спектральная призма сильнее всего отклоняет фиолетовые лучи, дифракционная решетка, наоборот, сильнее отклоняет красные лучи.
Важной характеристикой всякого спектрального прибора является разрешающая способность.
|
Разрешающая способность спектрального прибора — это безразмерная величина
|
где — минимальная разность длин волн двух спектральных линий, при которой эти линии воспринимаются раздельно.
Определим разрешающую способность дифракционной решетки. Положение середины k-го максимума для длины волны
определяется условием
|
|
(5.44) |
Края k—го максимума (то есть ближайшие дополнительные минимумы) для длины волны l расположены под углами, удовлетворяющими соотношению:
|
|
(5. |
Два близких максимума воспринимаются раздельно в том случае, если середина одного максимума совпадает с краем другого (критерий Рэлея).
Таким образом, середина максимума для длины волны
совпадает с краем максимума для длины волны l в том случае, если
|
|
(5.46) |
Отсюда находим
|
|
(5.47) |
Следовательно, разрешающая способность дифракционной решетки
|
|
(5. |
пропорциональна порядку спектра k и числу щелей N.
Дополнительная информация
http://www.physics.spbstu.ru/forstudents/lectures/zaharov/19.pdf – Н.Г. Захаров. Практические занятия. Дифракция света.
http://allphysics.ru/feynman/difraktsiya – Фейнмановские лекции по физике. Дифракция.
http://physics.nad.ru/Physics/Cyrillic/optics.htm – Анимации: преломление света на границе стекло-воздух, дисперсия света в стеклянной призме, дифракция Фраунгофера.
http://pymath.ru/viewtopic.php?f=77&t=811&sid=63be0a3e99f9a32260b53dcfaad3c271 – Видеоурок «Дифракция Фраунгофера на щели».
http://pymath.ru/viewtopic.php?f=77&t=756&sid=63be0a3e99f9a32260b53dcfaad3c271 – Видеоурок «Постановка задачи дифракции на круглом отверстии Френеля».
4.3 Двухщелевая дифракция — University Physics Volume 3
Цели обучения
К концу этого раздела вы сможете:
- Описать комбинированный эффект интерференции и дифракции с двумя щелями, каждая из которых имеет конечную ширину
- Определение относительной интенсивности интерференционных полос на дифракционной картине
- Определите пропущенные порядки, если таковые имеются
Когда мы изучали интерференцию в эксперименте Юнга с двумя щелями, мы игнорировали эффект дифракции в каждой щели.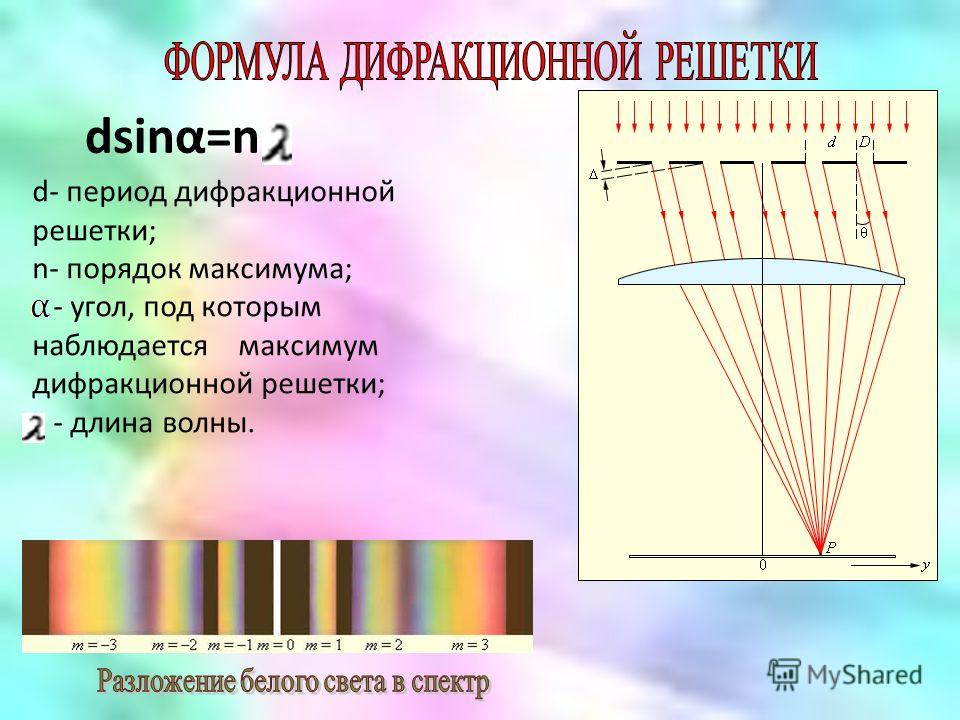 Мы предполагали, что щели настолько узкие, что на экране вы видите только интерференцию света всего от двух точечных источников. Если щель меньше длины волны, то на рис. 4.10 (а) видно, что на экране наблюдается только распространение света, а не пики и провалы. Поэтому было разумно исключить в этой главе эффект дифракции. Однако, если вы сделаете щель шире, рис. 4.10 (b) и (c) показывают, что вы не можете игнорировать дифракцию. В этом разделе мы изучаем сложности эксперимента с двумя щелями, которые возникают, когда вам также необходимо учитывать дифракционный эффект каждой щели.
Мы предполагали, что щели настолько узкие, что на экране вы видите только интерференцию света всего от двух точечных источников. Если щель меньше длины волны, то на рис. 4.10 (а) видно, что на экране наблюдается только распространение света, а не пики и провалы. Поэтому было разумно исключить в этой главе эффект дифракции. Однако, если вы сделаете щель шире, рис. 4.10 (b) и (c) показывают, что вы не можете игнорировать дифракцию. В этом разделе мы изучаем сложности эксперимента с двумя щелями, которые возникают, когда вам также необходимо учитывать дифракционный эффект каждой щели.
Чтобы рассчитать дифракционную картину для двух (или любого количества) щелей, нам нужно обобщить метод, который мы только что использовали, для одной щели. То есть поперек каждой щели мы размещаем равномерное распределение точечных источников, излучающих вейвлеты Гюйгенса, а затем суммируем вейвлеты от всех щелей. Это дает интенсивность в любой точке экрана. Хотя детали этого вычисления могут быть сложными, окончательный результат довольно прост:
.
 Двухщелевая дифракционная картина
Двухщелевая дифракционная картина
Дифракционная картина двух щелей шириной a , разделенных расстоянием d , представляет собой интерференционную картину двух точечных источников, разделенных d , умноженную на дифракционную картину щели шириной a .
Другими словами, местоположений интерференционных полос задаются уравнением дифракционные эффекты согласно уравнению 4.4. [Обратите внимание, что в главе об интерференции мы написали dsinθ=mλdsinθ=mλ и использовали целое число m для обозначения интерференционных полос. В уравнении 4.1 также используется м , но на этот раз для обозначения дифракционных минимумов. Если оба уравнения используются одновременно, рекомендуется использовать другую переменную (например, n ) для одного из этих целых чисел, чтобы они были различны. ]
]
Эффекты интерференции и дифракции действуют одновременно и обычно дают минимумы при разных углы. Это приводит к сложной картине на экране, в которой отсутствуют некоторые максимумы интерференции от двух щелей, если максимум интерференции находится в том же направлении, что и минимум дифракции. Такой отсутствующий пик мы называем отсутствующим порядком. Один из примеров дифракционной картины на экране показан на рис. 4.11. Сплошная линия с несколькими пиками разной высоты — интенсивность, наблюдаемая на экране. Это результат интерференции волн от отдельных щелей и дифракции волн внутри одной щели.
Рисунок
4.11
Дифракция от двойной щели. Фиолетовая линия с пиками одинаковой высоты — результат интерференции волн от двух щелей; синяя линия с одним большим горбом посередине — дифракция волн внутри одной щели; а толстая красная линия — это произведение двух, то есть картина, наблюдаемая на экране. График показывает ожидаемый результат для ширины щели a=2λa=2λ и расстояния между щелями d=6λd=6λ. Максимум порядка m=±3m=±3 для интерференции отсутствует, поскольку минимум дифракции происходит в том же направлении.
Максимум порядка m=±3m=±3 для интерференции отсутствует, поскольку минимум дифракции происходит в том же направлении.
Пример 4.3
Интенсивность полос
На рис. 4.11 показано, что интенсивность полос при m=3m=3 равна нулю, но как насчет других полос? Рассчитайте интенсивность полосы при m=1m=1 относительно I0,I0, интенсивности центрального пика.
Стратегия
Определите угол интерференционной полосы с двумя щелями, используя уравнение из Interference, затем определите относительную интенсивность в этом направлении из-за дифракции, используя уравнение 4.4.
Решение
Из главы об интерференции мы знаем, что яркие интерференционные полосы возникают при dsinθ=mλdsinθ=mλ, или
sinθ=mλd.sinθ=mλd.
Из уравнения 4.4,
I=I0(sinββ)2, где β=ϕ2=πasinθλ.I=I0(sinββ)2, гдеβ=ϕ2=πasinθλ.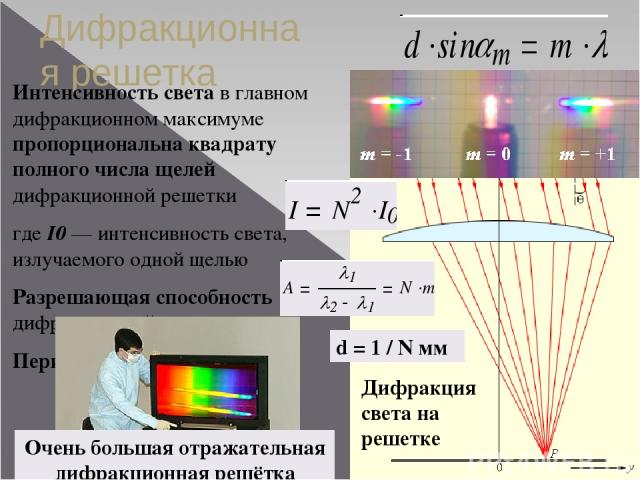
Подстановка сверху,
β=πasinθλ=πaλ·mλd=mπad.β=πasinθλ=πaλ·mλd=mπad.
Для a=2λa=2λ, d=6λd=6λ и m=1m=1,
β=(1)π(2λ)(6λ)=π3.β=(1)π(2λ)(6λ )=π3.
Тогда интенсивность равна
I=I0(sinββ)2=I0(sin(π/3)π/3)2=0,684I0.I=I0(sinββ)2=I0(sin(π/3)π/3)2=0,684 I0.
Значение
Обратите внимание, что этот подход относительно прост и дает результат, почти такой же, как и более сложный анализ с использованием векторов для определения значений интенсивности двухщелевой интерференции (тонкая линия на рис. 4.11). Метод фазора учитывает нисходящий наклон интенсивности дифракции (синяя линия), так что пик около м=1м=1 возникает при значении θθ немного меньшем, чем мы показали здесь.
Пример 4.4
Двухщелевая дифракция
Предположим, что в эксперименте Юнга щели шириной 0,020 мм разнесены на 0,20 мм.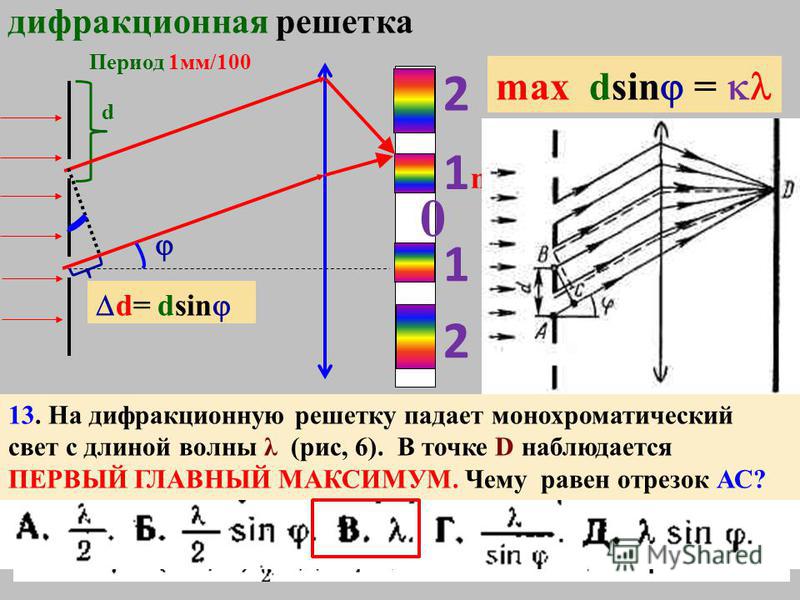 Если щели освещаются монохроматическим светом с длиной волны 500 нм, сколько ярких полос наблюдается в центральном пике дифракционной картины?
Если щели освещаются монохроматическим светом с длиной волны 500 нм, сколько ярких полос наблюдается в центральном пике дифракционной картины?
Раствор
Из уравнения 4.1 угловое положение первого дифракционного минимума равно ×10−5м=2,5×10−2рад.
Используя dsinθ=mλdsinθ=mλ для θ=2,5×10−2радθ=2,5×10−2рад, находим
m=dsinθλ=(0,20 мм)(2,5×10−2рад)(5,0×10−7м)= 10,m=dsinθλ=(0,20 мм)(2,5×10-2рад)(5,0×10-7м)=10,
, что является максимальным порядком интерференции, который находится внутри центрального пика. Заметим, что m=±10m=±10 — недостающие порядки, так как θθ точно совпадает. Соответственно, мы наблюдаем яркие полосы для
m=−9,−8,−7,−6,−5,−4,−3,−2,−1,0,+1,+2,+3,+ 4,+5,+6,+7,+8 и+9m=-9,-8,-7,-6,-5,-4,-3,-2,-1,0,+1, +2,+3,+4,+5,+6,+7,+8 и+9
всего 19 ярких полос.
Проверьте свое понимание 4.3
Для эксперимента в примере 4.4 покажите, что m=20m=20 также является отсутствующим порядком.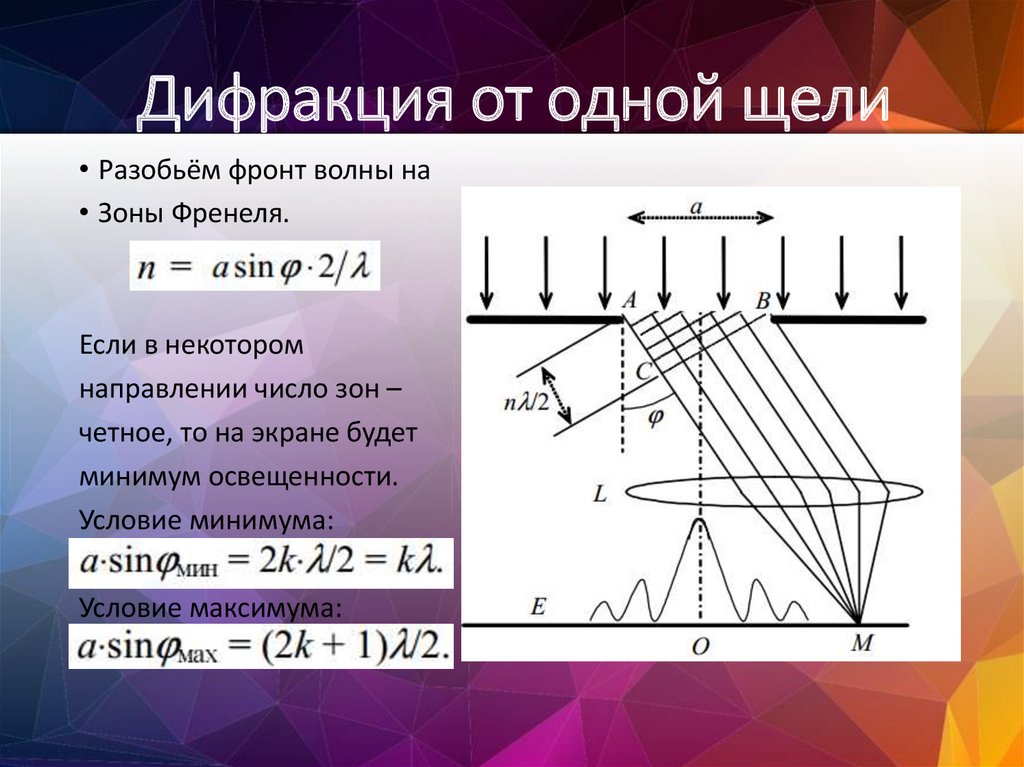
Интерактивный
Исследуйте эффекты двухщелевой дифракции. В этой симуляции, написанной Фу-Квун Хвангом, выберите N=2N=2 с помощью ползунка и посмотрите, что произойдет, если вы зададите ширину щели, расстояние между щелями и длину волны. Можете ли вы сделать заказ «пропавшим без вести»?
Однощелевая дифракция: вывод, формула и модель
Определение: что такое однощелевая дифракция?
Дифракция на одной щели — наиболее простая экспериментальная установка, позволяющая наблюдать дифракционные эффекты. При прохождении света через щель, ширина которой порядка длины световой волны, на экране, находящемся на некотором расстоянии от щели, наблюдается отчетливая дифракционная картина. Интенсивность зависит от угла, на который преломляются лучи.
Принцип Гюйгенса
Согласно принципу Гюйгенса, каждая свободная точка на фронте волны будет действовать как источник вторичных сферических волн. Новый волновой фронт представляет собой поверхность, касательную ко всем вторичным сферическим волнам. Поэтому каждую часть щели можно рассматривать как излучатель волн.
Поэтому каждую часть щели можно рассматривать как излучатель волн.
Однощелевая дифракционная картина
Все волны, проходящие через щель, интерферируют, образуя дифракционную картину, состоящую из ярких и темных полос. Яркие полосы обусловлены конструктивной интерференцией, а темные области — деструктивной интерференцией. Число представляет порядок ярких и темных полос. Интенсивность полос состоит из центрального максимума, окруженного максимумами и минимумами по обе стороны от него. Центральный максимум ярче остальных максимумов. Максимумы быстро уменьшаются по мере удаления от центра.
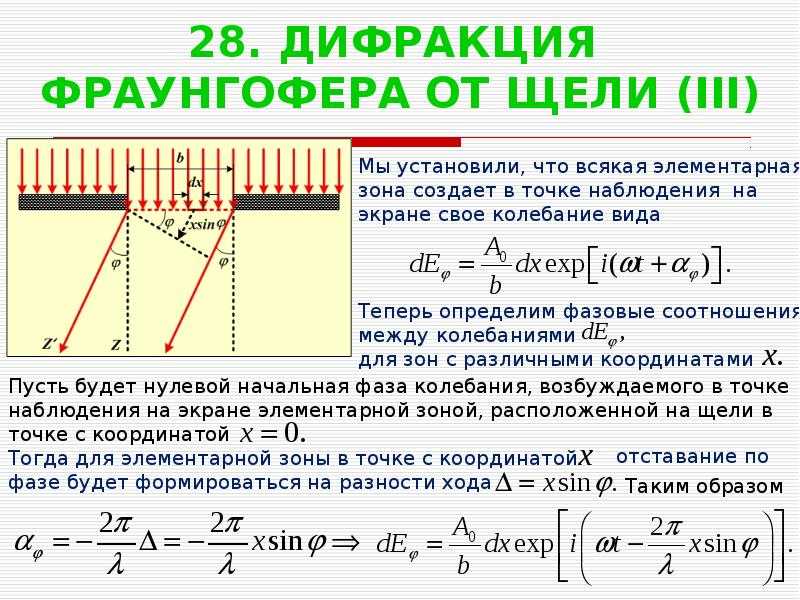
Уравнение дифракции с одной щелью
Для изучения дифракционной картины на экране используется эксперимент с одной щелью. Рассмотрим монохроматический источник света, который проходит через щель AB шириной a , как показано на рисунке. В точке P на экране вторичные волны интерферируют деструктивно и создают темную полосу. Пусть D будет расстоянием между щелью и экраном, а y будет расстоянием между точкой P и точкой O, центром экрана. AC перпендикулярен BP. Пусть θ — угол дифракции, а θ’ — угол ВАС.
AC перпендикулярен BP. Пусть θ — угол дифракции, а θ’ — угол ВАС.
Предположим, что экран находится на значительном расстоянии от щели, т. е. D >> a . Следовательно,
θ = θ’
And,
sin θ ≈ tan θ ≈ θ = y/D
Разность хода между двумя лучами AP и BP определяется как,
Δ = BP – AP = BC
В прямоугольном треугольнике BCA
sin θ’ = sin θ = BC/BA
BC = BA sin θ = a sin θ
Следовательно,
Δ = a sin θ
Дифракционные минимумы
Условие для минимумов или темной полосы:
Разность хода = целое число, кратное длине волны
или, Δ = nλ (n=±1, ±2, ±3, … и т. д.)
или, a sin θ = nλ
или, ay/D = nλ
или, y n = nλD/a
Это уравнение дает расстояние n-й темной полосы от центра.
Ширина полосы определяется выражением,
β = y n+1 – y n = (n+1)λD/a – nλD/a
или, β = λD/a
Дифракционные максимумы
Условие для максимумов или яркой полосы:
Разность хода = нецелое кратное длина волны
или, Δ = (n+1/2)λ (n=±1, ±2, ±3, … и т.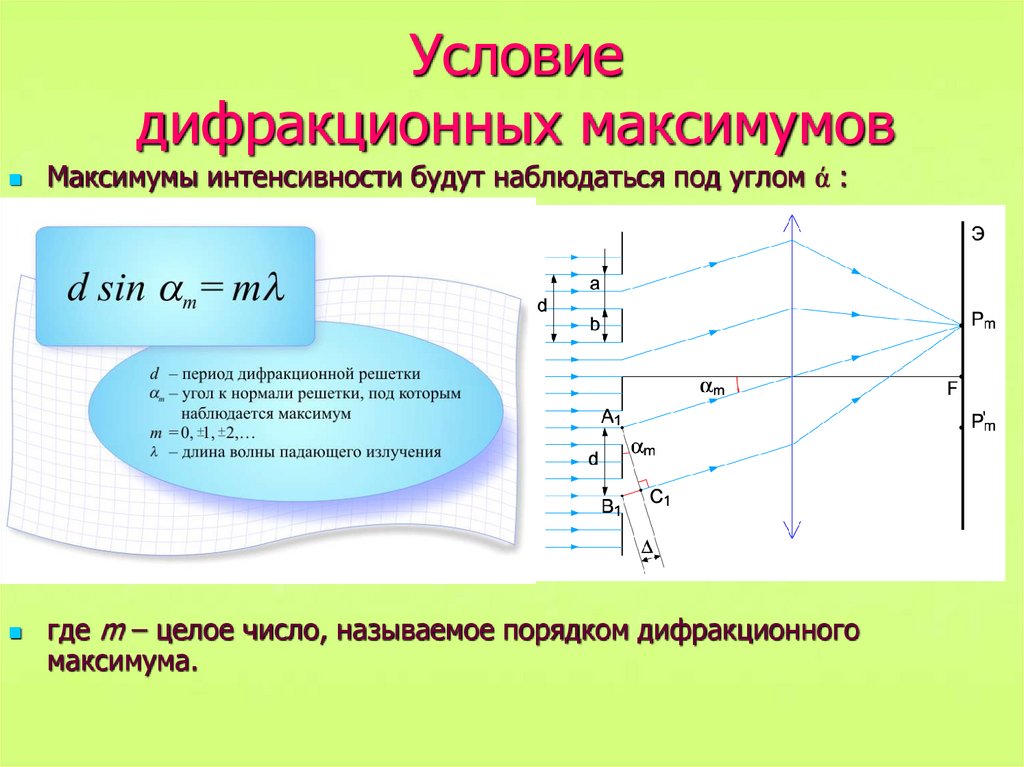

 35)
35) 37)
37) 41)
41) 43)
43) 45)
45) 48)
48)