Функция передачи модуляции | это… Что такое Функция передачи модуляции?
ТолкованиеПеревод
- Функция передачи модуляции
Часто́тно-контра́стная характери́стика, функция передачи модуляции в полиграфии, оптике, фотографии и т. п. — один из параметров, характеризующих качество системы, воспроизводящей изображения (такими системами, в частности, являются оптические приборы и светочувствительные материалы).
Изучается резольвометрией.
Обычно измеряется и рассматривается не как одно число, а в виде графиков зависимостей контраста.
Частотно-контрастная характеристика — безразмерная величина T, определяемая как отношение величины контраста репродукции (изображения, получаемого с помощью воспроизводящей системы), к контрасту соответствующей области оригинала (воспроизводимого объекта).
Значение частотно-контрастной характеристики T зависит от пространственной частоты деталей оригинала N: чем больше частота N, тем ниже T.

При определении частотно-контрастной характеристики оценивают распределение освещенности на участках репродукции в сравнении с известным распределением яркостей оригинала. В качестве оригинала при оценке частотно-контрастной характеристики используют периодические решетки (миры) с линейчатой структурой. По результатам измерения строят график зависимости частотно-контрастной характеристики от частоты.
где Emax, Emin — максмальная и минимальная освещённости итогового изображения, Lmax Lmin — максимальная и минимальная яркости оригинала.
Форма графика такой зависимости и его абсолютные величины описывают интегральную характеристику Микроконтраст оптической системы, светочувствительного материала или фотографического процесса.
Используемые на практике графики зависимости частотно-контрастной характеристики от угла изображения (используется мира фиксированной пространственной частоты и измеряется контраст получаемого изображения) могут ошибочно называться «частотно-контрастной характеристикой» и часто приводятся как графики MTF (англ.
 Modulation Transfer Function).
Modulation Transfer Function).Графики MTF трёх объективов. Сплошные линии — центр кадра. Пунктир — края. Красные линии — Гелиос-44-2 (диафрагма 2), фиолетовые — объективы оптической схемы Тессар (2.8), зелёный —
Значение пространственной частоты изображения при определённом (обычно 0.7) значении частотно-контрастной характеристики, выраженное в «линиях на мм», «парах линий на мм» или «обратных мм», обычно называется разрешающей способностью оптической системы или светочувствительного материала.
Содержание
- 1 Сравнение графиков MTF
- 2 В цифровой технике
- 3 См. также
- 4 Ссылки
Сравнение графиков MTF
На рисунке приведены примеры MTF для трёх объективов. Сплошные графики — результат измерений в центре поля изображеня. Пунктирные — на краю поля зрения.
Несмотря на то, что «зелёный» объектив имеет более низкое значение контраста, чем «фиолетовый», в центре кадра, на краях он позволяет увидеть, пусть и с малым контрастом, мелкие детали изображения.
 «фиолетовый» же имеет очень сильное падение контраста и разрешающей способности к краям. В результате, сравнивая эти два объектива только по одному или двум числам разрешающей способности в центре и на краях, невозможно получить объективной картины того, насколько изображение с одного и с другого объектива будет отвечать задачам фотографа.
«фиолетовый» же имеет очень сильное падение контраста и разрешающей способности к краям. В результате, сравнивая эти два объектива только по одному или двум числам разрешающей способности в центре и на краях, невозможно получить объективной картины того, насколько изображение с одного и с другого объектива будет отвечать задачам фотографа.Так и сравнение зелёного объектива с красным. Незначительное различие в формальных числах разрешающей способности (22 и 28 линий на миллиметр в центре на полностью открытой диафрагме) сопровождается радикальной разницей в качестве изображения из-за неспособности «красного» объектива разрешить более 30-40 линий на миллиметр при любой оценке контраста.
Кроме того, все эти измерения дают принципиально различные результаты при диафрагмировании и изменении фокусного расстояния объектива (для объективов с переменным фокусным расстоянием).
В цифровой технике
Особенностями рассмотрения MTF в цифровой технике являются:
- фиксированный размер светочувствительного элемента и периодическая структура их расположения (в плёночной фотографии размеры и расположение зёрен фотоматериала случайны).

- взаимозависимость между контрастом деталей и собственными шумами матрицы (в плёночной фотографии есть аналогичная связь с зернистостью плёнки).
- наличие преобразования изображения из внутреннего, «сырого» (RAW) представления изображения в окончательную картинку (JPEG или TIFF) и зависимость результата от параметров этого преобразования.
Любая цифровая камера получает с матрицы изображение в так называемом формате RAW. Структура этих данных мало пригодна непосредственно как для рассматривания, так и для получения частотно-контрастной характеристики аппарата.
Тем не менее, эти сырые данные обрабатываются либо на компьютере либо фотоаппаратом. И после обработки получается файл, в универсальном формате, обычно JPG, с информацией, привычной для восприятия и вполне пригодной для резольвометрии.
В процессе обработки устанавливаются:
- чувствительность
- контраст
- насыщенность цвета
- резкость
В камерах эти настройки фиксированы или регулируются дискретно, выбором из набора определённых производителем камеры величин.

Более широкие возможности предоставляют программы преобразования RAW на компьютере.
Однако изменение всех этих настроек «в сторону увеличения», в конечном итоге, даёт увеличение уровня шума. Поэтому сравнивать MTF у разной цифровой техники необходимо при одинаковом количестве шумов и, если используются какие-либо алгоритмы шумоподавления, то при сопосотавимых параметрах работы этих алгоритмов.
См. также
- Локальный цвет
Ссылки
- (рус.) Подробно о графиках MTF.
- (англ.) Табличка разрешений K-mount объективов.
- В. И. Кузичев Частотно-контрастная характеристика // Фотокинотехника: Энциклопедия / Главный редактор Е. А. Иофис. — М.: Советская энциклопедия, 1981.
- (рус.) БСЭ Статья «Частотно-контрастная характеристика».
- (рус.) Разрешение. Мифы и реальность. MTF и её измерение.
Wikimedia Foundation. 2010.
- Функция для галочки
- Функция ограниченной вариации
Игры ⚽ Нужен реферат?
Полезное
Теория оптических систем
Теория оптических систем
ОглавлениеПРЕДИСЛОВИЕВВЕДЕНИЕ Глава I. 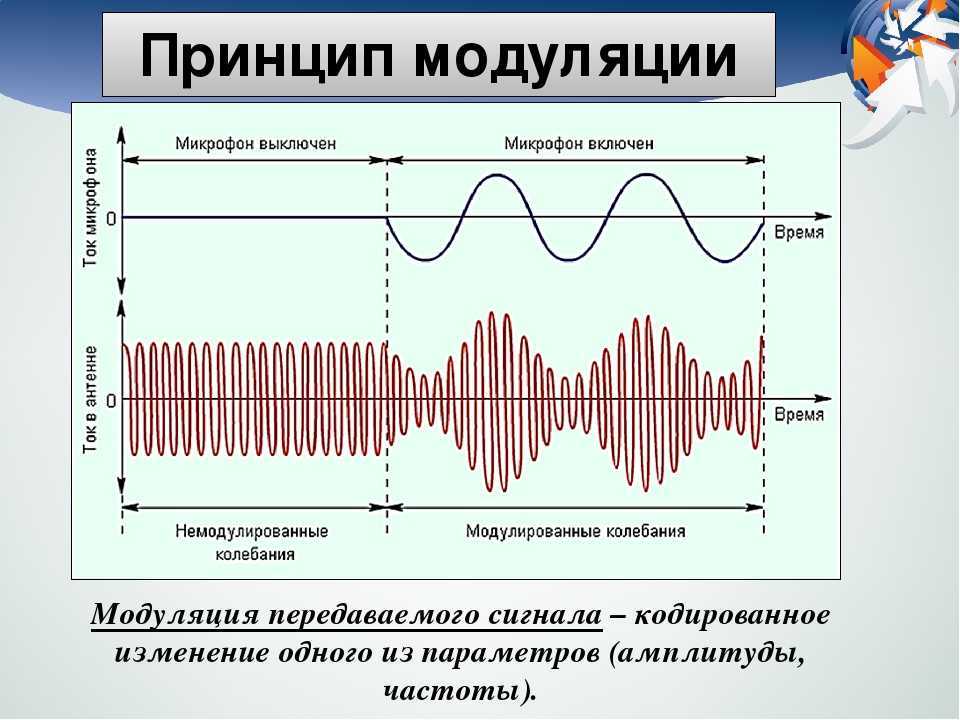 ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ ОСНОВНЫЕ ПОЛОЖЕНИЯ И ЗАКОНЫ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ1. Принцип Ферма 2. Показатель преломления 3. Правила знаков 4. Законы преломления и отражения 5. Полное внутреннее отражение 6. Преломляющие и отражающие поверхности Глава II. ПРЕЛОМЛЕНИЕ И ОТРАЖЕНИЕ ЛУЧЕЙ 7. Преломление лучей плоской поверхностью 8. Преломление лучей сферической поверхностью 9. Отражение лучей плоской поверхиостью 10. Отражение лучей сферической поверхностью 11. Преломление лучей несферической поверхностью 12. Отражение от несферических поверхностей Глава III. ИДЕАЛЬНАЯ ОПТИЧЕСКАЯ СИСТЕМА 13. Понятие об идеальной оптической системе и ее свойства. Линейное увеличение 14. Кардинальные элементы идеальной оптической системы 15. Зависимости между положениями и размерами предмета и изображения 16. Угловое увеличение. Узловые точки 17. Продольное увеличение 18. Построение хода лучей через оптическую систему, заданную кардинальными элементами 19.  Изображение наклонных плоскостей предметов Изображение наклонных плоскостей предметов20. Расчет хода луча через идеальную систему 21. Оптические системы из нескольких компонентов Глава IV. ОПТИКА ПАРАКСИАЛЬНЫХ И НУЛЕВЫХ ЛУЧЕЙ 23. Инвариант Гюйгенса-Гельмгольца 24. Расчет хода нулевых лучей Глава V. ДЕТАЛИ ОПТИЧЕСКИХ СИСТЕМ 25. Материалы, применяемые для изготовления оптических деталей 26. Линзы 27. Плоскопараллельные пластины 29. Отражательные призмы 30. Преломляющие призмы и клинья 31. Световоды и волоконная оптика 32. Линзы Френеля. Аксиконы. Оптические растры. Градиентные и дифракционные элементы Глава VI. ОГРАНИЧЕНИЕ ПУЧКОВ ЛУЧЕЙ В ОПТИЧЕСКИХ СИСТЕМАХ 34. Входной и выходной зрачки 35. Угловое и линейное поля. Виньетирование. Входное и выходное окна 36. Действующее отверстие входного зрачка Глава VII. ОПТИЧЕСКИЙ ПРИБОР КАК ПЕРЕДАТЧИК ЭНЕРГИИ ИЗЛУЧЕНИЯ 37. Оптическое излучение. Поток излучения 38.  Энергетические и световые величины и их единицы Энергетические и световые величины и их единицы39. Связь между световыми и энергетическими величинами 40. Распространение излучения 41. Коэффициент пропускания оптической системы 42. Прохождение потока излучения через светофильтр 43. Освещенность Изображения, создаваемая потоком излучения при действии оптической системы Глава VIII. РАСЧЕТ ХОДА ЛУЧЕЙ ЧЕРЕЗ ОПТИЧЕСКУЮ СИСТЕМУ 44. Формулы для расчета хода лучей на ЭВМ 45. Формулы для расчета хода бесконечно тонких астигматических пучков 46. Выбор начальных данных для расчета хода лучей Глава IX. МОНОХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ 47. Общие положения о вычислении аберраций оптической системы 48. Аберрации третьего порядка 49. Условия нормировки вспомогательных лучей 50. Сферическая аберрация 51. Меридиональная кома 52. Условие синусов и условие изопланатизма 53. Астигматизм и кривизна поверхности изображения 54. Дисторсия Глава X. ХРОМАТИЧЕСКИЕ АБЕРРАЦИИ ОПТИЧЕСКИХ СИСТЕМ 56.  Хроматизм увеличения Хроматизм увеличения57. Сферохроматическая аберрация и хроматические аберрации широких наклонных пучков Глава XI. ГЛАЗ КАК ОПТИЧЕСКАЯ СИСТЕМА 59. Основные характеристики глаза 60. Недостатки глаза и их коррекция Глава XII. ОПТИЧЕСКИЕ ОСВЕТИТЕЛЬНЫЕ СИСТЕМЫ 61. Назначение и виды осветительных систем 62. Оптическая схема прожектора дальнего действия 63. Зеркальные осветительные системы 64. Линзовые конденсоры Глава XIII. ЛУПА И МИКРОСКОП 65. Лупа и ее характеристики 66. Оптическая схема микроскопа и его основные характеристики 67. Разрешающая способность микроскопа 68. Глубина изображаемого пространства для микроскопа 69. Объективы и окуляры микроскопа 70. Осветительные системы микроскопов Глава XIV. ТЕЛЕСКОПИЧЕСКАЯ СИСТЕМА 71. Схема телескопической системы и ее основные характеристики 72. Разрешающая способность телескопической системы 73. Основные сведения об объективах и окулярах телескопических систем 74.  Фокусировка окуляра телескопической системы Фокусировка окуляра телескопической системы75. Применение коллектива в зрительной трубе 76. Расчет зрительной трубы Кеплера 77. Схема зрительной трубы Галилея и ее расчет 78. Расчет призменного монокуляра 79. Расчет зрительной трубы с линзовой оборачивакщей системой 80. Основные сведения о зрительных трубах переменного увеличения 81. Стереоскопические телескопические системы 82. Зрительная труба с электронно-оптическим преобразователем и ее расчет Глава XV. ФОТОГРАФИЧЕСКИЙ ОБЪЕКТИВ 83. Основные характеристики фотообъектива 84. Разрешающая способность и функция передачи модуляции фотографической системы 85. Глубина изображаемого пространства и глубина резкости 86. Определение выдержки при фотографировании 87. Основные типы фотографических объективов Глава XVI. ОПТИКА ТЕЛЕВИЗИОННЫХ СИСТЕМ 88. Оптические характеристики передающих и приемных телевизионных трубок 89. Объективы передающих телевизионных камер и их основные характеристики 90.  Разрешающая способность и ФПМ телевизионной системы Разрешающая способность и ФПМ телевизионной системы91. Телевизионная система с «бегущим лучом» Глава XVII. ПРОЕКЦИОННЫЕ СИСТЕМЫ 92. Виды и особенности проекционных систем 93. Эпископическая проекционная система 94. Диаскопическая проекционная система 95. Габаритный и светоэнергетический расчеты проекционного прибора с зеркальной осветительной системой Глава XVIII. ОПТИЧЕСКИЕ ФОТОЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ 96. Некоторые характеристики и параметры приемников излучения 97. Определение диаметра входного зрачка оптической фотоэлектрической системы по интегральным характеристикам 98. Определение диаметра входного зрачка оптической фотоэлектрической системы по спектральным характеристикам 99. Оптические фотоэлектрические системы с приемником излучения, расположенным в плоскости изображения источника 100. Оптические фотоэлектрические системы, в которых изображение источника больше светочувствительной поверхности приемника 101. Оптическая фотоэлектрическая система с приемником излучения, расположенным в выходном зрачке 102.  Некоторые принципиальные схемы оптических фотоэлектрических систем Некоторые принципиальные схемы оптических фотоэлектрических системГлава XIX. ОПТИЧЕСКИЕ СИСТЕМЫ ДЛЯ ЛАЗЕРОВ 104. Параметры пучка лазера и основные соотношения при его преобразовании оптической системой 105. Оптические системы для концентрации излучения лазера 106. Оптические системы для уменьшения расходимости лазерного пучка 107. Оптическая фотоэлектрическая система с лазером 108. Оптические системы, применяемые в голографии Глава XX. ОПТИЧЕСКИЕ СИСТЕМЫ ДВОЯКОЙ СИММЕТРИИ 109. Характеристика трансформированного изображения и его получение 110. Цилиндрический и сфероцилиндрический объективы-анаморфоты 111. Цилиндрическая афокальная система Глава XXI. АБЕРРАЦИОННЫЙ РАСЧЕТ ОПТИЧЕСКИХ СИСТЕМ 112. Общие сведения о методах аберрационного расчета оптических систем 113. Допустимые остаточные аберрации в различных оптических системах 114. Связь между параметрами 1-го и 2-го вспомогательных лучей 115. Преобразование сумм Зейделя для оптической системы, состоящей из тонких компонентов 116. 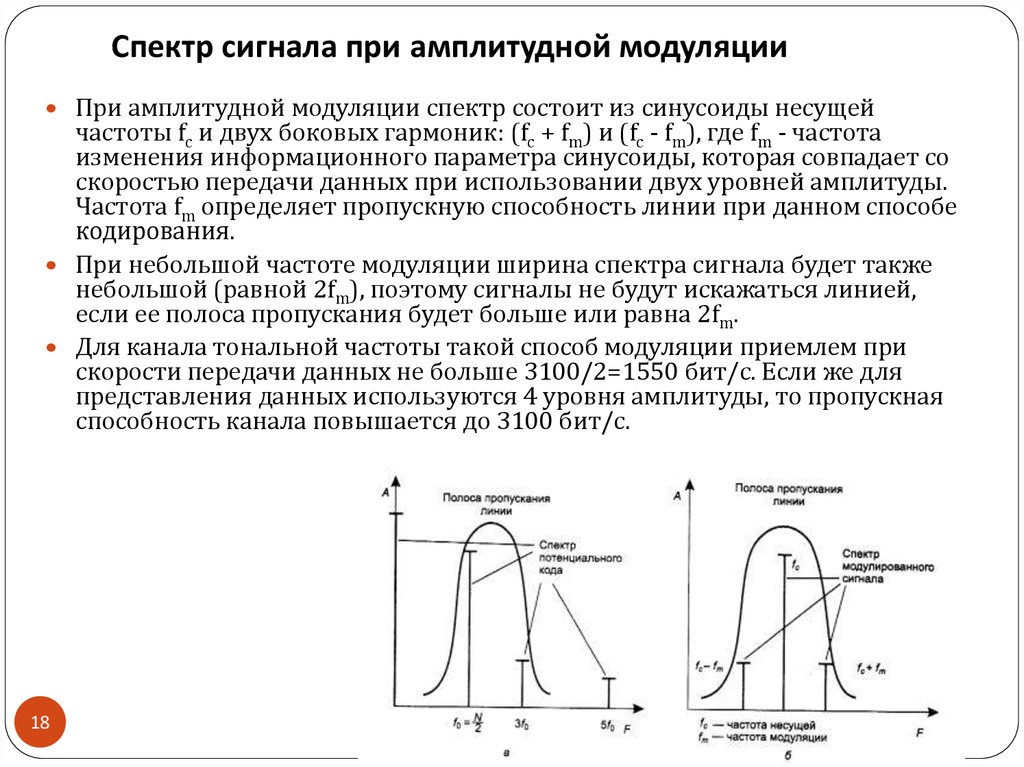 Основные параметры тонких компонентов Основные параметры тонких компонентов117. Аберрации оптических систем с иесферическими поверхностями 118. Расчет оптической системы на минимум сферической аберрации 119. Расчет двухлинзового склеенного объектива 120. Расчет двухливэового несклеенного объектива 121. Расчет светосильного двухкомпоиентного объектива 122. Расчет объектива типа триплета 123. Расчет зеркальных систем 124. Расчет зеркально-линзовых систем 125. Об автоматизированной коррекции оптических систем на ЭВМ 126. Суммирование аберраций 127. О допусках в оптических системах 128. Оценка качества изображения по результатам аберрационного расчета 129. Волновая аберрация оптической системы |
Что такое передаточная функция модуляции?
Передаточная функция модуляции, или MTF, — это параметр, используемый для оценки характеристик объектива. MTF обеспечивает количественный и стандартизированный способ характеристики оптических систем, поэтому метрика используется как оптическими дизайнерами, так и микроскопистами для сравнения линз и определения идеальной для системы обработки изображений.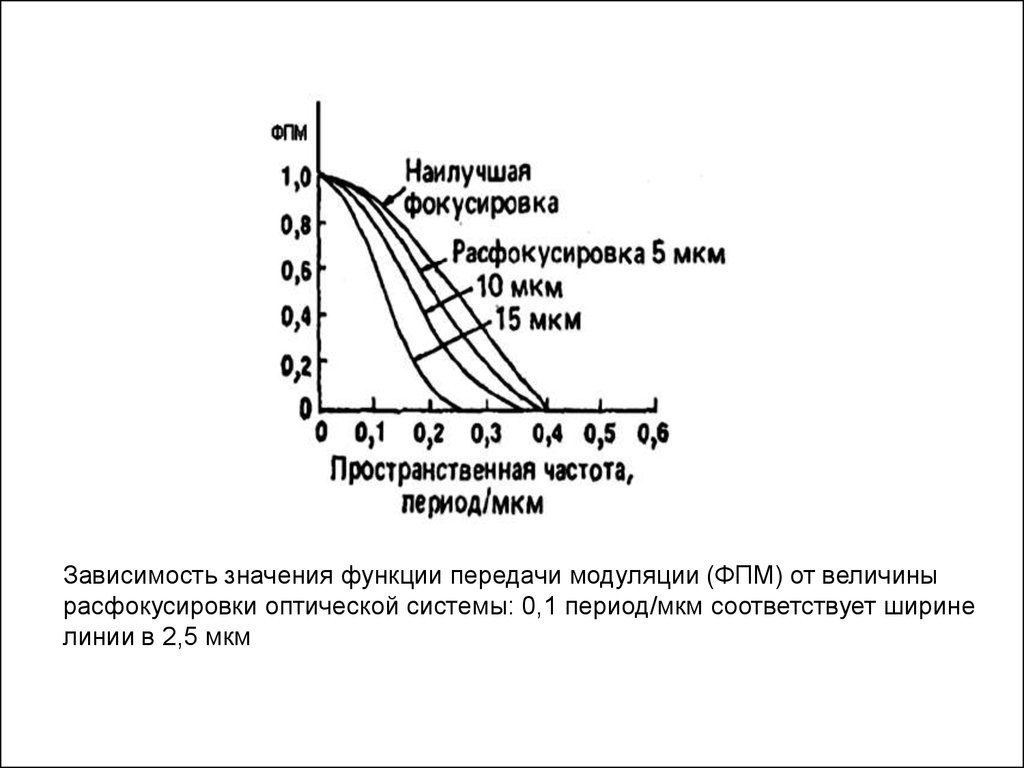
Оптические данные MTF используются для ряда инструментов, включая секвенаторы ДНК, анализаторы клеток, сканеры слайдов и промышленное инспекционное оборудование. Чтобы помочь процессу оптического проектирования, в этом техническом документе подробно рассматривается MTF и объясняются различные способы его использования.
Понимание измерения MTF
И разрешение, и контрастность необходимы для того, чтобы изображение выглядело четким. Проще говоря, разрешение — это способность передавать детали, а контрастность — это способность различать светлые и темные области. Даже при высоком разрешении низкая контрастность будет препятствовать четкому различению деталей образца. Высококачественная оптика передает больший контраст на более высоких частотах (т. е. с более высоким разрешением), поэтому важно измерять эту способность оптики при проектировании системы визуализации. Это можно сделать через МТФ.
MTF измеряет способность объектива преобразовывать контраст образца в изображение, используя пространственную частоту (разрешение). Пространственная частота указывает количество пар линий (т. е. одна черная и одна белая линия) на миллиметр (лин/мм). Как правило, для измерения MTF объектива используются различные диаграммы с чередующимися черными и белыми линиями на равном расстоянии друг от друга (рис. 1). Затем контраст наносится на график MTF в зависимости от пространственной частоты, как показано на рисунке 2 ниже.
Пространственная частота указывает количество пар линий (т. е. одна черная и одна белая линия) на миллиметр (лин/мм). Как правило, для измерения MTF объектива используются различные диаграммы с чередующимися черными и белыми линиями на равном расстоянии друг от друга (рис. 1). Затем контраст наносится на график MTF в зависимости от пространственной частоты, как показано на рисунке 2 ниже.
Рисунок 1. Примеры различных пространственных частот. | Рисунок 2. Пример графика MTF, показывающий контраст (MTF) в зависимости от пространственной частоты. На графике показан контраст 50% при пространственной частоте 30 пар линий/мм. |
Как читать график MTF
На графике MTF на рис. 2 поле зрения фиксировано, по горизонтальной оси отложена пространственная частота (лп/мм), а по вертикальной оси показана контрастность. Диаграмма показывает, что с помощью этого объектива можно достичь контраста 50% при пространственной частоте 30 пар линий/мм.
Диаграмма показывает, что с помощью этого объектива можно достичь контраста 50% при пространственной частоте 30 пар линий/мм.
В большинстве объективов контраст выше в центре поля зрения, чем по краям. По этой причине диаграмма MTF может также отображать кривые в сагиттальном и меридиональном направлениях. Эти кривые иллюстрируют изменение контраста в зависимости от расстояния от центра изображения.
Сагиттальное указывает исполнение в радиальном направлении (от центра к углу изображения), а меридиональное указывает исполнение в концентрическом направлении (круговое). Контраст в сагиттальном и меридиональном направлениях изменяется из-за влияния внеосевых аберраций (т. е. оптических ошибок в разных точках поля), таких как кома и астигматизм.
В целом, сходные сагиттальные и меридиональные характеристики создают более однородное изображение. Это означает, что если сагиттальные и меридиональные кривые расположены ближе друг к другу на диаграмме MTF, то изображения будут иметь более равномерную производительность как по оси X (горизонтальной), так и по оси Y (вертикальной). Зазор, с другой стороны, обычно указывает на неравномерное изображение с аберрациями. В идеале вы хотите, чтобы кривые были ближе друг к другу для более равномерного изображения.
Зазор, с другой стороны, обычно указывает на неравномерное изображение с аберрациями. В идеале вы хотите, чтобы кривые были ближе друг к другу для более равномерного изображения.
Как рассчитать MTF
MTF показывает, как контраст на поверхности объекта отражается на плоскости изображения. Контраст рассчитывается по следующей формуле. Соотношение контрастности между поверхностью объекта и плоскостью изображения составляет ЧКХ.
Рис. 3. Контраст между поверхностью объекта слева и плоскостью изображения справа.
MTF можно рассчитать для одной длины волны (монохроматический свет) или для белого света, в зависимости от вашего применения. Например, для лазерных приложений для флуоресцентной или многофотонной визуализации могут потребоваться данные MTF для одной длины волны, в то время как для общих приложений визуализации могут потребоваться данные MTF для белого света. Графики MTF для каждой длины волны также можно сравнивать друг с другом, чтобы определить общую производительность устройства.
Рис. 4. Кривые MTF для одной длины волны и белого света
OEM-поставщики оптики могут предоставить информацию и диаграммы MTF для оптических компонентов, что позволит вам оценить оптику для вашей системы.
Как используется функция передачи модуляции?
1. Сравнение оптических характеристик с идеальным дифракционным пределом.
Дифракционный предел указывает абсолютный предел разрешения в оптической системе. Сравнивая значение дифракционного предела с MTF системы линз, можно оценить, насколько характеристики системы линз близки к теоретическому значению.
Кривая MTF может с первого взгляда показать разницу между идеальной оптической системой и построенной системой. Сравнивая MTF следующих двух оптических систем (рис. 5), вы можете видеть, что система 1 имеет более высокую производительность, чем система 2, поскольку она ближе к значению дифракционного предела.
Наглядное сравнение позволяет увидеть, какая система ближе к дифракционному пределу.
2. Сравнение характеристик различных объективов.
ЧКХ является хорошим индикатором, когда вы хотите сравнить характеристики различных объективов, поскольку он показывает, какой из объективов имеет более высокий контраст на определенной пространственной частоте. Как мы упоминали ранее, более высокая контрастность приведет к улучшению качества изображения. Диаграммы MTF позволяют легко сравнивать контрастность оптики, поскольку вы можете визуально увидеть, какая кривая MTF выше.
В качестве примера рассмотрим приведенный ниже график MTF (рис. 6). Вы можете видеть, что производительность MTF для оптики A лучше, чем для оптики B, поскольку кривая выше. Эта визуальная информация может помочь вам выбрать правильный объектив для вашей системы.
Рис. 6. Кривые MTF для двух разных объективов. Оптика A имеет более высокую кривую, чем оптика B, что указывает на лучшие оптические характеристики.
3. Определение ЧКХ при различных положениях фокуса в поле зрения.
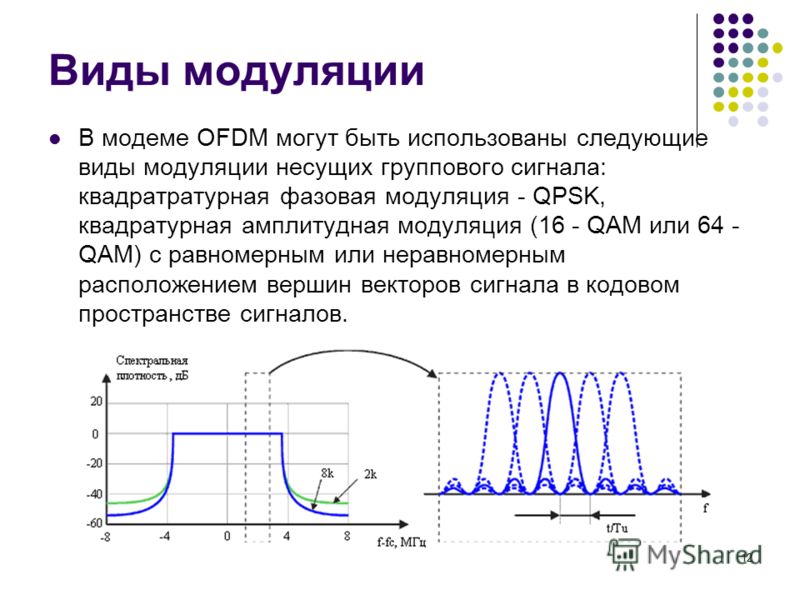
Диаграмма MTF также может показать вам, насколько чувствительна оптика к расфокусировке, иллюстрируя разницу MTF между осевым и внеосевым положениями фокуса. Положение фокусировки по оси относится к центру поля зрения, что обеспечивает резкое сфокусированное изображение. Внеосевое положение фокуса относится к положению в углу поля.
На рис. 7 ниже видно, что MTF в положении фокусировки по оси составляет 60 %, а MTF в положении фокусировки вне оси составляет 40 %. Видно, что внеосевая ФПМ ухудшилась на 20%. Допустимые числа варьируются в зависимости от приложения. Если цифры неприемлемы, рассмотрите возможность изменения конструкции или перехода на другие оптические компоненты.
В идеале кривая MTF для внеосевого положения должна быть как можно ближе к кривой для осевого положения для получения сфокусированного изображения. Разрыв между осевой и внеосевой кривыми (как показано на рис. 7 ниже) указывает на проблемы с расфокусировкой из-за аберраций.
Рис.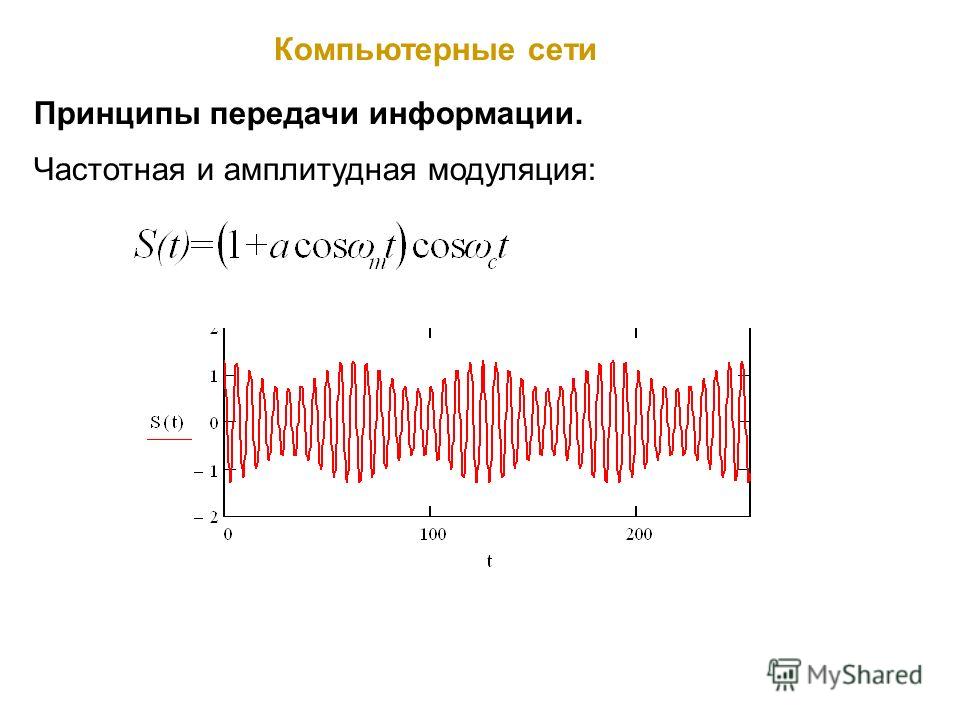 7. Кривые ЧКХ при различных положениях фокуса (вершины кривых) в поле зрения. Разрыв между осевой и внеосевой кривыми указывает на проблемы с расфокусировкой.
7. Кривые ЧКХ при различных положениях фокуса (вершины кривых) в поле зрения. Разрыв между осевой и внеосевой кривыми указывает на проблемы с расфокусировкой.
4. Определение идеальной высоты изображения для сенсора.
Высота изображения — это расстояние от центра до края изображения. Диаграмма MTF позволяет визуально определить идеальную высоту изображения в месте расположения сенсора оптической системы. Вы также можете проверить разницу в производительности между осевым и внеосевым положениями датчика.
На рис. 8 ниже показан пример. Посмотрите на MTF в центре и вне оси датчика. MTF в центральном положении составляет 70%. MTF меридионального направления на расстоянии 5 мм от центра составляет 50%. Обычно, чем дальше от центра, тем сильнее ухудшается ЧКХ из-за влияния внеосевых аберраций. В этом примере MTF меридионального становится равным 20% на расстоянии 10 мм от центра. Для оптимальной производительности не забудьте проверить MTF на высоте изображения, необходимой для приложения, при сборке системы.
Рисунок 8. Диаграмма MTF для изображений разной высоты. MTF ухудшается по мере удаления от центра.
Другой полезный способ использования диаграмм ЧКХ — это проверка ЧКХ различных оптических компонентов системы, таких как объектив и тубус. Это позволяет вам увидеть, есть ли ухудшение MTF из-за одного из оптических компонентов. С помощью этой информации вы можете настроить компоненты для достижения оптимальной производительности, необходимой для системы. Например, можно рассчитать MTF только объектива, тубуса и оптической системы, сочетающей объектив и тубус.
Рисунок 9. Графики MTF для объектива (слева) и тубуса (справа).
Рис. 10. Диаграмма MTF, показывающая комбинированные оптические характеристики объектива и тубуса.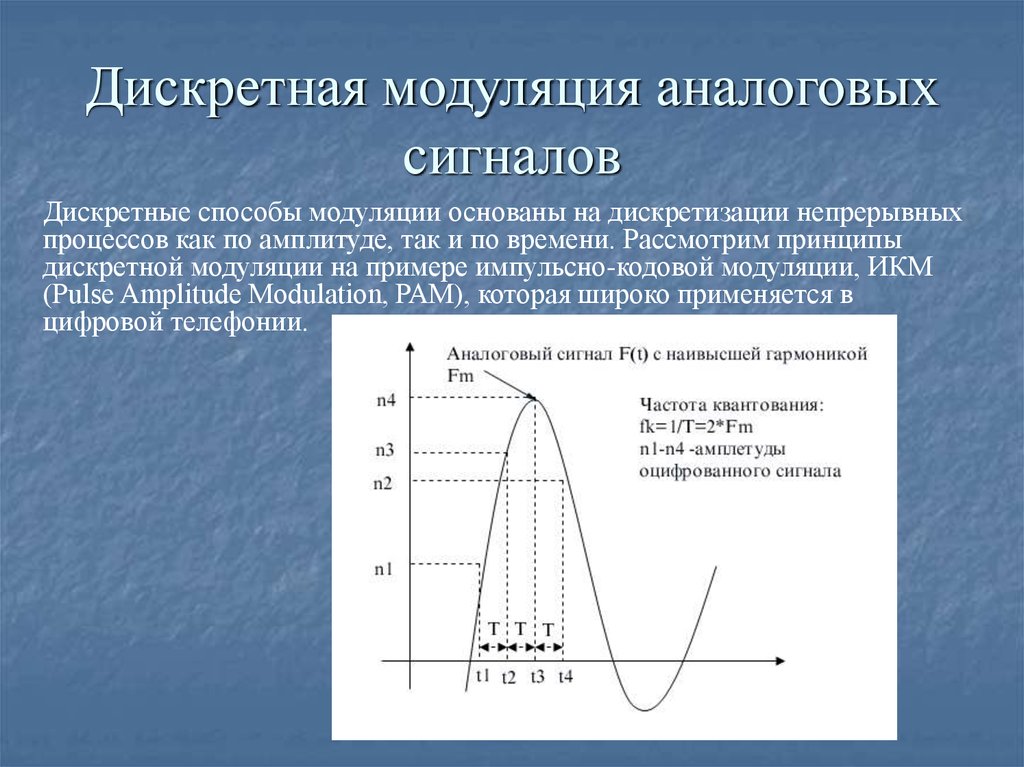
Выводы
Знание MTF оптики при правильных условиях поможет вам построить оптическую систему, необходимую для вашего прибора. Отметим, что при оценке оптической системы с ФПМ необходимо выбрать датчик с оптимальным шагом пикселя и частотой Найквиста. Для получения дополнительной информации, пожалуйста, обратитесь к нашему техническому документу «Что следует учитывать при выборе камеры для микроскопа».
Если у вас есть вопросы о данных MTF, свяжитесь с нами. Наши специалисты всегда готовы помочь.
Данные MTF предоставлены Olympus
Olympus раскрывает данные MTF на условиях NDA (соглашение о неразглашении). Эти данные могут быть использованы для построения оптической системы с более высокими оптическими характеристиками.
Автор
Ю Кикучи, инженер-оптик
Olympus Scientific Solutions
Передаточная функция модуляции
Optipedia • Книги SPIE Press открыты для вашего ознакомления.
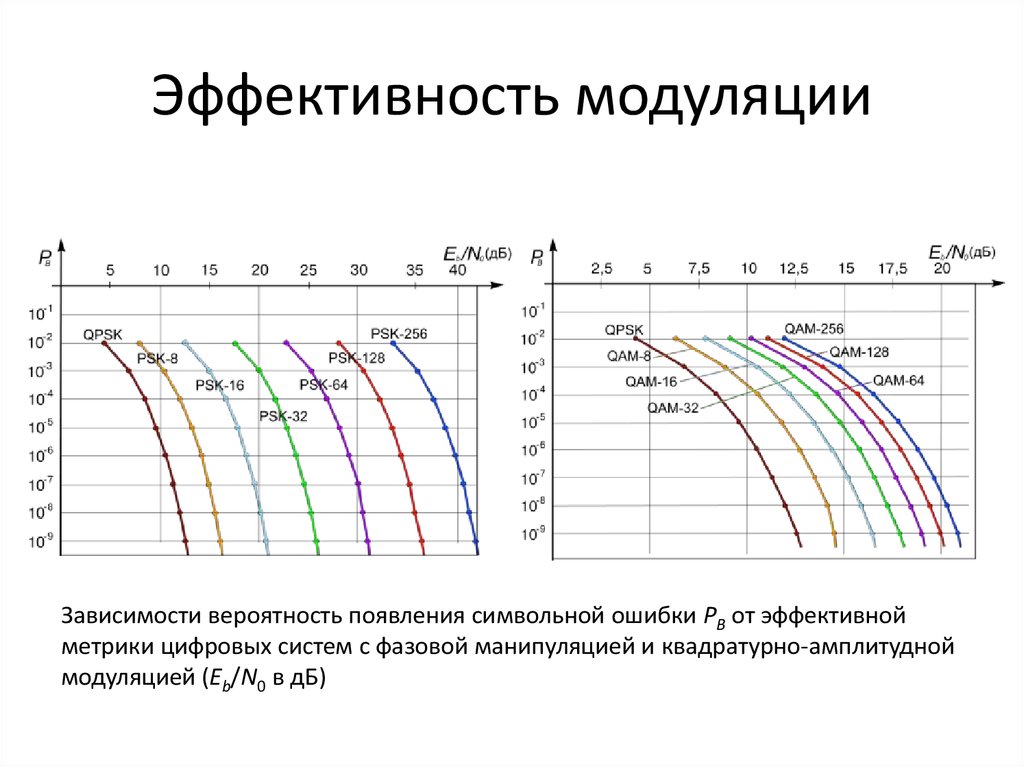
Передаточная функция модуляции представляет собой отклик величины оптической системы на синусоидальные колебания различных пространственных частот. Когда мы анализируем оптическую систему в частотной области, мы рассматриваем отображение синусоидальных входных сигналов (рис. 1.8), а не точечные объекты.
Рисунок 1.8 Синусоидальная цель различных пространственных частот.
Инвариантная к линейному сдвигу оптическая система отображает синусоиду как другую синусоиду. Ограниченное пространственное разрешение оптической системы приводит к уменьшению глубины модуляции М изображения по сравнению с тем, что было в распределении объектов (рис. 1.9). Глубина модуляции определяется как амплитуда изменения освещенности, деленная на уровень смещения:
Рисунок 1.9 Глубина модуляции уменьшается при переходе от объекта к изображению.
Из рис. 1.10 видно, что глубина модуляции является мерой контраста, при этом
Условие M = 0 означает, что, хотя уровень освещенности изображения все еще не равен нулю, нет пространственных изменений это сияние. Когда форма волны имеет минимальное значение, равное нулю, существует единичная глубина модуляции — каким бы ни был максимальный уровень освещенности. Низкие уровни глубины модуляции труднее отличить от неизбежных уровней шума, присущих любой практической системе.
Когда форма волны имеет минимальное значение, равное нулю, существует единичная глубина модуляции — каким бы ни был максимальный уровень освещенности. Низкие уровни глубины модуляции труднее отличить от неизбежных уровней шума, присущих любой практической системе.
Рисунок 1.10 Определение глубины модуляции.
Конечный размер импульсной характеристики оптической системы вызывает заполнение впадин синусоиды и понижение пиковых уровней. Результатом этого является уменьшение глубины модуляции изображения по сравнению с глубиной модуляции объекта. Определяя передачу модуляции (МП) как отношение модуляции в изображении к модуляции в объекте
, мы находим, что уменьшение передачи модуляции зависит от пространственной частоты. Ограниченное разрешение оптики более важно на высоких пространственных частотах, где масштаб деталей меньше. Как видно на рис. 1.11, когда мы строим передачу модуляции в зависимости от пространственной частоты, мы получаем MTF, обычно являющуюся убывающей функцией пространственной частоты.

 Modulation Transfer Function).
Modulation Transfer Function).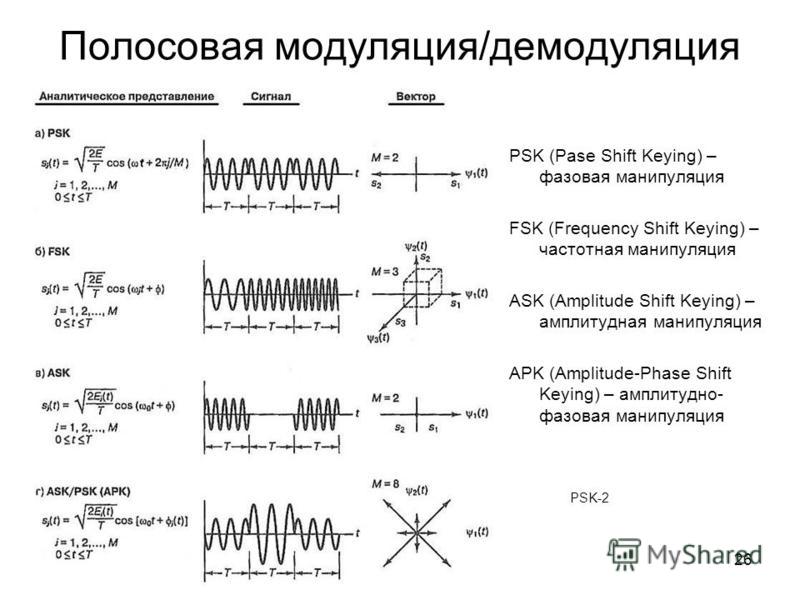 «фиолетовый» же имеет очень сильное падение контраста и разрешающей способности к краям. В результате, сравнивая эти два объектива только по одному или двум числам разрешающей способности в центре и на краях, невозможно получить объективной картины того, насколько изображение с одного и с другого объектива будет отвечать задачам фотографа.
«фиолетовый» же имеет очень сильное падение контраста и разрешающей способности к краям. В результате, сравнивая эти два объектива только по одному или двум числам разрешающей способности в центре и на краях, невозможно получить объективной картины того, насколько изображение с одного и с другого объектива будет отвечать задачам фотографа.
 П. и др. Теория оптических систем: Учебник для студентов приборостроительных специальностей вузов/Н. П. Заказнов, С. И. Кирюшин, В. Н. Кузичев.— 3-е изд., перераб. и доп. — М.: Машиностроение, 1992. — 448 с.
П. и др. Теория оптических систем: Учебник для студентов приборостроительных специальностей вузов/Н. П. Заказнов, С. И. Кирюшин, В. Н. Кузичев.— 3-е изд., перераб. и доп. — М.: Машиностроение, 1992. — 448 с.