Гауссово размытие: Быстрое размытие по Гауссу / Хабр

3.3. Гауссово размывание

3.3. Гауссово размывание

3.3.1. Общая информация

Рисунок 17.11. Пример применения фильтра «Гауссово размывание»

Исходное изображение

Результат обработки

Расширение Гауссово размывание действует на каждый пиксель активного слоя или выделения, устанавливая среднее общее значение на базе всех значений пикселей, находящихся в радиусе, настроенном в диалоге. Более высокое значение выдаст больший объём размывания. Можно настроить более сильное размывания в каком-то одном направлении, для этого нажмите на значок звена цепочки так, чтобы звено стало разорванным, и после этого измените радиус. GIMP поддерживает две реализации Гауссова размывания: FIR и RLE. Оба фильтра выдают аналогичный итоговый результат, но в разных случах какой-то один из фильтров может работать быстрее другого.

3.3.2. Активация фильтра

Этот фильтр можно найти в меню изображения Фильтры → Размывание → Гауссово размывание…

3.

3.3. Параметры

Рисунок 17.12. Параметры фильтра «Гауссово размывание»

Presets, «Input Type», Clipping, Blending Options, Preview, Split view

	Примечание
	Эти параметры описываются в Раздел 2, «Общие свойства».

Размер по X, Размер по Y

Здесь можно настроить интенсивность размывания. Изменяя соотношение горизонтального размывания к вертикальному, можно получить эффект размытия в движении.

Фильтр

Авто: попробовать выбрать нужный фильтр автоматически.

FIR: расшифровывается как «конечная импульсная характеристика». Для фотографий или сканированных изображений.

RLE: расшифровывается как «кодирование длин серий». Гауссово размывание с фильтром RLE лучше всего использовать для созданных на компьютере изображений с большими областями постоянной интенсивности.

Политика «бездны»

Политика «бездны» (обработка границ) подчиняется Политика «бездны».

Обрезать по границе ввода

Нужно ли обрезать границу вывода по границе ввода: этот параметр удаляет нежелательные пиксели, созданные размыванием по краям изображения.

Рисунок 17.13. Пример

Верхний правый угол изображения, масштаб x800

Параметр «Обрезать по границе ввода» не отмечен

Параметр «Обрезать по границе ввода» отмечен

Фильтр «Гауссово размывание» не сохраняет границы изображения:

Слева: исходное изображение

В середине: медианный фильтр

Справа: Гаусс

Фильтр Гауссова размытия | Бесплатное онлайн-приложение

Фильтр Гауссова размытия | Бесплатное онлайн-приложение

Примените Фильтр Гауссова размытия к своим изображениям с помощью современного браузера, такого как Chrome, Opera и Firefox.

При поддержке aspose.com и aspose.cloud

Поделиться в Facebook

Поделиться в Twitter

Поделиться в LinkedIn

Другие приложения

Cloud API

Оставить отзыв

Добавить в закладки

Нажмите Ctrl + D, чтобы добавить эту страницу в избранное, или Esc чтобы отменить действие

Aspose.Imaging Фотофильтр

Как применить Фильтр Гауссова размытия к изображениям с помощью Aspose.Imaging Фотофильтр

1. Щелкните внутри области загрузки файла, чтобы загрузить изображения или перетащите файлы изображений
2. Дождитесь загрузки изображения, настройте параметры фильтра, если они доступны, затем нажмите кнопку Применить
3. Измените формат выходного изображения, если необходимо; Нажмите кнопку «Получить результат»
4. Ссылка на скачивание обработанных изображений будет доступна сразу после завершения операции модификации
5. Вы также можете отправить ссылку на обработанный файл изображения на свой адрес электронной почты
6. Обратите внимание, что файл будет удален с наших серверов через 24 часа, а ссылки для скачивания перестанут работать по истечении этого периода времени

Часто задаваемые вопросы

1. ❓ Как добавить Фильтр Гауссова размытия к изображению?

   Во-первых, вам нужно добавить файл изображения для фильтрации: перетащите файл изображения или щелкните внутри белой области, чтобы выбрать файл. Чтобы применить операцию фильтра, вам нужно настроить желаемые эффекты и формат вывода, а затем нажать кнопку «Получить результат». Когда модификация изображения будет завершена, вы сможете загрузить результат.

2. ❓ Как применить Фильтр Гауссова размытия к многостраничному изображению?

   Все просто — выполните те же действия, что и при добавлении Фильтр Гауссова размытия к простому изображению. Но кроме того, есть возможность выбрать страницу для редактирования.

3. 🛡️ Безопасно ли обрабатывать изображения с помощью бесплатного приложения Aspose.Imaging Photo Filter?

   Конечно! Ссылка для скачивания файлов результатов будет доступна сразу после завершения операции модификации. Мы удаляем загруженные файлы через 24 часа, и ссылки для скачивания перестанут работать по истечении этого периода времени. Никто не имеет доступа к вашим файлам. Приложение Photo Filter абсолютно безопасно.

   Когда пользователь загружает свои файлы из сторонних сервисов, они обрабатываются таким же образом.

   Единственное исключение из вышеуказанных политик возможно, когда пользователь решает поделиться своими файлами через форум, запросив бесплатную поддержку, в этом случае только наши разработчики имеют доступ к ним для анализа и решения проблемы.

4. 💻 Можно ли добавить Фильтр Гауссова размытия в изображения в Linux, Mac OS или Android?

   Да, вы можете использовать бесплатное приложение Aspose.Imaging Photo Filter в любой операционной системе с веб-браузером. Наш сервис фильтрации изображений работает онлайн и не требует установки программного обеспечения.

5. 🌐 Какой браузер следует использовать для применения Фильтр Гауссова размытия к изображению?

   Для фильтрации изображения можно использовать любой современный браузер, например, Google Chrome, Firefox, Opera, Safari.

6. ❓ Могу ли я использовать полученное изображение в коммерческих целях?

   Несмотря на то, что наши приложения бесплатны, вы не ограничены в коммерческом использовании полученных изображений, избегая при этом нарушения прав третьих лиц на исходные изображения. Например, вы можете создать NFT (не взаимозаменяемый токен) из своего изображения и попытаться продать его на торговых площадках NFT.

Error explanation placeholder

Email:

 Сделайте этот форум закрытым, чтобы он был доступен только вам и нашим разработчикам

Вы успешно сообщили об ошибке, Вы получите уведомление по электронной почте, когда ошибка будет исправлена Click this link to visit the forums.

 

Gaussian Blur

California State UniversityHelloSan BernardinoWorldDepartment of Computer ScienceИсходное изображениеИзображение размыто с помощью Gaussian blur
с σ = 2

Gaussian blur описывает размытие изображения Гауссова функция. это широко используемый эффект в графическом программном обеспечении, как правило, для уменьшения шума изображения и уменьшения деталь. Визуальный эффект этой техники размытия — плавное размытие, напоминающее размытие изображения через полупрозрачный экран, отчетливо отличается от боке эффект, создаваемый расфокусированным объективом или тенью объекта при обычном освещении.

Гауссово сглаживание также используется в качестве этап предварительной обработки в алгоритмах компьютерного зрения, чтобы улучшать структуры изображений в разных масштабах — см. Представление в масштабном пространстве и масштабное пространство выполнение.

Математически применение размытия по Гауссу к изображению — это то же самое. как свертка изображение с функцией Гаусса; это тоже известно как двумерное преобразование Вейерштрасса. К контраст, свертка по кругу (т. е. размытие круглого прямоугольника) будет более точно воспроизводит эффект боке. Поскольку Фурье преобразование гауссиана является другим гауссианом, применяя Размытие по Гауссу уменьшает высокочастотные искажения изображения. компоненты; Таким образом, размытие по Гауссу является фильтром нижних частот. фильтр.

Механика

Размытие по Гауссу можно использовать для получения гладкого цифрового изображения полутонового отпечатка в градациях серого.

Размытие по Гауссу — это тип фильтра размытия изображения, который использует Функция Гаусса (которая также используется для нормального распределения в статистике) для расчета преобразования, применяемого к каждый пиксель изображения. Уравнение функции Гаусса в одном размерность

Gxy=12πσe-x22σ2

В двух измерениях это произведение двух таких гауссиан, один в направлении:

Gxy=12πσ2e-x2+y22σ2

Где x — расстояние от начала координат в по горизонтальной оси, y — расстояние от начала координат вертикальной оси, а σ — стандартное отклонение Гауссово распределение. Применительно к двум измерениям эта формула создает поверхность, контуры которой концентричны круги с гауссовым распределением от центральной точки. Значения из этого распределения используются для построения матрицы свертки, которая применяется к исходному изображению. Новое значение каждого пикселя установлено на средневзвешенное значение этого пикселя район. Исходное значение пикселя получает самое тяжелое вес (имеющий наибольшее значение Гаусса) и соседние пиксели получать меньшие веса по мере их расстояния до исходного пикселя увеличивается. Это приводит к размытию, которое сохраняет границы и края лучше, чем другие, более равномерные фильтры размытия; смотрите также масштаб-пространство выполнение.

Теоретически функция Гаусса в каждой точке изображения будет ненулевым, а это означает, что все изображение должно быть включены в расчеты для каждого пикселя. На практике, когда вычисление дискретной аппроксимации функции Гаусса, пиксели на расстоянии более 3 σ достаточно малы, чтобы считается фактически нулевым. Таким образом, вклад пикселей снаружи этот диапазон можно игнорировать. Как правило, программа обработки изображений нужно только рассчитать матрицу с размерностью ⌈ 6σ ⌉ + ⌈ 6σ ⌉ (где ⌈ ⌉ — функция потолка), чтобы обеспечить результат, достаточно близкий к тому, который получен с помощью всего гауссова распределение.

Помимо круговой симметрии, размытие по Гауссу может применяться к двумерному изображению как к двум независимым одномерные расчеты, и поэтому называется линейно разъемный . То есть эффект применения двухмерного матрица также может быть достигнута путем применения серии одномерные матрицы Гаусса в горизонтальном направлении, затем повторите процесс в вертикальном направлении. В с вычислительной точки зрения, это полезное свойство, поскольку вычисление может быть выполнено за время O(wkernelwimagehimage)+O(hkernelwimagehimage) (где h — высота,

w — высота. ширина; см. обозначение Big O), в отличие от O (wkernelhkernelwimagehimage) для неотделимого ядра.

Применение нескольких последовательных размытий по Гауссу к изображению имеет тот же эффект, что и при применении одного большего размытия по Гауссу, радиус — это квадратный корень из суммы квадратов размытия радиусы, которые были фактически применены. Например, применяя последовательно размытие по Гауссу с радиусами 6 и 8 дает те же результаты, что и применяя одно размытие по Гауссу с радиусом 10, так как 62+82=10. Из-за этого отношения, время обработки не может быть сэкономлено за счет имитации размытие по Гауссу с последовательными более мелкими размытиями — необходимое время будет по крайней мере так же хорош, как выполнение одного большого размытия.

Два уменьшенных изображения флага Содружество Наций. Перед уменьшением масштаба размытие по Гауссу был применен к нижнему изображению, но не к верхнему. Размытие делает изображение менее резким, но препятствует образованию алиасинга артефакты.

Размытие по Гауссу обычно используется при уменьшении размера изображение. При понижении разрешения изображения обычно примените фильтр нижних частот к изображению перед передискретизацией. Это чтобы ложная высокочастотная информация не появлялась в уменьшенном изображении (псевдоним). Размытие по Гауссу имеет приятный свойства, такие как отсутствие острых краев, и, следовательно, не ввести звон в отфильтрованное изображение.

Фильтр нижних частот

Размытие по Гауссу — это фильтр нижних частот, ослабляющий высокие частоты. частотные сигналы.

Его амплитуда Боде график (логарифмическая шкала в частотной области) представляет собой параболу.

Образец матрицы Гаусса

Это выборочная матрица, полученная путем выборки фильтра Гаусса. ядра (с σ = 0,84089642) в середине каждого пикселя, а затем нормализация.

Обратите внимание, что центральный элемент (в [4, 4]) имеет наибольшую значение, симметрично уменьшающееся по мере увеличения расстояния от центра.

( 0.000000670.000022920.000191170.000387710.000191170.000022920.000000670.000022920.000786330.006559650.013303730.006559650.000786330.000022920.000191170.006559650.054721570.110981640.054721570.006559650.000191170.000387710.013303730.110981640.225083520.110981640.013303730.000387710.000191170.006559650.054721570.110981640.054721570.006559650.000191170.000022920.000786330.006559650.013303730.006559650.000786330.000022920.000000670.000022920.000191170.000387710.000191170 .000022920.00000067 )

Обратите внимание, что 0,22508352 (центральное) в 1177 раз больше, чем 0,00019117, которое находится сразу за пределами 3σ.

Реализация

Эффект размытия по Гауссу обычно создается путем свертки изображение с ядром гауссовых значений. На практике лучше всего воспользоваться свойством размытия по Гауссу линейно отделимым путем разделения процесса на два прохода.

В первом проходе а одномерное ядро ​​используется для размытия изображения только в горизонтальном или вертикальном направлении. Во втором проходе другой одномерное ядро ​​используется для размытия в оставшемся направлении. Полученный эффект такой же, как при свертывании с двумерное ядро ​​за один проход, но требует меньше расчеты.

Дискретизация обычно достигается путем выборки гауссова ядро фильтра в дискретных точках, обычно в позициях соответствующие середине каждого пикселя. Это снижает вычислительные затраты, но для очень маленьких ядер фильтра точка выборка функции Гаусса с очень небольшим количеством выборок приводит к большая ошибка. В этих случаях точность сохраняется (при незначительном вычислительные затраты) путем интегрирования функции Гаусса по площадь каждого пикселя.

При преобразовании непрерывных значений Гаусса в дискретные значения, необходимые для ядра, сумма значений будет отличается от 1. Это приведет к затемнению или осветлению изображение. Чтобы исправить это, значения можно нормализовать, разделив каждый член ядра суммой всех членов ядра.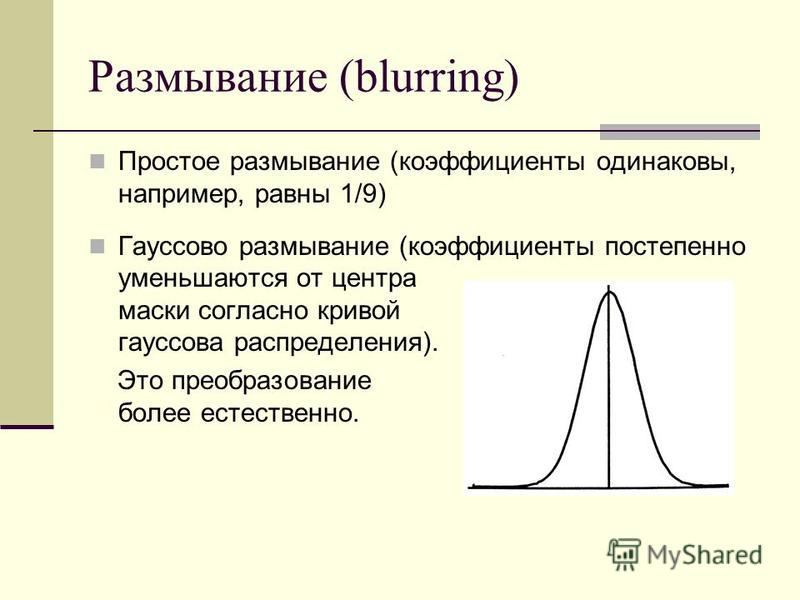

Размытие по Гауссу OpenCV | Работа с Gaussian Blur()

В следующей статье представлен обзор для OpenCV Gaussian Blur. При решении проблем, связанных с компьютерным зрением, иногда необходимо уменьшить четкость изображений или сделать их различимыми, и это можно сделать с помощью ядер фильтра нижних частот, среди которых размытие по Гауссу является одним из них, который использует функция, называемая функцией Gaussian Blur(), для удаления шума с изображения или уменьшения деталей изображения, а функция Gaussian Blur() возвращает размытое изображение, а размытие по Gaussian широко используется на этапах предварительной обработки перед построением моделей в машинном обучении или глубокое обучение и в графическом программном обеспечении.

Синтаксис для определения функции Gaussian Blur() в OpenCV:

GaussianBlur(source_image, kernel_size, sigmaX)

Где

• source_image размыто с использованием функции Gaussian.
• kernel_size — это матрица, представляющая размер ядра.
• sigmaX — это переменная, представляющая стандартное отклонение ядра Гаусса в направлении X, и она имеет тип double.

Работа Gaussian Blur() в OpenCV

• Чтобы иметь возможность уменьшить четкость изображений или сделать изображения четкими, удалить шум с изображений или уменьшить детали изображений, мы используем Gaussian размытие.
• Размытие по Гауссу использует функцию под названием Gaussian Blur(), чтобы уменьшить четкость изображений или сделать их различимыми, или удалить шум с изображений, или уменьшить детали изображений.
• Изображение, которое нужно размыть, считывается с помощью функции imread().
• Затем изображение вместе с матрицей, представляющей размер ядра Гаусса и стандартное отклонение ядра Гаусса, передается в качестве параметров функции Gaussian Blur().
• Функция Gaussian Blur() размывает изображение и возвращает размытое изображение в качестве выходных данных.

Примеры размытия по Гауссу в OpenCV

Ниже приведены примеры размытия по Гауссу в OpenCV:

Пример #1 затем отобразите размытое изображение в качестве вывода на экран.

Код:

# импорт всех необходимых модулей
import numpy as np
import cv2 as cv
# чтение изображения, которое необходимо размыть, с помощью функции imread()
imageread = cv.imread('C: /Users/admin/Desktop/images/tree.jpg')
# применение функции GaussianBlur() к изображению для размытия изображения и отображения его на экране
resultimage = cv.GaussianBlur(imageread, (7, 7) ), 0)
cv.imshow('Blurred_image', resultimage)
cv.waitKey(0)
cv.destroyAllWindows()

Вывод:

В приведенной выше программе мы импортируем необходимые модули. Затем мы читаем изображение, которое нужно размыть, с помощью функции imread(). Затем мы применяем к изображению функцию Gaussian Blur(), чтобы размыть изображение и отобразить его как вывод на экране. Пример № 2

Код:

# импорт всех необходимых модулей
import numpy as np
import cv2 as cv
# чтение изображения, которое необходимо размыть, с помощью функции imread()
imageread = cv.imread('C: /Users/admin/Desktop/images/educba.jpg')
# применение функции GaussianBlur() к изображению для размытия изображения и отображения его на экране
resultimage = cv.GaussianBlur(imageread, (7, 7) ), 0)
cv.imshow('Blurred_image', resultimage)
cv.waitKey(0)
cv.destroyAllWindows()

Вывод:

В приведенной выше программе мы импортируем необходимые модули. Затем мы читаем изображение, которое нужно размыть, с помощью функции imread(). Затем мы применяем к изображению функцию Gaussian Blur(), чтобы размыть изображение и отобразить его как вывод на экране. Пример №3

Код:

# импорт всех необходимых модулей
import numpy as np
import cv2 as cv
# чтение изображения, которое необходимо размыть, с помощью функции imread()
imageread = cv. imread('C: /Users/admin/Desktop/images/plane.jpg')
# применение функции GaussianBlur() к изображению для размытия изображения и отображения его на экране
resultimage = cv.GaussianBlur(imageread, (7, 7) ), 0)
cv.imshow('Blurred_image', resultimage)
cv.waitKey(0)
cv.destroyAllWindows()

Вывод:

В приведенной выше программе мы импортируем необходимые модули. Затем мы читаем изображение, которое нужно размыть, с помощью функции imread(). Затем мы применяем к изображению функцию Gaussian Blur(), чтобы размыть изображение и отобразить его как вывод на экране. Пример № 4

Код:

# импорт всех необходимых модулей
import numpy as np
import cv2 as cv
# чтение изображения, которое необходимо размыть, с помощью функции imread()
imageread = cv.imread('C: /Users/admin/Desktop/images/car.jpg')
# применение функции GaussianBlur() к изображению для размытия изображения и отображения его на экране
resultimage = cv.