Гистограмма пример: Семь основных инструментов контроля качества

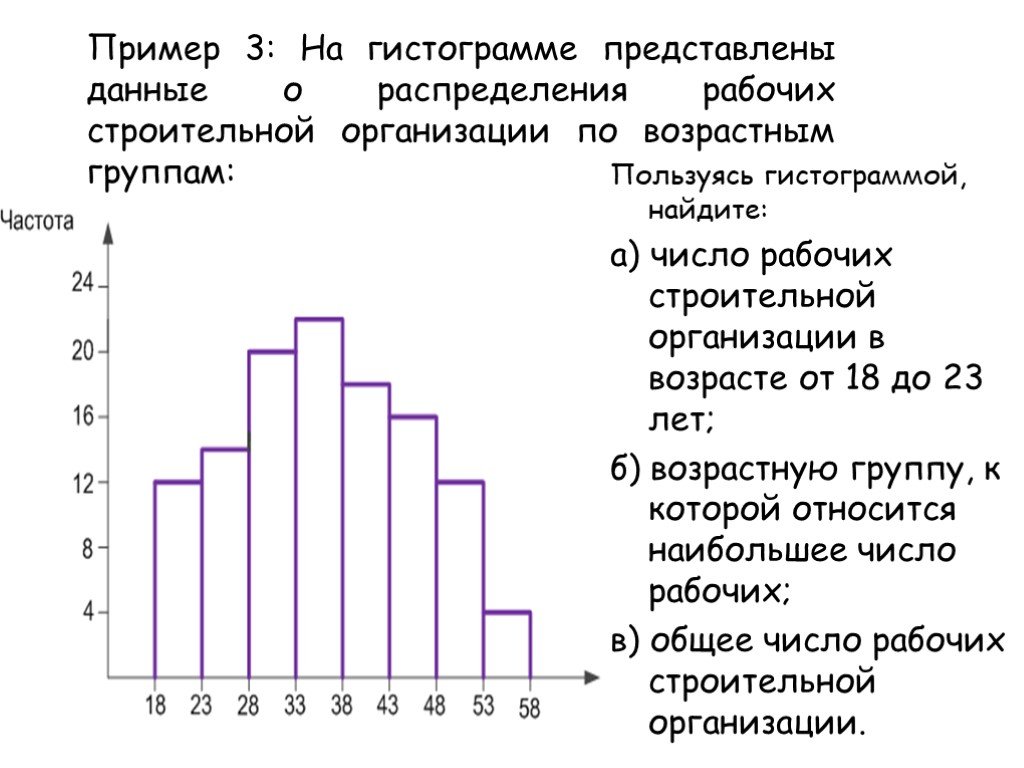
Полигон и гистограмма, полигон в статистике это

Гистограмма представляет собой ступенчатую фигуру в виде прямоугольников. Длина каждого прямоугольника представляет собой равный одинаковый частотный интервал и вычисляется по формуле:

x_i-x_i-1

Высоты гистограммы определяется по формуле:

Формула размаха выборки R:

R=x_max−x_min

Количество интервалов в выборке определяется по формуле:

k≈1+log₂n≈1+3,221·lgn

 Длина l интервала гистограммы, формула:

l=R/n

  Формула эмпирической плотности распределения выборки имеет вид:

х_i — значения частот;

n_i— частоты;

w_i — относительные частоты;

n — объём выборки;

---

Пример 

В водоёме проведены измерения температуры воды в течение 20 дней.

Статистика отчета измерений:

11, 15, 18, 14, 12, 13, 11, 14, 18, 19, 18, 14, 15, 16, 14, 18, 21, 17, 13, 16

  Построить гистограмму относительных, абсолютных и накопленных частот выборки, вычислить эмпирическую плотность распределения частот.

  Решение. 

  По условию задачи объем выборки равен 20.

Отсортируем и упорядочим вариационный ряд, начиная от самого минимального значения, получим:

11, 11, 12, 13, 13, 14, 14, 14, 14, 15, 15, 16, 16, 17, 18, 18, 18, 18, 19, 21

  Найдем размах выборки

R=21-11=10

Количество интервалов в выборке равно:

k≈log₂20+1≈5,32

Округляя до целого числа, имеем

k=5

Определим длину каждого интервала

l=10/5=2

Получаем таблицу интервалов

Номер интервала	Абсолютная частота, n i	Частотный интервал
1.	3	[11;13)
2.	6	[13;15)
3.	4	[15;17)
4.	5	[17;19)
5.	2	[19;21)

Таблица относительных частот и эмпирическая плотность распределения частоты

Частотный интервал	Относительная частота, wi=ni/n	Эмпирическая плотность распределения частоты ni/Δ
[11;13)	0.15	1.5
[13;15)	0.3	3
[15;17)	0. 2	2
[17;19)	0.25	0.25
[19;21)	0.1	0.1

График гистограммы абсолютных частот

График гистограммы относительных частот

 

График гистограммы накопленных частот

   

Полигон это тоже самое, что и многоугольник распределения вероятностей или частот и строится для дискретной случайной величины.

Полигон в статистике

— это график (или ломанная линия), отрезки которой соединяют точки с координатами х_i, w_i в прямоугольной системе координат между собой (см. рисунок ниже) и наглядно показывает распределение частот как для количественных, так и  порядковых значений переменных, то плотность распределения случайной величины.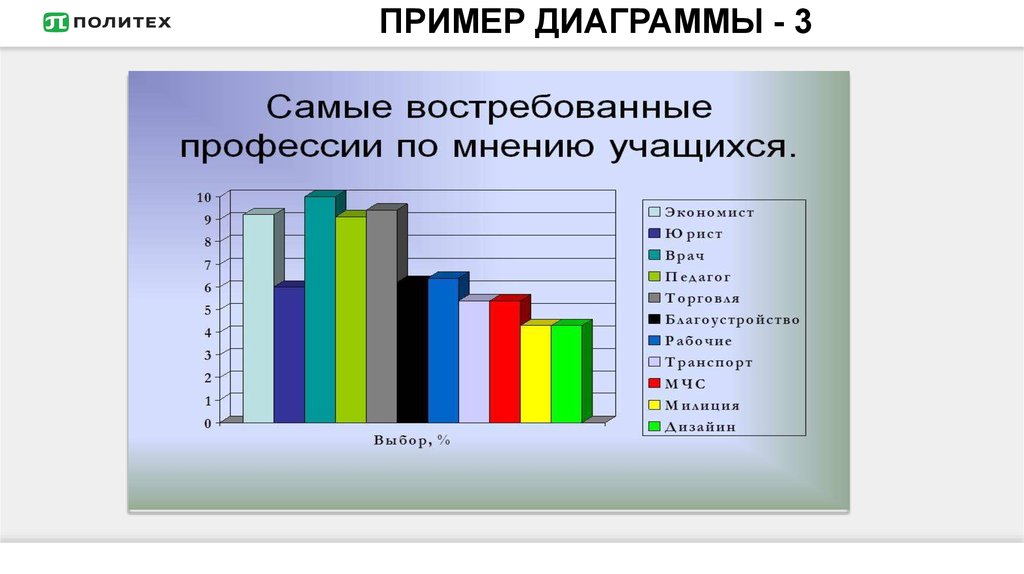

Для построения полигона частот на оси абсцисс откладывают варианты х_i, а на оси ординат — соответствующие им частоты n_i  и соединяют точки.

 Пример графика полигона частот х_i, n_i 

Пример графика полигона относительных частот х_i, w_i 

Способы создания гистограмм с помощью Python / Хабр

За последний год я сталкивалась с необходимостью рисования гистограмм и столбчатых диаграмм достаточно часто для того, чтобы появилось желание и возможность об этом написать. Кроме того, мне самой довольно сильно не хватало подобной информации. В этой статье приведен обзор 3 методов создания таких графиков на языке Python.

Начнем с того, чего я сама по своей неопытности не знала очень долго: столбчатые диаграммы и гистограммы — разные вещи. Основное отличие состоит в том, что гистограмма показывает частотное распределение — мы задаем набор значений оси Ox, а по Oy всегда откладывается частота.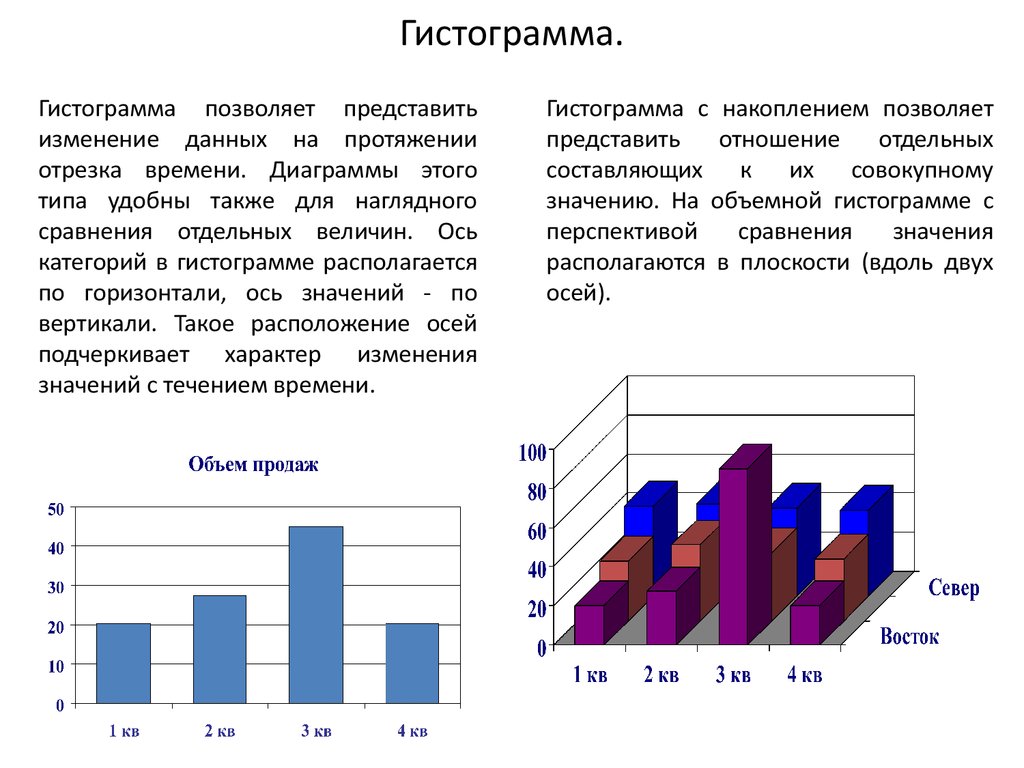 В столбчатой диаграмме (которую в англоязычной литературе уместно было бы назвать barplot) мы задаем и значения оси абсцисс, и значения оси ординат.

Для демонстрации я буду использовать избитый набор данных библиотеки scikit learn Iris. Начнем c импортов:

import pandas as pd
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn import datasets
iris = datasets.load_iris()

Преобразуем набор данных iris в dataframe — так нам удобнее будет с ним работать в будущем.

data = pd.DataFrame(data= np.c_[iris['data'], iris['target']], columns= iris['feature_names'] + ['target'])

Из интересующих нас параметров data содержит информацию о длине чашелистиков и лепестков и ширине чашелистиков и лепестков.

Используем Matplotlib
Построение гистограммы
Cтроим обычную гистограмму, показывающую частотное распределение длин лепестков и чашелистиков:

fig, axs = plt. subplots(1, 2)
n_bins = len(data)
axs[0].hist(data['sepal length (cm)'], bins=n_bins)
axs[0].set_title('sepal length')
axs[1].hist(data['petal length (cm)'], bins=n_bins)
axs[1].set_title('petal length')

Построение столбчатой диаграммы

Используем методы matplotlib-а, чтобы сравнить ширину листьев и чашелистиков. Это кажется удобнее всего делать на одном графике:

x = np.arange(len(data[:50]))  
width = 0.35  

Для примера и в целях упрощения картинки возьмем первые 50 строк dataframe.

fig, ax = plt.subplots(figsize=(40,5))
rects1 = ax.bar(x - width/2, data['sepal width (cm)'][:50], width, label='sepal width')
rects2 = ax.bar(x + width/2, data['petal width (cm)'][:50], width, label='petal width')
ax.set_ylabel('cm')
ax.set_xticks(x)
ax.legend()

Используем методы seaborn

На мой взгляд, многие задачи по построению гистограмм проще и эффективнее выполнять с помощью методов seaborn (кроме того, seaborn выигрывает еще и своими графическими возможностями, на мой взгляд).

Я приведу пример задач, решающихся в seaborn с помощью одной строчки кода. Особенно seaborn выигрышный, когда надо построить распределение. Скажем, нам надо построить распределение длин чашелистиков. Решение этой задачи таково:

sns_plot = sns.distplot(data['sepal width (cm)'])
fig = sns_plot.get_figure()

Если же вам необходим только график распределения, сделать его можно так:

snsplot = sns.kdeplot(data['sepal width (cm)'], shade=True)
fig = snsplot.get_figure()

Подробнее о построении распределений в seaborn можно почитать тут.

Pandas-гистограммы

Здесь все просто. На самом деле, это оболочка matplotlib.pyplot.hist(), но вызов функции через pd.hist() иногда удобнее менее поворотливых конструкций matplotlib-a. В документации библиотеки pandas можно прочитать больше.

Работает это так:

h = data['petal width (cm)'].hist()
fig = h.get_figure()

Спасибо, что прочитали до конца! Буду рада отзывам и комментариям!

примеров гистограмм | 6 лучших примеров гистограммы с объяснением

Гистограмма — это статистический инструмент для представления распределения набора данных.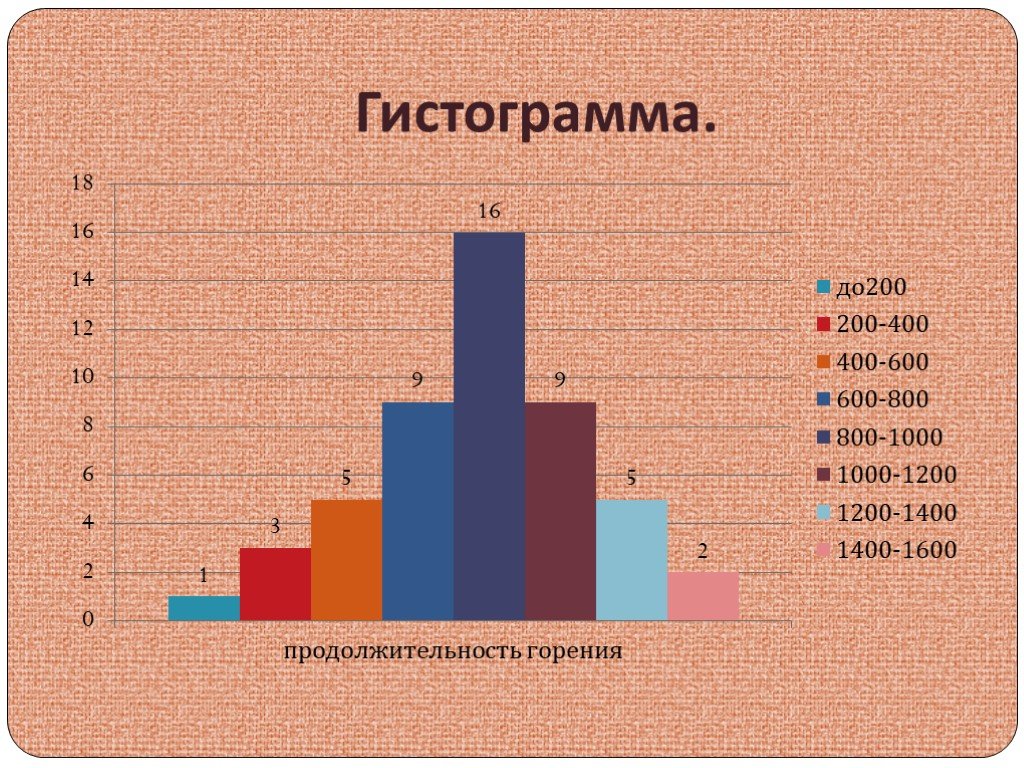 Это общая оценка распределения вероятностей непрерывного ряда переменных данных. На самом деле это график, который отвечает на все запросы с лежащим в основе частотным распределением набора непрерывных и вероятных данных, он дает представление о плотности данных. На гистограмме частота появления для каждого бина указывается площадью столбца. В этой статье мы собираемся предоставить вам лучшие примеры гистограмм.

Примеры гистограммы

Существует много примеров гистограммы. Некоторые из них:

• Бимодальные
• Симметричный, одномодальный
• Перекошено вправо
• Перекос влево
• Мультимодальный
• Симметричный

1. Бимодальная гистограмма

Когда гистограмма имеет два пика, она называется бимодальной гистограммой. Он имеет два значения, которые чаще всего встречаются в наборе данных.

Пример 1

Как и во многих ресторанах, в 14:00 и 19:00 можно ожидать гораздо больше посетителей, чем в любое другое время дня и ночи. Это делает график гистограммы бимодальным, поскольку в течение всего дня есть два отдельных периода времени, которые соответствуют двум пиковым временам обслуживания в ресторане.

Пример 2

В Индии люди обычно ухаживают за собой по выходным. Итак, если изобразить гистограмму за все 7 дней посещения людьми салонов и салонов, то субботы и воскресенья будут двумя крайностями. Распределение данных будет примерно таким, как показано ниже:

2. Симметричная, унимодальная гистограмма

Гистограмма является унимодальной, если имеется только один горб. Это означает, что частота возникновения события распределяется таким образом, что нет никаких крайностей.

Пример 1

Профессор Брук хотел увидеть и подсчитать часы, потраченные его учениками на предстоящий тест. Он получил следующие числа: 1, 3, 2, 1, 5, 1, 4, 3, 2, 1, 1, где каждое число представляет собой количество часов, потраченных каждым студентом на учебу. Те же данные представлены на гистограмме, и мы видим справедливый баланс между левым и правым хвостами.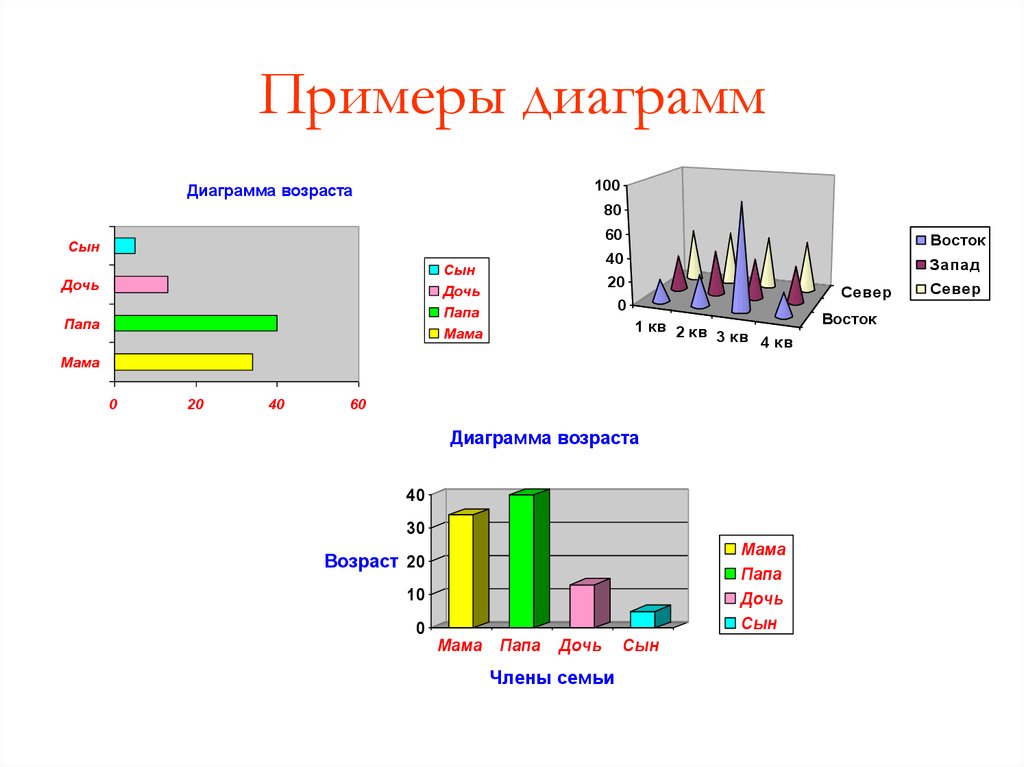

3. Гистограмма с перекосом вправо

Это гистограмма, в которой очень мало больших значений находится справа, а большая часть данных находится на левой стороне. Говорят, что такие данные смещены вправо. Они также известны как распределения с положительной асимметрией.

Пример 1

На сложных экзаменах всегда трудно получить отличные оценки, чтобы сказать больше 90%. Однако многим учащимся удается получить хорошие оценки.

Пример 2

Обычно существует очень большая разница между богатыми, средними и бедными людьми. Богатство людей в стране сосредоточено в руках немногих, а остальное население живет в условиях нехватки денег. Его естественная граница находится в нуле. График в обоих случаях будет примерно таким, как показано ниже:

4. Гистограмма с перекосом влево

Это гистограмма, в которой очень мало больших значений находится слева, а большая часть данных находится справа. Такие данные называются перекошенными влево.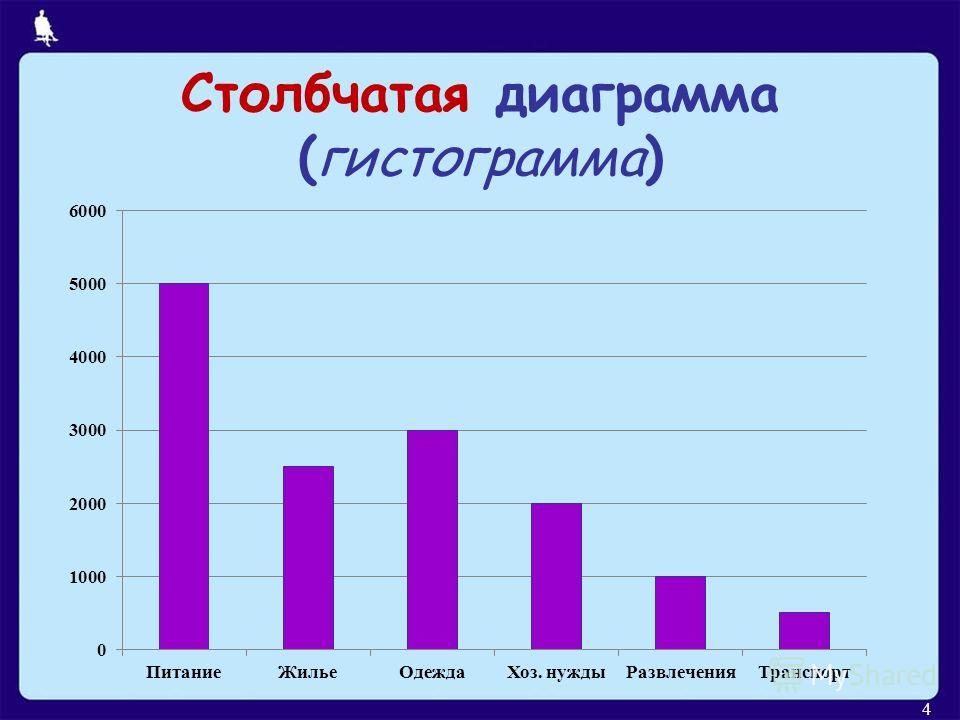 Они также известны как распределения с отрицательной асимметрией . Это потому, что есть длинный вытянутый хвост в отрицательном направлении.

Пример 1

В любом обычном офисе сотрудники, как правило, пьют меньше чая или кофе, но с приближением позднего часа их усталость возрастает, и они склонны пить больше чая и кофе. Такие данные могут быть представлены гистограммой с перекосом влево, как показано на графике ниже.

Пример 2

В компании много сотрудников с должностями высшего, среднего и оперативного уровня.
Их зарплата также варьируется таким же образом. График для тех же данных будет примерно похож на приведенную ниже гистограмму:

5. Мультимодальная гистограмма

На гистограмме мультимодальное распределение показано как непрерывное распределение вероятностей с двумя или более модами. В мультимодальной гистограмме мы узнаем, что выборка или данные не являются однородными, а наблюдение или вывод представляют собой перекрывающееся распределение.

Пример 1

Предположим, среди 50 молодых людей поколения миллениалов проводится опрос о том, за чем они в настоящее время следят в GOT, Marvels, DC, IPL, предстоящем чемпионате мира, ответ может быть крайним из двух или более.

Пример 2

Хорхе, управляющий филиалом, решил работать в то время, когда любой клиент ожидает выполнения своей работы в банке. После опроса 10 клиентов он получил результат 5, 8, 20, 10, 3, 6, 12, 25, 9, 11 (в мин.). Графическое распределение тех же данных будет примерно похоже на приведенную ниже гистограмму:

6. Симметричная гистограмма

В гистограмме, если они имеют одинаковую форму с обеих сторон носителя, данные симметричны. Две стороны выглядят одинаково, если гистограмма складывается между ними.
Итак, асимметричное распределение — это распределение данных, при котором одна из двух половин является зеркальным отражением другой половины.

Пример 1

Если мы проведем обследование среди 25 мужчин для измерения их веса и роста, данные часто будут следовать схеме симметричного распределения. Данные большинства людей будут находиться в пределах определенного количества типичных значений с небольшими крайностями в любом направлении.

Пример 2

Предположим, XUZ Pvt. Ltd — это компания, в которой каждый 15 сотрудников тратит на обед эти деньги: 10, 5, 15, 23, 7, 9, 11, 18, 13, 4, 12, 8, 15, 3, 8,5 долларов. График для тех же данных будет похож на график ниже.

Заключение – Примеры гистограммы

Гистограмма обеспечивает визуальную интерпретацию числовых данных. Это делается путем отображения количества точек данных, которые попадают в указанный диапазон значений, известный как бины. Итак, мы видим, что примеров гистограмм из нашей повседневной жизни может быть бесчисленное множество. Из одного и того же набора данных может быть много гистограмм с разными целями и ситуациями. Гистограмма — очень полезный инструмент для интерпретации базы данных.

Гистограмма очень важна, так как она отображает большой объем данных и частоту значений данных. Также медиану и распределение данных можно определить по гистограмме. Кроме того, он может показывать выбросы или пробелы в данных, если таковые имеются. Диаграммы гистограмм передают информацию о наборе данных быстрее, чем таблицы.

Рекомендуемые статьи

Это руководство по примерам гистограмм. Здесь мы обсудили 6 лучших практических примеров графиков гистограмм с подробным объяснением. Вы также можете просмотреть другие наши рекомендуемые статьи, чтобы узнать больше —

1. Примеры монополистической конкуренции
2. Топ 7 реальных примеров глобализации
3. Примеры ценных бумаг, удерживаемых до погашения
4. Пример оценки риска

1.6.2 — Гистограммы | СТАТ 500

Если имеется много точек данных и мы хотели бы увидеть распределение данных, мы можем представить данные с помощью гистограммы частот или гистограммы относительных частот

.

Гистограмма похожа на гистограмму, но предназначена для количественных данных. Для создания гистограммы данные необходимо сгруппировать по интервалам классов. Затем создайте подсчет, чтобы показать частоту (или относительную частоту) данных в каждом интервале. Относительная частота — это частота в определенном классе, деленная на общее количество наблюдений. Столбцы имеют ширину, равную интервалу классов, и высоту, соответствующую частоте (или относительной частоте).

Пример гистограммы

Джессика взвешивается каждую субботу в течение последних 30 недель. В таблице ниже показан ее зарегистрированный вес в фунтах.

135	137	136	137	138	139
140	139	137	140	142	146
148	145	139	140	142	143
144	143	141	139	137	138
139	136	133	134	132	132

Создайте гистограмму ее веса.

---

Ответ

Для гистограмм обычно требуется от 5 до 20 интервалов. Поскольку диапазон данных составляет от 132 до 148, удобно иметь класс шириной 2, так как это даст нам 9интервалы.

• 131,5-133,5
• 133,5-135,5
• 135,5-137,5
• 137,5-139,5
• 139,5-141,5
• 141,5-143,5
• 143,5-145,5
• 145,5-147,5
• 147,5-149,5

Причина, по которой мы выбрали конечные точки как 0,5, состоит в том, чтобы избежать путаницы, принадлежит ли конечная точка интервалу слева от нее или интервалу справа от нее. Альтернативой является указание соглашения о конечной точке. Например, Minitab включает левую конечную точку и исключает правую конечную точку.

Имея интервалы, можно построить таблицу частот, а затем нарисовать гистограмму частот или получить гистограмму относительных частот, чтобы построить гистограмму относительных частот. Следующая гистограмма создается программой Minitab, когда мы указываем средние точки для определения интервалов в соответствии с интервалами, выбранными выше.

Гистограмма пример: Семь основных инструментов контроля качества