Гистограмма в Эксель: как создать, график, условия
Microsoft Office Excel предназначен для создания таблиц с большим количеством информации, с которой можно проводить различные математические операции. Иногда провести качественный анализ данных из-за большого объема достаточно трудно. Необходимо графическое отображение информации. В редакторе существует несколько видов диаграмм, и сегодня подробно рассмотрим, что собой представляет гистограмма в excel.
Содержание
- Создание
- Настройка графика
- Примеры графиков
Создание
Гистограмма это один из способов представления информации по данным таблицы в виде прямоугольников одинаковой ширины, высота которых отражает различие между числами. Рассмотрим, как сделать простейшую столбчатую диаграмму:
- Заполняете таблицу цифрами, которые необходимо будет проанализировать. Для примера возьмем расход топлива для четырех машин в нескольких гаражах на одном предприятии.
- Выделяете диапазон вместе с заголовками строк и столбцов, затем переходите во вкладку Вставка на Панели инструментов, ищете кнопку гистограмма и из выпадающего списка выбираете нужный шаблон.

- В итоге получилась гистограмма с группировкой данных по гаражам:
Настройка графика
Для форматирования полученной диаграммы в редакторе существует три дополнительные вкладки: конструктор, макет, формат.
Внутри первой вкладки можно изменить тип диаграммы, блок работы с данными, готовые макеты, где уже заложены различные сочетания настроек, а также набор стилей, которые отвечают за цветовое оформление гистограммы.
Также панель содержит интересную функцию – перемещение. Она позволяет размещать диаграмму на том же рабочем листе или на отдельной страничке внутри книги без потери связи с исходной таблицей данных.
Второй дополнительный ярлык содержит меню вставки дополнительных объектов, блок подписи диаграммы, осей, а также создания легенды, поле работы с осями и сеткой, настройки фона графика, если он есть, а также инструменты анализа данных, которые показывают зависимость в виде одной черты поверх основной диаграммы.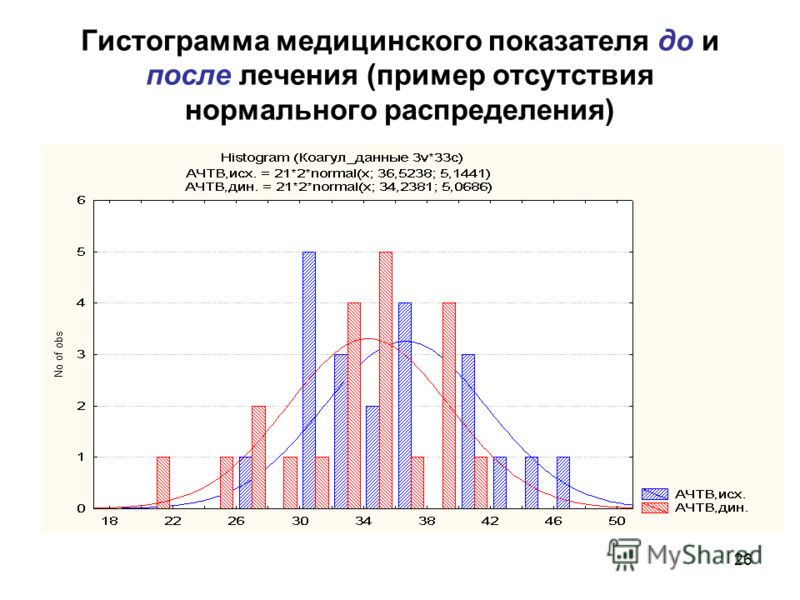
Последняя вкладка Формат позволяет настраивать фигуры, объекты WordArt, а также определять порядок группировки диаграмм и их размеры.
Как видите, Excel содержит большой набор инструментов для редактирования и форматирования гистограмм.
Примеры графиков
Рассмотрим практическое использование столбчатых графиков. Такой вид отображения данных получил широкое применение в статистике.
- Гистограмма распределения позволяет анализировать числовые ряды с выделением пика. При этом графики могут отображать зависимость по одной из математических функций: логарифмической, экспоненциальной, гамма-функции и прочие. Для примера покажем гистограмму нормального распределения.
- Гистограмма частот представляет собой ступенчатую фигуру, в основании которой находятся равные интервалы, а высоту каждого отрезка формирует частота.
- Диаграмма с накоплением нужна для отображения соотношения между двумя периодами, то есть показывает графическую разность между первым и последним значением за определенный промежуток времени.
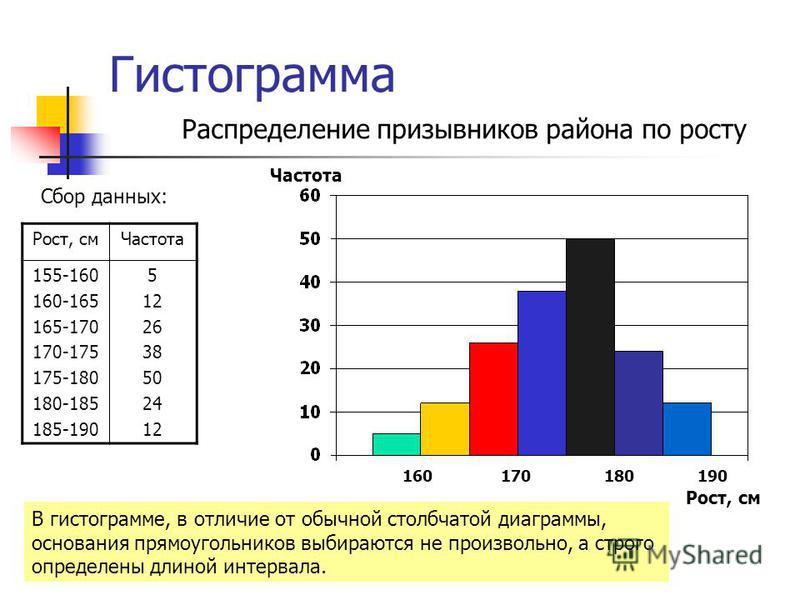 Отлично подходит для анализа изменения объема товарно-материальных ценностей на складах. Для упрощения создания такой гистограммы в excel есть готовый шаблон.
Отлично подходит для анализа изменения объема товарно-материальных ценностей на складах. Для упрощения создания такой гистограммы в excel есть готовый шаблон.
Как видите, гистограммы помогают проводить качественный анализ информации в графическом виде, при этом excel имеет большой набор инструментов для настройки диаграммы, что позволяет представить данные в любом удобном для пользователя формате.
Гистограмма | Кинезиолог
Краткое описание:
Библиографическая ссылка для цитирования: Сазонов В.Ф. Законы распределения случайных величин [Электронный ресурс] // Кинезиолог, 2009-2021: [сайт]. Дата обновления: 27.10.2021. URL: https://kineziolog.su/content/gistogramma(дата обращения: __.__.20__). _________________________Что такое гистограмма и как она строится.
Примеры построения гистограмм с использованием различных формул для определения количества групп Перейти
Онлайн-калькулятор для автоматического построения диаграммы по данным своего исследования Перейти
Что такое гистограмма
Гистограмма является наглядным отображением метода группировки, то есть распределения множества результатов измерений какой-либо величины по группам, в соответствии с существенным для данной группы признаком.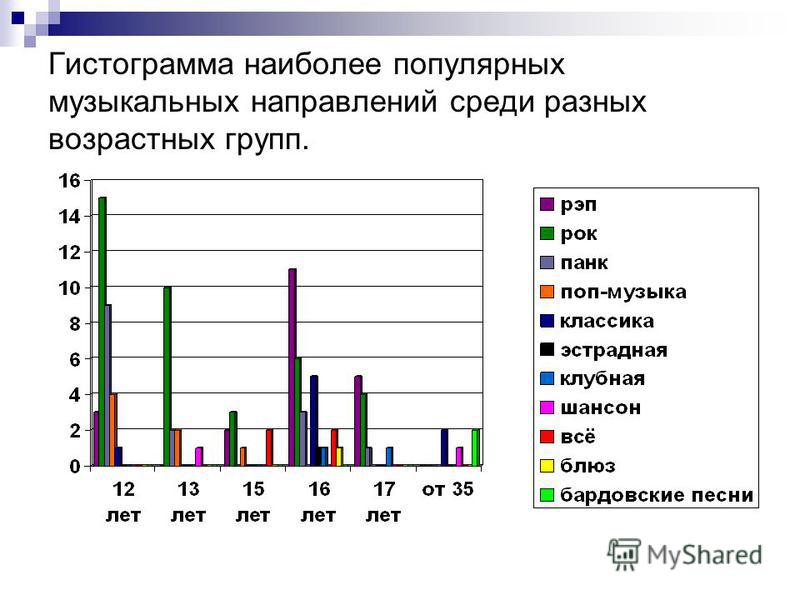 Методы группировки широко применяются для обработки первичных данных.
Методы группировки широко применяются для обработки первичных данных.
Рисунок. Пример гистограмм. Источник изображения: https://planetcalc.ru/484/
Под первичными данными в статистике мы понимаем статистические ряды, которые называют рядами динамики, если речь идет об изменении явления во времени, либо рядами распределения, если речь идет о составе или структуре исследуемого явления.
Если речь идет о рядах, построенных на основе качественных признаков (например, предприятия по формам собственности), то такие ряды называются атрибутивными, если ряды построены по количественным признакам (например, предприятия по объему товарооборота), то они называются вариационными.
В зависимости от прерывности вариации признака различают дискретные и интервальные вариационные ряды.
Гистограмма представляет собой столбчатую диаграмму, построенную по полученным данным, которые разбиваются на несколько групп.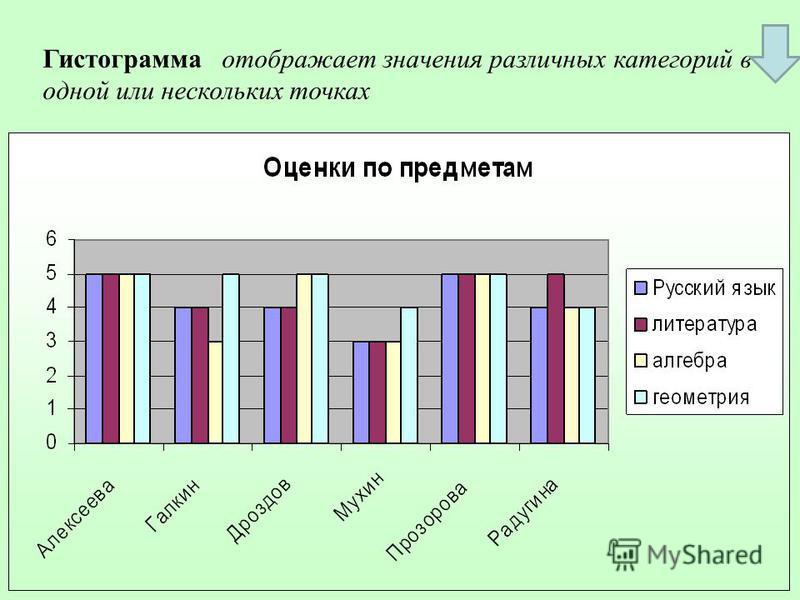 Число данных, попавших в каждую группу (частота), выражается высотой столбика, соответствующего данной группе.
Число данных, попавших в каждую группу (частота), выражается высотой столбика, соответствующего данной группе.
Гистограмму можно строить для любых рядов, при этом, если это атрибутивный либо дискретный вариационный ряд (например, число рабочих в каждом тарифном разряде), то число выделяемых групп равно числу вариантов значений признака. В случае же интервального вариационного ряда число групп будет зависеть от величины интервала, используемого для группировки данных.
Интервал — разница между максимальным и минимальным значениями признака в каждой группе. Понятно, что чем больше групп, тем меньше интервал и наоборот. Группы в таком случае иногда называют также классами интервалов.
Например, можно разбить полученные данные о численности рабочих на предприятиях на следующие группы:
до 25 человек,
25–50 человек,
50–100 человек,
свыше 100 человек.
Тогда гистограмма будет содержать 4 столбика, высота которых будет соответствовать числу предприятий попавших в данную группу.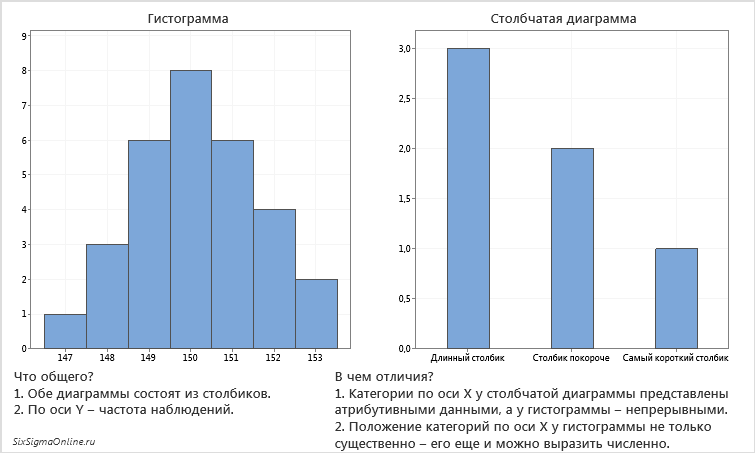
Заметим, кстати, что вышеприведенное распределение является примером использования неравных интервалов, выделенных, что называется, программой исследования, т. е. нами самими.
Вопрос выбора величины интервала (числа групп), используемого для группировки элементов интервального вариационного ряда, далеко не праздный. Помимо того, что гистограмма является отличным средством визуализации данных, она также является ни чем иным, как приближением функции распределения вероятности (см. картинку). Т. е. величина столбика каждой группы показывает вероятность того, что следующее значение измеряемой величины попадет в данную группу.
Слишком большое число групп может дать слишком «скачущий» график, слишком малое – слишком «сглаженный». В идеале, очевидно, хотелось бы иметь число групп, дающее наименьшее отклонение от функции распределения вероятности, т. е. позволяющее дать наиболее точную оценку настоящей функции распределения вероятности изучаемого явления.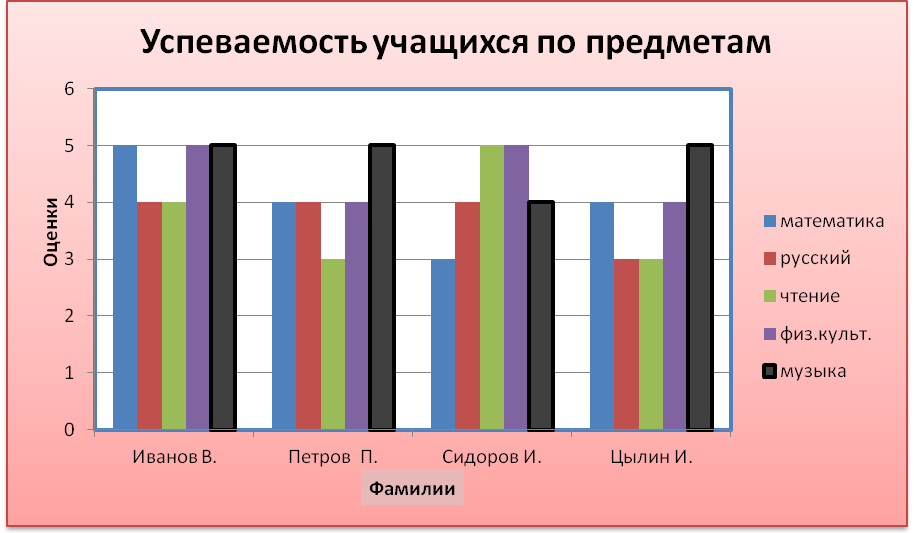
В общем, математики этим занялись.
Первым, по всей видимости, был Стерджесc (Sturges, 1926). Он рассмотрел идеализированную частотную гистограмму из k классов, где i-ое значение было равно биномиальному коэффициенту . При достаточно больших k форма гистограммы приближалась к форме нормального распределения. Сумма всех значений была равна
.
Таким образом, для n результатов измерений величины, подчиняющейся нормальному распределению, число классов, используемых при построении гистограммы следует брать как и форма полученной гистограммы будет приближаться к форме нормального распределения для достаточно большого k. Это и есть формула Стерджесса. В этом виде она попала практически во все учебники по статистике.
Формула эта в настоящее время подвергается критике как раз за то, что она явным образом использует биномиальное распределение для аппроксимации нормального распределения, что не всегда применимо. Считается, что эта формула позволяет строить удовлетворительные гистограммы при числе измерений менее 200.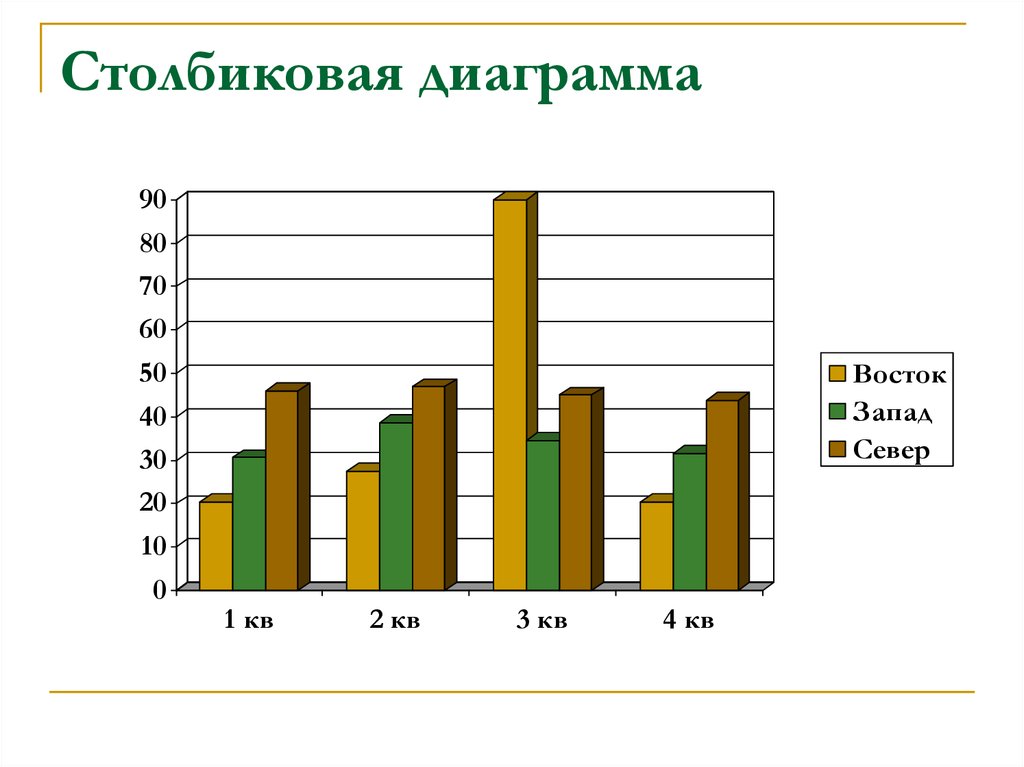
Существует целый ряд альтернативных формул, некоторые из которых вычисляют длину интервала, после чего определяется число требуемых классов (см. здесь).
Рассмотрим пару таких формул:
Формула Скотта (Scott, 1979)
, где h — длина интервала, s — стандартное отклонение значений ряда измерений
Формула Фридмана Диакониса (Freedman and Diaconis, 1981)
, где h — длина интервала, (IQ) — разница между верхним и нижним квартилем.
Эти формулы довольно просты и обоснованы статистической теорией, и считаются предпочтительнее формулы Стерджесса.
Источники:
https://planetcalc.ru/484/
Определение, примеры, части, построение графика, типы, применение
Введение
Статистика — это раздел математики, который занимается изучением сбора, анализа, интерпретации, представления и организации данных определенным образом. Другими словами, статистика — это раздел математики, который вращается вокруг сбора данных. После сбора данных мы должны найти способы сжать их в табличной форме, чтобы изучить их характерные черты. Такое расположение называется представлением данных. Одной из таких форм представления данных являются гистограммы. Что такое гистограмма и как она используется для представления, интерпретации и анализа данных? Давайте узнаем.
После сбора данных мы должны найти способы сжать их в табличной форме, чтобы изучить их характерные черты. Такое расположение называется представлением данных. Одной из таких форм представления данных являются гистограммы. Что такое гистограмма и как она используется для представления, интерпретации и анализа данных? Давайте узнаем.
Прежде чем мы узнаем больше о гистограммах, давайте вспомним, что мы подразумеваем под частотой, поскольку она является неотъемлемой частью понимания гистограмм.
Распределение частот
Таблица частот или распределение частот – это метод представления необработанных данных в форме, из которой можно легко понять информацию, содержащуюся в необработанных данных. Эта таблица частот показывает, сколько раз переменная встречается в необработанных данных. Давайте разберемся на примере.
Пример
Ниже указан возраст 25 учащихся 8 класса школы. Узнайте частоту каждого класса.
15, 16, 16, 14, 17, 17, 16, 15, 15, 16, 16, 17, 15, 16, 16, 14, 16, 15, 14, 15, 16, 16, 15, 14, 15
Решение
Были даны следующие данные о возрасте 25 учащихся 8 класса школы
15, 16, 16, 14, 17, 17, 16, 15, 15, 16, 16 , 17, 15, 16, 16, 14, 16, 15, 14, 15, 16, 16, 15, 14, 15
Нам нужно найти частоту каждого класса.
Сначала приведем данные в табличную форму. Мы видим, что есть 4 ученика в возрасте 14 лет, а есть 8 учеников в возрасте 15 лет. Точно так же мы можем видеть, что есть 10 учеников в возрасте 16 лет, а есть 3 ученика в возрасте 17 лет. Следовательно, 4 — это частота для 14-летнего возраста 8 – частота для 15-летнего возраста, 10 – частота для 16-летнего возраста и 17 – частота для 17-летнего возраста. Представив эти данные в виде таблицы, мы будем иметь,
| Age | Frequency |
| 14 | 4 |
| 15 | 8 |
| 16 | 10 |
| 17 | 3 |
Выше приведена необходимая таблица частот для заданных данных.
Определение
Гистограмма представляет собой графическое представление распределения данных. Другими словами, гистограмма — это диаграмма, отображающая распределение значений числовой переменной в виде ряда столбцов. Наборы прямоугольников, расположенных рядом друг с другом, используются для построения гистограмм, в которых каждый столбец представляет собой тип данных.
Давайте разберемся на примере.
Пример
В следующей таблице приведено число учащихся VI класса в школе в течение академических лет в 1996 году — 97–2001 — 2001 год.
| Академический год | 1996 — 97 | 1997 — 98 | 1996 — 97 | 1997 — 98 | 1996 — 971997 — 98 | 1996 — | 1997 — 98 | 1996 — | 1997 — 98 | 1998 — 99 | 1999 — 2000 | 2000 — 2001 | ||
| Количество студентов | 50 | 75 | 80 | 150 | 75 | 80 | 150 | 75 | 80 | 150 | 80 | 150 | 120 |
Представьте приведенные выше данные в виде гистограммы.
Solution
We have been given the data –
| Academic Year | 1996 – 97 | 1997 – 98 | 1998 – 99 | 1999 – 2000 | 2000 – 2001 |
| Количество студентов | 50 | 75 | 80 | 150 | 120 |
Для этих данных необходимо подготовить гистограмму. По оси x отложим годы, а по оси y количество учащихся. Гистограмма для этих данных должна быть –
Давайте разберемся в различных частях гистограммы.
Части гистограммы
Гистограмма состоит из многих частей. Полную гистограмму составляют следующие части:
Заголовок . Заголовок — самая важная часть гистограммы. Описание гистограммы, например, о чем она, все заявлено в заголовке.
ось x – ось x – это горизонтальная ось гистограммы, которая описывает интервалы классов, на которые были разделены частоты.
y – ось – ось y – это вертикальная ось гистограммы, описывающая диапазон частот гистограммы.
Полосы — Полосы представляют собой прямоугольники, представляющие количество раз, когда значения встречались в интервале. Покрываемый интервал представлен шириной полосы.
Теперь научимся строить гистограмму.
Как построить гистограмму?
Ниже приведены шаги, необходимые для построения гистограммы для заданного набора данных –
- Выбор подходящего масштаба для представления весов по горизонтальной оси или по оси X является первым шагом. Это также может быть выражено в виде обозначения интервалов классов по оси абсцисс.
- Следующим шагом является выбор подходящего масштаба для представления частот по вертикальной оси или по оси Y. Это также может быть выражено в виде обозначения интервалов классов по оси ординат.
- Важно отметить, что на двух предыдущих шагах интервалы классов должны быть исключительными.
- Следующий шаг включает в себя рисование полос, соответствующих каждому из заданных весов, используя их частоты. Эти полосы рисуются путем построения прямоугольников с основаниями в качестве интервалов классов и соответствующими частотами в качестве высот.
- Так как по горизонтальной оси отмечены границы классов, а по вертикальной — частоты, то на каждом интервале классов строится прямоугольник.
- Между двумя последовательными стержнями не должно быть зазора.
Давайте разберем вышеописанные шаги на примере.
Пример
Предположим, учитель хочет проанализировать успеваемость двух групп учащихся по математике. Посмотрев на их выступления, она обнаружила, что некоторые студенты набрали менее 20 баллов, а некоторые другие набрали 70 баллов и выше. Поэтому она решила сгруппировать их в интервалы разного размера следующим образом:
| Оценки | Количество студентов |
| 0 – 20 | 7 |
| 20 – 30 | 10 |
| 30 – 40 | 10 |
| 40 – 50 | 20 |
| 50 – 60 | 20 |
| 60 — 70 | 15 |
| 70 выше | 8 |
| Всего | 9042 |
CRATIOR CREATE AISTOGRAM.
Решение
Нам даны данные с неравномерным распределением интервалов классов. От нас требуется построить график гистограммы из приведенных выше данных. Поскольку интервалы классов находятся в разных пропорциях, нам придется внести некоторые изменения в представление данных. Из приведенных выше данных мы можем заметить, что если размер класса равен 20, длина прямоугольника равна 7. Это означает, что когда размер класса равен 10, длина прямоугольника будет 720 x 10 = 3,5. Аналогичным образом мы можем изменить данную таблицу следующим образом –
| Marks | Number of Students | Width of the Class | Length of the Class |
| 0 – 20 | 7 | 20 | 3.5 |
| 20 – 30 | 10 | 10 | 10 |
| 30 – 40 | 10 | 10 | 10 |
| 40 – 50 | 20 | 10 | 20 |
| 50 – 60 | 20 | 10 | 20 |
| 60 – 70 | 15 | 10 | 15 |
| 70 above | 8 | 10 | 2,67 |
| Итого | 90 |
Используя эту таблицу, теперь можно создать гистограмму как – гистограмма.
Характеристики гистограммы
Ниже приведены общие характеристики гистограммы –
- Гистограмма используется для отображения непрерывных данных в виде категорий.
- В гистограмме нет промежутков между столбцами, в отличие от гистограммы.
- Ширина полос одинакова.
- Масштабы горизонтальной и вертикальной осей не обязательно должны начинаться с 0.
Распространенная ошибка, которая часто возникает при использовании гистограммы, заключается в том, что ее ошибочно принимают за гистограмму. Однако гистограмма и гистограмма сильно отличаются друг от друга. Итак, каковы различия между ними? Давайте узнаем.
Гистограмма и гистограмма
Гистограмма и гистограмма обычно используются для представления частотного распределения данных. Несмотря на то, что они оба имеют некоторое сходство, у них есть и свои различия. Ниже приведены различия между гистограммой и гистограммой
| Гистограмма | 0042 |
Используется для представления статистической информации в виде полос для отображения частотного распределения непрерывных данных. | Используется для сравнения частоты, общего количества, суммы или среднего значения данных в различных классификациях с использованием горизонтальных или вертикальных полос. |
| Гистограмма представляет количественные данные | Гистограмма представляет данные по категориям |
| Между столбцами гистограммы нет пробелов. | Между столбцами гистограммы есть пробелы. |
| В гистограмме элементы сгруппированы вместе | В гистограмме элементы взяты по отдельности |
| В гистограмме ось X должна представлять только непрерывные данные, выраженные в виде чисел. | На гистограмме ось X может представлять что угодно. |
| Частота показана площадью каждого прямоугольника | Высота показывает частоту, а ширина не имеет значения. |
Types of Histograms
Based on the frequency distribution of the data, there are four types of histograms –
- Uniform histogram
- Symmetric or Bell-shaped histogram
- Bimodal histogram
- Probability histogram
Давайте узнаем об этом один за другим.
Равномерная гистограмма
Чрезвычайно совместимые данные представлены однородной гистограммой. На этой гистограмме частота каждого класса во многом связана с частотой других. Количество классов в однородной гистограмме довольно мало, и в каждом классе одинаковое количество элементов. Ниже приведено общее представление однородной гистограммы –
Симметричная гистограмма
Основной характеристикой симметричной гистограммы является то, что она имеет холмик в центре и сужение, связанное с ним, как слева, так и справа. Из-за этой характеристики симметричная гистограмма также известна как гистограмма в форме колокола. Другими словами, когда по центру гистограммы проведена вертикальная линия, а две стороны одинаковы по размеру и форме, говорят, что гистограмма симметрична. Ниже приведено общее представление симметричной или колоколообразной гистограммы –
Бимодальная гистограмма
Бимодальная гистограмма, как следует из названия, имеет два пика вместо одного. Такое представление возникает, когда в наборе данных есть наблюдения за двумя разными типами людей или объединенными группами. Другими словами, бимодальная гистограмма имеет два отдельных класса или интервала, одинаково представляющих максимальную частоту распределения. Ниже приведено общее представление бимодальной гистограммы –
Такое представление возникает, когда в наборе данных есть наблюдения за двумя разными типами людей или объединенными группами. Другими словами, бимодальная гистограмма имеет два отдельных класса или интервала, одинаково представляющих максимальную частоту распределения. Ниже приведено общее представление бимодальной гистограммы –
Гистограмма вероятности
Гистограмма вероятности используется для графического представления дискретного распределения вероятности. Каждый прямоугольник на гистограмме вероятности центрируется по значению x. Также на этой гистограмме каждый прямоугольник и вероятность соответствующего значения пропорциональны друг другу. Ниже приводится общее представление гистограммы вероятности –
Применение гистограмм
Гистограммы широко используются для различных статистических целей. Ниже приведены некоторые области, в которых гистограмма широко используется для представления частотных распределений –
Фондовая биржа
Гистограммы широко используются на фондовых биржах для идентификации различных групп инвесторов или различных мест.
Медицинские и клинические исследования
Гистограмма находит применение в медицинских и клинических исследованиях, где она используется с целью выявления наличия или отсутствия определенных состояний среди различных групп людей.
Фотография
Гистограммы используются в фотографии для обработки изображений, а также для оцифровки.
Шесть сигм
В шести сигмах гистограмма используется для изучения структуры дефектов в различных категориях образцов.
Решенные примеры
Пример 1 В следующей таблице указан срок службы 400 светодиодных ламп. Нарисуйте гистограмму для приведенных ниже данных.
| Срок службы | Количество ламп |
| 300 – 400 | 14 |
| 400 – 500 | 56 |
| 500 – 600 | 60 |
| 600 – 700 | 86 |
| 700 – 800 | 74 |
| 800 – 900 | 62 |
| 900 – 1000 | 48 |
Решение Мы получили срок службы 400 светодиодных ламп в виде следующих данных.
| Срок службы | Number of Lamps |
| 300 – 400 | 14 |
| 400 – 500 | 56 |
| 500 – 600 | 60 |
| 600 – 700 | 86 |
| 700 — 800 | 74 |
| 800 — 900 | 62 |
| 900 — 1000 | 48 |
. Мы обязаны для подготовки. В приведенных выше данных мы видим, что существует равное распределение интервалов классов. Поэтому мы можем использовать таблицу как есть для создания соответствующей гистограммы.
Гистограмма приведенных выше данных будет выглядеть следующим образом:
Пример 2 29, 27, 21, 19, 45, 14, 34, 37, 34, 23, 45, 24, 42, 8, 47, 22, 31, 17, 13, 38, 26, 3, 34, 29, 11, 22, 7, 15, 24, 38, 31, 21, 35
Подготовьте гистограмму для приведенных выше данных.
Решение Мы получили оценки, полученные 40 студентами на экзамене. Оценки –
Оценки –
27, 18, 15, 21, 48, 25, 49, 29, 27, 21, 19, 45, 14, 34, 37, 34, 23, 45, 24, 42, 8, 47, 22, 31, 17, 13, 38, 26, 3, 34, 29, 11, 22, 7, 15, 24, 38, 31, 21, 35
Для этого нам необходимо подготовить гистограмму. Мы видим, что данные представлены в необработанном виде, и нам сначала нужно определить интервалы классов и подготовить таблицу частот для данных данных. Таблица частот для этих данных будет –
| Интервал класса (диапазон оценок) | Number of Students |
| 0 – 10 | 3 |
| 10 – 20 | 8 |
| 20 – 30 | 14 |
| 30 – 40 | 9 |
| 40 — 50 | 6 |
| Всего | 40 |
Сейчас, что существует равное распределение интервалов класса, поэтому мы можем использовать таблицу, как и для создания соответствующих соответствующих. график гистограммы.
график гистограммы.
Гистограмма приведенных выше данных будет выглядеть так, как показано ниже:
Ключевые факты и сводка
- Гистограмма представляет собой диаграмму, на которой показано распределение значений числовой переменной в виде ряда столбцов.
- Таблица частот или распределение частот – это метод представления необработанных данных в форме, из которой можно легко понять информацию, содержащуюся в необработанных данных.
- Описание гистограммы, например, что она собой представляет, указано в заголовке.
- Ось x – это горизонтальная ось гистограммы, которая описывает интервалы классов, на которые были разделены частоты.
- Ось Y — это вертикальная ось гистограммы, описывающая диапазон частот гистограммы.
- Полосы — это прямоугольники, представляющие количество раз, когда значения встречались в интервале. Покрываемый интервал представлен шириной полосы.
- В зависимости от частотного распределения данных существует четыре типа гистограмм: однородная гистограмма, симметричная или колоколообразная гистограмма, бимодальная гистограмма и гистограмма вероятности.

- Чрезвычайно совместимые данные представлены однородной гистограммой.
- На симметричной гистограмме в центре имеется холмик, а сужение, связанное с ним, есть как слева, так и справа.
- Бимодальная гистограмма, как следует из названия, имеет два пика вместо одного.
- Гистограмма вероятности используется для графического представления дискретного распределения вероятности.
Гистограмма (на тему больницы) Рабочие листы по математике
Построение статистических дисплеев Рабочие листы по математике для 6-го класса
Понимание графиков в картинках и гистограмм. Рабочие листы по математике для 2-го класса
Мы тратим много времени на изучение и сбор информации на этом сайте. Если вы сочтете это полезным в своем исследовании, используйте приведенный ниже инструмент, чтобы правильно указать ссылку Helping with Math в качестве источника. Мы ценим вашу поддержку!
R Гистограмма (с примерами)
Гистограмма — это графическое отображение данных с использованием столбцов разной высоты.
Гистограмма используется для суммирования дискретных или непрерывных данных, измеренных на шкале интервалов.
Создание гистограммы в R
В R мы используем функцию hist() для создания гистограмм. Например,
температуры <- c(67 ,72 ,74 ,62 ,76 ,66 ,65 ,59 ,61 ,69 ) # гистограмма вектора температур результат <- история (температуры) print(result)
Вывод
Создать гистограмму
В приведенном выше примере мы использовали функцию hist() для создания гистограммы вектора температуры .
Гистограмма, которую мы создали выше, проста и понятна, мы можем добавить к ней так много всего.
Добавить заголовок и метку к гистограмме в R
Чтобы добавить заголовок и метку к нашей гистограмме в R, мы передаем параметр main и параметр xlab соответственно внутри функции
температуры <- c(67 ,72 ,74 ,62 ,76 ,66 ,65 ,59 ,61 ,69 ) # гистограмма вектора температур результат <- hist(температуры, main = "Гистограмма температуры", xlab = "Температура в градусах Фаренгейта" ) печать(результат)
Выход
Добавить заголовок и метку к гистограмме На приведенном выше рисунке мы видим, что мы добавили заголовок и метку к гистограмме вектора температуры .
история(температуры, main = "Максимальная температура за неделю", xlab = "Температура в градусах Фаренгейта")
Здесь,
-
main- добавляет заголовок"Максимальная температура за неделю" -
xlab- добавляет метку"Температура в градусах Фаренгейта"
Изменить цвет столбцов гистограммы в R
В R мы передаем параметр
col внутрь hist() , чтобы изменить цвет столбцов. Например,
температуры <- c(67 ,72 ,74 ,62 ,76 ,66 ,65 ,59 ,61 ,69 ) # гистограмма вектора температур результат <- hist(температуры, main = "Гистограмма температуры", xlab = "Температура в градусах Фаренгейта", столбец = "красный") печать(результат)
Вывод
Изменить цвет гистограммы В приведенном выше примере мы использовали параметр col внутри barplot() для изменения цвета столбцов.
результат <- история(температуры, .Гистограмма примеры: Семь основных инструментов контроля качества


