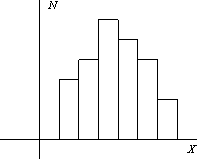ГИСТОГРАММА РАСПРЕДЕЛЕНИЯ — это… Что такое ГИСТОГРАММА РАСПРЕДЕЛЕНИЯ?
- ГИСТОГРАММА РАСПРЕДЕЛЕНИЯ
- — график распределения частот для непрерывной переменной ( также: Шкала измерительная). Предназначен для визуального представления распределения непрерывной переменной, состоит из соприкасающихся прямоугольников, основанием которых служат интервалы группировки в точных границах, а высотой — вычисленные значения плотности распределения .
Социология: Энциклопедия. — Минск: Интерпрессервис; Книжный Дом. А.А. Грицанов, В.Л. Абушенко, Г.М. Евелькин, Г.Н. Соколова, О.В. Терещенко. 2003.
- ГИПОТЕЗА
- ГЛОБАЛИЗАЦИЯ
Смотреть что такое «ГИСТОГРАММА РАСПРЕДЕЛЕНИЯ» в других словарях:
ГИСТОГРАММА — один из видов графич; представления экспериментальных данных. Г. строится следующим образом. Весь диапазон наблюденных значений X1 ,…, Х п нек рой случайной величины Xделится на kинтервалов группировки (обычно равных) точками ; подсчитывается… … Математическая энциклопедия
Гистограмма (значения) — Гистограмма: Гистограмма способ графического представления табличных данных. Гистограмма (статистика) это функция, приближающая плотность вероятности некоторого распределения, построенная на основе выборки из него. Гистограмма (фотография) это… … Википедия
Гистограмма — фигура, получающаяся на плоскости, где введены декартовы координаты и по оси абсцисс отложены группированные наблюдения, а по оси ординат число соответствующих наблюдений. Верхняя часть контура Г. есть статистический аналог плотности… … Геологическая энциклопедия
гистограмма — – это способ графического представления распределения числовых (непрерывных) данных, часто используемый в разведочном анализе данных для иллюстрации основных характеристик распределения. Диапазон возможных значений переменной делится на отрезки,… … Словарь социологической статистики
Гистограмма — (histogram) График распределения частот, который строится при помощи прямоугольников, чья площадь пропорциональна частоте нахождения данной величины в интервале, на котором построен данный прямоугольник. Бизнес. Толковый словарь. М.: ИНФРА М ,… … Словарь бизнес-терминов
ГИСТОГРАММА — (от греч. histo столб и gramma черта, буква) англ. histogram; нем. Histograma. Столбчатая диаграмма, вид графического изображения количественного распределения по к. л. признаку; обычно представляет собой совокупность смежных прямоугольников,… … Энциклопедия социологии
Гистограмма (статистика) — У этого термина существуют и другие значения, см. Гистограмма. Гистограмма в математической статистике это функция, приближающая плотность вероятности некоторого распределения, построенная на основе выборки из него. Содержание 1 Определение 2… … Википедия
Гистограмма — Пример гистограммы У этого термина существуют и другие значения, см. Гистограмма (значения). Гистограмма (от др. греч … Википедия
Гистограмма (фотография) — У этого термина существуют и другие значения, см. Гистограмма. Изображение и гистограмма на дисплее камеры. Гистограмма (в фотографии … Википедия
ГИСТОГРАММА — – 1) график, имеющий вид прямоугольников, основание которых (обычно по оси абсцисс) соответствует интервалу; в случае неравномерных интервалов и резких колебаний гистограмма предпочтительнее полигону частот; 2) столбиковая диаграмма, состоящая из … Современный образовательный процесс: основные понятия и термины
sociology_encyclopedy.academic.ru
Типы распределений и соответствующие им гистограммы | Бережливые шесть сигм | Тематический раздел | База знаний
В предыдущей статье нам удалось выделить основные характеристики числового ряда, которые можно показать с помощью гистограмм – это среднее значение популяции, разброс и функция распределения. Так как последняя характеристика зачастую представляет наибольший интерес, ее анализ и примеры некоторых, наиболее часто встречающихся распределений требуют дополнительного внимания.
Гистограмма позволяет анализировать частотное распределение числового ряда, а соответственно дает возможность выделить наиболее вероятные число или диапазон – другими словами, пик. Гистограмма с ярко выраженным пиком называется унимодальной:
Если мы можем различить у гистограммы два ярко выраженных пика, то гистограмма называется бимодальной. Во многих случаях это значит, что выборки происходят из двух разных популяций, так как наличие двух мод в одной популяции маловероятное явление:
Гистограммы с большим количеством пиков (многомодальные) встречаются крайне редко и, зачастую свидетельствуют о присутствии специальных факторов, влияющих на исследуемую систему или процесс. Если каждый интервал гистограммы содержит примерно равное количество значений, то такая гистограмма называется однородной или гистограммой равномерного распределения:
Гистограмма называется симметричной, если она имеет симметричную форму относительно центральной линии (правая и левая стороны одинаковой формы). Ассиметричные гистограммы бывают со скосом влево или вправо от осевой линии. Если левая сторона гистограммы вытянута значительно больше, чем правая (или левый «хвост” значительно длиннее правого), то говорят, что гистограмма имеет отрицательную асимметрию:
Соответственно, у гистограммы с положительной асимметрией больше в сторону выдаётся правая сторона (или правый «хвост” значительно длиннее левого):
Если наблюдаемая величина подчиняется нормальному закону распределения, гистограмма числового ряда будет иметь унимодальную симметрическую форму:
Нормальному закону распределения может подчиняться любая величина, на которую не влияют специальные факторы (например, связывающие или ограничивающие): когда она подвержена влиянию большого числа случайных помех. Считается, что из всех распределений чаще всего встречается именно нормальное.
Частным случаем нормального распределения является логарифмическое распределение. Оно является непрерывным унимодальным распределением и имеет положительную асимметрию. Этому распределению с заданной степенью приближения, подчиняется, например, размер фракций гравия, камня и т.п. Аналогичные примеры: длительность часто повторяемого события (время выполнения операции на конвейере), или размер зарплат на предприятии – как правило, значительно большее количество сотрудников имеет среднюю зарплату, но есть персонал, у которого она значительно выше (правый хвост гистограммы).
Гамма-распределение – это двухпараметрическое семейство абсолютно непрерывных распределений. Они применяются в различных отраслях экономики и техники, теории и практике испытаний надежности. В частности, гамма-распределению могут быть подчинены такие величины, как общий срок службы изделия, время наработки до k-го отказа (k = 1, 2, …, и т.д.). Также, это распределение используется в логистике для описания спроса в моделях управления запасами.
Экспоненциальное распределение – непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события. Например, время между появлениями двух последовательных клиентов (заказчиков в бизнесе или просто покупателей в магазине) будет случайной величиной с экспоненциальным распределением:
Логистическая функция распределения – по форме похожа на функцию нормального распределения, её главное предназначение – моделирование данных бинарного типа. Используется, например, в медико-биологических исследованиях для анализа эффекта различных лекарств, ядов и т.д. От нормального распределения логистическое отличается длинными «хвостами” – данными, находящимися в крайних, отдалённых от центра, позициях:
Вот далеко не полный перечень типов распределений и соответствующих им гистограмм. Внешнее отличие построенной Вами гистограммы от перевернутого колокола еще совсем не означает, что данные собраны неправильно или, что процесс нестабилен. Однако это всегда заставляет исследователя задуматься и постараться найти объяснение такому результату.
sixsigmaonline.ru
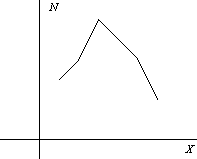
Полигон и гистограмма статистического распределения
Для наглядности статистическое распределение значения признака иллюстрируется полигоном распределения или гистограммой.
Для построения
полигона на координатной плоскости
изображают ломаную с вершинами в точках
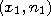 ,
,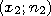 , … ,
, … ,
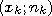 .
Движение лини полигона характеризует
частотность того или иного значения
наблюдаемого признака: чем выше очередная
вершина полигона, тем чаще наблюдалось
соответствующее ему значение в рамках
проведенного эксперимента.
.
Движение лини полигона характеризует
частотность того или иного значения
наблюдаемого признака: чем выше очередная
вершина полигона, тем чаще наблюдалось
соответствующее ему значение в рамках
проведенного эксперимента.
|
|
|
|
(a) Полигон статистического распределения |
(b) Гистограмма статистического распределения |
Гистограмма — это
ступенчатая фигура, составленная из
серии прямоугольников. Основаниями
прямоугольников гистограммы служат
отрезки
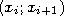 ,
а высотами — отрезки
,
а высотами — отрезки .
Высоты прямоугольников гистограммы
демонстрируют частотность значений
наблюдаемого признака: чем выше
прямоугольник, тем чаще соответствующий
признак наблюдался в рамках проведенного
исследования.
.
Высоты прямоугольников гистограммы
демонстрируют частотность значений
наблюдаемого признака: чем выше
прямоугольник, тем чаще соответствующий
признак наблюдался в рамках проведенного
исследования.
При изучении
непрерывно изменяющегося признака для
построения полигона выбирают точки
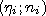 ,
где
,
где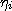 —
это середина отрезка
—
это середина отрезка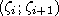
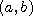 ,
в пределах которого изменяется наблюдаемый
признак. Для построения гистограммы в
непрерывном случае в качестве оснований
гистограммы используют отрезки разбиения
,
в пределах которого изменяется наблюдаемый
признак. Для построения гистограммы в
непрерывном случае в качестве оснований
гистограммы используют отрезки разбиения .
. Значение репрезентативности выборки для статистического распределения
Если выборка для
проведения исследования является
репрезентативной, то полученные данные
о статистическом распределении признака
дает достаточно точное представление
о распределении признака в генеральной
совокупности. Следует иметь в виду, что
увеличение объема выборки всегда
приводит к повышению ее репрезентативности,
таким образом, чем больше объем выборки
 ,
тем точнее выборочное распределение
отражает действительное состояние дел.
,
тем точнее выборочное распределение
отражает действительное состояние дел.
Примеры статистических распределений Пример с делением испытуемыми данного отрезка на две части внутренней точкой
В двух словах, эксперимент состоял в следующем: двум группам испытуемых экспериментальной (группа студентов-дизайнеров) и контрольной (группа студентов-инженеров), в качестве задания предлагалось:
изобразить на стандартном листе бумаги отрезок прямой линии произвольно,
разместить на этом отрезке одну точку произвольно,
вычислить коэффициент отношения меньшего из получившихся отрезков к большему.
В результате каждый испытуемый демонстрировал некоторый числовой показатель k, заключенный между нулем и единицей. Экспериментальная гипотеза состояла в том, что дизайнеры продемонстрируют больший разброс значений этого показателя, причем, разница окажется статистически значимой.
Здесь мы подробно разберем ряд действий, связанных с анализом данных в контрольной группе.
В испытании принимали участие 50 студентов факультета инженерных систем и природоохранного строительства Самарского государственного архитектурно-строительного университета. Стало быть — объем выборочной совокупности равен 50.
Испытуемыми были продемонстрированы следующие результаты (код испытуемого составлен из его инициалов, коэффициент k вычисляется как отношение длины меньшего из получившихся отрезков к длине большего из них).
|
№ |
Код |
Значение |
|
1 |
К. О. |
0,174 |
|
2 |
Л. Д |
0,666 |
|
3 |
Б. О |
0,625 |
|
4 |
Н. Е. |
0,455 |
|
5 |
Х. А. |
0,614 |
|
6 |
М. У. |
0,286 |
|
7 |
П. Р. |
0,417 |
|
8 |
К. А. |
0,591 |
|
9 |
Р. О. |
0,750 |
|
10 |
М. А. |
0,429 |
|
11 |
П. У. |
0,500 |
|
12 |
М. А. |
0,250 |
|
13 |
Р. А. |
0,391 |
|
14 |
Т. О. |
0,750 |
|
15 |
С. Т. |
0,504 |
|
16 |
Я. В. |
0,750 |
|
17 |
Б. Е. |
0,542 |
|
18 |
С. Е. |
0,771 |
|
19 |
Ч. Е. |
0,545 |
|
20 |
П. О. |
0,578 |
|
21 |
И. С. |
0,750 |
|
22 |
Б. А. |
0,330 |
|
23 |
Ш. Б. |
0,299 |
|
24 |
Я. Р. |
0,780 |
|
25 |
П. П. |
0,528 |
|
26 |
Ф. И. |
0,200 |
|
27 |
К. О. |
0,449 |
|
28 |
Н. Е. |
0,429 |
|
29 |
К. Р. |
0,500 |
|
30 |
К. Ан. |
0,659 |
|
31 |
Л. А. |
0,482 |
|
32 |
М. А. |
0,551 |
|
33 |
Д. М. |
0,414 |
|
34 |
С. О. |
0,638 |
|
35 |
Ш. А. |
0,328 |
|
36 |
О. Т. |
0,586 |
|
37 |
К. О. |
0,400 |
|
38 |
Е. Л. |
0,504 |
|
39 |
Р. Я. |
0,621 |
|
40 |
С. О. |
0,323 |
|
41 |
У. Т. |
0,635 |
|
42 |
М. Р. |
0,472 |
|
43 |
К. О. |
0,450 |
|
44 |
Ш. О. |
0,380 |
|
45 |
М. В. |
0,500 |
|
46 |
К. И. |
0,659 |
|
47 |
Ш. Е. |
0,355 |
|
48 |
А. С. |
0,684 |
|
49 |
Т. Е. |
0,695 |
|
50 |
Ч. А. |
0,526 |
Итак, коэффициент деления отрезка k — это непрерывная случайная величина, принимающая значения из отрезка от 0 до 1. Каждому наблюдаемому значению k поставить в соответствие его наблюдаемую частоту, конечно, можно, однако это не охарактеризует распределение генеральной совокупности: большинство частот окажутся равными между собой, так как большинство наблюдаемых значений встречается в рамках эксперимента не более одного раза.
Поэтому для построения статистического распределения разделим отрезок возможных значений коэффициента k на 5 равных частей и сгруппируем наблюдаемые значения по факту принадлежности тому или иному промежутку. Прежде всего следует упорядочить полученные значения:
|
№ |
Код |
Значение |
|
1 |
К. О. |
0,174 |
|
2 |
Ф. И. |
0,200 |
|
3 |
М. А. |
0,250 |
|
4 |
М. У. |
0,286 |
|
5 |
Б. А. |
0,299 |
|
6 |
С. О. |
0,323 |
|
7 |
Ш. А. |
0,328 |
|
8 |
Б. А. |
0,330 |
|
9 |
Ш. Е. |
0,355 |
|
10 |
Ш. О. |
0,380 |
|
11 |
Р. О. |
0,391 |
|
12 |
К. С. |
0,400 |
|
13 |
Д. М. |
0,414 |
|
14 |
П. Р. |
0,417 |
|
15 |
М. А. |
0,429 |
|
16 |
Н. Е. |
0,429 |
|
17 |
К. З. |
0,449 |
|
18 |
К. О. |
0,450 |
|
19 |
Н. Е. |
0,455 |
|
20 |
Р. Н. |
0,472 |
|
21 |
Л. А. |
0,482 |
|
22 |
М. А. |
0,500 |
|
23 |
К. Р. |
0,500 |
|
24 |
П. У. |
0,500 |
|
25 |
С. Т. |
0,504 |
|
26 |
Е. Л. |
0,504 |
|
27 |
Ч. А. |
0,526 |
|
28 |
П. А. |
0,528 |
|
29 |
Б. Е. |
0,542 |
|
30 |
Ч. Е. |
0,545 |
|
31 |
М. А. |
0,551 |
|
32 |
О. Т. |
0,568 |
|
33 |
П. Е. |
0,578 |
|
34 |
К. А. |
0,591 |
|
35 |
Р. Я. |
0,621 |
|
36 |
У. Т. |
0,635 |
|
37 |
С. О. |
0,638 |
|
38 |
Б. О. |
0,652 |
|
39 |
К. И. |
0,659 |
|
40 |
К. А. |
0,659 |
|
41 |
Л. Д. |
0,666 |
|
42 |
Т. Е. |
0,684 |
|
43 |
А. С. |
0,695 |
|
44 |
П. О. |
0,750 |
|
45 |
Р. О. |
0,750 |
|
46 |
И. С. |
0,750 |
|
47 |
Я. В. |
0,750 |
|
48 |
С. Е. |
0,771 |
|
49 |
Т. О. |
0,775 |
|
50 |
Я. Р. |
0,780 |
Все наблюдаемые значения сосредоточены в интервале от 0,174 до 0,780. Разделим этот интервал на 5 равных частичных интервалов и подсчитаем частоты попаданий k в эти частичные интервалы:
|
Интервал |
0,1740– – 0,2952 |
0,2952– –0,4164 |
0,4164– – 0,5376 |
0,5376– – 0,6588 |
0,6588– –0,7800 |
|
Частота |
4 |
9 |
15 |
10 |
12 |
Полученная таблица и есть статистическое распределение наблюдаемого признака (коэффициента деления отрезка). Используя относительные частоты вместо частот, можно записать его в виде:
|
Интервал |
0,1740– –0,2952 |
0,2952– –0,4164 |
0,4164– –0,5376 |
0,5376– –0,6588 |
0,6588– – 0,7800 |
|
Относительная частота |
0,08 |
0,18 |
0,30 |
0,20 |
0,24 |
Для большей наглядности полученные данные о распределении признака k можно изобразить в виде гистограммы. При этом мы используем относительные частоты распределения, так как в этом случае вертикальные значения гистограммы не зависят от объема выборки, они заведомо не превосходят 1.
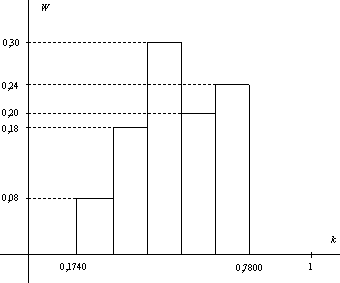
Гистограмма распределения коэффициента деления отрезка.
Аналогично исследуется распределение коэффициента k, в экспериментальной группе (группе студентов-дизайнеров).
studfile.net
Полигон и гистограмма | matematicus.ru
Гистограмма представляет собой ступенчатую фигуру в виде прямоугольников. Длина каждого прямоугольника представляет собой равный одинаковый частотный интервал и вычисляется по формуле:
xi-xi-1
Высоты гистограммы определяется по формуле:
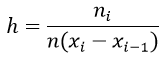
Формула размаха выборки R:
R=xmax−xmin
Количество интервалов в выборке определяется по формуле:
k≈1+log2n≈1+3,221·lgn
Длина l интервала гистограммы, формула:
l=R/n
Формула эмпирической плотности распределения выборки имеет вид:
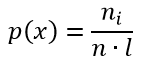
хi — значения частот;
ni— частоты;
wi — относительные частоты;
n — объём выборки;
В водоёме проведены измерения температуры воды в течение 20 дней.
Статистика отчета измерений:
11, 15, 18, 14, 12, 13, 11, 14, 18, 19, 18, 14, 15, 16, 14, 18, 21, 17, 13, 16
Построить гистограмму относительных, абсолютных и накопленных частот выборки, вычислить эмпирическую плотность распределения частот.
Решение.
По условию задачи объем выборки равен 20.
Отсортируем и упорядочим вариационный ряд, начиная от самого минимального значения, получим:
11, 11, 12, 13, 13, 14, 14, 14, 14, 15, 15, 16, 16, 17, 18, 18, 18, 18, 19, 21
Найдем размах выборки
R=21-11=10
Количество интервалов в выборке равно:
k≈log220+1≈5,32
Округляя до целого числа, имеем
k=5
Определим длину каждого интервала
l=10/5=2
Получаем таблицу интервалов
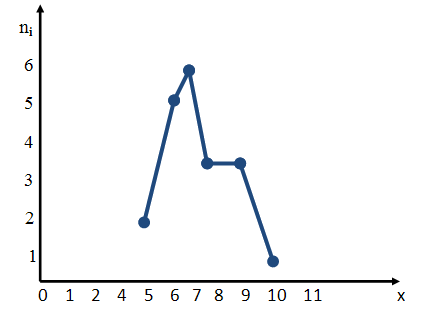
| Номер интервала | Абсолютная частота, ni | Частотный интервал |
| 1. | 3 | [11;13) |
| 2. | 6 | [13;15) |
| 3. | 4 | [15;17) |
| 4. | 5 | [17;19) |
| 5. | 2 | [19;21) |
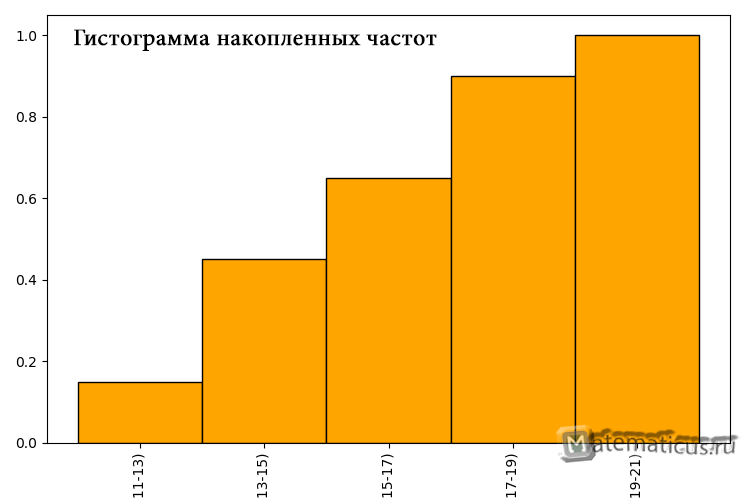
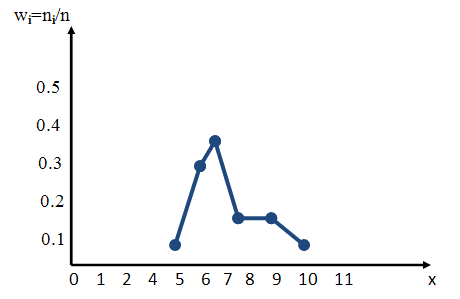
Таблица относительных частот и эмпирическая плотность распределения частоты
| Частотный интервал | Относительная частота, wi=ni/n | Эмпирическая плотность распределения частоты ni/Δ |
| [11;13) | 0.15 | 1.5 |
| [13;15) | 0.3 | 3 |
| [15;17) | 0.2 | 2 |
| [17;19) | 0.25 | 0.25 |
| [19;21) | 0.1 | 0.1 |
График гистограммы абсолютных частот
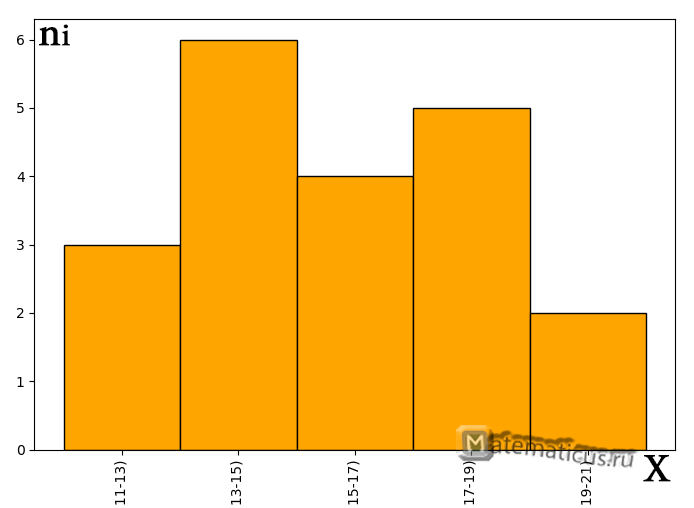
График гистограммы относительных частот
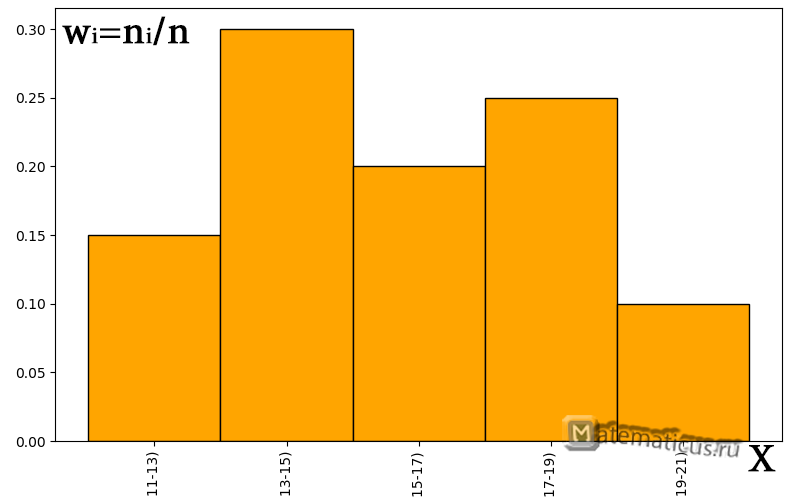
График гистограммы накопленных частот
Для построения полигона частот на оси абсцисс откладывают варианты хi, а на оси ординат — соответствующие им частоты ni и соединяют точки.
Пример графика полигона частот хi, ni
Пример графика полигона относительных частот хi, wi
www.matematicus.ru
Гистограмма — QUORACE
Гистограммы позволяют сделать при контроле качества предварительную оценку закона распределения случайной величины, т.е. понять, как происходит разброс значений, есть ли влияющие факторы и как они влияют на измеряемый результат.
Гистограмма является столбчатым графиком и позволяет наглядно представить характер распределения случайной величины
Построение гистограммы происходит следующим образом
1. Создаётся план исследования, проводятся измерения, результаты заносятся в таблицу. Результатом может быть, как фактическое измеренное значение, например, момент затяжки 20 Н*м, так и отклонение от требуемого значения, например, запись отклонения в 0,05 мм при оценке диаметра изделия.
В Таблице 1 приведён пример для 40 результатов измерений момента силы (Н*м).
Заданный момент силы равен 25,5 Н*м, отклонения ±1,5 Н*м. Он будет рассмотрен для построения гистограмм.
Таблица 1.
2. В полученной выборке находят минимальное и максимальное значение Xmin и Xmax (Таблица 2).
3. Вычисляют разницу R=Xmax-Xmin (Таблица 2).
4. Разницу R разбивают на z равных интервалов (L), где z=√N, N – объём всей выборки (количество измеренных значений параметра) (Таблица 2). Для точного анализа выборка должна быть представительной, т.е. быть достаточной для проведения анализа и его точной интерпретации. Представительной считается выборка от 35 до 100 значений, обычно N=100. Длина интервала L=R/x должна быть больше цены деления шкалы измерительного устройства, которым выполнялись измерения.
Таблица 2.
5. Подсчитываются частоты попадания значений в интервалы, составляется таблица распределения и строится его графическое изображение. При этом частоты значений, оказавшиеся на границе интервалов, поровну распределяют между соседними интервалами (Рис.1)
Рис.1
Имея таблицу распределения значения X(среднее арифметическое) и S2 (стандартное отклонение) можно рассчитать по формулам
Где xi – среднее значение i-го интервала
Или воспользовавшись соответствующими функциями в MS Excel
СРЗНАЧ() для X
СТАНДОТКЛОН.В() или СТАНДОТКЛОН.Г() для S2
Зная X и S2 можно оценить индекс воспроизводимости процесса (Ср), который будет рассмотрен в другой статье.
Исходя из гистограммы, рассмотренной в примере, можно сделать вывод о том, что часть значений находится вне допусков и большинство значений уходят в сторону двух пиков по левую и правую границу допусков, что характерно для выборки, объединяющей результаты двух процессов, когда происходит смешивание двух распределений с далеко отстоящими средними значениями. В данном случае необходимо применить метод стратификации и провести анализ ещё раз. В данном случае можно предположить, что измерения проводились двумя различными ключами, что и дало такой результат. Разделение данных по различным ключам позволит исключить двойные пики в гистограмме.
Таким образом, существуют некоторые основные типы гистограмм исходя из графического представления которых можно сделать выводы о характере популяции.
Существует восемь основных типов гистограмм:
- Нормальное распределение. Обычный тип. Форма колокола.
Симметричная форма с пиком примерно в центре интервала характерна для нормального распределения. Отклонения от данной формы могут указывать на наличие различных причин, влияющих на распределение. - Распределение с двумя пиками.
В центре интервала низкая частота попадания, зато есть два пика по левую и правую стороны интервала. Подобное распределение говорит о том, что в выборку включены значения, объединяющие различные процессы, например, смешаны результаты контроля двух станков или была произведена различная настройка контролирующего инструмента. - Плато
При подобном распределении можно говорить о влиянии условий, аналогичных предыдущей гистограмме, отличие в том, что средние значения нескольких распределений отличаются незначительно. Необходимо провести расслоение данных, снизить вариабельность процессов. - Распределение гребенчатого типа.
Чередующиеся высокие и низки значения обычно указывают на ошибки измерений или ошибки в способе группировки данных, также на систематическую погрешность в способе округления данных. Существуют незначительная вероятность того, что это распределение типа плато. Если значения в таблицу заносятся человеком, то наличие пиков на целых числах может быть обусловлено влиянием человека при округлении значений. Человеку свойственно отдавать предпочтения при записи круглым числам - Положительно или отрицательно скошенное распределение.
Среднее значение гистограммы локализовано слева или справа от центра размаха. Частоты резко спадают к противоположному от пика концу. Форма ассиметрична. Подобное распределение возможно, когда невозможно получение значений больше или меньше определённой величины, либо при наличии одностороннего поля допуска, также это может быть влияние точности заготовок при их механической обработке. - Усечённое распределение, с обрывом справа или слева.
Среднее арифметическое гистограммы локализовано далеко слева или справа от центра размаха, частоты резко спадают в противоположном от пика направлении. Подобные распределения встречаются при стопроцентном просеивании изделий из-за плохой воспроизводимости процессов, т.е., например, часть распределения изъята при контроле качества. - Распределение с изолированным пиком.
На ряду с обычным распределением любого типа по одну сторону от распределения находится маленький пик. Причиной может быть включение данных из другого распределения или появление ошибки измерения. Стоит перепроверить измерения и вычисления, может возможно выделить условия (оборудование, время), которые могут служить причиной образования изолированного пика. - Распределение с пиком на краю.
Имеется большой пик по одну из сторон размаха. Подобное распределение может быть при объединении всех несоответствий, близких к одному из концов размаха в одну категорию, либо на неаккуратную запись данных.
Если существуют границы допуска, то следует нанести их на гистограммы. Исходя из положения распределения относительно границ допуска на гистограмме можно делать выводы о необходимости принятия решений.
Есть пять типичных случаев расположения распределения относительно границ допуска
- Гистограмма находится в допуске.
Состояние процесса стабильно, необходимо поддерживать процесс в данном состоянии - Гистограмма находится в допуске, но вплотную к границам.
Необходимо уменьшить разброс до меньшего значения. - Гистограмма за границами допуска слева (или справа).
Необходимо сместить среднее значение ближе к центру. - Гистограмма за границами допуска слева и справа.
Необходимы действия, направленные на снижение вариаций процесса. - Гистограмма за границами допуска слева и справа, пик смещён вправо (или влево).
Необходимо провести действия, аналогичные для 3 и 4 случая одновременно, для снижения вариаций и смещения среднего.
quorace.com
это… Что такое гистограмма: гистограмма в статистике, использование гистограмм
Добавлено в закладки: 0
Что такое гистограмма? Описание и определение понятия
Гистограмма – это один из видов диаграмм, представляющий собой графическое изображение определенных статистических показателей и величин в виде столбиков. Основанием для составления диаграммы служит количественный признак. В общем виде, Гистограмма – это ряд смежных прямоугольников, выстраивающихся в ряд на прямой линии. При этом, площадь каждого из них является пропорциональной частоте, данной величине представленной в данной совокупности.
Гистограмм (от др.-греч. черта, буква, написание) — способ графического представления табличных данных.
Гистограмма в статистике
Рассмотрим более детально термин гистограмма
 В большинстве статистических расчетов имеем дело либо со случайными данными, которые получены в ходе какого-либо эксперимента (выводящиеся из файла или печатаются непосредственно в документе), либо с результатами генерации случайных чисел, которые рассмотрены в предыдущих разделах встроенными функциями, которые моделируют то или иное явление методом Монте-Карло.
В большинстве статистических расчетов имеем дело либо со случайными данными, которые получены в ходе какого-либо эксперимента (выводящиеся из файла или печатаются непосредственно в документе), либо с результатами генерации случайных чисел, которые рассмотрены в предыдущих разделах встроенными функциями, которые моделируют то или иное явление методом Монте-Карло.
Гистограммой называется график, который аппроксимирует по случайным данным плотность их распределения. При построении гистограммы область значений случайной величины (а,b> разбивают на некоторое количество bin сегментов, а затем подсчитывают процент попадания данных в каждый сегмент.
Гистограмма представляет собой столбчатой график, который построен по полученным за определенный период (к примеру, за неделю или за месяц) данным, разбиваемые на несколько интервалов; число данных, которые попадают в каждый из интервалов (частота), должно выражаться высотой столбика.
Данные для построения гистограммы собирают в течение длительного периода – недели, месяца, года и т. д.
Гистограмма – это серия столбиков одинаковой ширина, но разной высота, которая показывает рассеяние и распределения данных. Ширина столбика – это интервал в диапазоне наблюдений, высотой – количество данных, которая приходится на ту или иную часть интервала, т.е. част ость. По существу, гистограмма может отображать распределение исследуемого показателя. Гистограмме позволено оценить характер рассеивания показателя и разобираться в там, на чём следует сосредотачивать усилия пo улучшению.
- Симметричная
Большинство значений располагаются по обе стороны от центра распределение (центральной тенденции) с отклонением, которое сбалансировано по обе стороны от центра. - С наклоном
Большинство значений располагаются слева от центральная тенденции. Такому типу распределения данных может произойти, в случае когда есть естественное препятствие, или в случае сортировки данных (товары, не соответствующие определенному стандарту, должны удалятся из набора данных). - Асимметричная
На таком графике присутствует длинный “хвост” по одну сторону от центральная тенденция. По одну сторону наблюдается больше отклонений, чем по другую, указывается тем самым на то, что в течение процесса происходит сдвиг определённых переменных значений. - Двухмодальная
В двух модальном типе присутствует две вершины. Это обычно происходит,если происходит смешение двух различных групп данных (категорию невысоких людей смешивают с категорией очень высоких людей). По факту, у нас есть две гистограммы, которые объединены вместе.
Как построить гистограмму?
Чтобы построить гистограмму, нарисуйте горизонтальную и вертикальную оси. Горизонтальная ось (Х) будет отображать интервалы; вертикальная ось (Y), будет отображать частоты. Нарисуйте полоску, которая представляет собой частотность данных в каждом классе. Полоски должны соприкасаться друг с другом.
Использование гистограмм
Гистограмму используют для изображения только интервальных рядов.
Количественные соотношения некоторого показателя представлены в виде прямоугольников, площади которых пропорциональны. Чаще всего для удобства восприятия ширину прямоугольников берут одинаковую, при этом их высота определяет соотношения отображаемого параметра.
В статистике гистограмма — геометрическое изображение эмпирической функции плотности вероятности некоторой случайной величины, которое построено по выборке.
В фотографии гистограммой называют графическое представление распределения яр костей фотоснимка.
Гистограмма – это один из тех немногих способов графического представления данных, доступность и легкость восприятия которого не вызывает сомнения. Она прекрасно подходит для описания больших массивов данных, равнин как и для характеристики небольшого числового ряда.
Гистограмм называют двухмерный график, по горизонтальная ось который откладываются переменные или числовых интервалов, а по вертикальность – частота возникновения переменная (в заданном интервале). Чаще всего гистограмма составляют из прямоугольников с шириной, равной величине интервала и площадью, которая пропорциональна соответствующая частоте возникновения переменная. Другими сливами, площадь прямоугольнику соответствует количеству значения, попадающих в определенный интервал: чем большее значение, тем больше площадь – при равных значениях интервала, больший столбик будет соответствовать большему количеству значений
Мы коротко рассмотрели определение термина гистограмма, гистограмма в статистике, использование гистограмм. Оставляйте свои комментарии или дополнения к материалу.
biznes-prost.ru
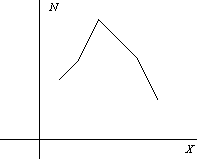
Полигон и гистограмма статистического распределения
Для наглядности статистическое распределение значения признака иллюстрируется полигоном распределения или гистограммой.
Для построения
полигона на координатной плоскости
изображают ломаную с вершинами в точках
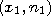 ,
,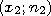 , … ,
, … ,
 .
Движение лини полигона характеризует
частотность того или иного значения
наблюдаемого признака: чем выше очередная
вершина полигона, тем чаще наблюдалось
соответствующее ему значение в рамках
проведенного эксперимента.
.
Движение лини полигона характеризует
частотность того или иного значения
наблюдаемого признака: чем выше очередная
вершина полигона, тем чаще наблюдалось
соответствующее ему значение в рамках
проведенного эксперимента.
|
|
|
|
(a) Полигон статистического распределения |
(b) Гистограмма статистического распределения |
Гистограмма — это
ступенчатая фигура, составленная из
серии прямоугольников. Основаниями
прямоугольников гистограммы служат
отрезки
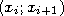 ,
а высотами — отрезки
,
а высотами — отрезки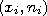 .
Высоты прямоугольников гистограммы
демонстрируют частотность значений
наблюдаемого признака: чем выше
прямоугольник, тем чаще соответствующий
признак наблюдался в рамках проведенного
исследования.
.
Высоты прямоугольников гистограммы
демонстрируют частотность значений
наблюдаемого признака: чем выше
прямоугольник, тем чаще соответствующий
признак наблюдался в рамках проведенного
исследования.
При изучении
непрерывно изменяющегося признака для
построения полигона выбирают точки
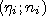 ,
где
,
где —
это середина отрезка
—
это середина отрезка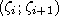 ,
образующего разбиение интервала
,
образующего разбиение интервала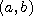 ,
в пределах которого изменяется наблюдаемый
признак. Для построения гистограммы в
непрерывном случае в качестве оснований
гистограммы используют отрезки разбиения
,
в пределах которого изменяется наблюдаемый
признак. Для построения гистограммы в
непрерывном случае в качестве оснований
гистограммы используют отрезки разбиения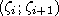 .
.
Значение репрезентативности выборки для статистического распределения
Если выборка для
проведения исследования является
репрезентативной, то полученные данные
о статистическом распределении признака
дает достаточно точное представление
о распределении признака в генеральной
совокупности. Следует иметь в виду, что
увеличение объема выборки всегда
приводит к повышению ее репрезентативности,
таким образом, чем больше объем выборки
 ,
тем точнее выборочное распределение
отражает действительное состояние дел.
,
тем точнее выборочное распределение
отражает действительное состояние дел.
Примеры статистических распределений Пример с делением испытуемыми данного отрезка на две части внутренней точкой
В двух словах, эксперимент состоял в следующем: двум группам испытуемых экспериментальной (группа студентов-дизайнеров) и контрольной (группа студентов-инженеров), в качестве задания предлагалось:
изобразить на стандартном листе бумаги отрезок прямой линии произвольно,
разместить на этом отрезке одну точку произвольно,
вычислить коэффициент отношения меньшего из получившихся отрезков к большему.
В результате каждый испытуемый демонстрировал некоторый числовой показатель k, заключенный между нулем и единицей. Экспериментальная гипотеза состояла в том, что дизайнеры продемонстрируют больший разброс значений этого показателя, причем, разница окажется статистически значимой.
Здесь мы подробно разберем ряд действий, связанных с анализом данных в контрольной группе.
В испытании принимали участие 50 студентов факультета инженерных систем и природоохранного строительства Самарского государственного архитектурно-строительного университета. Стало быть — объем выборочной совокупности равен 50.
Испытуемыми были продемонстрированы следующие результаты (код испытуемого составлен из его инициалов, коэффициент k вычисляется как отношение длины меньшего из получившихся отрезков к длине большего из них).
|
№ |
Код |
Значение |
|
1 |
К. О. |
0,174 |
|
2 |
Л. Д |
0,666 |
|
3 |
Б. О |
0,625 |
|
4 |
Н. Е. |
0,455 |
|
5 |
Х. А. |
0,614 |
|
6 |
М. У. |
0,286 |
|
7 |
П. Р. |
0,417 |
|
8 |
К. А. |
0,591 |
|
9 |
Р. О. |
0,750 |
|
10 |
М. А. |
0,429 |
|
11 |
П. У. |
0,500 |
|
12 |
М. А. |
0,250 |
|
13 |
Р. А. |
0,391 |
|
14 |
Т. О. |
0,750 |
|
15 |
С. Т. |
0,504 |
|
16 |
Я. В. |
0,750 |
|
17 |
Б. Е. |
0,542 |
|
18 |
С. Е. |
0,771 |
|
19 |
Ч. Е. |
0,545 |
|
20 |
П. О. |
0,578 |
|
21 |
И. С. |
0,750 |
|
22 |
Б. А. |
0,330 |
|
23 |
Ш. Б. |
0,299 |
|
24 |
Я. Р. |
0,780 |
|
25 |
П. П. |
0,528 |
|
26 |
Ф. И. |
0,200 |
|
27 |
К. О. |
0,449 |
|
28 |
Н. Е. |
0,429 |
|
29 |
К. Р. |
0,500 |
|
30 |
К. Ан. |
0,659 |
|
31 |
Л. А. |
0,482 |
|
32 |
М. А. |
0,551 |
|
33 |
Д. М. |
0,414 |
|
34 |
С. О. |
0,638 |
|
35 |
Ш. А. |
0,328 |
|
36 |
О. Т. |
0,586 |
|
37 |
К. О. |
0,400 |
|
38 |
Е. Л. |
0,504 |
|
39 |
Р. Я. |
0,621 |
|
40 |
С. О. |
0,323 |
|
41 |
У. Т. |
0,635 |
|
42 |
М. Р. |
0,472 |
|
43 |
К. О. |
0,450 |
|
44 |
Ш. О. |
0,380 |
|
45 |
М. В. |
0,500 |
|
46 |
К. И. |
0,659 |
|
47 |
Ш. Е. |
0,355 |
|
48 |
А. С. |
0,684 |
|
49 |
Т. Е. |
0,695 |
|
50 |
Ч. А. |
0,526 |
Итак, коэффициент деления отрезка k — это непрерывная случайная величина, принимающая значения из отрезка от 0 до 1. Каждому наблюдаемому значению k поставить в соответствие его наблюдаемую частоту, конечно, можно, однако это не охарактеризует распределение генеральной совокупности: большинство частот окажутся равными между собой, так как большинство наблюдаемых значений встречается в рамках эксперимента не более одного раза.
Поэтому для построения статистического распределения разделим отрезок возможных значений коэффициента k на 5 равных частей и сгруппируем наблюдаемые значения по факту принадлежности тому или иному промежутку. Прежде всего следует упорядочить полученные значения:
|
№ |
Код |
Значение |
|
1 |
К. О. |
0,174 |
|
2 |
Ф. И. |
0,200 |
|
3 |
М. А. |
0,250 |
|
4 |
М. У. |
0,286 |
|
5 |
Б. А. |
0,299 |
|
6 |
С. О. |
0,323 |
|
7 |
Ш. А. |
0,328 |
|
8 |
Б. А. |
0,330 |
|
9 |
Ш. Е. |
0,355 |
|
10 |
Ш. О. |
0,380 |
|
11 |
Р. О. |
0,391 |
|
12 |
К. С. |
0,400 |
|
13 |
Д. М. |
0,414 |
|
14 |
П. Р. |
0,417 |
|
15 |
М. А. |
0,429 |
|
16 |
Н. Е. |
0,429 |
|
17 |
К. З. |
0,449 |
|
18 |
К. О. |
0,450 |
|
19 |
Н. Е. |
0,455 |
|
20 |
Р. Н. |
0,472 |
|
21 |
Л. А. |
0,482 |
|
22 |
М. А. |
0,500 |
|
23 |
К. Р. |
0,500 |
|
24 |
П. У. |
0,500 |
|
25 |
С. Т. |
0,504 |
|
26 |
Е. Л. |
0,504 |
|
27 |
Ч. А. |
0,526 |
|
28 |
П. А. |
0,528 |
|
29 |
Б. Е. |
0,542 |
|
30 |
Ч. Е. |
0,545 |
|
31 |
М. А. |
0,551 |
|
32 |
О. Т. |
0,568 |
|
33 |
П. Е. |
0,578 |
|
34 |
К. А. |
0,591 |
|
35 |
Р. Я. |
0,621 |
|
36 |
У. Т. |
0,635 |
|
37 |
С. О. |
0,638 |
|
38 |
Б. О. |
0,652 |
|
39 |
К. И. |
0,659 |
|
40 |
К. А. |
0,659 |
|
41 |
Л. Д. |
0,666 |
|
42 |
Т. Е. |
0,684 |
|
43 |
А. С. |
0,695 |
|
44 |
П. О. |
0,750 |
|
45 |
Р. О. |
0,750 |
|
46 |
И. С. |
0,750 |
|
47 |
Я. В. |
0,750 |
|
48 |
С. Е. |
0,771 |
|
49 |
Т. О. |
0,775 |
|
50 |
Я. Р. |
0,780 |
Все наблюдаемые значения сосредоточены в интервале от 0,174 до 0,780. Разделим этот интервал на 5 равных частичных интервалов и подсчитаем частоты попаданий k в эти частичные интервалы:
|
Интервал |
0,1740– – 0,2952 |
0,2952– –0,4164 |
0,4164– – 0,5376 |
0,5376– – 0,6588 |
0,6588– –0,7800 |
|
Частота |
4 |
9 |
15 |
10 |
12 |
Полученная таблица и есть статистическое распределение наблюдаемого признака (коэффициента деления отрезка). Используя относительные частоты вместо частот, можно записать его в виде:
|
Интервал |
0,1740– –0,2952 |
0,2952– –0,4164 |
0,4164– –0,5376 |
0,5376– –0,6588 |
0,6588– – 0,7800 |
|
Относительная частота |
0,08 |
0,18 |
0,30 |
0,20 |
0,24 |
Для большей наглядности полученные данные о распределении признака k можно изобразить в виде гистограммы. При этом мы используем относительные частоты распределения, так как в этом случае вертикальные значения гистограммы не зависят от объема выборки, они заведомо не превосходят 1.
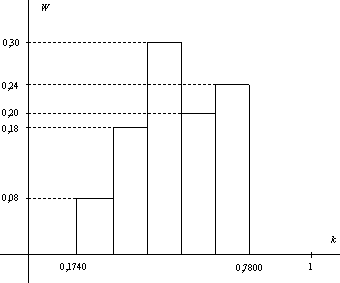
Гистограмма распределения коэффициента деления отрезка.
Аналогично исследуется распределение коэффициента k, в экспериментальной группе (группе студентов-дизайнеров).
studfile.net