Электронный учебник — Словарь 2М
Электронный учебник — Словарь 2М2М гистограммы. Этот термин был впервые использован Пирсоном в 1895 г.) 2М гистограммы являются графическими представлениями распределения частот выбранных переменных, на которых для каждого интервала (класса) рисуется столбец, высота которого пропорциональна частоте класса.
2М гистограммы
— Висячие столбцы. Гистограмма висячих
столбцов является «наглядным критерием
проверки на нормальность распределения»,
который помогает определить области
распределения, где возникают расхождения между
наблюдаемыми и ожидаемыми нормальными
частотами. В то время как стандартным способом
представления подогнанного к наблюдаемому
распределению нормального распределения
является наложение на гистограмму наиболее
подходящей нормальной кривой, гистограмма
висячих столбцов предлагает противоположный
способ: столбцы, представляющие наблюдаемые
частоты для последовательных диапазонов
значений, «подвешиваются» к наиболее
подходящей нормальной кривой.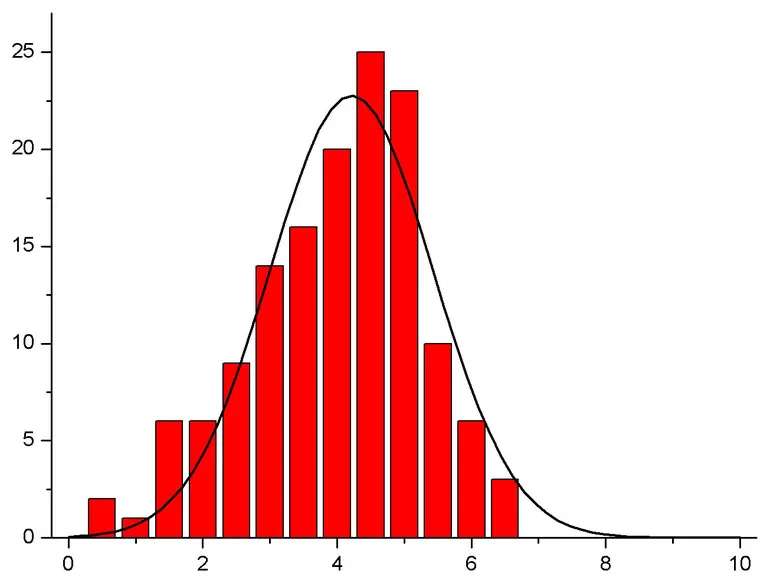
Если исследуемое распределение хорошо
приближается нормальной кривой, то нижние ребра
всех столбцов должны образовать прямую
горизонтальную линию.
2М гистограммы -
Простые. Эта гистограмма представляет
собой столбчатую диаграмму распределения частот
для выбранной переменной (если выбрано более
одной переменной, то для каждой из них будет
построен отдельный график).
2М гистограммы -
С двойной осью Y. Гистограмму с двойной осью
Y можно считать комбинацией двух по-разному
масштабированных составных гистограмм. Для этой
гистограммы можно выбрать две различные группы
переменных. Для каждой из выбранных переменных
будет изображено распределение частот, но
частоты переменных из первого списка
(называемого Левая ось Y) будут
откладываться по левой оси Y, а частоты
переменных из второго списка (называемого Правая
ось Y) будут откладываться по правой оси Y. Имена всех переменных из двух списков будут
внесены в условные обозначения и будут
сопровождаться буквами Л или П,
обозначающими соответственно левую или правую
ось Y.
Имена всех переменных из двух списков будут
внесены в условные обозначения и будут
сопровождаться буквами Л или П,
обозначающими соответственно левую или правую
ось Y.
Этот график полезен для сравнения
распределений переменных с разными частотами.
2М гистограммы - Составные. Составные гистограммы изображают распределение частот для нескольких переменных на одном 2М графике. В отличие от гистограмм с двойной осью Y частоты для всех переменных откладываются по левой оси Y.
2М диаграммы
диапазонов — Отрезки.
На диаграмме диапазонов такого типа диапазоны
представлены «отрезками» с горизонтальными
черточками на обоих концах (см. следующий
рисунок). Средние точки обозначены маркерами
точек.
Средние точки обозначены маркерами
точек.
2М диаграммы
диапазонов — Прямоугольники.
На диаграмме такого типа диапазон
изображается в виде прямоугольника (верхняя
сторона которого соответствует верхней границе
диапазона, а нижняя сторона — нижней). Средние
точки изображаются либо маркерами точек, либо
горизонтальными линиями, «пересекающими»
прямоугольник.
2М диаграммы
диапазонов — Столбцы.
На диаграмме диапазонов такого типа средняя
точка представлена столбцом (т.е. верх столбца
задается значением средней точки), а диапазон
(представленный «отрезком»)
накладывается на столбец.
2М
диаграммы диапазонов — Столбцы ошибок. На
двумерной диаграмме диапазонов такого типа
диапазоны или столбцы ошибок определяются
исходными значениями выбранных переменных.
Средние точки изображаются маркерами точек. Для
каждого наблюдения строится один диапазон или
столбец ошибок. В простейшем случае нужно
выбрать три переменные, одна из которых будет
соответствовать средним точкам, другая — верхним
границам, а оставшаяся — нижним границам.
В простейшем случае нужно
выбрать три переменные, одна из которых будет
соответствовать средним точкам, другая — верхним
границам, а оставшаяся — нижним границам.
2М диаграммы
размаха. На диаграммах размаха (этот термин
был впервые использован Тьюки в 1970 г.) диапазоны
или характеристики распределения значений
выбранной переменной (или переменных)
изображаются отдельно для групп наблюдений,
заданных значениями категориальной
(группирующей) переменной. Для каждой группы
наблюдений вычисляется центральная тенденция
(например, медиана или среднее) и вариационные
статистики или статистики диапазона (например, квартили, стандартные
ошибки или стандартные
отклонения), и выбранные значения изображаются
на диаграмме размаха выбранного типа. Также
могут быть изображены точки выбросов.
2М
диаграммы размаха/медианы (блоковые
статистические графики). Этот тип блоковых
статистических графиков представляет собой диаграмму размаха для медиан (а
также минимаксных значений и 25-й и 75-й
процентилей) для столбцов или строк блока. Каждый
прямоугольник отображает данные из одного
столбца или строки.
Каждый
прямоугольник отображает данные из одного
столбца или строки.
2М диаграммы размаха — Отрезки. На диаграмме размаха такого типа диапазон (т.е. стандартная ошибка, стандартное отклонение, минимум-максимум или константа) представлен в виде отрезка (с горизонтальными черточками на обоих концах, как на показанном ниже рисунке).
2М диаграммы
размаха — Прямоугольники. На диаграмме
размаха такого типа вокруг средней точки (т.е.
среднего или медианы) рисуется прямоугольник,
который отражает выбранный диапазон (т.е.
стандартную ошибку, стандартное отклонение,
минимум-максимум или константу).
2М
диаграммы размаха — Прямоугольники — Отрезки.
На диаграммах размаха этого типа вокруг средней
точки (т.е. среднего или медианы) рисуются
прямоугольник, представляющий выбранный
диапазон (т.е. стандартную ошибку, стандартное
отклонение, минимум-максимум или константу), и
отрезок, также отражающий выбранный диапазон,
концы которого расположены вне прямоугольника
(см.
2М диаграммы размаха/средние (блоковые статистические графики). Этот тип блоковых статистических графиков представляет собой диаграмму размаха для средних (а также стандартных ошибок и стандартных отклонений) для столбцов или строк блока. Каждый прямоугольник отображает данные из одного столбца или строки.
2М диаграммы размаха — Столбцы ошибок. На статистических 2М диаграммах размаха такого типа диапазоны или столбцы ошибок вычисляются по данным. Центральная тенденция (например, медиана или среднее) и диапазон или вариационные статистики (например, значения минимума и максимума, квартили, стандартные ошибки или стандартные отклонения) вычисляются для каждой переменной, и выбранные значения представляются в виде столбцов ошибок.
На показанном выше рисунке диапазоны выбросов и крайних точек представлены
на «классической» диаграмме
размаха (о диаграммах размаха см. в работе
Тьюки — Tukey, 1977).
в работе
Тьюки — Tukey, 1977).
2М диаграммы рассеяния. Диаграмма рассеяния визуализирует зависимость между двумя переменными X и Y (например, весом и высотой). Данные изображаются точками в двумерном пространстве, где оси соответствуют переменным (X — горизонтальной, а Y — вертикальной оси).
Две координаты, которые определяют положение каждой точки, соответствуют значениям двух переменных.
См. также раздел Сокращение
объема выборки.
2М диаграммы
рассеяния Вороного. Эта особая диаграмма
рассеяния одной переменной является в большей
степени аналитическим средством, нежели просто
методом графического представления данных.
Предлагаемые ею решения помогают моделировать
множество явлений в естественных и социальных
науках (см. Coombs, 1964 г.; Ripley, 1981 г.). Программа
разделяет пространство между точками данных,
представленными координатами X, Y в двумерном
пространстве.
Использование этого метода сильно зависит от области исследования; однако во многих случаях к этой диаграмме полезно добавлять дополнительные измерения, используя категоризацию (см. следующий рисунок).
См. также раздел Сокращение
объема выборки.
2М диаграммы
рассеяния — Простая. Простая диаграмма
рассеяния визуализирует зависимость между двумя
переменными X и Y (например, весом и высотой). Точки
данных изображаются точками в двумерном
пространстве, где оси соответствуют переменным.
Две координаты (X и Y), которые определяют
положение каждой точки, соответствуют значениям
двух переменных для этой точки. Если две
переменные сильно связаны, то множество точек
данных принимает определенную форму (например,
прямой линии или кривой). Если же переменные не
связаны, то точки образуют «облако» (на
следующем рисунке показан каьегоризованный
график для двух типов данных).
Если две
переменные сильно связаны, то множество точек
данных принимает определенную форму (например,
прямой линии или кривой). Если же переменные не
связаны, то точки образуют «облако» (на
следующем рисунке показан каьегоризованный
график для двух типов данных).
Подгонка функций к диаграмме рассеяния позволяет выявить структуру связей между переменными (см. следующий рисунок).
Другие примеры диаграмм рассеяния можно найти
в разделах Выбросы и Закрашивание. См. также
раздел Сокращение
объема выборки.
2М диаграммы
рассеяния — С двойной осью Y. Диаграмму
рассеяния такого типа можно рассматривать как
комбинацию двух составных
диаграмм рассеяния для одной переменной X и
двух различных наборов (списков) переменных Y.
Для переменной X и каждой из переменных Y будет
построена диаграмма рассеяния, но переменные из
первого списка (называемого Левая ось Y)
будут откладываться по левой оси Y, в то
время как переменные из второго списка
(называемого Правая ось Y), будут
откладываться по правой оси Y. Имена всех
переменных Y из двух списков будут включены
в условные обозначения, сопровождаемые буквой (Л)
или (П), обозначающей левую или правую ось Y
соответственно.
Имена всех
переменных Y из двух списков будут включены
в условные обозначения, сопровождаемые буквой (Л)
или (П), обозначающей левую или правую ось Y
соответственно.
Диаграммы рассеяния с двойной осью Y можно использовать для сравнения структуры нескольких корреляционных зависимостей путем изображения их на одном графике. При этом в силу независимости масштабов, используемых для двух списков переменных, этот график облегчает сравнение переменных, значения которых принадлежат разным диапазонам.
См. также раздел Сокращение
объема выборки.
2М диаграммы
рассеяния — Составная. В отличие от простой
диаграммы рассеяния, на которой одна переменная
представлена по горизонтальной, а вторая — по
вертикальной оси, составная диаграмма рассеяния
состоит из нескольких зависимостей и изображает
несколько корреляций : значения одной переменной
(X) откладываются по горизонтальной оси, а по
вертикальной оси откладываются значения
нескольких переменных (Y). Для каждой переменной Y
используется разный цвет и вид точек, который
указан в условных обозначениях, так что на
графике можно отличить зависимости для
различных переменных.
Для каждой переменной Y
используется разный цвет и вид точек, который
указан в условных обозначениях, так что на
графике можно отличить зависимости для
различных переменных.
Диаграмма рассеяния составного типа используется для сравнения структуры нескольких корреляционных зависимостей путем изображения их на одном графике, использующем один общий масштаб (например, для выявления основной структуры факторов или измерений при анализе дискриминантных функций).
См. также раздел Сокращение
объема выборки.
2М диаграммы рассеяния — Частоты . На диаграммах частот изображаются частоты перекрывающихся точек для двух переменных, чтобы наглядно представить веса точек данных или другие измеряемые параметры.
См. также раздел Сокращение
объема выборки.
2М круговая
диаграмма. Термин «круговые
диаграммы» впервые был использован Хаскеллом
в 1922 году. На этих графиках пропорции отдельных
значений переменной X представлены в виде
круговых секторов.
Термин «круговые
диаграммы» впервые был использован Хаскеллом
в 1922 году. На этих графиках пропорции отдельных
значений переменной X представлены в виде
круговых секторов.
2М линейные графики. На линейных графиках отдельные точки данных соединены линией.
Эти графики являются простым способом
представления и исследования
последовательностей значений. Графики
трассировочного типа можно использовать для
воспроизведения следа (а не последовательности).
Также линейные графики применяются для
изображения непрерывных функций, теоретических
распределений и т.п.
2М линейные графики — Агрегированные. Агрегированные линейные графики изображают последовательность средних для последовательных подмножеств выбранной переменной.
Можно выбрать число последовательных
наблюдений, по которым будет вычислено среднее, а
при необходимости диапазон значений в каждом
подмножестве будет выделен значками типа
отрезков. Агрегированные линейные графики
используются для представления и исследования
последовательностей большого числа значений.
Агрегированные линейные графики
используются для представления и исследования
последовательностей большого числа значений.
2М линейные графики — Простые. Простые линейные графики используются для представления и исследования последовательностей значений (обычно когда порядок значений является существенным).
Кроме того, линейные последовательные графики
применяются при построении графиков непрерывных
функций, таких как функции подгонки или
теоретические распределения. Заметьте, что
пустая ячейка данных (т.е. пропущенные данные)
«разрывает» линию.
2М линейные
графики — С двойной осью Y. Линейный
график с двойной осью Y можно рассматривать
как комбинацию двух по-разному масштабированных составных линейных
графиков. Для каждой выбранной переменной
используется свой шаблон линии; и при этом все
переменные, выбранные в списке Левая ось Y,
будут откладываться по левой оси Y, а
переменные, выбранные в списке Правая ось Y,
будут откладываться по правой оси Y.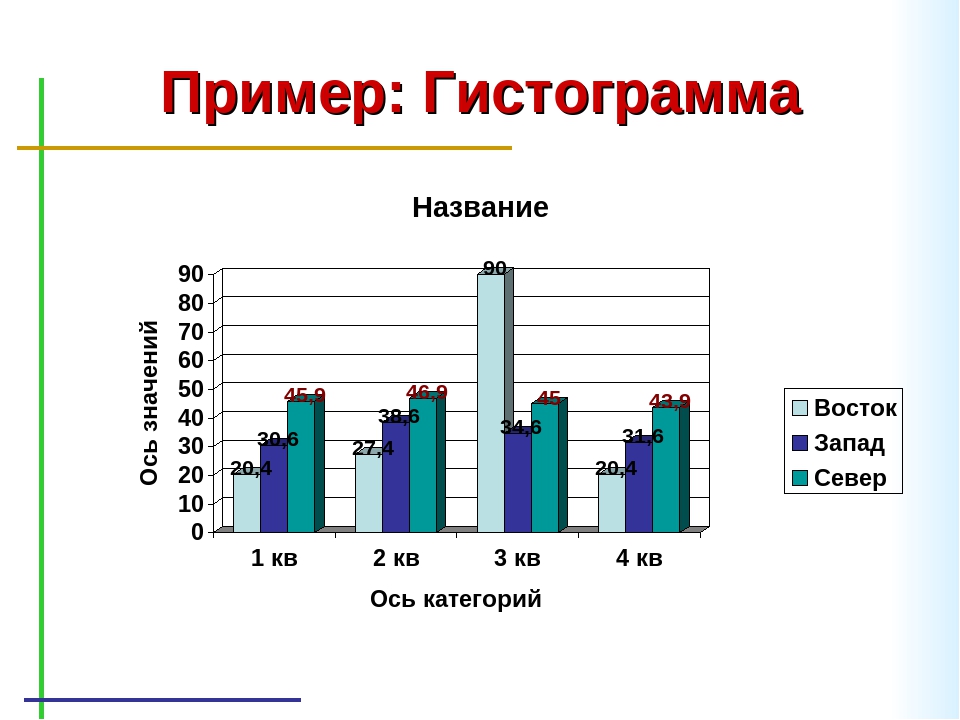 Имена
всех переменных будут указаны в условных
обозначениях вместе с буквой Л для
переменных, относящихся к левой оси Y, и с
буквой П для переменных, относящихся к
правой оси Y.
Имена
всех переменных будут указаны в условных
обозначениях вместе с буквой Л для
переменных, относящихся к левой оси Y, и с
буквой П для переменных, относящихся к
правой оси Y.
Линейный график с двойной осью Y можно
использовать для сравнения последовательностей
значений нескольких переменных, накладывая их
линейные представления на один график. В то же
время в силу независимости шкал, используемых
для двух осей, этот график может облегчить
сопоставление переменных трудно поддающихся
сравнению (т.е. имеющих значения в разных
диапазонах).
2М линейные
графики — Составные. В отличие от простых линейных
графиков, на которых представлена
последовательность значений одной переменной,
на составном линейном графике изображаются
несколько последовательностей значений
(переменных). Для каждой переменной используется
и указывается в условных обозначениях свой
шаблон и цвет линии.
Этот тип линейных графиков используется для
сравнения последовательностей значений
нескольких переменных (или нескольких функций)
путем изображения их на одном графике,
использующем один общий масштаб (например, для
сравнения нескольких одновременных
экспериментальных процессов, социальных
явлений, цен акций или товаров, форм кривых
текущих характеристик и т.п.).
2М линейные
графики — Трассировочные XY. На
трассировочных графиках сначала строится
диаграмма рассеяния двух переменных, а затем
отдельные точки данных соединяются линией (в
порядке их считывания из файла данных). В этом
смысле трассировочные графики визуализируют
«путь» последовательного процесса
(движение, изменение явления во времени и т.п.).
2М
линейные графики (профили наблюдений). В
отличие от простых
линейных графиков, на которых значения одной
переменной изображаются в виде одной линии
(точки данных соединяются линией), на линейных
графиках профилей наблюдений одна линия
рисуется для значений выбранных переменных для
одного наблюдения (строки), т.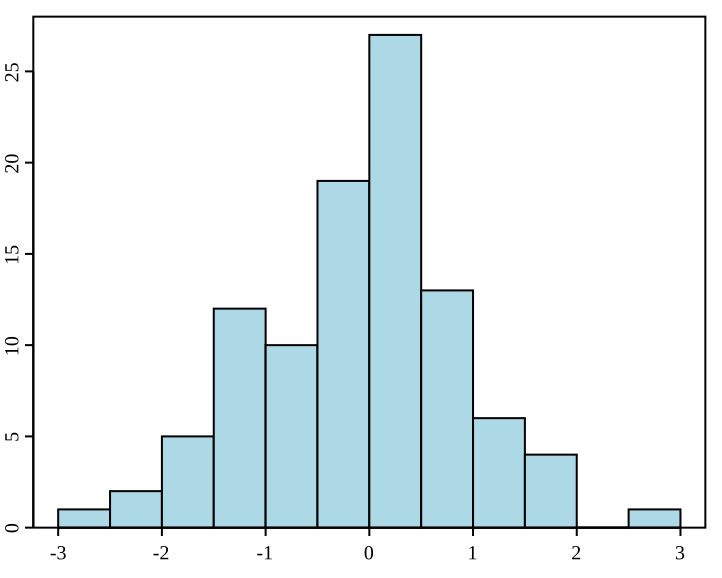 е. для каждого из
выбранных наблюдений строится один линейный
график. Линейные графики профилей наблюдений
являются простым способом наглядного
представления значений одного наблюдения
(например, результатов нескольких тестов).
е. для каждого из
выбранных наблюдений строится один линейный
график. Линейные графики профилей наблюдений
являются простым способом наглядного
представления значений одного наблюдения
(например, результатов нескольких тестов).
2М линейный график (или категоризованный
линейный график) медиан с квантилями и
минимаксными диапазонами
С помощью диалогового окна Статистические 2М
диаграммы размаха можно построить 2М линейный
график медиан с квантилями и минимаксными
столбцами диапазонов. В этом окне нужно выбрать
медиану в качестве средней точки, процентили (с
коэффициентом 25) для прямоугольника, и мин-макс
для отрезка. Наконец, остается пометить поле
Соединить средние точки, чтобы медианы на
графике были соединены линией.
Таким же образом можно построить
категоризованный 2М линейный график медиан с
квантилями и минимаксными диапазонами, выбирая
те же пункты в диалоговом окне Статистические
категоризованные диаграммы размаха.
2М
последовательные/наложенные графики — Зонные.
На графике этого типа последовательности
значений каждой выбранной переменной будут
представлены последовательными областями,
расположенными одна над другой.
2М
последовательные/наложенные графики — Линейные.
На графике этого типа последовательности
значений каждой выбранной переменной будут
представлены последовательными линиями,
расположенными одна над другой.
2М
последовательные/наложенные графики — Смешанные
ступенчатые. На графике этого типа
последовательности значений переменных,
выбранных в первом списке, будут представлены
последовательными ступенчатыми областями,
расположенными одна на другой, а
последовательности значений переменных,
выбранных во втором списке, -
последовательными ступенчатыми линиями,
расположенными одна над другой (над областью,
отвечающей последней переменной из первого
списка).
2М
последовательные/наложенные графики — Смешанные
линейные. На графике этого типа
последовательности значений переменных,
выбранных в первом списке, будут представлены
последовательными областями, расположенными
одна на другой, а последовательности значений
переменных, выбранных во втором списке, -
последовательными линиями, расположенными
одна над другой (над областью, отвечающей
последней переменной из первого списка).
2М
последовательные/наложенные графики -
Столбчатые диаграммы. На графике
этого типа последовательности значений каждой
выбранной переменной будут представлены
последовательными сегментами вертикальных
столбцов, расположенных друг над другом.
2М
последовательные/наложенные графики -
Ступенчатые. На графике этого типа
последовательности значений каждой выбранной
переменной будут представлены ступенчатыми
линиями, расположенными одна над другой.
2М
последовательные/наложенные графики -
Ступенчатые зонные. На графике этого
типа последовательности значений каждой
выбранной переменной будут представлены
ступенчатыми областями, расположенными одна над
другой.
2М столбчатые диаграммы. На столбчатой диаграмме последовательность значений представлена в виде столбцов (одному наблюдению соответствует один столбец). Если выбрано несколько переменных, то для каждой из них будет построен отдельный график. Можно построить составную диаграмму, где все переменные будут отображены одновременно в виде групп столбцов (одна группа для каждого наблюдения, как на следующем рисунке).
Европейский портал информации здравоохранения
В предыдущих видеоуроках мы объясняли, как найти показатель в хранилище данных и загрузить его данные в R. Сейчас мы рассмотрим, как на основе таких данных строить простые гистограммы.
Весь процесс подробно показан в видеоролике ниже. Обратите внимание: в меню ролика доступны русские субтитры.
1. Для R существует множество пользовательских пакетов, с помощью которых можно создавать простые диаграммы. В нашем руководстве будет рассмотрен пакет ggplot2. Он должен быть установлен в вашей RStudio и включен в код:
install-packages(“ggplot2”, dependencies = TRUE)
Require(“ggplot2”)
2. В одном из предыдущих уроков мы объясняли, как загрузить через API (ИПП) данные показателя. Эти данные мы и будем использовать. Взгляните на данные в блоке «data_from_api» – он должен содержать данные показателя с идентификатором HFA_74. В метаданных будет указано, что код HFA_74 соответствует показателю «младенческая смертность на 1000 живорождений».
3. Сделайте копию набора данных и назовите его блоком «barchart», запустив следующий код:
barchart <- data_from_api
4. Обратите внимание, что в блоке приводятся данные за определенные годы (1970–2015) в разбивке по полу (девочки, мальчики, все) и по группам стран. Значения для групп стран – это средневзвешенные по численности населения субрегиональные показатели для определенных групп стран в регионе. Допустим, вы хотите получить данные за 2013 г. для всего населения и без средних значений. Для этого нужно установить 2013 г. в фильтре для данных, запустив следующий код. Он работает очень быстро.
Обратите внимание, что в блоке приводятся данные за определенные годы (1970–2015) в разбивке по полу (девочки, мальчики, все) и по группам стран. Значения для групп стран – это средневзвешенные по численности населения субрегиональные показатели для определенных групп стран в регионе. Допустим, вы хотите получить данные за 2013 г. для всего населения и без средних значений. Для этого нужно установить 2013 г. в фильтре для данных, запустив следующий код. Он работает очень быстро.
barchart <- barchart [barchart$dimensions$YEAR == 2013,]
barchart <- barchart [barchart$dimensions$SEX == “ALL”,]
barchart <- barchart [barchart$dimensions$COUNTRY != “”2013,]
5. Обратите внимание, что в получившихся данных содержится именно нужная нам информация. На основе этих данных можно построить гистограмму, запустив следующий код:
dat <- data.frame(country = barchart$dimensions$COUNTRY,
values = as.numeric(barchart$value$display))
ggplot(data=dat, aes(x.country, y=values, fill=country)) +
geom_bar(stat=”identity”) +
ggtitle(“Infant deaths per 1000 live births”)
6. Диаграмма отображается в правом нижнем углу на вкладке Plots. На ней показана младенческая смертность на 1000 живорождений в странах Европейского региона ВОЗ за 2013 год. Видно, что максимальный показатель младенческой смертности составляет около 20 смертей на 1000 живорождений, а минимальный – около 2 смертей.
7. Используя функции пакета ggplot2, можно менять цвет столбцов и подписывать их. Можно также менять структуру диаграммы, сортируя лежащий в ее основе набор данных. Дополнительную информацию можно найти на сайте пакета ggplot2 -http://www.ggplot2.org/ и других интернет-ресурсах.
8. Вы можете преобразовать построенную диаграмму в изображение или файл формата PDF. Подобным образом можно загружать из API другие данные, фильтровать их и визуализировать, используя наиболее подходящие пакеты и типы диаграмм. Так вы сможете создавать скрипты для обращения к хранилищу данных и всегда иметь в своем распоряжении новейшие данные ЕРБ ВОЗ для статистического анализа.
Гистограмма с переменной шириной столбцов
Имеем, в качестве примера, вот такую табличку с информацией по количеству сотрудников и стоимостью четырех известных IT-компаний:
Задача: необходимо наглядно отобразить оба параметра для сравнения по всем компаниям.
Можно попытаться построить типичную в таких случаях пузырьковую (точечную) диаграмму. Можно попробовать поиграть с трехмерными диаграммами или торнадо. А можно немного «пошаманить» и сделать плоскую гистограмму со столбцами переменной ширины.
Этап 1. Подготовка данных
Половина успеха при построении любых нестандартных типов диаграмм в Excel, заключается в правильной подготовке таблицы с данными для диаграммы. В нашем случае, исходную табличку придется ощутимо переделать и превратить в нечто похожее на:
Давайте разберем все изменения, которые были сделаны.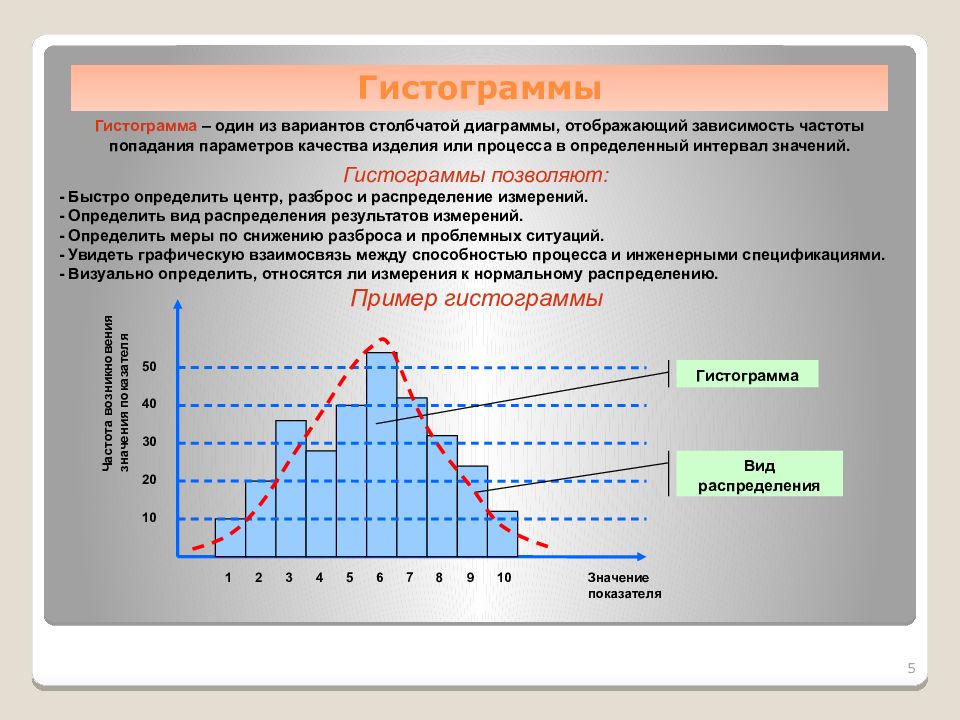
- Каждая компания превратилась из строки в столбец.
-
По каждой компании должен быть блок из 5 ячеек, где первая и последняя ячейки с нулями, а три центральных содержат одинаковые значения — стоимость каждой компании.
- Добавлены вспомогательные столбцы Пустышка и Подписи, в которых напротив центральных значений каждого блока размещены стоимости и названия компаний. Эти колонки понадобятся нам чуть позже для правильного размещения подписей к столбикам.
-
Первый (неподписанный) столбец представляет из себя чуть более хитрую штуку. Не залитые голубым цветом в нем ячейки — это количества сотрудников по каждой компании (92, 126, 54, 380), но взятые последовательно с нарастающим итогом. Т.е. для Apple это 92, для Microsoft уже 92+126=218, для Google 92+126+54=272 и т.д. Голубые же ячейки будут впоследствии, своего рода, «переходниками» и содержат среднее арифметическое соседних ячеек, т.е.
 для Apple это (0+92)/2=46, для Microsoft (92+218)/2=155 и т.д.
для Apple это (0+92)/2=46, для Microsoft (92+218)/2=155 и т.д.
Этап 2. Строим диаграмму
Выделим в нашей таблице все столбцы кроме последних двух и на вкладке Вставка (Insert) выберем для построения вариант диаграммы С областями с накоплением (Stacked Area):
На выходе должно получиться что-то похожее:
Основная проблема в том, что Excel на автомате интерпретирует подписи к оси X не как числа, а как текст — интервалы между подписями не соответствуют математической разнице между числами, да и сами подписи повторяются. Именно поэтому наша диаграмма еще не похожа на желаемую, но это, на самом деле, легко исправить. Щелкните правой кнопкой мыши по горизонтальной оси и выберите в контекстном меню команду Формат оси (Axis Format). В открывшемся окне переключите Тип оси с Автовыбора на Ось дат (Date Axis) и все сразу изменится!
В открывшемся окне переключите Тип оси с Автовыбора на Ось дат (Date Axis) и все сразу изменится!
В этом же окне можно настроить шаг делений по горизонтальной оси — для нашего примера я поменял параметр Единицы измерения с месяцев на дни и задал значение 50.
Этап 3. Добавляем подписи
Теперь неплохо бы добавить в нашу диаграмму подписи с названиями компаний. Скопируйте столбец Пустышка (выделить диапазон G11:G25 и нажать Ctrl+C), выделите диаграмму и вставьте скопированные данные прямо в нее (нажать Ctrl+V) — к нашей диаграмме должен добавиться новый ряд, выглядящий как крыши домов над нашими прямоугольниками:
Теперь щелкните правой кнопкой мыши по любой «крыше» и выберите команду Изменить тип диаграммы для ряда (Change series chart type). В открывшемся окне измените тип диаграммы для добавленного ряда на обычный график с маркерами:
Затем щелкните правой кнопкой мыши по графику и выберите Добавить подписи данных (Add Data Labels). Excel подпишет значения стоимости компании на каждом «пике».
Excel подпишет значения стоимости компании на каждом «пике».
Дальнейший ход действий зависит от того, какая у вас версия Excel. Если у вас последние Excel 2013 или 2016, то все будет проще. Щелкните правой кнопкой мыши по подписям, выберите команду Формат подписей (Format Data Labels) и затем включите флажок Значения из ячеек (Values from cells). Останется выделить данные из последнего столбца в нашей таблице, чтобы они попали на диаграмму в подписи к столбикам вместо чисел:
Если же у вас более древние версии Excel, то придется либо изменять подписи вручную (несколько одиночных щелчков по подписи, пока не начнет мигать курсор, а потом вбить название компании), либо использовать специальную бесплатную надстройку XYChartLabeler (дай бог здоровьичка Rob Bovey — ее автору, спасшему много-много моих нервных клеток и времени).
P.S.
Excel 2016 стал первой версией за последние 20 лет, где Microsoft, наконец-то, добавила новые типы диаграмм (водопад, Парето, Маримекко и др. ) в стандартный набор. Очень хочется верить, что «лед тронулся» и в следующих обновлениях мы увидим еще больше красивых и наглядных вариантов. Возможно, когда-нибудь и описанная выше гистограмма с переменной шириной столбцов будет строиться без «шаманских танцев» из этой статьи, а за два движения. Будем надеяться 🙂
) в стандартный набор. Очень хочется верить, что «лед тронулся» и в следующих обновлениях мы увидим еще больше красивых и наглядных вариантов. Возможно, когда-нибудь и описанная выше гистограмма с переменной шириной столбцов будет строиться без «шаманских танцев» из этой статьи, а за два движения. Будем надеяться 🙂
Ссылки по теме
Построение полигона, гистограммы, кумуляты, огивы
Для наглядности строят различные графики статистического распределения, и, в частности, полигон и гистограмму.
Полигон
Гистограмма
В случае интервального статистического распределения целесообразно построить гистограмму.
Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною
, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты
.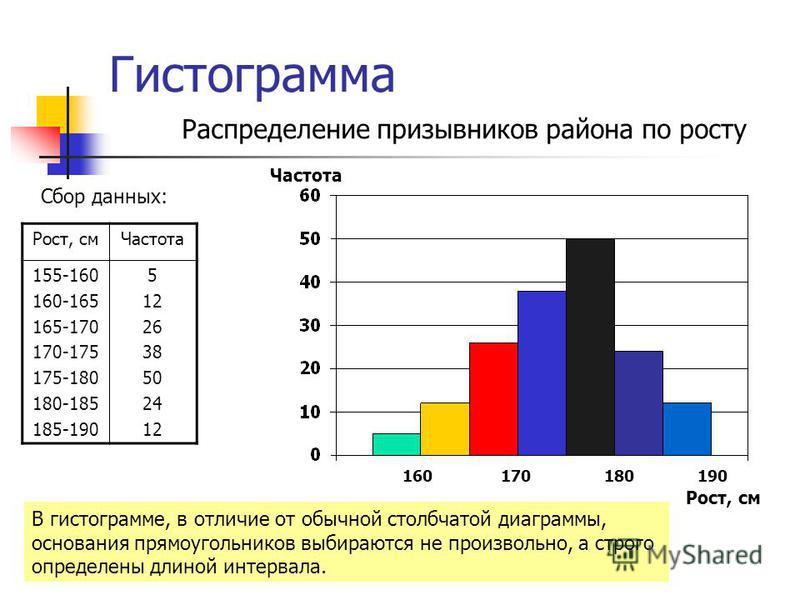 Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.
Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.
В случае построения гистограммы относительных частот (гистограммы частостей) высоты в случае равных интегралов должны быть пропорциональны относительной частоте , а в случае неравных интервалов высота равна плотности относительной частоты .
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
Пример 2
Построить гистограмму частот и относительных частот (частостей)
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).
| 2-4 | 4-8 | 8-13 | 13-15 | 15-17 | 17-20 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим плотности частоты:
| Интервалы, | Длина интервала, | Плотность частоты, | |
| 2 – 4 | 15 | 2 |
7. 500 500
|
| 4 – 8 | 35 | 4 | 8.750 |
| 8 – 13 | 64 | 5 | 12.800 |
| 13 – 15 | 55 | 2 | 27.500 |
| 15 – 17 | 21 | 2 | 10.500 |
| 17 – 20 | 10 | 3 |
3. 333 333
|
| Итого | 200 | — | — |
Гистограмма частот
Кроме этой задачи на другой странице сайта есть пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения признака — на оси ординат.
Пример 4
Построить кумулятивную кривую:
| 2 | 5 | 8 | 11 | 14 | 17 | |
| 15 | 35 | 64 | 55 | 21 | 10 |
Решение
Вычислим накопленные частоты:
| Накопленные частоты, | ||
| 2 | 15 | 15 |
| 7 | 35 | 50 |
| 8 | 64 | 114 |
| 15 | 55 | 169 |
| 16 | 21 | 190 |
| 17 | 10 | 200 |
| Итого | 200 | — |
Кумулятивная кривая
Если вам сейчас не требуется платная помощь с решением задач, контрольных работ и типовых расчетов, но может потребоваться в дальнейшем, то, чтобы не потерять контакт
вступайте в группу ВК
сохраните контакт WhatsApp (+79688494598)
сохраните контакт Телеграм (@helptask) .
Возможно срочное (от нескольких часов до суток) решение задач, а также онлайн-помощь на экзамене/зачете/самостоятельной.
Оплата на банковскую карту.
Заявку можно оставить прямо в чате ВКонтакте, WhatsApp или Telegram, предварительно сообщив необходимые вам сроки решения и скинув условие задач.
Гистограмма и ящик с усами на пальцах / Хабр
В этой заметке я хочу описать два типа графиков для одномерных данных, а именно
- гистограмма
- ящик с усами
Рассмотрим произвольную выборку вещественных чисел , будем обозначать порядковую статистику , такую что .
Скорее всего все поменять этот тип графика из школьной или университетской программы, который выглядит приблизительно так как на картинке.
Прежде всего необходимо помнить, что значения входной выборки располагаются по оси x, а по оси y располагается число раз, которое данное значение встретилось (назовем их отсчеты). Гистограмма позволяет огрубить и сделать набор данных более компактным, при этом не умаляя его специфичность.
Важными характеристиками гистограммы являются следующие:
- число столбцов (которые называются bins или bars)
- абсолютные или плотностные отсчеты по оси y
- как сгруппированы данные
Столбцы
В подавляющем большинстве случаев гистограмма определена на отрезке
, где
— исходная выборка,
вспомогательные константы, округляющие до ближайших “читаемых” чисел, которые в каждом случае зависят от масштаба и, обычно, это делители десятки в масштабе исходных данных. Если вдруг стало интересно, как ставить отсечки в данных, то можно посмотреть ссылку:
R (pretty).
Так же обычно гистограммы делят отрезок I на подотрезки равной длины и, вот, выбор числа отрезков является искусством, хотя можно привести несколько формул:
- Правило Стёрджеса (Не фотограф).
- Правило Скотта.
- Правило Фридмана-Дьякониса.
где
— число столбцов,
— размер исходной выборки,
— оценка стандартного отклонения,
— интерквартильное расстояние, которое еще встретится ниже.
Так же можно отметить несколько правил здравого смысла:
- хорошо чтобы в большинстве столбцов было больше одного исходного значения
- каждый столбец гистограммы требует хотя бы одного пикселя по ширине, и в целом ограничение “не более 200” столбцов достаточно распространено
В противном случае, если число столбцов избыточно, а исходных данных мало, гистограмма будет напоминать штрих-код, как например на рисунке ниже.
Ось Y
Гистограммы бывают в абсолютных значениях, когда по оси y откладывается количество элементов исходной выборки попавших в каждый из интервалов, и в относительных, когда сумма столбцов нормируются на единицу, в этом случае гистограмма является оценкой плотности распределения и с точки зрения графика меняется лишь масштаб.
Так как обычная гистограмма является оценкой плотности, то мы можем суммировать столбцы и получить оценку функции вероятности следующим образом: . Два следующих графика построены по одним и тем же данным, слева не нормализованная гистограмма, справа аккумулированные значения нормализованной гистограммы.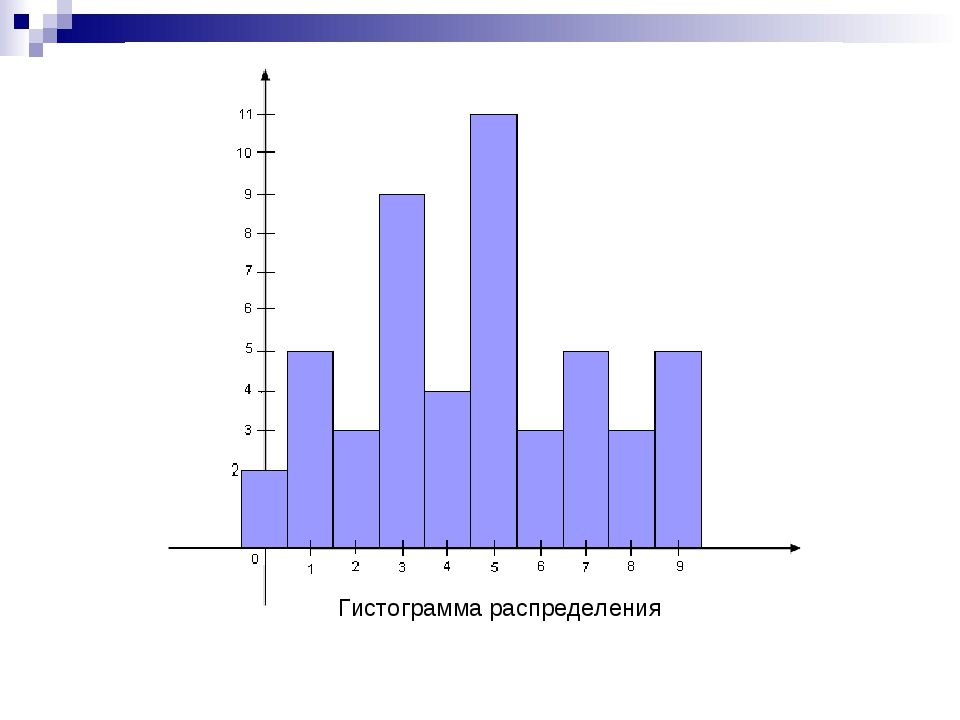
Группировка данных
До сих пор был рассмотрен случай, когда у нас есть характеристика, на которую мы просто хотим взглянуть, обычно намного более интересно сравнивать поведение одной и той же характеристики для различных подгрупп. В таком случае гистограмма будет иметь следующий вид.
В данном случае, ширина каждого столбца для каждой группы уменьшается пропорционально числу групп и слегка сдвигаются друг относительно друга, в качестве альтернативы можно рассмотреть полупрозрачное перекрытие, которое будет выглядеть следующим образом для тех же данных.
В сухом остатке
Для отрисовки гистограммы необходимо определить
- Число столбцов
- Нужна ли нормализация и аккумулирование данных
- Способ отображения различных групп
Для отрисовки гистограммы для каждой группы требуется хранить следующие значения:
- значение границ столбцов, где самое первое значение -координата левой границы самого левого столбца, а последнее — -координата правой границы самого правого столбца
- значений — количество элементов попавших в каждый из столбцов.

“Ящик с усами” не имеет официально устоявшегося названия, а называть его “ящиком с усами“ у меня язык не поворачивается, тем более когда ящиков несколько, а диаграмма размаха хоть и не очень частотное, но более благозвучное название. Приведем пример трех ящиков слева отображены соответствующие значения исходных данных (не являются частью диаграммы размаха). Прежде всего необходимо отметить, что в случае диаграмм размаха, исходная характеристика откладывается по оси Y, а ось X условна и представляет собой группирующую переменную.
Чтобы нарисовать ящик для одной группы про исходные данные необходимо знать всего три характеристики:
- Первый квартиль
- Медиану
- Третий квартиль
Иногда к “обязательному” набору добавляют следующие дополнительные:
Таким образом, ящик с усами в разрезе будет выглядеть следующим образом.
Некоторые моменты требуют пояснения. Ящик, то есть объект между и , практически везде ограничен этими значениями, а вот “усы” могут различаться и если вас действительно интересуют числа, необходимо уточнять, что имеется в виду в каждом отдельном случае.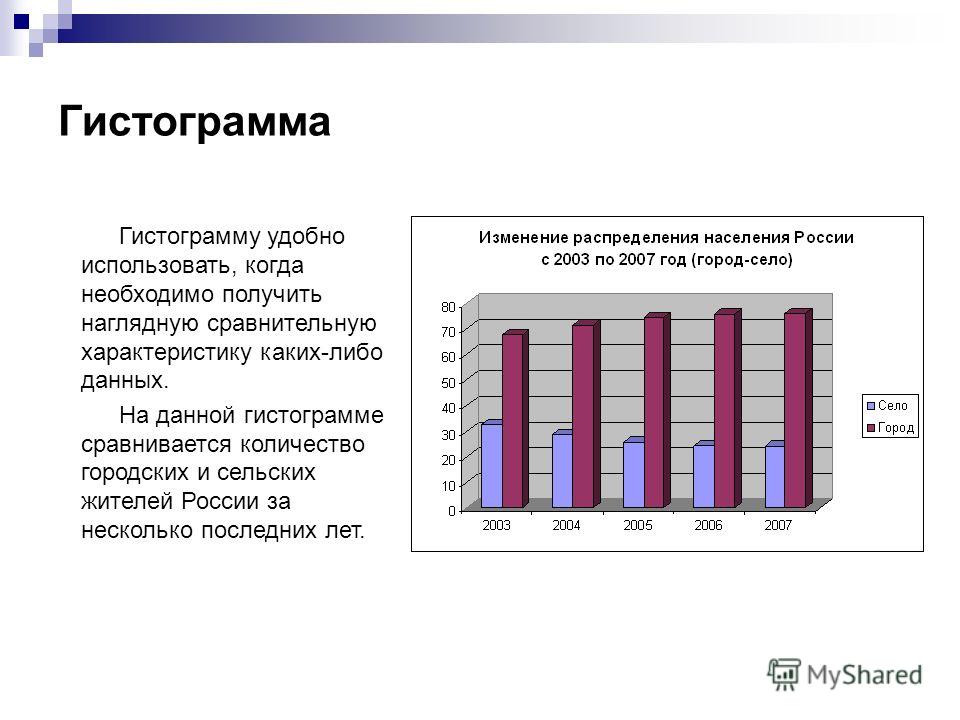 Самое важное это длина усов: исходим из того, что она .
Самое важное это длина усов: исходим из того, что она .
Отметки минимума и максимума часто опускаются, экстремальные точки, то есть выходящие за пределы усов тоже опускаются либо рисуются точками или звездочками. В зависимости от структуры данных желание отрисовывать экстремальные значения может значительно увеличить объем данных для отрисовки диаграммы размаха.
Магическое число появилось в работе Тьюки Exploratory Data Analysis (1977) и причина его появления не очень ясна, но с тех времен ничего не менялось, многие инструменты предлагают его в качестве значения по умолчанию, но позволяют выставлять произвольное, вплоть до нуля, в этом случае, “усы” будут покрывать весь отрезок от минимального до максимального значений исходных данных.
Есть предположение, что возникло следующим образом. Ширина усов составляет , известно, что для симметричных распределений совпадает с абсолютным отклонением от медианы (MAD), которая в свою очередь, является оценкой дисперсии с коэффициентом . А значит, , мы получаем не безызвестные 3 сигмы влево, 3 сигмы вправо.
А значит, , мы получаем не безызвестные 3 сигмы влево, 3 сигмы вправо.
Иногда в качестве концов усов предлагается интервал , в таком случае очевидно, что всегда (если исходных данных больше 20) должны получаться точки, не попадающие внутрь интервала и поэтому их обычно игнорируют при таком подходе.
В сухом остатке
Для отрисовки “диаграммы размаха” необходимо определить:
- способ группировки данных
- длину усов
- нужно ли отмечать экстремальные значения
Для отрисовки “ящика с усами” для одной группы требуется всего 3 числа.
Как построить гистограмму в Excel
Чтобы понять как построить гистограмму в Excel, предлагаю немного теории. Итак, гистограмма — это диаграмма, на которой данные выделены с помощью столбиков.
Гистограммы бывают:
- Простые прямоугольные, объемные, цилиндрические, конусные и пирамидальные. Без комментариев , ибо что тут рассказывать . Ставьте, кому что нравится, на саму диаграмму не влияет, отличий в построении не имеет.

- Сгрупированные или с накоплением. Если у вас больше одного ряда данных, то вы сможете показывать данные нескольких рядов, но относящихся к одному периоду, в одном столбике. Грубо говоря, при гистограмме с накоплением столбики располагаются друг над другом. Соответственно при группировке столбики находятся рядом.
- Нормированные. Опять-таки, если у вас больше одного ряда данных, то Excel сможет показать эти данные в одном столбике, при этом в качестве исходных данных будут браться не сами цифры, а их доли в процентах от общей суммы. Имеет смысл использовать, когда у вас сравнимые данные.
Инструкция по созданию диаграммы
- Создаем таблицу. Я придумал небольшое производство столов и стульев, использовав по ходу генератор случайных чисел, точнее его аналог для простых целей — функцию СЛЧИС.
- Потом выбираем на вкладке «Вставка» нужную диаграмму. Я выбрал обычную сгруппированную, она самая первая в списке.

- Появится гистограмма с минимальными настройками прямо на листе.Нам такого счастья не надо, поэтому правой кнопки мыши по диаграмме вызываем контекстное меню и выбираем отдельный лист.
- Переходим на лист диаграммы. Там появляются новые вкладки «Макет», «Конструктор» и «Формат». На вкладке «Макет» мы
- Ставим название диаграммы
- Ставим названия осей
- Добавляем таблицу данных
- Делаем небольшие корректировки по легенде, области построения.
Все это делается в два клика, поупражняйтесь. Кое-какие настройки делать с гистограммой явно лишнее, например, промежуточные линии сетки.
- На вкладке «Формат» можно задать форматирование каждого элемента диаграммы, в том числе:
- Заливку, контуры, цвет столбиков
- Стили надписей
- Размеры и порядок элементов
- и многое другое, что порой делать вообще не нужно.
Вот что у меня получилось.
На этом примере видно, как не стоит злоупотреблять излишним форматированием
- На вкладке «Конструктор» можно поменять тип диаграммы, ввести новые данные, переместить диаграмму и задать какой-то стиль.
 Здесь давайте посмотрим внимательнее на типы доступных гистограмм.
Здесь давайте посмотрим внимательнее на типы доступных гистограмм.
Гистограмма с накоплением
Как видите, данные по каждому периоду теперь содержатся друг над другом. Обычно, это нужно, чтобы наглядно посмотреть изменение общего объема производства и долю каждой составляющей.
Нормированная гистограмма с накоплением
Здесь фактические данные заменяются их долями, процентами. Это нужно для определения динамики вкладов отдельных категорий в общую копилку. Как я уже говорил выше, годится не для всех данных.
В принципе все, остальные типы — лишь производные от трех описанных выше, а форматированием не отличаются вообще.
5-минутное видео по теме:
Эксель Практик
«Глаза боятся, а руки делают»
P.S. Понравилась статья? Подпишитесь на рассылку в правой части страницы (Бесплатный курс «Топ-10 инструментов Excel») и будьте в курсе новых событий.
Как сделать гистограмму в Excel
Гистограмма является отличным инструментом визуализации данных. Это наглядная диаграмма, с помощью которой можно сразу оценить общую ситуацию, лишь взглянув на неё, без изучения числовых данных в таблице. В Microsoft Excel есть сразу несколько инструментов предназначенных для того, чтобы построить гистограммы различного типа. Давайте взглянем на различные способы построения.
Урок: Как создать гистограмму в Microsoft Word
Построение гистограммы
Гистограмму в Экселе можно создать тремя способами:
- С помощью инструмента, который входит в группу «Диаграммы»;
- С использованием условного форматирования;
- При помощи надстройки Пакет анализа.
Она может быть оформлена, как отдельным объектом, так и при использовании условного форматирования, являясь частью ячейки.
Способ 1: создание простой гистограммы в блоке диаграмм
Обычную гистограмму проще всего сделать, воспользовавшись функцией в блоке инструментов «Диаграммы».
- Строим таблицу, в которой содержатся данные, отображаемые в будущей диаграмме. Выделяем мышкой те столбцы таблицы, которые будут отображены на осях гистограммы.
- Находясь во вкладке «Вставка» кликаем по кнопке «Гистограмма», которая расположена на ленте в блоке инструментов «Диаграммы».
- В открывшемся списке выбираем один из пяти типов простых диаграмм:
- гистограмма;
- объемная;
- цилиндрическая;
- коническая;
- пирамидальная.
Все простые диаграммы расположены с левой части списка.
После того, как выбор сделан, на листе Excel формируется гистограмма.
С помощью инструментов, расположенных в группе вкладок «Работа с диаграммами» можно редактировать полученный объект:
- Изменять стили столбцов;
- Подписывать наименование диаграммы в целом, и отдельных её осей;
- Изменять название и удалять легенду, и т.д.
Урок: Как сделать диаграмму в Excel
Способ 2: построение гистограммы с накоплением
Гистограмма с накоплением содержит столбцы, которые включают в себя сразу несколько значений.
- Перед тем, как перейти к созданию диаграммы с накоплением, нужно удостовериться, что в крайнем левом столбце в шапке отсутствует наименование. Если наименование есть, то его следует удалить, иначе построение диаграммы не получится.
- Выделяем таблицу, на основании которой будет строиться гистограмма. Во вкладке «Вставка» кликаем по кнопке «Гистограмма». В появившемся списке диаграмм выбираем тот тип гистограммы с накоплением, который нам требуется. Все они расположены в правой части списка.
- После этих действий гистограмма появится на листе. Её можно будет отредактировать с помощью тех же инструментов, о которых шёл разговор при описании первого способа построения.
Способ 3: построение с использованием «Пакета анализа»
Для того, чтобы воспользоваться способом формирования гистограммы с помощью пакета анализа, нужно этот пакет активировать.
- Переходим во вкладку «Файл».
- Кликаем по наименованию раздела «Параметры».

- Переходим в подраздел «Надстройки».
- В блоке «Управление» переставляем переключатель в позицию «Надстройки Excel».
- В открывшемся окне около пункта «Пакет анализа» устанавливаем галочку и кликаем по кнопке «OK».
- Перемещаемся во вкладку «Данные». Жмем на кнопку, расположенную на ленте «Анализ данных».
- В открывшемся небольшом окне выбираем пункт «Гистограммы». Жмем на кнопку «OK».
- Открывается окно настройки гистограммы. В поле «Входной интервал» вводим адрес диапазона ячеек, гистограмму которого хотим отобразить. Обязательно внизу ставим галочку около пункта «Вывод графика». В параметрах ввода можно указать, где будет выводиться гистограмма. По умолчанию — на новом листе. Можно указать, что вывод будет осуществляться на данном листе в определенных ячейках или в новой книге. После того, как все настройки введены, жмем кнопку «OK».

Как видим, гистограмма сформирована в указанном вами месте.
Способ 4: Гистограммы при условном форматировании
Гистограммы также можно выводить при условном форматировании ячеек.
- Выделяем ячейки с данными, которые хотим отформатировать в виде гистограммы.
- Во вкладке «Главная» на ленте жмем на кнопку «Условное форматирование». В выпавшем меню кликаем по пункту «Гистограмма». В появившемся перечне гистограмм со сплошной и градиентной заливкой выбираем ту, которую считаем более уместной в каждом конкретном случае.
Теперь, как видим, в каждой отформатированной ячейке имеется индикатор, который в виде гистограммы характеризует количественный вес данных, находящихся в ней.
Урок: Условное форматирование в Excel
Мы смогли убедиться, что табличный процессор Excel предоставляет возможность использовать такой удобный инструмент, как гистограммы, совершенно в различном виде. Применение этой интересной функции делает анализ данных намного нагляднее.
Применение этой интересной функции делает анализ данных намного нагляднее.
Опишите, что у вас не получилось. Наши специалисты постараются ответить максимально быстро.
Помогла ли вам эта статья?
ДА НЕТСделайте гистограммы в Excel | Создатель гистограмм для Excel
Дом » Гистограммы и анализ возможностей
Устали делать гистограммы в Excel?
- Пакет инструментов анализа данных Excel занимает слишком много времени и требует слишком много шагов?
- Сложно ли показать пределы спецификации или нормальную кривую на гистограмме Excel?
- Слишком сложно рассчитать метрики возможностей процесса Cp Cpk? Показатели брака? Сигма?
vimeo.com/video/3585?autoplay=1&muted=1″ frameborder=»0″ allow=»autoplay; fullscreen» allowfullscreen=»»/>
Что такое гистограмма?
Гистограммы показывают разброс или дисперсию переменных данных.Верхняя (USL) и нижняя (LSL) спецификации заказчика определяют, насколько хорошо процесс соответствует требованиям заказчика. Измерения, выходящие за пределы спецификации, представляют собой точки данных, которые не соответствуют требованиям заказчика.
Как работает средство создания гистограмм макросов QI?
QI Macros устанавливается прямо в Excel:
- Point — Просто выберите данные на листе Excel.
- Щелкните — в меню «Макросы QI» в Excel и выберите «Гистограмма с Cp Cpk».
- Анализируйте и улучшайте — Макросы QI предложат вам указать пределы спецификации, выполнить вычисления гистограммы и нарисовать гистограмму с кривой для вас.

Чем хорош QI Macros Histogram Maker в Excel?
- Вычисляет более 20 показателей анализа возможностей процесса, включая Cp Cpk и Pp Ppk.
- Рисует колоколообразную кривую.
- Интерактивно:
- Расчеты можно просматривать и обновлять в таблице Excel, созданной с помощью макросов QI.
- Позволяет экспериментировать с тем, как ограничения спецификации влияют на Cp Cpk, изменяя их в таблице расчетов гистограммы.
- Позволяет настроить интервалы бина гистограммы и приблизительное количество полос.
Я очень впечатлен программой QI Macros. Я работаю с Excel восемь часов в день и думал, что написал макросы, которые сделали меня эффективным. Только макросы контрольных диаграмм и гистограмм в QI Macros сэкономили мне часы работы и позволили мне представить данные руководству в понятном формате.
— Кайл Допп
Решения First Choice
Почему выбирают макросы QI для анализа возможностей и построения гистограмм?
Доступный
- Только 299 долларов США — меньше с оптовыми скидками
- Без годовой платы
- Бесплатная техническая поддержка
Простота использования
- Работает прямо в Excel
- Вычисляет Cp Cpk Pp Ppk
- Точные результаты, не беспокоясь
Проверено и надежно
- 100 000 пользователей в 80 странах
- Празднование 20-летия
- Five Star CNET Rating — Не содержит вирусов
Создайте и используйте гистограмму — ArcGIS Insights
Гистограммы объединяют числовые данные в группы с равным интервалом, называемые ячейками, и отображают частоту значений в каждой ячейке. Гистограмма создается с использованием одного числового поля или поля коэффициент / соотношение.
Гистограмма создается с использованием одного числового поля или поля коэффициент / соотношение.
Гистограммы могут ответить на такие вопросы о ваших данных, как: Каково распределение числовых значений и их частота встречаемости в наборе данных? Есть выбросы?
Пример
Неправительственная организация здравоохранения изучает уровень ожирения среди подростков в США. Гистограмма частоты ожирения среди молодежи в каждом штате может использоваться для определения распределения показателей ожирения, включая наиболее и наименее распространенные частоты и общий диапазон.
Гистограмма выше показывает нормальное распределение и указывает, что наиболее часто встречающиеся значения находятся в диапазоне от 10 до 14 процентов.
Увеличение или уменьшение количества ячеек может повлиять на то, как вы анализируете свои данные. Пока данные не меняются, его внешний вид может. Важно выбрать подходящее количество бункеров для ваших данных, чтобы шаблоны в данных не были неправильно истолкованы. Слишком мало интервалов может скрыть важные закономерности, а слишком большое число интервалов может сделать небольшие, но ожидаемые колебания данных важными.На следующем рисунке показан пример подходящего количества ячеек для данных. Каждая ячейка содержит диапазон примерно 1%, и данные можно исследовать в более мелком масштабе, чтобы увидеть закономерности, которые не видны при использовании шести ячеек. В этом случае возникает закономерность нормального распределения вокруг среднего с небольшим, но, вероятно, не значительным перекосом влево.
Слишком мало интервалов может скрыть важные закономерности, а слишком большое число интервалов может сделать небольшие, но ожидаемые колебания данных важными.На следующем рисунке показан пример подходящего количества ячеек для данных. Каждая ячейка содержит диапазон примерно 1%, и данные можно исследовать в более мелком масштабе, чтобы увидеть закономерности, которые не видны при использовании шести ячеек. В этом случае возникает закономерность нормального распределения вокруг среднего с небольшим, но, вероятно, не значительным перекосом влево.
Создать гистограмму
Чтобы создать гистограмму, выполните следующие действия:
- Выберите числовое поле или поле «коэффициент / соотношение».
- Создайте гистограмму, выполнив следующие действия:
- Перетащите выбранные поля на новую карточку.
- Наведите указатель мыши на зону сброса карты.

- Перетащите выбранные поля на гистограмму.
Совет:
Вы также можете создавать диаграммы, используя меню «Диаграмма» над панелью данных или кнопку «Тип визуализации» на существующей карточке. Для меню «Диаграмма» будут включены только диаграммы, совместимые с выбранными вами данными. Для меню типа визуализации будут отображаться только совместимые визуализации (включая карты, диаграммы или таблицы).
Гистограммы также можно создать с помощью функции «Просмотр гистограммы», доступ к которой осуществляется с помощью кнопки «Действие» в разделе «Найти ответы»> «Как оно распространяется?».
Примечания по использованию
Гистограммы обозначаются отдельными значениями. Вы можете использовать кнопку «Параметры слоя», чтобы изменить цвет символа и цвет контура, которые будут применены ко всем ячейкам.
При создании гистограммы Insights автоматически вычисляет соответствующее количество интервалов для отображения ваших данных. Вы можете изменить количество ячеек с помощью ползунка вдоль оси x или щелкнув количество ячеек и введя новое число.
Вы можете изменить количество ячеек с помощью ползунка вдоль оси x или щелкнув количество ячеек и введя новое число.
Если выбранное количество интервалов не делится равномерно на диапазон данных, то интервалы будут вычисляться с использованием десятичных значений. В гистограммах в качестве меток ячеек отображаются округленные целые числа, а не десятичные дроби. Округленные целые числа предназначены только для отображения, а десятичные значения используются для всех вычислений. В случае, когда ячейка включает значения данных, близкие к верхнему или нижнему пределу, а метка округлена, начальное и конечное значения ячейки могут отображаться некорректно, поскольку метки отображают округленные значения, а не десятичные дроби.
Используйте кнопку статистики диаграммы для отображения среднего, медианного и нормального распределения данных. Кривая нормального распределения представляет ожидаемое распределение случайной выборки непрерывных данных, где наибольшая частота значений сосредоточена вокруг среднего, а частота значений уменьшается по мере увеличения или уменьшения значений от среднего. Кривая нормального распределения полезна для определения наличия смещения в ваших данных (например, данные имеют более высокую частоту низких значений) или выбросов.
Кривая нормального распределения полезна для определения наличия смещения в ваших данных (например, данные имеют более высокую частоту низких значений) или выбросов.
Используйте кнопку «Тип визуализации» для прямого переключения между гистограммой и градуированной картой символов или сводной таблицей.
Используйте кнопку «Перевернуть карточку» для просмотра обратной стороны карточки. Вкладка «Информация о карте» предоставляет информацию о данных на карте, а вкладка «Экспорт данных» позволяет пользователям экспортировать данные с карты.
На обратной стороне гистограммы отображаются следующие вычисленные значения: среднее значение, медиана, стандартное отклонение, асимметрия и эксцесс (упрощенно). Асимметрия и эксцесс описаны в следующей таблице:
| Статистика | Описание |
|---|---|
Асимметрия | Асимметрия определяет симметричность распределения данных. Значения асимметрии могут быть нулевыми, отрицательными или положительными, как показано ниже:
|
Эксцесс | Эксцесс описывает форму частотного распределения и дает меру вероятности того, что распределение приведет к выбросам. Упрощенные значения эксцесса могут быть нулевыми, отрицательными или положительными, как показано ниже:
|
Отзыв по этой теме?
График гистограммы— MATLAB
Алгоритм биннинга, заданный как одно из значений в этой таблице.
Значение | Описание |
|---|---|
| По умолчанию |
| Правило Скотта оптимально, если данные близки к нормальному распространению. Это правило также подходит для большинства других дистрибутивов.(-1/3) . |
| Правило Вольноотпущенника-Диакониса менее чувствительно
к выбросам в данных, и может быть больше
подходит для данных с распределениями с тяжелым хвостом. |
| Целочисленное правило полезно с целым числом
data, поскольку он создает корзину для каждого целого числа.Это
использует ширину бункера 1 и размещает края бункера наполовину
между целыми числами. Чтобы случайно не создать
слишком много ящиков, вы можете использовать это правило, чтобы создать
ограничение в 65536 ячеек (2 16 ). Примечание |
| Правило Стерджеса популярно благодаря
простота.Он выбирает количество ящиков, которые будут |
| Правило квадратного корня широко используется в других
программные пакеты. |
гистограмма не всегда выбирает количество интервалов, используя эти точные
формулы. Иногда количество бункеров немного регулируют, чтобы края бункера падали на
«красивые» номера.
Для данных datetime метод bin может быть одной из этих единиц времени:
'секунда' | 'месяц' |
'минута' | 'четверть' |
' день ' | ' декада ' |
' неделя ' | ' век ' |
Для данных продолжительности метод бункера может быть одной из этих единиц.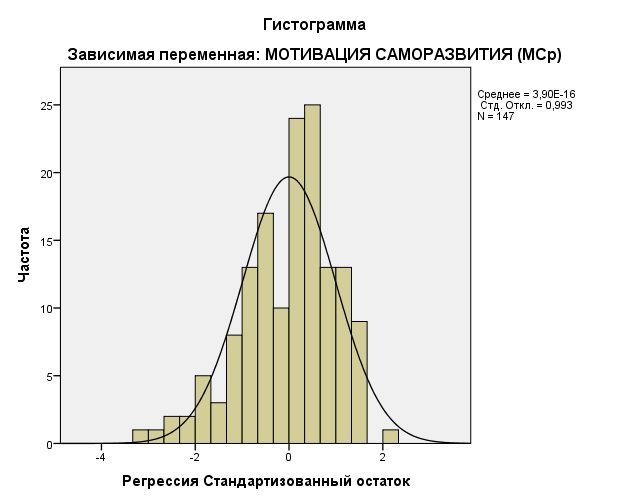 времени:
времени:
'секунда' | 'день' |
'минута' | 'год' |
Если вы укажете BinMethod с данными даты, времени или продолжительности, то
Гистограмма может использовать максимум 65 536 интервалов (или
2 16 ).Если для указанной продолжительности ячеек требуется больше ячеек,
тогда гистограмма использует большую ширину ячейки, соответствующую максимальному
количество бункеров.
Эта опция не применяется к гистограммам категориальных данных.
Примечание
Если вы установите BinLimits , NumBins , BinEdges ,
или свойство BinWidth , затем свойство BinMethod установлен на «ручной» .
Пример: гистограмма (X, 'BinMethod', 'integer') создает
гистограмма с ячейками, центрированными по целым числам.
- обзор | Темы ScienceDirect
Мы начнем с определений базовой одномерной статистики изображения, которая применяется к одноканальным изображениям, а затем расширим обсуждение до многомерной статистики , чтобы включить мультиспектральные и мультисенсорные изображения.
4.3.1 Гистограмма
Гистограмма изображения описывает статистическое распределение пикселей изображения с точки зрения количества пикселей на каждом DN. Он вычисляется просто путем подсчета количества пикселей в каждом «бункере» DN и деления на общее количество пикселей в изображении: N ,
(4.1) histDN = количество (DN) / N
.
Гистограмма часто связана с функцией плотности вероятности (PDF) статистики,
(4.2) histDN≈PDF (DN)
, но эта связь математически проблематична, потому что (1) PDF определяется для непрерывного переменных, и (2) он правильно используется только для статистических распределений случайного процесса.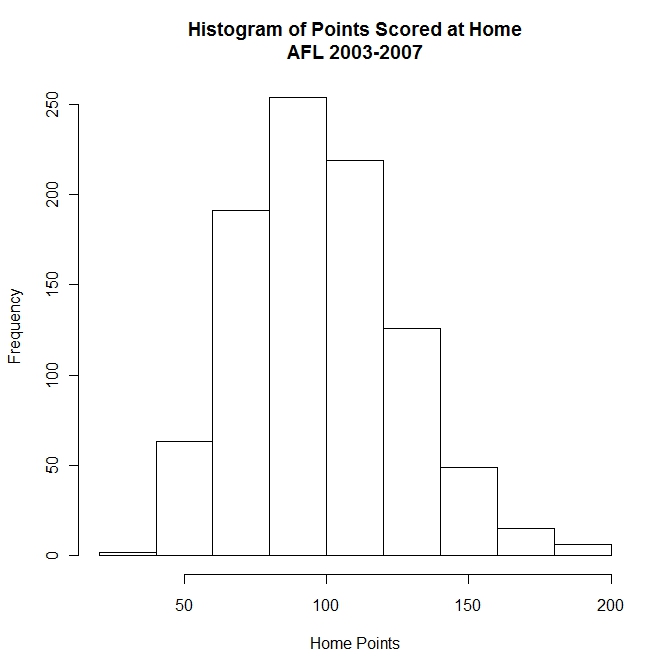 Помимо вопроса о сравнении дискретных и непрерывных переменных, изображения редко рассматриваются как экземпляры случайного процесса, а скорее как отдельные массивы данных. 2 Гистограмма, следовательно, является более подходящим описанием для цифровых изображений.
Помимо вопроса о сравнении дискретных и непрерывных переменных, изображения редко рассматриваются как экземпляры случайного процесса, а скорее как отдельные массивы данных. 2 Гистограмма, следовательно, является более подходящим описанием для цифровых изображений.
Гистограммы больших изображений участков суши, как правило, одномодальные (т. Е. Имеют один «пик») с расширенным хвостом в сторону более высоких DN s, то есть более высоких яркостей сцены (рис. 4-3). Важно помнить, что гистограмма изображения указывает только количество пикселей на каждом DN ; он не содержит информации о пространственном распределении этих пикселей.Однако иногда пространственную информацию можно вывести из гистограммы. Например, сильно бимодальная гистограмма обычно указывает на два доминирующих материала в сцене, такие как земля и вода. Нельзя сделать вывод о том, насколько пиксели в каждой категории пространственно связаны. Например, изображения в ближнем ИК-диапазоне сцены со множеством небольших озер и сцены прибрежной зоны океана могут иметь похожие бимодальные гистограммы.
РИСУНОК 4-3. Пример гистограммы изображения в сравнении с распределением Гаусса с тем же средним значением и дисперсией.Обратите внимание на асимметрию гистограммы, которая не является нетипичной и кажется мультимодальной.
Гистограмма изображения - полезный инструмент для увеличения контрастности . Например, обычная методика повышения контрастности «расширяет» диапазон DN s и «зажимает» или ограничивает его на одном или обоих концах, что приводит к определенному проценту насыщенных пикселей. Соответствующие пороговые значения DN могут быть получены из гистограммы в процентах от общего количества пикселей в изображении.
Нормальное распределение
В дистанционном зондировании, как и в большинстве областей науки и техники, часто математически удобно принять нормальное распределение (гауссово) для независимых, одинаково распределенных выборок из случайного процесса. В одном измерении это непрерывное распределение имеет вид
(4. 3) N (f; μ, σ) = 1σ2πe - [(f-μ) 22σ2]
3) N (f; μ, σ) = 1σ2πe - [(f-μ) 22σ2]
, который имеет знакомую форму, показанную на рис. 4-3. Центроид распределения равен μ, а его ширина пропорциональна σ.Хотя нормальное распределение не подходит в качестве глобальной модели для большинства изображений, оно широко используется для моделирования распределения подмножеств пикселей, имеющих сходные характеристики в изображении, в целях классификации (глава 9).
4.3.2 Кумулятивная гистограмма
Некоторые алгоритмы обработки изображений, в частности выравнивание гистограмм, сопоставление гистограмм и удаление полос (Richards and Jia, 1999), требуют функции, совокупной гистограммы (chist) , полученной из гистограммы следующим образом ,
(4.4) chistDN = ∑DN = DNminDNhistDN
.
Совокупная гистограмма - это доля пикселей в изображении с DN , меньшим или равным указанному DN. Это монотонная функция DN , так как она может только увеличиваться по мере накопления каждого значения гистограммы. Поскольку гистограмма, как определено в формуле. (4-1) имеет единицу площади, асимптотический максимум кумулятивной гистограммы равен единице (рис. 4-4). В этой нормализованной форме кумулятивная гистограмма также называется кумулятивной функцией распределения (CDF ) (Castleman, 1996), хотя эта связь имеет те же теоретические проблемы, что и уравнение.(4-2).
Поскольку гистограмма, как определено в формуле. (4-1) имеет единицу площади, асимптотический максимум кумулятивной гистограммы равен единице (рис. 4-4). В этой нормализованной форме кумулятивная гистограмма также называется кумулятивной функцией распределения (CDF ) (Castleman, 1996), хотя эта связь имеет те же теоретические проблемы, что и уравнение.(4-2).
РИСУНОК 4-4. Сравнение примерной кумулятивной гистограммы изображения с кумулятивной гауссовой гистограммой с использованием тех же данных, что и на рис. 4-3.
4.3.3 Статистические параметры
Среднее значение DN можно рассчитать двумя способами:
(4.5) μ = 1N∑p = 1NDNp = ∑DN = DNminDNmaxDN × histDN
Первый подход добавляет DN s всех пикселей изображения и делится на общее количество пикселей, чтобы получить среднее значение DN. Второй подход взвешивает каждый DN по соответствующему значению гистограммы (часть изображения, имеющего это DN ) и суммирует взвешенные DN с. Если гистограмма уже доступна, последняя форма, известная как первый момент гистограммы, является более эффективным вычислением. Разница DN определяется выражением
Если гистограмма уже доступна, последняя форма, известная как первый момент гистограммы, является более эффективным вычислением. Разница DN определяется выражением
(4.6) σ2 = 1N-1∑p = 1N (DNp-μ) 2 = NN-1∑DN = DNminDNmax (DN-μ) 2 × histDN
, где либо расчет может быть использован, как в формуле. (4-5). Вторая форма - это секундный момент гистограммы. В сумме по пикселям используется N -1, а не N , когда среднее значение должно быть оценено на основе данных, а не априори из распределения (Press et al., 1992). Стандартное отклонение DN , σ, является квадратным корнем из дисперсии.
Среднее значение и дисперсия достаточны для определения нормального или гауссовского распределения (уравнение (4-3)). Если гистограмма унимодальная и симметричная, гауссово распределение может быть неплохой моделью для реальных данных. Однако, как отмечалось ранее, глобальные гистограммы изображений имеют тенденцию быть асимметричными, а иногда и мультимодальными. Независимо от того, является ли распределение нормальным или нет, среднее значение и дисперсия DN полезны.Как обсуждается ниже, стандартное отклонение изображения можно использовать как меру контраста изображения, поскольку оно является мерой ширины гистограммы, то есть разброса в DN с.
Независимо от того, является ли распределение нормальным или нет, среднее значение и дисперсия DN полезны.Как обсуждается ниже, стандартное отклонение изображения можно использовать как меру контраста изображения, поскольку оно является мерой ширины гистограммы, то есть разброса в DN с.
Иногда полезны другие статистические параметры, включая режим ( DN , при котором гистограмма максимальна), медиана ( DN , которая делит область гистограммы пополам, при этом 50% пикселей ниже медианы и 50% выше), и меры более высокого порядка асимметрии (асимметрия),
(4.7) асимметрия = 1N∑p = 1N (DNp-μσ) 3 = ∑DN = DNminDNmax (DN-μσ) 3 × histDN
и эксцесс (резкость пика относительно нормального распределения) (Press et al. , 1986; Pratt, 1991),
(4.8) эксцесс = [1N∑p = 1N (DNp-μσ4)] - 3 = [∑DN = DNminDNmax (DN-μσ) 4 × histDN] -3
Асимметрия равна нулю для любой симметричной гистограммы. Гистограмма с длинным хвостом в сторону большего DN s имеет положительную асимметрию, что типично для изображений дистанционного зондирования. Для нормального распределения эксцесс равен нулю.Если гистограмма имеет положительный эксцесс, то пик более резкий, чем пик гауссианы; отрицательный эксцесс означает, что пик менее резкий, чем пик по Гауссу. Обратите внимание, что асимметрия и эксцесс нормированы на σ и не имеют единиц измерения, в отличие от среднего и стандартного отклонения. Для данных изображения, представленных на рис. 4-3, мы имеем μ = 34,1, σ = 9,12, асимметрию = 1,78 и эксцесс = 4,32, что указывает на степень асимметрии и резкости пика гистограммы. Асимметрия и эксцесс весьма чувствительны к выбросам , пикселям с DN s далеко от основного распределения из-за их высокого порядка.
Агрегация гистограмм | Руководство по Elasticsearch [7.15]
Агрегирование гистограммы
Агрегирование на основе источника значений с несколькими сегментами, которое может применяться к извлеченным числовым значениям или значениям числового диапазона.
из документов. Он динамически создает сегменты фиксированного размера (также известные как интервал) по значениям. Например, если
документы имеют поле, содержащее цену (числовую), мы можем настроить эту агрегацию для динамического создания корзин с
интервал 5 (в случае цены может составлять 5 долларов).Когда выполняется агрегирование, поле цены каждого документа
будет оцениваться и округляться до ближайшего к нему сегмента - например, если цена составляет 32 , а размер ведра
равно 5 , тогда округление даст 30 , и, таким образом, документ «упадет» в корзину, связанную с
ключ 30 .
Чтобы сделать это более формальным, вот используемая функция округления:
bucket_key = Math.floor ((значение - смещение) / интервал) * интервал + смещение
Для значений диапазона документ может быть разделен на несколько сегментов.Первый сегмент вычисляется из нижнего граница диапазона точно так же, как вычисляется сегмент для одного значения. Последний сегмент вычисляется в том же путь от верхней границы диапазона, и диапазон считается во всех сегментах между ними и включая эти два.
Интервал должен быть положительным десятичным числом, а смещение должно быть десятичным в [0, интервал) (десятичное число больше или равно 0 и меньше интервал )
Следующий фрагмент "сегментирует" товары на основе их цены с интервалом 50 :
POST / sales / _search? Size = 0
{
"aggs": {
"Цены": {
"гистограмма": {
"поле": "цена",
«интервал»: 50
}
}
}
} И ответ может быть следующий:
{
...
"агрегаты": {
"Цены": {
"ведра": [
{
«ключ»: 0,0,
«doc_count»: 1
},
{
«ключ»: 50,0,
«doc_count»: 1
},
{
«ключ»: 100,0,
«doc_count»: 0
},
{
«ключ»: 150,0,
«doc_count»: 2
},
{
«ключ»: 200,0,
«doc_count»: 3
}
]
}
}
} Минимальное количество документов
Ответ, приведенный выше, показывает, что ни один из документов не имеет цены в диапазоне [100, 150) .По умолчанию
ответ заполнит пробелы в гистограмме пустыми сегментами. Можно изменить это и запросить сегменты с
более высокое минимальное количество благодаря настройке min_doc_count :
POST / sales / _search? Size = 0
{
"aggs": {
"Цены": {
"гистограмма": {
"поле": "цена",
«интервал»: 50,
«min_doc_count»: 1
}
}
}
} Ответ:
{
...
"агрегаты": {
"Цены": {
"ведра": [
{
«ключ»: 0.0,
«doc_count»: 1
},
{
«ключ»: 50,0,
«doc_count»: 1
},
{
«ключ»: 150,0,
«doc_count»: 2
},
{
«ключ»: 200,0,
«doc_count»: 3
}
]
}
}
} По умолчанию гистограмма возвращает все сегменты в пределах диапазона самих данных, то есть документы с
наименьшие значения (на которых с гистограммой) будут определять минимальный сегмент (сегмент с самым маленьким ключом) и
документы с наивысшими значениями определяют максимальный сегмент (сегмент с самым высоким ключом).Часто, когда
при запросе пустых корзин это вызывает путаницу, особенно когда данные также фильтруются.
Чтобы понять, почему, давайте рассмотрим пример:
Допустим, вы фильтруете свой запрос, чтобы получить все документы со значениями от 0 до 500 , кроме того, вы хотите
чтобы разрезать данные по цене, используя гистограмму с интервалом 50 . Вы также указываете "min_doc_count": 0 , как вы
люблю получать все ведра, даже пустые.Если случится так, что все товары (документы) имеют цены выше 100 ,
первое ведро, которое вы получите, будет с ключом 100 . Это сбивает с толку, как часто вам хотелось бы
чтобы получить эти ведра от 0 до 100 .
С настройкой extended_bounds теперь вы можете "принудительно" агрегировать гистограмму, чтобы начать построение сегментов на определенном мин. Значение , а также продолжать наращивать ведра до значения макс. (даже если документов больше нет).С использованием extended_bounds имеет смысл только тогда, когда min_doc_count равно 0 (пустые сегменты никогда не будут возвращены, если min_doc_count больше 0).
Обратите внимание, что (как следует из названия) extended_bounds - это , а не сегментов фильтрации. То есть, если extended_bounds.min больше
чем значения, извлеченные из документов, документы по-прежнему будут определять, какой будет первая корзина (и
то же самое и с расширенными границами .max и последнее ведро). Для фильтрации сегментов следует вложить агрегацию гистограммы
под диапазоном фильтруйте агрегацию с соответствующими настройками от / до .
Пример:
POST / sales / _search? Size = 0
{
"запрос": {
"constant_score": {"filter": {"range": {"price": {"to": "500"}}}}
},
"aggs": {
"Цены": {
"гистограмма": {
"поле": "цена",
«интервал»: 50,
"extended_bounds": {
«мин»: 0,
«макс»: 500
}
}
}
}
} При агрегировании диапазонов сегменты основываются на значениях возвращенных документов.Это означает, что ответ может включать сегменты вне диапазона запроса. Например, если ваш запрос ищет значения больше 100, и у вас есть диапазон охватывающий от 50 до 150 и интервал 50, этот документ будет разделен на 3 сегмента - 50, 100 и 150. Как правило, это лучше всего рассматривать шаги запроса и агрегирования как независимые - запрос выбирает набор документов, а затем агрегация группирует эти документы независимо от того, как они были выбраны. См. Примечание о диапазоне ковша поля для получения дополнительной информации и примера.
hard_bounds является аналогом extended_bounds и может ограничивать диапазон сегментов в гистограмме. это
особенно полезно в случае диапазонов открытых данных, которые могут привести к очень большому количеству сегментов.
Пример:
POST / sales / _search? Size = 0
{
"запрос": {
"constant_score": {"filter": {"range": {"price": {"to": "500"}}}}
},
"aggs": {
"Цены": {
"гистограмма": {
"поле": "цена",
«интервал»: 50,
"hard_bounds": {
«мин»: 100,
«макс»: 200
}
}
}
}
} В этом примере, даже если диапазон, указанный в запросе, составляет до 500, гистограмма будет иметь только 2 сегмента, начиная с 100 и 150.Все остальные сегменты будут опущены, даже если в результатах присутствуют документы, которые должны попасть в эти сегменты.
По умолчанию возвращаемые сегменты сортируются по их ключу по возрастанию, хотя поведение порядка можно контролировать с помощью
настройка порядка . Поддерживает те же функции order , что и Terms Aggregation .
По умолчанию ключи сегмента начинаются с 0, а затем продолжаются через равные интервалы. интервал , эл.грамм. если интервал равен 10 , первые три сегмента (при условии
внутри них есть данные) будет [0, 10) , [10, 20) , [20, 30) . Ведро
границы могут быть смещены с помощью параметра смещение .
Лучше всего это проиллюстрировать на примере. Если имеется 10 документов со значениями от 5 до 14, использование интервала 10 приведет к
два ведра по 5 документов в каждом. Если используется дополнительное смещение 5 , будет только одна отдельная корзина [5, 15) , содержащая все 10
документы.
По умолчанию сегменты возвращаются в виде упорядоченного массива. Также возможно запросить ответ в виде хеша вместо ключа ведра ключи:
POST / sales / _search? Size = 0
{
"aggs": {
"Цены": {
"гистограмма": {
"поле": "цена",
«интервал»: 50,
"keyed": правда
}
}
}
} Ответ:
{
...
"агрегаты": {
"Цены": {
"buckets": {
"0.0": {
«ключ»: 0,0,
«doc_count»: 1
},
«50.0 ": {
«ключ»: 50,0,
«doc_count»: 1
},
"100.0": {
«ключ»: 100,0,
«doc_count»: 0
},
"150.0": {
«ключ»: 150,0,
«doc_count»: 2
},
"200.0": {
«ключ»: 200,0,
«doc_count»: 3
}
}
}
}
} Параметр отсутствует параметр определяет, как следует обрабатывать документы, в которых отсутствует значение.
По умолчанию они будут игнорироваться, но их также можно рассматривать как если бы они
имел значение.
POST / sales / _search? Size = 0
{
"aggs": {
"количество": {
"гистограмма": {
"поле": "количество",
«интервал»: 10,
«пропавших без вести»: 0
}
}
}
} Документы без значения в поле количества |
При выполнении агрегирования гистограммы по полям гистограммы вычисляется общее количество отсчетов для каждого интервала.
Например, выполнение агрегирования гистограммы по следующему индексу, в котором хранятся предварительно агрегированные гистограммы. с показателями задержки (в миллисекундах) для разных сетей:
PUT metrics_index / _doc / 1
{
"network.name": "net-1",
"latency_histo": {
"значения": [1, 3, 8, 12, 15],
«считает»: [3, 7, 23, 12, 6]
}
}
PUT metrics_index / _doc / 2
{
"network.name": "net-2",
"latency_histo": {
"значения": [1, 6, 8, 12, 14],
«считает»: [8, 17, 8, 7, 6]
}
}
POST / metrics_index / _search? Size = 0
{
"aggs": {
"latency_buckets": {
"гистограмма": {
"поле": "latency_histo",
«интервал»: 5
}
}
}
} Гистограмма Агрегация суммирует счетчики каждого интервала, вычисленные на основе значений , и
верните следующий вывод:
{
...
"агрегаты": {
"Цены": {
"ведра": [
{
«ключ»: 0,0,
«doc_count»: 18
},
{
«ключ»: 5,0,
«doc_count»: 48
},
{
«ключ»: 10,0,
«doc_count»: 25
},
{
«ключ»: 15,0,
«doc_count»: 6
}
]
}
}
} Агрегация гистограмм - это агрегация сегментов, которая разбивает документы на сегменты, а не вычисляет показатели по полям, например агрегации показателей делают.Каждая корзина представляет собой набор документов, на которых могут работать субагрегации. С другой стороны, поле гистограммы - это предварительно агрегированное поле, представляющее несколько значений внутри одного поля: ведра числовых данных и количество предметов / документов для каждого ведра. Это несоответствие между ожидаемыми входными данными гистограммы. (ожидаются необработанные документы) и поле гистограммы (которое предоставляет сводную информацию) ограничивают результат агрегации только количество документов для каждого сегмента.
Следовательно, при выполнении агрегации гистограммы по полю гистограммы никакие субагрегации не допускаются.
Кроме того, при выполнении агрегирования гистограммы по полю гистограммы отсутствует параметр не поддерживается.
1.6.2 - Гистограммы
Если имеется много точек данных, и мы хотели бы увидеть распределение данных, мы можем представить данные в виде частотной гистограммы или гистограммы относительной частоты .
Гистограмма похожа на гистограмму, но предназначена для количественных данных. Чтобы создать гистограмму, данные необходимо сгруппировать в интервалы классов. Затем создайте подсчет, чтобы показать частоту (или относительную частоту) данных в каждом интервале. Относительная частота - это частота в определенном классе, деленная на общее количество наблюдений. Ширина полосок соответствует интервалу классов, а высота - частоте (или относительной частоте).
Пример гистограммы
Джессика взвешивается каждую субботу в течение последних 30 недель.В таблице ниже показаны ее зарегистрированные веса в фунтах.
135 | 137 | 136 | 137 | 138 | 139 |
140 | 139 | 137 | 140 | 142 | 146 |
148 | 145 | 139 | 140 | 142 | 143 |
144 | 143 | 141 | 139 | 137 | 138 |
139 | 136 | 133 | 134 | 132 | 132 |
Создайте гистограмму ее веса.
Ответ
Для гистограмм обычно требуется от 5 до 20 интервалов. Поскольку диапазон данных составляет от 132 до 148, удобно иметь класс шириной 2, поскольку это даст нам 9 интервалов.
- 131,5–133,5
- 133,5–135,5
- 135,5–137,5
- 137,5–139,5
- 139,5–141,5
- 141,5–143,5
- 143,5–145,5
- 145,5–147,5
- 147,5–149,5
Причина, по которой мы выбираем конечные точки как.5, чтобы избежать путаницы, принадлежит ли конечная точка интервалу слева от него или интервалу справа. Альтернативой является указание соглашения о конечной точке. Например, Minitab включает левую конечную точку и исключает правую конечную точку.
Имея интервалы, можно построить таблицу частот, а затем нарисовать гистограмму частот или получить гистограмму относительных частот для построения гистограммы относительных частот. Следующая гистограмма создается Minitab, когда мы указываем средние точки для определения интервалов в соответствии с интервалами, выбранными выше.
Если мы не укажем среднюю точку для определения интервалов, Minitab по умолчанию выберет другой набор интервалов классов, в результате чего будет получена следующая гистограмма. Согласно соглашению включить левую и исключить правую конечную точку, наблюдение 133 включено в класс 133-135.
Обратите внимание, что различный выбор интервалов классов приведет к разным гистограммам. Гистограммы относительной частоты строятся почти так же, как гистограммы частот, за исключением того, что вертикальная ось представляет относительную частоту, а не частоту.Для визуального сравнения распределения двух наборов данных лучше использовать относительную частоту, а не гистограмму частот, поскольку для всех относительных частот используется одна и та же вертикальная шкала - от 0 до 1.
Как пользоваться гистограммой камеры
Гистограмма - это графическое представление тонального диапазона на фотографии, и ее анализ тонального диапазона изображения обеспечивает точную проверку экспозиции. Гистограмма отображает диапазон тонов изображения от самых темных в левой части графика (0 в цифровом выражении) до самых светлых в правой части (255 в цифровом выражении).
Вы можете думать об этом так: экспонометр считывает сцену до того, как вы сделаете снимок; гистограмма анализирует только что сделанный снимок. Вы можете выбрать, чтобы гистограмма отображалась на ЖК-дисплее камеры вместе с отображением воспроизведения вашей фотографии (точную процедуру см. В руководстве к вашей камере Nikon).
Вот что такое гистограмма. Но почему это важный, фундаментальный инструмент цифровой фотографии? Просто потому, что ваше понимание гистограммы подскажет вам, нужно ли отрегулировать экспозицию, и укажет, как это сделать.
Однако первое, что нужно понять, это то, что не всегда необходимо использовать гистограмму. На самом деле, выборочное использование лучше всего. Мало кто из фотографов смотрит на гистограмму для каждой сделанной фотографии. В большинстве случаев измеритель вашей камеры точно и точно установит правильную экспозицию для сцены.
Но вы должны проверить гистограмму, когда освещение сцены особенно сложно; когда в одной сцене присутствуют участки глубокой тени и яркого света; и когда вы собираетесь сделать серию изображений в одной и той же обстановке и хотите убедиться, что ваша экспозиция соответствует цели.
Взглянув на гистограмму, вы узнаете, какие части фотографии переэкспонированы или недоэкспонированы. Передержка означает отсутствие деталей в светлых участках; недодержка, потеря детализации в тенях. Гистограмма мгновенно покажет ситуацию: сильная концентрация в левой части графика означает, что изображение недоэкспонировано и вы потеряли детали в теневых областях; сильная концентрация справа означает, что ваши блики могут быть нечеткими. Средство? Вы можете увеличить выдержку, закрыть диафрагму или уменьшить ISO, чтобы исправить передержку; противоположные настройки служат для коррекции недодержки.
Вот кое-что, что вы, возможно, захотите использовать в связи с гистограммой: предупреждение о передержке светлых участков.

 country, y=values, fill=country)) +
country, y=values, fill=country)) + для Apple это (0+92)/2=46, для Microsoft (92+218)/2=155 и т.д.
для Apple это (0+92)/2=46, для Microsoft (92+218)/2=155 и т.д.

 Здесь давайте посмотрим внимательнее на типы доступных гистограмм.
Здесь давайте посмотрим внимательнее на типы доступных гистограмм.

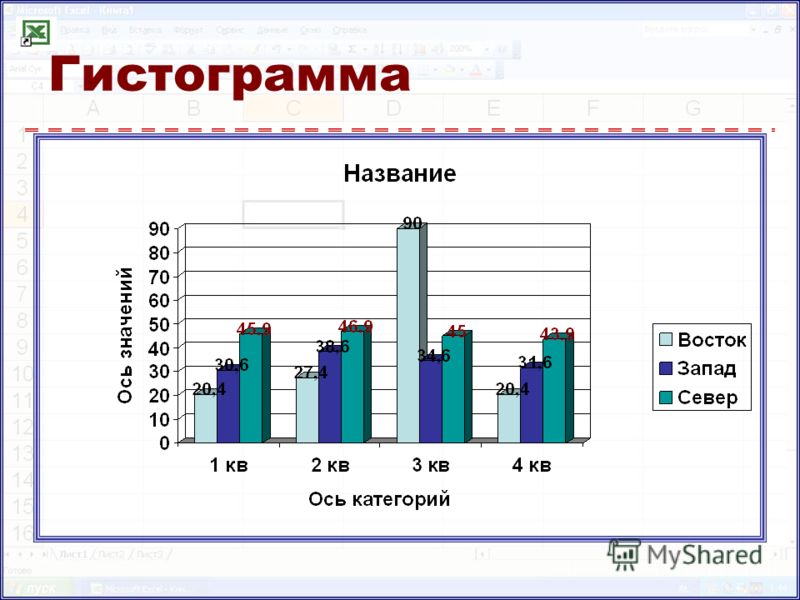
 Измерение асимметрии определяет, находится ли большинство значений распределения слева или справа от среднего. Асимметрия нормального распределения равна нулю, показывая равное количество данных по обе стороны от среднего.
Измерение асимметрии определяет, находится ли большинство значений распределения слева или справа от среднего. Асимметрия нормального распределения равна нулю, показывая равное количество данных по обе стороны от среднего. Распределения с относительно тяжелыми хвостами называются лептокуртическими и имеют эксцесс больше нуля.Распределения с относительно светлыми хвостами называются платикуртическими и имеют эксцесс меньше нуля. Эксцесс нормального распределения равен трем, или, при использовании упрощенного эксцесса, эксцесс нормального распределения равен нулю (это находится по той же формуле, что и эксцесс, минус 3).
Распределения с относительно тяжелыми хвостами называются лептокуртическими и имеют эксцесс больше нуля.Распределения с относительно светлыми хвостами называются платикуртическими и имеют эксцесс меньше нуля. Эксцесс нормального распределения равен трем, или, при использовании упрощенного эксцесса, эксцесс нормального распределения равен нулю (это находится по той же формуле, что и эксцесс, минус 3).
 (-1/3) ,
где
(-1/3) ,
где  Если диапазон данных больше
чем 65536, то целочисленное правило использует вместо этого более широкие интервалы.
Если диапазон данных больше
чем 65536, то целочисленное правило использует вместо этого более широкие интервалы.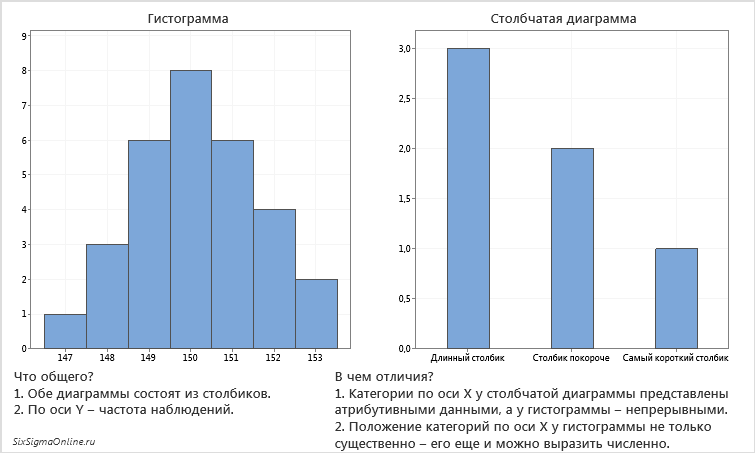 Выбирает количество ящиков
быть
Выбирает количество ящиков
быть