Идеальная фигура в геометрии: Идеальная фигура — amphiboly — ЖЖ — Главная

Содержание

Идеальная фигура — amphiboly — ЖЖ

location: да

music: ——————?

Круг — наиболее идеальная геометрическая фигура. Вы спросите: «Почему?», я отвечу: «Потому что круг не имеет углов. Вообще».
И с этим не поспоришь. Это аксиома. Круг он и есть круг. Ну, нет у него углов, потому что он круглый. И неоткуда им там взяться. В отличии от всех остальных геометрических фигур у круга нет и никогда не было никаких углов. Они ему не нужны, без надобности. Потому что это фигура такая. Круглая. Круг. Идеальная, я бы даже сказал. А раз идеальная — то и углы, которые постоянно зачем-то нужно сглаживать, не нужны. Конечно же это огромный плюс, когда дело касаемо обыкновенной геометрии, а вот если, к примеру, взять бытовой вопрос: “Ваш дом круглый, тогда как?”.
Первое, что приходит на ум — недоумение, а здоров ли Ваш оппонент, который задаёт такой провокационный вопрос? Но, спешу Вас успокоить — здоров.

И вопрошающий совсем даже не болен, как может показаться в начале. Да, круглые дома существуют, и не только в воспалённом воображении вашего собеседника (хотя такое и трудно вообразимо). Не знаю точное количество таковых, но то что два дома в природе существуют — однозначно.
Конечно, такое может показаться абсурдом, круглый дом, в голове сразу возникают ряд трудноразрешимых вопросов от осознания факта самого существования таких домов, которые где-то даже заводят в тупик и ступор, но факт остается фактом: Такие дома есть.
Трудно себе представить дом без углов, не правда ли? Это кажется чем-то невероятным, неправильным, не логичным. Но факты — вещь упрямая. И с этим не поспоришь.

Вот куда, скажите на милость, например, ставить расшалившихся детей? Как их наказывать, если дом круглый и у него нет углов? Вообще. Отсутствуют как данность.
В любом мало-мальски приличном доме есть специально отведённое место для воспитательных мер — угол. Ребенок нашалил, напроказничал, и тут же получил соответствующее наказание — постановку в угол.

До тех пор, пока не одумается и не поймёт собственную вину. Пусть стоит в углу. Думает. Хорошее место для размышлений, для познания мира. Если в доме хороший ремонт, то можно изучать красивые узоры на обоях. Если не очень — отколупывать ногтём шелушащуюся краску или старую штукатурку. Одним словом, в углу всегда найдётся чем заняться. Рано или поздно всё равно выпустят: Ну, не звери же родители? А как урок — угол вещь незаменимая в воспитательных целях. Факт.
И как, скажите, прикажете быть родителям, которые проживают в круглом доме? Как воспитывать ребёнка, будущего члена общества с понятиями о чувстве вины и наказании за содеянное? Дилемма. Тот ещё вопрос.

Или вот, ещё, ситуация: Человек с гостями культурно отдыхал. Выходной у него. Долго отдыхал. Всю ночь. Бывает такое? Бывает. Все мы люди, все мы человеки, и ни что человеческое нам не чуждо. Отдых человеку положен для расслабления уставшего организма и для поднятия бодрости духа в последующей трудовой деятельности.

Отдыхал человек долго, весело, со всеми втекающими и вытекающими последствиями. Дело ближе к утру. Основные гости разъехались и остался один — самый стойкий — гость. Но и он — гость дорогой — тоже спешно засобирался домой, потому что дела и всё такое. Пора и честь знать.
Гостеприимный же хозяин — буде не совсем трезв — решил сделать самому стойкому гостю презент. Ну, что тут удивительного, скажете Вы, презент он и есть презент. Подарок то бишь. Но презент преподнёс не простой, а… музыкальный. Называется — труба. Обычная такая труба, классическая. С костяным мундштуком и вентилями. Всё равно хозяину она не нужна (не обучен игре на оной), а гостю — приятно. Подарок же. И вот, гость спешно засобирался домой, с подарком на пару. Хвать его подмышку и был таков. Хозяин расслабился, размяк — хорошо. Можно и вздремнуть, апосля нелегкой ночки. Прыг в кроватку и давай давить на массу. Благодать.

Но, вдруг, во сне — слышь, Чу! — взбесившийся слон. И так он этот слон трубит неприятно, что сил нет никаких.

Топочет, значит, лапами своими громко, трубит в хобот: Спать не даёт, мешает.
Глаза конечно сами собой — хоть и с неохотой — разлепаются. Хозяин садится на кроватке, но трубящий слон не пропадает. Наоборот, такое ощущение, что трубит он где-то совсем рядом, где-то в голове, ну, или под окном. Что почти одно и тоже. Почти. Наконец, слегка очухавшись, хозяин понимает, что тут что-то не так. Выходит шатающейся походкой на балкон, смотрит вниз, а там, а там… нет, не слон, конечно же. Там гость дорогой стоит!
Гость, как и положено гостю под утро — всё ещё не трезв. И мало того что не трезв, он вполне себе весел и бодр (если не считать неустойчивого переминания с ноги на ногу и некой мягкости тела, гибкости). Стоит он внутри КРУГЛОГО дома и… правильно — трубит. Как тот слон из сна.
А утро хорошее такое: летнее, теплое, почти певчее. Для птах небесных. Соловушки должны петь, жаворонки ранние всякие. Но не поют. Молчат. Зато поёт гость. Точнее не поёт, а трубит в подарочную трубу.

И громко так трубит, что эхо от его трубения разносится аж по всему круглому дому. Это почти тоже самое, что в колодец крикнуть. Ты туда — ого, а оттуда — ого-го-го-го. С эхом красивым, с реверберацией. И эхо это самое носится по кругу, громко так, зычно. Долго носится, не хочет покидать пределы круглого дома. Потому что круг — это почти та же труба или колодец бездонный, а значит — идеальное место для звука. Есть где разгуляться. И гость доволен — подарок-то не пустяшный оказался, полезный — и уже слушатели первые (зрители), почитатели таланта так сказать, появились. Из окон.

Нет, ну понятно, что когда дом круглый, то сразу изо всех щелей, они, аки тараканы, слушатели, вылезают. Ручками машут, брависсимо кричат. Хозяину гостеприимному спросони кажется что все радуются, аплодируют, счастливы бесплатному концерту. Раннему. Ведь не каждый день на бесплатный концерт трубача попадаешь. Но нет, не радуются. Прислушавшись гостеприимный хозяин понимает — ругаются. А чего ругаются? Подумаешь, ну, даёт человек сольный концерт под открытым небом, так лето же!!! Опен эйр почти.

Другие бы радовались халяве, за так, а они… потому как слышит хозяин гостеприимный, что слова-то всё более не лестные доносятся в адрес дорогого гостя. Маму вспоминают евойную зачем-то. И не только её. Много кого ещё, аж язык не поворачивается повторить такое. А гостю хоть бы хны: Знай себе трубит и трубит. Радуется подарку. На лице улыбка, удовольствие. Небо над ним чистое-чистое, лазурное я бы даже сказал. Деревья зеленые-зеленые, едва колышутся от слабого ветерка. Всё хорошо, если бы не слушатели грубияны. Но, ничего не поделаешь, публика ноне такова — вечно чем-то недовольна. Ладно бы критики музыкальные, профессионалы, а то так, обычные слушатели. Обыватели. Без образования. Им медведь ещё в детстве на ухо наступил, а туда же — критиковать.

И видит хозяин гостеприимный с балкона, что атмосфера в круглом домике накаляется. Нет, солнышко ещё не взошло пока (утро же раннее-раннее), но уже горячо почему-то. Да и где ему, солнышку, сквозь круг замкнутый пробиться? Вокруг лишь стены домика круглого.

Бетонные. Непроницаемые. Пока поднимешься, проберёшься внутрь — уж и полдень на дворе. Но до полдня пока ещё далеко, а в воздухе-то уже горячо. Это значит от ауры слушателей атмосфера накалилась. Нравится поди людям. Или то спросони так кажется? Но, не важно. Суть такова, что зрители/слушатели вдруг стали гостю дорогому дары преподносить. В начале гостеприимный хозяин подумал что то цветы, в знак благодарности за бесплатный концерт, но нет, то не цветы были. То были продукты. Пищевые. Наверное, слушатели подумали, что гость дорогой голоден и стали преподносить ему явства. Уж больно трубил он зычно. Так слоны обычно трубят, когда голодны. Или когда на водопой идут. Так как колодец круглого дома изначально иссохший, не предназначенный для водопоя — значит то голод был. Это так слушатели/зрители подумали. Наверняка.

Хозяин гостеприимный был против такого утверждения, потому как вдоволь потчевал гостей. Всякостями. И не только. Одних жидких продуктов использованных вон целая батарея стоит на кухне.

Ждёт своего часа. Мусорки. Так что неправда их, слушателей. Сыты гости остались. По самое горлышко.

И вот давай они гостя дорого кормить, потчевать, почти как в зоопарке. Почти. Кидают ему пищу всякую разнообразную. И много так кидают, будто хотят накормить надолго вперёд, на всю жизнь его оставшуюся. Но так ведь не бывает, чтобы навсегда, впрок, не правда ли?
Хозяин гостеприимный глаза со страху прикрыл (кабы не поубивали гостя ненароком дарами своими), стоит, к шлепкам доносящимся снизу прислушивается. Потом осмелел чуток и один глазик приоткрыл. Видит, стоит гость дорогой, ничего себе, молодец, лавирует между дарами. Изворачивается. А дары-то всё больше из овощных культур. Яблочки там, помидорки всяки, картошка свежая. Реже -вареная или яйца. Деликатес. Почти. Знают наверное, что слоны — вегетарианцы, предпочитают растительную пищу, потому и не бросают мясные полуфабрикаты/продукты. Только забывают слушатели неблагодарные, что гость наш — не слон. Человек он.

Могли бы и мясца подкинуть немного. Ради приличия.
В общем, слушатели кидают продукты, гость уворачивается от них. Отказывается от даров, одним словом. Категорически. Уже плюс. В подтверждении хозяина гостеприимного слов. О сытости. Хозяин конечно понимает, что всё это хорошо, дары, все дела, но надо как-то и остужать сложившуюся ситуацию. И тихо так, тихо, сложив ладошки рупором, зовёт гостя дорогого, пшикает ему: “Пшшш… Кшшш… Пшшш…“, и ручкой машет, а гость дорогой стоит и ноль внимания. Трубит знай себе и трубит, как ни в чём не бывало. И с каждой минутой всё лучше и лучше. Уже и на слона даже не похоже. Получается что-то. Музыка выходит, рождается. Талант у гостя оказывается к духовым инструментам!
Гостеприимный хозяин почесал за ухом и тоже решил что-нибудь швыркнуть, дабы гость дорогой всё же обратил на него внимание. Отвлёкся, значит, от музицирования. Перерыв сделал. Антракт небольшой. Перекур.
Шатающейся походкой вернулся в квартиру и стоит, как осинка на ветру, раздумывает: “Чем бы в него таким пульнуть/швыркнуть, чтобы понял, что зову я его?”.

Долго думал.

А тем временем на улице уже полемика началась. Обсуждение услышанного. Кричат слушатели неблагодарные, благим матом, не восторгаются ни разу. Нервничают почему-то. И на бис не требуют. Наверное где-то сфальшивил гость дорогой во время исполнения. Не понимают, что у гостя это всего-лишь первые шаги к успеху. Первый концерт сольный, можно даже сказать — дебют. Требуют гостя дорогого зачем-то к бабушке евойной домой возвращаться… А он не хочет, не желает! Ему и тут неплохо. Тоже в диалог вступил. Говорит, лучше бы они сами своих предков посетили, желательно прямо сейчас. Может и направление указать, всем желающим. А-то, говорит, моду взяли, продуктами зазря швыряеться. Родственников бы лучше своих покормили. Всё толку больше, чем тротуары засорять/мусорить. А он сыт. По горло. Из гостей только. И ладно бы ещё свежие продукты предлагали к дегустации, а то всё больше порченные да просроченные!!! Никакого уважения к талантам начинающим. Позор, говорит!

Хозяин же гостеприимный тем временем пока диалоги задушевные велись нашёл искомое: Зажигалку импортную! Вещь в хозяйстве конечно полезная, нужная: огонь разводить, прикурить, опять же, можно. .. дорогу осветить, если тёмно, но… придётся вернуть. Зажигалка то гостева была. Забыл он её второпях. Так что вернуть надобно. Обязательно. Для порядку.

Возвращается хозяин гостеприимный на балкон и шварк зажигалку вниз, что есть силы ослабшие, гостю под ноги прям. И ничего вроде, нормально бросил. Точно. Почти. В гостя не попал, а всего лишь рядом. Что тоже неплохо. Но, недоразумение вышло. Вернуть-то он вернул, только совсем не так, как хотелось.
  Зажигалка — будь она не ладна — упала под ноги гостю и… взорвалась. Обдав ярким пламенем и опалив одёжу начинающего таланта. Тихо вмиг стало во дворе. Прервался гость дорогой от обсуждения музыкальных тем и ходов со слушателями/зрителями. Стоит опешив. Слушатели тоже поутихли, головы повернули и смотрят на хозяина гостеприимного — изучают. А хозяин и рад бы вниманию, но не того хотел. Хотел просто вещь вернуть, да внимания гостева, а не общественного, общесоциального. Но, ничего не поделаешь, приходится улыбаться всем, радоваться, ручкой махать да глазиком подмигивать. Слегка нетрезвым.
Гость стоит, инструмент вниз опустил и брюки изучает, не прожглась ли где дырка? Кулаком зачем-то воздух сотрясает. Знать беда приключилась всё же — прожглась дырочка малая. Может и большая даже, сверху не видно. Ну, вот и опешил хозяин гостеприимный вдруг, сконфузился: мало того что вещь законную не вернул в цельности, так и другую подпортил. Стыдно стало хозяину гостеприимному, ручки в стороны разводит, сожаление выказывает. Гримасу виноватую гримасничает.
  А зрители/слушатели злобные, наоборот, аплодировать начали, восторгаться случившимся. Недобрые люди, однозначно. Может у гостя то единственный костюм концертный был, а они радуются, вещи порченой. Злыдни!
  Гость погоревал-погоревал маленько, изучил костюмчик подпорченный, и сел на бордюрчик каменный… Отошёл от шока недавнего и молвил слова, достойные киноленты какой-нибудь музыкально-новогодней комедьи:”Кто так строит, люди? Ну, кто так строит?!!”.
Огорчился конечно, голову свесил понурив и тяжело вздохнул. Потом собрался с силами, встал, и, пошатываясь, держа в руке инструмент музыкальный подарочный, поплелся по кругу круглому, по дому заколдованному, в поисках выхода Долго ли коротко бродил новоиспечённый талант музыкальный в центре идеальной фигуры неизвестно, но ещё некоторое время, изредка, раздавались звуки трубы музыкальной, но уже не как полноценные произведения, а как фразы обрывочные, вопли зверя подраненного, умирать собирающегося.

Вы, конечно, спросите: “А при чём здесь углы, в доме круглом? Точнее, их отсутствие? В чём трагедия истории сей, драматизм где упрятан?”, и будете правы, я отвечу: “Нет никакого драматизма. И углы не при чём! Потому что их нет. Вообще”. Потому что круг — это идеальная фигура, а раз так — то и углы ей не нужны, без надобности. Вообще. И гостю дорогому они тоже не нужны. Ему труба надобна. Инструмент музыкальный. А вот зрителям/слушателям недобрым углы бы понадобились, в воспитательных целях, так сказать. Они бы с радостью гостя дорогого по углам расставили, преподали урок показательный. Ну не любят у нас начинающих талантов, ох не любят!!! Но… и им не судьба, потому что круг — идеальная фигура, и углов там там нет. Вообще. Отсутствуют как данность. Так что и им остаётся лишь злиться да раздувать щёки от зависти, завидовать тем, кто проживает в домиках обычных, с углами и прочими прелестями. В не идеальных. В простых и обыкновенных. Квадратных.

Метки: free word

Posted on 20 июн, 2011 at 17:05 | Ссылка | Оставить комментарий | Поделиться | Пожаловаться

«Почему говорят, что круг — идеальная форма?» — Яндекс Кью

Геометрические фигуры и прямые линии

Прямые линии являются ключом к распознаванию форм, которые мы часто видим в реальном мире: геометрические фигуры .

В сегодняшнем посте мы будем классифицировать геометрические фигуры, образованные прямыми линиями, и подумаем, где их можно найти.

Начнем с самого простого:

Две прямые Можно ли составить фигуру из двух прямых?

Ну конечно можно! Однако мы не называем эту фигуру геометрической фигурой. Чтобы быть геометрической фигурой, она должна быть «замкнутой». То есть, если мы поместим шарик внутрь фигуры, он не сможет вырваться. На сделанном нами рисунке мяч мог улететь!

Если вы попытаетесь сдвинуть две линии, то увидите, что никоим образом ее нельзя замкнуть. Можно взять два прямых предмета, например, две палочки для еды, и попробовать.

Базовые геометрические фигуры

А теперь попробуем с тремя прямыми…
Готово! Теперь вы можете сделать фигуру, от которой мяч не сможет убежать.

Каждая из прямых линий, которые мы использовали, теперь действует как часть фигуры.

Будем называть каждую прямую стороной фигуры . Итак, эта фигура имеет три стороны и называется треугольником. Когда мы говорим «треугольник», мы имеем в виду либо расположение трех линий, либо окружающее их пространство.

Можете ли вы представить, где мы можем найти треугольники вокруг нас? Я нашел несколько в Smartick , посмотрим, узнаете ли вы их!

4-сторонние геометрические фигуры

Давайте посмотрим, что мы можем сделать с 4 прямыми линиями…

Мы могли бы сделать, например,

Мы называем эти фигуры четырехугольниками. Есть несколько особых четырехугольников, у которых есть пары параллельных сторон. То есть есть две стороны, которые параллельны друг другу, и две другие тоже. Кроме того, параллельные стороны равны. Как мы могли сделать это? Получаем две равные стороны и ставим их параллельно друг другу:

Как расположить две другие стороны так, чтобы они тоже были параллельны? Вот и все! Просто объединив их вместе.

На данный момент у нас есть три возможности:

Все стороны равны, образуя ромб.

Где найти алмазы?

Я нашел два!

Если четыре угла фигуры прямые, то мы создали прямоугольник.

Мы можем найти много прямоугольников вокруг себя… Я уверен, что вы можете придумать множество!

Если мы создадим геометрическую фигуру, которая удовлетворяет обоим вышеуказанным условиям, а также имеет все равные стороны и четыре прямых угла, то это квадрат.

Геометрические фигуры с более чем 4 сторонами

Мы можем продолжать добавлять все линии, которые мы хотим, чтобы создать разные фигуры с разным количеством сторон. Они особенно важны, когда у них равные стороны. Например, следующим будет пятиугольник (5-сторонний).
Мы можем найти их, например, в рисунке футбольных мячей.

И затем у нас есть шестигранник (6-гранный).
Мы можем найти их… в ульях! Откуда пчелы умеют делать такие идеальные геометрические фигуры?

А потом семиугольники, восьмиугольники, эннагоны, нонагоны… чего-то не хватает? Конечно! Что мы можем сделать с изогнутыми линиями? Кривые линии не имеет смысла классифицировать, потому что они различаются гораздо больше… но я могу сказать вам, что есть очень, очень важная изогнутая фигура, о которой, я уверен, вы уже знаете… круг !

Мы получаем круг, когда сохраняем расстояние от точки. Например, с помощью компаса мы устанавливаем точку с помощью стрелки. Затем, сохраняя отверстие, рисуем карандашом окружность. Вы можете найти множество кругов вокруг себя, на колесах вашего автомобиля или на теннисном мяче.
Если вы хотите, вы можете продолжить изучение элементарной математики с помощью Smartick!

Подробнее:

Автор
Последние сообщения

Smartick

Команда создания контента.
Мультидисциплинарная и мультикультурная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать наилучший математический контент.

Последние сообщения Smartick (посмотреть все)

Понимание составных фигур в геометрии

Основные термины

o Составная цифра

Очевидно, что не все геометрические фигуры представляют собой простые многоугольники или окружности. Во многих случаях геометрическая фигура состоит из множества различных фигур, таких как треугольники, четырехугольники, окружности и т. д. Такая фигура называется составной фигурой . Хотя такие фигуры имеют произвольную форму, а это означает, что мы не можем вывести простые формулы для их площадей, периметров или других характеристик, мы часто можем использовать то, что мы узнали о более простых геометрических фигурах, для вычисления этих величин для более сложных составных фигур. Ключом к решению таких задач является разделение составной фигуры на набор более простых фигур, характеристики которых мы знаем, как получить или вычислить. Поэтому мы сосредоточимся на применении того, что мы узнали о различных простых геометрических фигурах, для анализа составных фигур. Ряд практических задач иллюстрирует базовый подход.
Составные фигуры
Как упоминалось выше, составные фигуры лучше всего анализировать, разделив их на более мелкие фигуры, характеристики которых мы можем легко определить. Крайне важно вспомнить характеристики более простых фигур, таких как квадраты и круги. Рассмотрим, например, следующую фигуру, площадь и периметр которой мы хотим вычислить.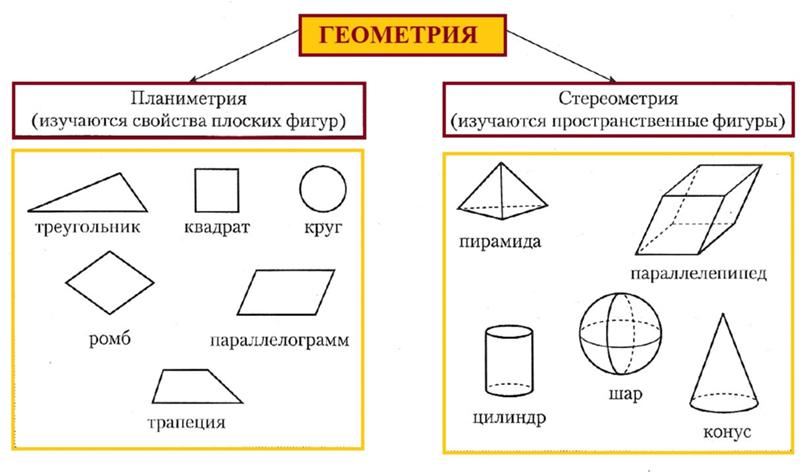
Фигура представляет собой трапецию, но предположим, что вы не помните формулу площади трапеции. Напомним, что прямоугольник содержит четыре прямых угла; таким образом, если мы разделим фигуру вертикальной линией, как показано ниже, мы создадим прямоугольник и прямоугольный треугольник.
Теперь, поскольку противоположные стороны прямоугольника равны, мы можем заполнить некоторые пробелы в том, что знаем о фигуре. Применяя простую арифметику, мы находим, что основание треугольника равно 2 дюймам.
Наконец, давайте применим теорему Пифагора, чтобы найти длину единственной оставшейся неизвестной стороны, x .

Теперь у нас есть все необходимое для расчета площади A и периметр P этой фигуры.

Практическая задача : Найдите площадь и периметр фигуры ниже.
77
7
Хотите узнать больше? Почему бы не пройти онлайн-курс по геометрии?
Решение : При осмотре мы видим, что эта фигура состоит из двух прямоугольников и треугольника. Разделим фигуру соответствующим образом и, используя свойства прямоугольников, заполним как можно больше «пробелов».
Это дает нам достаточно информации, чтобы найти площадь фигуры, но мы также должны найти гипотенузу h треугольника, если мы хотим вычислить периметр. Опять же, мы можем использовать теорему Пифагора. Тогда площадь A (используя формулы для прямоугольников и треугольников) и периметр P фигуры будут следующими.

Практическая задача : Найдите длину отрезка пунктирной линии на рисунке ниже.
Решение : Эта задача немного отличается от примеров, которые мы видели до сих пор. Снова разделим фигуру на треугольник и прямоугольник. Сейчас мы удалим неизвестный сегмент линии.
Теперь мы должны применить то, что мы знаем о треугольниках. Треугольник в верхней части рисунка равнобедренный, поэтому мы знаем, что два угла при основании равны. Давайте также добавим неизвестный отрезок обратно на картинку.
Вспоминая то, что мы знаем о параллельных прямых, неизвестный отрезок делит равнобедренный треугольник на два прямоугольных треугольника. Поскольку два угла при основании конгруэнтны (как и два прямых угла), два новых угла, образованных при вершине треугольника, также должны быть конгруэнтны.
Таким образом, по условию ASA мы знаем, что два треугольника конгруэнтны. Каждое из оснований должно иметь длину 2 единицы. Используя эту информацию (как показано ниже), мы применяем теорему Пифагора для вычисления высоты треугольника. Мы уже знаем, что «высота» прямоугольника равна 6 единицам.

Таким образом, длина отрезка (вертикальной) пунктирной линии составляет 9,46 единицы.
Фигуры могут также включать круги или их части. В таких случаях может потребоваться вычисление площади сектора или длины дуги при определении площади или периметра (соответственно) фигуры. Однако те же самые принципы, которые использовались выше, применимы и в этих случаях. Следующие практические задачи дают вам возможность проверить свои навыки в этой области.
Практическая задача : Найдите выражение для площади заштрихованной области.
Решение : Все, что нам дано для этой фигуры, это то, что каждый из белых кругов имеет радиус r . Таким образом, мы знаем, что белая площадь в четыре раза больше площади одного из белых кругов.

Фигура уже показана как полукруг (половина круга) и прямоугольник. Поскольку каждый из белых кругов имеет диаметр 2 r , мы знаем, что каждая сторона прямоугольника равна 4 r (таким образом, прямоугольник является квадратом).
Таким образом, площадь квадрата равна 16 r ² . Кроме того, радиус полукруга равен 2 r , так что его площадь следующая.

Теперь мы можем объединить всю эту информацию, чтобы вычислить площадь заштрихованной области.

Практическая задача : Каков диаметр круга, содержащего прямоугольник, показанный ниже?
Решение : У этой проблемы есть некоторые сложности, но мы можем ее решить. Наиболее важным моментом в этом случае является то, что вершины прямоугольника лежат на окружности; таким образом, мы можем провести радиусы от центра круга до каждого угла прямоугольника.
Здесь мы разделили прямоугольник на четыре треугольника. По условию SSS мы видим, что на фигуре есть две пары конгруэнтных треугольников: два треугольника со сторонами r, r, и 4, и два треугольника со сторонами r , r и 2. Теперь нам нужно показать, что два радиуса на самом деле образуют диагональ прямоугольника — это условие не выполняется.
Идеальная фигура в геометрии: Идеальная фигура — amphiboly — ЖЖ