Угловое расстояние — Википедия Переиздание // WIKI 2
В математике (в частности, в геометрии и тригонометрии) и во всех естественных науках (например, в астрономии и геофизике) угловое расстояние — это мера видимого расстояния между двумя точками или объектами, выраженная в угловых единицах дуги, при условии, что наблюдатель находится в вершине угла концами которого являются две рассматриваемые точки. Угловой диаметр является частным случаем углового размера.
Угловое расстояние является фундаментальной величиной в астрономии, определяющей положение любого объекта на небесной сфере по его небесным координатам: либо в угловых единицах, либо во времени. Азимут, высота, склонение или прямое восхождение объекта на небе, среди прочего, являются небесными координатами. Любое из них — это угловое расстояние до точки или плоскости отсчета: горизонта, небесного экватора, меридиана и т. д.
Использование
Термин угловое расстояние технически синонимичен самому углу, но предназначен для обозначения линейного расстояния (часто огромного и неизвестного) между этими объектами (например, звездами, наблюдаемыми с Земли).

Для визуальных наблюдений без претензий на точность можно вычислить угловое расстояние, конечно, с приближениями порядка степени, и, конечно, очень грубо.
Отдельные вариации — длина руки, толщина пальцев и т. д. — меняют значения в первых приближениях, но не так важны для определения местоположения звезды или планеты, видимой невооруженным глазом или для связи созвездия с соседями.
Измерение
Поскольку угловое расстояние концептуально совпадает с углом, оно измеряется в тех же единицах, например, градусах или радианах и с использованием таких приборов, как гониометры или оптические приборы, специально предназначенные для поворота в четко определенных направлениях и записи соответствующих углов (такие как телескопы).
Вычисление
Чтобы рассчитать угловое расстояние θ в угловых секундах для двойной звёздные системы, экзопланеты, объекта Солнечной системы и других астрономических объектов, используется размер большой полуоси, выраженной в астрономических единицах (а.е.), деленное на расстояние D, выраженное в парсеках, согласно формуле для малых углов — tan ( a D ) {\displaystyle \tan({\frac {a}{D}})} :
- θ ≈ a D {\displaystyle \theta \approx {\dfrac {a}{D}}}
Учитывая два угловых положения, каждое из которых определяется прямым восхождением (RA), α ∈ [ 0 , 2 π ] {\displaystyle \alpha \in [0,2\pi ]} и склонением (dec), δ ∈ [ − π / 2 , π / 2 ] {\displaystyle \delta \in [-\pi /2,\pi /2]} угловое расстояние между двумя точками можно рассчитать, используя следующую формулу:
- θ = cos − 1 [ sin ( δ 1 ) sin ( δ 2 ) + cos ( δ 1 ) cos ( δ 2 ) cos ( α 1 − α 2 ) ] {\displaystyle \theta =\cos ^{-1}\left[\sin(\delta _{1})\sin(\delta _{2})+\cos(\delta _{1})\cos(\delta _{2})\cos(\alpha _{1}-\alpha _{2})\right]}
См. также
Литература
 Эта страница в последний раз была отредактирована 26 июня 2020 в 03:28.
Эта страница в последний раз была отредактирована 26 июня 2020 в 03:28.
- УГЛОВОЕ РАССТОЯНИЕ
-
УГЛОВОЕ РАССТОЯНИЕ, в астрономии — расстояние на небесной сфере между двумя небесными телами, измеренное по дуге большого круга, проходящего через них, с наблюдателем в центре. Например, угловое расстояние между двумя звездами Большой Медведицы, находящимися на одной линии с Полярной звездой, равно 5°.
Научно-технический энциклопедический словарь.
- УГЛОВАЯ СКОРОСТЬ
- УГЛОВОЕ УСКОРЕНИЕ
Смотреть что такое «УГЛОВОЕ РАССТОЯНИЕ» в других словарях:
Угловое расстояние — Длина дуги, выраженная в угловых единицах (т. е. в радианах, градусах, дуговых минутах или секундах), которая соответствует данному углу наблюдения. Например, угловое расстояние между двумя точками на небесной сфере представляет собой угол между… … Астрономический словарь
угловое расстояние — kampinis atstumas statusas T sritis Standartizacija ir metrologija apibrėžtis Atstumas, išreikštas kampo matavimo vienetais. atitikmenys: angl. angular distance vok. Winkelentfernung, f rus. угловое расстояние, n pranc. distance angulaire, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
угловое расстояние — kampinis atstumas statusas T sritis fizika atitikmenys: angl. angular distance; angular separation vok. Winkelentfernung, f rus. угловое расстояние, n pranc. distance angulaire, f … Fizikos terminų žodynas
Угловое разрешение — Разрешение способность оптического прибора измерять линейное или угловое расстояние между близкими объектами, показывать раздельно близко расположенные объекты. Содержание 1 Угловое разрешение 2 Линейное разрешение 3 Общие сведения … Википедия
Угловое (Крым) — У этого термина существуют и другие значения, см. Угловое . Село Угловое укр. Углове крымскотат. Acı Bolat Страна … Википедия
угловое увеличением — 3.1 угловое увеличением (angular magnification M): Угловое увеличение М оптического прибора есть отношение угла наблюдения объекта, опирающегося на входной зрачок прибора (aприб), к углу наблюдения объекта глазом без прибора (aгл) Примечание В… … Словарь-справочник терминов нормативно-технической документации
ЗЕНИТНОЕ РАССТОЯНИЕ — угловое расстояние небесного светила или земного предмета от зенита. Обозначается г, отсчитывается вдоль круга высоты от 0 до 180°. С высотой h связано соотношением z = 90° h … Естествознание. Энциклопедический словарь
Зенитное расстояние — угловое расстояние небесного светила от зенита. Обозначается Z и отсчитывается вдоль круга высоты от 0 до 180˚. С высотой h связано соотношением Z = 90˚ h … Астрономический словарь
зенитное расстояние — угловое расстояние небесного светила или земного предмета от зенита. Обозначается z, отсчитывается вдоль круга высоты от 0 до 180º. С высотой h связано соотношением z = 90º – h. * * * ЗЕНИТНОЕ РАССТОЯНИЕ ЗЕНИТНОЕ РАССТОЯНИЕ, угловое расстояние… … Энциклопедический словарь
ПОЛЯРНОЕ РАССТОЯНИЕ — Расстояние между полюсом и данной точкой на земной поверхности. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней. Михельсон А.Д., 1865. ПОЛЯРНОЕ РАССТОЯНИЕ Угловое расстояние звезды от видимого… … Словарь иностранных слов русского языка
Угловой размер, линейный размер и расстояние
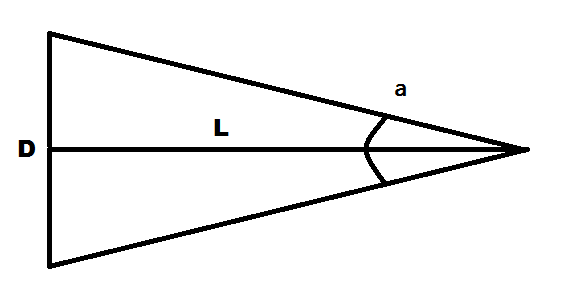
Угловой размер — это угол между линиями, соединяющими диаметрально противоположные точки измеряемого объекта и глаз наблюдателя.
Посмотрим на рисунок: здесь отрезок D — измеряемый объект, отрезок L — линия наблюдения, перпендикулярная отрезку D и являющаяся его серединным перпендикуляром, и угол а — угловой размер отрезка D.
Очевидные соотношения между величинами (вспомним тригонометрию):
Таким образом, наблюдатель, зная, например, линейный размер объекта, по угловому размеру объекта может определить расстояние до него. Помню, раньше для этих целей военные бинокли снабжали специальными риcками для определения углового размера.
Ну и обратные задачи тоже имеют место — зная, например, расстояние и линейный размер объекта, можно определить его угловой размер; и наконец, зная расстояние и угловой размер, можно определить линейный размер. Последние задачи актуальны для астрономии. Там используют термин
Ниже калькуляторы, рассчитывающие неизвестные по всем соотношениям. В качестве данных по умолчанию используется расстояние от Земли до Солнца, диаметр Солнца и средний угловой диаметр Солнца, наблюдаемого с Земли.

Расстояние по угловому и линейному размеру
Угловой размерТочность вычисленияЗнаков после запятой: 2
save Сохранить extension Виджет

Линейный размер по угловому размеру и расстоянию
Угловой размерТочность вычисленияЗнаков после запятой: 2
Линейный размер
save Сохранить extension Виджет

Угловой размер по расстоянию и линейному размеру
Угловой размер
save Сохранить extension Виджет
- Угловое расстояние
-
Длина дуги, выраженная в угловых единицах (т. е. в радианах, градусах, дуговых минутах или секундах), которая соответствует данному углу наблюдения. Например, угловое расстояние между двумя точками на небесной сфере представляет собой угол между двумя воображаемыми линиями, направленными от наблюдателя к этим точкам.
Астрономический словарь. EdwART. 2010.
- Угловой диаметр
Смотреть что такое «Угловое расстояние» в других словарях:
УГЛОВОЕ РАССТОЯНИЕ — УГЛОВОЕ РАССТОЯНИЕ, в астрономии расстояние на небесной сфере между двумя небесными телами, измеренное по дуге большого круга, проходящего через них, с наблюдателем в центре. Например, угловое расстояние между двумя звездами Большой Медведицы,… … Научно-технический энциклопедический словарь
угловое расстояние — kampinis atstumas statusas T sritis Standartizacija ir metrologija apibrėžtis Atstumas, išreikštas kampo matavimo vienetais. atitikmenys: angl. angular distance vok. Winkelentfernung, f rus. угловое расстояние, n pranc. distance angulaire, f … Penkiakalbis aiškinamasis metrologijos terminų žodynas
угловое расстояние — kampinis atstumas statusas T sritis fizika atitikmenys: angl. angular distance; angular separation vok. Winkelentfernung, f rus. угловое расстояние, n pranc. distance angulaire, f … Fizikos terminų žodynas
Угловое разрешение — Разрешение способность оптического прибора измерять линейное или угловое расстояние между близкими объектами, показывать раздельно близко расположенные объекты. Содержание 1 Угловое разрешение 2 Линейное разрешение 3 Общие сведения … Википедия
Угловое (Крым) — У этого термина существуют и другие значения, см. Угловое . Село Угловое укр. Углове крымскотат. Acı Bolat Страна … Википедия
угловое увеличением — 3.1 угловое увеличением (angular magnification M): Угловое увеличение М оптического прибора есть отношение угла наблюдения объекта, опирающегося на входной зрачок прибора (aприб), к углу наблюдения объекта глазом без прибора (aгл) Примечание В… … Словарь-справочник терминов нормативно-технической документации
ЗЕНИТНОЕ РАССТОЯНИЕ — угловое расстояние небесного светила или земного предмета от зенита. Обозначается г, отсчитывается вдоль круга высоты от 0 до 180°. С высотой h связано соотношением z = 90° h … Естествознание. Энциклопедический словарь
Зенитное расстояние — угловое расстояние небесного светила от зенита. Обозначается Z и отсчитывается вдоль круга высоты от 0 до 180˚. С высотой h связано соотношением Z = 90˚ h … Астрономический словарь
зенитное расстояние — угловое расстояние небесного светила или земного предмета от зенита. Обозначается z, отсчитывается вдоль круга высоты от 0 до 180º. С высотой h связано соотношением z = 90º – h. * * * ЗЕНИТНОЕ РАССТОЯНИЕ ЗЕНИТНОЕ РАССТОЯНИЕ, угловое расстояние… … Энциклопедический словарь
ПОЛЯРНОЕ РАССТОЯНИЕ — Расстояние между полюсом и данной точкой на земной поверхности. Объяснение 25000 иностранных слов, вошедших в употребление в русский язык, с означением их корней. Михельсон А.Д., 1865. ПОЛЯРНОЕ РАССТОЯНИЕ Угловое расстояние звезды от видимого… … Словарь иностранных слов русского языка
Выехали вы в поле для проведения экскурсии по звёздному небу для любителей астрономии, а вас спрашивают: «Какое угловое расстояние между двумя яркими звёздами А и Б?» или «Какой угловой размер созвездия Орион?», что вы на это скажете? Полезете гуглить в интернет или придумаете любое число, всё равно никто не проверит? На самом деле есть не очень точный, но уж наверняка точнее чем наугад способ определения угловых размеров на небе с помощью пальцев.
Тут недавно Московский планетарий опубликовал и социальные сети быстро подхватили памятку «быстрое определение угловых размеров на небе с помощью пальцев вытянутой руки». Начнём с неё:

(по клику изображение откроется в новой вкладке)
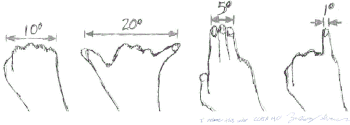
На примере астеризма Ковш созвездия Большая Медведица показаны угловые расстояния между звёздами, а также схематически вытянутая рука и расстояние между пальцами. Например, «ширина» мизинца равна 1°, кулак — 10°, «коза» с большим пальцем — 20°.
Ещё один вариант с пальцами руки и дополнительными «позами»:

Здесь добавились 3 пальца от указательного до безымянного — итого 5°. А также 25° — расстояние от большого пальца до мизинца в максимальной растянутости пальцев.
Кстати, обратите внимание, 1″ (одна секунда) — это примерно диаметр 5-копеечной монеты с расстояния в 4 километра. А теперь вспомните, например, Туманность Сатурн (NGC 7009) в созвездии Водолей имеет видимый размер 0,58′ или 34″. Без телескопа никак…
На просторах интернета нашёл ещё один интересный вариант определения размеров. Смотрим ниже:

Вариант с 3 — 4 — 6° выглядит очень любопытно. Во-первых, позволяет определить расстояние между объектами, которые лежат не на одной линии, а во-вторых, косточки указательного пальца так же могут выступать в качестве линейки.
Напоследок добавлю картинку для сравнения размеров большого пальца и диаметра полной Луны:

0,5° или 30′ — угловой диаметр полной Луны. Для сравнения диаметры планет Солнечной системы (1′ = 60″):
| Меркурий | 5″ — 13″ |
| Венера | 10″ — 66″ |
| Марс | 4″ — 25″ |
| Юпитер | 30″ — 50″ |
| Сатурн | 15″ — 20″ |
| Уран | 3,5″ — 5″ |
| Нептун | 2,2″ — 3″ |
Ну что, теперь, думается мне, вы не растеряетесь и сможете с лёгкостью определить расстояние между удалёнными пунктами на небесной сфере или размеры крупных объектов. А зная угловой размер и удалённость от наблюдателя, можно определить и линейный размер (онлайн-калькулятор).
Угловое расстояние Википедия
В математике (в частности, в геометрии и тригонометрии) и во всех естественных науках (например, в астрономии и геофизике) угловое расстояние — это мера видимого расстояния между двумя точками или объектами, выраженная в угловых единицах дуги, при условии, что наблюдатель находится в вершине угла концами которого являются две рассматриваемые точки. Угловой диаметр является частным случаем углового размера.
Угловое расстояние является фундаментальной величиной в астрономии, определяющей положение любого объекта на небесной сфере по его небесным координатам: либо в угловых единицах, либо во времени. Азимут, высота, склонение или прямое восхождение объекта на небе, среди прочего, являются небесными координатами. Любое из них — это угловое расстояние до точки или плоскости отсчета: горизонта, небесного экватора, меридиана и т. д.
Использование[ | ]
Термин угловое расстояние технически синонимичен самому углу, но предназначен для обозначения линейного расстояния (часто огромного и неизвестного) между этими объектами (например, звездами, наблюдаемыми с Земли).
Для визуальных наблюдений без претензий на точность можно вычислить угловое расстояние, конечно, с приближениями порядка степени, и, конечно, очень грубо.
Отдельные вариации — длина руки, толщина пальцев и т. д. — меняют значения в первых приближениях, но не так важны для определения местоположения звезды или планеты, видимой невооруженным глазом или для связи созвездия с соседями.
Измерение[ | ]
Поскольку угловое расстояние концептуально совпадает с углом, оно измеряется в тех же единицах, например, градусах или радианах и с использованием таких приборов, как гониометры или оптические приборы, специально предназначенные для поворота в четко определенных направлениях и записи соответствующих углов (такие как телескопы).
Вычисление[ | ]
Чтобы рассчитать угловое расстояние θ в угловых секундах для двойной звёздные системы, экзопланеты, объекта Солнечной
Измерение расстояния и начального азимута между точками без проекционных преобразований
Длина дуги большого круга – кратчайшее расстояние между любыми двумя точками находящимися на поверхности сферы, измеренное вдоль линии соединяющей эти две точки (такая линия носит название ортодромии) и проходящей по поверхности сферы или другой поверхности вращения. Сферическая геометрия отличается от обычной Эвклидовой и уравнения расстояния также принимают другую форму. В Эвклидовой геометрии, кратчайшее расстояние между двумя точками – прямая линия. На сфере, прямых линий не бывает. Эти линии на сфере являются частью больших кругов – окружностей, центры которых совпадают с центром сферы.
Начальный азимут — азимут, взяв который при начале движения из точки А, следуя по большому кругу на кратчайшее расстояние до точки B, конечной точкой будет точка B. При движении из точки A в точку B по линии большого круга азимут из текущего положения на конечную точку B постоянно меняется. Начальный азимут [angles-rhumb.html отличен от постоянного], следуя которому, азимут из текущей точки на конечную не меняется, но маршрут следования не является кратчайшим расстоянием между двумя точками.
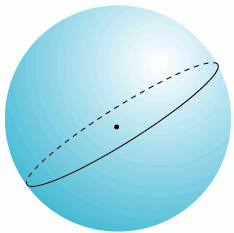
 большой круг
большой круг
Через любые две точки на поверхности сферы, если они не прямо противоположны друг другу (то есть не являются антиподами), можно провести уникальный большой круг. Две точки, разделяют большой круг на две дуги. Длина короткой дуги – кратчайшее расстояние между двумя точками. Между двумя точками-антиподами можно провести бесконечное количество больших кругов, но расстояние между ними будет одинаково на любом круге и равно половине окружности круга, или pi*R, где R – радиус сферы.
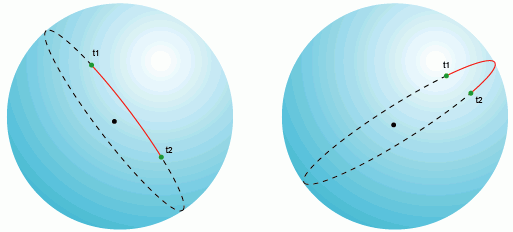
 расстояние большого круга
расстояние большого круга
На плоскости (в прямоугольной системе координат), большие круги и их фрагменты, как было упомянуто выше, представляют собой дуги во всех проекциях, кроме гномонической, где большие круги — прямые линии. На практике это означает, что самолеты и другой авиатранспорт всегда использует маршрут минимального расстояния между точками для экономии топлива, то есть полет осуществляется по расстоянию большого круга, на плоскости это выглядит как дуга.
 Маршрут Нью-Йорк — Пекин
Маршрут Нью-Йорк — Пекин
Форма Земли может быть описана как сфера, поэтому уравнения для вычисления расстояний на большом круге важны для вычисления кратчайшего расстояния между точками на поверхности Земли и часто используются в навигации.
Вычисление расстояния этим методом более эффективно и во многих случаях более точно, чем вычисление его для спроектированных координат (в прямоугольных системах координат), поскольку, во-первых, для этого не надо переводить географические координаты в прямоугольную систему координат (осуществлять проекционные преобразования) и, во-вторых, многие проекции, если неправильно выбраны, могу привести к значительным искажениям длин в силу особенностей проекционных искажений.
Известно, что более точно описывает форму Земли не сфера, а эллипсоид, однако в данной статье рассматривается вычисление расстояний именно на сфере, для вычислений используется сфера радиусом 6372795 метров, что может привести к ошибке вычисления расстояний порядка 0.5%.
Существует три способа расчета сферического расстояния большого круга (подробнее).
[править] Сферическая теорема косинусов
В случае маленьких расстояний и небольшой разрядности вычисления (количество знаков после запятой), использование формулы может приводить к значительным ошибкам связанным с округлением. Графическое изображение формул здесь и далее — из Википедии.
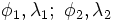 — широта и долгота двух точек в радианах
— широта и долгота двух точек в радианах
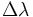 — разница координат по долготе
— разница координат по долготе
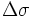 — угловая разница
— угловая разница
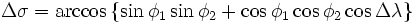
Для перевода углового расстояния в метрическое, нужно угловую разницу умножить на радиус Земли (6372795 метров), единицы конечного расстояния будут равны единицам, в которых выражен радиус (в данном случае — метры).
[править] Формула гаверсинусов
Используется, чтобы избежать проблем с небольшими расстояниями.
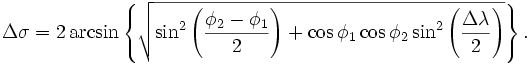
[править] Модификация для антиподов
Предыдущая формула также подвержена проблеме точек-антиподов, чтобы ее решить используется следующая ее модификация.
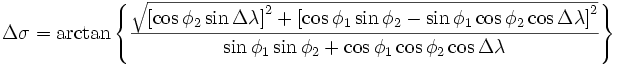
[править] Реализация на Avenue
На языке Avenue, используя последнюю формулу для вычисления расстояния большого круга между двумя точками, можно использовать следующий код. Точки для вычисления передаются другим скриптом, либо добавляются в начало данного в виде pnt = point.make(long, lat) (скачать скрипт):
'pnt1, pnt2 - точки между которыми вычисляются расстояния 'pi - число pi, rad - радиус сферы (Земли), num - количество знаков после запятой pi = 3.14159265358979 rad = 6372795 num = 7 'получение координат точек в радианах lat1 = pnt1.getY*pi/180 lat2 = pnt2.getY*pi/180 long1 = pnt1.getX*pi/180 long2 = pnt2.getX*pi/180 'косинусы и синусы широт и разниц долгот cl1 = lat1.cos cl2 = lat2.cos sl1 = lat1.sin sl2 = lat2.sin delta = long2 - long1 cdelta = delta.cos sdelta = delta.sin 'вычисления длины большого круга p1 = (cl2*sdelta)^2 p2 = ((cl1*sl2) - (sl1*cl2*cdelta))^2 p3 = (p1 + p2)^0.5 p4 = sl1*sl2 p5 = cl1*cl2*cdelta p6 = p4 + p5 p7 = p3/p6 anglerad = (p7.atan).SetFormatPrecision (num)
dist = anglerad*rad
'вычисление начального азимута
x = (cl1*sl2) - (sl1*cl2*cdelta)
y = sdelta*cl2
z = (-y/x).ATan.AsDegrees
if (x < 0) then z = z+180 end
z = -(z + 180 mod 360 - 180).AsRadians
anglerad2 = z - ((2*pi)*((z/(2*pi)).floor)) angledeg = (anglerad2*180)/pi'возврат значений длины большого круга и начального азимута
distlist = {dist, angledeg}
return distlist
Для вызова процедуры расчета длин приведенной выше, можно также воспользоваться следующим скриптом, результатом его работы будет расчет длин между точкой testpont до всех точек активной темы вида и запись результата в поле Newdist атрибутивной таблицы этой темы:
atheme = av.getactivedoc.getactivethemes.get(0)
aftab = atheme.getftab
f_shape = aftab.findfield("Shape")
f_dist = aftab.findfield("dist")
f_ang = aftab.findfield("ang")
'testpoint - точка отсчета
testpoint = point.make(25.85, 55.15)
aftab.seteditable(true)
'для каждой точки темы до которых считают расстояния от точки отсчета
for each rec in aftab
pnts = {}
apoint = aftab.returnvalue(f_shape, rec)
pnts.add(apoint.getx)
pnts.add(testpoint.getx)
pnts.add(apoint.gety)
pnts.add(testpoint.gety)
'Вызов процедуры расчета расстояний
'"Calc-distance" - название скрипта с процедурой в проекте
param = av.run("Calc-distance", pnts)
aftab.setvalue(f_dist, rec, param.get(0))
aftab.setvalue(f_ang, rec, param.get(1))
end
aftab.seteditable(false)
[править] Реализация на языке Python
Реализует полный вариант расчета через atan2(), более универсальнее, чем вариант для Avenue. (скачать скрипт)
import math
#pi - число pi, rad - радиус сферы (Земли)
rad = 6372795
#координаты двух точек
llat1 = 77.1539
llong1 = -120.398
llat2 = 77.1804
llong2 = 129.55
#в радианах
lat1 = llat1*math.pi/180.
lat2 = llat2*math.pi/180.
long1 = llong1*math.pi/180.
long2 = llong2*math.pi/180.
#косинусы и синусы широт и разницы долгот
cl1 = math.cos(lat1)
cl2 = math.cos(lat2)
sl1 = math.sin(lat1)
sl2 = math.sin(lat2)
delta = long2 - long1
cdelta = math.cos(delta)
sdelta = math.sin(delta)
#вычисления длины большого круга
y = math.sqrt(math.pow(cl2*sdelta,2)+math.pow(cl1*sl2-sl1*cl2*cdelta,2))
x = sl1*sl2+cl1*cl2*cdelta
ad = math.atan2(y,x)
dist = ad*rad
#вычисление начального азимута
x = (cl1*sl2) - (sl1*cl2*cdelta)
y = sdelta*cl2
z = math.degrees(math.atan(-y/x))
if (x < 0):
z = z+180.
z2 = (z+180.) % 360. - 180.
z2 = - math.radians(z2)
anglerad2 = z2 - ((2*math.pi)*math.floor((z2/(2*math.pi))) )
angledeg = (anglerad2*180.)/math.pi
print 'Distance >> %.0f' % dist, ' [meters]'
print 'Initial bearing >> ', angledeg, '[degrees]'
[править] Реализация в Excel
Скачать пример расчета расстояния большого круга и начального азимута в Excel. Демонстрирует расчеты через закон косинусов, гаверсинус, полное уравнение и полное уравнение через atan2().
Можно также воспользоваться следующей функцией:
Public Function Distance_A_B(Lat1 As Double, Long1 As Double, Lat2 As Double, Long2 As Double)
'определение расстояний между географическими координатами. Координаты должны быть десятичными
'расстояние выводится в метрах
With Application.WorksheetFunction
Distance_A_B = .Atan2(Sin(.Pi() * Lat1 / 180) * Sin(.Pi() * Lat2 / 180) + Cos(.Pi() * Lat1 / 180) * Cos(.Pi() * Lat2 / 180) * Cos(Abs(.Pi() * Long2 / 180 - .Pi() * Long1 / 180)), _
((Cos(.Pi() * Lat2 / 180) * Sin(.Pi() * Long2 / 180 - .Pi() * Long1 / 180)) ^ 2 + (Cos(.Pi() * Lat1 / 180) * Sin(.Pi() * Lat2 / 180) - Sin(.Pi() * Lat1 / 180) * Cos(.Pi() * Lat2 / 180) * Cos(Abs(.Pi() * Long2 / 180 - .Pi() * Long1 / 180))) ^ 2) ^ 0.5) * 6372795
End With
End Function
[править] Проверочный набор данных
Если все считается правильно, должны быть получены следующие результаты (координаты точек даны как широта/долгота, расстояние в метрах, начальный угол в десятичных градусах):
| # | Точка 1 | Точка 2 | Расстояние | Угол |
| 1 | 77.1539/-139.398 | -77.1804/-139.55 | 17166029 | 180.077867811 |
| 2 | 77.1539/120.398 | 77.1804/129.55 | 225883 | 84.7925159033 |
| 3 | 77.1539/-120.398 | 77.1804/129.55 | 2332669 | 324.384112704 |
[править] Ссылки по теме
- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
javascript — Angular 2: передача данных в маршруты?
Переполнение стека- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
- Товары
- Клиенты
- Случаи использования
- Переполнение стека Публичные вопросы и ответы
- Команды Частные вопросы и ответы для вашей команды
- предприятие Частные вопросы и ответы для вашего предприятия
- работы Программирование и связанные с ним технические возможности карьерного роста
- Талант Нанимать технический талант
- реклама Связаться с разработчиками по всему миру
