Точка, линия, прямая, луч, отрезок, ломанная
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположениеТочка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
ABCточка 1, точка 2, точка 3
123Можно нарисовать на листке бумаги три точки "А" и предложить ребёнку провести линию через две точки "А". Но как понять через какие? AAAЛиния — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
abcЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру.Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороныДаже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
BAПрямые могут быть
- пересекающимися, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторонуУ луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
BAЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
CBAОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.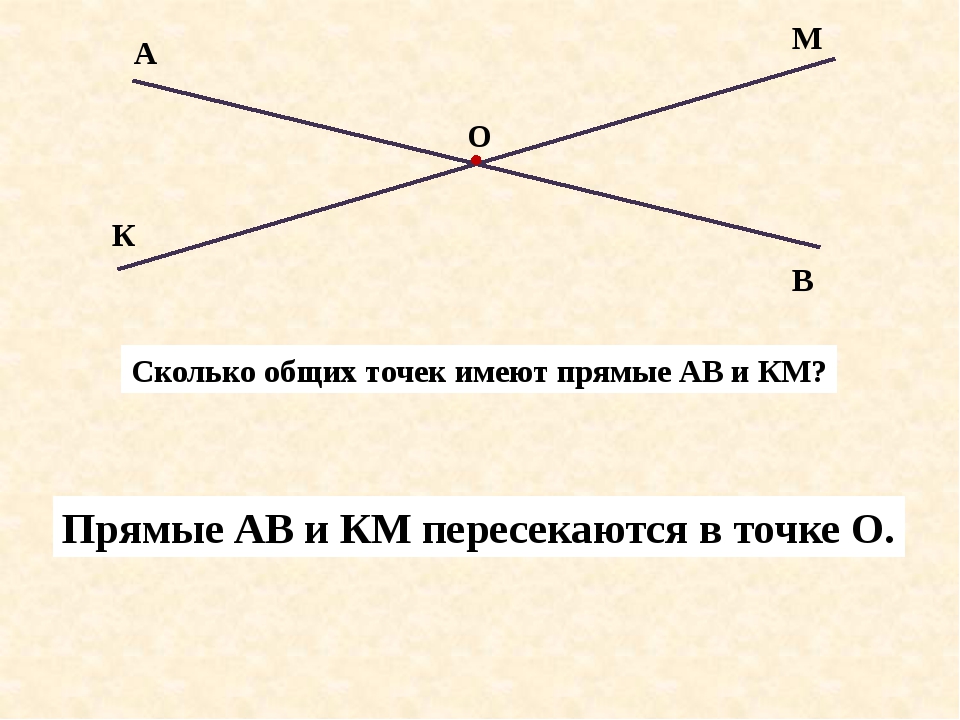 Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
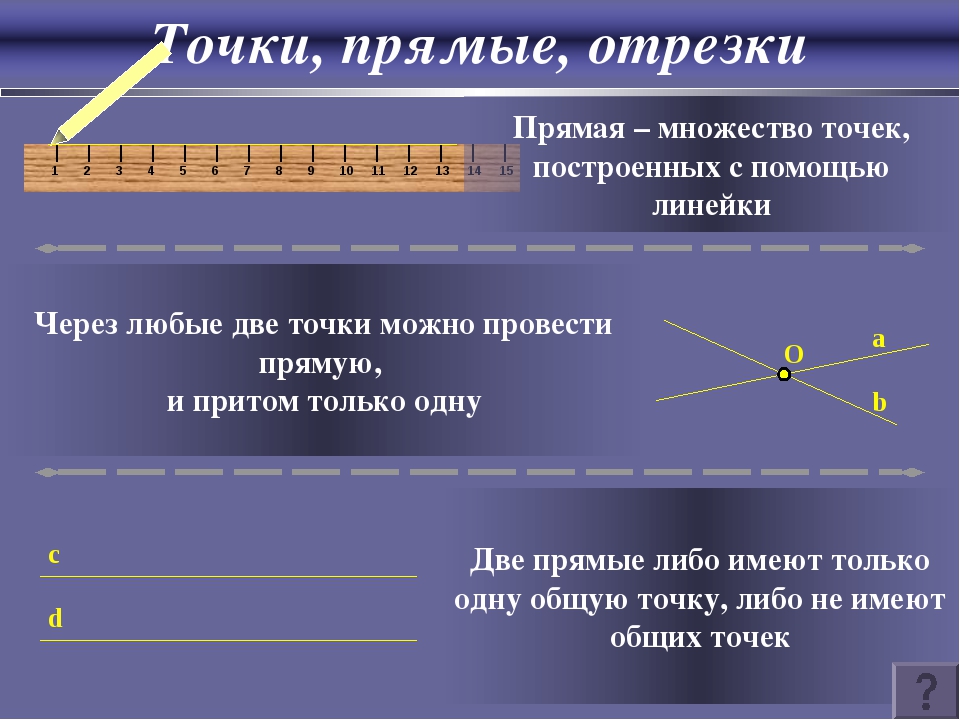
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
BAпрямая линия AB
BAОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ BA✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
BAЗадача: где прямая, луч, отрезок, кривая?Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
ABCDE646212752Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее, а у какой больше вершин? У первой линии все звенья одинаковой длины, а именно по 13см.Многоугольник — это замкнутая ломанная линияУ второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
ABCDEF120605812298141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
треугольники
четырёхугольники: квадрат, прямоугольник, дельтоид, ромб, параллелограмм, трапеция
пятиугольники
Как выглядит прямая и луч. Что можно назвать прямым. Как выстроить нужный угол без транспортира
Несмотря на то что геометрия относится к числу точных наук, ученые не могут однозначно дать определение термину «прямая». В самом общем виде можно дать такое определение: «Прямая — это линия, путь вдоль которой равен расстоянию между двумя точками».
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности.
К основным понятиям геометрии относятся точка, прямая и плоскость, они даются без определения, но определения других геометрических фигур даются через эти понятия. Плоскость, как и прямая, — это первичное понятие, не имеющее определения. Это утверждение устанавливается следующей аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.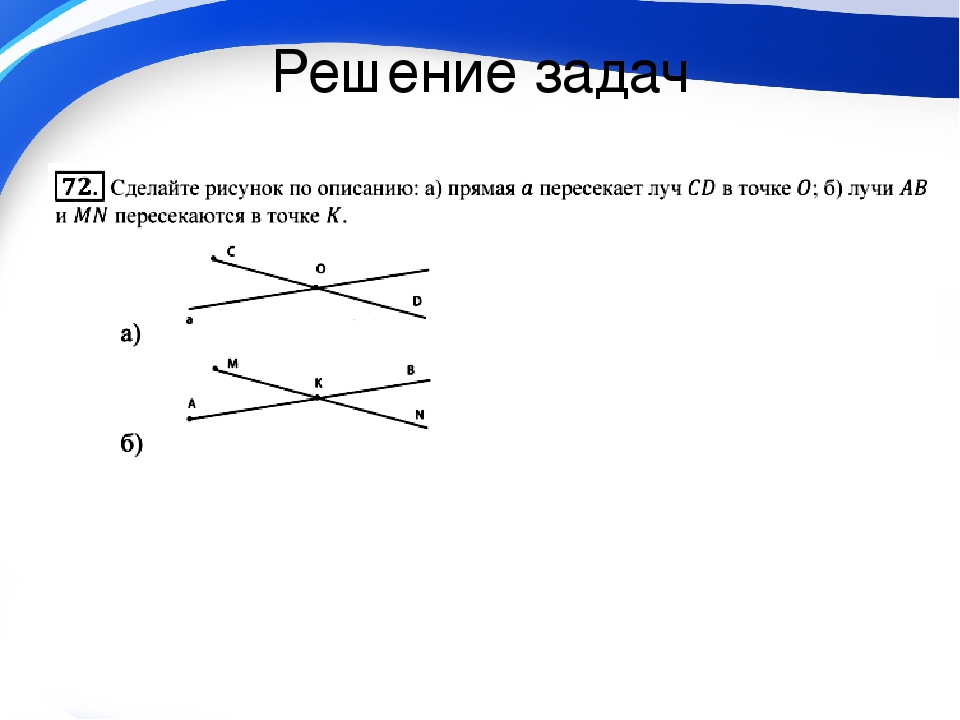
Задача: где прямая, луч, отрезок, кривая? Вершины ломаной(похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная. Задача: какая ломанная длиннее, а у какой больше вершин? Смежные стороны многоугольника — это смежные звенья ломанной. Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка.
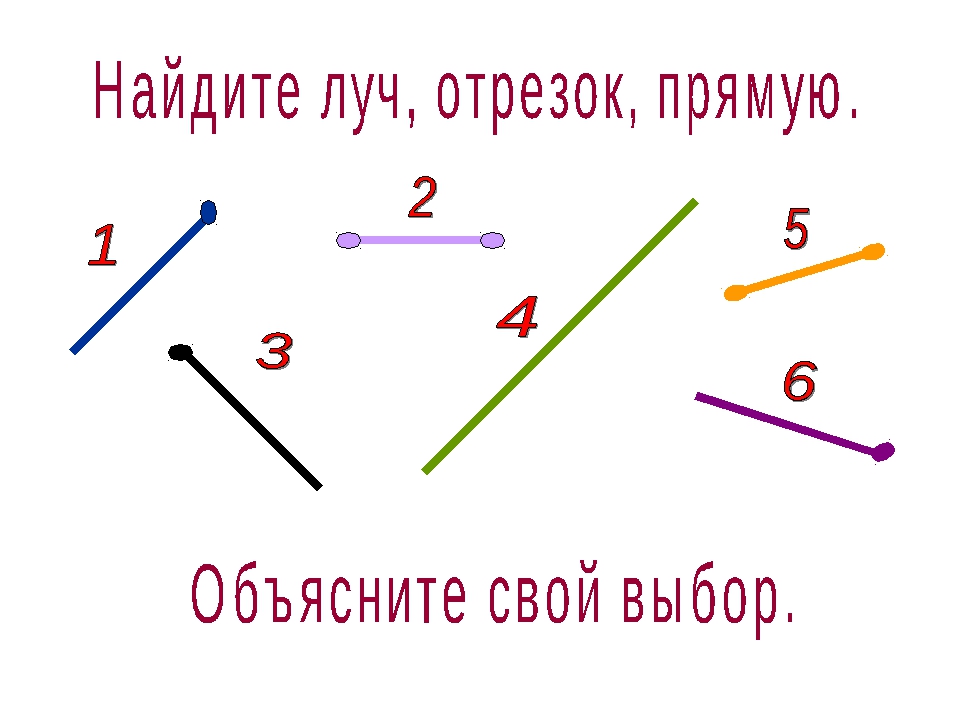 Символически записываем отрезок \(AB\).
Символически записываем отрезок \(AB\).
Что такое точка в математике?
Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. С. Вписанный угол, опирающийся на полуокружность, — прямой. Здесь собраны основные определения, теоремы, свойства фигур на плоскости.
Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенно определяется аксиомами геометрии.
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны. Лучом называют часть прямой линии, ограниченную с одной стороны. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
В последнем случае эти буквы указывают концы отрезка.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса. В рамках задачи важно только его местоположение
Точка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие? A A A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a b cЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру.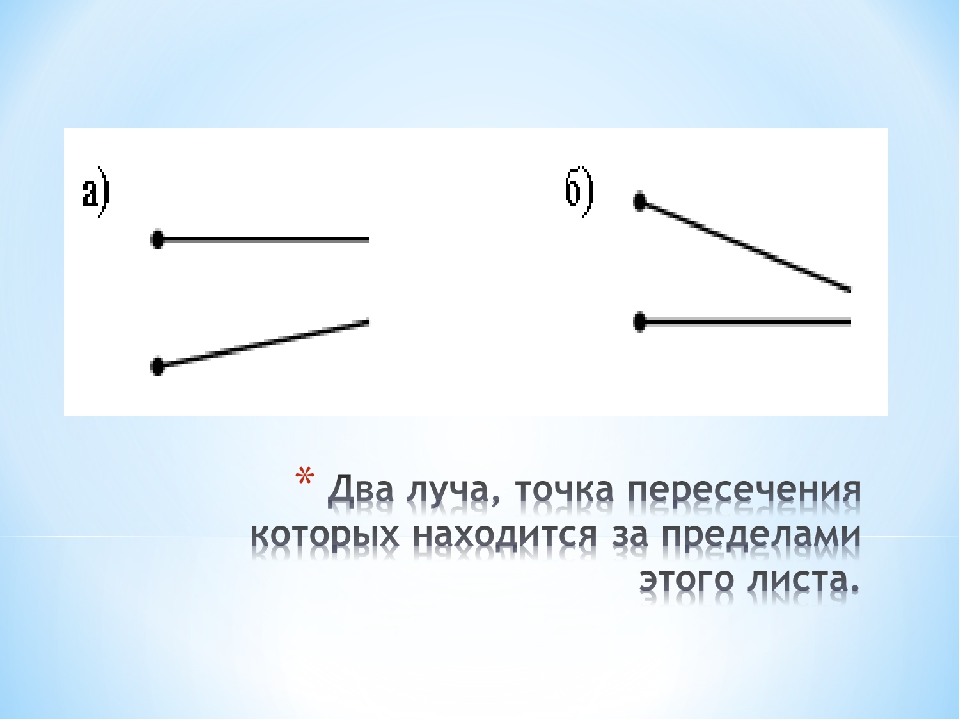 Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
B AПрямые могут быть
- пересекающимися, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.
- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
B AЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B AОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
 Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точками
Через одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Aпрямая линия AB
B AОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B A ✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого.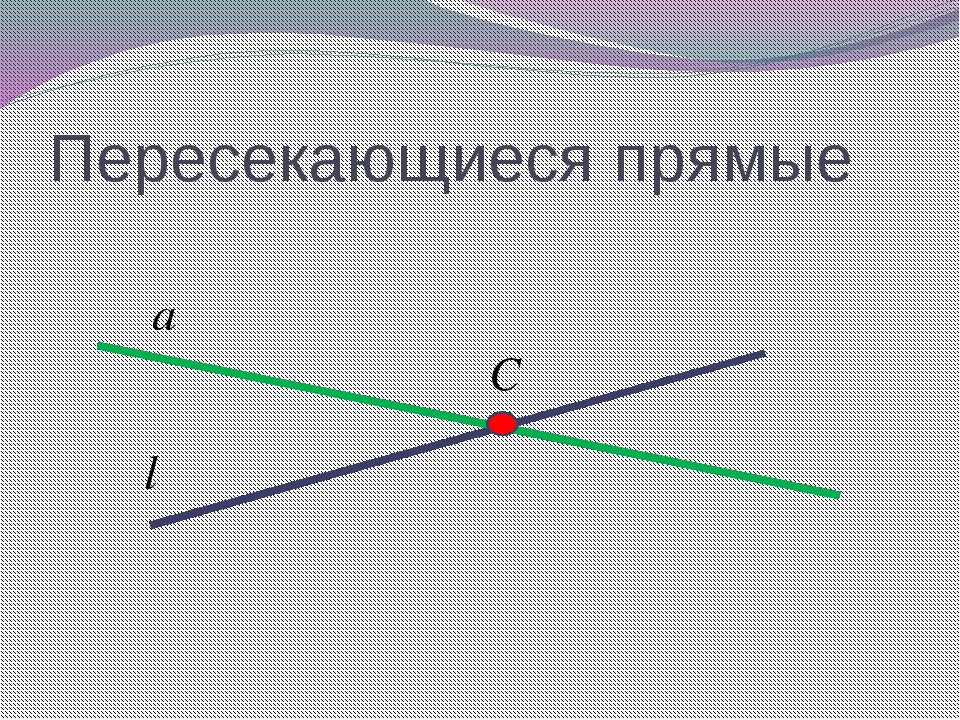 Смежные звенья не должны лежать на одной прямой.
Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т.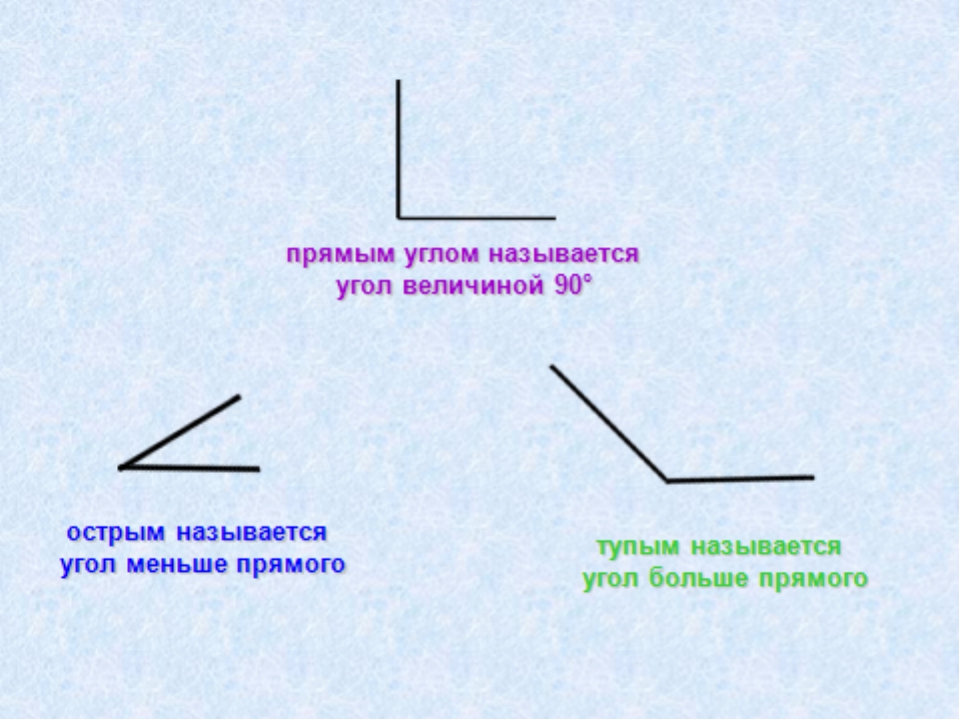 д.
д.
Мы рассмотрим каждую из тем, а в конце будут даны тесты по темам.
Точка в математике
Что такое точка в математике? Математическая точка не имеет размеров и обозначается заглавными латинскими буквами: A, B, C, D, F и т.д.
На рисунке можно видеть изображение точек A, B, C, D, F, E, M, T, S.
Отрезок в математике
Что такое отрезок в математике? На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка. Концы отрезка — две граничные точки.
На рисунке мы видим следующее: отрезки ,,,, и , а также две точки B и S.
Прямая в математике
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности. Прямая в математике обозначается двумя любыми точками прямой. Для объяснения понятия прямой ученику можно сказать, что прямая — это отрезок, который не имеет двух концов.
На рисунке изображены две прямые: CD и EF.
Луч в математике
Что же такое луч? Определение луча в математике: луч — часть прямой, которая имеет начало и не имеет конца. В названии луча присутствуют две буквы, например, DC. Причем первая буква всегда обозначает точку начала луча, поэтому менять местами буквы нельзя.
На рисунке изображены лучи: DC, KC, EF, MT, MS. Лучи KC и KD — один луч, т.к. у них общее начало.
Числовая прямая в математике
Определение числовой прямой в математике: прямая, точки которой отмечают числа, называют числовой прямой.
На рисунке изображена числовая прямая, а также луч OD и ED
Как известно из геометрии, «прямое» значит что-то, не имеющее изгибов и поворотов. Точное направление, ровное шоссе, откровенную беседу тоже называют этим же словом. Это понятие, конечно, используется и в других областях жизнедеятельности, в том числе в литературе и в обычном общении людей между собой.
Что можно назвать прямым
Для того чтобы разобраться со значением слова «прямая», вспомним, как мы используем его в обычной речи. Затем пройдемся по каждому пункту отдельно. Итак, простым перечислением можно назвать следующие фразы с данным словом:
Затем пройдемся по каждому пункту отдельно. Итак, простым перечислением можно назвать следующие фразы с данным словом:
- прямая дорога;
- прямой разговор;
- прямой угол;
- прямая зависимость;
- прямая линия;
- прямое значение;
- прямая речь;
- прямой рейс;
- прямое направление;
- и так далее.
В каждом случае объяснение значения будет совершенно различным, несмотря на использование во всех словосочетаниях одного и того же слова. Например, прямое направление — это просто указание на то, в какую сторону нужно двигаться. А прямой рейс — это сообщение о том, что движение состоится из одного пункта в другой без остановок и изменений маршрута.
Как отличить прямое, ровное от кривого
Что такое прямая? В учебниках геометрии есть объяснение этого понятия. Прямой называют простейшую — ровную линию, не имеющую ни начала, ни конца. Ограниченная двумя точками часть прямой называется отрезком. Что такое прямая и отрезок, мы разобрались.
Любая черта может быть изогнутой или волнистой, то есть кривой. Если последовательно соединить несколько самостоятельных «натянутых» отрезков без соблюдения одного направления (в разные стороны), то получится кривая или ломаная линия. Когда черта состоит из дуг, изгибов и плавных поворотов, ее называют изогнутой, волнистой. Что такое прямая в геометрии? Если идти от обратного, то это каждая линия, которая не является кривой, волнистой, ломаной или изогнутой.
Что общего между прямым разговором и прямой речью
Судя по объяснению авторитетных словарей, прямым разговором называется серьезная беседа, требующая откровенности и правдивости от всех участников этого процесса. Для этого не обязательно знать, что такое прямая речь, достаточно без утайки рассказывать о том, что спрашивают, или делать конкретные предложения. Во время прямых разговоров иногда выясняются разные тайны или сокрытые подробности событий. Чаще всего такие беседы происходят между близкими людьми, друзьями или родственниками.
А вот чтобы точно передать или записать данную беседу на бумагу, уже необходимо вспомнить что такое прямая речь, слова автора и другие термины литераторов.
Правописание требует, чтобы слова говорящего отделялись от слов автора (рассказчика) двоеточием, кавычками, запятыми и тире. На выделение речи влияет расположение слов «героя» в тексте, в абзаце, в строке и так далее. То есть прямой речью называют воспроизведенные дословно чьи-либо слова, включенные в основной сюжет рассказа.
Крылатая птица и крылатые слова
Мы выяснили, что такое прямая в геометрии и в литературе, пора двигаться далее. Кстати, в предыдущем предложении одно из слов было использовано в переносном смысле (двигаться). То есть было образовано второе, не прямое значение, связанное с основным только названием. Произошел перенос наименования по действию. Оказывается, некоторые слова, которыми мы пользуемся, имеют разные значения:
- прямое, или основное;
- переносное, или вторичное.

Что такое прямое значение слова? Ответ заложен в самом вопросе. Это название признака, действия, предмета или явления, которое сразу же вызывает о них представление, вне зависимости от контекста. Многозначность понятия формируется переносом названия на что-то другое, никак не связанное с основным, прямым значением слова. Например:
- двигаться на телеге — двигаться по тексту;
- золотой самородок — золотые руки;
- шоколадная конфета — шоколадная кожа.
Какой угол является прямым
Прежде всего любой угол — это самостоятельная геометрическая фигура. Если соединить между собой три точки, лежащие не на одной прямой, то острие (или вершина) этой конструкции и будет являться углом. Если внутри любой окружности провести несколько пересекающихся между собой линий, то в точке их пересечения образуется несколько углов с парными значениями. Количество их будет равняться числу проведенных линий, умноженному на два.
Все углы измеряются в градусах, и полное значение суммы всех углов в круге равно 360 градусам. Углы бывают острые и тупые, прямые и развернутые, смежные, вертикальные и дополнительные.
Углы бывают острые и тупые, прямые и развернутые, смежные, вертикальные и дополнительные.
Что такое прямой угол? Как его получить, где найти? Внутри круга, разделенного проведенными через его центр двумя перпендикулярными между собой линиями, образуется четыре одинаковых угла. Они называются прямыми и значение каждого из них — 90 градусов.
Как выстроить нужный угол без транспортира
Иногда в обычной жизни необходимо применить или вычислить точное значение угла. Существует несколько простых способов для этого.
- Если взять лист от любой тетради или книги, то все его углы равны 90 градусам.
- При складывании такого листа с аккуратным совмещением двух соседних сторон образуется угол в 45 градусов.
- Если по одной стороне тетрадного или любого другого листа бумаги отмерить 10 см, а по другой — 17,3 см, а затем соединить эти точки линией, то можно получить шаблон, углы которого равняются 90, 60 и 30 градусам.
Что такое прямая зависимость результата от действий? На конкретный ответ могут повлиять самые разные факторы. Одно неизменно: если выполнять действия в нужном направлении, делать последовательные шаги и применять полученные знания на практике, то результат будет обязательно положительным.
Одно неизменно: если выполнять действия в нужном направлении, делать последовательные шаги и применять полученные знания на практике, то результат будет обязательно положительным.
О параллельных прямых и фантастических мирах
Что такое прямая? Точка — это основное понятие в что-то, не имеющее частей. Ровная, вытянутая линия без начала и конца, которая имеет бесконечное количество точек, является прямой.
Чтобы объяснить, что такое математики применяют разные определения и сравнения. Вот одна из аксиом: линии прямые, которые нигде и никогда не могут пересекаться, являются параллельными. Можно использовать еще один способ, чтобы определить параллельность линий. Если из каждой точки на одной из прямых выстроить перпендикулярно (то есть под прямым углом) ко второй равные отрезки, то эти прямые не смогут пересекаться и будут являться параллельными.
Что такое параллельные прямые, ясно. А как это связано с фантастическими мирами? Ответ достаточно прост, так как и в этом случае имеет место перенос понятий, о которых шла речь выше. Возможная реальность, не пересекающаяся, а находящаяся рядом с нашей, в одном и том же пространстве и времени, и является параллельным миром. Считается верным утверждение, что процессы, которые происходят там, никак не влияют на наш мир.
Возможная реальность, не пересекающаяся, а находящаяся рядом с нашей, в одном и том же пространстве и времени, и является параллельным миром. Считается верным утверждение, что процессы, которые происходят там, никак не влияют на наш мир.
Несколько общеизвестных аксиом
В математическом мире аксиома — это утверждение, для которого не требуются доказательства. Ниже приведены некоторые из таких истин.
Любую из геометрических или иных фигур можно увеличить с соблюдением пропорций.
Две прямые, расходящиеся в одном направлении, обязательно будут сходиться в другом.
Если две прямые параллельны третьей, то они параллельны и друг другу.
Если две прямые линии сближаются, они когда-нибудь пересекутся.
Если прямые сближаются, они не смогут разойтись в том же направлении без пересечения.
Через две любые точки можно провести окружность или прямую.
Сумма трех углов является одинаковой у всех треугольников, и она равна суме двух прямых углов.
Прямоугольник — это фигура с четырьмя прямыми углами.
Представим мир без геометрии
Знания о том, что такое прямая, отрезок, точка, угол, нужны не только школьникам и студентам для получения хороших оценок. Их применяют архитекторы и дизайнеры, портные и строители, геодезисты и геологи, мебельщики и автомобилестроители, а также огромное количество других специалистов. Разве кто-то хочет носить уродливое платье или жить в доме с кривыми, падающими стенами?
Что такое прямой угол? Линии, отрезки, плоскости, точки и углы — это, можно сказать, основа архитектуры. Наука о домостроении так же невозможна без математических вычислений и геометрических понятий, как и литература без слов, точек, запятых, восклицательных знаков и прямой речи.
Что такое прямая дорога? Это путь, ведущий из одного пункта в другой (или от одного понятия к другому, от невежественности к эрудиции, например), с возможными остановками во времени, но без отклонений от выбранного маршрута.
Точка и прямая являются основными геометрическими фигурами на плоскости.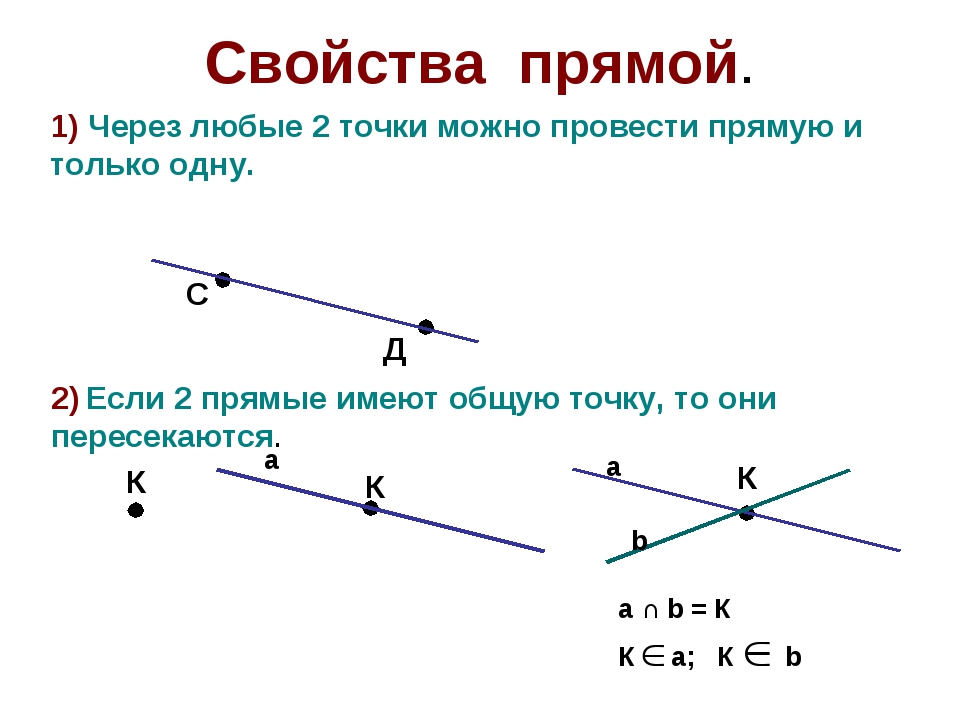
Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др., а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками.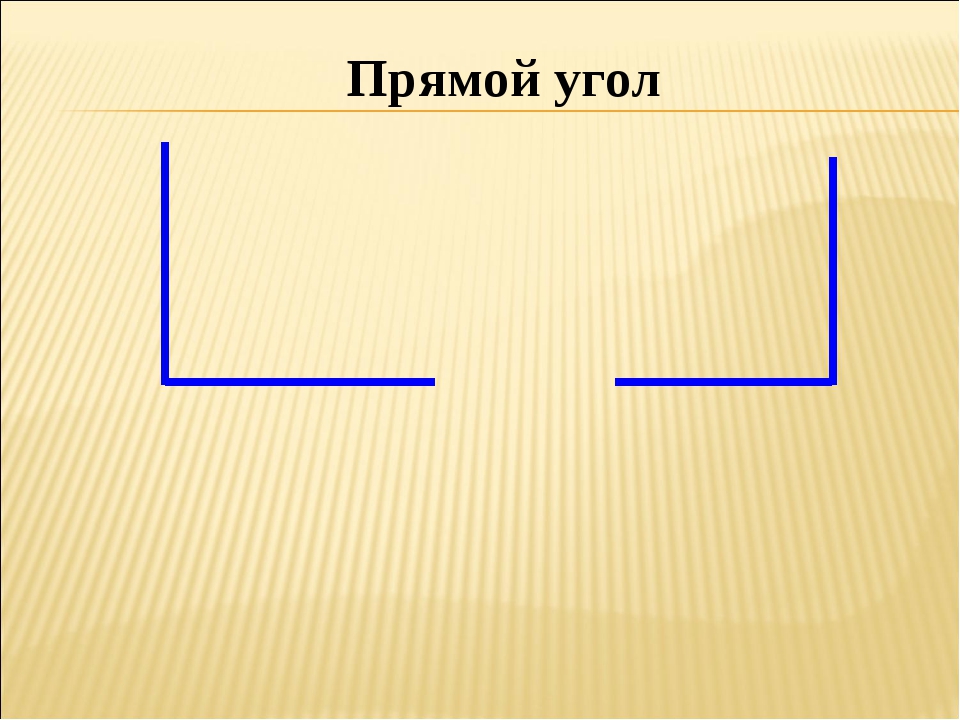 Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.
Получается, что прямая бесконечна: у неё нет ни начала, ни конца; у луча есть только начало, но нет конца, а отрезок имеет начало и конец. Поэтому только отрезок мы можем измерить.
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.
Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Отрезок — что это такое
Обновлено 24 июля 2021- Отрезок — это…
- Разница между ним, лучом и прямой
- Вектор
- Ломаная линия
- Отрезок времени
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Одним из понятий геометрии, с которым знакомятся еще в начальной школе, является отрезок. Уйма задач по математике и геометрии строится на понятиях отрезка и прямой.
Понимание, что такое отрезок, поможет решать всевозможные задачи и примеры на уроках математики как в школе, так и в высших учебных заведениях.
Отрезок — это геометрическая фигура
Согласно определению в словаре, отрезком называют часть прямой, ограниченную двумя точками, находящимися на ней. Именно по обозначениям этих точек и дается название отрезка.
На рисунке, изображенном ниже, показан отрезок AB. Точки A и B являются концами отрезка.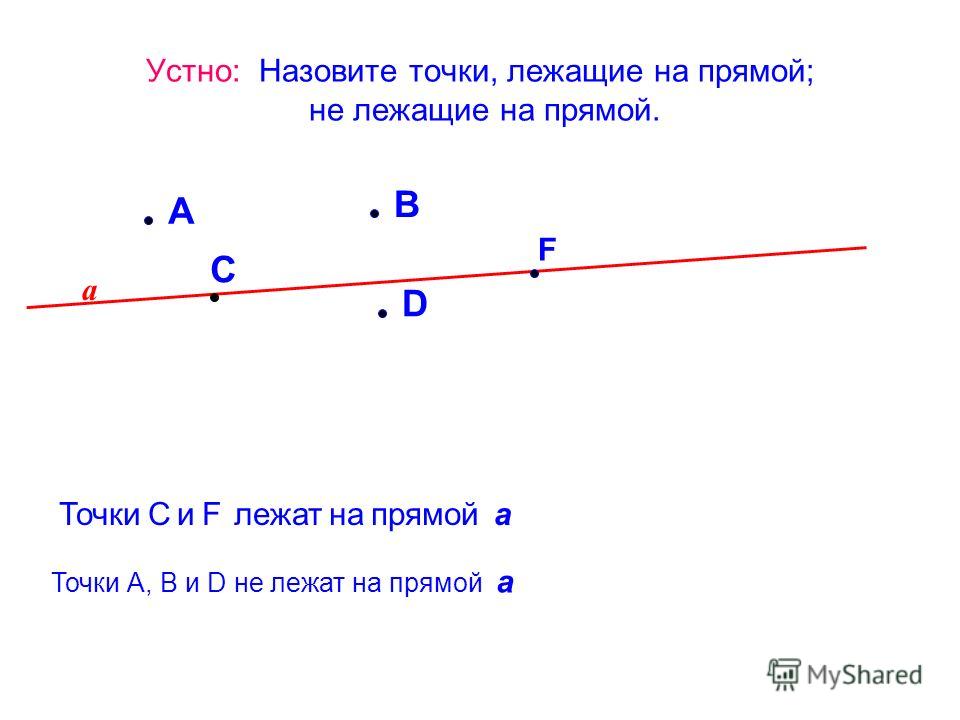 Длиной отрезка называют расстояние между его концами.
Длиной отрезка называют расстояние между его концами.
В математике принято обозначать точки, и соответственно отрезки, большими буквами латинского алфавита. Если нужно нарисовать отрезок, чаще всего его изображают без прямой, а лишь от одного конца до другого.
Также можно сказать, что отрезок — это совокупность всех точек, которые лежат на одной прямой и находятся между двумя заданными точками, которые являются концами данного отрезка.
Если на отрезке между его концами отметить еще одну точку, она разделит данный отрезок на два. Длину отрезка АВ можно посчитать, просуммировав длины отрезков АС и СВ.
Разница между отрезком, лучом и прямой
Школьники иногда путают понятия прямой, луча и отрезка. И вправду, эти понятия очень схожи между собой, однако имеют принципиальное различие:
- Прямой называется линия, которая не искривляется, а также не имеет начала и конца.
- Луч — это часть прямой, ограниченная одной точкой.
 Он имеет начало и не имеет конца.
Он имеет начало и не имеет конца. - Отрезок ограничивается двумя точками. Он имеет и начало, и конец.
Точка, находящаяся на прямой, делит ее на два луча. Количество же отрезков на одной прямой может быть бесконечным.
Чтобы различать эти фигуры на рисунке, в начале и конце рисуемой линии ставятся или не ставятся точки. Рисуя луч, точка ставится в одном конце, а изображая отрезок — в обоих концах. Прямая не имеет концов, поэтому точки в конце линии не ставятся.
Направленный отрезок — это вектор
Отрезки бывают двух видов:
- Ненаправленные.
- Направленные.
Для ненаправленных отрезков, АВ и ВА — одинаковые отрезки, так как направление не имеет значения.
Если же говорить о направленных отрезках, порядок перечисления его концов имеет решающее значение. В таком случае, АВ➜ и ВА➜ — разные отрезки, так как они противоположно направленные.
Направленные отрезки называются векторами.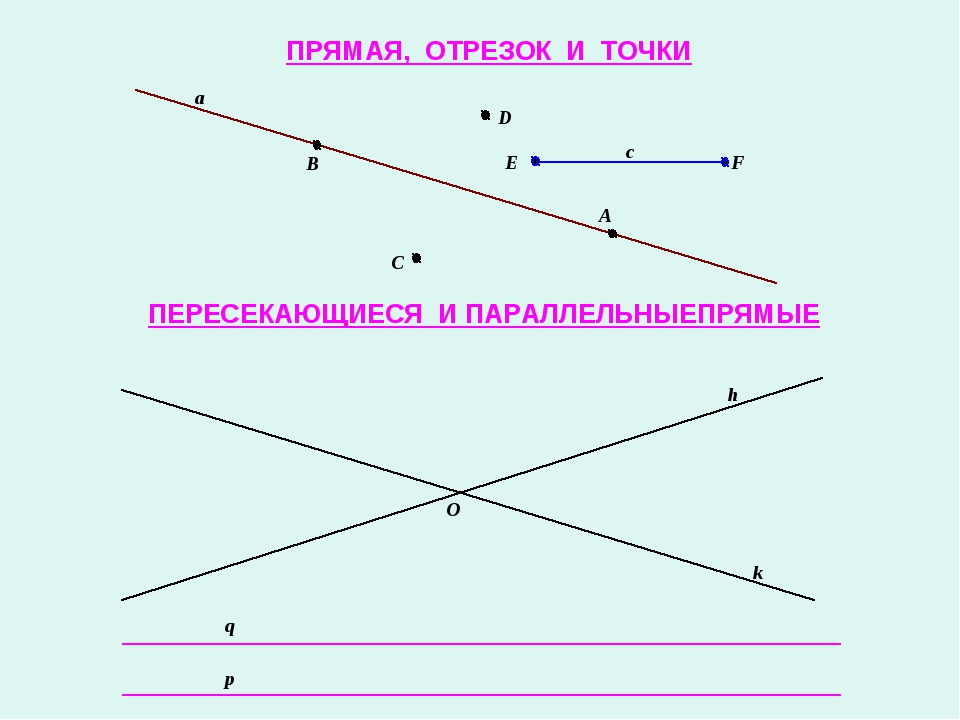 Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.
Векторы могут обозначаться как двумя заглавными буквами латинского алфавита со стрелочкой над ними, так и одной маленькой буквой со стрелочкой.
Модулем вектора называется длина направленного отрезка. Обозначается как АВ➜. Модули векторов АВ➜ и ВА➜ равны.
Векторы часто рассматривают в системе координат. Модуль вектора равен квадратному корню суммы квадратов координат концов вектора.
Коллинеарными векторами называются те, что лежат на одной или на параллельных прямых.
Ломаная линия — это множество соединенных отрезков
Ломаная линия состоит из множества отрезков, которые называются ее звеньями. Эти отрезки соединены друг с другом своими концами и не расположены под углом 180°.
Вершинами ломаной являются следующие точки:
- Точка, с которой началась ломаная.
- Точка, которой ломаная закончилась.
- Точки, в которых соединяются смежные звенья (отрезки ломаной).
Число вершин ломаной всегда на один больше, чем количество ее звеньев.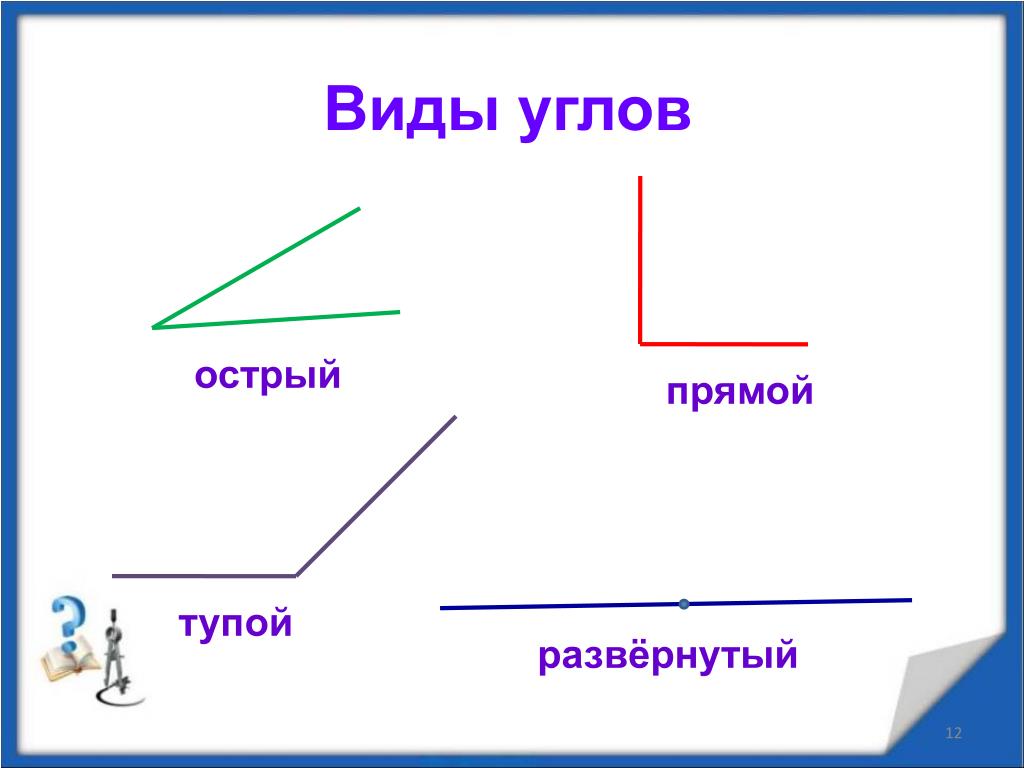 Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.
Обозначается ломаная перечислением всех ее вершин начиная с одного конца и заканчивая другим.
Например, ломаная ABCDEF состоит из отрезков AB, BC, CD, DE и EF и вершин A, B, C, D, E и F. Звенья AB и BC являются смежными, так как имеют общий конец — точку В. Длина ломаной вычисляется как сумма длин всех ее звеньев.
Любая замкнутая ломаная является геометрической фигурой — многоугольником.
Сумма углов многоугольника кратна 180° и вычисляется по следующей формуле 180*(n-2), где n — количество углов или отрезков, составляющих данную фигуру.
Отрезок времени
Интересно, что слово отрезок применимо не только к геометрическим понятиям, но и как временной термин.
Отрезком времени называют период между двумя событиями, датами. Он может измеряться как секундами или минутами, так и годами или даже десятилетиями.
Время в целом в таком случае определяется как временная прямая.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Эта статья относится к рубрикам:
точка, прямая, отрезок, луч, ломаная линия
Точка и прямая являются основными геометрическими фигурами на плоскости.
Древнегреческий учёный Евклид говорил: «точка» – это то, что не имеет частей». Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол. Точка является основой для построения любой геометрической фигуры.
Прямая линия или просто прямая – это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Точки обозначают заглавными латинскими буквами А, В, С, D, Е и др., а прямые теми же буквами, но строчными а, b, c, d, e и др. Прямую можно обозначить и двумя буквами, соответствующими точкам, лежащим на ней. Например, прямую a можно обозначить АВ.
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Простейшие геометрические фигуры на плоскости – это отрезок, луч, ломаная линия.
Отрезок – это часть прямой, которая состоит из всех точек этой прямой, ограниченных двумя выбранными точками.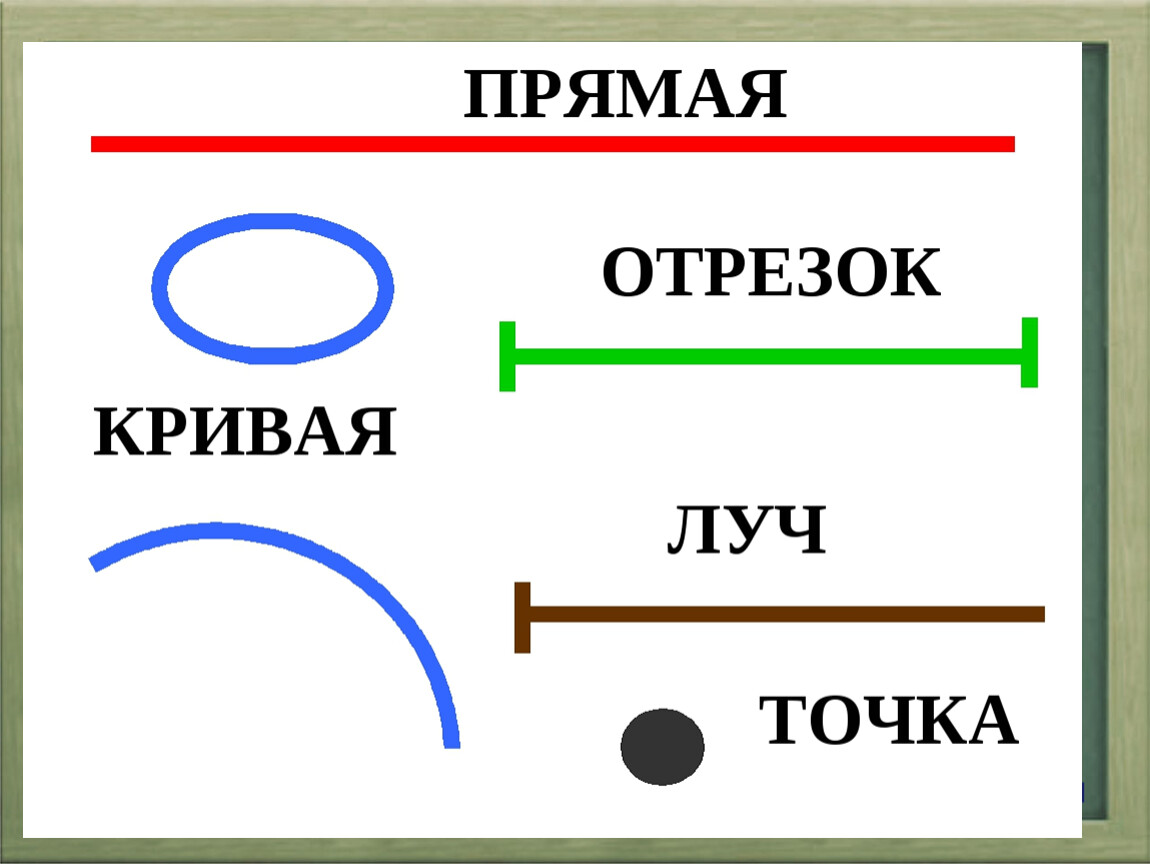 Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Эти точки – концы отрезка. Отрезок обозначается указанием его концов.
Луч или полупрямая – это часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой или началом луча. Луч имеет точку начала, но не имеет конца.
Полупрямые или лучи обозначаются двумя строчными латинскими буквами: начальной и любой другой буквой, соответствующей точке, принадлежащей полупрямой. При этом начальная точка ставится на первом месте.
Получается, что прямая бесконечна: у неё нет ни начала, ни конца; у луча есть только начало, но нет конца, а отрезок имеет начало и конец. Поэтому только отрезок мы можем измерить.
Несколько отрезков, которые последовательно соединены между собой так, что имеющие одну общуюточкуотрезки (соседние) располагаются не на одной прямой, представляют собой ломаную линию.
Ломаная линия может быть замкнутой и незамкнутой. Если конец последнего отрезка совпадает с началом первого, перед нами замкнутая ломаная линия, если же нет – незамкнутая.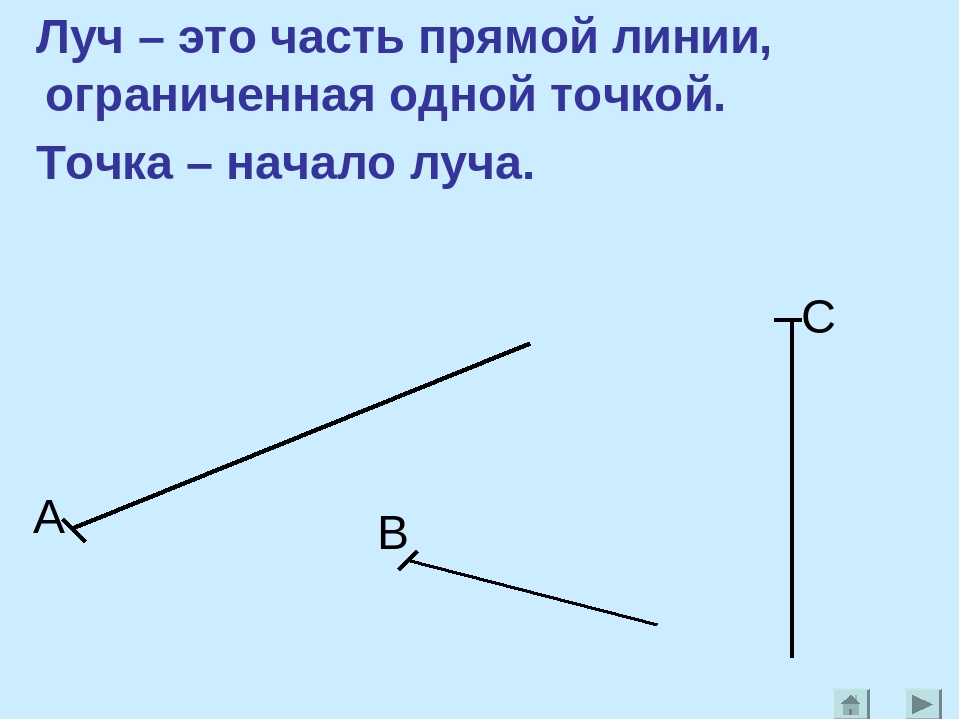
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
точка и прямая линия, отрезок, луч, ломаная линия
К основным геометрическим фигурам на плоскости относятся точка и прямая линия. Отрезок, луч, ломаная линия — простейшие геометрические фигуры на плоскости.
Точка — это самая малая геометрическая фигура, которая является основой всех прочих построений (фигур) в любом изображении или чертеже.
Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.
Прямую линию, или прямую, можно представить себе как бесчисленное множество точек, которые расположены на одной линии, не имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:
На листе бумаги мы видим только часть прямой линии, так как она бесконечна. Прямая изображается так:
Часть прямой линии, ограниченная с двух сторон точками, называется отрезком прямой, или отрезком. Отрезок изображается так:
Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца. Луч изображается так:
Если на прямой вы поставили точку, то этой точкой прямая разбивается па два луча, противоположно направленных. Такие лучи называются дополнительными.
Ломаная линия — это несколько отрезков, соединенных между собой так, что конец первого отрезка является началом второго отрезка, а конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку) отрезки расположены не на одной прямой. Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.
Выше изображена трехзвенная ломаная линия.
Если конец последнего отрезка ломаной совпадает с началом первого отрезка, то такая ломаная линия называется замкнутой. Примером замкнутой ломаной служит любой многоугольник:
Четырехзвенная замкнутая ломаная линия — четырехугольник
Трехзвенная замкнутая ломаная линия — треугольник
Плоскость, как и прямая, — это первичное понятие, не имеющее определения. У плоскости, как и у прямой, нельзя видеть ни начала, ни конца. Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.
Примером плоскости является поверхность вашего рабочего стола, тетрадный лист, любая гладкая поверхность. Плоскость можно изобразить как заштрихованную
геометрическую фигуру:
Прямая и обратная пропорциональность. Формулы, обозначение, примеры
Основные определения
Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.
Виды зависимостей:
- Прямая зависимость. Чем больше одна величина, тем больше вторая. Чем меньше одна величина, тем меньше вторая величина.
- Обратная зависимость. Чем больше одна величина, тем меньше вторая. Чем меньше одна величина, тем больше вторая.
Зависимости также можно классифицировать по формам: функциональная и статистическая.
Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.
В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.
Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.
Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.
Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.
Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.
Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.
Есть две разновидности пропорциональностей:
- Прямая пропорциональность. Это зависимость, при которой увеличение одного числа ведет к увеличению другого во столько же раз. А уменьшение одно числа ведет к уменьшению другого во столько же раз.
- Обратная пропорциональность. Это зависимость, при которой уменьшение одного числа ведет к увеличению другого во столько же раз. А увеличение числа наоборот ведет к уменьшению другого во столько же раз.

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.
Прямо пропорциональные величины
Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.
Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».
Свойство прямо пропорциональной зависимости:
Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.
Примеры прямо пропорциональной зависимости:
- при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;
- периметр квадрата и его сторона — прямо-пропорциональные величины;
- стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.
|
Формула прямой пропорциональности y = kx, где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности. |
Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента прямой пропорциональности:
y/x = k
Графиком прямо пропорциональной зависимости величин является прямая линия.
Например, при k = 2 график выглядит так:
Пример 1.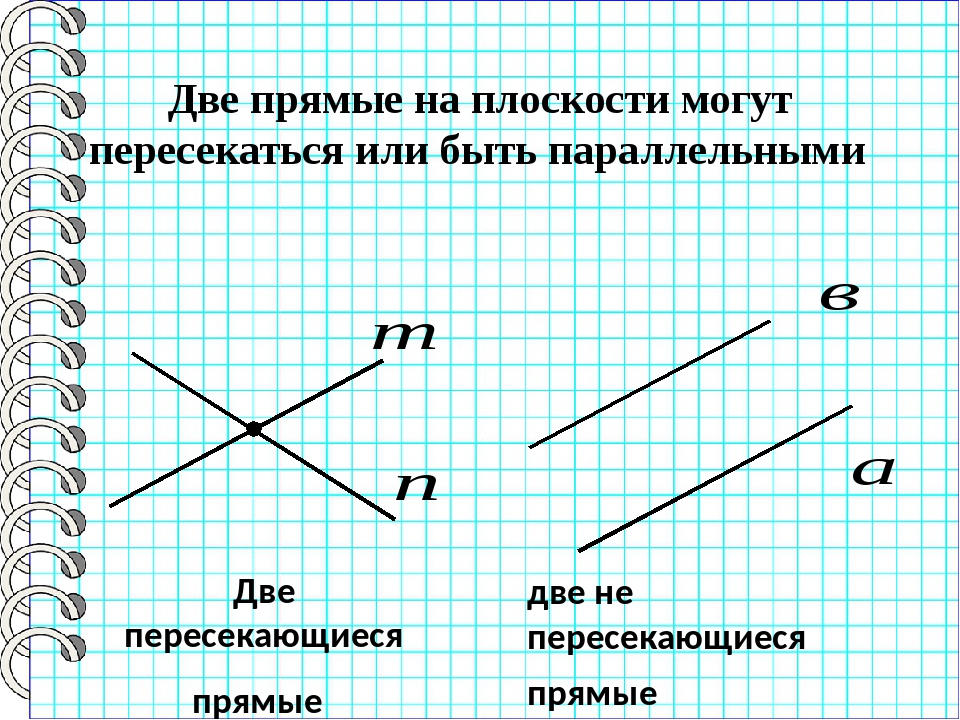
В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.
Как решаем:
- Вспомним формулу для определения пути через скорость и время: S = V * t.
- Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений: 70 * 2 = V * 7
- Найдем скорость второго автомобиля: V = 70 * 2/7 = 20
Ответ: 20 км/ч.
Пример 2.
Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?
Как рассуждаем:
Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.
Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.
Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:
Таким образом:
- х = 1 (блогер) * 30 (раз) : 12/8 (дней).
- х = 1 * 30 : 12/8
- х = 20
Ответ: 20 человек напишут 420 постов за 12 дней.
Обратно пропорциональные величины
Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.
Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».
Свойство обратной пропорциональности величин:
Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.
Примеры обратно пропорциональной зависимости:
- время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины;
- при одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи;
- количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене.

|
Формула обратной пропорциональности y = k/x где y и x — это переменные величины, k — постоянная величина, которую называют коэффициентом обратной пропорциональности. |
Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.
Формула коэффициента обратной пропорциональности:
xy = k.
Графиком обратно пропорциональной зависимости величин является гипербола.
Свойства функции обратной пропорциональности:
- Область определения — множество всех действительных чисел, кроме x = 0.
D(y): (-∞; 0) U (0; +∞).
- Область значений — все действительные числа, кроме y = 0.

Е(у): (-∞; 0) U (0; +∞).
- Не имеет наибольших и наименьших значений.
- Является нечетной, и ее график симметричен относительно начала координат.
- Непериодическая.
- Ее график не пересекает оси координат.
- Не имеет нулей.
- Если k > 0 (аргумент возрастает), функция пропорционально убывает на каждом из своих промежутков. Если k < 0 (аргумент убывает), функция пропорционально возрастает на каждом из своих промежутков.
- При возрастании аргумента (k > 0) отрицательные значения функции находятся в промежутке (-∞; 0), а положительные — (0; +∞). При убывании аргумента (k < 0) отрицательные значения расположены на промежутке (0; +∞), положительные — (-∞; 0).
Потренируемся
Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?
Как рассуждаем:
- В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.

- Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.
- Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:
Как решаем:
- Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию: 30 : 24 = 5 : х
- Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член: х = 24 * 5 : 30; х = 4
- Значит, 30 человек раскрутят канал за 4 дня.
Ответ: за 4 дня.
Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?
Как рассуждаем:
Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.
Обозначим: =
v1 = 75 км/ч
v2 = 52 км/ч
t1 = 13 ч
t2 = х
Как решаем:
- Составим пропорцию: v1/v2 = t2/t1.

Соотношения равны, но перевернуты относительно друг друга.
- Подставим известные значения: 75/52 = t2/13
Ответ: 18 часов 45 минут.
Уравнение прямой, виды уравнения прямой на плоскости
В прошлом материале мы рассмотрели основные моменты, касающиеся темы прямой на плоскости. Теперь же перейдем к изучению уравнения прямой: рассмотрим, какое уравнение может называться уравнением прямой, а также то, какой вид имеет уравнение прямой на плоскости.
Определение уравнения прямой на плоскости
Допустим, что есть прямая линия, которая задана в прямоугольной декартовой системе координат Oху.
Определение 1Прямая линия – это геометрическая фигура, которая состоит из точек. Каждая точка имеет свои координаты по осям абсцисс и ординат. Уравнение, которое описывает зависимость координат каждой точки прямой в декартовой системе Oxy, называется уравнением прямой на плоскости.
Фактически, уравнение прямой на плоскости – это уравнение с двумя переменными, которые обозначаются как x и y. Уравнение обращается в тождество при подстановке в него значений любой из точек прямой линии.
Давайте посмотрим, какой вид будет иметь уравнение прямой на плоскости. Этому будет посвящен весь следующий раздел нашей статьи. Отметим, что существует несколько вариантов записи уравнения прямой. Объясняется это наличием нескольких способов задания прямой линии на плоскости, и также различной спецификой задач.
Общее уравнение прямой линии
Познакомимся с теоремой, которая задает вид уравнения прямой линии на плоскости в декартовой системе координат Oxy.
Теорема 1Уравнение вида Ax+By+C=0 , где x и y – переменные, а А, В и C – это некоторые действительные числа, из которых A и B не равны нулю, задает прямую линию в декартовой системе координат Oxy. В свою очередь, любая прямая линия на плоскости может быть задана уравнением вида Ax+By+C=0 .
Таким образом, общее уравнение прямой на плоскости имеет вид Ax+By+C=0 .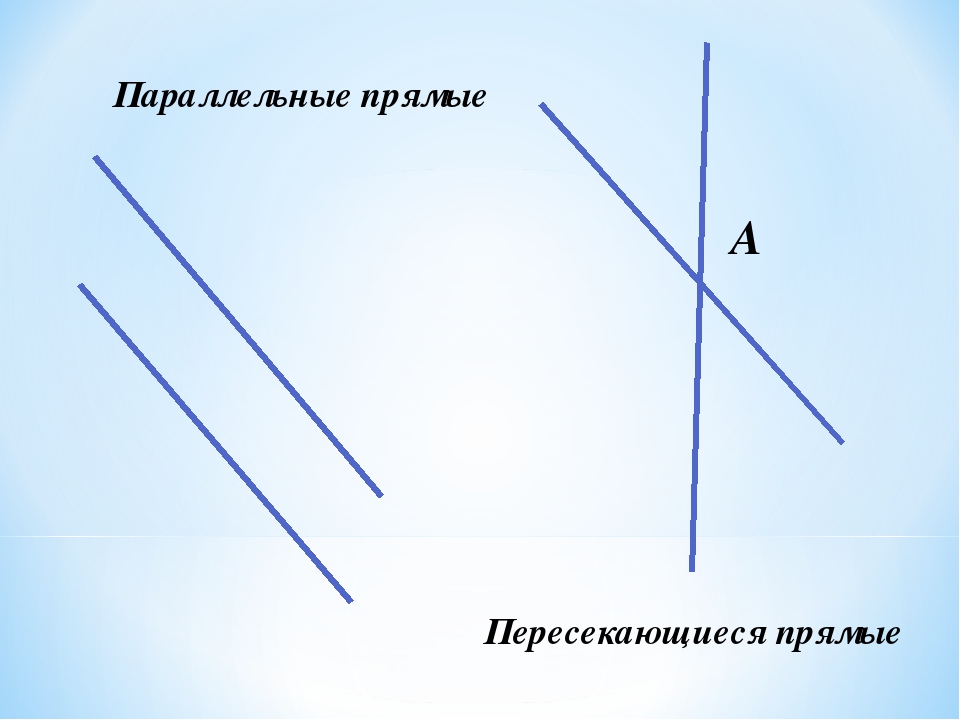
Поясним некоторые важные аспекты темы.
Пример 1Посмотрите на рисунок.
Линия на чертеже определяется уравнением вида 2x+3y-2=0 , так как координаты любой точки, составляющей эту прямую, удовлетворяют приведенному уравнению. В то же время, определенное количество точек плоскости, определяемых уравнением 2x+3y-2=0, дают нам прямую линию, которую мы видим на рисунке.
Общее уравнение прямой может быть полным и неполным. В полном уравнении все числа А, В и C отличны от нуля. Во всех остальных случаях уравнение считается неполным. Уравнение вида Ax+By=0 определяет прямую линию, которая проходит через начало координат. Если A равно нулю, то уравнение Ax+By+C=0 задает прямую, расположенную параллельно оси абсцисс Ox. Если B равно нулю, то линия параллельна оси ординат Oy.
Вывод: при некотором наборе значений чисел А, В и C с помощью общего уравнения прямой можно записать любую прямую линию на плоскости в прямоугольной системе координат Oху.
Прямая, заданная уравнением вида Ax+By+C=0 , имеет нормальный вектор прямой с координатами A, B .
Все приведенные уравнения прямых, которые мы рассмотрим ниже, могут быть получены из общего уравнения прямой. Также возможен и обратный процесс, когда любое из рассматриваемых уравнений может быть приведено к общему уравнению прямой.
Разобраться во всех нюансах темы можно в статье «Общее уравнение прямой». В материале мы приводим доказательство теоремы с графическими иллюстрациями и подробным разбором примеров. Особое внимание в статье уделяется переходам от общего уравнения прямой к уравнениям других видов и обратно.
Уравнение прямой в отрезках
Уравнение прямой в отрезках имеет вид xa+yb=1 , где a и b – это некоторые действительные числа, которые не равны нулю. Абсолютные величины чисел a и b равны длине отрезков, которые отсекаются прямой линией на осях координат. Длина отрезков отсчитывается от начала координат.
Благодаря уравнению можно легко построить прямую линию на чертеже. Для этого необходимо отметить в прямоугольной системе координат точки a, 0 и 0, b , а затем соединить их прямой линией.
Построим прямую, которая задана формулой x3+y-52=1 . Отмечаем на графике две точки 3, 0, 0, -52 , соединяем их между собой.
Дополнительно рекомендуем ознакомиться с материалом, изложенным в статье «Уравнение прямой в отрезках».
Уравнение прямой с угловым коэффициентом
Эти уравнения, имеющие вид y=k·x+b должны быть нам хорошо известны из курса алгебры. Здесь x и y – это переменные, k и b – это некоторые действительные числа, из которых k представляет собой угловой коэффициент. В этих уравнениях переменная у является функцией аргумента x.
Дадим определение углового коэффициента через определение угла наклона прямой к положительному направлению оси Ox.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание Определение 2Для обозначения угла наклона прямой к положительному направлению оси Ox в декартовой системе координат введем величину угла α . Угол отсчитывается от положительного направления оси абсцисс до прямой линии против хода часовой стрелки. Угол α считается равным нулю в том случае, если линия параллельна оси Ox или совпадает с ней.
Угол α считается равным нулю в том случае, если линия параллельна оси Ox или совпадает с ней.
Угловой коэффициент прямой – это тангенс угла наклона этой прямой. Записывается это следующим образом k=tg α . Для прямой, которая располагается параллельно оси Oy или совпадает с ней, записать уравнение прямой с угловым коэффициентом не представляется возможным, так как угловой коэффициент в этом случае превращается в бесконечность (не существует).
Прямая, которая задана уравнением y=k·x+b, проходит через точку 0, b на оси ординат. Это значит, что уравнение прямой с угловым коэффициентом y=k·x+b , задает на плоскости прямую линию, которая проходит через точку 0, b и образует угол α с положительным направлением оси Ox, причем k=tg α .
Пример 3Изобразим прямую линию, которая определяется уравнением вида y=3·x-1.
Эта линия должна пройти через точку (0, -1) . Угол наклона α=arctg 3=π3 равен 60 градусов к положительному направлению оси Ox. Угловой коэффициент равен 3
Обращаем ваше внимание, что с помощью уравнения прямой с угловым коэффициентом очень удобно искать уравнение касательной к графику функции в точке.
Больше материала по теме можно найти в статье «Уравнение прямой с угловым коэффициентом». Помимо теории там размещено большое количество графических примеров и подробный разбор задач.
Каноническое уравнение прямой на плоскости
Данный вид уравнения имеет вид x-x1ax=y-y1ay, где x1, y1, ax, ay- это некоторые действительные числа, из которых ax и ay не равны нулю.
Прямая линия, заданная каноническим уравнением прямой, проходит через точку M1(x1, y1) . Числа ax и ay в знаменателях дробей представляют собой координаты направляющего вектора прямой линии. Это значит, что каноническое уравнение прямой линии x-x1ax=y-y1ay в декартовой системе координат Oxy соответствует линии, проходящей через точку M1(x1, y1) и имеющей направляющий вектор a→=(ax, ay) .
Пример 4Изобразим в системе координат Oxy прямую линию, которая задается уравнением x-23=y-31. Точка M1(2, 3) принадлежит прямой, вектор a→(3, 1) является направляющим вектором этой прямой линии.
Каноническое уравнение прямой линии вида x-x1ax=y-y1ay может быть использовано в случаях, когда ax или ay равно нулю. Наличие ноля в знаменателе делает запись x-x1ax=y-y1ay условной. Уравнение можно записать следующим образом ay(x-x1)=ax(y-y1) .
Наличие ноля в знаменателе делает запись x-x1ax=y-y1ay условной. Уравнение можно записать следующим образом ay(x-x1)=ax(y-y1) .
В том случае, когда ax=0 , каноническое уравнение прямой принимает вид x-x10=y-y1ay и задает прямую линию, которая расположена параллельно оси ординат или совпадает с этой осью.
Каноническое уравнение прямой при условии, что ay=0 , принимает вид x-x1ax=y-y10 . Такое уравнение задает прямую линию, расположенную параллельно оси абсцисс или совпадающую с ней.
Больше материала на тему канонического уравнения прямой смотрите здесь. В статье мы приводим целый ряд решений задач, а также многочисленные примеры, которые позволяют лучше овладеть темой.
Параметрические уравнения прямой на плоскости
Данные уравнения имеют вид x=x1+ax·λy=y1+ay·λ , где x1, y1, ax, ay — это некоторые действительные числа, из которых ax и ay не могут быть одновременно равны нулю. В формулу вводится дополнительный параметр λ , который может принимать любые действительные значения.
Назначение параметрического уравнения в том, чтобы установить неявную зависимости между координатами точек прямой линии. Для этого и вводится параметр λ .
Числа x, y представляют собой координаты некоторой точки прямой. Они вычисляются по параметрическим уравнениям прямой при некотором действительном значении параметра λ .
Пример 5Предположим, что λ=0 .
Тогда x=x1+ax·0y=y1+ay·0⇔x=x1y=y1 , т. е. точка с координатами (x1, y1) принадлежит прямой.
Обращаем ваше внимание на то, что коэффициенты ax и ay при параметре λ в данном виде уравнений представляют собой координаты направляющего вектора прямой линии.
Пример 6Рассмотрим параметрические уравнения прямой линии вида x=2+3·λy=3+λ . Прямая, заданная уравнениями, в декартовой системе координат проходит через точку (x1, y1) и имеет направляющий вектор a→=(3, 1) .
Больше информации ищите в статье «Параметрические уравнения прямой на плоскости».
Нормальное уравнение прямой
Нормальное уравнение прямой имеет вид ,Ax+By+C=0, где числа А, В, и C таковы, что длина вектора n→=(A, B) равна единице, а C≤0 .
Нормальным вектором линии, заданной нормальным уравнением прямой в прямоугольной системе координат Oху, является вектор n→=(A, B) . Эта прямая проходит на расстоянии C от начала координат в направлении вектора n→=(A, B) .
Еще одним вариантом записи нормального уравнения прямой линии является cos α·x+cos β·y-p=0 , где cos α и cos β — это два действительных числа, которые представляют собой направляющие косинусы нормального вектора прямой единичной длины. Это значит, что n→=(cos α, cos β) , справедливо равенство n→=cos2 α + cos2 β=1 , величина p≥0 и равна расстоянию от начала координат до прямой.
Пример 7Рассмотрим общее уравнение прямой -12·x+32·y-3=0. Это общее уравнение прямой является нормальным уравнением прямой, так как n→=A2+B2=-122+32=1 и C=-3≤0 .
Уравнение задает в декартовой системе координат 0ху прямую линию, нормальный вектор которой имеет координаты -12, 32 . Линия удалена от начала координат на 3 единицы в направлении нормального вектора n→=-12, 32 .
Обращаем ваше внимание на то, что нормальное уравнение прямой на плоскости позволяет находить расстояние от точки до прямой на плоскости.
Если в общем уравнении прямой Ax+By+C=0 числа А, В и С таковы, что уравнение Ax+By+C=0 не является нормальным уравнением прямой, то его можно привести к нормальному виду. Подробнее об этом читайте в статье «Нормальное уравнение прямой».
Прямая линия — уравнения, формулы, определения, примеры
Прямая линия — это бесконечная одномерная фигура, не имеющая ширины. Прямая линия — это комбинация бесконечных точек, соединенных по обе стороны от точки. На прямой линии нет кривой. Прямая линия может быть горизонтальной, вертикальной или наклонной. Если мы нарисуем угол между любыми двумя точками на прямой, мы всегда получим 180 градусов. В этом мини-уроке мы исследуем мир прямых линий, разбираясь в уравнениях прямых линий в различных форматах и как решать вопросы, основанные на прямых линиях.
Введение в прямую линию
Прямая линия — это линия бесконечной длины, на которой нет кривых. Прямая линия может быть образована и между двумя точками, но оба конца простираются до бесконечности. Прямая линия — это фигура, образованная, когда две точки \ (A (x_1, y_1) \) и \ (B (x_2, y_2) \) соединены кратчайшим расстоянием между ними, а концы линии растянуты до бесконечности.
На изображении ниже показана прямая линия между двумя точками A и B.Прямая линия AB представлена как: \ (\ overline {\ text {AB}} \)
Хотя прямые линии не имеют определенного начала или конца, они представлены в нашей повседневной жизни такими примерами, как железнодорожные пути или автострады.
Прямые бывают разных типов. Как правило, прямые линии классифицируются на основе их совмещения. Их выравнивание относится к углу, который они образуют с осью x или осью y. По совмещению прямых они бывают следующих типов:
- Горизонтальные линии
- Вертикальные линии
- Наклонные или наклонные линии
Давайте изучим их один за другим.
Горизонтальные линии
Линии, нарисованные горизонтально и параллельные оси x или перпендикулярные оси y, называются горизонтальными линиями. Они образуют угол 0 o или 180 o с осью x и угол 90 o или 270 o с осью y.
На данном рисунке \ (\ overline {\ text {AB}} \) — горизонтальная линия.
Вертикальные линии
Линии, нарисованные вертикально и параллельные оси y или перпендикулярные оси x, называются вертикальными линиями.Они образуют угол 90 o или 270 o с осью x и угол 0 o или 180 o с осью y.
На данном рисунке \ (\ overline {\ text {CD}} \) — вертикальная линия.
Наклонные или наклонные линии
Линии нарисованы под наклоном или образуют угол, отличный от 0 o , 90 o , 180 o , 270 o , 360 o с горизонтальными или вертикальными линиями, называются наклонными или наклонными линий.
На данном рисунке \ (\ overline {\ text {EF}} \) и \ (\ overline {\ text {GH}} \) — наклонные линии.
Уравнение прямой
Уравнение прямой — это линейное уравнение. Прямая линия на декартовой плоскости может иметь различные представления в зависимости от известных переменных, углов и констант. Наклон прямой линии определяет направление прямой и говорит о ее крутизне. Он рассчитывается как разница в координатах y / разница в координатах x, что также называется превышением пробега.Уравнение прямой бывает разной формы. Это следующие:
Общее уравнение прямой
Общее уравнение прямой может быть задано как ax + by + c = 0, где
- a, b, c — константы, а
- x, y — переменные.
- Уклон -a / b
Форма уклона и пересечения по оси Y
Прямая линия с наклоном m = tanθ, где θ — это угол, образованный линией с положительной осью x, а точка пересечения с y как b определяется выражением y = mx + b, где m — наклон.
Форма уклона
Прямая линия с наклоном m = tanθ, где θ — угол, образованный линией с положительной осью x и проходящей через точку \ ((x_1, y_1) \), задается следующим образом: Форма точки наклона как \ (y — y_1 = m (x — x_1) \)
Двухточечная форма
Прямая линия, проходящая через точки \ ((x_1, y_1) \) и \ ((x_2, y_2) \), задается в двухточечной форме как: \ (y — y_1 = (\ dfrac {y_2 — y_1}) {x_2 — x_1}) (x — x_1) \)
Форма перехвата
Прямая линия, имеющая точку пересечения по оси x как a и точку пересечения с y как b, как показано на рисунке ниже, где точка A находится на оси x (здесь вертикально), а точка B находится на оси y (здесь горизонтально), является задается в виде перехвата как x / a + y / b = 1
Уравнение линий, параллельных оси X или оси Y
Уравнение прямой, параллельной оси x, имеет вид: y = ± a, где
- a — расстояние линии от оси абсцисс.
 Значение a равно + ve, если оно лежит выше оси x, и n -ve, если оно лежит ниже оси x.
Значение a равно + ve, если оно лежит выше оси x, и n -ve, если оно лежит ниже оси x.
Уравнение прямой, параллельной оси y. определяется выражением: x = ± b, где
- b — расстояние от оси Y до прямой. Значение b равно + ve, если оно лежит справа от оси y, и -ve, если оно лежит слева от оси y.
Ниже показано изображение линий, параллельных оси x и оси y соответственно.
Угол, образованный линией с положительной осью x, является наклоном прямой.Разные линии образуют разные углы с осью x. Линия может иметь наклон от положительного, отрицательного, нулевого или даже бесконечного наклона. Посмотрим на некоторые случаи.
Нулевой наклон
Если линия образует угол 0 o с осью x, наклон линии равен 0. Наклон линии представлен как m = tanθ
Здесь θ = 0 o . Следовательно, m = tan0 = 0. Следовательно, линия с наклоном 0 параллельна оси x.
Положительный наклон
Если линия образует угол между 0 o и 90 o с осью x, наклон линии положительный.
Отрицательный наклон
Если линия образует угол между 90 o и 180 o с осью x, наклон линии отрицательный.
Бесконечный наклон
Если линия образует угол 90 o с осью x, или линия параллельна оси y, наклон линии не определен или бесконечен.
Как известно, наклон прямой m = tan θ
Здесь θ = 90 o .уклон m = tan 90 o , не определен. Следовательно, линия с бесконечным наклоном параллельна оси y.
Свойства прямой
Свойства прямых описаны ниже.
- Прямая линия бесконечна. Мы никогда не сможем вычислить расстояние между двумя крайними точками линии.
- Прямая линия имеет нулевые площади, нулевой объем. но у него бесконечная длина.
- Прямая линия — это одномерная фигура.
- Бесконечное количество линий может проходить через одну точку, но есть только одна уникальная линия, которая проходит через две точки.

Связанные темы
Вот список связанных тем по прямой:
Важные примечания
Вот список из нескольких моментов, которые следует помнить при изучении прямой линии:
- Прямая линия не может проходить через три неколлинеарных точки.
- Если две прямые l и m совпадают, они подчиняются соотношению l = k × m, где k — действительное число.
- Острый угол \ (\ theta \) между двумя линиями с уклоном \ (m_1 \) и \ (m_2 \), где \ (m_2> m_1 \) может быть вычислен по формуле \ (tan \ theta = \ dfrac { m_2 — m_1} {1 + m_2 \ times m_1} \).
-
Пример 1: Павел рисует линию на декартовой плоскости с уравнением y = 2x — 1, а его сестра рисует прямую 2y = x + 1, Пол говорит, что линии пересекаются во 2-м квадранте, а его сестра говорит, что линии пересекаются в 1-м квадранте, кто прав.
Решение
Дано:
Полом нарисована линия y = 2x — 1его сестра нарисовала линию 2y = x +1
Давайте решим эти два уравнения одновременно, чтобы найти точку пересечения.

у = 2х — 12y = x + 1
Когда мы решаем эти два уравнения одновременно, мы получаем
x = 1 и y = 1
Обе линии пересекаются в точке (1, 1)
Точка пересечения находится в первом квадрантеОтвет: Сестра Пола верна
-
Пример 2: Колония расположена в декартовой плоскости, дом Мэтью расположен в точке (4, 3), а дом Джима расположен в точке (7, -2), две дороги должны быть построены из квадрата, расположенного в ( 3, 2), выясните, перпендикулярны ли эти две дороги друг другу (при условии, что дороги образуют прямую линию).
Решение
Рассмотрим дом Мэтью, расположенный в точке P (4, 3)
Дом Джима находится в точке Q (7, -2)
Площадьнаходится в точке R (3, 2)
, применяя формулу для вычисления наклона линии между двумя точками
\ (m = \ dfrac {y_2 — y_1} {x_2 — x_1} \)
Наклон прямой между точкой P и R равен
\ (m_1 = \ dfrac {3 — 2} {4 — 3} \)
\ (m_1 = 1 \)
Наклон прямой между точкой Q и R равен
\ (m_2 = \ dfrac {-2 — 2} {7 — 3 } \)
\ (m_2 = \ dfrac {-4} {4} \)
\ (m_2 = -1 \)
Если две прямые перпендикулярны друг другу, то произведение их наклонов равно -1.
\ (m_1 \ times m_2 = 1 \ times -1 \)
\ (m_1 \ times m_2 = -1 \)Ответ: Дороги перпендикулярны друг другу.
перейти к слайду
Разбивайте сложные концепции с помощью простых визуальных элементов.
Математика больше не будет сложным предметом, особенно если вы понимаете концепции посредством визуализации.
Забронируйте бесплатную пробную версию Класс
Часто задаваемые вопросы (FAQ)
Что вы используете, чтобы нарисовать прямую линию?
Прямая линия может быть проведена с помощью линейки, т-квадратов и т. Д.Различные геометрические инструменты, имеющие гладкую и плоскую поверхность, также можно использовать для проведения прямой линии между двумя точками. Прямая линия, проведенная между двумя точками, называется отрезком. Линейки — широко используемый инструмент для проведения прямой линии между двумя точками или прямой линии в целом.
В чем разница между параллельными и перпендикулярными линиями?
Угол между двумя параллельными линиями равен 0 градусов, а угол между двумя перпендикулярными линиями равен 90 ∘ .Параллельные линии выровнены в направлении друг друга, а перпендикулярные линии выровнены под углом 90 ∘ друг к другу. Наклоны параллельных линий равны друг другу, тогда как наклоны перпендикулярных линий не равны друг другу, а наклон одной линии равен отрицательному обратному наклону другой линии.
Какой угол наклона прямой?
Угол, образованный линией с положительной осью x, — это наклон линии, разные линии под разными углами с осью x.Линия может иметь наклон от положительного, отрицательного, нулевого или даже бесконечного наклона. Наклон линии конкретно измеряется с помощью оси x или горизонтальной линии. Чтобы измерить наклон любой линии, мы проводим горизонтальную линию из любой точки данной линии и измеряем угол против часовой стрелки от горизонтальной линии до данной линии, а затем вычисляем tanθ данного угла.
Что такое общее уравнение прямой?
Общее уравнение прямой может быть задано как ax + by + c = 0, где
- a, b, c — константы, а
- x, y — переменные.
Какой угол между двумя перпендикулярными линиями?
Угол между двумя перпендикулярными линиями составляет 90 градусов. Две перпендикулярные линии выровнены таким образом, что произведение наклонов двух линий равно -1. Перпендикулярные линии видны повсюду, например, угол стола, угол комнаты и т. Д., И мы можем измерить угол между сторонами и узнать, что угол между перпендикулярными линиями равен 90 градусам.
Что такое параллельные линии?
Две прямые называются параллельными, если они лежат в одной плоскости и никогда не пересекаются.Параллельные линии отличаются друг от друга на угол 0 или 180 градусов. Они выровнены в одном направлении друг с другом. Если у нас есть две параллельные прямые, на которых нам известен наклон одной прямой, то мы можем приравнять наклон другой прямой к первой и узнать наклон другой прямой.
Прямые и изогнутые линии — Геометрия
Давным-давно (плюс-минус 2000 лет) существовала культура, которой мы обязаны значительной частью математики, которую мы знаем сегодня: Древняя Греция. Наиболее важный вклад, вероятно, был внесен Евклидом, который собрал всю информацию, которая была известна о математике в то время, и скомпилировал ее в книгах под названием The Elements . Он не только собирал и систематизировал математику, но также «логически» организовал, или, скажем так, создал систему, которая организовывала контентный материал в соответствии с его подразумеваемой логикой (дедуктивное рассуждение). Так в игру вступили аксиомы и теоремы… (из аксиомы следует теорема), представляете, насколько это было важно? Трудно понять…
Евклид зарезервировал большую часть своих книг для g eometry (грекам это нравилось!). Фактически, именно в этом разделе его работы оставались нетронутыми до 19 века (но теперь все дело в высшей математике) . Итак, действительно, то, что мы сегодня изучаем в школе, началось более двух тысяч лет назад!
Итак, действительно, то, что мы сегодня изучаем в школе, началось более двух тысяч лет назад!
Сегодняшний пост посвящен изучению прямых и изогнутых линий, как Евклид изучал много лет назад.
Есть много способов определить прямые и изогнутые линии; наиболее подробный способ их определения следующий:
- Прямая линия — это последовательность точек, выровненных в одном направлении. Или, другими словами, чтобы перейти от одной точки к другой, мы никогда не меняем направления.
- Напротив, точки кривой линии меняют направление от одной точки к другой.
Мы можем наблюдать эти линии на следующем изображении:
Но это не единственный способ их определить! Оригинальный способ (и тот, который они используют в настоящее время в математике) больше похож на метод, который использовал сам Евклид. Подумайте о двух моментах на листе бумаги. Сколько способов вы можете перейти от одной точки к другой?
Если нет препятствий, есть множество способов сделать это… например:
И это еще не все! Верно? Итак, вот ключевой вопрос: какая линия из всех линий, которые мы можем провести, самая короткая? Другими словами: какой самый короткий путь из пункта А в пункт Б? Вот и все! Последняя строка, синяя. Вот как мы определяем прямую линию.
Вот как мы определяем прямую линию.
Между двумя точками линия, соединяющая их, является прямой, если это кратчайшее возможное расстояние между ними.
Если линия не является кратчайшим расстоянием между двумя точками, это кривая линия.
Но подождите! А как насчет второй линии, которую мы нарисовали? Это особый случай, потому что это не одна строка, а несколько строк.
- Линия, соединяющая A и C.
- Линия, соединяющая C и D.
- Линия, соединяющая D и E.
- Линия, соединяющая E и B.
Итак, нам все еще нужно знать, что такое линия… как мы узнаем, есть ли у нас одна или несколько линий? Здесь все становится немного сложнее, но я постараюсь объяснить это изо всех сил.
Вообще говоря, линия не может иметь углов (это то, что мы называем производной в математике). Если линия имеет угол, это не просто одна линия, а несколько линий.В нашем примере у нас есть 3 угла.
Теперь мы можем разделить то, что мы сначала назвали линией, на несколько частей, потому что «линия, соединяющая A с B» больше не правильная, потому что это не линия!
Как вы думаете, сколько прямых линий можно провести между A и B? Всего один, правда? Зато можно нарисовать много изогнутых линий! Евклид и все последовавшие за ним математики долгое время думали так же. До тех пор, пока в 19-м веке не появился человек по имени Гаусс, который подумал… что же произойдет, если я нанесу A и B на сферу? Например, самолет, который вылетает из Бостона в Мумбаи, не может следовать по прямой (при условии, что мы не можем проложить туннель), так какой же путь он выберет? И самое главное, существует ли еще один?
Мы рассмотрим эту загадку в одном из следующих постов…
Между тем, если вы хотите продолжить изучение математики, создайте учетную запись на Smartick!
Подробнее:
Развлечение — любимый способ обучения нашего мозга
Дайан Акерман
Smartick — увлекательный способ изучения математики- 15 веселых минут в день
- Адаптируется к уровню вашего ребенка
- Миллионы учеников с 2009 года
Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создать максимально возможное математическое содержание.
Что такое прямой угол? — Определение, факты и пример
Что такое прямой угол?
Два соединяющихся луча образуют угол. Общая точка, где встречаются эти два луча, называется вершиной, а лучи — плечами угла.
Мера угла — это величина поворота или поворота точки от одного плеча к другому вдоль его вершины.
Когда стороны угла лежат в противоположном направлении, они образуют прямой угол. Углы образуют прямую линию через вершину.
Прямой угол также называется «плоский угол ».
На рисунке OX и OY — руки угла. Общая точка O, где встречаются лучи, называется вершиной.
Как изобразить прямой угол?
Существуют различные способы представления прямых углов в соответствии с системой измерения.
-
Записывается как 180 °
-
Также записывается как π
Все углы, указанные на рисунке, прямые.
Свойства прямого угла
-
В прямом угле лучи смотрят в противоположных направлениях.
-
Прямой угол меняет направление точки
-
Прямой угол составляет ровно половину оборота.
-
Прямой угол можно также образовать, сложив два прямых угла.
Построение прямого угла с помощью транспортира
-
Начертите прямую OA со стрелкой на A.
-
Теперь держите транспортир на этой линии так, чтобы базовая линия транспортира была выровнена по OA. Буква A должна быть направлена в сторону 0 ° транспортира.
-
Начинайте с 0 ° и двигайтесь к отметке 180 ° транспортира.Достигнув 180 °, отметьте точку B на бумаге.
-
Соедините вершину прямой OA с точкой B.
 второй луч OB будет иметь стрелку в точке B.
второй луч OB будет иметь стрелку в точке B.
Прямые углы в жизни
|
Интересные факты
|
Построение прямых линий: обзор
Purplemath
В этом обзоре мы начнем с построения прямых линий, а затем перейдем к другим графикам. Единственное существенное различие, на самом деле, заключается в том, сколько точек вам нужно построить, чтобы построить хороший график. Но это увеличенное количество точек будет зависеть от «интересных» проблем, связанных с различными типами графиков.
Прежде чем мы начнем, позвольте мне сказать следующее: вы должны сделать аккуратных графиков, что означает, что вы должны использовать линейку. Если у вас нет линейки, возьмите ее. Сейчас. Дешевая пластиковая шестидюймовая машина очень поможет, и вы можете получить от своего инструктора большие «баллы», используя ее.
MathHelp.com
И нет, использование миллиметровой бумаги , а не не освобождает вас от использования линейки.
Прямолинейное построение графиков
Предположим, нам дано уравнение y = 3 x + 2 для построения графика. Поскольку переменные в этом уравнении имеют простую форму — просто x , в отличие, скажем, от x 2 или | x | — это уравнение отображается в виде простой прямой линии. Чтобы начать построение этого уравнения, нам нужно нарисовать так называемую «Т-диаграмму».
Поскольку переменные в этом уравнении имеют простую форму — просто x , в отличие, скажем, от x 2 или | x | — это уравнение отображается в виде простой прямой линии. Чтобы начать построение этого уравнения, нам нужно нарисовать так называемую «Т-диаграмму».
Т-диаграмма выглядит так:
Затем мы выберем значения для x , подставим их в уравнение и решим это уравнение для соответствующих значений y .
Мы должны быть осторожны, чтобы не забыть выбрать хотя бы одно или два отрицательных значения для x ; использование только положительных чисел может впоследствии ввести в заблуждение, поэтому лучше не создавать эту дурную привычку сейчас. Также мы должны попытаться нанести минимум три точки. Так намного безопаснее: если мы ошибемся в одном пункте, мы узнаем, потому что эта точка не будет совпадать с другими.
Вот как выглядит T-диаграмма с некоторыми подключенными значениями:
Некоторым людям нравится добавлять третий столбец, в котором они записывают фактические точки сюжета, который выглядит так:
(Если вы используете графический калькулятор, вы, вероятно, можете попросить калькулятор заполнить Т-образную диаграмму за вас.Найдите в руководстве утилиту «ТАБЛИЦА» или просто прочтите главу о построении графиков. Когда вы узнаете, как использовать эту утилиту, вы можете просто скопировать свою Т-диаграмму с экрана калькулятора.)
Теперь, когда у нас есть точки на графике, мы рисуем НАСТОЯЩИЙ аккуратный набор осей, используя нашу линейку. Это означает рисование ЧЕТНОЙ, СОГЛАСОВАННОЙ шкалы на осях (то есть рисование равномерно распределенных отметок для чисел на осях) и, возможно, даже маркировку осей их переменными. Мы рисуем стрелки на концах осей, где числа становятся больше (это то, что обозначают стрелки, я знаю!), И рисуем стрелки НИГДЕ ЕЩЕ.
Для сравнения:
Это хороший график:
Это плохой график:
(Кстати, вы заметили, что мои отметки 5 и 10 на моих осях выше длиннее, чем у других? Это не то, что мы «должны» делать, но я на собственном опыте убедился, что это может быть очень полезно, когда Я рассчитываю, чтобы изложить свои соображения.)
Теперь наносим точки:
Точки совпадают правильно, поэтому мы знаем, что мы правильно выполнили вычисления и построили график. Теперь мы можем поставить линейку напротив точек и провести линию:
График представляет собой красивую прямую линию, идущую вверх (чего и следовало ожидать, потому что уравнение имеет положительное значение наклона м = 3) и пересекает ось y на значении пересечения y б = 2.
И помните: на концах линий графика нет стрелок. Да, я знаю, что многие американские учебники для средних и старших классов рисуют вещи именно так. Остальной мир (и остальная математика) рисует свои линии, как показано выше. Независимо от вашего нынешнего возраста, вы можете рисовать «взрослые» графики уже сейчас.
Партнер
Иногда они дают нам уравнение типа 2 y — 4 x = 3.Первое, что я всегда хочу сделать, это решить уравнение для « y =». (Среди прочего, форма « y =» — единственный способ, которым мой графический калькулятор может принять уравнение.) Процесс решения работает следующим образом:
2 y — 4 x = 3
2 y = 4 x + 3
y = 2 x + 1,5
Тогда мы можем построить график как обычно.
Кстати, часто неплохо использовать значения x , которые немного разбросаны. Если нанесенные точки расположены слишком близко друг к другу, мы можем оказаться не совсем уверены в угле линии, которую строим. Для строки выше я, вероятно, выбрал бы такие точки, как x = –4, x = –2, x = 0 и x = 2.
Иногда мы хотим быть более конкретными в отношении значений, которые мы выбираем для x .Например, предположим, что нам нужно построить график y = (2/3) x + 4. Мы можем значительно облегчить нашу жизнь, выбрав значения x , кратные 3. Поступая таким образом, мы будем иметь возможность вычеркнуть 3 в знаменателе и, таким образом, избежать дробей в точках нашего графика. Я имею в виду, что выбор x = 5 сам по себе не является неправильным, но выбор x = 3 даст нам гораздо более приятное значение y для точки, нанесенной на график для этого уравнения. Если бы знаменатель дроби был, скажем, 7, тогда было бы полезно выбрать значения x , кратные 7.И так далее.
(Если вы хотите более подробно изучить построение линейных уравнений в виде графиков, см. «Построение графиков линейных уравнений».)
URL: https://www.purplemath.com/modules/graphing.htm
Линейные функции и прямые
6.2 — Линейные функции и прямые линии6.2 — Линейные функции и прямые
Линейные функции
Щелкните здесь, чтобы просмотреть функции. Линейные функции — самые простые из всех типов функций. Линейная функция принимает на вход число x и возвращает число. m x + b как выход:m и b — постоянные. Проще говоря, x умножается на м (это называется масштабированием на коэффициент м ). а затем добавляется b (это называется смещением на величину b ).Используя обозначение функции, линейная функция выглядит так:
f ( x ) = m x + b .Если мы положим y = f ( x ), то это будет выглядеть так:
y = м x + b .Это называется уравнением прямой линии , потому что если мы построим точки, которые удовлетворяют этому уравнению на графике y против x , тогда, как мы увидим ниже, все точки лежат на прямой линии.
Типичное использование линейной функции — преобразование одного набора единиц в другой. Простой пример: если i — это расстояние, измеренное в дюймах, а c — то же самое. расстояние в сантиметрах; тогда c = 2,54 i . Это просто масштабирование. Более сложный пример: если c — температура измеряется в градусах Цельсия и f то же самое температура измеряется в градусах Фаренгейта; тогда f = 1.8 с + 32. Это масштабирование и сдвиг.
Уравнение прямой
В разделе 6.1 мы ввели декартову плоскость с осью x , нарисованной горизонтально, и осью y , нарисованной вертикально. Предположим, что m и b — константы. Мы хотим построить график линейной функции:y = м x + b ,на этой плоскости и покажите, что график представляет собой прямую линию.Для этого составляем следующую таблицу значений значений y (то есть выражения м x + b ) по сравнению с x :
Обратите внимание на следующее:
- Каждая строка таблицы показывает точку на графике.
- В одной из строк указано, что когда x = 0, тогда y = b . Таким образом, точка (0, b ) это точка на графике. Поскольку эта точка лежит на оси y , число b называется точкой пересечения y .
- При переходе от одной строки таблицы к следующей, значение x увеличивается на 1, а значение y увеличивается на m . Потому что увеличение устойчиво, точки должны лежать на прямой , а не на какой-то другой кривой.
- Более крупный м , тем быстрее увеличивается y . Если м отрицательно, то значение y фактически уменьшается .Номер м известен как склон .
- x не обязательно должно быть целым числом — это может быть любое действительное число. Потому что вещественные числа плотные, точки на графике бесконечно близко друг к другу и образуют сплошную линию (т.е. без зазоров).
| Вывод: Уравнение y = м x + b ,где m и b — константы, это уравнение прямой . м называется уклоном и b называется перехват y . Эта форма уравнения называется пересечением угла наклона . форма . Возможны и другие формы; Нажмите здесь, чтобы увидеть их. |
Нахождение уравнения прямой
Учитывая график прямой, есть несколько способов найти ее уравнение.
Метод 1: Этот метод работает, только если видна точка пересечения y .
- Найдите любые две точки,
( x 1 , y 1 ) и
( x 2 , y 2 ), на линии и
подставьте их координаты в следующую формулу, чтобы получить м :
- Получите b из просмотра пересечения y графика.
- Подставьте полученные числа для m и b в уравнение y = m x + b .
Метод 2: Этот метод работает, даже если точка пересечения y не видна.
- Как и в методе 1, найдите любые две точки,
( x 1 , y 1 ) и
( x 2 , y 2 ), на линии и
подставьте их координаты в следующую формулу, чтобы получить м :
- Подставьте полученное число для м в
уравнение y = m x + b .Также возьмите одну из точек, скажем ( x 1 , y 1 ),
и подставим его координаты в уравнение. Это дает:
y 1 = m x 1 + b
- Это может не выглядеть так, но это уравнение имеет только одну переменную, b , и вы легко можете решить эту проблему.
- Подставьте полученные числа для m и b в уравнение y = m x + b .
Метод 3: Этот метод имеет то преимущество, что он использует только алгебру, а не геометрию, и может применяться к любому типу функции, а не только к прямой линии:
- Найдите две точки,
( x 1 , y 1 ) и
( x 2 , y 2 ), которые находятся на линии.
Возьмите первую точку ( x 1 , y 1 ) и
подставляем его в уравнение прямой,
y = м x + b .Это дает:
y 1 = m x 1 + b
Аналогичным образом возьмем вторую точку ( x 2 , y 2 ) и подставляем его в уравнение прямой, y = м x + b . Это дает:y 2 = m x 2 + b
- Вместе эти два уравнения составляют систему двух уравнений с двумя неизвестными: m и b .Мы можем решить их для m и b , используя метод исключения.
Чтобы быть конкретным, если мы вычтем первое уравнение из второго, то b будет
исключаем и получаем уравнение:
y 2 — y 1 = м x 2 — м x 1 ,
которое при решении для м дает то же уравнение, что и в двух других методах, а именно: - Найти b обратной подстановкой.Чтобы быть конкретным, замените номер, который вы полученное для м в одно уравнение системы уравнений, скажем в y 1 = m x 1 + b . Это может не выглядеть так, но это уравнение имеет только одну переменную, b , и вы легко можете решить эту проблему.
Пример: Воспользуйтесь методом 1, чтобы найти уравнение прямой на графике справа.
Решение: Две точки на этой линии: ( x 1 , y 1 ) = (0, 15) и ( x 2 , y 2 ) = (3, 0). Подставляя эти координаты в формулу наклона, получаем
= -5.При осмотре перехватчик y
b = 15.Подставляя эти два значения для m и b в уравнение прямой линии, y = m x + b , дает
y = −5 x + 15.
Пример: Используйте метод 3, чтобы найти уравнение прямой на графике справа.
Решение: Две точки на этой линии — это (7, 15) и (1, 3). Подставляем координаты точки (7, 15) в уравнение прямой, y = m x + b , а затем проделайте то же самое с точкой (1, 3). Это дает систему двух уравнений с двумя неизвестными: m и b .Неизвестный b можно исключить, вычитая уравнения:
Решение относительно m дает m = 2. Подставляя назад m = 2, скажем, в первое уравнение, дает 15 = 7 · 2 + b , что легко решается и дает b = 1. Подставляя эти два значения для m и b в уравнение прямой линии, y = m x + b , дает
y = 2 x + 1.
Если вы нашли эту страницу в ходе веб-поиска, вы не увидите
Оглавление в рамке слева.
Щелкните здесь, чтобы отобразить его.
Уклон прямой
Purplemath
Одно из самых важных свойств прямой — это то, как она отклоняется от горизонтали.Эта концепция отражена в так называемом «наклоне» линии.
Давайте посмотрим на прямую
y = ( 2 / 3 ) x — 4. Ее график выглядит так:MathHelp.com
Чтобы найти наклон, нам понадобятся две точки от прямой.
Я выберу два значения x , вставлю их в линейное уравнение и решу для каждого соответствующего значения y . Если, скажем, я выберу x = 3, тогда:
Теперь предположим, что я выбрал x = 9; затем:
(Между прочим, я выбрал эти два значения x именно потому, что они были кратны трем; таким образом я знал, что смогу очистить знаменатель дроби, так что в итоге я получу хорошее, аккуратные целые числа для моих результирующих значений y .Это не правило, что вы должны это делать, но это полезный метод.)
Итак, две найденные мной точки (3, –2) и (9, 2) находятся на линии
y = ( 2 / 3 ) x — 4.Чтобы найти уклон, обозначенный как « м », мы можем использовать следующую формулу:
(Почему « м » вместо «уклон», а не, скажем, « с »? Официальный ответ: никто не знает.)
В случае, если вы раньше не сталкивались с числами переменных, меньшими, чем заданные, они называются «индексами». Индексы обычно используются для различения похожих вещей или, например, для отсчета в последовательностях. В случае формулы наклона нижние индексы просто указывают на то, что у нас есть «первая» точка (координаты которой обозначены индексом «1») и «вторая» точка (координаты которой имеют индекс «2»). Другими словами, нижние индексы указывают не более чем на то, что у нас есть две точки, с которыми мы работаем.
(Вам решать, какую точку обозначить как «первую», а какую — как «вторую». Как подсказывает логика, угол линии не изменится только потому, что вы посмотрели на две точки в в другом порядке.)
Для вычисления уклонов по формуле наклона важно, чтобы мы вычитали x и y в том же порядке . Для наших двух точек, если мы выберем (3, –2) в качестве нашей «первой» точки, то получим следующее:
Первое значение y выше, –2, было взято из точки (3, –2); второе значение y , 2, пришло из точки (9, 2); x — значения 3 и 9 были взяты из двух точек в том же порядке .
Если бы, с другой стороны, мы взяли координаты точек в обратном порядке, результат был бы точно таким же:
Как видите, порядок, в котором вы перечисляете точки, на самом деле не имеет значения, пока вы вычитаете значения x в том же порядке, в котором вы вычитали значения y . Из-за этого формулу наклона можно записать, как указано выше, или, альтернативно, ее также можно записать как:
Позвольте мне подчеркнуть этот момент:
Не имеет значения, какую из двух формул «наклона» вы используете, и неважно, какую точку вы выберете в качестве «первой», а какую — в качестве «второй».Значение только имеет значение, так это то, что вы вычитаете свои x -значения в том же порядке , как вы вычитали свои y -значения.
Для тех, кому интересно, эквивалентность двух приведенных выше формул наклона может быть доказана, если принять во внимание следующее:
y 1 — y 2 = y 1 + (- y 2 )
= — л 2 + л 1
= — y 1 — (- y 2 )
= — ( y 2 — y 1 )
Аналогично:
x 1 — x 2 = x 1 + (- x 2 )
= — x 2 + x 1
= — x 1 — (- x 2 )
= — ( x 2 — x 1 )
Затем первая формула преобразуется во вторую следующим образом:
м = ( y 1 — y 2 ) / ( x 1 — x 2 ) = [- ( y 2
Как вы можете видеть выше, выполнение вычитания в так называемом «неправильном» порядке служит только для создания двух знаков «минус», которые затем отменяются.Результат: не беспокойтесь слишком сильно о том, какая точка является «первой», потому что это на самом деле не имеет значения. (И, пожалуйста, не присылайте мне электронное письмо, в котором утверждается, что порядок имеет какое-то значение или что одна из двух приведенных выше формул почему-то «неправильная». Если вы думаете, что я ошибаюсь, вставьте пары точек в обе формулы и попробуйте доказать, что я неправ! И продолжайте вставлять, пока не «увидите», что математика на самом деле верна.)
Вернемся к строке
y = ( 2 / 3 ) x — 4 и найдем для нее еще несколько точек.Если я положу x = –3, тогда:Если я положу x = 0, то:
Это дает мне две точки: (–3, –6) и (0, –4). Если я нанесу эти две точки на линию, я получу две синие точки, показанные ниже:
Если я поднимусь вверх от первой точки ко второй (при движении вправо по оси x ), я получу:
Следующая точка, которую я использую, — (3, –2).Обозначив точку и начертив ступеньку, я получу:
А теперь внимательно посмотрите на эти ступеньки. Подсчитайте их по сетке, видимой на заднем плане. Вы увидите, что, переходя от одной намеченной точки к другой, я продвигался на два шага вверх и на три шага вперед. В терминах, привычных для строительной отрасли, эти ступеньки имеют (вертикальный) «подъем», равный 2, и (горизонтальный) «подъем», равный 3. Когда люди говорят о «уклоне» как о «подъеме над спуском», это означает что они имеют в виду.(Для получения дополнительной информации попробуйте здесь.)
Давайте найдем наклон другого линейного уравнения:
-
Найдите наклон
y = –2 x + 3
На графике линия выглядит так:
Я выберу пару значений для x и найду соответствующие значения для y .Выбирая x = –1, я получаю:
y = –2 (–1) + 3 = 2 + 3 = 5
Выбирая x = 2, я получаю:
y = –2 (2) + 3 = –4 + 3 = –1
Тогда точки (–1, 5) и (2, –1) находятся на прямой y = –2 x + 3. Наклон прямой вычисляется как:
Между прочим, если вы посмотрите на график и начнете с любой точки на линии (для простоты выберите ту, которая также лежит на сетке), вы заметите, что ступенька идет вниз.Вы спускаетесь на два, больше на одного; вниз два, больше одного; вниз два, больше одного. И это соответствует наклону, который мы нашли выше:
(два меньше) / (больше одного) = (–2) / (1) = –2
-
Найдите наклон прямой, проходящей через точки (–3, 5) и (4, –1).
В данном случае мне не нужно искать очки, потому что они уже мне их дали.Итак, я сразу перейду к формуле:
.м = (5 — (–1)) / (- 3 — 4)
= (5 + 1) / (- 3 + (–4)) = (6) / (- 7)
= — (6/7)
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в поиске уклона по паре точек. Попробуйте выполнить указанное упражнение или введите свое собственное.Затем нажмите кнопку, чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
(Щелкнув «Нажмите, чтобы просмотреть шаги», вы попадете прямо на сайт Mathway, если вы хотите проверить их программное обеспечение или получить дополнительную информацию.)
URL: https://www.purplemath.com/modules/slope.htm
Прямая линия выглядит изогнутой
Если вы посмотрите на прямую линию, и она кажется волнистой или изогнутой, это может указывать на проблемы со зрением.Искаженное зрение — распространенный симптом ряда заболеваний зрения, часто связанных с возрастом и ухудшением качества зрения.
Если вы видите изогнутые линии там, где вы знаете, что линия на самом деле прямая, возможно, вы страдаете от состояния, известного как дегенерация желтого пятна, или от одного из связанных заболеваний глаз, перечисленных ниже.
Что может вызывать волнообразное зрение?
1. Дегенерация желтого пятна
Дегенерация желтого пятна — распространенное возрастное нарушение зрения, которое может привести к ухудшению качества зрения и частичной потере зрения.Это влияет на центральное поле зрения , и часто больной теряет способность видеть прямо перед собой — хотя они, как правило, сохраняют периферическое зрение.
Это наиболее частая причина того, что прямые линии выглядят изогнутыми.
Нет лекарства, и качество зрения со временем ухудшится, но окулист может предложить помощь в управлении состоянием и приспособлении к потере зрения.
Узнайте больше об этом состоянии, прочитав полное руководство по дегенерации желтого пятна
2.Астигматизм
Астигматизм — это состояние, при котором глаз не может правильно обрабатывать свет.
Это часто вызывает рефракцию, когда изображения кажутся искаженными, поскольку глаз изо всех сил пытается обработать то, что он видит. Глаз пытается уловить свет в сетчатке в нескольких точках, а не в одной, и это вызывает нарушение зрения.
Симптомы могут вызывать тревогу, но астигматизм можно исправить с помощью контактных линз или очков.В крайних случаях для окончательного решения проблемы может быть рекомендована лазерная хирургия.
3. Сморщивание желтого пятна / отек желтого пятна
Желтое пятно в задней части глаза может стать жертвой ряда болезней и расстройств, влияющих на зрение. Макулярная складка и отек желтого пятна — частые примеры заболеваний глаз, которые могут привести к искажению зрения.
- Макулярный отек — это отек, который вызывает искажение зрения.
- Макулярный отек — это повреждение или сжатие стекловидного тела, которое защищает глаз и облегчает движение глаз.
Оба состояния требуют оценки офтальмологом, который может порекомендовать соответствующее лечение на основе собственных симптомов и состояния пациента.
Использование диаграммы Амслера для проверки зрения
Если прямая линия выглядит изогнутой или у вас есть какие-либо проблемы со зрением, ваш офтальмолог может диагностировать такие состояния, как дегенерация желтого пятна, с помощью инструмента, известного как сетка Амслера.

 Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
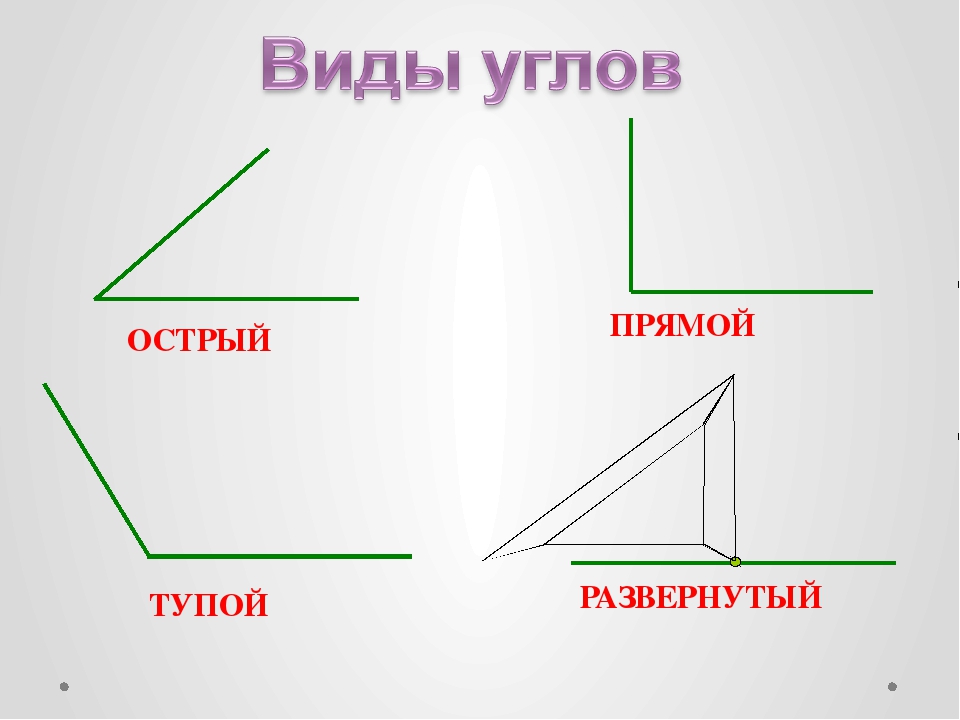 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.
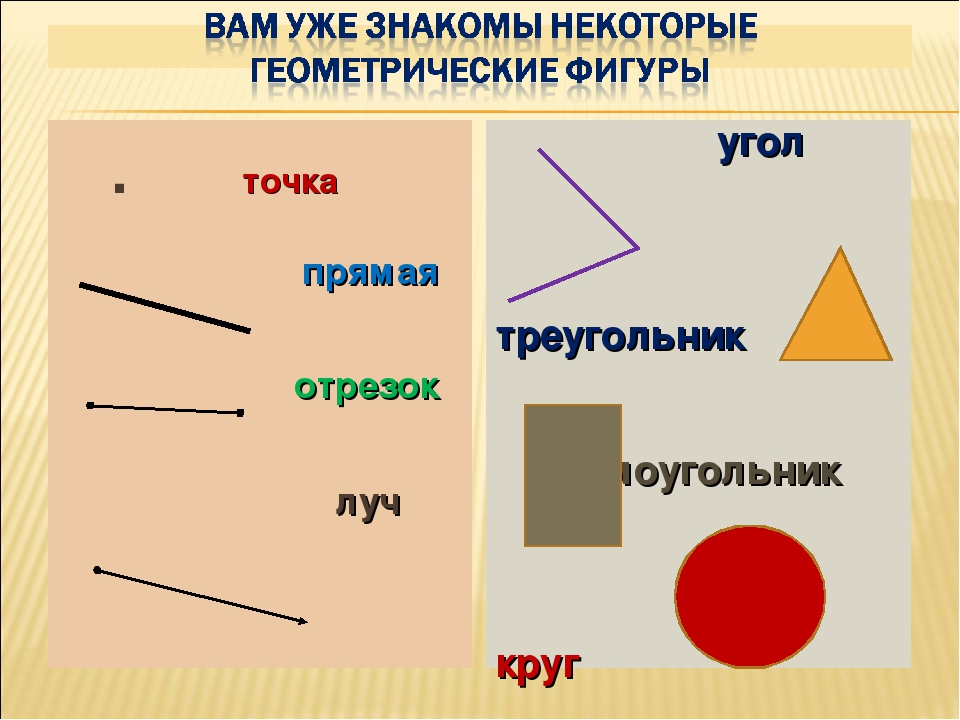 У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
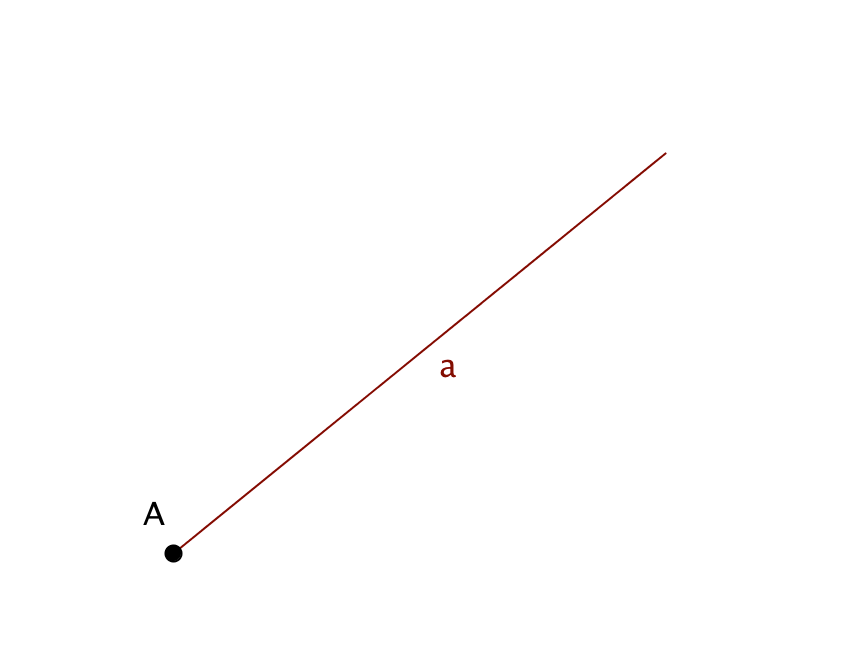 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.
 Он имеет начало и не имеет конца.
Он имеет начало и не имеет конца.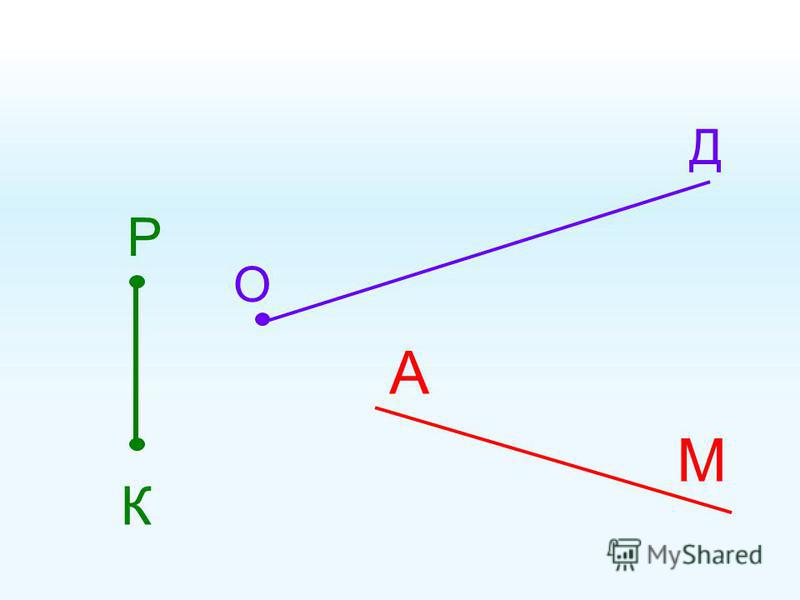
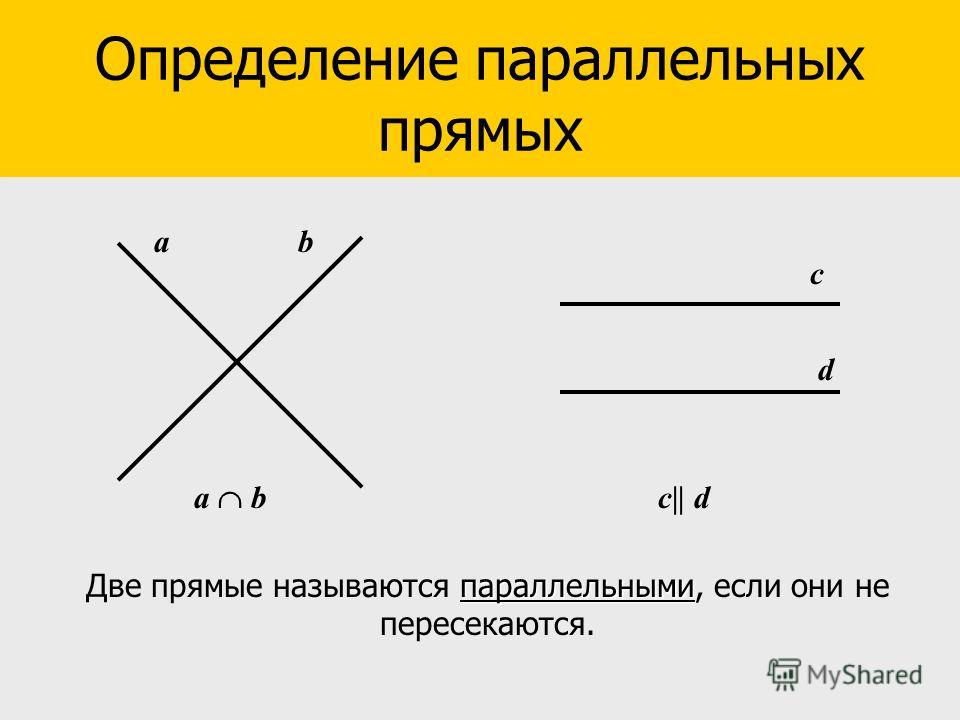

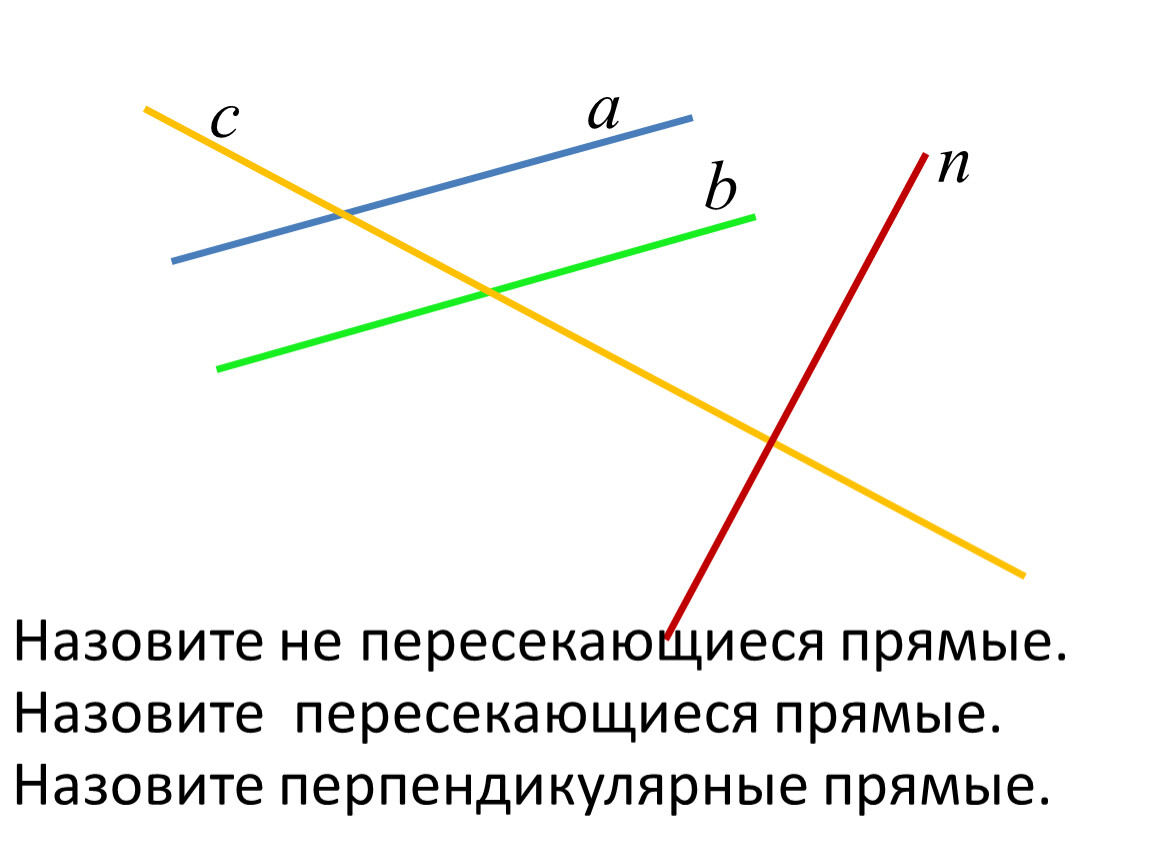


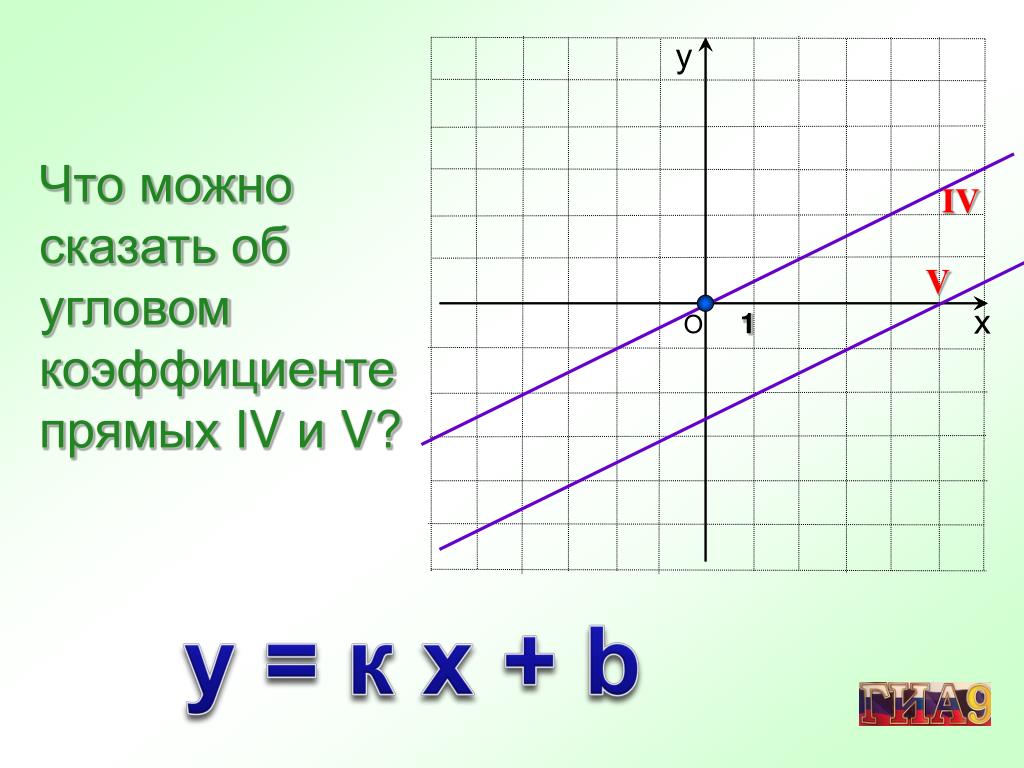 Значение a равно + ve, если оно лежит выше оси x, и n -ve, если оно лежит ниже оси x.
Значение a равно + ve, если оно лежит выше оси x, и n -ve, если оно лежит ниже оси x. 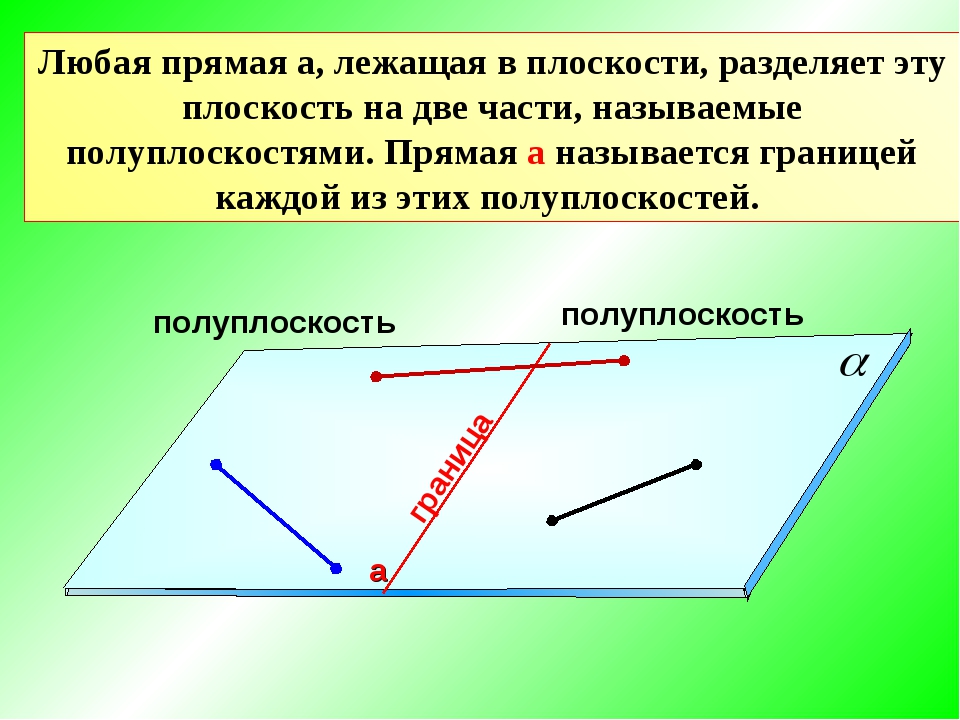
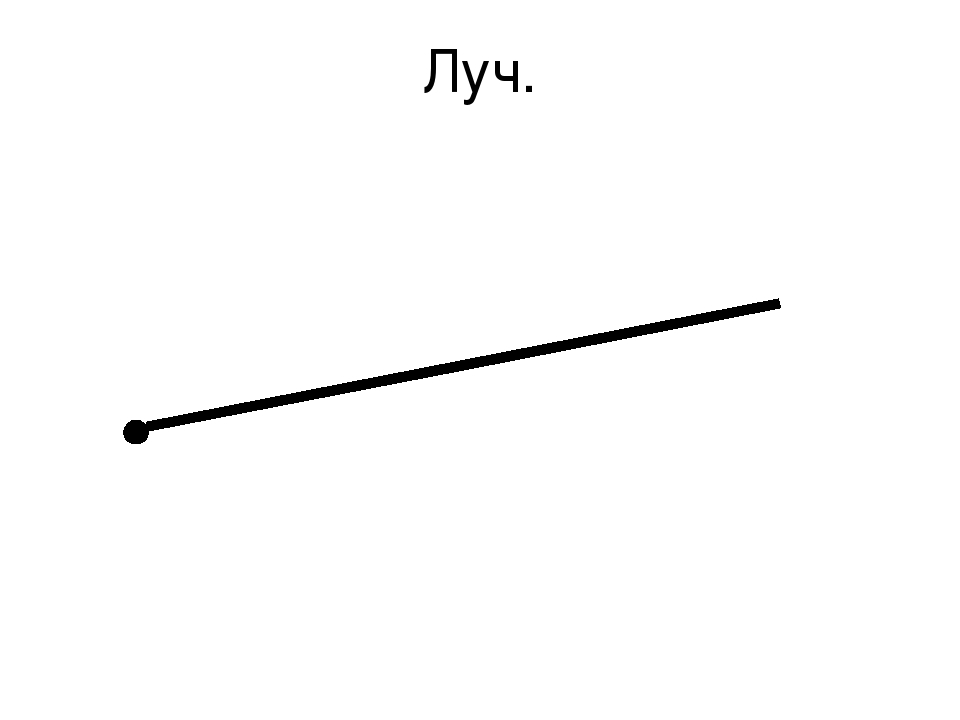
 второй луч OB будет иметь стрелку в точке B.
второй луч OB будет иметь стрелку в точке B.