ОСНОВЫ КОМПОЗИЦИИ: Золотое сечение — PhotoDzen.com
15 Апреля 2015
Композиция — это распределение предметов и фигур в пространстве, установление соотношения объёмов, света и тени, цвета и т. п. Существуют разные способы и правила для создания гармоничной композиции. Когда мы смотрим вокруг невооруженным глазом, наш мозг быстро выхватывает интересные сюжеты, объекты. Камера же фиксирует все подряд. Поэтому это ваша задача выбрать основной объект, сделать центром внимания в кадре, а окружающие его другие объекты превратить в фон или сделать частью истории, которую Вы хотите «рассказать» своим снимком.
Фотографии с правильно выбранной композицией заставляют задержать на них взгляд и рассмотреть детали. Они рассказывают историю, создают настроение и заставляют задуматься.
Золотое сечение в фотографии — основной и мощный инструмент для получения динамичных, интересных снимков. Правило золотого сечения встречается и в природе, причем повсеместно.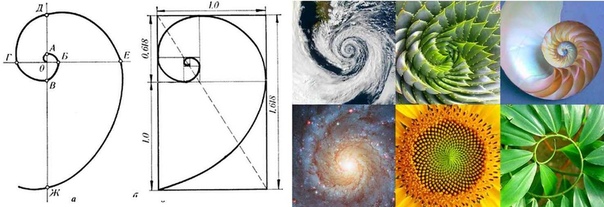
Для желающих узнать больше — видео:
Мы затронем только практическую часть применения золотого сечения в фотографии. Кадр условно делиться на три части по горизонтали и вертикали:
При пересечении горизонтальной и вертикальной линии образуется особая точка – «точка силы» или «узел внимания». Их четыре – именно в этих точках лучше располагать главные объекты кадра, именно на них останавливается взгляд в независимости от формата кадра или картины.
Практические советы:
- Если расположитьлинию горизонта по одной из горизонтальных линий, то кадр будет смотреться гармоничней. Но на какой из линий, на верхней или нижней?
- Если вы хотите сконцентрировать внимание зрителя на земле или воде – то лучше на верхней.
- Если же вы делаете акцент на интересном, выразительном небе – то на нижней.
- Если вы снимаете портрет, то лучше размещать глаза на верхней горизонтальной линии.
- Если вы снимаете человека в полный рост, то лучше размещать его на правой или левой вертикальной линии.
- Очень важно следить за тем, в какую сторону направляется человек, или куда направлен его взгляд. Например, если человек смотрит

В современных фотоаппаратах уже есть функция-подсказка, которая отображает линии правила третей на мониторе или в видоискателе.
Размещайте важные части композиции вдоль линий, а самое главное — на их пересечении.
Золотое сечение может прослеживаться не только в прямоугольной сетке, но и в диагоналях или спирали. Принцип расположения предметов – тот же, по основным линиям и в точках их пересечений.
Фото: Steve McCurry
Фото: Joe McNally
Фото: Richard Barnabe
ДИАГОНАЛЬНОЕ ЗОЛОТОЕ СЕЧЕНИЕ
Применяя правило золотого сечения проводим диагонали и получаем прямоугольник состоящий из трех секторов. Этот прямоугольник можно поворачивать как угодно Если скомпонуете свой кадр так, чтобы три разных объекта примерно располагались в этих секторах, а главные объекты в более крупных секциях — то композиция будет выглядеть очень гармонично.
Это правило используется, если у вас в кадре есть несколько областей, различающихся по смыслу.
СПИРАЛЬНОЕ ЗОЛОТОЕ СЕЧЕНИЕ
Спирали очень распространены в природе. Форма спирально завитой раковины привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике. Гёте называл спираль — «кривой жизни».
Используя эту спираль при построении композиции в кадре (ее можно перевернуть вверх ногами или в другую сторону), мы получим кадр с четко выраженным предметом в центре спирали.
Фото: Джона Лемьё (John Lemieux)
Фото: Анри Картье-Брессон
Больше фотографируйте и экспериментируйте. Удачи!
Другие статьи о композиции в фотографии:
Золотое сечение в фотографии
Сила линий в фотографии
Формат кадра в фотографии
Контраст в фотографии (Часть 1)
Контраст в фотографии (Часть 2)
Точка съемки и выбор плана
Ракурс
Геометрия в фотографии
Равновесие
ШедЭврика природы: последовательность Фибоначчи
ШедЭврика природы: последовательность Фибоначчи
опубликовано 19-07-2021 в Библиотеки
Последовательность Фибоначчи и золотое сечение показывают, как математика и искусство соотносятся в природных и рукотворных явлениях.
Большинство из нас слышали о золотой середине, золотом веке Древней Греции, золотой молодёжи, золотых шлягерах в музыке и даже о золотом сердце. А как насчёт золотого сечения?
Понятие золотого сечения тесно связано с последовательностью Фибоначчи – рядом чисел, в котором каждое последующее число является суммой двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и так далее до бесконечности. Данная последовательность была названа в честь математика Леонарда Пизанского по прозвищу Фибоначчи. При делении любого числа из последовательности на число, стоящее перед ним в ряду, результатом всегда будет величина 1.618 – число золотого сечения, обозначаемое греческой буквой φ («фи»).
На золотом сечении строится такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. В геометрии прямоугольник с таким отношением сторон зовётся золотым прямоугольником.
Отрезав от золотого прямоугольника квадрат, сторона которого равна меньшей стороне прямоугольника, мы снова получим золотой прямоугольник меньших размеров. Этот процесс можно продолжать до бесконечности. Продолжая отрезать квадраты, мы будем получать все меньшие и меньшие золотые прямоугольники. Причем располагаться они будут по логарифмической спирали, которая также называется золотой спиралью.
Связи и закономерности золотого сечения можно найти не только в математике, но и в природе, архитектуре и строительстве, а также в искусстве.
Некоторые примеры золотого сечения в природе можно увидеть в спиралевидном узоре семян подсолнечника, чешуйках сосновой шишки, разворачивании растущего папоротника и раковинах улиток.
Пропорции различных частей человеческого тела составляют число, очень близкое к золотому сечению, включая соотношение фаланг пальцев, предплечье по отношению к кисти, спираль уха и даже молекулу ДНК. В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения.
В строении черт лица человека также есть множество примеров, приближающихся по значению к формуле золотого сечения.
Золотое сечение проявляется и в некоторых неживых природных явлениях, например, вихревые потоки ураганов и совершенные формы снежинок. Во Вселенной все известные человечеству галактики и все тела в них существуют в форме спирали, соответствующей формуле золотого сечения.
Многие признанные шедевры живописи созданы по правилу золотого сечения, в том числе Рождение Венеры Сандро Боттичелли, Тайная вечеря
Любое произведение искусства, спроектированное в точном соответствии с золотыми пропорциями, являет собой совершенную эстетическую форму. Примерами памятников архитектуры, возведённых по правилам золотого сечения, являются: египетские пирамиды, Пантеон, Тадж Махал, Парфенон, Собор Нотр-Дам де Пари, храм Василия Блаженного и др.
Гармония золотого сечения играет заметную роль и в музыке и находит свое отражение, например, в определённых пропорциях при построении композиции, когда на точку золотого сечения обычно приходится наиболее яркое или неожиданное музыкальное решение.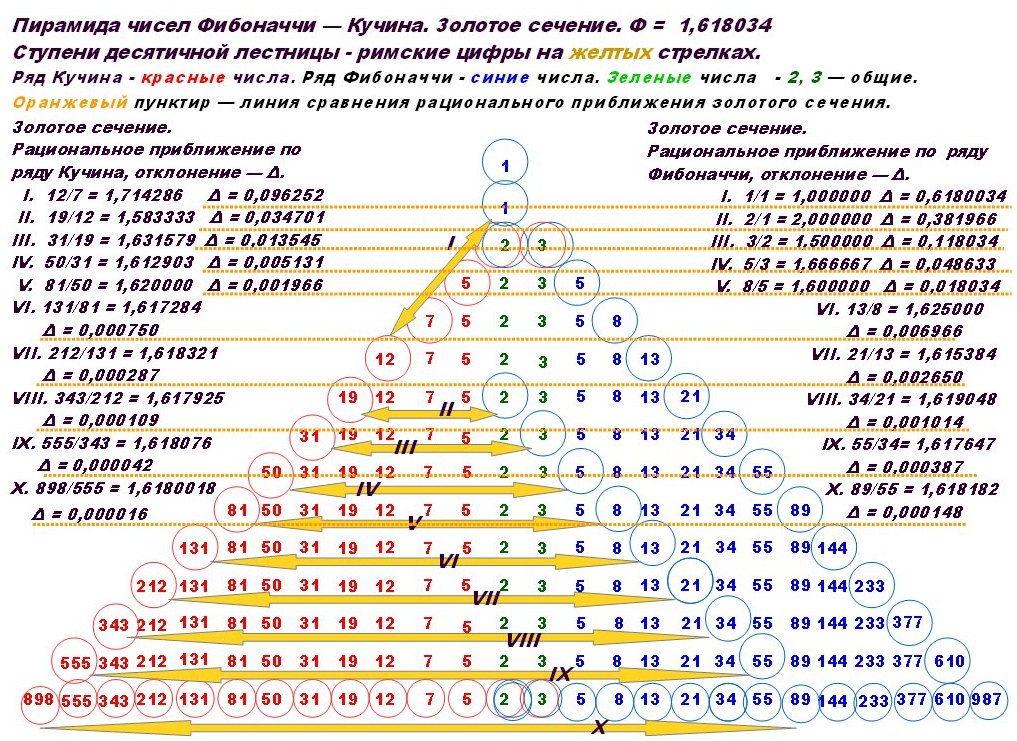
Примечательно, что еще одно творение человека — фондовый рынок — демонстрирует удивительные характеристики золотого сечения. Инвесторы используют такие инструмент технического анализа, как дуги Фибоначчи, коррекции Фибоначчи и веер Фибоначчи, для обоснования прогнозов движения цен в отношении отдельных акций или для всего фондового рынка.
Таким образом последовательность Фибоначчи проявляется в самых разнообразных формах, от молекул ДНК до галактик во Вселенной, и создается впечатление, что гармония золотого сечения повсюду вокруг нас.
Больше интересного из области математики про последовательность Фибоначчи и не только вы можете узнать из баз данных EBSCO Academic Search Ultimate и Applied Science & Technology Source Ultimate.
Числа Фибоначчи
Звезда. Орбиты планет. Сосновая шишка. Все эти природные формы не случайны. Они связаны с такими понятиями, как золотое сечение и числа Фибоначчи, за которыми стоит некое идеальное математическое соотношение. Когда мы видим что-то красивое, гармоничное, симметричное в природе или искусстве, то, скорее всего, оно имеет «золотое» соотношение частей и целого, близкое к 1,6 — его еще называют «числом бога».
Последовательность Фибоначчи выглядит так:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711…
Если вы заметили, каждое последующее число равно сумме двух предыдущих. Эту последовательность первым открыл европейцам математик и путешественник Леонардо Пизанский, Фибоначчи было его прозвищем (считается, что оно образовано от слов «сын Боначчи»). В 1202 году он опубликовал монументальный 460-страничный сборник по алгебре и арифметике под названием «Книга абака», основанный на математических знаниях индусов и арабов. Этот труд настолько опережал свое время, что просвещенному человечеству потребовалось еще несколько веков, чтобы осилить и осмыслить эти сведения. Числа Фибоначчи стали применяться в математике в эпоху Возрождения и в Новое время.
Этот труд настолько опережал свое время, что просвещенному человечеству потребовалось еще несколько веков, чтобы осилить и осмыслить эти сведения. Числа Фибоначчи стали применяться в математике в эпоху Возрождения и в Новое время.
Согласно легенде, на бесконечную последовательность чисел, каждое из которых является суммой двух предыдущих, Леонардо натолкнула нехитрая задачка о кроликах. Можете попробовать ее решить и проверить, получится ли у вас нужная последовательность.
Задача о кроликах1 января у вас в закрытом загоне скрестилась пара кроликов: самка и самец. 1 февраля они произвели на свет детей — самку и самца. Новорожденные кролики становятся зрелой парой через месяц и затем еще через месяц дают жизнь новой разнополой паре животных. Вопрос: сколько пар кроликов у вас будет через год? Учтите, что каждая половозрелая пара дает жизнь только одной паре и в ней всегда один самец и одна самка, все кролики из задачи бессмертны и точно доживут до 1 января следующего года. Посчитали?
Посчитали?
Теперь проверьте себя:
1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
13 + 8 = 21
21 + 13 = 34
34 + 21 = 55
55 + 34 = 89
89 + 55 = 144
144 + 89 = 233
233+ 144 = 377
Правильный ответ: через год будет 377 пар кроликов.
С точки зрения математики у последовательности Фибоначчи имеется много интересных свойств. Если взять пару соседних чисел из этого ряда и разделить большее число на меньшее, результат будет постепенно приближаться к числу золотого сечения (~1,6).
А что такое золотое сечение?И тут настало время поговорить о принципе золотого сечения. Так называют идеальное соотношение частей и целого, которое лежит в основе таких понятий, как гармония, красота, идеал. Этим принципом руководствовался Леонардо да Винчи, когда рисовал своего «Витрувианского человека», ему же пытаются соответствовать современные дизайнеры, архитекторы, ювелиры, художники. Золотое сечение встречается и в природе, и в науке, и в технике. И это тот редкий пример, когда математическая формула передает такое сложное понятие, как красота.
И это тот редкий пример, когда математическая формула передает такое сложное понятие, как красота.
Представьте отрезок. Разделите его на два меньших отрезка — a и b, при этом a должно быть равно отношению a:b. Это и будет «золотой» пропорцией. Иными словами, золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок относится к большей части так, как сама большая часть относится к меньшей. В виде формулы вышесказанное можно записать так: (a + b):a=a:b. Золотое сечение выражается числом Ф (фи), оно равно 1,6180339887, но обычно округляется до 1,618 или 1,62. Если выразить золотое сечение в процентном соотношении, то оно составит 62% к 38%.
Где искать золотое сечение?Математики утверждают, что правило золотого сечения действует и в природе, и в космосе. Наглядный пример красоты и совершенства в природе — это растения и цветы. Внимательные ботаники давно разглядели в многообразии форм растительной жизни четкие математические закономерности: многие природные узоры, орнаменты, формы подчиняются правилу золотого сечения, вернее, одному из его частных случаев — последовательности Фибоначчи.
Внимательные ботаники давно разглядели в многообразии форм растительной жизни четкие математические закономерности: многие природные узоры, орнаменты, формы подчиняются правилу золотого сечения, вернее, одному из его частных случаев — последовательности Фибоначчи.
Многолетние наблюдения ботаников показали, что растения, чья структура или плоды подчиняются правилам золотого сечения, гораздо более выносливы, а не просто красивы. В одном из исследований по шишкам сибирской сосны или кедра было установлено, что если шишки сильно уклоняются от правильного расположения чешуек, то их семена очень слабо жизнеспособны. Иными словами, только у гармоничной красивой шишки будут жизнеспособные семена.
Числа Фибоначчи можно найти даже у себя. Посмотрите на свои руки: на обеих по пять пальцев. Два из них (большие) состоят из двух фаланг, а у остальных восьми — по три фаланги. 2, 3, 5, 8 — это как раз одни из первых чисел последовательности Фибоначчи. Совпадение? Математики считают, что это закономерно — правило золотого сечения действует повсюду.
Даже в космосе можно найти число идеальной пропорции. Возьмем Солнечную систему. Планеты вращаются по траектории эллипса, а значит, у их траекторий есть минимальный и максимальный радиус. Удивительно, но соотношение этих радиусов у всех планет Солнечной системы совпадает с числом золотого сечения, погрешность составляет доли процента. В то же время соотношение орбит планет нашей Солнечной системы очень близко к коэффициенту золотого сечения. Этот факт был известен еще Кеплеру, и, опираясь на него, он пытался построить некую универсальную систему мироздания.
«Золотая пропорция — это не только критерий красоты, — говорит профессор физического факультета МГУ, доктор физико-математических наук Павел Короленко. — Не только явление, которое позволяет проникнуть в суть понятия красивого. Но это и явление, которое несет в себе некую эвристическую ценность. Задает некое направление в исследованиях, проводимых в математике, физике, биологии. Я считаю, что это очень важное достоинство этого феномена».
Подробнее о золотом сечении и числах Фибоначчи рассказывается в фильме канала «Наука» — «В поисках абсолютной гармонии».
Зачем нужна математика?Единственное существо, которое научилось жить вечноВ поисках эликсира молодостиЗолотое сечение в фотографии и правило третей.
Золотое сечение в фотографии одно из основных понятий и главных правил для построения правильной и гармоничной композиции. Создание фотографии бесспорно творческий процесс, но, как и в любой другой области искусства, здесь также присутствуют свои правила и принципы. И хотя в наши дни они очень часто нарушаются или игнорируются, в целях создания гипер авангардных фотоснимков, все-таки их нужно знать.
Правило золотого сечения или «божественная пропорция», было впервые открыто итальянским математиком Леонардо Фибоначчи (приблизительно в 1200 г.), который первый заметил, что в окружающей природе существует своего рода схема-дизайн, которая невероятным образом очень приятно воспринимается человеческим глазом. Со времен Ренессанса, художники уже активно использовали правило золотого сечения и создавали свои картины, применяя главную цифру правила в отношении соотношения сторон — 1:1,618. Использование данного правила помогает создавать сильную композицию органичным и естественным способом.
Со времен Ренессанса, художники уже активно использовали правило золотого сечения и создавали свои картины, применяя главную цифру правила в отношении соотношения сторон — 1:1,618. Использование данного правила помогает создавать сильную композицию органичным и естественным способом.
Принцип золотого сечения нашел свое выражение в двух схемах-фигурах, известных как Спираль Фибоначчи и Сетка Фибоначчи.
Использование спирали во время компоновки кадра, позволяет создать гармоничную композицию, и при ее просмотре взгляд зрителя будет естественным образом скользит вдоль фотографии.
В чем главное отличие этих двух понятий? Посмотрите на следующие фотографии.
Главное отличие в соотношение сторон. Параметры золотого сечения 1:0.618:1, а правило третей – 1:1:1. Вывод можно сделать такой: правило третей немного более упрощенная версия правила золотого сечения, в его классическом варианте. Оно было впервые озвучено в 1797 г. Согласно данному правилу, кадр делиться воображаемыми линиями по горизонтали и вертикали на трети, где главные композиционные детали располагаются на точках пересечения линий. Применение данного правила создает более динамичную композицию, тем самым открывая зрителю глубокий смысл фотографии, приглашая его к активному взаимодействию во время просмотра. Чтобы понять данное правило в действие рассмотрим следующие фотографии.
Согласно данному правилу, кадр делиться воображаемыми линиями по горизонтали и вертикали на трети, где главные композиционные детали располагаются на точках пересечения линий. Применение данного правила создает более динамичную композицию, тем самым открывая зрителю глубокий смысл фотографии, приглашая его к активному взаимодействию во время просмотра. Чтобы понять данное правило в действие рассмотрим следующие фотографии.
Многие исследования доказали, что во время просмотра фотографии, для человеческого взгляда более естественно концентрироваться на одной из точек пересечения, чем в центре кадра. Если на фотографии вы хотите сделать акцент, на определенном предмете, то его необходимо расположить на одной из четырех точек. Желаете сделать акцент на переднем плане фотографии? Тогда лучше, сформировать кадр так, чтобы линия горизонта проходила вдоль верхней линии сетки (соотношение 2:1) и наоборот. Хотите показать красивый узор на небе? Тогда линия горизонта, должна проходить вдоль нижней линии сетки.
В видоискателе большинства современных, профессиональных фотоаппаратов можно увидеть сетку, созданную по принципу правила третей, она значительно облегчает фокусирование и правильное распределение акцентов.
Есть такое популярное выражение «Правила создана для того, чтобы их нарушать». И в свадебной фотографии, правило третей очень часто нарушается, в целях создания интересных кадров. Чтобы расти в артистическом плане, я считаю, что правило иногда нужно нарушать, только в любом случае их надо знать и уметь хорошо применять их на практике.
Золотое сечение и числа Фибоначчи в фотографии
Эта статья посвящена основным правилам и понятиям, связанным как непосредственно с процессом съемки, так и с последующей обработкой получившегося снимка в графических редакторах. Речь пойдет о правилах «Золотого Сечения», геометрических пропорциях, которые при правильном и грамотном их использовании позволяют создавать удивительные и гармоничные работы.
Золотое сечение — воистину первое, о чем следует знать начинающему фотографу! Оно же иногда называется — правилом третей. О эстетической ценности этого правила — было известно еще в древнейшие времена. Сознательно использовать правило третей начал — великий да Винчи, за ним это правило начали использовать и другие художники, а вслед за ними и фотографы, и кинооператоры, и архитекторы, дизайнеры. Начнём с математики.
Математическая интерпретация
Математически «Золотое сечение» определяется следующим образом — отношение целого к большей части должно равняться отношению большей части к меньшей. Если разделить отрезок прямой на две неравные части, чтобы его длина (а+в) относилась к большей части (а) так, как эта большая часть к меньшей (в), получим результат, который и называют «Золотое Сечение». Это число равняется 1.618 или 0.618. Части же целого отрезка (а+в), взятого за 1, выражают в относительных величинах: а=0.62…, в=0.38 или в процентах 62% и 38%.![]()
Рис.1
Эти числа и получили название «золотых».
Принято считать, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные. Именно в такой пропорции выбирали размеры хостов известные художники.
Примером же использования правила «Золотого сечения» в фотографии может являться расположение основных компонентов кадра в особых точках — «зрительных центрах». Часто используются четыре точки, расположенные на расстоянии 3/8 и 5/8 от соответствующих краёв плоскости.
Рис.2
Практическое использование правила «Золотого сечения» при компоновке кадра.
Разумеется, в момент съемки мы не в состоянии просчитать и зрительно отложить в уме необходимые пропорции. Поэтому на момент съемки используется упрощенный вариант построения «Золотого сечения» или правило «Трети». Заключается оно в следующем: мы мысленно делим кадр на три части по горизонтали и вертикали и, в точках пересечения воображаемых линий, размещаем ключевые детали снимаемой сцены. Простейшая сетка «Третей» выглядит следующим образом: (рис 3).
Простейшая сетка «Третей» выглядит следующим образом: (рис 3).
Рис.3
Таким образом, кадр, сформированный по правилу золотого сечения, может выглядеть, к примеру, так: (рис 4,5)
Рис.4
Рис.5
Разумеется, мы можем комбинировать размещение объекта в зависимости от замысла фотографа и объекта съемки. На рис. 6 — 9 показаны различные варианты использования правила.
Рис.6
Рис.7
Рис.8
Рис.9
Далее небольшое отступление относительно ЗП (заднего плана).
При использовании правила «Золотого сечения» нельзя забывать про линию горизонта.
Правильная постановка горизонта должна соответствовать, в зависимости от композиции, одной из линий горизонтальных третей, верхней или нижней. На рис.10 показано позиционирование горизонта по нижней линии трети.
Рис.10
По поводу «золотого сечения» можно говорить бесконечно. Ниже я хочу привести различные варианты сеток, созданных по правилу «Золотого сечения», для различных композиционных вариантов. Для того, чтобы понять эти принципы, необходимо самостоятельно экспериментально попробовать совместить сетки с вашими фотографиями. Базовые сетки выглядят так (рис.11-17):
Для того, чтобы понять эти принципы, необходимо самостоятельно экспериментально попробовать совместить сетки с вашими фотографиями. Базовые сетки выглядят так (рис.11-17):
Рис.11
Рис.12
Рис.13
Рис.14
Рис.15
Рис.16
Рис.17
Правило «Равновесия».
Композиционно кадр необходимо строить так, чтобы объекты на нем были уравновешены. Что это значит? А значит это, что гармонично будут смотреться снимки, на которых либо соблюдена симметрия (рис.18 — в данном случае уравновешивающими элементами являются столбы справа и слева), либо основной объект экспозиции компенсирован дополнительным или второстепенным (рис.19 — журавль слева уравновешивает композицию справа).
Рис.18
Рис.19
Как пел В. Цой: «Нужно место для шага вперед»!
Любой снимок, даже построенный по правилу «Золотого сечения», может быть неправильно воспринят и не понят, только лишь потому, что не учтено направление движение (взгляда, действия) объекта съемки. На рис.20 у девушки совершенно не остается места для продолжения движения (она уходит из кадра), хотя кадр и построен в соотношениях «Золотого сечения». На рис.21 такое пространство у нее есть. Повторюсь, данное правило касается не только движения (людей, животных машин), но и взгляда (портрет), динамики поворота тела, лица, или сюжетного действия.
На рис.20 у девушки совершенно не остается места для продолжения движения (она уходит из кадра), хотя кадр и построен в соотношениях «Золотого сечения». На рис.21 такое пространство у нее есть. Повторюсь, данное правило касается не только движения (людей, животных машин), но и взгляда (портрет), динамики поворота тела, лица, или сюжетного действия.
Рис.20
Рис.21
Текст: Д.И. Жамков
Числа Фибоначчи — элементы числовой последовательности, в которой каждое последующее число равно сумме двух предыдущих чисел. Название по имени итальянского математика средневековой Европы Леонардо Пизанского по прозвищу Фибоначчи, что обозначает «хороший сын родился».
Числа Фибоначчи так же называют золотым сечением. Не вдаваясь в математику, можно сказать лишь одно — изображения, которые согласуются с золотым сечением и числами Фибоначчи особенно благоприятны для человеческого глаза.
Многие фотографы и дизайнеры придерживаются пропорций 1:1. 618 для построения более удачной композиции.
618 для построения более удачной композиции.
Эта последовательность была хорошо известна в Индии, где применялась в метрических науках. Позже многие исследователи начали замечать эту последовательность в природе и космосе.
Следующие два видео и последующие за ним изображения помогут вам лучше понять как это работает на практике.
Ниже представлены фотографии, которые сделаны с применением пропорций Фибоначчи.
Что такое числа Фибоначчи 🚩 Хобби и развлечения 🚩 Другое
Вам понадобится
- Числа Фибоначчи – это бесконечный ряд чисел, в котором каждое последующее число равно сумме двух предыдущих и в 1,618 раз больше предыдущего:
- 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610…
Инструкция
Ряд Фибоначчи начинается с единицы. К ней прибавляется предыдущее число (0):1 + 0 = 1
К полученной единице вновь прибавляется предыдущее число (1): 1 + 1 = 2
И так далее: 2 + 1 = 3; 3 + 2 = 5; 5 + 3 = 8; 8 + 5 = 13; 13 + 8 = 21 .
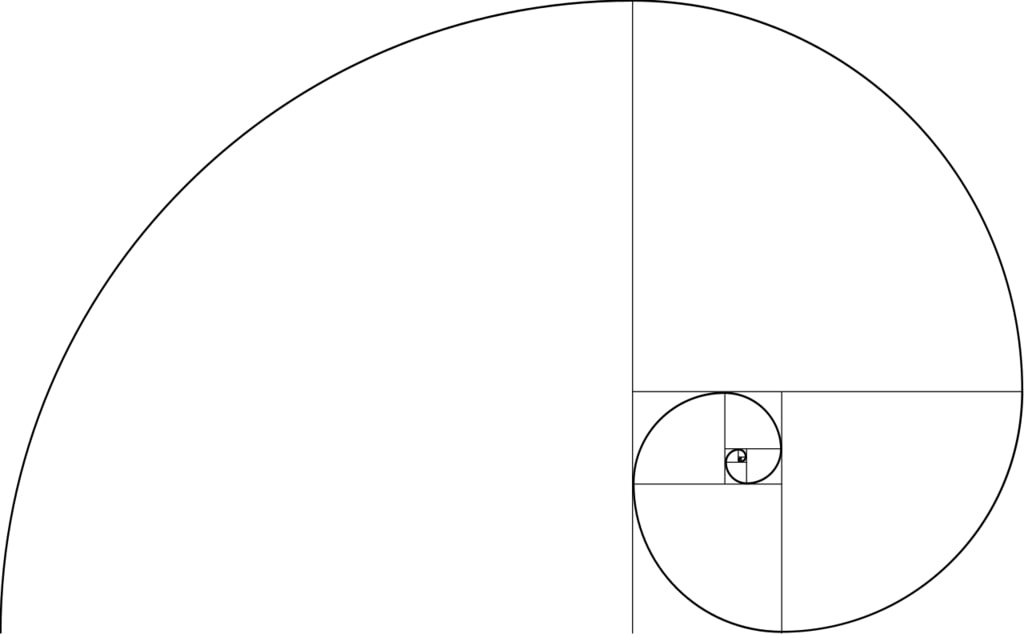 ..
.. Начиная с 3, каждое следующее число в ряду Фибоначчи будет в 1,6 раз больше предыдущего. Проверим:
5/3 = 1, 6
8/5 = 1,6
13/8 = 1,6
21/13 = 1,6 …….. 610 / 377 = 1,6
Если последовательность чисел Фибоначчи наглядно изобразить в виде прямоугольника и затем соединить плавными линиями, то получится спираль, подобная раковине наутилуса.
1.61803399 – это число Phi, отражающее правило золотого сечения при создании идеальных пропорций, которое нашло применение в изобразительном искусстве и архитектуре.
Точно неизвестно, способен ли человеческий глаз отличить гармонию от дисгармонии, но многие архитекторы, художники, дизайнеры и фотографы используют в своих творениях правило Золотого сечения. Оно проявлено во многих зданиях-шедеврах, от Парфенона до Сиднейского оперного театра и Национальной галереи в Лондоне.
Долгое время золотое сечение считалось божественной мерой, отражающей законы мироздания.
Совместные труды современных биологов, физиков и математиков пролили свет на тайну этого числового ряда. Числа Фибоначчи встречаются в природе повсеместно. Всё, что имеет форму, образуется, растёт, стремится занять место в пространстве, – имеет тенденцию к спиральности.
Числа Фибоначчи встречаются в природе повсеместно. Всё, что имеет форму, образуется, растёт, стремится занять место в пространстве, – имеет тенденцию к спиральности.
Последовательность чисел Фибоначчи есть в расположении листьев на стеблях, ветвей на стволах, которые растут в определённом количестве, под определённым углом. Это явление называется филлотаксис.
В качестве примеров филлотаксиса можно привести: упорядоченность соцветий, семян подсолнуха, строение сосновых шишек, ананаса и брокколи.
Правило Фибоначчи также есть в строении пчелиных сот. И, в так называемых, «родословных древах» пчёл.
Числа Фибоначчи скрыты в пропорциях человеческого тела, если бы они были идеальными. А также в отдельных частях тела, например, в строении кисти руки.
Генетические закономерности человека по числу возможных предков на линии наследования Х-хромосомы тоже соответствуют правилам чисел Фибоначчи.
Таким образом, прослеживается некий формообразующий принцип, алгоритм, которому подчиняется природа и различные её проявления.
Кто этот Архитектор Вселенной, попытавшийся сделать её идеальной? Осуществил ли он свои намерения или ему помешали мутации, ошибки и сбои в задуманной программе.
Использование золотого сечения в фотографии для лучшей композиции
Фотография начинается с композиции. То, как вы создаете сцену, является основным строительным блоком для получения хорошей картинки, и одной из композиционных техник, которая всегда была решающей, является Золотое сечение.
Вот что это значит и как вы можете использовать его для немедленного улучшения ваших фотографий.
Что такое золотое сечение?
Допустим, у вас есть линия. Существует математическое правило, которое гласит, что любая линия может быть разделена таким образом, что более длинный сегмент делится на более короткий
чтобы добиться подобного эффекта, но знайте, что хорошая оригинальная композиция всегда будет превосходить кадрирование, не говоря уже о том, что она лучше научит кадрировать фотографии.
Что такое Фи Грид?
Многие фотографы предпочитают использовать сетку на основе Фи при составлении своих снимков. Естественно, эта техника называется Фи Грид. Это вариация «Правила третей», одного из базовых принципов фотографии
,
Правило третей делит фрейм на три строки и три столбца одинакового размера, в результате чего получается 1: 1: 1 по вертикали и 1: 1: 1 по горизонтали. Phi Grid разделяет рамку аналогичным образом, но уменьшает средний ряд и средний столбец в соответствии с золотым соотношением, в результате чего получается 1: 1,618: 1 по вертикали и 1: 1,618: 1 по горизонтали.
Вот быстрое сравнение:
Пересечение линий сетки — это то место, к которому естественным образом обращается глаз, поэтому используйте их для выравнивания изображения. Школа цифровой фотографии предлагает пример использования Phi Grid в подробной статье, которую стоит прочитать полностью:
Я выровнял горизонт с верхней линией сетки Фи. На мой взгляд, когда вы выравниваете горизонт с сеткой с правилом третей, разделение слишком… очевидно.
Я думаю, что это оставило бы слишком много того, что не является предметом на изображении. На этой фотографии небо и облака — прекрасное дополнение к тому, что я пытаюсь передать на фотографии: церковь внизу справа и знаменитая улица Дюваль слева. Но если небо больше, чем на фотографии, зритель может подумать, что небо на самом деле является объектом.
Спираль Фибоначчи
В геометрии золотое сечение также может быть выражено как особый тип прямоугольника. Предположим, вы берете линию x + y выше и поворачиваете ее прямоугольником, где ширина равна x, а длина равна x + y.
Если вы разделите площадь этого прямоугольника на ряд квадратов, он образует спираль последовательности Фибоначчи, как демонстрирует LiveScience:
Если вы читали «Код да Винчи», вы знаете последовательность Фибоначчи: вы начинаете с цифры 1, добавляете предыдущее целое число и составляете бесконечный ряд чисел с этим шаблоном. Так что сериал выглядит так:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…
Фибоначчи обнаружил, что эта «золотая спираль» появляется в нескольких местах по всей природе, от молекул ДНК до цветочных лепестков, от ураганов до Млечного пути. Что еще более важно, спираль Фибоначчи приятна человеческому глазу.
Что еще более важно, спираль Фибоначчи приятна человеческому глазу.
Адриан Беджан, профессор машиностроения в Школе инженерии имени Пратта при Герцоге, говорит, что золотое сечение эстетически приятно из-за эволюции человеческого зрения.
Короче говоря, наш мозг должен обрабатывать все, что видят наши глаза. Чем быстрее он сможет что-то обработать, тем приятнее это будет. Любое изображение с золотым сечением обрабатывается мозгом быстрее, поэтому оно посылает сигнал, что такое изображение эстетично.
Как использовать спираль Фибоначчи
Что касается реальной фотографии, вам не нужно беспокоиться о технических объяснениях. Спирали Фибоначчи полезны почти для всех видов фотографии, но особенно хороши для пейзажей и широких снимков
,
У Apogee Photo есть отличный пример того, как его использовать:
Осенью был туманный вечер, и я хотел запечатлеть цвета заката, которые проникали сквозь туман, а также красивый малиновый цвет осенней листвы. Я стремился включить одного человека, который выделялся, идя по тропинке, листву падения на переднем плане и линии дерева как центральную точку фокуса в моем кадре.
Чтобы сделать это, я поместил эти аспекты в центр моего воображаемого прямоугольника, зная, что он содержит несколько ключевых точек фокусировки, связанных с отношением, и включил туман в сцену вдоль широкой дуги спирали.
Как вы можете видеть, спираль в основном имеет способ естественного движения вашего глаза от фокуса наружу. Вы можете увидеть еще несколько примеров спирали Фибоначчи, следуя этим удивительным фотографам природы в Instagram
,
Лучшие приложения для золотого сечения
Правильное приложение камеры может сделать вас лучшим фотографом
, но не каждое приложение камеры поддерживает Phi Grid или спираль Фибоначчи.
Если вы пользуетесь телефоном Android, то получите Camera Zoom FX ($ 3). Это одно из 10 приложений, которые каждый должен установить первым на Android
и не зря. Он поддерживает как сетку Фи, так и спираль Фибоначчи в качестве оверлеев. Просто выберите нужную сетку, составьте изображение и снимайте.
Если у вас iPhone, то Camera Awesome [больше не доступен] имеет спираль Фибоначчи, чтобы делать больше потрясающих фотографий
, Чтобы использовать Phi Grid, вам понадобится платное приложение, такое как Phi Camera [Больше не доступно].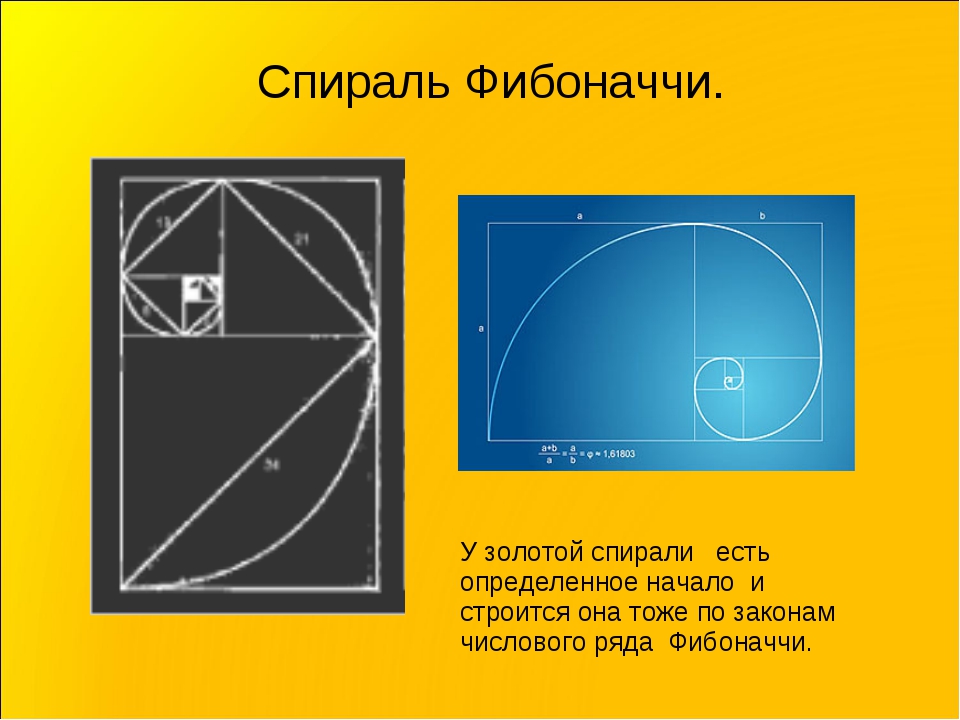
Золотое сечение против правила третей
В Интернете много споров о том, что лучше: золотое сечение или правило третей. Видео выше дает некоторое представление о двух стилях, но мы хотим услышать от вас: какая техника композиции лучше и почему?
Изображение предоставлено: LiveScience, Школа цифровой фотографии, Apogee Photo
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — одна из самых известных формул в математике.
Каждое число в последовательности представляет собой сумму двух предшествующих ему чисел. Итак, последовательность такова: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 и так далее. Математическое уравнение, описывающее его: Xn + 2 = Xn + 1 + Xn
Оплот средней школы и студентов, его называют «секретным кодом природы» и «универсальным правилом природы». Говорят, что он определяет размеры всего, от Великой пирамиды в Гизе до культовой морской ракушки, которая, вероятно, украшала обложку вашего школьного учебника математики.
Говорят, что он определяет размеры всего, от Великой пирамиды в Гизе до культовой морской ракушки, которая, вероятно, украшала обложку вашего школьного учебника математики.
И, скорее всего, почти все, что вы знаете об этом, неверно.
Разрозненная история
Итак, что же на самом деле стоит за этой знаменитой сценой?
Многие источники утверждают, что он был впервые обнаружен или «изобретен» Леонардо Фибоначчи. Итальянский математик, родившийся около 1170 года нашей эры, первоначально был известен как Леонардо Пизанский, сказал Кейт Девлин, математик из Стэнфордского университета. По словам Девлина, только в 19 веке историки придумали прозвище Фибоначчи (что примерно означает «сын клана Боначчи»), чтобы отличить математика от другого известного Леонардо Пизанского.[Большие числа, определяющие Вселенную]
Но Леонардо из Пизы на самом деле не обнаружил последовательность, — сказал Девлин, который также является автором книги «В поисках Фибоначчи: поиски заново забытого математического гения, изменившего мир» (Принстон University Press, 2017). Древние санскритские тексты, в которых использовалась индуистско-арабская система счисления, впервые упоминают об этом, и те, что предшествуют Леонардо Пизанскому на столетия.
Древние санскритские тексты, в которых использовалась индуистско-арабская система счисления, впервые упоминают об этом, и те, что предшествуют Леонардо Пизанскому на столетия.
«Это было всегда», — сказал Девлин Live Science.
Однако в 1202 году Леонардо Пизанский опубликовал огромный фолиант «Liber Abaci», математическую «поваренную книгу» о том, как проводить вычисления », — сказал Девлин.«Liber Abaci», написанная для торговцев, излагает индуистско-арабскую арифметику, полезную для отслеживания прибылей, убытков, остатков ссуд и т. Д., Сказал Девлин.
В одном месте книги Леонардо Пизанский вводит последовательность с задачей с участием кроликов. Задача состоит в следующем: начните с кролика-самца и кролика-самки. Через месяц они созревают и производят помет с еще одним кроликом и самкой. Через месяц эти кролики размножаются и выходят, как вы уже догадались, еще один самец и самка, которые также могут спариваться через месяц.(Игнорируйте здесь невероятно невероятную биологию.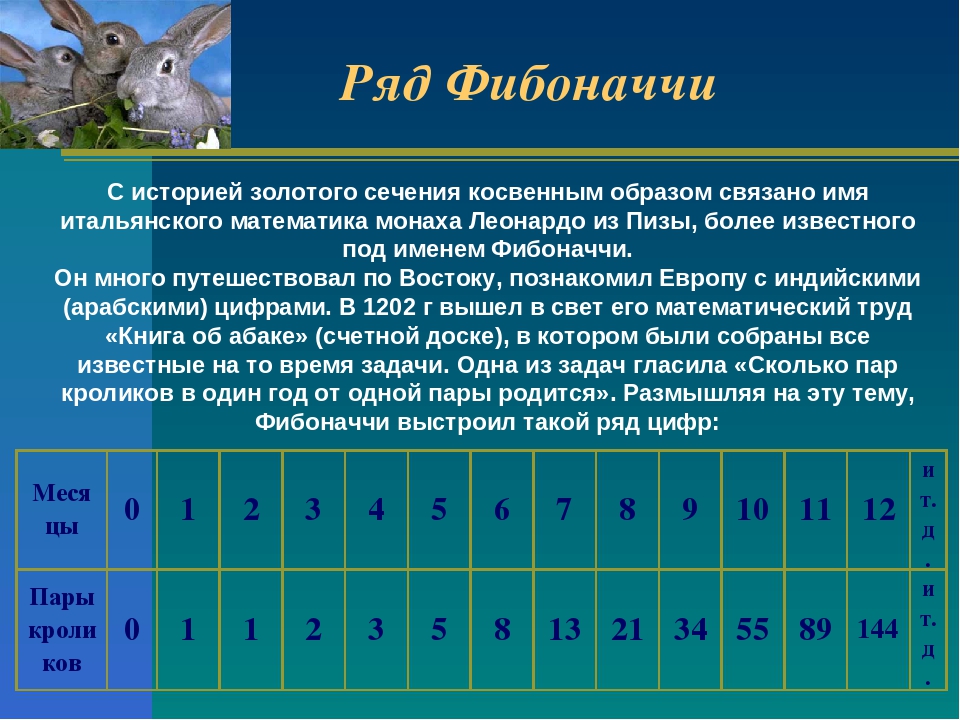 ) Сколько кроликов у вас будет через год? Оказывается, ответ — 144, и формула, использованная для получения этого ответа, теперь известна как последовательность Фибоначчи. [11 самых красивых математических уравнений]
) Сколько кроликов у вас будет через год? Оказывается, ответ — 144, и формула, использованная для получения этого ответа, теперь известна как последовательность Фибоначчи. [11 самых красивых математических уравнений]
«Liber Abaci» впервые представила последовательность в западном мире. Но после нескольких скудных абзацев о разведении кроликов Леонардо Пизанский никогда больше не упоминал последовательность. Фактически, об этом почти забыли до 19 века, когда математики больше работали над математическими свойствами последовательности.В 1877 году французский математик Эдуард Лукас официально назвал задачу о кролике «последовательностью Фибоначчи», — сказал Девлин.
Последовательность Фибоначчи и золотое сечение — красноречивые уравнения, но не такие волшебные, как могут показаться. (Изображение предоставлено Shutterstock)
Воображаемое значение
Но каково именно значение последовательности Фибоначчи? Помимо того, что это изящный инструмент обучения, он обнаруживается в нескольких местах на природе. Однако, по словам Девлина, архитектурой вселенной управляет не какой-то секретный код.
Однако, по словам Девлина, архитектурой вселенной управляет не какой-то секретный код.
Это правда, что последовательность Фибоначчи тесно связана с тем, что сейчас известно как золотое сечение (которое даже не является истинным соотношением, потому что это иррациональное число). Проще говоря, соотношение чисел в последовательности, когда последовательность стремится к бесконечности, приближается к золотому сечению, которое составляет 1,6180339887498948482 … Отсюда математики могут вычислить так называемую золотую спираль или логарифмическую спираль, коэффициент роста которой равен золотое сечение. [9 самых значительных чисел в мире]
«Золотое сечение», кажется, действительно отражает некоторые типы роста растений, — сказал Девлин.Например, спиральное расположение листьев или лепестков на некоторых растениях соответствует золотому сечению. Сосновые шишки имеют золотую спираль, как и семена подсолнечника, согласно «Филлотаксису: системное исследование морфогенеза растений» (Cambridge University Press, 1994). Но столько же растений не соблюдают это правило.
Но столько же растений не соблюдают это правило.
«Это не« единственное Божье правило »для выращивания растений, скажем так, — сказал Девлин.
И, возможно, самый известный пример из всех, морская раковина, известная как наутилус, на самом деле не выращивает новые клетки в соответствии с последовательностью Фибоначчи, сказал он.
Когда люди начинают рисовать связи с человеческим телом, искусством и архитектурой, связи с последовательностью Фибоначчи переходят от призрачных к совершенно вымышленным.
«Требуется большая книга, чтобы задокументировать всю дезинформацию о золотом сечении, большая часть которой является просто повторением одних и тех же ошибок разными авторами», — писал Джордж Марковски, математик, работавший в то время в Университете штата Мэн. в статье 1992 года в College Mathematics Journal.
Большая часть этой дезинформации может быть отнесена к книге 1855 года немецкого психолога Адольфа Цайзинга.Цейзинг утверждал, что пропорции человеческого тела основаны на золотом сечении. Золотое сечение породило «золотые прямоугольники», «золотые треугольники» и всевозможные теории о том, где возникают эти знаковые измерения. С тех пор люди говорят, что золотое сечение можно найти в размерах пирамиды в Гизе, Парфенона, «Витрувианского человека» Леонардо да Винчи и ряда зданий эпохи Возрождения. По словам Девлина, общие утверждения о том, что это соотношение «исключительно приятно» для человеческого глаза, были сформулированы некритически.
Золотое сечение породило «золотые прямоугольники», «золотые треугольники» и всевозможные теории о том, где возникают эти знаковые измерения. С тех пор люди говорят, что золотое сечение можно найти в размерах пирамиды в Гизе, Парфенона, «Витрувианского человека» Леонардо да Винчи и ряда зданий эпохи Возрождения. По словам Девлина, общие утверждения о том, что это соотношение «исключительно приятно» для человеческого глаза, были сформулированы некритически.
Все эти утверждения, когда они проверяются, оказываются в значительной степени ложными, сказал Девлин.
«Мы хорошие распознаватели образов. Мы можем видеть закономерности независимо от того, есть они или нет», — сказал Девлин. «Это все просто принятие желаемого за действительное».
Что такое последовательность Фибоначчи? И как это применимо к гибкой разработке
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — это последовательность чисел, в которой число представляет собой сложение двух последних чисел, начиная с 0 и 1.
Последовательность Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55…
Как правило, пишется выражение:
X n = X n-1 + X n-2
Руководство по гибкой разработке
Это руководство представляет собой основу для перехода вашей команды к гибкой разработке.
Спираль Фибоначчи и золотое сечение
Последовательность Фибоначчи часто визуализируется в виде графика, такого как тот, что в заголовке этой статьи.Каждый квадратик показывает площадь следующего числа в последовательности. Затем спираль Фибоначчи рисуется внутри квадратов, соединяя углы прямоугольников.
Квадраты идеально подходят друг к другу, потому что соотношение между числами в последовательности Фибоначчи очень близко к золотому сечению [1], которое составляет приблизительно 1,618034. Чем больше числа в последовательности Фибоначчи, тем ближе отношение к золотому сечению.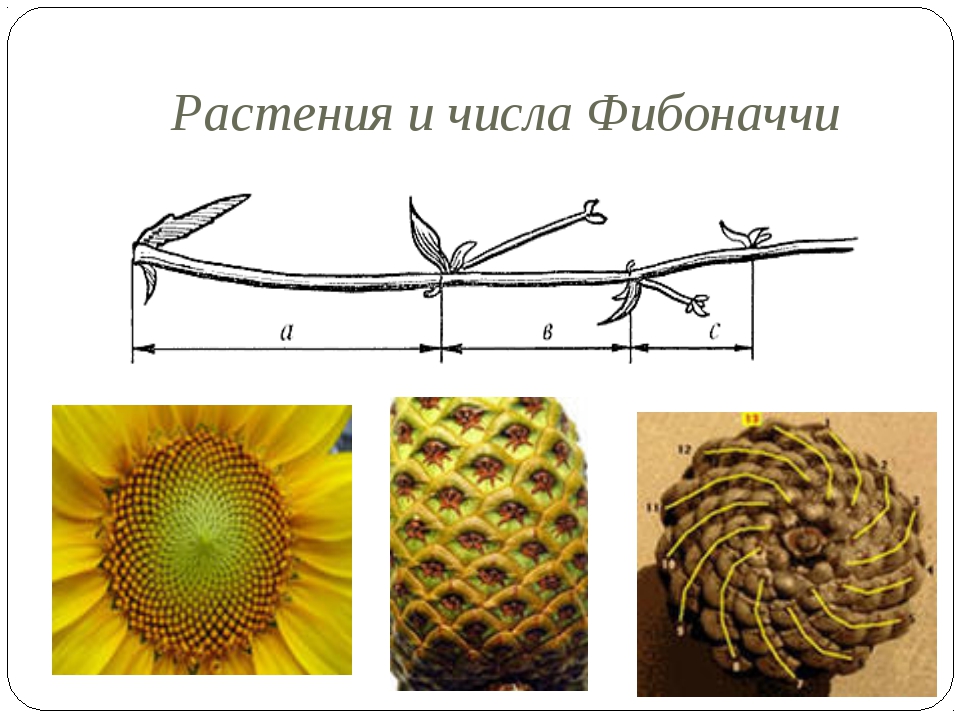
Спираль и результирующий прямоугольник также известны как золотой прямоугольник [2].
Истоки последовательности Фибоначчи
Фиббоначи (Леанардо Пизано Боголло [3], его прозвище Фибоначчи) впервые представил серию чисел, известную как последовательность Фибоначчи, в своей книге Liver Abaci [4] в 1202 году. Фибоначчи был членом влиятельной итальянской торговой семьи. 12 и 13 века. Будучи частью торговой семьи, математика была неотъемлемой частью бизнеса. Фибоначчи путешествовал по Ближнему Востоку и Индии и был очарован математическими идеями из своих путешествий.Его книга, Liver Abaci , была беседой о математических методах в торговле, которые Фибоначчи наблюдал во время своих путешествий.
Фибоначчи известен двумя важными вкладами в западную математику:
- Он помог распространить использование индуистских систем записи чисел в Европе (0,1,2,3,4,5 вместо римских цифр).
- На первый взгляд незначительный ряд чисел позже назвал в его честь Последовательность Фибоначчи.

Фибоначчи открыл последовательность, задав следующий вопрос:
Если пару кроликов поместить в закрытое пространство, сколько кроликов родится там, если мы предположим, что каждый месяц пара кроликов производит еще пар и что кролики начинают рожать детенышей через два месяца после их рождения?
- Начало: Вначале кролики не рождаются, так как исходная пара еще не успела забеременеть и родилась (0) .
- Первый месяц: рождается одна пара кроликов (1) .
- Второй месяц: снова рождается одна пара кроликов, так как новые кролики еще не созрели для рождения детенышей (1) .
- Третий месяц: две пары кроликов размножаются, а одна пара не готова, поэтому рождаются две пары кроликов (2) .
- Четвертый месяц: три пары кроликов размножаются, а две пары кроликов не готовы, поэтому рождаются три пары кроликов.
 (3) .
(3) . - Пятый месяц: пять пар кроликов производят, а три еще не готовы, поэтому рождается пять пар кроликов. (5) .
- И так далее.
Хотя вопрос Фибоначчи о кроликах — нереальный сценарий, последовательность можно наблюдать в природе, например, в массиве семян подсолнечника и других растений, а также в форме галактик и ураганов.
Семена подсолнечника — это яркая демонстрация последовательности Фибоначчи в природе.
Важность последовательности Фибоначчи
Хотя эта серия чисел из этой простой головоломки может показаться несущественной, она была заново открыта в удивительно разнообразных формах, от разделов продвинутой математики [5] до приложений в информатике [6], статистике [7], природе [ 8] и гибкой разработки.
Как последовательность Фибоначчи используется в гибкой разработке
Теперь вы можете сказать себе: « Это хорошо, но какое отношение это имеет к гибкой разработке? », и это отличный вопрос. Какое отношение имеет последовательность Фибоначчи к гибкой разработке? Интересно, что последовательность Фибоначчи — полезный инструмент для оценки времени выполнения задач.
Какое отношение имеет последовательность Фибоначчи к гибкой разработке? Интересно, что последовательность Фибоначчи — полезный инструмент для оценки времени выполнения задач.
Оценка задач в Agile
Большая часть управления Agile-командой — это оценка времени, которое потребуется для выполнения задач.Система баллов часто используется, чтобы дать общую оценку масштаба или размера конкретной задачи. Чем больше и сложнее, тем больше очков, а меньше — меньше. Затем менеджеры могут просматривать и расставлять приоритеты задач в соответствии с назначенной шкалой.
Использование последовательности Фибоначчи с вашей командой
Чтобы использовать последовательность Фибоначчи, проинструктируйте свою команду оценивать задачи из последовательности Фибоначчи до 21.
1, 2, 3, 5, 8, 13, 21
Одна из самых маленьких простых задач и двадцать один из больших проектов.Что касается того, почему вы должны использовать последовательность Фибоначчи вместо, скажем, размеров футболки, проверьте мою следующую статью о . 5 причин, по которым использование последовательности Фибоначчи сделает вас лучше при оценке задач в Agile Development .
5 причин, по которым использование последовательности Фибоначчи сделает вас лучше при оценке задач в Agile Development .
А чтобы узнать больше о руководстве командой Agile eLearning Development, ознакомьтесь с нашим приятным электронным руководством The Agile Guide to Agile Development.
Статьи по теме:
1. 5 причин, по которым использование последовательности Фибоначчи делает вас лучше в гибкой разработке
2.8 компонентов и использование диаграмм Burndown в гибкой разработке
3. Электронная книга: Agile Guide to Agile Development
Список литературы
- Золотое сечение
- Золотой прямоугольник
- Леонардо Пизано Фибоначчи
- Liber Abaci Фибоначчи: перевод на современный английский книги расчетов Леонардо Пизано (Источники и исследования по истории математики и физических наук)
- Последовательность Фибоначчи
- Почему числа Фибоначчи важны в информатике?
- Числа Фибоначчи, статистическая сходимость и приложения
- Фибоначчи в природе
Что такое ретрейсменты Фибоначчи и соотношения Фибоначчи?
Уровни коррекции Фибоначчи популярны среди технических трейдеров. Они основаны на ключевых числах, определенных математиком Леонардо Фибоначчи в 13 веке. Последовательность чисел Фибоначчи не так важна, как математические отношения, выраженные в виде отношений, между числами в ряду.
Они основаны на ключевых числах, определенных математиком Леонардо Фибоначчи в 13 веке. Последовательность чисел Фибоначчи не так важна, как математические отношения, выраженные в виде отношений, между числами в ряду.
В техническом анализе коррекция Фибоначчи создается путем взятия двух крайних точек (обычно пика и впадины) на графике акций и деления вертикального расстояния на ключевые соотношения Фибоначчи 23,6%, 38,2%, 50%, 61,8% и 100%.
После определения этих уровней рисуются горизонтальные линии, которые используются для определения возможных уровней поддержки и сопротивления.
Ключевые выводы
- Уровни коррекции Фибоначчи — популярные инструменты, которые трейдеры могут использовать для построения линий поддержки, определения уровней сопротивления, размещения стоп-лоссов и установки целевых цен.
- Восстановление Фибоначчи создается путем взятия двух крайних точек на графике акций и деления вертикального расстояния на ключевые соотношения Фибоначчи: 23,6%, 38,2%, 50%, 61,8% и 100%.
 Уровни коррекции Фибоначчи
Уровни коррекции Фибоначчи - страдают теми же недостатками, что и другие универсальные торговые инструменты, поэтому их лучше всего использовать вместе с другими индикаторами.
Как работают соотношения Фибоначчи
Прежде чем мы сможем понять, почему были выбраны эти соотношения, давайте рассмотрим числовой ряд Фибоначчи.
Последовательность чисел Фибоначчи выглядит следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. Д. Каждый член в этой последовательности представляет собой просто сумму двух предыдущих условия, и последовательность продолжается бесконечно. Одной из замечательных характеристик этой числовой последовательности является то, что каждое число приблизительно равно 1.618 раз больше предыдущего числа. Эта общая взаимосвязь между каждым числом в серии является основой соотношений, используемых техническими трейдерами для определения уровней восстановления.
Ключевое соотношение Фибоначчи 61,8% находится путем деления одного числа в ряду на число, которое следует за ним. Например, 21, разделенное на 34, равно 0,6176, а 55, разделенное на 89, равняется примерно 0,61798.
Например, 21, разделенное на 34, равно 0,6176, а 55, разделенное на 89, равняется примерно 0,61798.
Соотношение 38,2% определяется путем деления числа в ряду на число, расположенное в двух точках справа.Например, 55, разделенное на 144, примерно равно 0,38194.
Соотношение 23,6% находится путем деления одного числа в ряду на число, которое находится на три знака вправо. Например, деление 8 на 34 дает примерно 0,23529.
Восстановление Фибоначчи и прогнозирование цен на акции
По неизвестным причинам эти отношения Фибоначчи, кажется, играют роль на фондовом рынке, как и в природе. Технические трейдеры пытаются использовать их для определения критических точек, в которых динамика цены актива может развернуться.
Уровни коррекции Фибоначчи — наиболее широко используемый из всех торговых инструментов Фибоначчи. Отчасти это связано с их относительной простотой, а отчасти с их применимостью практически к любому торговому инструменту. Их можно использовать для построения линий поддержки, определения уровней сопротивления, размещения стоп-лоссов и установки целевых цен. Коэффициенты Фибоначчи могут даже выступать в качестве основного механизма в стратегии торговли против тренда.
Коэффициенты Фибоначчи могут даже выступать в качестве основного механизма в стратегии торговли против тренда.
Уровни коррекции Фибоначчи — это горизонтальные линии, которые указывают возможные местоположения уровней поддержки и сопротивления.Каждый уровень связан с одним из вышеуказанных соотношений или процентов. Он показывает, насколько цена откатилась от предыдущего движения. Направление предыдущего тренда, вероятно, сохранится. Однако цена актива обычно восстанавливается до одного из указанных выше соотношений до того, как это произойдет.
На следующем графике показано, как появляется коррекция Фибоначчи. Большинство современных торговых платформ содержат инструмент, который автоматически рисует горизонтальные линии. Обратите внимание, как цена меняет направление по мере приближения к уровням поддержки и сопротивления.
Изображение Сабрины Цзян © Investopedia 2020
В дополнение к коэффициентам, описанным выше, многим трейдерам также нравится использовать уровень 50%.
Уровень коррекции 50% на самом деле не является соотношением Фибоначчи. Однако трейдеры часто используют его из-за тенденции цен на активы продолжать движение в определенном направлении после 50% -ного восстановления.
Плюсы и минусы коррекции Фибоначчи
Несмотря на популярность ретрейсментов Фибоначчи, у этих инструментов есть некоторые концептуальные и технические недостатки, о которых трейдерам следует помнить при их использовании.
Использование ретрейсмента Фибоначчи субъективно. Трейдеры могут использовать этот технический индикатор по-разному. Те трейдеры, которые получают прибыль с помощью коррекции Фибоначчи, проверяют ее эффективность. В то же время те, кто теряет деньги, говорят, что это ненадежно. Другие утверждают, что технический анализ — это случай сбывающегося пророчества. Если все трейдеры наблюдают и используют одни и те же соотношения Фибоначчи или другие технические индикаторы, ценовое действие может отражать этот факт.
Основополагающий принцип любого инструмента Фибоначчи — это числовая аномалия, не имеющая никакого логического доказательства.Соотношения, целые числа, последовательности и формулы, полученные из последовательности Фибоначчи, являются только продуктом математического процесса. Это не делает торговлю по Фибоначчи ненадежной по своей природе. Однако это может быть неудобно для трейдеров, которые хотят понять логику стратегии.
Кроме того, стратегия восстановления Фибоначчи может указывать только на возможные коррекции, развороты и отскоки против тренда. Эта система изо всех сил пытается подтвердить любые другие индикаторы и не дает легко идентифицируемых сильных или слабых сигналов.
Итог
Торговые инструменты Фибоначчи страдают от тех же проблем, что и другие универсальные торговые стратегии, такие как теория волн Эллиотта. Тем не менее, многие трейдеры добиваются успеха, используя коэффициенты Фибоначчи и коррекции для размещения сделок в рамках долгосрочных ценовых трендов.
Восстановление Фибоначчи может стать еще более мощным при использовании в сочетании с другими индикаторами или техническими сигналами. Курс технического анализа Investopedia Academy охватывает эти индикаторы, а также то, как преобразовать модели в действенные торговые планы.
Определение линий чисел Фибоначчии их использование
Что такое числа и линии Фибоначчи?
Числа Фибоначчи используются для создания технических индикаторов с использованием математической последовательности, разработанной итальянским математиком, обычно называемым «Фибоначчи», в 13 веке. Последовательность чисел, начинающаяся с нуля и единицы, создается путем сложения двух предыдущих чисел. Например, ранняя часть последовательности — 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т. Д.
Затем эту последовательность можно разбить на коэффициенты, которые, по мнению некоторых, позволяют понять, куда будет двигаться данный финансовый рынок.
Последовательность Фибоначчи важна из-за так называемого золотого сечения 1,618 или его обратной величины 0,618. В последовательности Фибоначчи любое данное число примерно в 1,618 раз больше предыдущего, без учета первых нескольких чисел. Каждое число также составляет 0,618 числа справа от него, опять же без учета первых нескольких чисел в последовательности.Золотое сечение широко распространено в природе, где оно описывает все, от количества жилок на листе до магнитного резонанса спинов в кристаллах ниобата кобальта.
В последовательности Фибоначчи любое данное число примерно в 1,618 раз больше предыдущего, без учета первых нескольких чисел. Каждое число также составляет 0,618 числа справа от него, опять же без учета первых нескольких чисел в последовательности.Золотое сечение широко распространено в природе, где оно описывает все, от количества жилок на листе до магнитного резонанса спинов в кристаллах ниобата кобальта.
Изображение Сабрины Цзян © Investopedia 2021
Ключевые выводы
- Числа и линии Фибоначчи созданы с помощью соотношений, найденных в последовательности Фибоначчи.
- Общие числа Фибоначчи на финансовых рынках: 0,236, 0,382, 0,618, 1,618, 2,618, 4,236. Эти соотношения или проценты можно найти, разделив определенные числа в последовательности на другие числа.
- Хотя официально это не числа Фибоначчи, многие трейдеры также используют 0,5, 1,0 и 2,0.
- Цифры отражают, как далеко цена может зайти после очередного ценового движения.
 Например, если акция движется с 1 до 2 долларов, к этому могут быть применены числа Фибоначчи. Падение до 1,76 доллара — это откат на 23,6% от движения цены в 1 доллар (округлено).
Например, если акция движется с 1 до 2 долларов, к этому могут быть применены числа Фибоначчи. Падение до 1,76 доллара — это откат на 23,6% от движения цены в 1 доллар (округлено). - Два общих инструмента Фибоначчи — это коррекция и расширение. Уровни коррекции Фибоначчи измеряют, насколько далеко может зайти откат. Расширения Фибоначчи измеряют, насколько далеко может зайти импульсная волна.
Формулы для чисел и уровней Фибоначчи
У чисел Фибоначчи нет определенной формулы, это скорее числовая последовательность, в которой числа имеют определенные отношения друг с другом.
Как рассчитать уровни коррекции Фибоначчи
Числовую последовательность Фибоначчи можно использовать по-разному для получения уровней восстановления Фибоначчи или уровней расширения Фибоначчи. Вот как их найти. Как их использовать, обсуждается в следующем разделе.
Для коррекции Фибоначчи на графике необходимо выбрать две ценовые точки, обычно максимум и минимум колебания. Как только эти две точки выбраны, числа / линии Фибоначчи рисуются в процентах от этого движения.
Как только эти две точки выбраны, числа / линии Фибоначчи рисуются в процентах от этого движения.
Если акция вырастет с 15 до 20 долларов, то уровень 23,6% составит 18,82 доллара, или 20 долларов — (5 долларов x 0,236) = 18,82 доллара. Уровень 50% составляет 17,50 долларов, или 15 долларов — (5 долларов x 0,5) = 17,50 долларов.
Уровни расширения Фибоначчи также выводятся из числовой последовательности. По мере продвижения последовательности разделите одно число на предыдущее, чтобы получить коэффициент 1.618. Разделите число на два разряда слева, и получится 2,618. Разделите число на три слева, и получится 4,236.
Расширение Фибоначчи требует трех ценовых точек. Начало движения, конец движения, а затем точка где-то посередине (откат).
Если цена вырастет с 30 до 40 долларов, и эти два ценовых уровня являются точками один и два, то уровень 161,8% будет на 16,18 долларов (1,618 x 10 долларов) выше цены, выбранной для точки три. Если третий пункт равен 35 долларам, то 161. Уровень расширения 8% составляет 51,18 доллара (35 + 16,18 доллара).
Уровень расширения 8% составляет 51,18 доллара (35 + 16,18 доллара).
Уровни 100% и 200% не являются официальными числами Фибоначчи, но они полезны, поскольку проецируют движение, аналогичное (или кратному) тому, что только что произошло на ценовом графике.
Что вам говорят числа и линии Фибоначчи?
Некоторые трейдеры считают, что числа Фибоначчи играют важную роль в финансах. Как обсуждалось выше, последовательность чисел Фибоначчи может использоваться для создания соотношений или процентов, которые используют трейдеры.
К ним относятся: 23,6%, 38,2%, 50%, 61,8%, 78,6%, 100%, 161,8%, 261,8%, 423,6%.
Эти проценты применяются с использованием множества различных методов:
- Коррекции Фибоначчи. Это горизонтальные линии на графике, обозначающие области поддержки и сопротивления.
- Расширения Фибоначчи. Это горизонтальные линии на графике, указывающие, где может достигнуть сильная ценовая волна.

- Дуги Фибоначчи. Это похожие на компас движения, исходящие от максимума или минимума, которые представляют области поддержки и сопротивления.
- Веера Фибоначчи. Это диагональные линии, построенные с использованием максимума и минимума, которые представляют области поддержки и сопротивления.
- Часовые пояса Фибоначчи. Это вертикальные линии в будущее, предназначенные для прогнозирования основных ценовых движений.
Уровни коррекции Фибоначчи — наиболее распространенная форма технического анализа, основанного на последовательности Фибоначчи. Во время тренда можно использовать уровни восстановления Фибоначчи, чтобы определить, насколько глубоким может быть откат.Импульсные волны — это более крупные волны в направлении тренда, а откаты — это более мелкие волны между ними. Поскольку это волны меньшего размера, они будут составлять процент от большей волны. В это время трейдеры будут следить за соотношением Фибоначчи от 23,6% до 78,6%. Если цена останавливается около одного из уровней Фибоначчи, а затем начинает двигаться обратно в трендовом направлении, трейдер может открыть сделку в трендовом направлении.
Если цена останавливается около одного из уровней Фибоначчи, а затем начинает двигаться обратно в трендовом направлении, трейдер может открыть сделку в трендовом направлении.
Уровни Фибоначчи используются как ориентиры, возможных областей, где может развиться торговля.Цена должна подтвердить, прежде чем действовать на уровне Фибоначчи. Заранее трейдеры не знают, какой уровень будет значительным, поэтому им нужно подождать и посмотреть, какой уровень соответствует цене, прежде чем открывать сделку.
Дуги, вееры, расширения и часовые пояса — это схожие концепции, но они по-разному применяются к диаграммам. Каждая из них показывает потенциальные области поддержки или сопротивления, основанные на числах Фибоначчи, примененных к предыдущим ценовым движениям. Эти уровни поддержки или сопротивления могут использоваться для прогнозирования того, где цена может прекратить падение или рост в будущем.
Разница между числами Фибоначчи и числами Ганна
У. Д. Ганн был известным трейдером, который разработал несколько подходов к торговле, основанных на числах. Индикаторы, основанные на его работе, включают веер Ганна и квадрат Ганна. В веере Ганна, например, используются углы в 45 градусов, которые Ганн считал особенно важными. Работа Ганна в основном вращалась вокруг циклов и углов. С другой стороны, числа Фибоначчи в основном связаны с отношениями, полученными из последовательности чисел Фибоначчи.Ганн был трейдером, поэтому его методы были созданы для финансовых рынков. Методы Фибоначчи создавались не для торговли, а были адаптированы к рынкам трейдерами и аналитиками.
Д. Ганн был известным трейдером, который разработал несколько подходов к торговле, основанных на числах. Индикаторы, основанные на его работе, включают веер Ганна и квадрат Ганна. В веере Ганна, например, используются углы в 45 градусов, которые Ганн считал особенно важными. Работа Ганна в основном вращалась вокруг циклов и углов. С другой стороны, числа Фибоначчи в основном связаны с отношениями, полученными из последовательности чисел Фибоначчи.Ганн был трейдером, поэтому его методы были созданы для финансовых рынков. Методы Фибоначчи создавались не для торговли, а были адаптированы к рынкам трейдерами и аналитиками.
Ограничения использования чисел и уровней Фибоначчи
Использование исследований Фибоначчи является субъективным, поскольку трейдер должен использовать максимумы и минимумы по своему выбору. Выбор максимума и минимума повлияет на результаты, которые получит трейдер.
Еще один аргумент против методов торговли числами Фибоначчи состоит в том, что этих уровней так много, что рынок обязательно отскочит или изменит направление около одного из них, что делает индикатор значимым в ретроспективе. Проблема в том, что трудно узнать, какое число или уровень будут важны в реальном времени или в будущем.
Проблема в том, что трудно узнать, какое число или уровень будут важны в реальном времени или в будущем.
10.4: Числа Фибоначчи и золотое сечение
Известной и важной последовательностью является последовательность Фибоначчи, названная в честь итальянского математика Леонардо Пизано по прозвищу Фибоначчи, жившего с 1170 по 1230 год. Эта последовательность:
\ [\ {1,1,2,3,5,8,13,21,34,55, \ ldots \ ldots \ ldots \} \]
|
Эта последовательность определяется рекурсивно. Это означает, что каждый термин определяется предыдущими терминами. |
и так далее.
|
Последовательность Фибоначчи определяется, для всех, когда и. |
Другими словами, чтобы получить следующий член в последовательности, добавьте два предыдущих члена.
\ [\ {1,1,2,3,5,8,13,21,34,55,55 + 34 = 89,89 + 55 = 144, \ cdots \} \]
Обозначения, которые мы будем использовать для представления последовательности Фибоначчи, следующие:
\ [f_ {1} = 1, f_ {2} = 1, f_ {3} = 2, f_ {4} = 3, f_ {5} = 5, f_ {6} = 8, f_ {7} = 13, f_ {8} = 21, f_ {9} = 34, f_ {10} = 55, f_ {11} = 89, f_ {12} = 144, \ ldots \]
Пример \ (\ PageIndex {1} \): Рекурсивный поиск чисел Фибоначчи
Найдите 13, 14 и 15 числа Фибоначчи, используя приведенное выше рекурсивное определение последовательности Фибоначчи.
Во-первых, обратите внимание, что уже есть 12 чисел Фибоначчи, перечисленных выше, поэтому, чтобы найти следующие три числа Фибоначчи, мы просто складываем два предыдущих члена, чтобы получить следующий член, как указано в определении.
Следовательно, 13-е, 14-е и 15-е числа Фибоначчи равны 233, 377 и 610 соответственно.
Вычисление членов последовательности Фибоначчи может быть утомительным при использовании рекурсивной формулы, особенно при нахождении членов с большим n. {n} \ right]} {\ sqrt {5}} \]
{n} \ right]} {\ sqrt {5}} \]
|
Формула Бине является примером последовательности , явно определенной .Это означает, что условия последовательности не зависят от предыдущих условий. |
Иногда вместо приведенной выше формулы иногда используется несколько более удобная и упрощенная версия формулы Бине.
|
Упрощенная формула Бине : n-е число Фибоначчи определяется по следующей формуле:
Примечание. Символ означает «округление до ближайшего целого числа».” |
Пример \ (\ PageIndex {2} \): поиск явно
Найдите ценность использования упрощенной формулы Бине.
Рисунок \ (\ PageIndex {1} \): Работа калькулятора для
Пример \ (\ PageIndex {3} \): Поиск Явно
Найдите значение , используя упрощенную формулу Бине.
Рисунок \ (\ PageIndex {2} \): Работа калькулятора для
Пример \ (\ PageIndex {4} \): поиск Явно
Найдите значение , используя упрощенную формулу Бине.
Рисунок \ (\ PageIndex {3} \): Работа калькулятора для
В природе мы можем найти числа Фибоначчи вокруг нас. Количество ветвей на некоторых деревьях или количество лепестков некоторых ромашек часто являются числами Фибоначчи
.Рисунок \ (\ PageIndex {4} \): числа Фибоначчи и ромашки
а. Ромашка с 13 лепестками б. Ромашка с 21 лепестком
а. б.
(Ромашки, н.о.)
Числа Фибоначчи также появляются в спиральных структурах роста, таких как количество спиралей на кактусе или на грядках с семенами подсолнечника.
Рисунок \ (\ PageIndex {5} \): числа Фибоначчи и спиральный рост
а. Кактус с 13 спиралями по часовой стрелке b. Подсолнечник с 34 спиралями по часовой стрелке и 55 спиралями против часовой стрелки
а. б.
(Кактус, н.о.) (Подсолнечник, н.о.)
Другой интересный факт возникает при рассмотрении соотношений последовательных чисел Фибоначчи.
Похоже, что эти коэффициенты приближаются к цифре. Число, к которому приближаются эти отношения, — это особое число, называемое золотым сечением, которое обозначается (греческой буквой фи).Вы видели это число в формуле Бине.
|
Золотое сечение: \ [\ phi = \ frac {1+ \ sqrt {5}} {2} \] Золотое сечение имеет десятичное приближение \ (\ phi = 1,6180339887 \). |
Золотое сечение — это особое число по разным причинам. Его также называют божественной пропорцией, и он проявляется в искусстве и архитектуре.Некоторые утверждают, что это самое приятное для глаз соотношение. Чтобы найти это соотношение, греки разрезали отрезок на две части и позволили меньшему отрезку равняться одной единице. Самый приятный крой — это когда отношение полной длины к длинной части такое же, как отношение длинной части к короткой 1.
Его также называют божественной пропорцией, и он проявляется в искусстве и архитектуре.Некоторые утверждают, что это самое приятное для глаз соотношение. Чтобы найти это соотношение, греки разрезали отрезок на две части и позволили меньшему отрезку равняться одной единице. Самый приятный крой — это когда отношение полной длины к длинной части такое же, как отношение длинной части к короткой 1.
1
перемножим, чтобы получить
переставить, чтобы получить
решите это квадратное уравнение, используя формулу корней квадратного уравнения.
Золотое сечение — это решение квадратного уравнения, означающее, что оно обладает свойством. Это означает, что если вы хотите возвести в квадрат золотое сечение, просто добавьте к нему единицу. Чтобы проверить это, просто подключите.
Сработало!
Еще одна интересная связь между золотым сечением и последовательностью Фибоначчи возникает при использовании степеней.
И так далее.
Обратите внимание, что коэффициенты и числа, добавленные к члену, являются числами Фибоначчи.{n} = f_ {n} \ phi + f_ {n-1} \)
, где \ (f_ {n} \) — это n-е число Фибоначчи, а \ (\ phi \) — это золотое сечение .
Пример \ (\ PageIndex {5} \): Степени золотого сечения
Найдите следующее, используя правило золотой силы: a. и б.
Калькулятор Фибоначчи
Этот калькулятор Фибоначчи представляет собой инструмент для вычисления произвольных членов последовательности Фибоначчи.Вам больше никогда не придется добавлять термины вручную — наш калькулятор найдет для вас первые 200 терминов! Вы также можете установить свои собственные начальные значения последовательности, и пусть этот калькулятор сделает всю работу за вас. Обязательно ознакомьтесь с калькулятором геометрической последовательности!
Что такое последовательность Фибоначчи?
Последовательность Фибоначчи — это последовательность чисел, подчиняющаяся определенному правилу: каждый член последовательности равен сумме двух предыдущих членов. Таким образом, каждый член можно выразить следующим уравнением:
Fₙ = Fₙ₋₂ + Fₙ₋₁
Последовательность Фибоначчи обычно имеет первые два члена, равные F₀ = 0 и F₁ = 1.В качестве альтернативы вы можете выбрать F₁ = 1 и F₂ = 1 в качестве стартеров последовательности. В отличие от арифметической последовательности, вам нужно знать как минимум два последовательных члена, чтобы вычислить оставшуюся часть последовательности.
Правило последовательности Фибоначчи также действует для отрицательных членов — например, вы можете найти F₋₁ равным 1.
Первые пятнадцать членов последовательности Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 …
Интересно, что числа Фибоначчи подчиняются хорошо известному закону Бенфорда!
Формула для n-го семестра
К счастью, вычисление n-го члена последовательности не требует вычисления всех предыдущих членов.Существует простая формула, позволяющая найти произвольный член последовательности:
Fₙ = (φⁿ - ψⁿ) / √5
где:
- Fₙ — n-й член последовательности,
- φ — золотое сечение (равно (1 + √5) / 2, или 1,618 …)
-
ψ = 1 - φ = (1 - √5) / 2.
Наш калькулятор Фибоначчи использует эту формулу для нахождения произвольных членов в мгновение ока!
Формула для n-го члена с произвольными стартерами
Вы также можете использовать калькулятор последовательности Фибоначчи, чтобы найти произвольный член последовательности с разными стартовыми элементами.Просто откройте расширенный режим и установите два числа для первого и второго члена последовательности.
Калькулятор Фибоначчи использует следующую обобщенную формулу для определения n-го члена:
Fₙ = aφⁿ + bψⁿ
где:
-
а = (F₁ - F₀ψ) / √5 -
b = (φF₀ - F₁) / √5 - F₀ — это первый член последовательности,
- F₁ — второй член последовательности.
Отрицательные члены последовательности Фибоначчи
Если вы запишете несколько отрицательных членов последовательности Фибоначчи, вы заметите, что последовательность ниже нуля имеет почти те же числа, что и последовательность выше нуля.Вы можете использовать следующее уравнение, чтобы быстро вычислить отрицательные члены:
F₋ₙ = Fₙ * (-1) ⁿ⁺¹
Например, F₋₈ = F₈ * (-1) ⁸⁺¹ = F₈ * (-1) = -21
Спираль Фибоначчи
Если вы нарисуете квадраты со сторонами, длина которых равна каждому последовательному члену последовательности Фибоначчи, вы можете сформировать спираль Фибоначчи:
Спираль на изображении выше использует первые десять членов последовательности — 0 (невидимый), 1, 1, 2, 3, 5, 8, 13, 21, 34.
Божественная композиция с соотношением Фибоначчи (Правило третей на стероидах)
Вы любите мелкие детали? Что ж, если ты фотограф, тебе лучше быть. Открытие правила третей — большая веха для любого фотографа. Внезапно вы понимаете, что все, что вы когда-либо делали раньше, — это центр кадра правой кнопкой мыши по центру кадра, потому что именно там находится сетка фокусировки камеры. Имеет смысл, правда? Правило третей подняло вас на новые высоты в вашем фотографическом путешествии, перемещая объект в ту или иную сторону в кадре, вверх или вниз.Но разве некоторые из этих фотографий не выглядят слишком тесно из-за того, что расположены так близко по обе стороны от кадра? Конечно, в некоторых случаях это работает, но что, если есть еще одно правило, которое вы могли бы включить в свой фотографический репертуар?
Введите коэффициент Фибоначчи…
Также известный как Золотое Сечение, Фи или Божественная Пропорция, этот закон был прославлен Леонардо Фибоначчи около 1200 г. н.э. Он заметил, что существует абсолютное соотношение, которое часто встречается в природе, своего рода дизайн, который универсально эффективен для живых существ. и приятен человеческому глазу.Отсюда и прозвище «божественная пропорция».
Начиная с эпохи Возрождения, художники и архитекторы разрабатывали свои работы таким образом, чтобы соотношение было примерно 1: 1,618. Его можно найти по всему Парфенону, в известных произведениях искусства, таких как Мона Лиза и Тайная вечеря, и он используется до сих пор. Божественная пропорция использовалась такими компаниями, как Apple, для разработки продуктов, она, как говорят, использовалась Twitter для создания своей новой страницы профиля и использовалась крупными компаниями по всему миру для разработки логотипов.В большинстве фотографических кругов об этом не говорят, потому что это довольно продвинутый метод композиции и может сбить с толку многих людей. Гораздо проще просто говорить о «правиле третей», потому что оно точное, точное и простое в применении.
Это соотношение можно использовать по-разному для композиции фотографии. В Lightroom 3 даже есть опция наложения золотого сечения, когда вы собираетесь кадрировать изображение. Таким образом, вы можете выровнять сетку золотого сечения, чтобы она совпадала с линиями или интересными точками на вашей фотографии.На этом этапе вы можете сильно запутаться. Если да, пожалуйста, уделите несколько минут, чтобы посмотреть одно (или все) из этих видео, которые пытаются объяснить это соотношение.
Видео 1: Число натур: 1,618
Видео 2: Природа в числах
Видео 3: Золотое сечение
Хорошо, надеюсь, это прояснило ситуацию? К настоящему времени вы должны знать, что это НЕ теория заговора или нечеткая математика. Это реальный аспект композиции, который использовался известными историческими художниками и архитекторами и компаниями из списка Fortune 500.Применительно к фотографии это соотношение может создавать эстетически приятные композиции, которые могут быть магнитом для человеческого подсознания. Когда вы берете золотую середину соотношения Фибонначи и четыре раза воссоздаете его в сетку, вы получаете то, что выглядит как сетка с правилом третей. Однако при ближайшем рассмотрении вы увидите, что эта сетка не является точным разделением кадра на три части. Вместо сетки из 3 частей, которая идет 1 + 1 + 1 = кадр, вы получаете сетку, которая идет 1 + 0,618 + 1 = кадр. Вот несколько примеров сетки Фи, размещенной поверх некоторых изображений, на которых я использовал ее в прошлом…
В приведенном выше примере я поместил немного более доминирующий глаз лошади на одном из перекрестков Фи.Учтите, что если бы я поместил сетку по правилу третей поверх этой фотографии и выровнял бы ею глаз, голова бы загромождала левую часть кадра. На этой фотографии голова не по центру, она не сгущается с обеих сторон. Это правильно, согласны? Давайте посмотрим на другой…
Этот немного отличается. Если вы НАСТОЯЩИЙ приверженец деталей, то, возможно, заметили небольшую разницу между пересекающимися линиями на графике Фи и золотым пятном самого Фи.На этом изображении я убедился, что голова моего объекта выровнена по спирали, и поместил левый глаз примерно над зоной наилучшего восприятия. Хорошо, переходим…
На этой фотографии, сделанной из Ки-Уэста, я выровнял горизонт с верхней линией сетки Фи. На мой взгляд, когда вы выравниваете горизонт сеткой по правилу третей, разделение становится слишком… очевидным. Я думаю, что это оставит слишком много того, что не является предметом изображения. На этой фотографии небо и облака являются прекрасным дополнением к тому, что я пытаюсь передать на фотографии: церковь внизу справа и знаменитая улица Дюваля слева.Но если неба больше, чем на фотографии, зритель может подумать, что небо на самом деле является объектом. Вот еще один…
В этом примере я использовал несколько линий на сетке Phi для моей окончательной композиции. Я выровнял двери обеими вертикальными линиями, а также нижней горизонтальной линией. Это обеспечило идеальное количество потолка, ведущего взгляд зрителя к двери. Вот еще несколько примеров без сетки. Посмотрите, можете ли вы представить себе сетку поверх изображений, и определите, почему изображение было составлено таким, каким оно было.
Заключение
Надеюсь, эта статья пролила свет на несколько загадочную тему в мире фотографии. Соотношение Фибоначчи — мощный инструмент для компоновки фотографий, и его не следует сбрасывать со счетов как незначительное отличие от правила третей. Хотя сетки выглядят одинаково, использование Phi может иногда означать разницу между фотографией, которая просто щелкает, и фотографией, которая кажется не совсем правильной. Я, конечно, не говорю, что правилу третей нет места в фотографии, но Фи — гораздо более совершенный, гораздо более умный и исторически проверенный метод компоновки сцены.
Если вы хотите начать использовать этот мощный инструмент композиции в своей фотографии, вам повезло! Я включил наложение PNG как спирали Фибоначчи, так и сетки Фибоначчи. Просто щелкните эту ссылку для загрузки, чтобы начать их использовать. Эти наложения предназначены для использования в Photoshop. Просто поместите их в файл, над которым вы работаете, а затем отмасштабируйте их до нужного размера изображения.
