Магия чисел: что такое последовательность Фибоначчи
Последовательность Фибоначчи — это ряд чисел, в котором первые два элемента — 0 и 1, а все последующие равны сумме двух предыдущих. Ее можно проследить в некоторых явлениях природы, науке, архитектуре и искусстве. Разбираемся в том, что это такое и почему важно.
Леонардо Пизанский: математика и удача
Леонардо Пизанский (ок. 1170 — ок. 1250) был математиком. Он жил в Италии, а в 1190-х годах переехал в Алжир, где узнал об арабских и индийских приемах вычисления. В 1200 году Леонардо вернулся в Пизу, а в 1202 дописал свой первый труд по математике — «Книгу абака» (абаком он называл арифметику). Именно в этой работе была описана последовательность чисел, которую впоследствии назвали последовательностью Фибоначчи.
Фибоначчи — это прозвище Леонардо Пизанского, которое появилось только в XVI веке. Оно происходит от слов filius Bonacci, которые стояли на обложке «Книги абака». Их можно перевести как «сын Боначчо» (или «Боначчи», если трактовать это слово как фамилию, а не как имя).
По другой версии, Bonacci нужно тоже понимать как прозвище — в итальянском это слово означает «удача».
Последовательность Фибоначчи впервые была рассмотрена на примере вымышленной популяции кроликов. Математик сформулировал задачу: в загоне есть пара кроликов, которая каждый месяц производит на свет новую пару. Сколько всего кроликов будет через год? При этом надо учесть несколько условий:
Кролики могут принести потомство только на третий месяц жизни.
Кролики всегда рождаются парами — самка и самец.
Кролики не умирают в течение года.
При решении этой задачи возник ряд чисел, который выглядит так:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 — в конце года будет 233 пары кроликов.
Это и есть последовательность Фибоначчи, которую можно продолжать бесконечно.
Золотое сечение и спираль Фибоначчи
Если последовательно делить одно число ряда Фибоначчи на предыдущее, в конце концов (с деления 89 на 55) мы начнем получать число 1,618.
Именно этот коэффициент принято называть золотым сечением, или золотой пропорцией. А если мы попробуем изобразить это графически, то получим золотой прямоугольник — длины его сторон будут относиться друг к другу как 1,618 : 1.
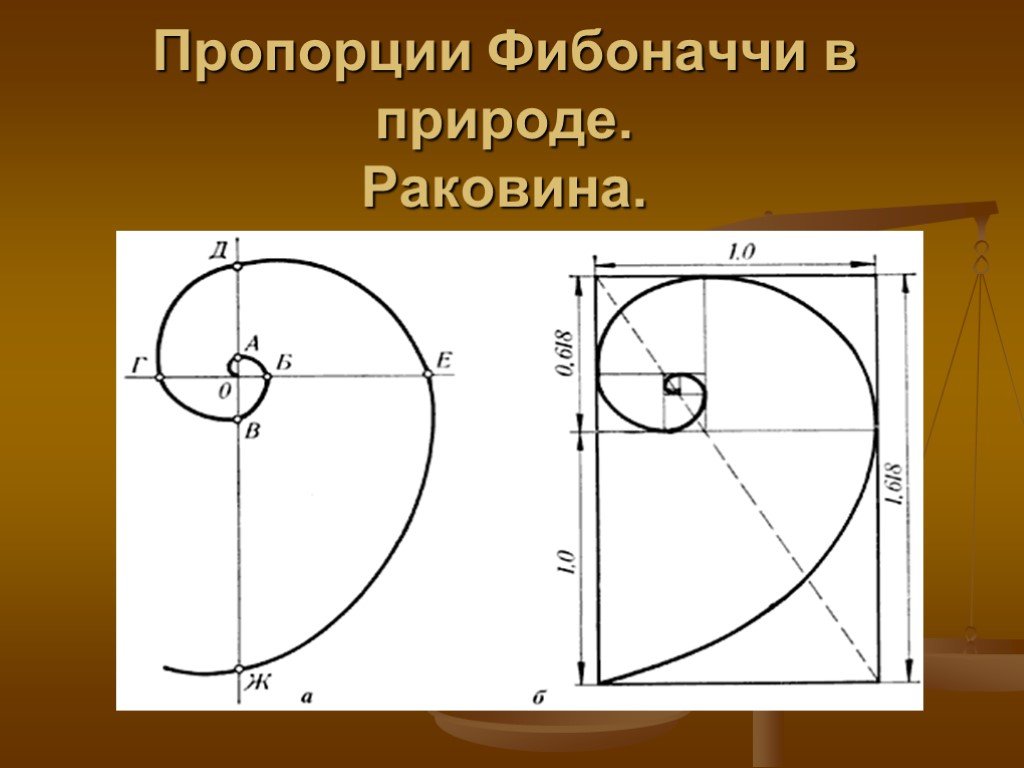
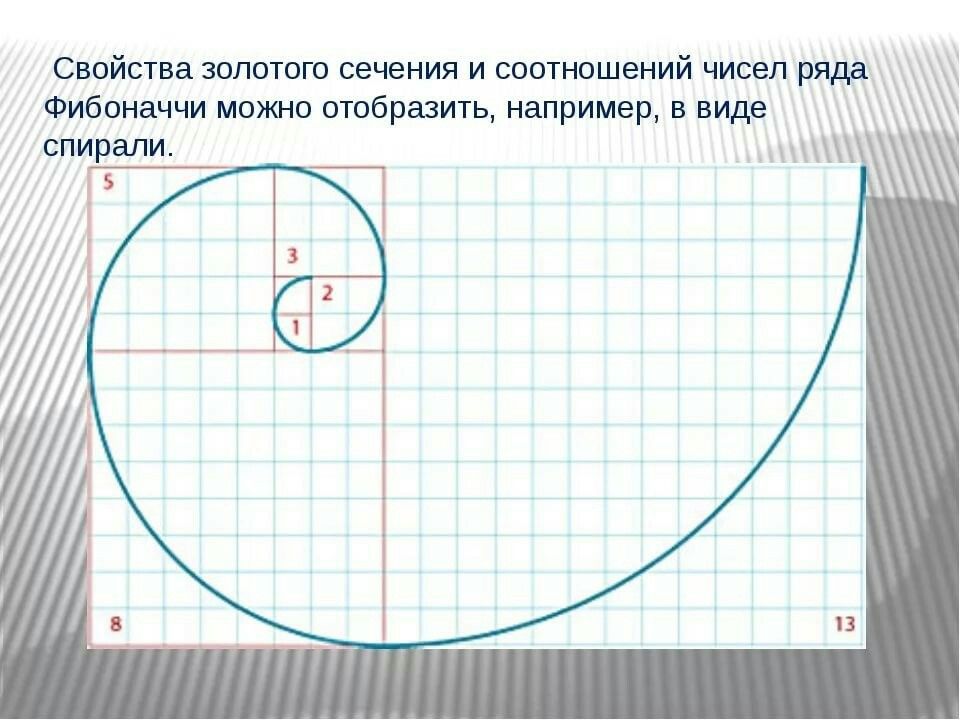
С помощью золотого прямоугольника можно построить спираль Фибоначчи.
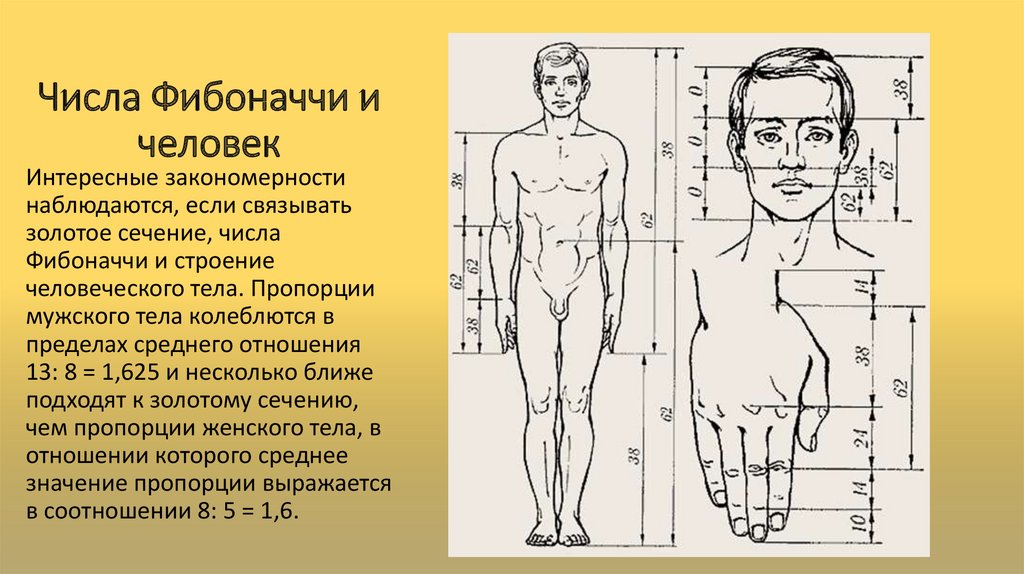
И золотая пропорция, и спираль Фибоначчи интересны тем, что они часто встречаются в природе. Например, семена в центре подсолнечника организованы в спираль и идут по и против часовой стрелки. Если анализировать каждую спираль отдельно, окажется, что это и есть спирали Фибоначчи. То же самое касается раковин некоторых улиток и даже строения человеческого уха. А если посчитать, как соотносится расстояние от точки пупа до коленей и от коленей до ступней в нашем теле, мы получим золотую пропорцию — 1 : 1,618.
Числа Фибоначчи в искусстве
Золотое сечение и спираль Фибоначчи часто используются в живописи или архитектуре. Пожалуй, самый известный пример — это работы Леонардо да Винчи.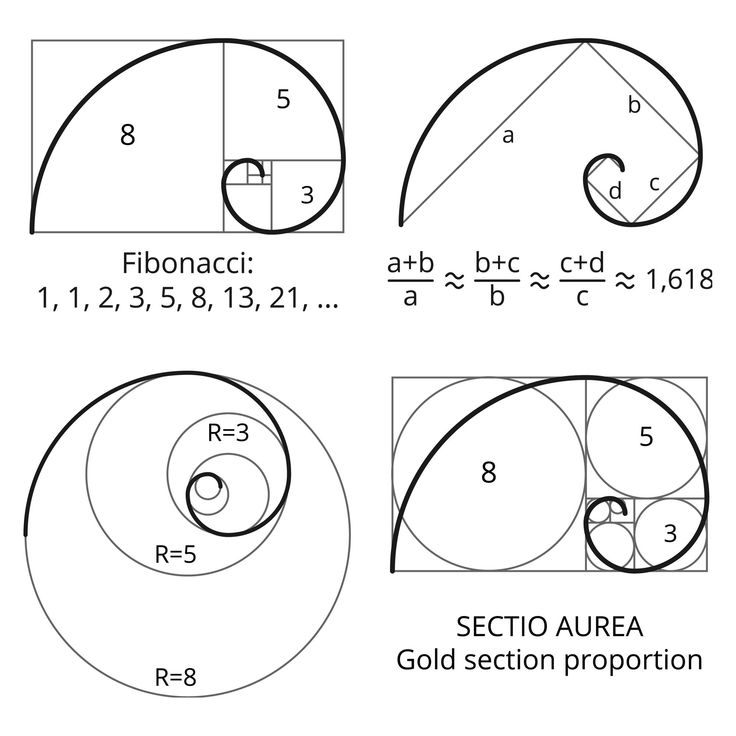
Композиция «Моны Лизы» построена на основе спирали Фибоначчи, а «Витрувианский человек» буквально изображает связь пропорций тела и золотого сечения.
С использованием золотой пропорции построены, например, египетские пирамиды Гизы, Собор Парижской Богоматери и Храм Василия Блаженного. А в 2005 году в Корнуолле (Великобритания) появился образовательный комплекс The Core («Ядро»). Его архитекторы вдохновлялись формой цветка подсолнечника. В итоге получилось здание, построенное по принципу спирали Фибоначчи.
Считается, что золотое сечение используется также в музыке и поэзии. В некоторых произведениях, например поэме Лермонтова «Бородино» или этюдах Шопена, кульминационные моменты разделяют композицию на части, соотношение которых близко к золотой пропорции.
Иллюстрация: magann / Depositphotos.com
Александра Смаракова
Теги
#эрудиция
#саморазвитие
фибоначчи прямоугольник свободный вектор | Загрузите это сейчас!
Этот сайт использует куки.
Продолжая просматривать, вы соглашаетесь на использование нами файлов cookie и других технологий отслеживания. Узнайте больше здесь.
Пожаловаться
Скачать (6,5 КБ)
спираль фибоначчи
золотая спираль
Шаблоны векторных 62
Белый зеленый округлённый прямоугольник картинки
Белый красный округлённый прямоугольник картинки
Золотая бабочка узор вектор материала
Золотой меч картинки
Прозрачный «Золотой глобус»
φ Последовательность Фибоначчи и золотое сечение ★ Фибоначчи
Узнать больше
Фибоначчи — это последовательность чисел, прославившаяся благодаря математику тринадцатого века Леонардо Пизано, который представил и объяснил решение алгебраической математической задачи в своей книге Liber Абаци (1228).
Было обнаружено, что последовательность Фибоначчи и отношения ее последовательных чисел широко распространены в природе, искусстве, музыке, биологии и других дисциплинах. Последовательность начинается с 0 и 1 и состоит из последующих чисел, в которых n-е число является суммой двух предыдущих чисел. Уравнение для нахождения числа Фибоначчи можно записать так:
Fn = F(n-1) + F(n-2). Начальными точками являются F1 = 1 и F2 = 1.
Каждое число в последовательности Фибоначчи обозначается нижним индексом 1, 2, 3, 4 …… чтобы указать, о каком члене последовательности идет речь. Таким образом, F16 относится к шестнадцатому числу Фибоначчи.
Последовательность Фибоначчи
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987 . . .
Что такое золотое сечение?
С последовательностью Фибоначчи связан еще один известный математический термин: 9.0009 Золотое сечение . Когда число в ряду Фибоначчи делится на предшествующее ему число, сами частные превращаются в ряды, которые следуют захватывающей схеме: 1/1 = 1, 2/1 = 2, 3/2 = 1,5 , 5/3 = 1.
666 …, 8/5 = 1,6 , 13/8 = 1,625 , 21/13 = 1,61538 , 34/21 = 1.619 , 55/34 = 1.6176 … и 89/89/34 = 1.6176 … и 89/ 55 = 1,618 … Первые десять соотношений приближаются к числовому значению 1,618034… которое называется «Золотым сечением» или «Золотым числом» и обозначается греческой буквой фи (Φ, φ). После этих первых десяти соотношений частные приближаются к Фи и, кажется, сходятся к нему, но никогда не достигают его полностью, потому что это иррациональное число. Фи (Φ), 1,61803 39887…, также является числом, полученным, когда вы делите линию на среднее и предельное соотношение, а затем делите всю линию на наибольшую среднюю часть; его обратное значение равно фи (φ), 0,61803 39887…, полученному при делении крайней (меньшей) части линии на (большую) среднюю. На изображении ниже отношение меньшей части линии (CB) к большей части (AC), то есть CB/AC, такое же, как отношение большей части AC ко всей линии AB.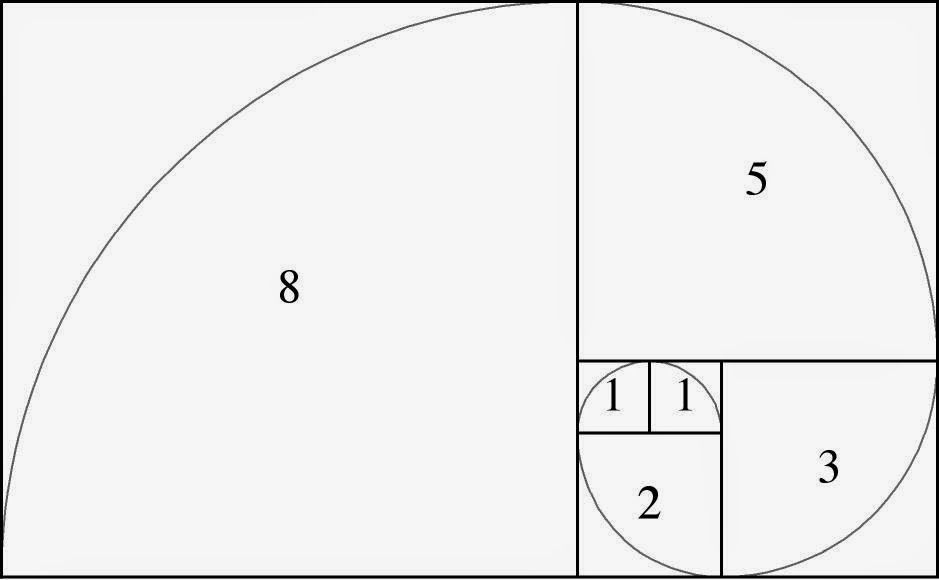
n)/(x – (1-x)), где x = (1+sqrt 5)/2 ~ 1,618. Ratio представляет собой фундаментальную математическую структуру, которая кажется распространенной — некоторые говорят, повсеместной — во всей Природе, особенно в организмах ботанического и зоологического царств.
Подробнее
Кто такой Леонардо Пизано (Фибоначчи)?
Мастер Леонардо Пизано (не путать с Леонардо да Винчи) был любимым государственным служащим Пизы, Италия, который добился известности при жизни (ок. 1170 – ок. 1250), но был забыт в течение двухсот лет. О нем или его многочисленных достижениях в математике не было написано никаких биографий; даже математики не знали, кто он такой, до 1494 года, когда уважаемый итальянский математик Лука Пачоли (1447–1517) кратко упомянул имя Леонардо в предисловии к своей собственной книге9.0005 Summa , отдавая ему должное за большинство идей, представленных в его собственной книге. Однако это замечательное одобрение не возродило наследие Леонардо, и его имя снова было быстро забыто.
Еще триста лет историческая анонимность скрывала достижения Леонардо Пизано, пока однажды историк математики по имени Пьетро Коссали (1748-1815) не заметил упоминание Пачоли и не начал самостоятельно исследовать работы Леонардо. Это было в 1797, спустя более пяти столетий после смерти Леонардо. Примечательно, что прошло еще сто лет, прежде чем Леонардо снова получил академическое признание и получил должное признание.
В 1870-х годах французский математик Эдуард Лукас присвоил имя «Фибоначчи» числовой последовательности, которая является решением знаменитой «задачи о кролике» в книге Леонардо Пизано Liber Abaci (1228). С тех пор Леонардо называют «Фибоначчи». ПОДРОБНЕЕ
Фибоначчи в искусстве и музыке
Как и Евклид до него, «Фибоначчи» считал вычисления формой искусства; для него это была чудесная вещь красоты, проникающая в искусство и звук.
Узнать больше
ФИБОНАЧЧИ В МАТЕМАТИКЕ
Основополагающая работа Леонардо Пизано, Liber Abaci , стала источником математических достижений в Европе в Средние века и повлияла на замену римских цифр современными арабскими цифрами.
Узнать больше
ФИБОНАЧЧИ В ПРИРОДЕ
Научные исследования находят доказательства того, что числа Фибоначчи и золотое сечение преобладают в природных объектах, от микроскопических пропорций строения тел живых существ на Земле до соотношения сил гравитации и расстояния между телами во Вселенной.
Узнать больше
ИСТОРИЯ ПОСЛЕДОВАТЕЛЬНОСТИ ФИБОНАЧЧИ
Серьезные ученые-математики все чаще начинают признавать, что Леонардо Пизано, возможно, был «самым выдающимся математическим гением Средневековья» и, безусловно, самым влиятельным всех средневековых писателей в продвижении индийско-арабских цифр среди европейских ученых.
Узнать больше
ПОДПИСАТЬСЯ НА НОВОСТИ И ОБНОВЛЕНИЯ
[mc4wp_form id=”71″]
404: Страница не найдена
Страница, которую вы пытались открыть по этому адресу, похоже, не существует.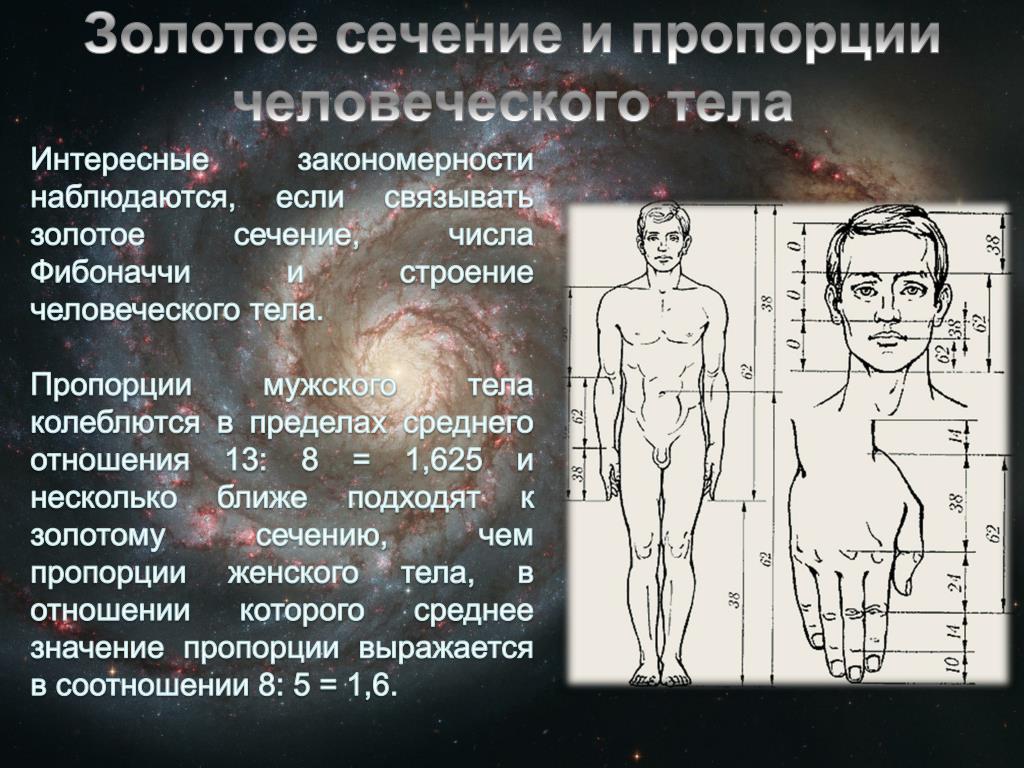
Обычно это результат плохой или устаревшей ссылки. Мы извиняемся за любые неудобства.
Что я могу сделать сейчас?
Если вы впервые посещаете TechTarget, добро пожаловать! Извините за обстоятельства, при которых мы встречаемся. Вот куда вы можете пойти отсюда:
Поиск- Пожалуйста, свяжитесь с нами, чтобы сообщить, что эта страница отсутствует, или используйте поле выше, чтобы продолжить поиск
- Наша страница «О нас» содержит дополнительную информацию о сайте, на котором вы находитесь, WhatIs.com.
- Посетите нашу домашнюю страницу и просмотрите наши технические темы
Поиск по категории
Сеть
- входная фильтрация
Ingress filtering — это метод, используемый предприятиями и интернет-провайдерами для предотвращения проникновения подозрительного трафика в …
- многопользовательский MIMO
Многопользовательский MIMO или MU-MIMO — это технология беспроводной связи, в которой используется несколько антенн для улучшения связи за счет .
.. - богон
Богон — это незаконный адрес интернет-протокола, который попадает в набор IP-адресов, которые официально не назначены…
..- E-Sign Act (Закон об электронных подписях в глобальной и национальной торговле)
Закон об электронных подписях (Закон об электронных подписях в глобальной и национальной торговле) — это федеральный закон США, в котором указывается, что в …
- личная информация (PII)
Личная информация (PII) — это любые данные, которые потенциально могут идентифицировать конкретное лицо.
- политика социальных сетей
Политика в отношении социальных сетей – это корпоративный кодекс поведения, содержащий рекомендации для сотрудников, размещающих контент в Интернете …
ИТ-директор
- управление корпоративными проектами (EPM)
Управление корпоративными проектами (EPM) представляет собой профессиональные практики, процессы и инструменты, связанные с управлением несколькими .
- Управление портфелем проектов: руководство для начинающих
Управление портфелем проектов — это формальный подход, используемый организациями для выявления, определения приоритетов, координации и мониторинга проектов …
- SWOT-анализ (анализ сильных и слабых сторон, возможностей и угроз)
SWOT-анализ представляет собой основу для выявления и анализа сильных и слабых сторон организации, возможностей и угроз.
HRSoftware
- Эффект хоторна
Эффект Хоторна — это изменение поведения участников исследования в ответ на их знание о том, что они …
- командное сотрудничество
Совместная работа в команде — это подход к коммуникации и управлению проектами, который делает упор на командную работу, новаторское мышление и равенство …
- самообслуживание сотрудников (ESS)
Самообслуживание сотрудников (ESS) — это широко используемая технология управления персоналом, которая позволяет сотрудникам выполнять множество связанных с работой .
Пропорция фибоначчи: Золотое сечение и пропорции Фибоначчи
