3. Ракурс | Композиция в фотографии
Ракурс — это позиция фотокамеры по отношению к главной теме. Как вы увидите, эта позиция сильно влияет на композицию, потому что в зависимости от нее мы можем усиливать объект фотографии в разной степени.
Этот элемент композиции можно использовать только на практике во время съемки, поэтому важно, чтобы мы всегда имели его ввиду. Позднее, в лаборатории, мы уже не сможем поменять угол съемки фотографии, если только мы не сделали одну и ту же фотографию со всех возможных ракурсов, как в фильме «Матрица», или же если мы не изменим угол при помощи функции искажения.
Съемка на уровне
Когда позиция фотокамеры — на том же уровне, что и объект фотографии. Это нейтральный и естественный ракурс.
Нижний ракурс съемки
Заключается в расположении фотокамеры ниже объекта или субъекта съемки. Достигнутым эффектом будет приподнимание субъекта, увеличение его размера и значимости. Нужно быть осторожным при использовании этого ракурса в близкой портретной съемке.
Обычно эффект получается обратным, мы не превознесем человека, но представим его в смешном виде, так как кожа подбородка и шея будут заметнее, чем все лицо.
Верхний ракурс съемки
Этот ракурс съемки заключается в том, чтобы фотокамера находилась выше объекта или субъекта фотографии. Обычно это уменьшает значение фотографируемого субъекта по отношению к остальным элементам. Он делает его маленьким и смешным.
Съемка на уровне земли
Это тот тип съемки, когда фотокамера находится почти на земле. Это редкая точка зрения для людей, поэтому она будто переносит зрителя фотографии в другой мир.
Этот ракурс эффективен для того, чтобы придать больше жизни неодушевленному предмету в фотографии.
Съемка сверху
Когда съемка фотографии происходит сверху перпендикулярно плоскости, где находится объект. Теряется перспектива, поэтому становится даже интересно сравнить реальные пропорции разных объектов фотографии.
Этого ракурса не так легко добиться при съемке объектов средних и больших размеров, так как для того, чтобы иметь отличный перпендикулярный угол, необходимо снимать с подъемного крана или будучи подвешенным в воздухе.
Пример 1 Съемка на уровне
«Erhu davant de les compres», Barcelona (2009)
Я сделал фотографию этого музыканта, играющего на эрху, когда тот выступал на Portal de Angel. Я использовал съемку на уровне субъекта, благодаря чему получил очень естественную фотографию.
Пример 1 Нижний ракурс
«Un predicador», Londres (2009)
В Гaйд Парке в Лондоне собираются болтуны, мечтатели и другие представители этой «среды обитания», любящие публичные места. Тем апрельским утром в 2009 году я сделал несколько фотографий, применяя нижний ракурс в композиции, с целью выделить героев, будто речь шла о пророках. По правде говоря, этот тип на фотографии кажется более значительным, чем он есть на самом деле.
Пример 1 Верхний ракурс
На этой фотографии изображены я и мои друзья во время экскурсии по восточному побережью США. Мирейа взобралась на скалу, закрепилась на ней и добилась верхнего ракурса, так что мы получились уменьшенными на фоне потрясающей прибрежной линии.
Пример 1 съемки на уровне земли
«L’infern d’un fotògraf», Barceona (2009)
Этот телевизор был оставлен в дверях на одной из улиц квартала Барселонетта в Барселоне. Решение наклониться и сделать фотографию на уровне земли позволило зрителю войти в этот другой мир. Что будет с телевизором? Какова его судьба?
Пример 1 съемки сверху
«Manifestació Plataforma per a la Defensa de Collserola», Barcelona (2008)
Эту фотографию, снятую сверху, я сделал во время выступления, проходившего рядом с храмом на горе Тибидабо. Угол наклона солнца в этот утренний час и выбранный ракурс позволяют следить за артистами через их тени.
Курс «Импрессионизм. Ракурсы»
Поделиться
Этот новый курс Академии Пушкинского в разделе Пушкинский INTRO будет посвящен разным ракурсам импрессионизма. От зарождения стиля до выдающихся произведений, вошедших в мировую историю искусства, от робких поисков нового до вершины мастерства.
Об этом и многом другом расскажут ведущие специалисты отдела искусства Европы и Америки XIX–XX веков. Старт курса 9 декабря.
Тест к курсу «Импрессионизм. Ракурсы»
Эдуард Мане — новая классика
С именем Мане связаны первые глобальные изменения в искусстве XIX века. Первого представителя французского модернизма нередко называют импрессионистом, однако формально Мане никогда не входил в группу импрессионистов и не участвовал в их выставках. В отличие от своих молодых современников, ориентированных прежде всего на стремительные изменения современной жизни, Эдуард Мане нередко обращался к искусству старых мастеров, вступая с ними в сложный, а порой и провокационный диалог.
Лекцию читает Анна Познанская, заместитель заведующего отделом искусства стран Европы и Америки XIX–XX веков.
Тест к лекции
Эдгар Дега. «За кулисами Парижской оперы»
Знаменитая Парижская опера стала центром художественных поисков Эдгара Дега на более чем четыре десятилетия.
Такое внимание к танцу, движению, а с ними – к особенностям освещения и контрастам цветов – превратило Дега не только в одного из величайших художников своего времени, но и в знаменитого экспериментатора. Дега воспринимал все здание Оперы как свой «дом» и обращался в своих произведениях к закулисью знаменитого театра и его обитателям – не только к балеринам, но и к музыкантам, певцам, посетителям в темноте лож. Как тайная жизнь Парижской оперы изменила Эдгара Дега, а он, в свою очередь, – историю мировой живописи? Об этом пойдет речь на лекции.
Лекцию читает Елена Коротких, научный сотрудник отдела искусства стран Европы и Америки ХIХ–ХХ веков.
Тест к лекции
Приключения импрессионизма за океаном. Новая живопись в США
Развитие импрессионизма в США связано с именами таких художников как Джон Сарджент, Уильям Меррит Чейз, Мэри Кэссетт, Фредерик Гассамм, которые, попав под обаяние нового парижского искусства, попытались перенести его на свой континент. Однако, американский импрессионизм имеет целый ряд специфических черт.
Мы сможем проследить его непростую историю от первых выставок французского искусства в Нью-Йорке и Бостоне до скандальной славы «школы мусорных ведер». Лекцию читает Александра Данилова, заведующая отделом искусства стран Европы и Америки XIX–XX веков.
Тест к лекции
Итальянские дивизионисты: художники света
Дивизионизм представляет собой наиболее значительное живописное явление в искусстве Италии на рубеже XIX–XX веков. Художники использовали оптическое смешение цветов для достижения максимальной яркости и светоносности своих полотен. Лекция посвящена анализу истоков итальянского дивизионизма, его соотношения с французским неоимпрессионизмом, рассмотрению творчества основных представителей данного течения и определению его роли в развитии искусства Италии в начале XX века. Лекцию читает Елена Стёпкина, младший научный сотрудник отдела искусства стран Европы и Америки XIX–XX веков.
Тест к лекции
Был ли импрессионизм в скульптуре?
Имена художников-импрессионистов большинство слушателей нашего курса назовет без труда.
Тест к лекции
Коллекционеры импрессионистов 1870–1930-х годов: любители и знатоки
Круг первых ценителей импрессионистов был очень пестрым, как и среда их друзей — от аристократов до оперных звезд, врачей и даже владельца пекарни. На рубеже XIX–XX веков добившиеся успеха художники стали отражением эмоций нового поколения коллекционеров и из Франции, и из других стран Европы и Америки. А в межвоенные годы для знатоков искусства собирание работ импрессионистов превратилось в тщательное составление личных музеев. О том, как менялись вкусы и взгляды коллекционеров, как и почему сохранились или не уцелели их собрания, рассказывает Алексей Петухов, старший научный сотрудник отдела искусства стран Европы и Америки XIX–XX веков.
Тест к лекции
Поль Сезанн. «От первой выставки импрессионизма до «отшельника из Экса»»
В парижской среде художников-новаторов уроженец Прованса Поль Сезанн считался нелюдимым и простоватым. И его почерк в искусстве, с самого начала сколь основательный, столь и страстный, и жизненная позиция ставили Сезанна в особое положение в любой ситуации, даже на первой выставке импрессионистов в 1874 году, в которой художник принял участие. К концу XIX века за ним закрепилось прозвище «отшельник из Экса», намекавшее на закрытость и таинственность. Как к Сезанну пришла запоздалая слава, почему его считают «отцом» современного искусства и как он на него повлиял — об этом пойдет речь на лекции. Лекцию читает Алексей Петухов, старший научный сотрудник отдела искусства стран Европы и Америки XIX–XX веков.
Тест к лекции
Ван Гог и Гоген: пути эскапизма
Дискуссия в рамках цикла, подготовленного совместно с просветительским проектом ScienceMe.
Подробности
Искусство быть одиноким: художники в изоляции
Дискуссия в рамках цикла, подготовленного совместно с просветительским проектом ScienceMe.
Подробности
Женская история импрессионизма
Дискуссия в рамках цикла, подготовленного совместно с просветительским проектом ScienceMe.
Подробности
Партнер Академии Пушкинского
Angles — Обзор геометрии (видео)
Привет и добро пожаловать в это видео об углах
Давайте начнем с определения луча . Луч — это линия с единственной конечной точкой, бесконечно простирающаяся в одном направлении.
Если мы возьмем этот луч и добавим к нему еще один луч с той же конечной точкой, мы получим угол .
Мы также создали вершину , которая является точкой пересечения двух лучей.
Вы можете думать об этом как об углу. Обычно мы видим вершины всякий раз, когда встречаются линии или многоугольников , например треугольников и четырехугольников.
Иногда у нас много ракурсов, поэтому, чтобы отличить их друг от друга, у нас есть система их именования.
Вот снова наш простой угол, но с добавлением нескольких точек на лучи:
Теперь мы можем называть наш угол углом ABC (∠ABC). При именовании углов тремя буквами точка вершины должна находиться посередине. Здесь B — вершина, поэтому B находится между A и C. На самом деле мы можем назвать это ∠CBA, и это так же правильно.
Если точка, которая является вершиной, является только частью одного угла, тогда мы можем использовать более короткое имя. В этом случае мы могли бы также назвать этот угол B. Однако будьте осторожны, потому что иногда одна точка может быть вершиной нескольких углов, например:
В этом случае нам пришлось бы называть углы по их длинные имена, потому что точка B является вершиной ∠ABC, ∠DBC и ∠DBA! Если бы мы попросили кого-нибудь просто посмотреть на ∠B, они бы не поняли, что из этого мы имели в виду. Поэтому важно быть точным при работе с более чем одним углом.
Иногда углы будут обозначаться числами внутри дуги, например:
Теперь у нас есть дополнительное имя для этого угла.
Теперь мы можем назвать его ∠1, или мы можем назвать его ∠ABC, или мы можем назвать его ∠B. Поскольку у большинства из нас три имени, будет справедливо, если у углов тоже будет куча. Но чаще всего нам нравится использовать буквы для обозначения наших углов, поскольку числа можно спутать с мерой угла. Иногда вы увидите строчные буквы вместо цифр или греческих символов, таких как \(\theta\) или \(\alpha\).
Говоря об измерениях, помните транспортир? Мы используем его для измерения углов. Если бы мы поместили один из них на наш надежный угол, мы бы обнаружили, что он измеряет 45 градусов:
. Если бы мы записали это, мы бы написали это так:
\(m∠ABC = 45°\)
Мера угла важна при классификации углов, как мы скоро увидим.
Давайте посмотрим на вариант нашего двухлучевого угла, но на этот раз давайте сделаем так, чтобы они были равны перпендикулярны друг к другу, что означает, что угол между ними составляет 90 градусов:
Здесь мы создали прямой угол .
Обратите внимание, что он имеет другой символ угла, чем наш первый угол. Вместо дуги у него квадрат. Всякий раз, когда мы видим угол с этим квадратом, мы знаем, что он точно равен 90 градусам. Чаще всего мы видим прямые углы в квадратов , прямоугольников и прямоугольных треугольников , но они могут появляться и в других местах.
Если угол имеет меру меньше 90 градусов, он называется остроугольным треугольником . Наш первоначальный угол был бы частью остроугольного треугольника, так как его мера составляет 45 градусов, что меньше 90:
угол , который выглядит так:
В этом случае угол ABC имеет размер 140 градусов, что больше 90. Тупые углы также должны быть меньше 180 градусов.
Это три основных типа углов, определяемых мерой, но есть еще два чудака, о которых нам нужно знать.
Первый прямой угол . Она выглядит как прямая линия и имеет меру 180 градусов.
Когда это нарисовано так, мы видим, что ∠ABC действительно существует и имеет меру 180 градусов. Это полезно знать, потому что это понадобится нам позже для понимания линейных пар.
Но прежде чем мы дойдем до этого, давайте посмотрим на другого чудака. Этот совсем не похож на ракурс:
Но на самом деле он называется полный угол . Представьте, что мы повернули точку А против часовой стрелки, а точка В осталась на месте, пока она снова не совместилась с точкой С. Сколько это градусов? Это весь круг, который, как мы знаем, составляет 360°.
Помните наш прямой угол? Что, если мы нарисуем это, но добавим еще один луч, выходящий из него, например:
Если мы знаем, что угол DBC равен 55 градусам, и мы знаем, что угол ABC является прямым углом и, следовательно, равен 180 градусам, мы действительно можем найти угол АВС! Как? Взяв весь прямой угол (∠ABC), равный 180 градусам, и вычтя меньший угол (∠DBC), равный 55 градусам.
\(180° – 55° = 125°\). это называется линейная пара . Два угла (∠ABD и ∠DBC) образуют прямую ∠ABC. А поскольку два меньших угла в сумме составляют 180 градусов, мы также можем сказать, что они являются дополнительными углами .
Нечто подобное происходит и с прямыми углами. Вот наш прямой угол, но с другим лучом посередине:
Угол DEF — прямой угол. Мы видим, что ∠DEG и ∠GEF вместе полностью заполняют ∠DEF, а это значит, что их сумма составляет 90 градусов. Итак, если мы знаем один из двух углов, мы можем найти другой, вычитая его меру из 9.0 градусов. Например, если ∠DEG равно 30°, то мы знаем, что ∠GEF равно 60°, потому что 90° – 30° = 60°. Углы, сумма которых равна 90°, называются дополнительными углами .
Вернемся к нашему тупому углу еще раз. Есть еще один тип ракурса, который скрывался у всех на виду, о котором нам нужно знать.
Мы видим, что угол ∠ABC тупой, а это значит, что он больше 90° и меньше 180°.
Но как насчет другой стороны?
Это называется угол рефлекса .
Всегда больше 180° и меньше 360°. Каждый острый, прямой и тупой угол имеет рефлекторный угол.
Далее давайте посмотрим, где мы увидим некоторые из этих углов в дикой природе или, по крайней мере, в задачах по геометрии.
Начнем с двух пересекающихся линий. В данном случае мы пронумеровали углы.
Всякий раз, когда мы видим подобную фигуру, зная один из углов, мы можем определить все остальные! Итак, если угол ∠1 равен 130°, мы можем вычислить угол ∠2, потому что эти два угла вместе образуют прямую и являются линейной парой и дополнительными. Таким образом, ∠2 должно быть равно 50°. То же самое работает для углов 1 и 3. И затем мы можем использовать то, что мы знаем о ∠2, чтобы соединить его с ∠4, чтобы найти этот угол. Когда все сказано и сделано, это выглядит так:
Обратите внимание, что углы, противоположные друг другу, имеют одинаковую меру.
Эти углы называются вертикальными углами , и они всегда конгруэнтны , что в геометрии говорит о том, что они имеют одинаковую меру.
Теперь давайте посмотрим на три пересекающиеся прямые:
Это называется секущей . Мы снова пронумеровали углы, и на двух линиях есть красные стрелки, указывающие на то, что они параллельны. Секущей не обязательно иметь параллельные линии, но когда они есть, это позволяет нам многое узнать о восьми углах, образованных пересекающимися линиями.
Но прежде чем мы дойдем до этого, давайте посмотрим на восемь углов. Мы видим, что они находятся в двух группах по четыре (углы 1-4 и 5-8). Угол 1 находится в верхнем левом положении в верхней группе углов. Если мы посмотрим на то же место в нижней группе углов, мы увидим, что ∠5 находится в верхнем левом месте для этой группы. Это означает, что ∠1 и ∠5 — соответствующие углы. Таким образом, ∠2 и ∠6 также являются соответствующими углами, потому что они находятся в правом верхнем углу для соответствующих групп.
∠3 и ∠7 также соответствуют, как и ∠4 и ∠8. В секущей, когда есть пара параллельных прямых, соответствующие углы равны. Когда прямые не параллельны, соответствующие углы не равны.
В случае нашей диаграммы с параллельными линиями, если мы знаем, что ∠2 равно 55°, мы знаем, что ∠6 также равно 55°. И как только мы это узнаем, мы можем использовать то, что мы узнали о вертикальных углах и линейных парах, чтобы найти все остальные:
Это все, что нам нужно знать, чтобы найти наши углы, но нам нужен еще кое-какой словарь, основанный на местоположении. быть в курсе с этими типами проблем. Внутренние углы — это углы между параллельными прямыми. В данном случае это ∠3, ∠4, ∠5 и ∠6. Внешние углы — это те, которые, как вы уже догадались, не лежат между параллельными прямыми. Итак, ∠1, ∠2, ∠7 и ∠8 — внешние углы.
Альтернативные углы — это углы, находящиеся по разные стороны от линии, пересекающей параллельные линии. А односторонние углы — это, конечно, углы, лежащие по одну сторону от этой линии.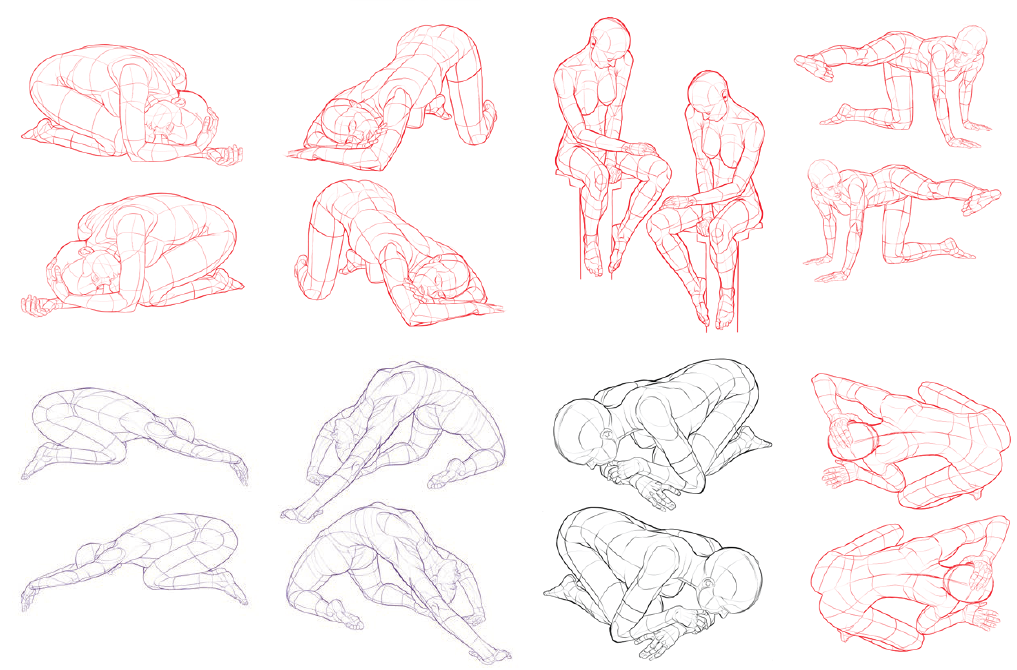
В вопросах о двух группах углов это используется для объединения внутренних или внешних углов с чередующимися или одинаковыми боковыми углами. Вопрос всегда будет относиться к другой группе углов. Что-то вроде «каков альтернативный внутренний угол для ∠3?» Мы бы посмотрели на другую группу углов, затем на другую сторону пересекающейся линии, а затем нашли бы единственный угол, который является внутренним углом, который будет равен ∠6. Тот же боковой внутренний угол для ∠3 равен ∠5.
Очень многое нужно усвоить за небольшой промежуток времени. Ссылаясь на изображение выше, попробуйте ответить на следующие вопросы, чтобы увидеть, утонуло ли оно:
1. Каков внешний угол, альтернативный ∠8?
2. Чему равен внешний угол той же стороны к ∠7?
3. Чему равен угол, соответствующий ∠5?
Спасибо за просмотр и удачной рыбалки!
Часто задаваемые вопросы
Q
Что такое дополнительные углы?
A
Дополнительные углы — это два угла, сумма величин которых равна 90 градусам.
Q
Что такое дополнительный угол?
A
Дополнительный угол — это угол, который в сумме с другим углом составляет 180°.
Пример. Какой угол примыкает к углу 107°?
180 – 107 = 73°
Q
Что такое вертикальные углы?
A
Вертикальные углы представляют собой пары углов, противоположных друг другу. Один вертикальный угол всегда равен другому вертикальному углу.
пр.
∠ABC и ∠DBE — вертикальные углы.
Q
Что такое соответствующие углы?
A
Соответствующие углы — это углы, которые находятся в одном и том же положении относительно поперечной и параллельной прямой, когда две прямые пересекаются секущей. Соответственные углы всегда имеют одну и ту же меру.
Пример.
∠1 и ∠2 — соответствующие углы.
Q
Что такое острый угол?
А
Острый угол – это угол, градусная мера которого меньше 90 градусов.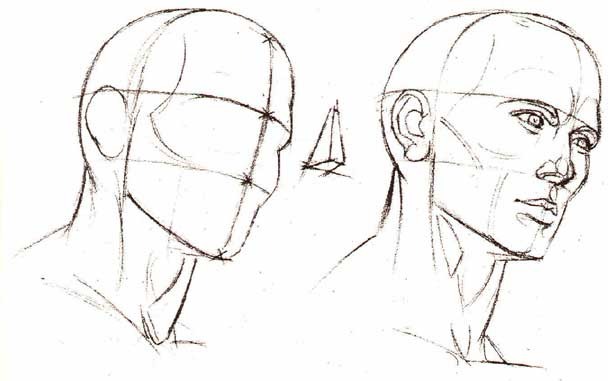
Q
Как найти угол треугольника?
A
Найдите угол прямоугольного треугольника по формулам: ) и \(tanθ=\frac {напротив} {смежный}\). Эти формулы можно запомнить, используя легочный SOH-CAH-TOA. Заполните заданные длины сторон и действуйте в обратном порядке, чтобы найти угол (ϴ). 9{-1}\frac{4}{5}\)
\(θ≈53,13°\)
Q
Что такое тупой угол?
A
Тупой угол — это любой угол, градусная мера которого больше 90°.
Пример.
Практические вопросы
Вопрос №1:
Описание какого угла соответствует приведенному ниже углу?
Прямой угол
Острый угол
Полный угол
Тупой угол
Показать ответ
Ответ:
Тупой угол имеет размер больше 90 градусов, но меньше 180 градусов.
Скрыть ответ
Вопрос № 2:
Решите для x .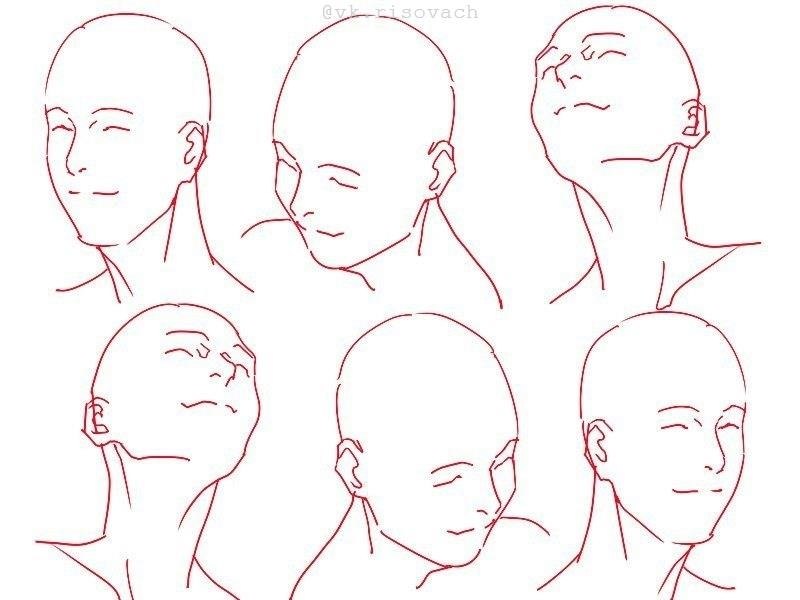
43 °
53 °
137 °
90 °
Покажите ответ
Ответ:
Сумма x и 37 ° будет
3, потому что эти две углы.
x можно рассчитать, вычитая 37 из 90. В любом случае \(x=53°\).Скрыть ответ
Вопрос №3:
Какая пара углов будет считаться вертикальными углами ?
Угол 6 и угол 8
Угол 3 и угол 8
Угол 5 и угол 8
Угол 1 и угол 8
Показать ответ
Ответ:
Вертикальные углы также известны как противоположные углы. Противоположные углы, или вертикальные углы, на схеме включают: 1 и 4, 2 и 3, 5 и 8, а также 6 и 7.
Скрыть ответ
Вопрос № 4:
Макс настраивает разбрызгиватель так, чтобы он опрыскивал участок газона под углом 90°.
Он планирует поворачивать разбрызгиватель каждые 15 минут, чтобы весь газон получал воду. Сколько раз нужно повернуть разбрызгиватель, чтобы полить весь газон?
Всего четыре раза
Всего пять раз
Всего два раза
Всего шесть раз
Показать ответ
Ответ:
Каждый раз, когда устанавливается дождеватель, он поливает четверть всего газона. Это означает, что разбрызгиватель необходимо повернуть четыре раза, чтобы достичь каждой секции. \(90°×4\text{sections}=360°\) (общий двор).
Скрыть ответ
Вопрос № 5:
Пешеходная дорожка пересекает железнодорожные пути, образуя поперечную линию. Если угол 1 равен 120 градусам, то чему равен угол 3?
120 градусов
70 градусов
50 градусов
60 градусов
Показать Ответ
Ответ:
Углы 1 и 3 являются дополнительными углами.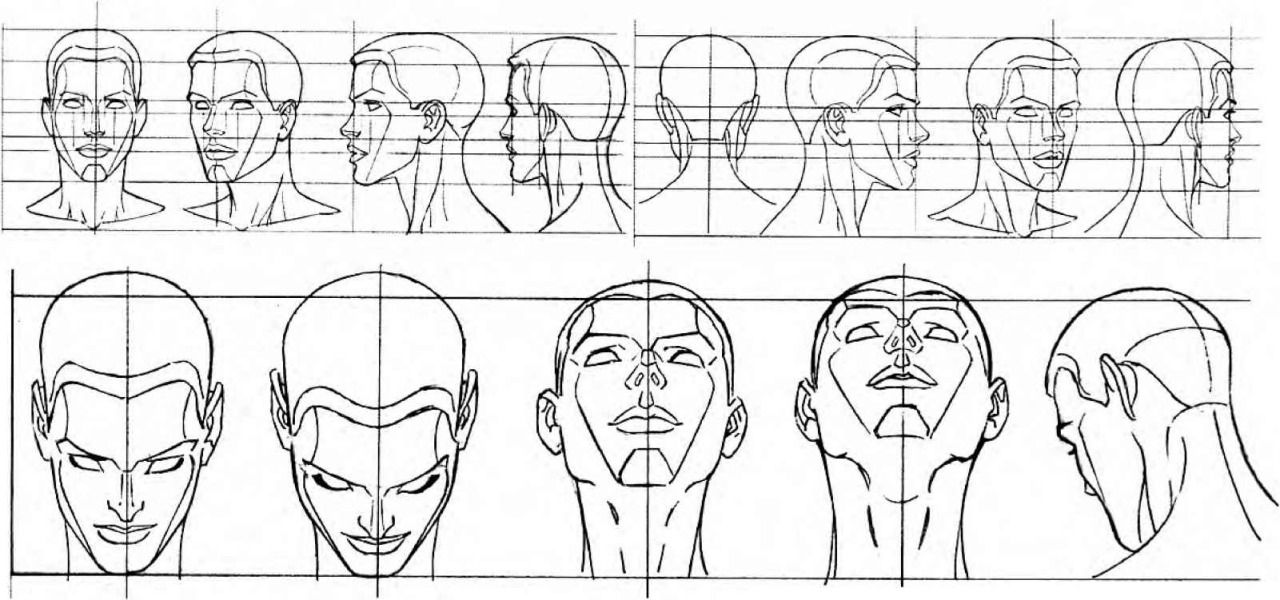
Сумма углов 1 и 3 будет 180 градусов. Если Угол 1 равен 120 градусам, то \(180-120\) дает нам значение Угла 3. Угол 3 равен 60 градусам.
Скрыть ответ
Углы
Углы используются в повседневной жизни. Инженеры и архитекторы используют углы для конструкций, дорог, зданий и спортивных сооружений. Спортсмены используют углы, чтобы повысить их производительность. Плотники используют углы, чтобы сделать стулья, столы и диваны. Художники используют свои знания ракурсов для набросков портретов и картины.Если две линии встречаются (или пересекаются) в одной точке, то образуется угол . Точка пересечения линий называется вершиной .
Ниже показан угол.
Линии AB и AC пересекаются в точке A , образуя
угол.
Точка A является вершиной угла, и линии, которые
встречаются, чтобы сделать угол, называются плечи уголка .
Именование углов
Размер угла Величина поворота от одного плеча угла к другому называется размер угла .
Размер угла измеряется в градусах ; и используемый символ
представлять степень. В полном обороте (или круге) 360.
Примечание:
градусов определяется таким образом, что угол одного полного оборота (или окружность) составляет 360 градусов.
Измерение углов
Транспортир используется для измерения углов.
В этом разделе мы будем
рассмотреть использование транспортира, который имеет форму полукруга и два
шкалы отмечены от 0 до 180.
Две шкалы облегчают нам измерение
углы смотрят в разные стороны.
Чтобы измерить размер угла ABC , поместите транспортир на
угла так, чтобы центр транспортира находился прямо над углом
вершина, В; а базовая линия транспортира проходит по плечу, BA ,
угла.
Используем внутреннюю шкалу для измерения угла ABC , так как плечо AB проходит через ноль внутренней шкалы . Следующий
внутренней шкалы вокруг транспортира, мы находим, что другое плечо, г. до н.э. г.,
проходит через внутреннюю шкалу в точке 60.
Чтобы измерить размер угла PQR , поместите транспортир на
угла так, чтобы центр транспортира находился прямо над углом
вершина, Q ; а базовая линия транспортира проходит по плечу PQ ,
угла.
Используем внешнюю шкалу для измерения угла PQR , так как плечо PQ проходит через ноль внешней шкалы . Следующий внешней шкалы вокруг транспортира, мы находим, что другой рычаг, QR , проходит через внешнюю шкалу на 120. Итак, размер угла PQR равен 120 градусов. Запишем это так:
Типы уголков
Острый угол больше 0 и меньше 90.
A Прямой угол ровно равен 90.
Обратите внимание, что прямой угол отмечен на схеме маленьким квадратом.
Тупой угол больше 90 и меньше 180.
A прямой угол точно равен 180.
Угол рефлекса больше 180 и меньше 360.
Перигон (или оборот ) — это угол, который точно равен
360.
Измерение углов отражения
Напомним, что:
Транспортир можно использовать для измерения величины острого угла (между
0 и 90) и тупой угол (от 90 до 180).