Размер матрицы в фотоаппарате: Матрица фотоаппарата. Типы и характеристики. — Главная

Содержание

Матрица фотоаппарата. Типы и характеристики.

Матрица фотоаппарата самая важная составляющая часть любой камеры. Именно она ответственна за создание изображения, после поступления на ее поверхность светового потока. Если описать матрицу научными словами, то это будет звучать следующим образом, микросхема состоящая из светочувствительных элементов, фотодиодов. Посмотрите следующий снимок, где показано месторасположение матрицы в блоке самого фотоаппарата («тушке»).

Матрица фотоаппарата самым прямым образом влияет на качество итогового изображения, что в сочетании с профессиональным фотообъективом приводит к точной и полной передаче всех деталей реальности.

1. Размер матрицы

2. Количество пикселей

3. Светочувствительность

Теперь подробнее о каждой из указанных характеристик.

Физический размер матрицы, т.е соотношение длины и ширины, измеряемой в миллиметрах, одна из самых важных характеристик матрицы. Чем больше размер, тем лучше будет качество фотографии. Почему? Большая по размеру матрицу, получает больше света, что в свою очередь связано с фактором ISO/светочувствительности. Даже при высоких значения ISO, количество шумов на фотоснимке, сделанном на профессиональную камеру с большой матрицей, будет минимальное. Чего нельзя сказать о фотоснимке сделанном, при участии маленькой матрицы.

Далее на картинке вы можете изучить самые распространенные размера матрицы в соотношение к диагонали.

Количество пикселей в матрице фотоаппарата влияет на размер изображения. Все профессиональные зеркальные фотокамеры снабжены матрицей с большим числом мегапикселей. Как результат, вы сможете распечатать большую фотографию, плакат или постер и все цвета и детали при этом, будут переданы в наилучшем качестве.

Типы матриц фотоаппарата.

По применяемой технологии матрицы бывают нескольких типов, но самые популярные из них:

— ПЗС (CCD — Charge Coupled Device). Данный тип матрицы выпускается практически всеми фирмами производителями фотокамер (Nikon, Canon, Sony и др.). Один из очевидных плюсов высокая чувствительность и маленький уровень шумов, что положительно влияет на качество фотографии, но высокое энергопотребление.

— КМПО (CMOS — Complementary Metal Oxide Semiconductor). Основные плюсы данного вида матрицы низкое энергопотребление и высокое быстродействие. В наши дни данный вид матрицы самый распространенный.

Далее, для примера я привела небольшую сравнительную характеристику фотокамер двух фирм лидеров производителей Nikon и Canon.

Профессиональные фотокамеры Nikon D5 (21,33 Мп), D810a (37,09 Мп) имеют КМОП-матрицу размером 35,9 x 24,0 мм. Компактные фотокамеры, например Nikon CoolPix L340, L2750 снабжены ПЗС матрицей.

Профессиональные фотокамеры Canon EOS – 1D X II Mark (21,5 Мп), EOS 5DS R (50,6 Мп) имеют CMOS матрицу. У Canon даже такие компактные камеры как PowerShot SX720 HS, SX 620HS также работают на КМПО матрице.

На этом я заканчиваю свою статью под названием «Матрица Фотоаппарата», дальше будет еще больше полезных и интересных статей. Подписывайтесь на обновления моего блога, и вы будете первыми получать новые статьи.

Размер матрицы фотоаппарата и её влияние на ГРИП

Матрица в цифровой фотокамере – это что-то вроде кадра на пленочных аппаратах. Проходящие через объектив лучи света попадают на нее и «рисуют» заданную картинку. Отличие матрицы от аналоговой технологии в том, что картинка не хранится на поверхности пленки, а записывается в память камеры в виде электронного файла.

Матрица представляет собой пластину, состоящую их фотодатчиков (пикселей). В зависимости от количества света, попадающего на пиксели, они генерируют сигнал определенной мощности. Зависимость здесь прямая: больше света – сильнее сигнал. Именно от количества этих фотодатчиков зависит размер будущей фотографии, уровень детализации изображения и наличие на картинке шумов.

Так, если матрица имеет 2592 пикселя в ширину и 1944 – в высоту, то камеру характеризуют как «пятимегапиксельную» (2592х1944=5038848). При прочих равных условиях, чем больше матрица, тем выше качество снимков.

CMOS матрица фотоаппарата Canon EOS1000D

Таким образом, размер матрицы является одной из важнейших характеристик аппарата. Но наряду с покупателями этот факт отлично известен производителям техники. И результатом борьбы за клиента стала подмена понятий. Вместо того, что ориентироваться на физический размер матрицы, измеряемый в миллиметрах, фотолюбители смотрят исключительно на пиксельность камеры, искусственно «подогнанную» в рекламных целях.

Увеличить количество фотодатчиков можно двумя разными способами: путем увеличения матрицы или же уменьшения площади самих датчиков. Первый метод (дорогой) приводит к реальному улучшению характеристик матрицы, а второй (дешевый) – позволяет поместить на неизменной площади пластины большее количество точек. Нетрудно догадаться, какой путь для себя выбирают производители массовой фототехники.

Размеры матрицы на камерах обозначаются геометрическим размером чипа. Причем точно вычислить физический размер пластины это обозначение не позволяет, а используется для сравнения матриц между собой. Для понимания реальных габаритов следует воспользоваться небольшой «шпаргалкой».

Самые маленькие матрицы обозначаются как 1/3.2?. Физический размер их равен 3,4х4,5 миллиметров, соотношение сторон – 4:3. Используются такие матрицы в недорогих фотоаппаратах.

Матрицы с аналогичным соотношением сторон, но несколько большего размера (4х5,4 мм) маркируются как 1 / 2.7?.

1/2,5? – обозначение пластины размером 4,3х5,8 миллиметров. Эти матрицы являются самыми распространенными в камерах любительского уровня с несменной оптикой.

Матрицы 1/1,8? характеризуются геометрическими размерами 5,3х7,2 мм; 2 / 3? – 6,6х8,8 мм; 4 / 3? – 18х13,5 мм. Соотношение сторон у всех этих фотопластин составляет 4:3.

Стороны более профессиональных матриц соотносятся между собой как 3:2. Встречаются они в зеркальных цифровых камерах среднего ценового диапазона. Размер DX и APS-C матриц – 24х18 миллиметров.

APS-C, APS-H и полнокадровая 35 мм матрицы

Самые дорогие фотоаппараты оснащаются полнокадровыми или среднеформатными матрицами, габариты которых составляют 36х24 и 60х45 миллиметров соответственно.

Как уже отмечалось выше, размер матрицы оказывает влияние на несколько ключевых величин: габариты камеры, наличие шумов и ГРИП. В первом случае всё очевидно: чем больше матрица, тем больше размер фотоаппарата, больше его вес и выше стоимость.

Наличие на изображении цифровых шумов определяется, кроме размера матрицы, еще настройками камеры (повышением резкости, функцией шуподавления). Рассматривать показатель шума как отдельный показатель было бы неправильно, потому что передача его идет параллельно с основным световым сигналом на фотодатчики. Характеризовать эту величину можно только в соотношении силы сигнала к шумам.

Что касается влияния физического размера матрицы на глубину резкости (ГРИП), то здесь ситуация неоднозначна.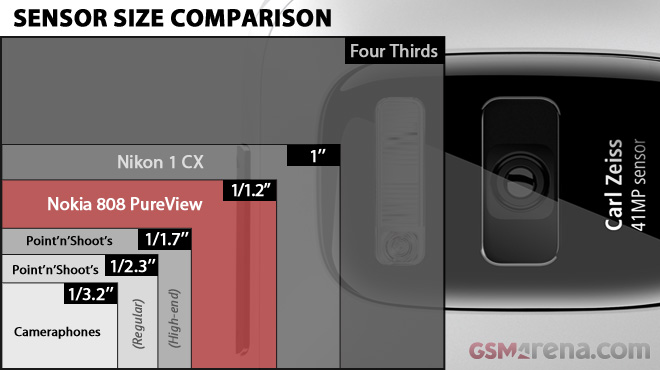 Дело в том, что сами по себе ширина и высота фотопластины не имеют принципиального значения. Глубина резкости зависит, прежде всего, от фокусного расстояния и светосильности объектива. А они, как правило, невелики на компактных камерах с маленькой матрицей. Соответственно, получение малой глубины резкости на так называемых «мыльницах» практически невозможно.

Кроме размера, матрицы различаются также по типам, наиболее распространенными из которых являются следующие три:

1) CCD-, или ПЗС-матрицы. Изначально целью изобретения этой технологии было использование ее при создании запоминающих устройств. Но способность ПЗС-матрицы получать определенный заряд в результате фотоэлектрического эффекта изменила ее основной функционал. На основе CCD работают камеры фирмы Sony и еще нескольких крупных производителей.

2) CMOS-, или КМОП-матрицы. Главной особенностью CMOS является пониженное энергопотребление, которое достигается за счет использования транзисторов. Такие матрицы используются, в основном, в тех устройствах, для которых уровень потребления электроэнергии является критичным фактором (в кадбкуляторах, например, или электронных часах).

3) LiveMOS-матрица. Впервые технология «живого» просмотра была применена компанией Olympus в 2006 году. В перечне характеристик камеры LiveMOS-матрицу обычно указывают как «Live View».

Стоит отметить, что отличия между типами матриц принципиальны только в отношении процесса их производства. Человеческому же глазу разница между ними невидна. Поэтому тип используемой матрицы должен восприниматься фотографами в качестве дополнительной информации, и не более того.

Источник: Фотокомок.ру – изучаем основы фотографии (при копировании или цитировании активная ссылка обязательна)

Сравнить размер сенсора(матрицы) фотоаппарата

Дело в том, что измерения могут быть очень запутанными и неясными. Лично я, могу понять, насколько большой APS-C сенсор, по сравнению с полнокадровым сенсором, но у меня были проблемы в понимании того, в каком отношении находится небольшой 1/2.33 (или «1») датчик с другими сенсорами. Когда компания Nokia объявила о выпуске 808 PureView, мне действительно стало интересно, насколько большой, или маленький этот датчик. Теперь есть новый сайт, который называется «Датчик изображения камеры» (cameraimagesensor.com). Тут, вы можете сравнивать размеры и технические характеристики датчиков изображения различных фотокамер.

Сайт cameraimagesensor.com позволяет выбрать конкретный продукт из списка, будь то обычная цифровая камера, камера среднего формата, CSC, DSLR или мобильное устройство, например смартфоны. После того как объект был выбран, вы увидите, размер датчика

на экране. Это не фотография в реальном размере, но она дает хорошее представление о том, как соотносятся разные датчики между собой.
Так, что если вы хотите знать, насколько маленьким будет датчик 1/2.3-inch по сравнению с Micro Four Third, или с APS-C, то у вас есть такая возможность. Вы можете сделать это очень просто и наглядно, не вникая в странные цифры и обозначения.

То на сколько, качественным будет изображение, очень влияет размер датчика. Если вы хотите получить хорошее изображение, высокого качества, с минимальным количеством шума, при покупке камеры, вам необходимо остановить свой выбор на фотокамере с большим датчиком.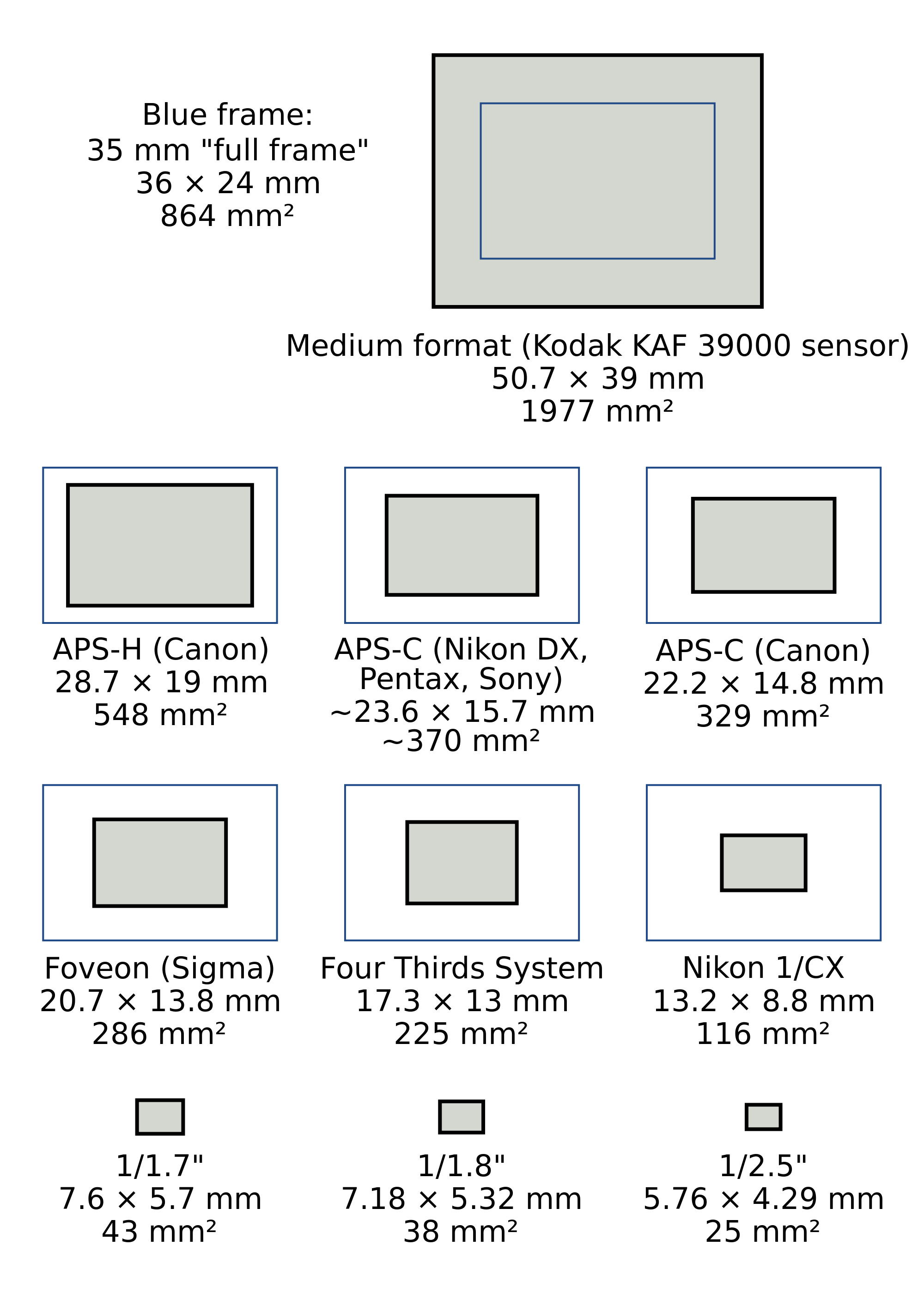
Таким образом, сайт cameraimagesensor.com, является замечательным мини-сайтом, с помощью которого вы можете получить визуальное представление о размере датчика изображения, и о других интересных технических характеристиках, таких как плотность пикселей, размер (высота) пикселя, размер сенсора в мм, и т.д.

Убедиться в интересных возможностях этого приложения вы можете прямо на нашем сайте, либо посетив сайт cameraimagesensor.com

Матрица фотоаппарата

Никого сейчас не удивишь цифровой фото камерой, каждая из которых наделена матрицей фотоаппарата. Что такое матрица фотоаппарата, почему ее название матрица цифрового фотоаппарата, какие ее функции.

Почти два столетия прошло с тех пор, как был создан первый прототип фотоаппарата. Принцип работы фотокамеры остался прежним: попадание светового потока через объектив и фиксация на светочувствительном элементе. Ранее использовались пленочные элементы с свойственной им химической реакцией. Новая эра фотоаппаратов преподнесла нам цифровые фотокамеры.

Матрица фотоаппарата, а точнее матрица цифрового фотоаппарата — это электронная схема, состоящая из миллионов крошечных светочувствительных диодов, которые реагируют на световой поток, попадающий на них. Один такой светодиод матрицы цифрового фотоаппарата приносит вашему изображению ровно один пиксель.

Теперь представьте себе матрицу фотоаппарата, передающую 12 миллионов пикселей. Сложно? Вовсе нет: 12 мегапикселей — это площадь матрицы в пикселях. К примеру, если соотношение сторон матрицы 3:4, то на матрице цифрового фотоаппарата будет располагаться 3 тысячи пикселей в столбце и таких столбцов 4 тысячи.

Как выглядит матрица фотоаппарата. Какой физический размер матрицы фотоаппарата?

Особенность электроники матрицы цифрового фотоаппарата заключается в накоплении эклектического заряда в зависимости от количества попадающего света на матрицу фотоаппарата. Если происходит переизбыток энергии на пикселе или группе пикселей матрицы цифрового фотоаппарата, то эта энергия начинает переходить на соседние пиксели.

В результате, когда фотографируете солнце вы получаете световой пучок разной окружности.

Важно знать: чем качественнее и дороже матрица, а главное, чем больше физический размер матрицы цифрового фотоаппарата, тем больше расстояние между её пикселями, тем менее заметен эффект распределения энергии на соседние пиксели.

Количество пикселей на матрице должно увеличиваться с увеличением качества и\или размера матрицы цифрового фотоаппарата. Иначе, новые пиксели теряют свою эффективность. Размер матрицы цифрового фотоаппарата — важная характеристика!

Для начала, что это такое. Раньше, в эпоху пленочных фотоаппаратов с этим было просто — вместо матрицы была светочувствительная пленка-негатив. Стандарт был 35мм (физический размер 24×36 мм). В современном же цифровом фотоаппарате вместо пленки устанавливается светочувствительная матрица — интегральная микросхема, состоящая из светочувствительных элементов (фотодиодов). Матрица предназначена для преобразования спроецированного на нее оптического изображения в поток цифровых данных.

Фотоматрица оцифровывает («нарезает» на пиксели) то изображение, которое формируется объективом фотоаппарата.

Существуют несколько типов матриц, применяемых в цифровых камерах, основные из которых CCD и CMOS. CCD-матрица обеспечивает лучшие показатели при съемке динамичных и мелких объектов, у нее низкий уровень шума и высокий коэффициент заполнения. CMOS-матрица же используется в изделиях, для которых критична конечная стоимость, благодаря своей недорогой стоимости, низкого энергопотребления.

Итак, физический размер матрицы. Необходимо отметить, что физический размер матрицы — одна из важнейших характеристик фотоаппарата, влияющих на качество получаемых фотографий. Физический размер — это ее геометрический размер (длина и ширина в миллиметрах). Однако чаще всего размеры фотосенсоров чаще всего обозначают в виде дробных частей дюйма, например 1 / 2.5″. Так как эта величина обратная, то и соответственно, размер матрицы больше, если число после дроби меньше.

Для примера, приведем соотношение наиболее часто используемых матриц:

Диагональ матрицы	Геометрический размер
1 / 3.2″	3.4 х 4.5мм
1 / 2.7″	4.0 х 5.4мм
1 / 2.5″	4.3 х 5.8мм
1 / 2.3″	4.6 х 6.2мм
1 / 1.8″	5.3 х 7.2мм
2 / 3″	6.6×8.8мм
1″	9.6 х 12.8мм
APS-C (матрица, в 1.6 раза меньше APS)	15 х 23мм
полный формат (APS)	24 х 36мм

Проще ориентироваться не на размер матрицы в обратных значениях дюйма, а на кроп-фактор. Кроп-фактор — это коэффициент, показывающий во сколько раз матрица фотоаппарата меньше полного формата. Например, для наиболее распространенного размера матрицы современных мыльниц 1 / 2.3″ кроп-фактор составит 5.62, т.е. матрица в 5. 62 раза меньше полноформатной.

Размер матрицы влияет на количество цифрового шума, передаваемого вместе с основным сигналом на матрицу. Наличие цифрового шума, в свою очередь, придает фотографии неестественный вид и создается впечатление, что на фотографии наложена матовая пленка. Чем больше физический размер матрицы, тем больше ее площадь и тем больше света на нее попадает, в результате чего полезный сигнал матрицы будет сильнее и соотношение сигнал / шум будет лучше. Это позволяет получать более яркую, качественную картинку с естественными цветами.

Выбираем фотоаппарат. Часть 4. Матрица и объектив

Главные параметры фотоаппарата, как уже неоднократно указывалось в предыдущих частях обзора, определяются характеристиками матрицы и оптики. Это те параметры, которые влияют на качество картинки в первую очередь. В последнее время стало модным гонятся за количеством пикселей в фотоаппарате и совсем не обращать внимания на физический размер матрицы. Это неправильно…

На первом месте должен стоять параметр — ФИЗИЧЕСКИЙ РАЗМЕР МАТРИЦЫ. Только от этого параметра и качества объектива зависят качества фотоаппарата и фотографий. Об этом много пишут, но не все читают специальную литературу. Я постараюсь очень коротко обобщить интернетовскую информацию по данному вопросу, а также сформулировать и пояснить основные понятия. Итак, матрица цифрового фотоаппарата состоит из множества отдельных светочувствительных элементов — пикселей, каждый такой элемент формирует одну точку на изображении. Чем больше разрешение матрицы, тем выше детализация получаемого снимка. Количество пикселей на матрице называется разрешением матрицы и измеряется в мегапикселях (миллионах пикселях). Каждый такой пиксель воспринимает свет и преобразует его в электрический заряд (чем ярче свет — тем сильней заряд). Если бы использовалась информация только о яркости света, то картинка получилась бы черно-белой. Чтобы она была цветной, ячейки покрывают цветными фильтрами, обычно это так называемые

RGB фильтры (Red – красный, Green – зеленый, Blue –синий).

Фильтр пропускает в ячейку лучи только своего цвета, поэтому каждый пиксель для процессора фотоаппарата имеет либо красный, либо зеленый, либо синий цвет и яркость этого цвета. Эти три цвета являются основными, а все остальные цвета получаются путем смешения основных. Процессор рассчитывает цвет каждого пикселя, анализируя информацию с соседних с ним пикселей. При этом сигнал с матрицы, для процессора будет выглядеть как сигнал от красных, зеленых и синих пикселей с различной яркостью. Таким образом, процессор формирует цифровое изображение. При печати изображения у пикселей появляется физический размер, и именно он и описывается разрешением при печати. Чем больше пикселей на дюйм (pixels per inch — ppi) будет на распечатке, тем менее заметными будут отдельные пиксели, и тем более реалистичным будет выглядеть отпечаток. Чем выше разрешение матрицы, тем более четкую и детализированную фотографию вы можете получить. Так же чем выше разрешение матрицы, тем большего размера фотографию вы можете напечатать без потери качества.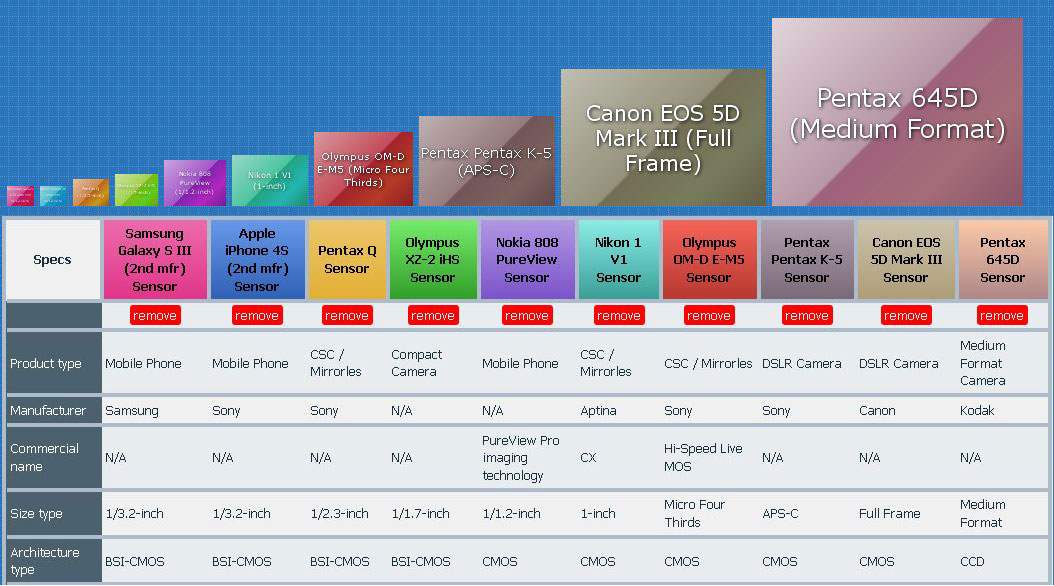

Для качественной печати фотографии 10х15 кв.см достаточно фотоаппарата с разрешением 2 Мпикс, для печати фото А4 – 10 Мпикс. Для демонстрации снимков на экране компьютера этого более чем достаточно, поэтому гнаться за большим числом мегапикселей не имеет особого смысла. Гораздо важнее обратить внимание на физический размер матрицы цифрового фотоаппарата. Практически все, кто только начинают пользоваться цифровыми фотоаппаратами либо даже и не слышали о таком понятии, как физический размер матрицы, либо слышали, но не понимают его значимости. А многие просто путают физический размер с разрешением. Однако, на самом деле, физический размер матрицы — это одна из важнейших характеристик, влияющих на качество получаемых фотографий. Ситуация осложняется и окончательно запутывается еще и потому, что вместо реальных геометрических размеров матрицы — длины и ширины в миллиметрах, в паспорте приводятся некие мифические цифры, о которых я упомянул выше и которые понять чрезвычайно сложно.

В Википедии есть хорошее описание размера матрицы.
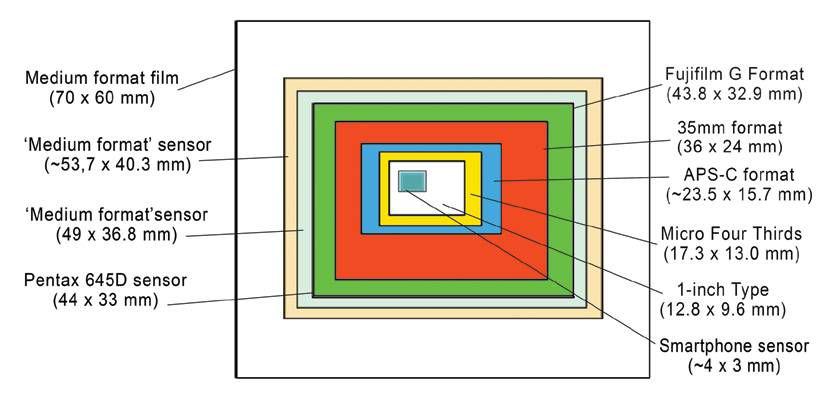
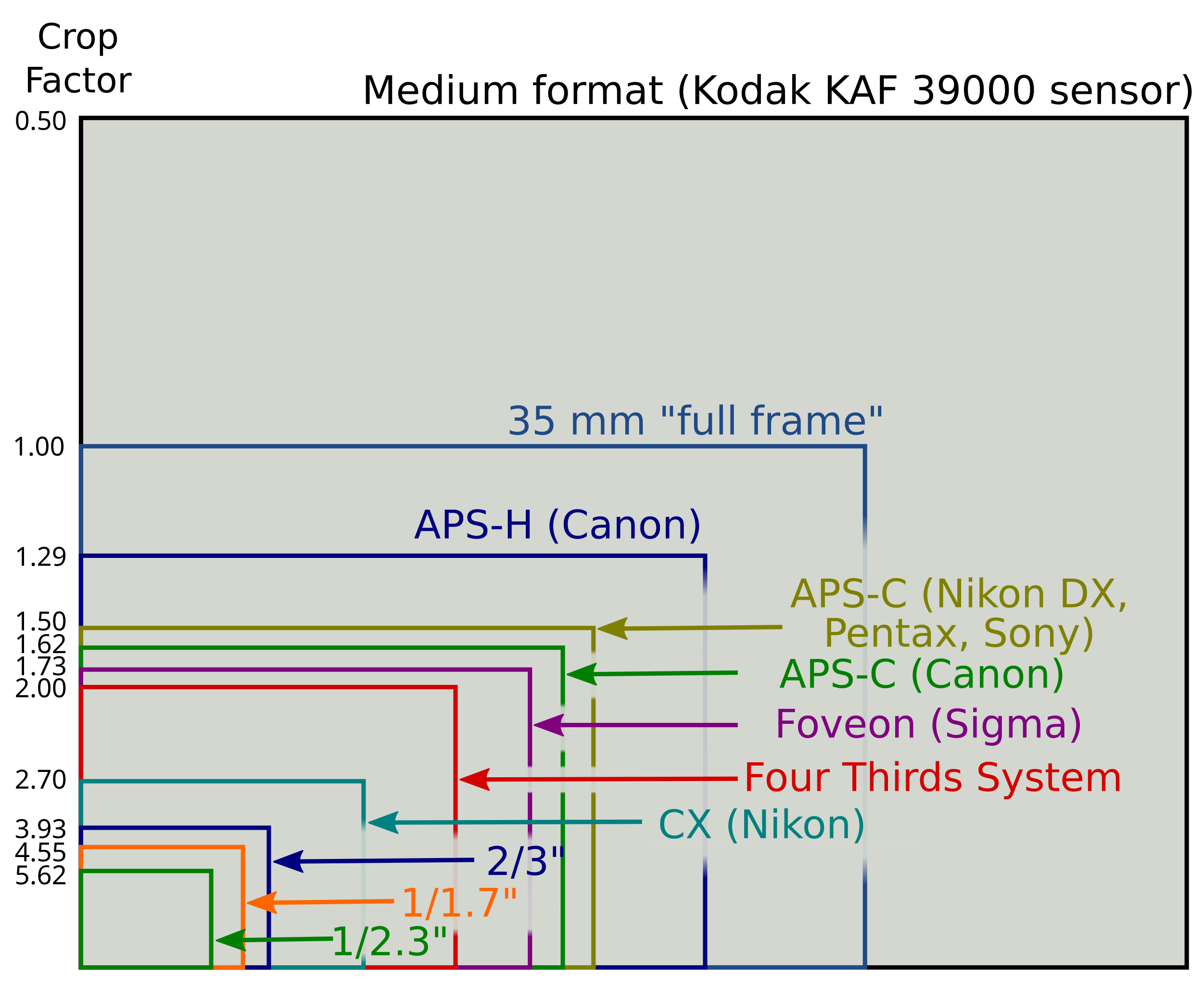
Размеры фотосенсоров чаще всего обозначают как “типоразмер” в виде дробных частей дюйма (например, 1/1.8″ или 2/3″), что фактически больше реального физического размера диагонали сенсора. Вот основные типоразмеры матриц, которые используются в цифровых камерах и вносятся в технический паспорт аппарата (в дюймах):

1 / 3.2 “; 1 / 2.7 “; 1 / 2,5″; 1 / 1,8″; 2 / 3″; APS-C

Эти обозначения происходят от стандартных обозначений размеров трубок телекамер в 1950-х годах. Они выражают не размер диагонали самой матрицы, а внешний размер колбы передающей трубки. Инженеры быстро установили, что по различным причинам диагональ полезной площади изображения составляет около двух третей диаметра трубки. Это определение стало устоявшимся (хотя и должно было быть давно отброшено). Не существует чёткой математической взаимосвязи между “типом” сенсора, выраженном в дюймах, и его фактической диагональю. Однако, в грубом приближении, можно считать, что диагональ матрицы составляет две трети типоразмера. Если добросовестно посчитать для каждого типоразмера сначала диагональ, а потом определить ее длину и ширину, и нарисовать основные типоразмеры матриц в реальном масштабе, то они будут выглядеть так:

На нижнем рисунке приведены реальные размеры матриц. Давайте теперь составим перечень матриц по типоразмерам:

Матрицы размера 1 / 3.2″ – самые маленькие матрицы, соотношение сторон 4:3, физический размер 3.4 х 4.5 кв.мм, используются в недорогих и компактных фотоаппаратах.
Матрицы размером 1 / 2.7″ , соотношение сторон 4:3, физический размер 4.0 х 5.4 кв.мм, используются в недорогих и компактных фотоаппаратах.
Матрицы размера 1 / 2,5″, соотношение сторон 4:3, то есть 4,3 х 5,8 кв.мм используются в большинстве компактных камер с несменной оптикой.
Матрицы размера 1 / 1,8″ , соотношение сторон 4:3, геометрический размер 5,3 х 7,2 кв. мм, используются в компактных камерах с несменной оптикой, среднего и выше среднего ценового диапазона (обычно в фотоаппаратах с разрешением от 8 Мпикс и более, но не обязательно).
Матрицы размера 2 / 3″ , соотношение сторон 4:3, физический размер 6,6 х 8,8 кв.мм иногда используются в дорогих компактных камерах с несменной оптикой.
Матрицы размера 4 / 3″ , физический размер 18 х 13,5 кв.мм, соотношение сторон 4:3, используются в дорогих камерах.
DX, APS-C формат, соотношение сторон 3:2, размер около 24 х 18 кв.мм. Матрицы таких размеров наиболее часто встречаются в цифровых зеркальных фотоаппаратах. Они соответствуют «полукадру» 35 мм кадра. Подавляющее большинство любительских, полупрофессиональных и даже профессиональных камер используют матрицы такого размера в силу того, что они относительно дёшевы в производстве и при этом размер пикселя остаётся довольно большим даже при 10 Мп разрешении.
Полнокадровая матрица размера 36 х 24 кв.мм, соотношение сторон 3:2, по размерам соответствующая классическому 35 мм кадру (3:2). На рынке представлено всего несколько моделей фотоаппаратов с матрицей такого размера. Такие матрицы дороги и сложны в производстве.

Самое высокое качество цифровых фотографий получается с матрицы размером 6х4,5 см. Это примерно 32-40 мегапикселей, а фотографии весят в среднем 160 мегабайт. Кстати, стоимость такой матрицы, без фотоаппарата, составляет 25 000 евро, а с аппаратом до 45 тысяч евро! Как видите, чем больше размер матрицы, тем меньшее увеличение необходимо для получения фотографии. Какое качество фотографии размером А-4 будет с каждой из этих матриц, как вы думаете? Возможно ли получить отличное качество большой фотографии с матрицы компакта размером с горошину, даже если производители пишут, что она размером в 12 мегапикселей? В то время как матрица в 12 мегапикселей у профессионального фотоаппарата имеет размер негатива фотопленки — 36мм x 24 мм, что в 1,5 раза больше матрицы APS-C и в 2 раза больше, чем матрица 4/3.

А теперь, когда мы выяснили основные физические размеры матриц, давайте поговорим о том, на что же эти размеры влияют.

Во-первых, размер матрицы влияет на размер и вес самой фотокамеры. Поскольку размеры оптической части линейно зависят от размера матрицы, то фотоаппарат с матрицей 1/1,8″ при прочих равных условиях будет больше по размеру, чем фотоаппарат с матрицей 1 / 2.7″ .

Во-вторых, размер матрицы влияет на количество цифрового шума, передаваемого вместе с основным сигналом на светочувствительные элементы матрицы.

Шумы могут возникать по множеству причин, это либо дефекты в структуре матрицы, либо токи утечки (заряд может пробивать изоляцию и переходить с одного пикселя на другой), так же шум возникает в результате нагрева матрицы (так называемый тепловой шум, когда при повышении температуры на 6-8 градусов шум увеличивается в 2 раза). Сам по себе показатель шума нет смысла рассматривать, о нем нужно говорить в соотношении сигнал/шум. Физический размер матрицы и размер каждого пикселя в отдельности значительно влияют на количество шумов. Чем больше физический размер матрицы, тем больше ее площадь и тем больше света на нее попадает, в результате чего полезный сигнал матрицы будет сильнее и соотношение сигнал/шум будет лучше. Это позволяет получать более яркую, качественную картинку с естественными цветами. Так же при большом размере каждого отдельного пикселя, слой изоляции, разделяющий пиксели друг от друга, толще и меньше зарядов ее пробивает, т.е. токов утечки меньше, а соответственно шумов меньше. Представьте, что на матрице одного и того же размера расположено либо 4 Мпикс, либо 8 Мпикс, и представьте толщину изоляции, которой они разделены друг от друга. Чем меньше пикселей приходится на единицу площади матрицы, тем лучше (выше реальная чувствительность, ниже уровень цветовых шумов, качественнее цветопередача). Кроме того, как уже было написано выше, матрица маленького размера из-за небольшого количества, попадающего на нее света, имеет слабый полезный сигнал, в результате его приходится сильнее усиливать, а вместе с полезным сигналом усиливаются и шумы, которые становятся более заметными.

Реальный размер матриц у современных аппаратов можно увидеть на странице Яндекс-маркет

Вывод

Следовательно, если вы хотите максимальное качество фотографий, покупаете фотоаппарат с максимально большой матрицей, насколько вам может позволить ваш бюджет. Поскольку физический размер матрицы напрямую связан с количеством попадающего на матрицу света, то чем матрица больше, тем качественней будут фотографии в условиях плохой освещенности. Однако, чудес не бывает, и увеличение размера матрицы неминуемо повлечет за собой увеличение размеров и стоимости фотоаппарата.

Теперь, я думаю, всем понятно, почему мыльницы с размером матрицы 5,27х3,96 кв.мм стоят намного дешевле, чем зеркалки с размером матрицы 15,1х22,7 кв.мм. Цена соответствует качеству.

Объектив.

И в заключение несколько слов об объективе. Во вторую очередь после матрицы качество снимка зависит от объектива. Объектив проецирует картинку на матрицу. Чем лучше объектив, тем четче и контрастнее будет картинка. Вот те параметры, которые должен иметь идеальный универсальный объектив.

1. Большой зум

2. Высокое качество картинки

3. Компактный размер

4. Низкая цена

К сожалению, идеальных объективов нет. Из этих четырех пунктов для реальных объективов в лучшем случае выполняются только три, а чаще 2. Одним словом, объектив не может быть компактным, светосильным, обладать супер-зумом и одновременно быть дешевым. Выбирайте, кому что больше нравится.

Чем больше светосила объектива, тем больше возможностей у фотографа снимать хорошие кадры без вспышки в режиме недостаточной освещенности. Со светосильным объективом нет необходимости применять вспышку, которая портит все, и нет необходимости увеличивать значение ISO матрицы, что всегда приводит к повышению шума уже при значении ISO -200 ед.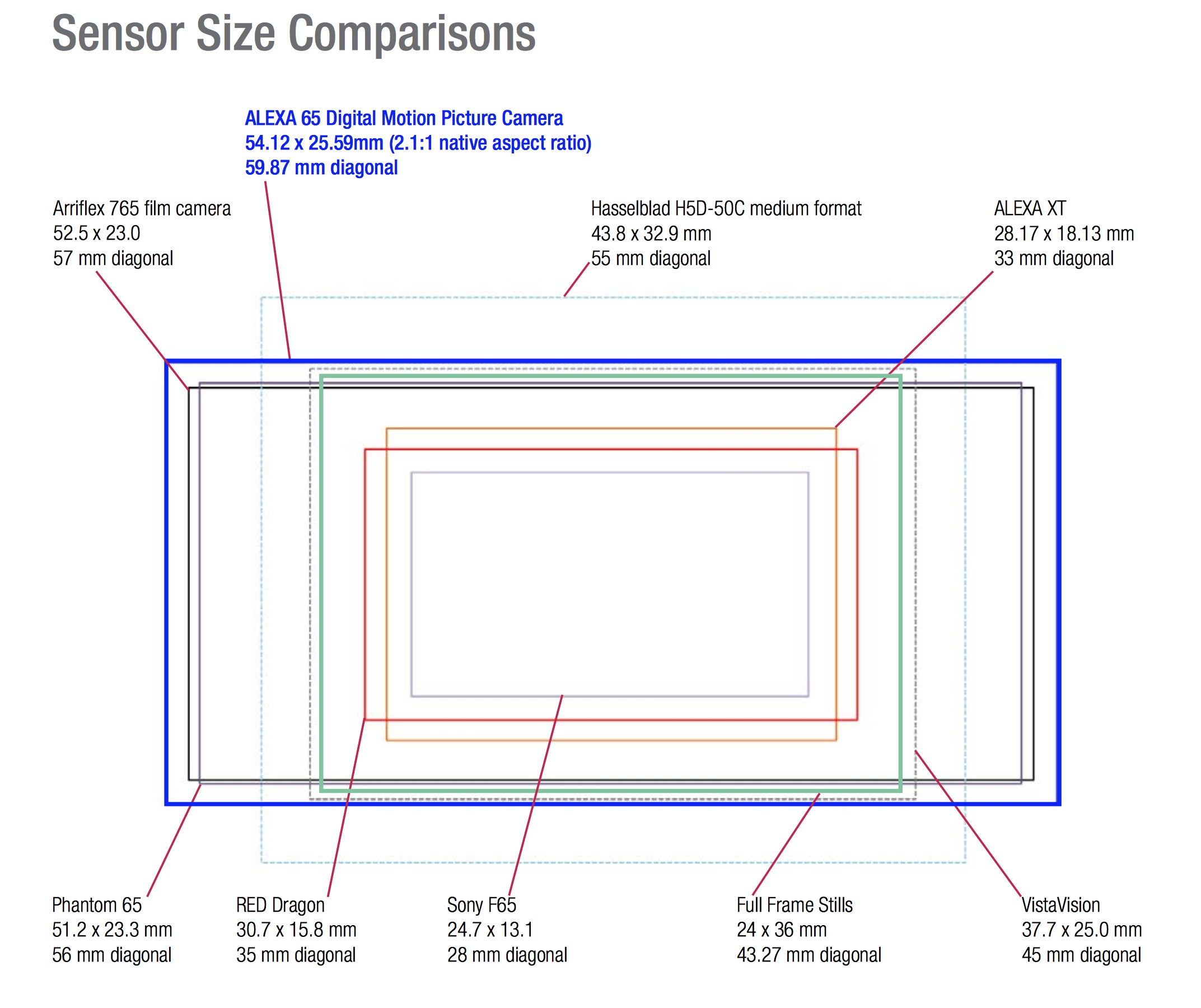

Диафрагма 1,8 – лучшее значение светосилы объектива компактного фотоаппарата.

Для зеркального фотоаппарата лучше купить объектив с максимальным значением диафрагмы 1,4.

Если вы хотите снимать репортаж, лучше купить объектив с переменным фокусным расстоянием – зум.

Если хотите делать фотографии высокого качества, выбирайте объективы с постоянным фокусным расстоянием.

Принимайте во внимание только оптическое значение увеличения фотоаппарата.

Фокусное расстояние. Чем меньше величина нижнего предела фокусного расстояния компактного фотоаппарата, тем лучше. Более широкоугольный в этом случае объектив позволит вам сделать более эффектные фотографии и снять всю вашу компанию в комнате. Обычный же объектив не позволит снять более трех человек.

Кстати! Новый объектив Nikon 50mm f/1.4G AF-S Nikkor будет работать с автофокусом и на дешевых зеркальных моделях Nikon.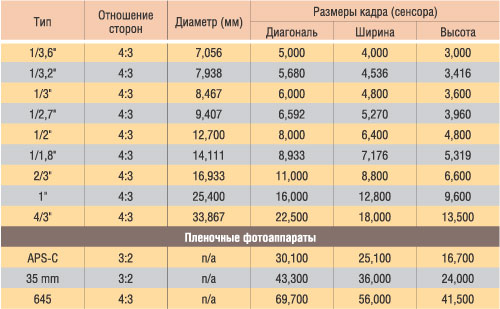

Удачного вам выбора и хороших покупок!

13.02.2014

Автор Михаил Назаров

♦ Рубрика: Фототехника.

Если вам понравилась наша статья, поделитесь, пожалуйста, ею с вашими друзьями в соц.сетях. Спасибо.

Матрица фотоаппарата ~ PhotoPoint

Матрица фотоаппарата, или как её еще называют фотоматрица, это микросхема, состоящая из фотодиодов (светочувствительных) элементов. Матрица используется во всех современных цифровых фокамерах и является одним из важнейших элементов. Её функцией заключается в преобразовании оптического изображения в поток цифровых данных.

В описании матрицы используется четыре основные характеристики:

Разрешение;
Светочувствительность;
Физический размер;
Соотношение сторон.

Ниже мы подробнее остановимся на каждой характеристики.

Разрешение матрицы фотоаппарата

Разрешение матрицы зависит от типа, плотности светочувствительных элементов и физического размера. В фотоматрицах разрешающая способность определяется размером пикселя. Размер пикселя может меняться в пределах 0,0025-0,0080 мм. Два пикселя отличаются друг от друга, когда между ними располагается третий, незасвеченный пиксель. В этом случае разрешающая способность соответствует расстоянию в два пикселя. В большинстве современных фотоаппаратов используются матрицы с разрешающей способностью 70-200 линий на миллиметр. 200 линий на миллиметр в матрицах крупноформатных зеркальных фотоаппаратов, а 70 в камерах мобильных телефонов и веб-камерах.

Светочувствительность фотоаппарата

Эта характеристика фотоаппарата определяет числовую зависимость параметров созданного изображения от экспозиции. Светочувствительность камеры измеряется в единицах ISO. Увеличение значения чувствительности влияет на увеличение цифрового шума в изображении. Использование больших значений ISO применяется при съемке в плохоосвещенных помещениях и в сумерках, когда важно снимать с быстрой выдержкой.

Физический размер матрицы фотоаппарата

Сравнение размеров матриц фирмы Nikon.

Слева на право — Nikon Coolpix P500 (размер 1/2,3 дюйм, разрешение 12,1 Мп), Nikon 1 J2 (размер 1 дюйм, разрешение 10,1 Мп), Nikon D3100 (размер APS-C, разрешение 14,2 Мп), Nikon D4 (полнокадровый размер, разрешение 16,2 Мп)

Физический размер матрицы определяется размером пикселя. Известно что, чем больше пиксель, тем больше света он собирает. Количество света попавшего на сенсор камеры влияет на производительность фотоаппарата и качество создаваемых им фотографий.

Размер матрицы имеет прямую зависимость с ГРИП. Фотоаппараты с наибольшей матрицей имеют наименьшую ГРИП, то есть объекты вне фокуса будут сильно размыты. У камер с маленькой матрицей на снимках ГРИП будет наибольшей, это значит, что объекты вне фокуса будут четкими.

Соотношение сторон матрицы фотоаппарата

Отношение сторон не имеет существенного влияния на качество фотографий, но является одним из критериев в описании матрицы:

Формат кадра 4:3 применяется в любительских цифровых фотоаппаратах;
Формат кадра 3:2 используется в зеркальных фотокамерах;
Есть модели, в которых применяется формат 16:9.

Заключение

Есть неправильный стереотип, что разрешение матрицы влияет на качество фотографий. Еще несколько лет назад наблюдалась так называемая мегапиксельная гонка, когда производители создавали камеры с большим разрешением. Этот маркетинговый ход привлекал клиентов, но по факту оказывалось, что мыльница с разрешение 10,0 Мп снимала более качественные снимки чем модель того же уровня с разрешением 16,0 Мп.

Существенное влияние на качество фотографий и видео имеет физический размер пикселя и матрицы, но никак не разрешение. Покупая недорогой компактный фотоаппарат учитывайте не столько разрешение матрицы, а его соотношение к размеру. Как известно, полнокадровые фотоаппараты (матрица соответствует формату пленки 35 мм) создают наиболее привлекательные изображения именно благодаря величине сенсора.

пикселей и таблицы цветов

Цифровая обработка изображений

Оцифровка изображения приводит к формированию элементов изображения, обычно называемых пикселей

Большинство систем визуализации имеют аналого-цифровые преобразователи (АЦП), которые принимают данные, полученные от ФЭУ, а затем оцифровывают информацию в матрицу с координатами X и Y
Чем больше пикселей в изображении, тем выше разрешение.
В ядерной медицине ключевым фактором лучшего разрешения является количество пикселей в изображении.
Размер матрицы определяет количество пикселей в изображении.Чтобы упростить это обсуждение, давайте посмотрим на матрицу 3 x 3, содержащую 9 пикселей

Вышеупомянутая матрица показывает значение счетчика в каждой ячейке, замечающее, что оно уменьшается в порядке убывания, при этом нижний правый угол содержит 50 пунктов, а верхний левый — 0 пунктов.

Это изменение количества отсчетов показывает изменение серой шкалы, где увеличение оттенков серого относится к уменьшению количества отсчетов

Шкала серого имеет 256 оттенков (2 ⁸) серого, что соответствует количеству отсчетов в изображении
При отображении счетчиков, полученных в результате сбора данных, компьютер применяет справочную таблицу (LUT), которая назначает количество / пиксель с координатами XY
С учетом указанной выше шкалы серого пиксель (пиксели) с максимальным количеством отсчетов является белым (или чистым), а пиксели с наименьшим количеством отсчетов — черными
Серая шкала также может быть инвертирована, когда самый горячий пиксель становится черным, а белый цвет означает отсутствие подсчета. Это называется обратным видео

LUT также может быть назначена многим типам цветовых шкал, которые могут дополнительно улучшить отображаемые данные и могут улучшить диагностическое качество исследования.
1. Комбинации LUT используют до трех основных цветов: R ed, G reen и B lue (помните ограбление?)
2. Смешивание цветов увеличивает разницу между количеством отсчетов в пикселях и количеством цветовых оттенков на отсчет (а)
3. Это дополнительно увеличивает возможность обнаружения незначительных изменений в счетах при использовании всех трех основных цветов.Согласно Perigees, можно использовать 262000 оттенков или комбинаций, однако, если каждый цвет представляет 2 ⁸ оттенков, тогда имеется 2 ⁸ x 2 ⁸ x 2 ⁸ = 1,67 x 10 ⁷ (красный, зеленый, и синий) комбинации
4. Пример того, как разные цветовые шкалы влияют на то, как мы визуально видим сканирование костей
Какие детали мы действительно видим?

В отношении оттенков серого человеческий глаз может видеть только изменение яркости примерно на 2%. Следовательно, учитывая 256 оттенков серого, требуется 5 оттенков в любом направлении, чтобы реализовать небольшое изменение шкалы
Человеческий глаз может видеть более 1 миллиона типов цветов, поэтому глаз более «чувствителен» к трехцветной шкале
Однако человеческий глаз более чувствителен к зеленому и желтому по сравнению с синим и красным
Понимая «ограниченное» разрешение наших шлюх и НМ, можно сказать, что незначительные изменения в количестве отсчетов на пиксель могут быть не видны.
Проверьте нашу способность видеть незначительные изменения цвета (оттенка).Всего 4 ряда. Первый и последний блоки в каждой строке нельзя перемещать. Расставьте поля в ряду, чтобы они соответствовали тонким изменениям цвета. Нажмите Test
Вот множество примеров LUT, используемых в ядерной медицине и диагностической радиологии. Щелкните изображение для увеличения

Глядя на ядерную кардиологию с отображением LUT, какую шкалу вы бы выбрали?

Размер матрицы — с плоской точки зрения (двухмерные изображения)

Размер пикселя
1. Определение размера пикселя указано выше для матрицы 128 и камеры размером 15 квадратных дюймов
2. Эта информация полезна не только для оценки разрешения, но и для возможности измерить размер поражения, зная количество пикселей, которые оно покрывает
Размеры матрицы ядерной медицины различаются и составляют:

32 x 32 (исследование потока)
64 x64 (исследование потока)
128 x 128 (потоковые или статические изображения)
256 x 256 (статические изображения)
512 x 512 (статические изображения)
256 x 1024 (сканирование всего тела)
512 x 1048 (сканирование всего тела)

Возникает вопрос: какая матрица лучше всего подходит для конкретной процедуры? Хотя примеры приведены выше, все же есть некоторые различия в различных вариантах выбора
При обдумывании матрицы необходимо учитывать количество приобретаемых отсчетов
Другой проблемой, вызывающей беспокойство, является режим байта и слова пикселя.
1. Рассмотрим 16 бит = 2 байта = 8 = 1 слово.Сколько отсчетов может вместить пиксель?
2. Если размер матрицы составляет 128 x 128 x 1 байт, это означает, что каждый пиксель может содержать 2 ⁸ отсчетов или до 256 отсчетов. Сколько там пикселей?
3. Что произойдет, если пиксель станет насыщенным или количество отсчетов превысит 256?
  1. Изображение перестает копироваться (это мой личный опыт) или
  2. Пиксель перестает получать, но остальная часть системы продолжает считать или
  3. Количество отсчетов в насыщенном пикселе возвращается и начинается снова с нуля и снова увеличивается
4. Пиксель также может быть в текстовом режиме, что соответствует 2 ⁸ x 2 ⁸ = 65.5 тыс. Отсчетов на пиксель. Шансы на насыщение пикселей практически отсутствуют. Большинство современных фотоаппаратов имеют возможность собирать в текстовом режиме
5. Вот пример того, как на разрешение влияют размер матрицы и глубина
Эффект частичного объема (PVE) ¹

Это лучше всего можно объяснить, посмотрев на край круга (вверху), где только часть пикселя собирает значения
Результат — потеря счета на краю получения изображения
На данном экзамене фактическое изображение круглое, но пиксели квадратные.
1. Это означает, что определенные области цилиндра собирают меньше отсчетов на основании того факта, что только часть пикселя собирает данные
2. Активность перетекает из цилиндра в частичный пиксель (пиксели)
3. Аналогичным образом активность также распространяется на пиксели, находящиеся за пределами цилиндра, области фона
Чистый результат обозначается как PVE
Вот как PVE может действительно сбить с толку полученные данные.На приведенном выше изображении ПЭТ-сканирование определяет опухоль, которая может прикрепляться или не прикрепляться к грудной стенке. КТ показывает, что это не часть стены, а объединенная ПЭТ / КТ-сканирование помогает врачу свести на нет эффект ПВЭ. Другой интересный момент заключается в том, что матрица для приведенного выше изображения в ПЭТ составляет 128, тогда как изображение КТ имеет матрицу 512

Размер матрицы и статистический шум

Предположим, вы собрали 1 миллион счетчиков за одно наводнение.Что такое процентный коэффициент вариации?
Что произойдет с резюме, если вы соберете такое же количество отсчетов в матрице 256?
Сколько отсчетов нужно сделать в 256-м матричном порядке, чтобы иметь такое же изменение, что и в 128-м?
Слишком много ошибок ~ шума вызывают проблемы с качеством изображения?

Регулировка изображения и дисплеи

Изображения можно настраивать в различных форматах — вверху графический дисплей, внизу — визуальные результаты
1. Необработанные данные отображаются на линейной кривой по мере увеличения числа, так же как и шкала серого
2. В изображении с большим количеством элементов может быть выполнена логарифмическая корректировка, которая увеличивает количество пикселей с низким количеством пикселей, в то время как пиксели с большим количеством пикселей имеют меньшую вариацию
3. При экспоненциальной регулировке пиксели с меньшим количеством изменяются незначительно, однако пиксели с большим количеством пикселей показывают большее изменение серого
4. Вычитание фона дает каждому пикселю один и тот же серый цвет (ноль), пока кривая не начнет подниматься
5. Повышение контрастности дает значение самого горячего пикселя для всех пикселей на плато, где изменение серого происходит по мере того, как кривая начинает опускаться
6. Вот что на самом деле делают с изображением различные настройки.На крайнем левом изображении , а не , корректировка
7. Изображения можно корректировать с помощью различных типов фильтров
Свернутое ядро (термин, используемый при фильтрации изображения)

Первый взгляд на сглаживающий фильтр
Компоненты — необработанные данные + свернутый фильтр = вывод измененных подсчетов. Другими словами, необработанные данные обрабатываются путем добавления мини-матрицы (свернутое ядро) с числовым значением, которое в той или иной форме изменяет исходную матрицу
Свернутое ядро умножает каждый пиксель на 1, а затем делит центральный пиксель на 9
Эта операция выполняется для каждого пикселя в исходной матрице (необработанные данные)

http: // www.slideshare.net/brucelee55/processing-methods-of-nuclear-medicine-images

Выше результаты сглаживающего фильтра

Фильтр улучшения края (ядро)

В варианте фильтрации взвешенное ядро, как показано выше, имеет разные значения в своей мини-матрице, которая изменяет необработанные данные совершенно другим способом
Обратите внимание, что центральный пиксель в ядре — единственное положительное значение, все остальные отрицательные
В результате пиксели с большим количеством пикселей значительно улучшаются.

Фильтрация нашла множество применений в ядерной медицине, а также в других областях цифровой обработки изображений.В Wiki есть интересная ссылка, касающаяся многих типов приложений-фильтров и запутанных ядер, которые идут с ними.

Разрешение

Размер

Для определения разрешения вы должны сначала определить зону сбора данных или размер головки детектора.
Если область изображения составляет 400 мм и вы используете матрицу 32 x 32, каков размер каждого пикселя?

Это можно рассчитать следующим образом: 400 мм / 32 пикселя = 12.5 мм или 1,25 см / пиксель
Это означает, что каждый пиксель соответствует размеру 1,25 см.
Если размер области с дефицитом фотонов составляет 3,0 см, то гипотетически вы должны иметь возможность разрешить ее, поскольку размер вашего пикселя меньше, чем область с недостаточным количеством отсчетов
Однако, если область дефицита фотонов была размером 6 мм, вы ее пропустите, потому что процесс болезни меньше, чем разрешение системы
Следовательно, увеличение размера матрицы становится критичным для разрешения меньшей области (холодной или горячей)

Разрешение и 64 x 64 при условии, что область изображения 400 мм x 400 мм

400 мм / 64 = 6.25 мм / пиксель
На этом этапе способность визуализировать холодное пятно размером 6 мм почти не отличается от пикселя
На самом деле вам следует применить матрицу 128 x 128, чтобы вы могли еще больше улучшить свое разрешение. Это дает размер пикселя 3,25 мм
Примечание: та же логика, описанная выше, может применяться, если в рассматриваемой области жарко или холодно.

Подробнее о размере матрицы

Каждый раз, когда вы увеличиваете матрицу, вы увеличиваете необходимое пространство для хранения на жестком диске.Время обработки также увеличивается в 4 900 10 раз.
Ключевой момент — Определение наилучшего разрешения изображения для системы

Как указано в ваших материалах для чтения, типичный размер детектора может быть 15 x 20 дюймов или 400 x 500 мм.
Использование коллиматора LEHR, который может разрешить объект диаметром 8 мм на глубине 10 см (это означает, что FWHM составляет 8 мм)
Гипотетически предлагается уменьшить количество мм / пиксель до разрешающей способности системы.
Однако разрешение выборки определило, что требуется втрое больше
Итак, если FWHM составляет 8 мм, то мм / пиксель должно быть 8 мм / 3 = 2.7

Если используется матрица 128, какой мм / пиксель? 500 мм (детектор) / 128 (матрица) = 3,9 мм / пиксель. Технически это недостаточно
Рекомендуется использовать матрицу 256 500 мм / 256 = 2,0 мм / пиксель
Следовательно, матрица 256 x 256 — это то, что необходимо для разрешения до 8-миллиметрового объекта. Какой размер пикселя?

Домашнее задание: пиксели и разрешение — это задание использует вышеуказанные данные для определения разрешения системы.

Режимы получения цифровых изображений
1. Режим кадра
  1. Считайте это статическим режимом, в котором счетчики адресованы координате пикселя XY в матрице
  2. Во время получения изображение сохраняется в буфере изображений, а затем сохраняется после остановки получения на жестком диске
  3. В динамическом режиме компьютер обычно имеет два буфера изображений, в которых счетчики регистрируются в первом, затем, когда время на каждый кадр заканчивается, полученное изображение сохраняется, в то время как следующее полученное изображение продолжается с буфером №2.
    1. Размер матрицы также важен, поскольку для хранения матрицы большего размера потребуется больше времени.
    2. Следовательно, динамические изображения обычно получаются в матрице 64
    3. Сбалансируйте концепции — динамическое изображение, количество отсчетов и размер матрицы
2. Режим стробированного кадра
  1. В этом случае количество буферов равно количеству собираемых кадров
  2. Состояние кадра запускается зубцом R и собирается за очень короткий период времени
  3. Каждый зубец R запускает состояние кадра, и счетчики собираются до тех пор, пока не будет достигнут определенный уровень
  4. Если есть вариации в частоте пульса, то обычно в конечных кадрах не будет активности в конце зубца R, что приведет к эффекту мигания.
  5. Стробированные исследования могут быть настроены на отклонение нерегулярных сокращений, и когда это происходит, буферы возвращаются к нулевым счетам, ожидая следующего хорошего зубца R
3. Режим списка
  1. Это не помещает счетчики в буфер, а вместо этого сохраняет все счетчики с местоположением XY и сохраняет их индивидуально
  2. Хорошим примером, где это может быть применено, является кардиостробирование, когда каждый кадр собирается индивидуально
  3. Если применяется, все подсчеты, положения XY, с каждым зубцом R.Затем технолог выбирает, какие зубцы R являются приемлемыми, составляя правильный сердечный цикл. Это те, у которых есть нормальные сокращения
  4. Этот вид приобретения используется редко
4. Цифровой зум (после или до)
  1. В этом случае масштабирование после получения изображения
    1. Если вы получили в матрице 128, а затем увеличили изображение в 2 раза, в результате вы получите изображение, которое теперь было в матрице 64
    2. Результат в потере разрешения
  2. Масштабирование перед захватом улучшает разрешение
    1. Считайте, что получаемая матрица 128 имеет увеличение x2.По сравнению с обычным масштабированием, предварительное масштабирование отображает 1/2 области изображения с тем же количеством пикселей
    2. Это улучшает разрешение
Устройства отображения
1. Существует множество типов дисплеев, о которых вы можете прочитать в своей книге
2. Ключевые моменты, о которых следует помнить:
  1. Разрешение ядерной медицины ограничено
  2. Разрешение устройства отображения должно быть не ниже разрешения изображения

Вернуться к началу документа
Вернуться к оглавлению

2/18

1.Эффект частичного объема в визуализации опухоли с помощью ПЭТ. Авторы M Soret, L Stephen, JNMT, Vol.48 # 66/07
2. Свертка изображений. Автор Людвиг, Портлендский государственный университет,

Модель проекционной камеры

| imatest

Не рекомендуется в текущей версии

Модель проекционной камеры описывает математику преобразования мировой точки в точку изображения. Это делается с помощью модели камеры с отверстиями.Вместе с моделью искажения, которая характеризует отклонение от модели точечного отверстия, этим методом можно моделировать большинство камер *.

Модель проекционной камеры учитывает только взаимосвязь между мировыми координатами и координатами изображения. Он не учитывает другие факторы, такие как функция передачи модуляции (MTF), оптические аберрации (например, хроматические аберрации, кома и т. Д.), Линейность и воспроизведение цвета, которые могут повлиять на качество изображения. \ top \) с точки зрения \ (j \) -й камеры (или создание камеры).j \ left (\ mathbf {X} _ {i} \ right) \)

Существует три компонента для применения модели проективного преобразования: внешние элементы, модель камеры-точечного отверстия и искажение точек для учета разницы между встроенной камерой и моделью-крошечным отверстием.

Проекция трехмерных точек в модели камеры-обскуры.

Изображение проецируемых точек.

Внутренние функции камеры описывают свойства модели камеры-обскуры, которые связывают относительные мировые координаты камеры относительно камеры с координатами изображения.В модели крошечного отверстия лучи проходят по прямой линии от объекта в сцене через крошечное отверстие к фокальной плоскости. Геометрия этого подобна треугольникам, связывающим мировые координаты с координатами изображения. Математическая модель для этого использует 5 параметров: фокусное расстояние в направлениях x и y, основная точка в направлениях x и y и перекос между направлениями x и y.

Параметры

Фокусное расстояние

В модели точечного отверстия фокусное расстояние, \ (f \) — это расстояние от точечного отверстия до фокальной плоскости вдоль оптической оси.Системы с большим фокусным расстоянием будут иметь большее увеличение в более узком поле зрения (FOV), тогда как меньшие фокусные расстояния будут иметь больший охват.

Возможно иметь разное фокусное расстояние вдоль каждого направления фокальной плоскости. В этом случае фокусное расстояние оси \ (y \) изменяется на \ (\ alpha \).

\ (f_y = \ alpha \ cdot f \)

Для настоящей камеры-обскуры \ (f_x = f_y \) (\ (\ alpha = 1 \)), однако на практике это может быть связано с факторами, включая производственные дефекты, искажение объектива и изображения, полученные с помощью системы сканирования.Интерпретация неравных фокусных расстояний заключается в том, что эффективная форма пикселя не является квадратной.

Принцип действия

Точка \ ((pp_x, pp_y) \) — это основная точка, которая представляет собой пиксельную координату пересечения оптической оси с фокальной плоскостью. Функция сдвига наклона-сдвига перемещает фокальную плоскость (и главную точку) вокруг оптической оси.

перекос

Фактор перекоса \ (s \) вводит сдвиговое преобразование изображения.Для многих камер это 0. Случаи, когда он не равен нулю, включают фотографирование изображения (введение гомографии) и несинхронизацию процесса выборки пикселей из устройства захвата кадра. Ненулевой перекос означает, что оси x и y камеры не перпендикулярны друг другу.

Внутренняя матрица

Внутренняя матрица, \ (\ mathbf {K} \) — это верхнетреугольная матрица, которая преобразует мировую координату относительно камеры в координату однородного изображения. Существует две общие и эквивалентные формы внутренней матрицы:

\ (\ mathbf {K} = \ begin {bmatrix} f & s & pp_x \\ 0 & f \ cdot \ alpha & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \)

\ (\ mathbf {K} = \ begin {bmatrix} f_x & s & pp_x \\ 0 & f_y & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \)

Многие камеры могут быть представлены с более простой внутренней матрицей. \ top \) будет точкой относительно камеры.Предположим, что

\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ begin {bmatrix} f & 0 & pp_x \\ 0 & f & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \ begin {bmatrix} X \\ Y \\ Z \ end {bmatrix} \)

\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ begin {bmatrix} f \ cdot X + pp_x \ cdot Z \\ f \ cdot Y + pp_y \ cdot Z \\ Z \ конец {bmatrix} \)

После преобразования в неоднородные координаты

\ (\ begin {bmatrix} x ‘\\ y’ \ end {bmatrix} = \ begin {bmatrix} \ displaystyle \ frac {f \ cdot X + pp_x \ cdot Z} {Z} \\ \ displaystyle \ frac { е \ cdot Y + pp_y \ cdot Z} {Z} \ end {bmatrix} = \ begin {bmatrix} f \ cdot \ displaystyle \ frac {X} {Z} + pp_x \\ f \ cdot \ displaystyle \ frac {Y } {Z} + pp_y \ end {bmatrix} \)

Проверка этого результата показывает, что расстояние от оптической оси (основной точки) пропорционально отношению расстояния мировых точек от оптической оси к расстоянию до камеры.Это означает, что точка, которая вдвое дальше от оптической оси и вдвое дальше от камеры, будет соответствовать той же точке изображения. Лучшая реконструкция точки с помощью одной камеры состоит в том, что точка находится где-то на линии.

шт.

Все эти значения вычисляются в единицах количества пикселей. Шаг пикселя \ (p \) используется для преобразования количества пикселей в физические единицы. Например:

\ (f [\ mathrm {mm}] = f [\ mathrm {пикселей}] \ cdot p \ left [\ frac {\ mu \ mathrm {m}} {\ mathrm {pixel}} \ right] \ cdot \ гидроразрыв {1 [\ mathrm {mm}]} {1000 [\ mu \ mathrm {m}]} \)

Обратный

Инверсия внутренней матрицы камеры используется для преобразования неискаженных точек изображения в линии от центра камеры.{-1} = \ displaystyle \ frac {1} {f} \ begin {bmatrix} 1 & 0 & -pp_x \\ 0 & 1 & -pp_y \\ 0 & 0 & f \ end {bmatrix} \)

Модель искажения камеры описывает отклонение физической камеры от модели проекционной камеры. Он преобразует неискаженные точки 2D-изображения в точки искаженного 2D-изображения (те, которые находятся за пределами камеры). Модель обратной дисторсии преобразует точки искаженного изображения в неискаженные.

Внешние элементы камеры описывают положение и ориентацию камеры в мире.Существует два способа описания преобразования координат между мировыми координатами и координатами относительно камеры: преобразование точки и преобразование осей (поза). Они оба имеют одинаковую форму матрицы вращения / переноса и являются противоположными друг другу.

Центр камеры соответствует расположению входного зрачка камеры. В панорамной фотографии это часто называют точкой отсутствия параллакса. Камеры с большим полем зрения (например, камеры «рыбий глаз») будут иметь разные положения входного зрачка при разных углах поля зрения.Для этих камер используется осевое расположение входного зрачка.

Преобразование точки

Описание преобразования точки преобразует мировую точку в точку относительно камеры. Его матрица вращения / переноса прямо умножается вправо на внутреннюю матрицу для формирования матрицы камеры.

\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right] \ left [\ begin {array} {ccc | c} &&& \\ & \ mathbf {R} && \ mathbf {t} \\ &&& \ end {array} \ right] \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ end {bmatrix} \)

В обозначении точечного преобразования камера расположена в \ (- \ mathbf {R} ^ \ top \ mathbf {t} \). {\ top} \ mathbf {t} \\ &&& \ end {array} \ right] \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ end {bmatrix} \)

В обозначении позы камеры центр камеры расположен в \ (\ mathbf {t} \).

Матрица камеры, \ (\ mathbf {P} \), представляет собой комбинацию внутренней матрицы камеры и точечного преобразования.

\ (\ mathbf {P} = \ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right] \ left [\ begin {array} { ccc | c} &&& \\ & \ mathbf {R} && \ mathbf {t} \\ &&& \ end {array} \ right] \)

Матрица камеры преобразует точки мира в координаты однородного изображения.

Мировые точки к точкам изображения

Преобразует мировую координату в координату относительно камеры путем умножения на мировую точку в преобразование точки изображения.Это преобразование является обратной позе.
Примените внутреннюю матрицу камеры к относительной координате камеры, чтобы получить однородную координату изображения.
Преобразует однородную координату изображения в неоднородную координату.
Примените модель искажения, чтобы определить положение изображения мировой точки на фокальной плоскости.

Обозначение преобразования точек

\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ underbrace {\ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right]} _ {\ mathrm {intrinics}} \ underbrace {\ left [\ begin {array} {ccc | c} &&& \\ & \ mathbf {R} && \ mathbf {t} \\ &&& \ конец {массив} \ right]} _ {\ mathrm {обратная \ поза}} \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ end {bmatrix} \)

\ (\ begin {bmatrix} x ‘\\ y’ \ end {bmatrix} = \ begin {bmatrix} \ mathrm {distort} _ {x} \! \! \ Left (\ displaystyle \ frac {x} {w } \ right) \\\ mathrm {искажать} _ {y} \! \! \ left (\ displaystyle \ frac {y} {w} \ right) \ end {bmatrix} \)

Обозначение преобразования осей

\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ underbrace {\ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right]} _ {\ mathrm {intrinics}} \ underbrace {\ left [\ begin {array} {ccc | c} &&& \\ & \ mathbf {R} ^ {\ top} && — \ mathbf { R} ^ {\ top} \ mathbf {t} \\ &&& \ end {array} \ right]} _ {\ mathrm {inverse \ pose}} \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ конец {bmatrix} \)

Изображение указывает на линии

Примените модель обратной дисторсии, чтобы неискажать точки изображения.Это помещает их в геометрию камеры-обскуры.
Преобразует координату изображения в однородную координату с весом \ (w \). Можно использовать любое действительное, отличное от нуля \ (w \), однако два общих из них — это 1 или расстояние от центра камеры до мировой точки.
Умножьте координату однородного изображения на значение, обратное внутренней матрице камеры. Этот вектор является вектором направления линии между точкой и центром камеры в координатах относительно камеры.

Примените поворот позы камеры (обратный матрице точечного преобразования) к вектору направления.\ top \ right | \ right | \) — расстояние от центра камеры (расположение входного зрачка) до мировой точки.

Калибровка камеры и трехмерная реконструкция

6tray (6) 906tray (906) ), перенос (и) и нормаль (и) плоскости. Подробнее …
Chess. Подробнее …
906 906 906 капли (крапинки) на карте несоответствия. Более…
906Подробнее …
6 906 центры в сетке кругов. Подробнее …
9026 906

Функции в этом разделе используют так называемую модель камеры-обскуры.В этой модели вид сцены формируется путем проецирования трехмерных точек на плоскость изображения с использованием преобразования перспективы.

\ [s \ vecthree {u} {v} {1} = \ vecthreethree {f_x} {0} {c_x} {0} {f_y} {c_y} {0} {0} {1} \ begin {bmatrix} r_ {11} & r_ {12} & r_ {13} & t_1 \\ r_ {21} & r_ {22} & r_ {23} & t_2 \\ r_ {31} & r_ {32} & r_ {33} & t_3 \ end {bmatrix} \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ end {bmatrix} \]

Таким образом, если изображение с камеры масштабируется с коэффициентом, все эти параметры должны быть масштабированы (умножены / разделены, соответственно) с одинаковым коэффициентом.Матрица внутренних параметров не зависит от просматриваемой сцены. Таким образом, после оценки его можно использовать повторно при фиксированном фокусном расстоянии (в случае зум-объектива). 2 \\ u = f_x * x » + c_x \\ v = f_y * y » + c_y \ end {множество}\]

\ (k_1 \), \ (k_2 \), \ (k_3 \), \ (k_4 \), \ (k_5 \) и \ (k_6 \) — коэффициенты радиального искажения.\ (p_1 \) и \ (p_2 \) — коэффициенты тангенциального искажения. \ (s_1 \), \ (s_2 \), \ (s_3 \) и \ (s_4 \) — коэффициенты искажения тонкой призмы. Коэффициенты более высокого порядка не рассматриваются в OpenCV.

На следующем рисунке показаны два распространенных типа радиального искажения: бочкообразное искажение (обычно \ (k_1> 0 \) и подушкообразное искажение (обычно \ (k_1 <0 \)).

В некоторых случаях датчик изображения может быть наклонен в чтобы сфокусировать наклонную плоскость перед камерой (условие Шеймпфуга).Это может быть полезно для измерения скорости изображения частиц (PIV) или триангуляции с помощью лазерного вентилятора. Наклон вызывает искажение перспективы \ (x » \) и \ (y » \). Это искажение можно смоделировать следующим образом, см., Например, [106].

\ [\ begin {array} {l} s \ vecthree {x » ‘} {y’ »} {1} = \ vecthreethree {R_ {33} (\ tau_x, \ tau_y)} {0} {- R_ {13} (\ tau_x, \ tau_y)} {0} {R_ {33} (\ tau_x, \ tau_y)} {- R_ {23} (\ tau_x, \ tau_y)} {0} {0} {1} R (\ tau_x, \ tau_y) \ vecthree {x »} {y »} {1} \\ u = f_x * x » ‘+ c_x \\ v = f_y * y’ » + c_y \ end { множество}\]

, где матрица \ (R (\ tau_x, \ tau_y) \) определяется двумя поворотами с угловым параметром \ (\ tau_x \) и \ (\ tau_y \), соответственно,

\ [R (\ tau_x, \ tau_y) = \ vecthreethree {\ cos (\ tau_y)} {0} {- \ sin (\ tau_y)} {0} {1} {0} {\ sin (\ tau_y)} {0} {\ cos (\ tau_y)} \ vecthreethree {1} {0} {0} {0} {\ cos (\ tau_x)} {\ sin (\ tau_x)} {0} {- \ sin (\ tau_x)} {\ cos (\ tau_x)} = \ vecthreethree {\ cos (\ tau_y)} {\ sin (\ tau_y) \ sin (\ tau_x)} {- \ sin (\ tau_y) \ cos (\ tau_x) } {0} {\ cos (\ tau_x)} {\ sin (\ tau_x)} {\ sin (\ tau_y)} {- \ cos (\ tau_y) \ sin (\ tau_x)} {\ cos (\ tau_y) \ cos (\ tau_x)}.\]

\ [(k_1, k_2, p_1, p_2 [, k_3 [, k_4, k_5, k_6 [, s_1, s_2, s_3, s_4 [, \ tau_x, \ tau_y]]]]) \]

вектор. То есть, если вектор содержит четыре элемента, это означает, что \ (k_3 = 0 \). Коэффициенты искажения не зависят от просматриваемой сцены. Таким образом, они также относятся к внутренним параметрам камеры. И они остаются неизменными независимо от разрешения снятого изображения. Если, например, камера была откалибрована для изображений с разрешением 320 x 240, абсолютно одинаковые коэффициенты искажения можно использовать для изображений 640 x 480 с той же камеры, в то время как \ (f_x \), \ (f_y \), \ ( c_x \) и \ (c_y \) необходимо соответствующим образом масштабировать.


enum	{ cv :: LMEDS = 4, cv :: RANSAC = 8, cv :: RHO = 16 }
	тип робастного алгоритма оценки Подробнее …

enum	{ cv :: SOLVEPNP_ITERATIVE = 0, cv :: SOLVEPNP_EPNP = 1, cv :: SOLVEPNP_P3P = 2, cv :: SOLVEPNP_DLS = 3, cv :: SOLVEPNP_UPNP = 4, cv :: SOLVEPNP_AP3P = 5, cv :: SOLVEPNP_MAX_COUNT }

перечисление	{ cv :: CALIB_CB_ADAPTIVE_THRESH = 1, cv :: CALIB_CB_NORMALIZE_IMAGE = 2, cv :: CALIB_CB_FILTER_QUADS = 4, cv :: CALIB_CB_FAST_CHECK = 8 }

enum	{ cv :: CALIB_CB_SYMMETRIC_GRID = 1, cv :: CALIB_CB_ASYMMETRIC_GRID = 2, cv :: CALIB_CB_CLUSTERING = 4 }

перечисление	{ cv :: CALIB_USE_INTRINSIC_GUESS = 0x00001, cv :: CALIB_FIX_ASPECT_RATIO = 0x00002, cv :: CALIB_FIX_PRINCIPAL_POINT = 0x00004, cv :: CALIB_ZERO_TANGENT_DIST = 0x00008, cv :: CALIB_FIX_FOCAL_LENGTH = 0x00010, cv :: CALIB_FIX_K1 = 0x00020, cv :: CALIB_FIX_K2 = 0x00040, cv :: CALIB_FIX_K3 = 0x00080, cv :: CALIB_FIX_K4 = 0x00800, cv :: CALIB_FIX_K5 = 0x01000, cv :: CALIB_FIX_K6 = 0x02000, cv :: CALIB_RATIONAL_MODEL = 0x04000, cv :: CALIB_THIN_PRISM_MODEL = 0x08000, cv :: CALIB_FIX_S1_S2_S3_S4 = 0x10000, cv :: CALIB_TILTED_MODEL = 0x40000, cv :: CALIB_FIX_TAUX_TAUY = 0x80000, cv :: CALIB_USE_QR = 0x100000, cv :: CALIB_FIX_TANGENT_DIST = 0x200000, cv :: CALIB_FIX_INTRINSIC = 0x00100, cv :: CALIB_SAME_FOCAL_LENGTH = 0x00200, cv :: CALIB_ZERO_DISPARITY = 0x00400, cv :: CALIB_USE_LU = (1 << 17) }

enum	{ cv :: FM_7POINT = 1, cv :: FM_8POINT = 2, cv :: FM_LMEDS = 4, cv :: FM_RANSAC = 8 }
	Алгоритм нахождения фундаментальной матрицы Подробнее…


	двойной резюме :: calibrateCamera (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, размер IMAGESIZE, InputOutputArray cameraMatrix, InputOutputArray distCoeffs, OutputArrayOfArrays rvecs, OutputArrayOfArrays tvecs, OutputArray stdDeviationsIntrinsics, OutputArray stdDeviationsExtrinsics, OutputArray perViewErrors, int flags = 0, TermCriteria критерии = TermCriteria (TermCriteria :: COUNT + TermCriteria :: EPS, 30, DBL_EPSILON))
	Находит внутренние и внешние параметры камеры из нескольких представлений шаблона калибровки.Подробнее …

double	cv :: calibrateCamera (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, Size imageSize, InputOutputArray cameraputrayvercs, InputArrayArray, OutputOutrays TermCriteria (TermCriteria :: COUNT + TermCriteria :: EPS, 30, DBL_EPSILON))

void	cv :: CalibrationMatrixValues (InputArray cameraMatrix, двойной размер и размер изображения, двойная апертура , double & focalLength, Point2d & PrincipalPoint, double & aspectRatio)
	Вычисляет полезные характеристики камеры на основе матрицы камеры.Подробнее …

void	cv :: composeRT (InputArray rvec1, InputArray tvec1, InputArray rvec2, InputArray tvec2, OutputArray rvec3crayArray, dr. (), OutputArray dr3dr2 = noArray (), OutputArray dr3dt2 = noArray (), OutputArray dt3dr1 = noArray (), OutputArray dt3dt1 = noArray (), OutputArray dt3dr2 = noArray (), OutputArray (), OutputdArray ()	Объединяет два преобразования поворота и сдвига.Подробнее …

void	cv :: computeCorrespondEpilines (InputArray points, int whichImage, InputArray F, OutputArray lines)
	Для точек в стереопаре соответствующие эпилины на другом изображении. Подробнее …

void	cv :: convertPointsFromHomogen (InputArray src, OutputArray dst)
	Преобразует точки из однородного в евклидово пространство.Подробнее …

void	cv :: convertPointsHomogen (InputArray src, OutputArray dst)
	Преобразует точки в / из однородных координат. Подробнее …

void	cv :: convertPointsToHomogen (InputArray src, OutputArray dst)
	Преобразует точки из евклидова пространства в однородное. Более…

void	cv :: rightMatches (InputArray F, InputArray points1, InputArray points2, OutputArray newPoints1, OutputArray newPoints2)
соответствующих точек. Подробнее …

void	cv :: decoposeEssentialMat (InputArray E, OutputArray R1, OutputArray R2, OutputArray t)
	.Подробнее …

int	cv :: decoposeHomographyMat (InputArray H, InputArray K, OutputArrayOfArrays вращений, OutputArrayOfArrays преобразований, OutputArrayOfArrays преобразований, OutputArrayOfArrays

void	cv :: decoposeProjectionMatrix (InputArray projMatrix, OutputArray cameraMatrix, OutputArray rotMatrix, OutputArray transVect, OutputArray OutputArrayMatrix = no, OutputArray rotMatrix, no, OutputArray noArray (), OutputArray eulerAngles = noArray ())
	Разбивает матрицу проекции на матрицу вращения и матрицу камеры.Подробнее …

void	cv :: drawChessboardCorners (Изображение InputOutputArray, Размер patternSize, Углы InputArray, bool patternWasFound)
Отображает обнаруженные углы

cv :: Mat	cv :: EstimationAffine2D (InputArray from, InputArray to, OutputArray inliers = noArray (), int method = RANSAC, double ransacReprojThreshold maxIters = 3, size 2000, двойная уверенность = 0.99, size_t RefinIters = 10)
	Вычисляет оптимальное аффинное преобразование между двумя наборами 2D точек. Подробнее …

int	cv :: EstimationAffine3D (InputArray src, InputArray dst, OutputArray out, OutputArray inliers, двойной ransacThreshold = 3, двойная уверенность = 0,99)		906 оптимальное аффинное преобразование между двумя наборами трехмерных точек. Подробнее …

cv :: Mat	cv :: EstimationAffinePartial2D (InputArray from, InputArray to, OutputArray inliers = noArray (), int method = RANSAC, double ransacReprojThreshold = 2000, двойная достоверность = 0.99, size_t RefinIters = 10)
	Вычисляет оптимальное ограниченное аффинное преобразование с 4 степенями свободы между двумя наборами 2D точек. Подробнее …

void	cv :: filterSpeckles (InputOutputArray img, double newVal, int maxSpeckleSize, double maxDiff, InputOutputArray buf = noArray ()

bool	cv :: find4QuadCornerSubpix (InputArray img, InputOutputArray углы, размер region_size)
	6 906 906 углов на шахматной доске более точных позиций 9025 906 -90
bool	cv :: findChessboardCorners (InputArray image, Size patternSize, OutputArray corners, int flags = CALIB_CB_ADAPTIVE_THRESH + CALIB_CB_NORMALIZE_IMAGE)

bool	cv :: findCirclesGrid (Изображение InputArray, Размер patternSize, Центры OutputArray, int flags, const Ptr & blobDetector, Параметры CirclesGridFinder

bool	cv :: findCirclesGrid (изображение InputArray, размер patternSize, центры OutputArray, int flags = CALIB_CB_SYMMETRIC_GRID, const Ptr

Mat	cv :: findEssentialMat (InputArray points1, InputArray points2, InputArray cameraMatrix, int method = RANSAC, double prob = 0.999, двойной порог = 1.0, OutputArray mask = noArray ())
	Вычисляет существенную матрицу из соответствующих точек на двух изображениях. Подробнее …

Mat	cv :: findEssentialMat (InputArray points1, InputArray points2, double focal = 1.0, Point2d pp = Point2d (0, 0), int method = RANSAC, double prob = 0.999, двойной порог = 1.0, маска OutputArray = noArray ())

Mat	cv :: findFundamentalMat (InputArray points1, InputArray points2, int method = FM_RANSAC, double param1 = 3., double param2 = 0,99, OutputArray mask = noArray ())
	Вычисляет фундаментальную матрицу из соответствующих точек на двух изображениях. Подробнее …

Mat	cv :: findFundamentalMat (InputArray points1, InputArray points2, OutputArray mask, int method = FM_RANSAC, double param1 = 3., Double param2 = 0.9926
Mat	cv :: findHomography (InputArray srcPoints, InputArray dstPoints, int method = 0, double ransacReprojThreshold = 3, OutputArray mask = noArray (), const int maxIters = 2000, const double trust = 0.995)
	Находит перспективное преобразование между двумя плоскостями. Подробнее …

Mat	cv :: findHomography (InputArray srcPoints, InputArray dstPoints, OutputArray mask, int method = 0, double ransacReprojThreshold = 3)	cv :: getOptimalNewCameraMatrix (InputArray cameraMatrix, InputArray distCoeffs, Size imageSize, double alpha, Size newImgSize = Size (), Rect * validPixROI = 0, bool centerPrincipalPoint = false) параметр свободного масштабирования.Подробнее …

Rect	cv :: getValidDisparityROI (Rect roi1, Rect roi2, int minDisparity, int numberOfDisparities, int SADWindowSize)		ROISSize исправленных изображений (возвращаемых cv :: stereoRectify ()) Подробнее …

Mat	cv :: initCameraMatrix2D (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints, InputArrayOfArrays image .0)
	Находит исходную матрицу камеры из соответствий точек 3D-2D. Подробнее …

void	cv :: matMulDeriv (InputArray A, InputArray B, OutputArray dABdA, OutputArray dABdB)
	вычисляет частичную производную матрицу для каждой производной матрицы . Подробнее …

void	cv :: projectPoints (InputArray objectPoints, InputArray rvec, InputArray tvec, InputArray cameraMatrix, InputArray Aspect distCoeffs, OutputArrayArrayo = 0, OutputArray, image )
	Проецирует трехмерные точки на плоскость изображения.Подробнее …

int	cv :: recoverPose (InputArray E, InputArray points1, InputArray points2, InputArray cameraMatrix, OutputArray R, OutputArray t, InputOutputArray mask = noArray 9038 (маска 6) 906	Восстановите относительное вращение и перенос камеры из оцененной основной матрицы и соответствующих точек на двух изображениях, используя проверку хиральности. Возвращает количество вставок, прошедших проверку. Более…

int	cv :: restorePose (InputArray E, InputArray points1, InputArray points2, OutputArray R, OutputArray t, double focal = 1.0, Point2d pp = Point2d (0, 0), InputOray mask = noArray ())

int	cv :: restorePose (InputArray E, InputArray points1, InputArray points2, InputArray cameraMatrix, OutputArray R, OutputArray t, double distanceThray (no inputOut mask) OutputArray triangulatedPoints = noArray ())

	поплавок резюме :: rectify3Collinear (InputArray cameraMatrix1, InputArray distCoeffs1, InputArray cameraMatrix2, InputArray distCoeffs2, InputArray cameraMatrix3, InputArray distCoeffs3, InputArrayOfArrays imgpt1, InputArrayOfArrays imgpt3, размер IMAGESIZE, InputArray R12, InputArray T12, InputArray R13, InputArray T13, OutputArray R1, OutputArray R2, OutputArray R3, OutputArr ay P1, OutputArray P2, OutputArray P3, OutputArray Q, double alpha, Size newImgSize, Rect * roi1, Rect * roi2, int flags)
	вычисляет преобразования ректификации для камеры с 3 головками, где все головы на той же линии.Подробнее …

void	cv :: reprojectImageTo3D (несоответствие InputArray, OutputArray _3dImage, InputArray Q, логический дескриптор изображение в трехмерное пространство. Подробнее …

void	cv :: Rodrigues (InputArray src, OutputArray dst, OutputArray jacobian = noArray ())
	Преобразует вектор вращения в вектор вращения наоборот.Подробнее …

Vec3d	cv :: RQDecomp3x3 (InputArray src, OutputArray mtxR, OutputArray mtxQ, OutputArray Qx = noArray (), OutputArray (), OutputArray (), No OutputArray (), OutputArray () )
	Вычисляет RQ-разложение матриц 3×3. Подробнее …

double	cv :: sampsonDistance (InputArray pt1, InputArray pt2, InputArray F)
	Вычисляет расстояние Сэмпсона между двумя точками.Подробнее …

int	cv :: resolveP3P (InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArrayOfArrays 9026s, 026 Поза объекта из 3-х 3D-2D точечных соответствий. Подробнее …

bool	cv :: resolvePnP (InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvecERINSVEPOLI_TEXT = false_VecText, intUpolic = false
	Находит позу объекта на основе соответствия точек 3D-2D.Подробнее …

bool	cv :: resolvePnPRansac (InputArray objectPoints, InputArray imagePoints, InputArray cameraMatrix, InputArray distCoeffs, OutputArray rvecvecvecount, false reprojectionError = 8.0, двойная достоверность = 0.99, OutputArray inliers = noArray (), int flags = SOLVEPNP_ITERATIVE)
	Находит позу объекта из соответствий точек 3D-2D с использованием схемы RANSAC.Подробнее …

	двойной резюме :: stereoCalibrate (InputArrayOfArrays objectPoints, InputArrayOfArrays imagePoints1, InputArrayOfArrays imagePoints2, InputOutputArray cameraMatrix1, InputOutputArray distCoeffs1, InputOutputArray cameraMatrix2, InputOutputArray distCoeffs2, размер IMAGESIZE, OutputArray R, T OutputArray , OutputArray E, OutputArray F, int flags = CALIB_FIX_INTRINSIC, TermCriteria критерии = TermCriteria (TermCriteria :: COUNT + TermCriteria :: EPS, 30, 1e-6))
	Калибровка стереокамеры.Подробнее …

void	cv :: stereoRectify (InputArray cameraMatrix1, InputArray distCoeffs1, InputArray cameraMatrix2, InputArray distCoeffs1, OutputArray Image Size, OutputArray Image , OutputArray P2, OutputArray Q, int flags = CALIB_ZERO_DISPARITY, double alpha = -1, Size newImageSize = Size (), Rect * validPixROI1 = 0, Rect * validPixROI2 = 0)
	Вычисляет исправление преобразований для каждой головы калиброванная стереокамера.Подробнее …

bool	cv :: stereoRectifyUncalibrated (InputArray points1, InputArray points2, InputArray F, Size imgSize, OutputArray h2, OutputArray h3, double threshold = 5) Вычисляет преобразование выпрямления для некалиброванной стереокамеры. Подробнее …

void	cv :: triangulatePoints (InputArray projMatr1, InputArray projMatr2, InputArray projPoints1, InputArray projPoints4 tri, OutputDangles точек Подробнее …

void	cv :: validateDisparity (InputOutputArray disparity, InputArray cost, int minDisparity, int numberOfDisparities, int disp12MaxDisparities, int disp12MaxDisparities,	, используя левое отклонение	, используя левое отклонение	) правильный чек. Матрица «стоимость» должна быть вычислена с помощью алгоритма стерео соответствия. Подробнее …

камер · PyTorch4D

Система координат камеры

При работе с 3D-данными пользователям необходимо знать 4 системы координат

Мировая система координат Это система, в которой живет объект / сцена — мир.
Система координат обзора камеры Это система, которая берет свое начало в плоскости изображения, а ось Z перпендикулярна плоскости изображения. В PyTorch4D мы предполагаем, что + X указывает влево, + Y указывает вверх и + Z указывает из плоскости изображения.Преобразование из мира в вид происходит после применения вращения ( R ) и перевода ( T ).
Система координат NDC Это нормализованная система координат, которая ограничивает в объеме визуализированную часть объекта / сцены. Также известен как объем просмотра. Согласно соглашению PyTorch4D, (+1, +1, znear) — это верхний левый ближний угол, а (-1, -1, zfar) — нижний правый дальний угол тома. Для неквадратных объемов сторона объема в XY с наименьшей длиной находится в диапазоне от [-1, 1] , а большая сторона — от [-s, s] , где s — это аспект соотношение и s> 1 (большее деление на меньшую сторону).Преобразование из вида в NDC происходит после применения матрицы проекции камеры ( P ).
Система координат экрана Это еще одно представление объема обзора с координатами XY , определенными в пиксельном пространстве вместо нормализованного пространства.

Иллюстрация четырех систем координат показана ниже.

Определение камер в PyTorch4D

Камеры в PyTorch4D преобразуют объект / сцену из мира в вид, сначала преобразуя объект / сцену для просмотра (с помощью преобразований R и T ), а затем проецируя трехмерный объект / сцену в нормализованное пространство через матрицу проекции P = K [R | T] , где K — собственная матрица.Параметры камеры в K определяют нормализованное пространство. Если пользователи определяют параметры камеры в пространстве NDC, то проекты преобразования указывают на NDC. Если параметры камеры определены в пространстве экрана, преобразованные точки находятся в пространстве экрана.

Обратите внимание, что базовый класс CamerasBase не делает никаких предположений о системах координат. Все вышеупомянутые преобразования являются геометрическими преобразованиями, определяемыми исключительно R , T и K .Это означает, что пользователи могут определять камеры в любой системе координат и для любых преобразований. Метод transform_points применит K , R и T к входным точкам как простое матричное преобразование. Однако, если пользователи хотят использовать камеры с рендерером PyTorch4D, им необходимо соблюдать допущения системы координат PyTorch4D (см. Ниже).

Мы предоставляем экземпляры общих типов камер в PyTorch4D и то, как пользователи могут гибко определять пространство проекции ниже.

Взаимодействие с модулем визуализации PyTorch4D

Средство визуализации PyTorch4D как для сеток, так и для облаков точек предполагает, что преобразованные камерой точки, то есть точки, переданные в качестве входных данных в растеризатор, находятся в пространстве NDC PyTorch4D. Таким образом, чтобы получить ожидаемый результат рендеринга, пользователи должны убедиться, что их входные 3D-данные и камеры соответствуют этим предположениям системы координат PyTorch4D. Система координат PyTorch4D предполагает + X: слева , + Y: вверх и + Z: от нас до сцены (справа).Путаница в отношении систем координат является обычным явлением, поэтому мы советуем вам потратить некоторое время на понимание ваших данных и системы координат, в которой они находятся, и преобразовать их соответствующим образом, прежде чем использовать средство визуализации PyTorch4D.

Примеры камер и их взаимодействия с модулем визуализации PyTorch4D можно найти в наших руководствах.

Типы камер

Все камеры наследуются от CamerasBase , который является базовым классом для всех камер. PyTorch4D предоставляет четыре различных типа камер. CamerasBase определяет методы, общие для всех моделей камер:

get_camera_center , который возвращает оптический центр камеры в мировых координатах
get_world_to_view_transform , который возвращает трехмерное преобразование из мировых координат в координаты обзора камеры (R, T)
get_full_projection_transform , который составляет преобразование проекции ( K ) с преобразованием мира в изображение (R, T)
transform_points , который принимает набор входных точек в мировых координатах и проецирует их в координаты NDC в диапазоне от [-1, -1, znear] до [+1, +1, zfar].
get_ndc_camera_transform , который определяет преобразование в пространство NDC PyTorch4D и вызывается при взаимодействии с модулем визуализации PyTorch4D. Если камера определена в пространстве NDC, возвращается преобразование идентичности. Если камеры определены в пространстве экрана, возвращается преобразование из экрана в NDC. Если пользователи определяют свою собственную камеру в пространстве экрана, им нужно подумать о преобразовании экрана в NDC. Мы предоставляем примеры для камер PerspectiveCameras и OrthographicCameras .
transform_points_ndc , который берет набор точек в мировых координатах и проецирует их в пространство NDC PyTorch4D
transform_points_screen , который принимает набор входных точек в мировых координатах и проецирует их на экранные координаты в диапазоне от [0, 0, znear] до [W-1, H-1, zfar]

Пользователи могут легко настраивать свои камеры. Для каждой новой камеры пользователи должны реализовать подпрограмму get_projection_transform , которая возвращает отображение P из координат обзора камеры в координаты NDC.

FoVПерспективаКамеры, FoVОртографические камеры

Эти две камеры соответствуют соглашению OpenGL для перспективных и ортогональных камер соответственно. Пользователь предоставляет поле ближнего znear и дальнего zfar , которое ограничивает объем обзора по оси Z . Объем обзора в плоскости XY определяется углом поля зрения ( fov ) в случае FoVPerspectiveCameras и min_x, min_y, max_x, max_y в случае FoVOrthographicCameras .Эти камеры по умолчанию находятся в пространстве NDC.

Перспективные камеры, Ортографические камеры

Эти две камеры следуют соглашению о многооконной геометрии для камер. Пользователь предоставляет фокусное расстояние ( fx , fy ) и главную точку ( px , py ). Например, camera = PerspectiveCameras (focal_length = ((fx, fy),), Principal_point = ((px, py),))

Проекция камерой трехмерной точки (X, Y, Z) в координатах обзора на точку (x, y, z) в пространстве проекции (NDC или экран) составляет

 
х = fx * X / Z + px
y = fy * Y / Z + py
г = 1 / Z


х = fx * X + px
y = fy * Y + py
г = Z

Пользователь может определять параметры камеры в NDC или в пространстве экрана.Параметры камеры экранного пространства являются общими, и в этом случае пользователь должен установить in_ndc на False , а также предоставить image_size = (высота, ширина) экрана, также известного как изображение.

get_ndc_camera_transform обеспечивает преобразование экрана в пространство NDC в PyTorch4D. Обратите внимание, что пространство экрана предполагает, что основная точка находится в пространстве с + X слева , + Y вниз и исходной точкой в верхнем левом углу изображения.Чтобы преобразовать в NDC, нам необходимо учесть масштабирование нормализованного пространства, а также изменение направления XY .

Ниже приведены примеры эквивалентных экземпляров PerspectiveCameras в NDC и пространстве экрана соответственно.

 
fcl_ndc = (1,2,)
prp_ndc = ((0,2, 0,5),)
camera_ndc = PerspectiveCameras (focal_length = fcl_ndc, Principal_point = prp_ndc)


image_size = ((128, 256),)
fcl_screen = (76,2,)
prp_screen = ((114,8, 31,75),)
camera_screen = PerspectiveCameras (focal_length = fcl_screen, Principal_point = prp_screen, in_ndc = False, image_size = image_size)

Взаимосвязь между экраном и спецификациями NDC камеры focal_length и main_point задается следующими уравнениями, где s = min (image_width, image_height) .Преобразование координат x и y между экраном и NDC точно такое же, как для px и py.

  fx_ndc = fx_screen * 2.0 / (с - 1)
fy_ndc = fy_screen * 2.0 / (с - 1)

px_ndc = - (px_screen - (image_width - 1) / 2.0) * 2.0 / (s - 1)
py_ndc = - (py_screen - (image_height - 1) / 2.0) * 2.0 / (s - 1)

Измерение положения и ориентации с использованием камеры, откалиброванной по геометрии проекции матриц Плюккера из трехмерных линий

В соответствии с методом 3D-линии в 2D-линию матрица преобразования P создается из n 3D линий L _i и n 2D проекционные линии l _i.Координаты 2D проекционных линий извлекаются с помощью преобразования Хафа ¹⁹. Результаты распознавания линий показаны на рис. 1. Результаты показывают, что преобразование Хафа может точно выделить линии.

Рисунок 1: Результаты эксперимента по извлечению строки.

( a — d ) Результаты распознавания линии в первой группе экспериментов, поскольку расстояния перемещения составляют 10 мм, 20 мм, 30 мм и 40 мм, соответственно. ( e — h ) Приведены результаты распознавания линий во второй группе экспериментов, поскольку расстояния перемещения составляют 10 мм, 20 мм, 30 мм и 40 мм, соответственно.

Различия между координатами репроецирующих линий и координатами линий, извлеченными с помощью преобразования Хафа, используются для оценки точности метода преобразования 3D-линии в 2D-линию. Сравнение средних логарифмических ошибок с использованием метода трехмерных линий и двухмерных линий и метода на основе точек ²⁰ показано на рис. 2. Разрешение изображения составляет 1024 × 768. Кроме того, для изучения взаимосвязи между ошибками и расстояние перемещения калибровочная доска перемещается на 10 мм, 20 мм, 30 мм и 40 мм соответственно.В первой группе экспериментов изображения снимаются на расстоянии измерения 1000 мм. Среднее значение средних логарифмических ошибок с использованием линейного метода составляет 1,11 × 10 ^-4, 1,67 × 10 ^-4, 2,78 × 10 ^-4 и 4,09 × 10 ^-4, соответствующих расстояниям перемещения. 10 мм, 20 мм, 30 мм и 40 мм. Среднее значение средних логарифмических ошибок точечного метода составляет 3,19 × 10 ^–4, 5,11 × 10 ^–4, 8,55 × 10 ^–4 и 1.41 × 10 ⁻³, что соответствует расстояниям перемещения 10 мм, 20 мм, 30 мм и 40 мм.

Рисунок 2

Средние логарифмические ошибки, связанные с расстоянием перемещения и линией, в методе от 3D-линии к 2D-линии и точечном методе в первой группе экспериментов.

Кроме того, вторая группа экспериментов проводится на меньшей дистанции измерения. Изображения наблюдаются камерой на расстоянии измерения 800 мм. Как и в первой группе экспериментов, метод 3D-линии в 2D-линию сравнивается с точечным методом для проверки точности измерения на рис.3. Среднее значение средних логарифмических ошибок при использовании построчного метода составляет 1,01 × 10 ^–4, 1,61 × 10 ^–4, 2,50 × 10 ^–4 и 3,99 × 10 ^–4, что соответствует расстояния перемещения 10 мм, 20 мм, 30 мм и 40 мм. Среднее значение средних логарифмических ошибок с использованием точечного метода составляет 3,12 × 10 ^–4, 4,81 × 10 ^–4, 8,08 × 10 ^–4 и 1,34 × 10 ^–3, что соответствует расстоянию перемещения 10 мм, 20 мм, 30 мм и 40 мм.Результаты обеих групп экспериментов показывают, что ошибки увеличиваются с увеличением расстояния перемещения. Более того, все ошибки метода 3D-линии в 2D-линии меньше, чем у метода, основанного на точках, на расстояниях перемещения. Результаты показывают, что линейный метод обеспечивает более высокую точность калибровки. Кроме того, ошибки изображений на расстоянии 800 мм меньше ошибок изображений на расстоянии 1000 мм. Оба метода обеспечивают более высокую точность измерения на небольшом расстоянии измерения.

Рис. 3

Средние логарифмические ошибки, связанные с расстоянием перемещения и линией, в методе от 3D-линии к 2D-линии и точечном методе во второй группе экспериментов.

Кроме того, три уровня гауссовских шумов добавлены для изучения эффектов шумов. Метод калибровки 3D-линии в 2D-линию также сравнивается с методом точечной калибровки в двух группах экспериментов. Ошибки измерения оцениваются с помощью

, где L ‘ — восстановленное расстояние перемещения калибровочной платы от первого места до следующего места. L — стандартное расстояние перемещения. L ‘ генерируется из P. Стандартные расстояния составляют 10 мм, 20 мм, 30 мм и 40 мм соответственно. Проведем 20 экспериментов на стандартных расстояниях. Результаты двух групп экспериментов показаны на рис. 4 и 5 соответственно. В первой группе экспериментов средние значения Δ L , использующие метод 3D-линии в 2D-линию без помех, составляют 0,26 мм, 0,43 мм, 0,84 мм и 1,35 мм, когда расстояния перемещения составляют 10 мм, 20 мм, 30 мм. , и 40 мм.Соответствующие погрешности точечного метода составляют 0,36 мм, 0,72 мм, 1,03 мм и 1,54 мм соответственно. Средние ошибки при использовании точечного метода, очевидно, больше, чем при использовании метода 3D-линия в 2D-линию. Когда уровень шума составляет 0,0001, средние ошибки при использовании метода от линии к линии составляют 0,31 мм, 0,56 мм, 0,99 мм и 1,51 мм по отношению к расстояниям перемещения 10 мм, 20 мм, 30 мм и 40 мм. Средние ошибки точечного метода составляют 0,42 мм, 0,80 мм, 1,14 мм и 1,70 мм. Средние ошибки линейного метода при уровне шума 0.005 составляют 0,35 мм, 0,55 мм, 0,98 мм и 1,63 мм, когда расстояния перемещения составляют 10 мм, 20 мм, 30 мм и 40 мм соответственно. Средние ошибки точечного метода при уровне шума 0,0005 составляют 0,44 мм, 0,84 мм, 1,18 мм и 1,79 мм соответственно. Средние ошибки линейного метода при уровне шума 0,01 составляют 0,39 мм, 0,64 мм, 1,16 мм и 1,64 мм при увеличении расстояния перемещения с 10 мм до 40 мм. Средние ошибки при использовании точечного метода составляют 0,46 мм, 0,92 мм, 1,24 мм и 1.95 мм.

Рис. 4. Погрешности измерения метода 3D-линия в 2D-линию (LLM) и точечного метода (PM) в первой группе экспериментов.

( a ) Погрешности измерения без помех. ( b — d ) Это ошибки измерения с шумами 0,001, 0,005 и 0,01 соответственно.

Рис. 5: Погрешности измерения метода 3D-линия в 2D-линию (LLM) и точечного метода (PM) во второй группе экспериментов.

( a ) Погрешности измерения без помех.( b — d ) Это ошибки измерения с шумами 0,001, 0,005 и 0,01 соответственно.

Вторая группа экспериментов проводится на расстоянии измерения 800 мм. Среднее значение Δ L метода 3D-линия в 2D-линию без помех составляет 0,14 мм, 0,49 мм, 0,63 мм и 1,23 мм с расстояниями перемещения 10 мм, 20 мм, 30 мм и 40 мм. Соответствующие средние ошибки точечного метода составляют 0,28 мм, 0,68 мм, 0,90 мм и 1,43 мм соответственно.Средние ошибки линейного метода меньше, чем точечного метода. Когда добавлен шум 0,0001, средние ошибки метода 3D-линии в 2D составляют 0,19 мм, 0,59 мм, 0,77 мм и 1,38 мм, что соответствует расстояниям перемещения 10 мм, 20 мм, 30 мм и 40 мм. Средние ошибки точечного метода составляют 0,34 мм, 0,76 мм, 1,00 мм и 1,55 мм. Средние ошибки линейного метода при уровне шума 0,005 составляют 0,21 мм, 0,65 мм, 0,84 мм и 1,46 мм при расстоянии перемещения 10 мм, 20 мм, 30 мм и 40 мм соответственно.Средние ошибки точечного метода при уровне шума 0,0005 составляют 0,37 мм, 0,85 мм, 1,07 мм и 1,67 мм при расстояниях перемещения 10 мм, 20 мм, 30 мм и 40 мм соответственно. Средние ошибки метода 3D-линии в 2D-линию при уровне шума 0,01 составляют 0,25 мм, 0,67 мм, 0,88 мм и 1,65 мм при увеличении расстояния перемещения от 10 мм до 40 мм. Средние ошибки при использовании точечного метода составляют 0,44 мм, 0,95 мм, 1,11 мм и 1,77 мм соответственно.

Чтобы объяснить приложению, как можно использовать эту технику, предоставляется наглядный пример для измерения положения и ориентации тележки.Детали этого примера проиллюстрированы на рис. 6, на котором тележка прикреплена трехмерной мишенью сверху и перемещается со смещениями 10 мм, 20 мм, 30 мм и 40 мм соответственно.

Рис. 6. Пример измерения положения и ориентации тележки с трехмерной мишенью.

( a ) Тележка перемещается с перемещениями d 10 мм, 20 мм, 30 мм, 40 мм соответственно. ( b ) Экспериментальное изображение измерения положения и ориентации.

Позиции t _x, t _y, t _z и ориентации α, β, γ тележки около ox, oy осей системы координат камеры в 20 различных местах показаны на рис. 7 (a – f). Поскольку ориентации α, β, γ стабильны в трех углах на рис. 7 (a – c), тележка перемещается по прямой. Согласно данным о положении тележки на рис.7 (г – е), перемещение тележки может быть решено с помощью нормы разности между вектором перемещения на первом месте и вектором перемещения на втором месте в системе координат камеры. Абсолютные и относительные погрешности восстановленных перемещений на рис. 7 (г – з) рассматриваются как индикаторы для проверки результатов измерения тележки. Результаты измерений перечислены в таблице 1.

Рисунок 7: Результаты измерения положения и ориентации тележки, прикрепленной к трехмерной мишени.

( a – c ) Углы поворота α, β, γ относительно осей o-x, o-y, o-z системы координат камеры. ( d – f) Есть переводы t _x, t _y, t _z вдоль ox, oy, oz осей координат камеры система. ( г ) Абсолютные ошибки восстановленных перемещений. ( h ) Относительные ошибки восстановленных перемещений.

Таблица 1 Средние, дисперсии, максимумы и минимумы углов поворота α, β, γ , переводы t _x, t _y, t _z, абсолютные и относительные ошибки восстановленных перемещений.

Поскольку смещение механизма составляет 10 мм, максимальные значения перемещений t _x, t _y, t _z равны -778.28 мм, 90,41 мм и 1121,14 мм соответственно. Минимумы перемещений t _x, t _y, t _z составляют -778,64 мм, 89,98 мм и 1120,76 мм соответственно. Максимумы углов поворота α, β, γ составляют 24,92 °, 44,34 ° и 52,86 ° соответственно. Минимумы углов поворота α, β, γ составляют 24,54 °, 44,05 ° и 52,45 ° соответственно. Средние ошибки измерения Δ L и относительные ошибки Δ L / d равны 0.18 мм и 1,85% соответственно. Когда смещение механизма увеличивается до 40 мм, максимальные перемещения t _x, t _y, t _z составляют -745,61 мм, 91,17 мм и 1123,78 мм соответственно. . Минимальные переводы t _x, t _y, t _z составляют −749,82 мм, 88,27 мм и 1120,13 мм соответственно.Максимальные углы поворота α, β, γ составляют 26,77 °, 46,37 ° и 55,43 ° соответственно. Минимальные углы поворота α, β, γ составляют 23,06 °, 42,99 ° и 51,55 ° соответственно. Средние ошибки измерения и относительные погрешности увеличиваются до 1,78 мм и 4,45% соответственно.

Согласно приведенному выше анализу и данным в Таблице 1, поскольку переводы t _y, t _z, очевидно, не меняются, направление ox перевода t _x — основное направление движения.Кроме того, углы поворота относительно трех осей немного различаются из-за того, что тележка перемещается по прямой линии. Среднее значение ошибок измерения увеличивается с увеличением перемещения перемещения. Относительная погрешность также увеличивается по мере увеличения смещения. Наконец, относительные ошибки в большинстве случаев не превышают 5%. Это показывает, что метод измерения применим в приложениях для определения ориентации и положения объекта.

Формирование изображения | Урок | Академия роботов

Теперь мы рассмотрим более математический способ описания процесса проекции, проекции точки из реального мира на плоскость изображения.В прошлой лекции мы рассмотрели это с очень интуитивной геометрической точки зрения. На этот раз мы посмотрим на это более математически.

Мы собираемся использовать модель проекции, отличную от той, что мы использовали в прошлый раз. Мы собираемся использовать модель, которая называется моделью «центральной проекции». Ключевыми элементами этой модели являются координатная рамка камеры, которую мы обозначаем буквой C. Плоскость изображения параллельна осям x и y камеры и расположена на расстоянии F в положительном направлении оси z.F эквивалентно фокусному расстоянию объектива, о котором мы говорили в прошлой лекции.

Теперь, чтобы спроецировать точку, мы пропускаем луч из точки в мире через плоскость изображения в исходную точку камеры. В модели с центральной проекцией вы заметите, что изображение не инвертируется, как это было в случае, о котором мы говорили в прошлой лекции. Мы можем написать уравнение для точки P в однородных координатах, мы умножим мировые координаты X, Y, Z на матрицу 3 x 4, чтобы получить однородные координаты проецируемой точки на плоскости изображения.

Давайте рассмотрим это уравнение более подробно. Довольно просто написать выражение для x̃, ỹ, z̃ через фокусное расстояние и мировую координату, X, Y, Z. Мы можем преобразовать однородные координаты в декартовы координаты, используя правило, о котором мы говорили в предыдущем разделе. и с небольшой перестановкой мы можем привести уравнение к этой форме, и это точно такая же форма, как мы получили в предыдущей лекции, глядя на похожие треугольники.

Что действительно удобно и полезно в этом однородном представлении процесса формирования изображения, так это то, что оно полностью линейно. У нас нет этого явного деления на Z, расстояние между камерой и объектом. Это подразумевается в том, как мы пишем уравнения в однородной форме.

Давайте снова посмотрим на это уравнение, и мы можем разделить эту матрицу на две части. Матрица справа имеет элементы, равные либо 0, либо 1, либо f — фокусному расстоянию объектива. Итак, эта матрица выполняет масштабирование и масштабирование.Это функция фокусного расстояния нашего объектива. Матрица слева имеет интересную форму, это всего лишь 3 x 4, и эта матрица выполняет уменьшение размерности, сжимая точки из трех измерений в два.

И пока мы считаем плоскость изображения сплошной. На самом деле плоскость изображения квантуется. Он состоит из массивного массива светочувствительных элементов, соответствующих пикселям выходного изображения. Размер каждого пикселя в этой сетке я обозначу греческой буквой ро.Таким образом, пиксели имеют равную ширину и высоту роу. Пиксели действительно очень маленькие, поэтому ширина и высота пикселя часто составляют порядка 10 микрон, может быть, немного больше, может быть, немного меньше.

Что нам теперь нужно сделать, так это преобразовать координату P, которую мы вычислили ранее и которая была в единицах измерения по отношению к началу плоскости изображения.

Нам нужно преобразовать его в единицы пикселей, и наша система координат пикселей имеет другое происхождение, о котором мы говорили в предыдущих лекциях.Координаты пикселей отсчитываются от верхнего левого угла изображения, поэтому нам нужно выполнить масштабирование, и нам нужно выполнить сдвиг, и это простая линейная операция. Итак, если у нас есть декартовы координаты x и y точки P на плоскости изображения, мы можем преобразовать их в эквивалентную координату пикселя, которую мы обозначаем координатами u и v, и мы можем представить это снова в однородной форме.

Здесь мы умножаем на матрицу, элементы матрицы — это размеры пикселя Pu и Pv и координаты так называемой главной точки.Главная точка — координата пикселя, где ось z исходного кадра пересекает плоскость изображения.

Однородные пиксельные координаты можно преобразовать в более знакомые декартовы пиксельные координаты u и v с помощью правила преобразования, которое мы рассмотрели ранее.

По сути, мы берем первый и второй элементы однородного вектора и делим его на третий элемент однородного вектора.

Теперь мы можем собрать все эти части вместе и написать полную модель камеры в виде трех матриц.Произведение первых двух матриц обычно обозначается символом K, и мы называем их внутренними параметрами. Все числа в этих двух матрицах являются функциями самой камеры. Неважно, где камера, куда она направлена, это всего лишь функция камеры. Эти числа включают высоту и ширину пикселей на плоскости изображения, координаты главной точки и фокусное расстояние объектива.
Третья матрица описывает внешние параметры, которые описывают, где находится камера, но ничего не говорят о типе камеры.

Элементы в этой матрице являются функцией относительной позы камеры по отношению к кадру начала координат мира. Фактически, это противоположность xi C.

Произведение всех этих матриц вместе называется матрицей камеры и часто обозначается символом C.

Таким образом, эта единственная матрица является единственной матрицей 3 x 4 — это все, что нам нужно для описания отображения от мировой координаты, X, Y и Z до однородного представления координаты пикселя на плоскости изображения.Эта координата плоскости однородного изображения может быть преобразована в знакомую координату плоскости изображения в декартовой системе координат, используя это правило преобразования. Итак, это очень простой и лаконичный способ выполнения перспективной проекции.

Давайте теперь рассмотрим, что происходит, когда я ввожу ненулевой масштабный коэффициент λ. Однородные элементы координат ũ, ṽ и w̃ все будут масштабированы по λ. Когда я конвертирую их в декартову форму, член λ будет разложен на числитель и знаменатель, поэтому результат не изменится.Это особое преимущество записи отношений в однородной форме. Это дает нам то, что называется масштабной дисперсией.

Поскольку мы можем умножить матрицу на произвольный масштабный коэффициент, это означает, что мы можем записать матрицу камеры в несколько упрощенной форме, которую мы называем нормализованной матрицей камеры. Мы делаем это, выбирая один конкретный элемент этой матрицы, имеющий значение 1, и обычно мы выбираем нижний правый элемент и устанавливаем его на 1.

Размер матрицы в фотоаппарате: Матрица фотоаппарата. Типы и характеристики.