Золотое сечение и числа Фибоначчи — Денис Войков на vc.ru
Введение
12 195 просмотров
Человек стремится к знаниям, пытается изучить мир, который его окружает. В процессе наблюдений появляются многочисленные вопросы, на которые, соответственно, требуется найти ответы. Человек ищет эти ответы, а находя их, появляются другие вопросы.
Оказывается, закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.
История происхождения чисел Фибоначчи и Золотого сечения
Леонардо был рожден в Пизе. Впоследствии получил прозвище Фибоначчи, что означает «хорошо рожденный сын». Когда Леонардо жил со своим отцом в странах Северной Африки, он изучал математику с арабскими учителями. Получив весь необходимый материал, он создал собственную книгу – «Книгу абака».
Основная задача, поясняющая возникновение ряда чисел Фибоначчи – задача о кроликах. Вопрос задачи звучит так: «Сколько пар кроликов в один год рождается от одной пары?». К задаче дано пояснение, что пара через месяц рождает ещё одну пару, а по природе кролики начинают объектом рождать потомство на второй месяц после своего рождения. Автор даёт нам решение задачи. Получается, что в первый месяц первая пара родит ещё одну. Во второй месяц первая пара родит ещё одну – будет три пары. В третий месяц родят две пары — изначально данная и рождённая в первый месяц. Получается пять пар. И так далее. Используя такую же логику в рассуждении, мы получим, что в четвёртый месяц будет 8 пар, в пятый– 13, в шестой – 21, в седьмой 34, в восьмой — 55, в девятый — 89, в десятый 144, в одиннадцатый – 233, в двенадцатый — 377[2](рис. 1).
Рисунок 1.
Задача о кроликах (Павел Малахов, 2017)
Из этой задачи и можно вывести саму последовательность чисел Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,… В основе этой последовательности лежит алгоритм: начиная с «1, 1» следующим числом будет сумма двух предыдущих чисел. Разделив любой член данной последовательности на член, который стоит перед ним, мы получим величину, называемую «пропорцией Золотого сечения» — примерно 1, 618[3].
Золотое сечение в живописи
В эпоху Возрождения художники открыли некие зрительные центры, которые, влияя на психику человека, невольно приковывают наше внимание. Данные точки не зависят от формата картины. Их всего четыре, они делят картину в пропорциях Золотого сечения- примерно 3/8 и 5/8 (рис.2).
Для того чтобы привлечь внимание зрителя к определенному элементу картины, необходимо совместить его с одним из зрительных центров. Данное открытие назвали «золотое сечение картины»[4].
Рисунок 2.
Золотое сечение картины (Войков Денис, 2020)
Золотое сечение в медицине
Правило золотого сечения используется в стоматологии, именно они используются при художественной реставрации зубов, их восстановлении. Рассмотрим эстетическое восстановление передних зубов, фронтального зубного ряда (рис. 3)[5].
Золотые пропорции включают в себя такие моменты:
— как ширина верхнего переднего зуба относится к ширине нижнего;
— как соотносятся между собой по ширине:
2 резца в нижнем фронтальном ряду;
двое резцов в верхнем ряду;
4 резца вверху;
— какое имеется расстояние между премолярами и т.д.
Рисунок 3. Золотое сечение на зубах (Стас Козловский, 2004)
Так же правило золотого сечения используется в косметологии и пластической хирургии. У людей с красивыми лицами существует идеальная пропорция между расстояниями от медиального угла глаза до крыла носа и от крыла носа до подбородка.
Это явление называется «динамической симметрией» или «динамическим равновесием».
Расстояние от линии смыкания губ до крыльев носа пропорционально расстоянию от линии губ до низшей точки подбородка в соотношении 1: 1,618. Ещё существует множество соотношений на лице, которые представлены на рисунке 4[6].
Рисунок 4. Золотая пропорция на лице человека (Joaquim Alves Gaspar, 2011)
Золотое сечение в психологии
Числа Фибоначчи и Золотое сечение чтобы также используется и в психологии. Например, чтобы выяснить, как развивается механизм творчества, В.В. Клименко воспользовался математикой, а именно законами чисел Фибоначчи и пропорцией «золотого сечения» — законами природы и жизни человека. Если развернуть в ряд числа Фибоначчи, то получим: 1,1, 2, 3, 5, 8, 13, 21, 34, 55, 89 и т.д. Отношение между числами Фибоначчи составляет 0,618. Развитие человека также происходит соответственно данной пропорции и подчиняется закону ее чисел, разделяя нашу жизнь на этапы с теми или иными доминантами механизма творчества [7].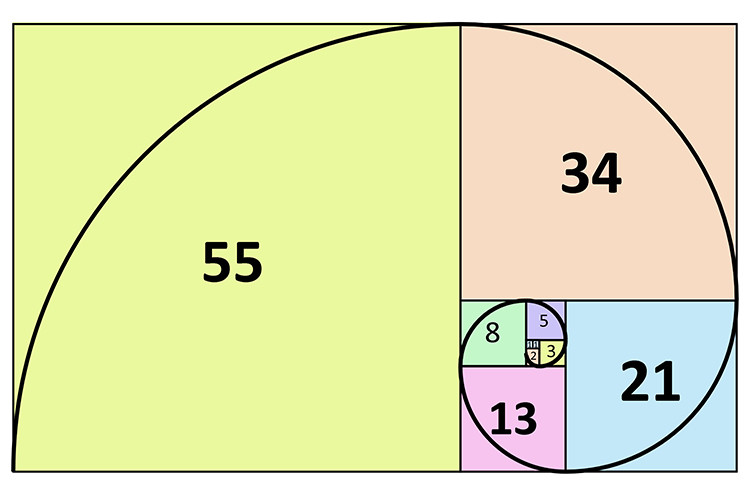
Числа Фибоначчи делят нашу жизнь на этапы по количеству прожитых лет:
• 0 —начало отсчета — ребёнок родился. У него еще отсутствуют не только психомоторика, мышление, чувства, воображение, но и оперативный энергопотенциал. Он — начало новой жизни, новой гармонии;
• 1 — ребенок овладел ходьбой и осваивает ближайшее окружение;
• 2 — понимает речь и действует, пользуясь словесными указаниями;
• 3 — действует посредством слова, задаёт вопросы;
• 5 — «возраст грации» — гармония психомоторики, памяти, воображения и чувств, которые уже позволяют ребёнку охватить мир во всей его целостности;
• 8 — на передний план выходят чувства. Им служит воображение, а мышление силами своей критичности направлено на поддержку внутренней и внешней гармонии…
Заключение
Закономерность явлений природы, строение и многообразие живых организмов на нашей планете, всё, что нас окружает, поражая воображение своей гармонией и упорядоченностью, законы мироздания, движение человеческой мысли и достижения науки – всё это можно объяснить последовательностью Фибоначчи.
В заключении отмечу, что данная работа является законченным исследованием и при этом имеет ряд перспектив. В дальнейшем возможно исследовать как числа Фибоначчи используются в биологии, химии, как это можно использовать и применять на практике в бытовых условиях.
Список источников информации
1. Воробьев Н.Н. Числа Фибоначчи. – 5-е изд. – М.: Наука, 1978 – 144с.
2. Загадки природы и числа Фибоначчи – [Электронный ресурс]. – URL: https://www.liveinternet.ru/users/4506755/post186633412 (дата обращения 23.08.2018)
3. Золотое сечение. – [Электронный ресурс]. – URL: https://ru.wikipedia.org/wiki% D0%97%D0%B% D0%B% D0%B% D1%82%D0%B% D0%B5% D1%81%D0%B5%D1%87%D0%B5%D0%B% D0%B8%D0%B5 (дата обращения 07.09.2018)
4. Правило золотого сечения в живописи – [Электронный ресурс] – URL: https://izo-life.ru/pravilo-zolotogo-secheniya/ (дата обращения 26.02.2021)
5. Золтое сечение в стоматологии – [Электронный ресурс] — URL: http://h809274671.nicwebsite.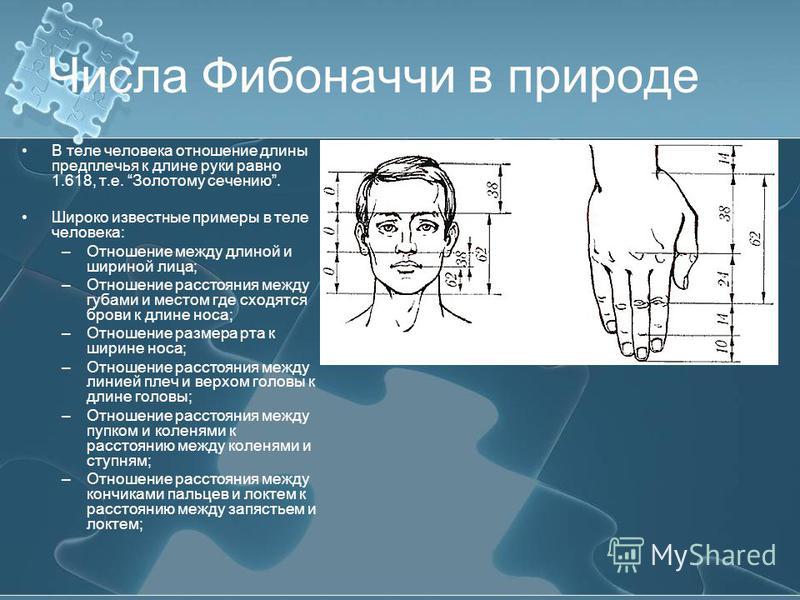
6. Идеальные пропорции лица – [Электронный ресурс] — URL: https://iakosmetolog.ru/interesno/idealnye-proporcii-lica.html (дата обращения 26.02.2021)
7. Числа Фибоначчи в психологии — [Электронный ресурс] — URL: https://megaobuchalka.ru/1/22657.html (дата обращения 09.09.2019).
Странная петля Фибоначчи: красота математического начала
Поговорим об удивительной последовательности Фибоначчи, золотом сечении и бактериях. Будьте готовы найти совпадения там, где не ожидали их увидеть.
Говоря об алгоритмах, нельзя не упомянуть о последовательности Фибоначчи. Она тесно связана с золотым сечением, которое мы снова и снова встречаем в природе, архитектуре, искусстве и даже романе Дэна Брауна. От раковин морских животных до сакральной геометрии, по-видимому, Золотое Сечение закодировано во многих аспектах нашей Вселенной.
Невозможно перечислить все места, где мы можем встретить эту удивительную последовательность, но самое невероятное – она появляется даже внутри самой себя.
В информатике последовательность – и различные стратегии ее вычисления – это хорошие обучающие инструменты. Последовательность Фибоначчи может быть вычислена с помощью простой рекурсии:
def fib(n):
if n <= 1:
return 1
return fib(n - 2) + fib(n - 1)Один из самых замечательных моментов этой реализации в том, что код очень близко соответствует самому определению.
Последовательность была описана в 1202 году Леонардо Фибоначчи. Она начинается с двух единиц, а последующие члены вычисляются путем сложения двух предыдущих. Третий член 1 + 1 = 2
1 + 2 = 3, далее 2 + 3 = 5. Вот первые несколько цифр:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 …
Рекурсивный код выше означает следующее: если n равно 0 или 1, функция вернет единицу, иначе – результат сложения fib(n-1) и fib(n-2), то есть сумму двух предыдущих членов.
Ряд Фибоначчи и золотое сечение
Кроме самой последовательности, Фибоначчи обнаружил ее связь с золотым сечением.
Золотое сечение – иррациональное число. Как и ? (число Пи), оно имеет бесконечное количество цифр после запятой, которые никогда не образуют повторяющихся шаблонов. Большинство из нас помнят ? как 3.14, а золотое сечение можно запомнить как 1.618. Буквенное представление этой величины – ? (фи, Phi).
Если взять n-ный член последовательности Фибоначчи и разделить его на (n-1)-ный, то полученный результат будет приблизительно равен золотому сечению. Чем дальше от начала, тем точнее приближение:
5/3 = 1.666 8/5 = 1.6 13/8 = 1.625 21/13 = 1.61538461538
Ряд Фибоначчи как алгоритмическая сложность
Вероятно, вы знаете, что рекурсивный код работает медленно. А знаете ли вы, что он работает медленно таким образом, который тесно связан с числом ??
Смоделируем наш пример с помощью дерева (так можно представить практически все рекурсивные функции).
Каждый вызов – это внутренний узел, а базовые случаи – листья. Дерево для fib(5) выглядит вот так:
Вы можете определить сложность этой функции как O(2n). Каждый вызов по существу приводит к еще двум вызовам – практически идеальный пример экспоненциального удвоения. Другими словами, дерево, представляющее наш код, имеет коэффициент ветвления 2, каждый узел имеет 2 дочерних элемента, поэтому на каждой глубине число узлов удваивается. Из одного узла получается 2, потом 4, потом 8…
Нотация «большое O» – это нечеткая линза, где оценка одновременно рекомендуется и требуется. Но действительно ли эта функция экспоненциально удваивается? Попробуем измерить время выполнения функции fib, определенной выше:
def time_fib(n):
start = time.clock()
digit = fib(n)
stop = time.clock()
return digit, (stop - start)
for i in range(1, 100):
digit, time_elapsed = time_fib(i)
print("{:3d} {:10d} {:5d}".
format(i, digit, round(time_elapsed)))
format(i, digit, round(time_elapsed)))Даже неуклюжий эмпирический анализ намекает на нашу странную петлю. После 32 итераций измерения приобретают знакомую форму…
n fib(b) time_elapsed 32 3524578 1 33 5702887 1 34 9227465 2 35 14930352 3 36 24157817 5 37 39088169 8 38 63245986 13 …
Компьютеры, часы и интерпретаторы неточны, и постепенно значение time_elapsed становится плохим приближением ряда Фибоначчи:
n fib(b) time_elapsed 39 102334155 24 40 165580141 37 41 267914296 59 42 433494437 95 43 701408733 155 44 1134903170 253
Тем не менее, даже грязная реализация выявила теоретическую истину. Рекурсивный метод вычисления n-ного члена последовательности Фибоначчи имеет алгоритмическую сложность, которая отражает эту последовательность. Если бы его сложность была O(2n), количество времени бы удваивалось, но этого не происходит.
Колония бактерий и ряд Фибоначчи
Можно смоделировать сложность этой функции, используя рекуррентное отношение – формальный математический язык для описания рекурсивных функций.
Не пугайтесь этого определения, тут все просто:
f (n) = f (n-1) + f (n-2)
Объем работы, который требуется для вычисления n-ного числа, – это объем работы, который требуется для вычисления предыдущих двух цифр вместе взятых. Другими словами, количество листовых узлов в рекурсивном дереве для вычисления n-ного члена последовательности отражает значение этого n-ного члена.
Возьмем конкретный пример:
f(5) = f(4) + f(3) f(4) = f(3) + f(2) f(3) = f(2) + f(1) f(2) = f(1) + f(0)
И f(1), и f(0) в нашем случае постоянны, так как метод просто возвращает 1. Поэтому можно сказать, что:
f (1) = 1 f (0) = 1
Если сложить все это снизу вверх, получится следующее:
f (2) = 1 + 1 = 2 f (3) = 2 + 1 = 3 f (4) = 3 + 2 = 5 f (5) = 5 + 3 = 8
Вы уже догадываетесь, к чему все это ведет?
Давайте попробуем развернуть формулу для f(5) вместо того, чтобы вставлять в нее реальные значения:
f(5) = f(4) + f(3)
f(5) = [f(3) + f(2)] + [f(2) + f(1)]
f(5) = {[f(2) + f(1)] + [f(1) + f(0)]} + {[f(1) + f(0)] + f(1)}
f(5) = {f(1) + f(0) + f(1) + f(1) + f(0)} + {f(1) + f(0) + f(1)}Все эти f(0) и f(1) – это листовые узлы дерева, которые имеют константное значение 1.
n
f(n) = f(n — 1) + f(n — 2) = ???
Есть все основания полагать, что второе выражение также будет расти экспоненциально, но медленнее, чем 2n. С другой стороны, рекурсивное дерево для функции роста бактерий будет иметь больше узлов, чем дерево для fib, хотя в обоих деревьях у узла либо 2 ребенка, либо ни одного. Они похожи, но не идентичны.
Опять золотое сечение
Оказывается, что для «линейных гомогенных рекуррентных отношений с постоянными коэффициентами» можно использовать изящный трюк, для нахождения короткого решения. К счастью, ряд Фибоначчи является таким отношением и мы можем представить его без использования рекурсии (и даже итерации) всего в одной формуле.
Доказательство этого трюка, называемое «теоремой о различных корнях», можно найти здесь.
Мы знаем, что ряд растет по экспоненте, а этот трюк помогает найти «корни» экспоненциальной функции. Он довольно прост: нужно взять нижние индексы функции f и превратить их в экспоненты по переменной r (root – корень), для которой мы их затем решим.
2 — r — 1 = 0
Полученное уравнение можно решить для r, используя квадратичную формулу.
r = [1 +- sqrt(1 — (4*(-1)))] / 2 r = (1 + sqrt(5)) / 2 r = (1 — sqrt(5)) / 2
Произошло нечто удивительное, даже если вы этого не заметили. Посчитайте на калькуляторе 1 + sqrt(5) / 2. Вы получите … 1.618: ?, золотое сечение. Поразительно.
Чтобы не потерять лес за деревьями, отметим, что это экспериментально демонстрирует экспоненциальный рост последовательности Фибоначчи с корнем экспоненты 1.618. Если n-ный член, разделенный на (n-1)-ный член приблизительно равен ?, то умножение (n-1)-ного члена на ? будет равно n-ному члену.
Отметим также, что второй корень – это другое замечательное число ? (Psi, пси), которое похоже на золотое сечение и примерно равно -0.618.
Конечно, технически будет правильно сказать, что верхняя граница рекурсивной функции O(2n), все же гораздо более приятно знать, что более жесткая граница – O(?n). n) / sqrt(5)
Это невероятно!
Перевод статьи Fibonacci’s Strange Loop: the beauty of mathematical inception by Tyler Elliot Bettilyon
Больше материалов по алгоритмам:
- Наиболее полный видеокурс по алгоритмам и структурам данных
- Анализ алгоритмов для начинающих: вводное руководство
- ТОП-15 алгоритмических задач, реализованных на C++
- Алгоритмы и структуры данных: развернутый видеокурс
- Как научиться решать алгоритмические задачи?
Фибоначчи и золотое сечение | Поговорим о науке
Неоновая вывеска «Золотая спираль» (Алина Курьянова, iStockphoto)
Неоновая вывеска «Золотая спираль» (Алина Курьянова, iStockphoto)
Читаемость
5.89
Узнать о «старой последовательности и ее отношениях» к формам в мире красоты и природы.
Красота в глазах смотрящегоЧто делает что-то «красивым»? Красота полностью субъективна? Если да, то почему некоторые вещи долгое время считались красивыми, хотя тенденции изменились? Может ли быть в природе какая-то закономерность, на которую люди реагируют подсознательно?
Греки говорили, что вся красота сводится к математике. Философы, социологи, биологи и математики искали общее качество, которое могло бы объяснить наше восприятие красоты.
Показана цветная фотография насекомого с двумя крыльями, окрашенными в оттенки синего. Узор на левом и правом крыльях является зеркальным отражением друг друга.
Крылья бабочки тёмно-синие вверху, у головы, становятся ярче до темно-синего в центре, у туловища, затем ярко-синего. Нижний край крыльев имеет толстую полосу черного цвета с рядами белых точек.
Между крыльями бабочки находится тонкое черное туловище и длинные усики. Он сидит на блестящем красном цветке с большой желтой тычинкой.
Оказывается, греки были правы насчет красоты и математики. Во многих вещах, которые люди называют красивыми, есть общий элемент. По мнению математиков еще древних греков и египтян, соотношение этого элемента равно 1:1,618. Это называется золотым сечением.
Числа Фибоначчи Так откуда взялось это «золотое» число? Соотношение основано на последовательности чисел, известных как числа Фибоначчи или последовательность Фибоначчи. Это было определено математиком Леонардо Боначчи около 1202 года.
Знаете ли вы?
Леонардо Боначчи стал известен как Леонардо Пизанский, потому что он был из Пизы. Он был даже более известен как Фибоначчи, что в переводе с итальянского означает «сын Боначчи». При жизни его не называли Фибоначчи.
Фибоначчи был одним из самых важных математиков в . Он познакомил западный мир с арабской системой счисления в своей книге 9.0045 Liber Abaci . Это та же система счисления, которую мы используем до сих пор.
В той же книге Фибоначчи представил свою знаменитую задачу о кроликах:
Некий человек поместил пару кроликов в место, окруженное стеной. Сколько пар кроликов может быть получено от этой пары за год, если предположить, что каждый месяц каждая пара рождает новую пару, от которой второй месяц становится продуктивным?
(стр. 283-284, перевод с оригинальной латыни)
Его решение этой задачи привело к ряду чисел. Первые два числа — это 0 и 1, а каждое последующее число — это сумма двух предшествующих ему чисел: 9.0003
Это Последовательность Фибоначчи. Отдельные числа в этой последовательности называются числами Фибоначчи.
The Fibonacci sequence can also be expressed using this equation:
F n = F (n-1) + F (n-2)Где n больше 1 (n>1).
Эта последовательность цифр может показаться не такой уж и большой. Но становится интереснее, когда мы делим каждое число на предыдущее.
Например: 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13
Для этих примеров ответы будут следующими: 1.000, 2.000, 1.500, 1.667 , 1,625 и 1,615.
Соотношения для первых семи пар чисел Фибоначчи (© Let’s Talk Science, 2022). Изображения – текстовая версия Показана цветная гистограмма с 0–2,0 по оси Y и 1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13 по оси x.
Слева направо: полоса с меткой 1/1 бледно-фиолетового цвета и достигает 1,0. Полоса с меткой 2/1 золотая и достигает 2,0. Полоса с меткой 3/2 имеет ярко-фиолетовый цвет и достигает значения 1,5. Полоса с пометкой 5/3 темно-фиолетового и достигает значения 1,667. Полоса с надписью 8/5 оранжевого цвета и достигает 1,6. Полоса с меткой 13/8 имеет бирюзовый цвет и достигает 1,625. Последний бар, помеченный 21/13, ярко-синего цвета и достигает 1,615. Эти соотношения написаны в центре каждого столбца.
Пунктирная линия проходит по графику на уровне 1,618033988749895. Это обозначено символом Phi. Горизонтальный овал с вертикальной линией через центр.
Золотое сечениеЗнаете ли вы?
Когда учащиеся смотрят на взаимосвязь между одним термином и следующим, они используют тип мышления, называемый рекурсивным мышлением .
Чем больше число Фибоначчи, тем больше отношение между каждой парой чисел приближается к 1,618033988749895. Этот номер называется Фи. Его также можно представить символом Φ, 21-й буквой греческого алфавита.
Фи — это золотое сечение. Он также обладает другими необычными математическими свойствами.
Знаете ли вы?
Золотое сечение также известно как Золотое сечение, Золотая середина и Божественная пропорция.
Золотое сечение также можно найти, используя две величины, например длины двух отрезков.
Две величины имеют золотое сечение, если их отношение равно отношению их суммы к большей из двух величин:
Соотношения отрезков в золотом сечении (© Let’s Talk Science, 2022). Изображение — текстовая версия, версияПоказан цветной рисунок отрезков и математическое уравнение.
Вверху находится длинная черная полоса с надписью Line Segment. Ниже находится более короткая синяя полоса с надписью «Длинный сегмент». Справа находится еще более короткая зеленая полоса с надписью «Короткий сегмент». При размещении встык синяя и зеленая полосы равны по длине черной полосе.
Уравнение находится под этой иллюстрацией. Слева слова «Длинный сегмент» синего цвета разделены словами «Короткий сегмент» зеленого цвета. Справа знак равенства. Затем слова Line Segment, выделенные черным цветом, разделены словами Long Segment, выделенными синим цветом. За ним следует еще один знак равенства. Далее 1+ квадратный корень из 5 делится на два. За ним следует еще один знак равенства. Справа ответ 1,61803…
Золотой прямоугольник (Источник: Ahecht [общественное достояние] через Wikimedia Commons). Изображение – Текст ВерсияПоказана цветовая диаграмма прямоугольника, разделенного на бледно-фиолетовый квадрат и меньший розовый прямоугольник.
Верхний и левый края квадрата отмечены синим, строчным шрифтом, курсивом a. Верхний край меньшего прямоугольника помечен красным, строчным шрифтом, курсивом b. Весь нижний край большего прямоугольника помечен буквой a + b курсивом зеленого цвета.
– это черно-белая иллюстрация прямоугольника, разделенного на более мелкие квадраты и прямоугольники, которые становятся меньше по мере перемещения по странице в сторону точки в правом нижнем квадранте.
Самый большой прямоугольник разделен на множество меньших фигур. Самый большой слева квадрат с цифрой 34.
Справа от квадрата находится вертикальный прямоугольник. Он разделен на квадрат с номером 21 и другой, меньший, горизонтальный прямоугольник.
Третий прямоугольник снова разделен. Квадрат справа имеет номер 13. Вертикальный прямоугольник далее делится на квадрат с номером 8 и горизонтальный прямоугольник, который снова делится. Следующий квадрат помечен 5. Рядом с ним другой вертикальный прямоугольник содержит квадрат с пометкой 3 и меньший горизонтальный прямоугольник, который, в свою очередь, содержит квадрат с пометкой 2. Наименьший квадрат не помечен, но похоже, что этот узор мог бы продолжаться, становясь все меньше и меньше с каждой итерацией.
На черно-белом изображении прямоугольника, разделенного на более мелкие квадраты и прямоугольники, наложенные синей спиральной линией.
Самый большой прямоугольник разделен на множество меньших фигур. Самый большой слева квадрат с номером 34. Синяя линия над ним изгибается из левого нижнего угла в правый верхний, образуя четверть круга.
Справа от квадрата находится вертикальный прямоугольник. Он разделен на квадрат с номером 21 и другой, меньший, горизонтальный прямоугольник. На квадрат с номером 21 наложена еще одна четверть круга, начиная с левого верхнего и заканчивая правым нижним углом.
Третий прямоугольник снова разделен. Квадрат справа помечен цифрой 13. На него наложена изогнутая синяя линия, идущая сверху справа и снизу слева.
Вертикальный прямоугольник далее делится на квадрат с цифрой 8 и горизонтальный прямоугольник, который снова делится. Синяя линия продолжает изгибаться по этим фигурам.
Следующий квадрат имеет номер 5. Рядом с ним другой вертикальный прямоугольник содержит квадрат с номером 3 и меньший горизонтальный прямоугольник, который, в свою очередь, содержит квадрат с номером 2. Синяя линия продолжает скручиваться по этим фигурам.
Самый маленький квадрат не помечен, но это точка, где синяя спираль заканчивается тугим завитком. Узор выглядит так, как будто он может продолжаться, разделяясь на все меньшие и меньшие формы, а спираль становится все туже и туже.
Спираль Фибоначчи против Золотой спирали
Термины Спираль Фибоначчи и Золотая спираль часто используются взаимозаменяемо. Но эти две спирали немного отличаются.
Спираль Фибоначчи создается путем создания спирали квадратов, размер которых увеличивается на числа в последовательности Фибоначчи. Итак: 1, 1, 2, 3, 5, 8, 13, 21 и т. д. Вы можете увидеть это в анимированной гифке ниже.
Как можно построить спираль Фибоначчи (© Let’s Talk Science, 2022)
Изображение – текст. Версия. Показан анимированный GIF-файл со спиралью , растущей из все более и более крупных квадратов разных цветов.
Первый квадрат крошечный и синий, с изогнутой белой линией от нижнего левого до верхнего правого угла. Второй квадрат появляется выше. Он намного больше, и линия изгибается снизу справа вверху слева. Третий квадрат снова больше. Он отображается слева от остальных, а линия изгибается от верхнего правого угла к нижнему левому. Четвертый квадрат отображается под остальными с линией, идущей сверху слева направо и снизу. Пятый квадрат оранжевого цвета и отображается справа с линией, идущей слева внизу и справа вверху. Пятый квадрат появляется поверх остальных, в розовом цвете, с линией от нижнего правого до верхнего левого. Последний квадрат настолько велик, что занимает больше половины страницы и заполняет все пространство слева от остальных. Он синего цвета с линией, изгибающейся от верхнего правого угла к нижнему левому.
Когда все квадраты собраны вместе, изогнутые линии на них образуют спираль. Эта спираль вырастает из крошечного пустого квадрата в правом нижнем углу страницы.
Золотая спираль, тем не менее, создается путем вложения все меньших и меньших золотых прямоугольников в большой золотой прямоугольник. Посмотрите на разницу в GIF ниже:
Как можно сделать золотую спираль (© Let’s Talk Science, 2022)
Изображение – Текст ВерсияПоказан анимированный GIF-файл, состоящий из прямоугольников и квадратов все меньшего и меньшего размера, расположенных друг над другом в виде спирали.
Первый прямоугольник синего цвета и занимает всю панель. Он имеет изогнутую белую линию через верхний левый угол. Вторая фигура — это розовый прямоугольник, который закрывает правую сторону синего, так что синяя часть теперь имеет квадратную форму. Он имеет изогнутую белую линию через верхний правый угол. Третий — оранжевый прямоугольник, который покрывает нижнюю часть розового, поэтому розовая область образует квадрат. Он имеет изогнутую белую линию в правом нижнем углу. Четвертый — фиолетовый прямоугольник, который закрывает левую часть оранжевого, образуя оранжевый квадрат. Далее идет красный прямоугольник, образующий фиолетовый квадрат, и зеленый прямоугольник, образующий красный квадрат. Наконец появляется крошечный синий квадратик рядом с белым того же размера.
Когда изображение готово, все изогнутые белые линии образуют спираль, закручивающуюся к последнему белому квадрату в правом нижнем квадранте панели.
Эти спирали кажутся знакомыми? Ну должны! Мы можем наблюдать ту же закономерность в природе.
Спираль Фибоначчи на подсолнухе (Let’s Talk Science с использованием изображения Дамиана Паулоса через iStockphoto).Предупреждение о неправильном представлении
Стоит отметить, что спирали, которые мы видим в природных объектах, не совсем соответствуют золотому сечению, но приближаются к нему.
Изображение — текстовая версияПоказана цветная фотография центра подсолнуха с наложенной на него синей спиралью.
Цветок с ярко-желтыми лепестками. Его центр состоит из крошечных заостренных темно-желтых структур, плотно упакованных в круг. Спираль демонстрирует, что крошечные заостренные структуры расположены по спирали.
Спираль Фибоначчи на внутренней стороне раковины наутилуса (Let’s Talk Science с использованием изображения, сделанного duncan1890 через iStockphoto). Изображение — текстовая версияПоказана цветная фотография раковины, разрезанной пополам, чтобы показать внутреннюю часть, с наложенной на нее красной спиралью. .
Стенки раковины закручиваются от центральной точки, становясь все шире и шире к внешнему краю. Эта структура разделена на изогнутые клиновидные участки, которые также увеличиваются в размерах от центральной точки. Спираль демонстрирует, что оболочка образует спираль Фибоначчи.
Спираль Фибоначчи на галактике Мессье 101 по прозвищу Галактика Вертушка (Давайте поговорим о науке с использованием изображения Европейского космического агентства и НАСА [CC BY 3. 0] через Wikimedia Commons). пространство с наложенной на него красной спиралью.Черный фон с белыми и золотыми точками. Центр водоворота выполнен из бледно-золотого цвета с тонкими линиями более темного золота по всему периметру. Тонкие белые хвосты вьются из центра, изгибаясь в пространство. Эти полосы полупрозрачного белого цвета перемежаются сгустками ярко-белого цвета.
Красная спираль, наложенная на фотографию, показывает, что эта галактика формирует спираль Фибоначчи.
Золотое сечение можно использовать и с другими формами. Золотые пропорции можно найти в узорах, включающих круги, треугольники, пятиугольники и другие формы.
Другие формы с их золотым сечением (Давайте поговорим о науке, используя изображение от primo-piano через iStockphoto). Изображение — версия текстаПоказана диаграмма пересекающихся треугольников, пятиугольников, квадратов и кругов с синими линиями, проведенными поверх них.
Самый большой треугольник остроугольный и содержит семь других, меньших треугольников. Его левый внешний край покрыт синей линией, обозначенной 1,618. Синяя линия поворачивает угол и продолжается на его нижнем краю, обозначенном цифрой 1. Этот треугольник разделен на равнобедренный и разносторонний треугольники. Разносторонний треугольник далее делится на еще один остроугольный и еще один равнобедренный треугольник. Синяя линия продолжается вокруг длинного, затем короткого края остроугольного треугольника. Этот треугольник снова делится на еще один остроугольный и еще один равнобедренный. Синяя линия продолжается вдоль основания остроугольного треугольника, который далее делится на еще один остроугольный и еще один равнобедренный. Синяя линия продолжается вдоль этого основания, и треугольник снова делится. Синяя линия заканчивается, когда она поворачивает за узкий угол вдоль основания наименьшего остроугольного треугольника. В целом синяя линия образует своего рода спираль с рядом острых углов и прямых краев, которые становятся короче и ближе к точке в правом нижнем углу самого большого треугольника.
Самый большой пятиугольник помечен цифрой 8. Его нижний край обведен синей линией. Внутри него меньший пятиугольник помечен цифрой 5, а синяя линия продолжается вдоль одного из его краев. Внутри него находятся меньшие пятиугольники, обозначенные цифрами 3 и 2, где линия продолжается вдоль края каждого из них. Два еще меньших пятиугольника не подписаны, но построены по тому же образцу. Все сегменты синей линии образуют спираль с тупыми углами и прямыми краями, которые становятся короче и ближе к точке в правом нижнем углу самого большого пятиугольника.
Самый большой квадрат помечен цифрой 8. Меньший квадрат, упирающийся в него справа, помечен цифрой 5. Синяя линия проведена из левого верхнего угла большого квадрата в левый верхний угол меньшего квадрата, образуя уклон вправо. Меньшие и меньшие квадраты, помеченные 3, 2 и 1, следуют той же схеме, и синяя линия продолжается по прямому наклону вниз до самого маленького квадрата в крайнем правом углу.
Самый большой круг обозначен d=8. Синяя линия покрывает верхнюю левую часть окружности. Внутри него круги меньшего размера обозначены цифрами 5, 3, 2 и 1. Синяя линия продолжается вдоль части окружностей каждого круга, образуя спираль. Это скручивается до самой маленькой точки в правом верхнем углу самого большого круга.
Итак, думаете ли вы, что золотое сечение делает вещи более красивыми, зависит от вас. Но, возможно, мы можем согласиться с тем, что последовательность Фибоначчи и золотое сечение интересны с математической точки зрения. Они также могут дать нам новый взгляд на природу и искусство.
Числа Фибоначчи и золотое сечение
Об этом курсе
9 665 недавних просмотров
Изучите математику, стоящую за числами Фибоначчи, золотым сечением и тем, как они связаны. Эти темы обычно не изучаются в типичном учебном плане по математике, но содержат много интересных результатов, которые по-прежнему доступны для продвинутого старшеклассника.
Гибкие срокиГибкие сроки
Сброс сроков в соответствии с вашим графиком.
Общий сертификатОбщий сертификат
Получите сертификат по завершении
100 % онлайн100 % онлайн
Начните сразу и учитесь по собственному графику.
Начальный уровеньНачальный уровень
Математика средней школы
Часов, чтобы закончитьПрибл. 10 часов на выполнение
Доступные языкиАнглийский
Субтитры: арабский, французский, португальский (европейский), итальянский, вьетнамский, немецкий, русский, английский, испанский
Чему вы научитесь
Числа Фибоначчи
- 90 соотношение
Fibonacci identities and sums
Continued fractions
Skills you will gain
- Recreational Mathematics
- Discrete Mathematics
- Elementary Mathematics
Flexible deadlines
Reset deadlines in accordance to your график.
Общий сертификат
Получение сертификата по завершении
100% онлайн100% онлайн
Начните сразу и учитесь по собственному расписанию.
Начальный уровеньНачальный уровень
Математика средней школы
Часов, чтобы закончитьПрибл. 10 часов на выполнение
Доступные языкиАнглийский
Субтитры: арабский, французский, португальский (европейский), итальянский, вьетнамский, немецкий, русский, английский, испанский
Instructor
Jeffrey R. Chasnov
Top Instructor
32 ПрофессорДепартамент математики
164 273 Учеников
6 Курсы
Предлагаемые
Университет науки и технологии. прогресс науки и техники, а также обучение нового поколения лидеров Азии и всего мира.
Отзывы
4.8
Заполненная звездаЗаполненная звездаЗаполненная звездаЗаполненная звездаЗаполненная звезда358 reviews
5 stars
82.
13%4 stars
15.47%
3 stars
1.81%
2 stars
0.47%
1 star
0.09%
ЛУЧШИЕ ОБЗОРЫ ОТ ЧИСЕЛ ФИБОНАЧЧИ И ЗОЛОТОГО СООТНОШЕНИЯ Конечно, это был отличный опыт, и я получил массу удовольствия, изучая его. Отличный курс!!
Заполненная звездаЗаполненная звездаЗаполненная звездаЗаполненная звездаЗаполненная звездаby BSA 30 августа 2017 г.
Очень хорошо спроектирован. Было очень весело проходить этот курс. Это тот курс, который может заинтересовать вас высшей математикой. Искренняя благодарность проф. Часнову и HKUST.
Filled StarFilled StarFilled StarFilled StarStarот UB6 июня 2018 г.
Этот курс сочетает в себе рациональное математическое мышление и эстетику искусства в природе. Получил удовольствие от этого. Спасибо Coursera и Гонконгскому университету науки и технологии
Filled StarFilled StarFilled StarFilled StarFilled Star от MH13 июля 2020 г.