Ряд обратных квадратов: Ряд обратных квадратов — Вики — Главная

{-s}}}\cdot \dots }

Произведение в правой части берётся по всем простым числам.

Формула суммы ряда обратных квадратов на серебряной монете Банка России 2007 года, посвящённой 300-летию со дня рождения Леонарда Эйлера

Содержание

1 История
2 Сходимость ряда
3 Первый метод Эйлера для нахождения суммы ряда
4 Второй метод Эйлера
5 Альтернативные способы нахождения суммы
- 5.1 Ряд Фурье
- 5.2 Метод разложения гиперболического котангенса
- 5.3 Другие подходы
6 Вариации и обобщения
7 Некоторые применения
8 Примечания
9 Литература
10 Ссылки

История

Пьетро Менголи

Впервые рассуждения о ряде обратных квадратов историки обнаружили в диссертации итальянского математика Пьетро Менголи (Novae quadraturae arithmeticae seu de additione fractionum, 1644 год, опубликована в 1650), но тогда задача не вызвала общего интереса.

Менголи определил, что ряд сходится, и нашёл сумму первых 10 членов^[3]:

19683291270080≈1,54977.{\displaystyle {\frac {1968329}{1270080}}\approx 1{,}54977.}

Позднее найти сумму ряда безуспешно пытались многие выдающиеся математики, в том числе Лейбниц, Стирлинг, де Муавр, Христиан Гольдбах, братья Якоб и Иоганн Бернулли. Они также вычислили несколько значащих цифр суммы ряда. Гольдбах показал, что сумма заключена в интервале (41/25; 5/3), Стирлинг в трактате «Methodus Differentialis» (1730) сумел вычислить довольно точное значение суммы: 1,644934066, однако никто не мог точно определить, с чем это значение может быть связано^[3]^[4]^[5].

Леонард Эйлер

Якоб Бернулли призвал в своей книге «Арифметические предложения о бесконечных рядах» (1689): «Если кому-либо удастся найти то, что до сих пор не поддавалось нашим усилиям, и если он сообщит это нам, то мы будем очень ему обязаны»

[2]^[6].

Но при жизни Якоба Бернулли решение так и не появилось.

Первым успеха добился Эйлер, спустя почти полвека после обращения Бернулли. Скорее всего, о данной проблеме Эйлеру рассказал Иоганн Бернулли, брат Якоба. Эйлер сообщил об открытии в заметке «О суммах обратных рядов» (De summis serierum reciprocarum, 1735 год)^[7] для журнала «Commentarii Academiae Scientiarum Imperialis Petropolitanae» Петербургской академии наук. Найденное им значение суммы Эйлер также сообщил письмом своему другу Даниилу Бернулли, сыну Иоганна Бернулли^[8]:

Недавно я нашёл, и совсем неожиданно, изящное выражение для суммы ряда, связанного с квадратурой круга… А именно, шестикратная сумма этого ряда равна квадрату периметра круга, диаметр которого 1.

Даниил рассказал отцу, который выразил сомнение в справедливости использованного Эйлером разложения синуса в бесконечное произведение (см. ниже). Поэтому в 1748 году Эйлер более строго обосновал результат в своей монографии «Введение в анализ бесконечно малых» (Introductio in analysin infinitorum, том I, глава X)^[9]. {2}}{6}},} используя уже известное в тот период приближённое значение числа π{\displaystyle \pi }, и убедился, что оба значения, в пределах точности счёта, совпадают. Впоследствии (1743) Эйлер опубликовал ещё два разных способа суммирования ряда обратных квадратов^[11].

Сходимость ряда

Чтобы убедиться, что ряд обратных квадратов сходится, достаточно доказать, что сходится следующий ряд^[12]:

1+11⋅2+12⋅3+13⋅4+14⋅5+…{\displaystyle 1+{\frac {1}{1\cdot 2}}+{\frac {1}{2\cdot 3}}+{\frac {1}{3\cdot 4}}+{\frac {1}{4\cdot 5}}+\dots }

Этот ряд мажорирует ряд обратных квадратов, потому что каждое слагаемое в нём (кроме первого) больше, чем в ряде обратных квадратов. Его можно представить в виде телескопической суммы:

1+(1−12)+(12−13)+(13−14)+…{\displaystyle 1+\left(1-{\frac {1}{2}}\right)+\left({\frac {1}{2}}-{\frac {1}{3}}\right)+\left({\frac {1}{3}}-{\frac {1}{4}}\right)+\dots }

Частичная сумма Sn{\displaystyle S_{n}} этого ряда равна 2−1n,{\displaystyle 2-{1 \over n},} поэтому ряд сходится, и его сумма равна 2. {2}}{6}}.}

Изложенный метод основан на разложении синуса в бесконечное произведение, однако Эйлер не дал этому разложению должного обоснования, ограничившись ссылкой на то, что и левая, и правая части, рассматриваемые как многочлены, имеют одни и те же корни: 0,±π,±2π,±3π,±4π…{\displaystyle 0,\pm \pi ,\pm 2\pi ,\pm 3\pi ,\pm 4\pi \dots } Иоганн и Даниил Бернулли указали на некорректность такого вывода, поскольку он применим только к многочленам конечной степени, а не к бесконечным рядам. В связи с этим Эйлер опубликовал ещё несколько способов суммирования, обоснованных более строго и приводящих к тому же результату

[11]. Тем не менее указанное разложение оказалось верным и было впоследствии доказано^[17].

Второй метод Эйлера

В 1741 году Эйлер учёл указанную выше критику своего первоначального метода и опубликовал другой метод суммирования, основанный на интегрировании рядов^[18]. Для этого рассматривается интеграл вида

E=∫01arcsin⁡x1−x2 dx=∫01arcsin⁡x darcsin⁡x=π28.

{2}}}+\dots }

Некоторые применения

См. также: Дзета-функция Римана § ζ(2)

Сумма ряда обратных квадратов, она же ζ(2),{\displaystyle \zeta (2),} появляется во многих задачах теории чисел.

Сумма делителей натурального числа N{\displaystyle N} растёт в среднем^[28] как линейная функция ζ(2)⋅N{\displaystyle \zeta (2)\cdot N}.

Вероятность того, что два случайным образом выбранных натуральных числа в интервале от 1 до N{\displaystyle N} окажутся взаимно простыми, с ростом N{\displaystyle N} стремится к 1/ζ(2).{\textstyle 1/\zeta (2).} Другими словами, средняя плотность взаимно простых чисел в числовом ряду^[29] равна 1/ζ(2).{\textstyle 1/\zeta (2).}

Пусть Q(x){\displaystyle Q(x)} — количество свободных от квадратов натуральных чисел в промежутке от 1 до x.{\displaystyle x.} Для него имеет место приближённая формула^[30]^[31]^[32]

Q(x)≈xζ(2){\displaystyle Q(x)\approx {\frac {x}{\zeta (2)}}}

Накопленная функция Эйлера^[en]

Φ(n):=∑k=1nφ(k),n∈N,{\displaystyle \Phi (n):=\sum _{k=1}^{n}\varphi (k),\quad n\in \mathbf {N} ,}

где φ(n){\displaystyle \varphi (n)} — функция Эйлера, имеет следующую асимптотику^[33]:

Φ(n)∼12ζ(2)⋅n2+O(nlog⁡n).

{2}+O\left(n\log n\right).}

Примечания

↑ Стюарт, Иэн. Невероятные числа профессора Стюарта = Professor Stewart’s incredible numbers. — М.: Альпина нон-фикшн, 2016. — С. 222—223. — 422 с. — ISBN 978-5-91671-530-9.
↑ ¹ ² ³ ⁴ Дербишир, 2010, с. 90—92, 103—109.
↑ ¹ ² Sofo, Anthony. The Basel Problem with an Extension (неопр.). Дата обращения: 3 августа 2020.
↑ Leonhard Euler biography (неопр.) (недоступная ссылка). Дата обращения: 16 апреля 2016. Архивировано 17 марта 2008 года.
↑ Euler et le problème de Bâle (неопр.). Дата обращения: 5 августа 2020. Архивировано 23 января 2021 года.
↑ Пойа Д. Математика и правдоподобные рассуждения. — Изд. 2-е, исправленное. — М.: Наука, 1975. — С. 40.
↑ Leonhard Euler. De summis serierum reciprocarum (неопр.). Дата обращения: 17 апреля 2016.
↑ Наварро, Хоакин. До предела чисел (неопр.). Дата обращения: 10 августа 2016. Архивировано 15 сентября 2016 года.
↑ ¹ ² История математики, том III, 1972, с. 337.
↑ Дербишир, 2010, с. 92.
↑ ¹ ² Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М.: ГИФМЛ, 1960. — С. 143—144. — 468 с.
↑ ¹ ² Воробьёв Н. Н. Теория рядов. — 4-е изд. — М.: Наука, 1979. — С. 52. — 408 с. — (Избранные главы высшей математики для инженеров и студентов втузов).
↑ ¹ ² Айгнер, Циглер, 2006, с. 49.
↑ Borwein, Borwein, Dilcher, 1989
↑ Антонио Дуран, 2014, с. 109—114.
↑ ¹ ² Кохась К. П., 2004.
↑ Фихтенгольц Г. М., 1966, с. 374—376.
↑ Фихтенгольц Г. М., 1966, с. 671.
↑ ¹ ² ³ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 3-е. — М.: Наука, 1963. — Т. III. — С. 443, 451. — 656 с.
↑ Фихтенгольц Г. М., 1966, с. 484.
↑ Фихтенгольц Г. М., 1966, с. 495—496.
↑ Robin Chapman.
↑ Wästlund, Johan. Summing inverse squares by euclidean geometry (неопр. ). Дата обращения: 6 августа 2020. Архивировано 24 февраля 2020 года.
↑ Why is pi here? And why is it squared? A geometric answer to the Basel problem на YouTube
↑ Жуков А. В. Вездесущее число «пи». — 2-е изд. — М.: Издательство ЛКИ, 2007. — С. 145. — 216 с. — ISBN 978-5-382-00174-6.
↑ ¹ ² Отрадных Ф. П. Математика XVIII века и академик Леонард Эйлер. — М.: Советская наука, 1954. — С. 33. — 39 с.
↑ Leonhard Euler, Institutiones calculi integrals
↑ Арнольд В. И. Динамика, статистика и проективная геометрия полей Галуа. — М.: МЦНМО, 2005. — С. 70. — 72 с.
↑ Cohen E. Arithmetical functions associated with arbitrary sets of integers (англ.) // Acta Arithmetica. — 1959. — Vol. 5. — P. 407—415. Архивировано 2 мая 2019 года. (см. также замечание к статье: Errata Архивная копия от 14 августа 2020 на Wayback Machine. Замечание касается «Corollary 3.3» на с. 413).
↑ Jia C.-H. The distribution of square-free numbers (англ.) // Science in China. Series A — Mathematics, Physics, Astronomy & Technological Science. — 1993. — Vol. 36, iss. 2. — P. 154—169. — doi:10.1360/ya1993-36-2-154.
↑ Pappalardi F. A Survey on k-freeness // Number Theory. Proceeding of the Conference in Analytic Number Theory in Honor of Prof. Subbarao (англ.) / Vol. Eds.: S. D. Adhikari, R. Balasubramanian, K. Srinivas. — Mysore: Ramanujan Mathematical Society, 2002. — P. 77—88. — 161 p. — (Lecture Notes Series: Number 1). — ISBN 9788190254510.
↑ Sinha K. Average orders of certain arithmetical functions (англ. ) // Journal of the Ramanujan Mathematical Society. — 2006. — Vol. 21, iss. 3. — P. 267—277. Архивировано 14 февраля 2012 года.
↑ Weisstein, Eric W. Totient Summatory Function (англ.) на сайте Wolfram MathWorld.

Литература

Айгнер М., Циглер Г. Доказательства из Книги. Лучшие доказательства со времён Евклида до наших дней. — М.: Мир, 2006. — С. 49. — 256 с. — ISBN 5-03-003690-3.
Дербишир, Джон. Простая одержимость. Бернхард Риман и величайшая нерешенная проблема в математике. — Астрель, 2010. — С. 90—92, 103—109. — 464 с. — ISBN 978-5-271-25422-2.
Дуран, Антонио. Поэзия чисел. Прекрасное и математика. — М.: Де Агостини, 2014. — 160 с. — (Мир математики: в 45 томах, том 27). — ISBN 978-5-9774-0722-9.
Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах.

— М.: Наука, 1972. — Т. III.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — Т. II. — С. 461—462, 490, 496, 671. — 800 с. — ISBN 5-9221-0155-2.
Borwein J. М., Borwein P. В., Dilcher K. Pi, Euler numbers, and asymptotic expansions // Amer. Math. Monthly. — 1989. — № 96. — P. 681—687.

Ссылки

Кохась К. П. Сумма обратных квадратов // Математическое просвещение. — 2004. — Вып. 8. — С. 142–163.
Соболевский А., доктор физ.-мат. наук (ИППИ РАН). Вокруг Базельской задачи: Бернулли, Эйлер, Риман (неопр.) (2014). — видеолекция. Дата обращения: 24 мая 2016.
Chapman, Robin. Evaluating ζ(2) (англ.) (1999). Дата обращения: 17 апреля 2016.

Pengelley D. J. Dances between continuous and discrete: Euler’s summation formula (англ.

2>6$%, и от $%1.65$% оно отличается на сколько-то тысячных. Тогда $%n=10$% должно дать хорошую точность. Пробуем (уже без «нелегальной» информации), и оно подходит. К слову сказать, $%n=9$% даёт оценку, которая чуть превышает нужную.

Здравствуйте

Математика – это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

1. Базельская задача

Для гармонического ряда аналогичная итерация дает сумму 14.3927257228, отчего гармонический ряд еще называют медленно расходящимся рядом.

Эйлер вычислил несколько первых знаков, после чего, обладая сверхъестественными способностями к вычислениям, увидел, что сумма базельского ряда равна
π 2 /6
После чего он строго доказал, что так оно и есть. Сделал он это еще в 1735 году, в Петербурге. Ход его рассуждений можно проиллюстрировать следующим образом: возьмем за основу известный ряд Тейлора:

Из школьного курса мы знаем, что при x=0, ± π, ± 2π, ± 3π . синус равен нулю.
Если рассмотреть в качестве примера алгебраическое уравнение 4-й степение:

Пусть его корни равны b, c, d и e. Тогда его можно разложить на линейные множители:

Ряд Тейлора, являясь многочленом, по основной теореме алгебры, можно аналогично представить в виде произведения одночленов:

Правая часть этого равенства преобразовывается к виду:

Если каждое выражение в скобках приравнять к нулю:
x 2 – π 2 = 0
Далее:
x 2 = π 2
Далее:
x 2 / π 2 = 1
Далее:
1 – x 2 / π 2 = 0
После чего правая часть становится равной:

При этом

Делим обе части равенства на x и получаем

Поскольку

имеем:
K ‘ =1
Получаем ряд:

После перемножения и расрытия скобок в правой части:

Делим обе части на -x 2 /π 2 и получаем:

что и требовалось доказать. Для 4-й степени:

Для 6-й степени:

ζ(8) = π 8 / 9450
ζ(10) = 691*π 10 / 638512875
ζ(12) = 2*π 12 / 18243225
ζ(14) = 3617*π 14 / 325641566250
.

Для положительных целых четных значений, кратных двум, Эйлер нашел упрощенную формулу с использованием чисел Бернулли:

или так

В 1755 году Эйлер опубликовал Наставления к дифференциальному исчислению, в которых подвел итог доказательству Базельской задачи.
На данный момент существует много ее различных доказательств, например, есть варианты, в которых используется только интегральное исчисление.

Ряд, состоящий из величин, обратных простым числам, расходится, причем еще медленнее, чем гармонический, примерно к ln(ln(p)) :

Сумма же гармонического ряда оценивается как ln(n+1) 2. Так появилась знаменитая дзета-функция Эйлера:

Он смог вычислить ее для любого четного значения S. Для нечетных функций простых формул до сих пор не найдено.
Таблица для первых 5 целых значений дзета-функции, с точностью до 12 знаков после запятой:
2 = 1.644934066848
3 = 1.202056903159
4 = 1.082323233711
5 = 1.036927755143
6 = 1. 017343061984

Дзета-функция определена не только для целых, но и рациональных чисел. Например, для s=1.1 она равна 10.58448, для s=1.0001 она равна 10000.577222.
В положительной области определения дзета-функция выглядит так:

Вообще, глядя на уравнение дзета-функции, можно сделать вывод, что она существует только для S > 1. Попробуйте подставить S 1.
На самом деле дзета-функция существует для любого значения, кроме 1, причем не только целого. В области слева от 1 дзета-функция выглядит так:

В начале отрицательной области определения дзета-функция выглядит так:

Для вычисления дзета-функции в области 1
Формула:

Между дзета-функцией и эта-функцией существует связь:

Например, чтобы вычислить дзета-функцию для 0.5, сначала с помощью ряда вычисляем эта-функцию для 0.5. Зная значения эта-функции, можно с помощью последней формулы вычислить аналогичные значения для дзета-функции. Так, например η(1/2)=0.604. . Отсюда ζ(1/2)= -1. 460.
Еще более странным выглядит алгоритм для вычисления дзета-функции для отрицательных значений. Эйлер в 1749 году предложил выразить ζ(1-x) через ζ(x). Т.е. например чтобы вычислить дзета-функцию ζ(-15), надо вычислить ζ(16) и подставить его в формулу, которая выглядит так:

Эта формула работает для целых S. Дзета-функция равна нулю всегда, когда S – отрицательное четное число. Эти нули еще называют тривиальными нулями дзета-функции.

Дзета-функция является фундаментальной функцией современной математики. Она может проявляться в самых неожиданных местах.
Так, для S=3 она равна 1.2020569. Это число называется постоянной Апери.
Постоянная Эйлера

очень важна, т.к. она используется самым неожиданным образом во множестве дисциплин: в статистике. квантовой механике, анализе и теории чисел. Существует связь между этой константой и дзета-функцией:

Существует связь между дзета-функцией и функцией Мебиуса. Областью определения функции Мебиуса являются натуральные числа 1,2,3. Вычисляется функция Мебиуса по следующему алгоритму:
μ(1)=1.
μ(n)=0, если среди делителей числа n есть квадрат.
μ(n)=-1, если число n – простое или является произведением нечетного числа различных простых чисе.
μ(n)= 1 , если число n является произведением четного числа различных простых чисел:

Существует связь между дзета-функцией и числом делителей натуральных чисел:

Существует связь между дзета-функцией и числом простых делителей натуральных чисел:

Существует связь между дзета-функцией и вероятностью выбора взаимно-простых чисел. Пусть имеется отрезок из натуральных чисел [1;N]. Из него случайно выбираем k целых чисел. Вероятность того, что эти числа взаимно просты в совокупности:

В частности, два случайно выбранных числа взаимно просты с вероятностью 6/π 2

3. Тождество Эйлера

Еще более загадочная связь существует между дзета-функцией и простыми числами. Эта связь также была установлена Эйлером. Он нашел ее, применив к дзета-функции классический алгоритм просеивания – решето Эратосфена. Доказательство может быть проиллюстрировано следующим образом:
Исходно дзета-функция имеет вид:

Умножим обе части равенства на 1/2 S , получим:

Вычитая второе из первого, удаляем все элементы с делителем 2:

Умножим обе части равенства на 1/3 S , получим:

Вычитая последнее из предпоследнего, удаляем все элементы с делителем 3:

Применяя в дальнейшем метод просеивания, умножая последовательно на величину, обратную очередному простому числу – 5, 7, 11, 13 и т.д., в конце концов получим:

Разделив последнюю формулу на все множители, получим знаменитое тождество Эйлера, в левой части которого стоит сумма величин, обратных степеням всех натуральных чисел, а в правой части стоит произведение величин, обратных степеням всех простых чисел:

которое можно записать так:

или так:

Впервые тождество упоминается Эйлером в мемуаре Various observations about infinite series, изданном в Петербурге в 1737 году, и выглядело оно вот так:

4.

О свойствах степенных рядов

У Эйлера есть работа (E352 по каталогу) о свойствах степенных рядов, которая по латински звучит как Remarques sur un beau rapport entre les series des puissances tant directes que reciproques. Ее английский перевод – Remarks on a beautiful relation between direct as well as reciprocal power series.
К моменту написания этой работы Эйлер уже определил свою знаменитую формулу для дзета-функции в виде обратного степенного ряда. Он также нашел явные формулу для четных натуральных степеней S. Но дзета-функция на тот момент была определена лишь для S > 1. В этой работе он расширяет область определения дзета-функцию на всю числовую область и выводит функциональное выражение, используя эта-функцию. Зная значение эта-функции, мы можем вычислить дзета-функцию в любой области значения, в том числе для S

Зная сумму одного из этих рядов, можно вычислить сумму другого ряда, точнее, если мы знаем сумму первого ряда для m, то сможем вычислить сумму второго ряда для : n = m+1.

Сумма первого ряда для m=1 равна 1/4 . В современных терминах это называется сумма Абеля, она определена для x, который по модулю меньше 1. Эта сумма получена исходя из того, что ряд

эквивалентен

Последнее выражение при x=1 равно 1/4.
Для других степеней аналогично:

Если подставить в правой части x=1, получим, что для второй степени сумма равна нулю, третьей – минус 2/16, четвертой – опять ноль, пятой – плюс 16/64, шестой – опять ноль и т.д.

В общем случае формула для вычисления n–й степени:

Каким образом Эйлер получил эти зависимости ? В качестве исходного ряда возьмем следующий:

Сначала умножим его на x, потом продифференцируем, и получим равенство для первой степени. Потом возьмем это равенство, умножим на x, опять продифференцируем, и получим равенство для второй степени, и т.д.

Далее Эйлер приводит формулы для расчета дзета-функции для четных положительных S. В общем виде формула выглядит так:

Здесь B – число Бернулли. Следующий код вычисляет первые несколько значений дзета-функцию по этой формуле с использованием чисел Бернулли:

Матем. просв., сер. 3, 2004, выпуск 8,

Наш семинар: математические сюжеты

Сумма обратных квадратов

Аннотация: В этой заметке мы рассказываем о том, как можно разными способами найти значение суммы
$$ 1+frac14+frac19+frac1<16>+frac1<25>+dotsb. $$
Вероятно, все изложенные здесь способы являются известными. Да и попытки устроить ревизию в этом хозяйстве уже тоже предпринимались.
Толчком к написанию этого текста послужило наблюдение, изложенное в параграфе 7, пополнению коллекции доказательств сильно помогли статья [12] и дискуссии в [18].

Полный текст: PDF файл (317 kB)
Список литературы: PDF файл HTML файл
Тип публикации: Научно-популярный, образовательный материал

Образец цитирования: К. 2 : Анализ-I

Сообщения без ответов | Активные темы | Избранное

Правила форума

В этом разделе нельзя создавать новые темы.

Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».

Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.

Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.

Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.

Verum

Помогите найти сумму ряда обратных квадратов: \sum 1/n^2

28. 04.2009, 14:22

25/04/09
5

Попробовал воспользоваться рядом,

Продифференцировал и получил

А вот найти сумму исходного ряда не могу(( не могу найти этот интеграл 🙁

gris

28. 04.2009, 14:46

Заслуженный участник

13/08/08
13984

А он не берётся в элементарных. Определённый интеграл можно через вычеты посчитать. Рассмотрите подинтегральное выражение для комплексного , разберитесь с ветвями логарифма и полюсами.

Только этот ряд ещё Эйлер считал и по другому.

Хорхе

28. 04.2009, 14:58

Заслуженный участник

14/02/07
2648

Можно несколькими способами — кроме означенного gris

ом, еще есть способ с рядами Фурье и (наверное, самый «элементарный») способ через двойной интеграл .

Тут оба способа довольно дотошно описаны (правда, на английском, но понять формулы можно на любом языке).

gris

28. 04.2009, 15:07

Заслуженный участник

13/08/08
13984

«Ряд из обратных квадратов» довольно популярный. Есть десятка два способов его вычисления. Если погуглить именно по этим словам или по «сумма обратных квадратов», то наверняка найдутся целые сборники решений.

Taras

28. 04.2009, 16:25

14/10/07
241
Киев, мм

а мне так нравится

Приравниваем коефициенты при получаем то, что хотим

ASA

28. 04.2009, 16:56

30/01/09
194

— дзета-функция Римана и, кажется, .

Добавлено спустя 15 минут 25 секунд:

Хорхе, оказывается, уже дал ссылку.

LetsGOX

28. 04.2009, 17:21

20/04/09
∞
113

Verum А эта штука случайно никак не выражается через замечательные пределы?

bundos

29.04.2009, 16:07

27/12/08
198

Используйте равентво Парсеваля для функции .

Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию

Страница 1 из 1

[ Сообщений: 8 ]

Модераторы: Модераторы Математики, Супермодераторы

Кто сейчас на конференции

Сейчас этот форум просматривают: нет зарегистрированных пользователей

Вы не можете начинать темы
Вы не можете отвечать на сообщения
Вы не можете редактировать свои сообщения
Вы не можете удалять свои сообщения
Вы не можете добавлять вложения

Найти:

∑ Сумма ряда онлайн

Препод очень удивится увидев твоё верное решение😉

Введите данные для подсчета суммы ряда

Найдем сумму ряда чисел. 2

Функция — Квадрат x

ctg(x)

Функция — Котангенс от x

arcctg(x)

Функция — Арккотангенс от x

arcctgh(x)

Функция — Гиперболический арккотангенс от x

tg(x)

Функция — Тангенс от x

tgh(x)

Функция — Тангенс гиперболический от x

cbrt(x)

Функция — кубический корень из x

gamma(x)

Гамма-функция

LambertW(x)

Функция Ламберта

x! или factorial(x)

Факториал от x

DiracDelta(x)

Дельта-функция Дирака

Heaviside(x)

Функция Хевисайда

Интегральные функции:

Si(x): Интегральный синус от x
Ci(x): Интегральный косинус от x
Shi(x): Интегральный гиперболический синус от x
Chi(x): Интегральный гиперболический косинус от x

В выражениях можно применять следующие операции:

Действительные числа: вводить в виде 7. 3; — возведение в степень
x + 7: — сложение
x — 6: — вычитание
15/7: — дробь

Другие функции:

asec(x): Функция — арксеканс от x
acsc(x): Функция — арккосеканс от x
sec(x): Функция — секанс от x
csc(x): Функция — косеканс от x
floor(x): Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
ceiling(x): Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
sign(x): Функция — Знак x
erf(x): Функция ошибок (или интеграл вероятности)
laplace(x): Функция Лапласа
asech(x): Функция — гиперболический арксеканс от x
csch(x): Функция — гиперболический косеканс от x
sech(x): Функция — гиперболический секанс от x
acsch(x): Функция — гиперболический арккосеканс от x

Постоянные:

pi: Число «Пи», которое примерно равно ~3. 14159..
e: Число e — основание натурального логарифма, примерно равно ~2,7183..
i: Комплексная единица
oo: Символ бесконечности — знак для бесконечности

Расходимость суммы обратных значений простых чисел

Сумма обратных величин простых чисел неограниченно растёт. Ось x представлена в логарифмической шкале, что показывает, что расхождение очень медленное. Красная линия является нижней оценкой и тоже растёт неограниченно.

Ряд обратных простых чисел расходится. То есть:

∑p prime1p=12+13+15+17+111+113+117+⋯=∞{\displaystyle \sum _{p{\text{ prime}}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}+{\frac {1}{17}}+\cdots =\infty }

Этот факт доказал Леонард Эйлер в 1737^[1], что усилило результат Евклида (3-й век до нашей эры), что существует бесконечно много простых чисел. {\infty }{\frac {1}{2n\ln n}}=\infty \end{aligned}}}

согласно интегральному признаку сходимости Коши — Маклорена. Это показывает, что ряд слева расходится.

Частичные суммы

В то время как частичные суммы обратных величин для простых чисел в конечном счёте достигает любое целое значение, они никогда не могут быть равны целому числу.

Одно из доказательств^[4] этого делается по индукции — первая частичная сумма равна 12{\displaystyle {\tfrac {1}{2}}} и она имеет вид oddeven{\displaystyle {\tfrac {odd}{even}}} (то есть нечётное/чётное). Если n-ая частичная сумма (для n⩾1{\displaystyle n\geqslant 1}) имеет вид oddeven{\displaystyle {\tfrac {odd}{even}}}, то (n+1){\displaystyle (n+1)}-ая сумма равна

oddeven+1pn+1=odd⋅pn+1+eveneven⋅pn+1=odd+eveneven=oddeven{\displaystyle {\frac {\text{odd}}{\text{even}}}+{\frac {1}{p_{n+1}}}={\frac {{\text{odd}}\cdot p_{n+1}+{\text{even}}}{{\text{even}}\cdot p_{n+1}}}={\frac {{\text{odd}}+{\text{even}}}{\text{even}}}={\frac {\text{odd}}{\text{even}}}}

поскольку (n+1){\displaystyle (n+1)}-ое простое число pn+1{\displaystyle p_{n+1}} нечётно. Поскольку сумма снова имеет вид oddeven{\displaystyle {\tfrac {odd}{even}}}, частичная сумма не может быть целым числом (2 делит знаменатель, но не делит числитель), что и доказывает утверждение.

Другое доказательство переписывает выражение для суммы первых n обратных значений для простых чисел (или суммы обратных значений любого множества простых) в терминах общего знаменателя, которое является произведением всех этих простых чисел. Тогда каждое из этих простых чисел делит все члены числителя, кроме одного, а потому не делит числитель в целом. Но каждое простое делит знаменатель. Таким образом, дробь неприводима и не является целым числом.

См. также

Теорема Евклида, гласящая, что существует бесконечно много простых чисел.
Теорема Бруна о сходимости суммы обратных значений простых чисел-близнецов к константе Бруна.

Примечания

↑ Euler, 1737, с. 160–188.
↑ Euler, 1748, с. 228, ex. 1.
↑ Mertens, 1874, с. 46–62.
↑ Lord, 2015, с. 128–130.

Литература

William Dunham. Euler The Master of Us All. — MAA, 1999. — P. 61–79. — ISBN 0-88385-328-0.
Leonhard Euler. Various observations concerning infinite series = Variae observationes circa series infinitas // Commentarii Academiae Scientiarum Petropolitanae. — 1737. — Т. 9.
Leonhard Euler. Introductio in analysin infinitorum. Tomus Primus. — Lausanne: Bousquet, 1748.
Mertens F. Ein Beitrag zur analytischer Zahlentheorie // J. Reine Angew. Math.. — 1874. — Т. 78.
Nick Lord. Quick proofs that certain sums of fractions are not integers // The Mathematical Gazette. — 2015. — Т. 99. — doi:10.1017/mag.2014.16.

Ссылки

Caldwell, Chris K. There are infinitely many primes, but, how big of an infinity? (неопр.).

Суммы квадратов, суммы кубов…

Суммы квадратов, суммы кубов.

2}4. $$

Заметно сложнее угадать формулу для суммы четвертых степеней. В отличие от предыдущих случаев, у $S_4(n)$ практически не видно общих делителей с $S_1(n)$ (кроме двойки). Зато можно заметить, что 14 и 98 делятся на 7, 55 и 979 на 11… Посмотрим на отношение $S_4/S_2$.

$n$	1	2	3	4	5	6
$S_2$	1	5	14	30	55	91
$S_4$	1	17	98	354	979	2275
$S_4/S_2$	1	17/5	7	59/5	89/5	25

Видно, что после домножения этого отношения на 5 получится последовательность целых чисел: 5, 17, 35, 59, 89, 125… Тут уже нельзя сказать, что разность соседних чисел неизменна… Все же посмотрим на эти разности: 12, 18, 24, 30… — закономерность сразу видна!

Таким образом, гипотеза состоит в том, что $$ S_4(n)/S_2(n)= \frac{5+6\cdot2+6\cdot3+\ldots+6n}5= \frac{6\frac{n(n+1)}2-1}5= \frac{3n^2+3n-1}5, $$ и соответственно $$ S_4(n)=\frac{n(n+1)(2n+1)(3n^2+3n-1)}{30}. 2}6$ (т. е. значений знаменитой дзета-функции), и в комбинаторике, и в теории чисел, и в топологии…

Литература

Д. Пойа. Математика и правдоподобные рассуждения (М.: Наука, 1975)
http://ilib.mccme.ru/djvu/polya/rassuzhdenija.htm
Мало где можно прочитать не о конкретной области математики, а о том, как вообще решать новую для себя математическую задачу. Подсказки и решение выше по существу следуют главе 7 этой замечательной книги.
Интервью с академиком И. М. Гельфандом // Квант, 1989, № 1, 3–12
http://kvant.mccme.ru/1989/01/akademik_izrail_moiseevich_gel.htm
В решении выше сделана попытка объяснить, как некоторые формулы для сумм степеней мог бы искать любой человек. Интересующимся математикой может быть интересно прочитать, как такую задачу решал в школьные годы один из выдающихся математиков 20 века (собственно про это — небольшой фразмент на стр. 8–9, но все интервью интересное).

В. С. Абрамович. Суммы одинаковых степеней натуральных чисел // Квант, 1973, № 5, 22–25
http://kvant.

наверх

2}{6}$$

5. Перейдите на google.com и выполните поиск о проблеме Базеля и дзета-функции Римана.

О суммах рядов обратных величин | Марко Тавора, доктор философии.

Изображение Пита Линфорта с Pixabay

В 1735 году известный математик Леонард Эйлер опубликовал статью « De summis serierum reciprocarum » (О суммах ряда обратных величин), показанную на рис. 1 (нажмите на эту ссылку, чтобы прочитать полную статью). ). В этой работе великий мастер нашел общую замкнутую формулу суммы:

Уравнение 1: Сумма обратных величин четных степеней целых чисел.

Удивительно умный метод Эйлера «с тех пор очаровывает математиков». Эйлер ранее доказал проблему Базеля в 1734 году. Этот результат расширяет проблему Базеля с показателя 2 до любого четного показателя.

Рисунок 1: Эйлер и его знаковая статья « De summis serierum reciprocarum » (источник).

Три первых примера:

Уравнение 2: Три первых примера уравнения. 1, для k = 1, 2 и 3.

Первая — это Базельская проблема, впервые доказанная Эйлером за год до этого.

Обратите внимание, что первый случай в уравнении. 2 — это Базельская проблема, также решенная Эйлером (в 1734 г.), рассмотренная в одной из моих недавних статей.

Рисунок 2: Страница из Seki Kōwas Katsuyo Sanpō от 1712 года, где он сводит в таблицу биномиальные коэффициенты и числа Бернулли (источник).

Но прежде чем приступить к замечательному доказательству Эйлера, необходимо объяснить понятие чисел Бернулли.

Рисунок 3: Один из нескольких выдающихся математиков в своей семье, Якоб Бернулли, открыл числа Бернулли, в честь которых они названы (источник). Числа были найдены независимо друг от друга японским математиком Секи Кова.

Это первая часть доказательства. Начнем с того, что напомним читателю концепцию ряда Тейлора. Ряд Тейлора можно быстро определить как «разложение в ряд функции относительно точки». Тема ряда Тейлора обширна, поэтому вместо того, чтобы подробно исследовать ее здесь, я ограничусь только одним случаем — разложением экспоненциальной функции e ˣ. Он определяется по формуле:

Уравнение 3: Ряд Тейлора для экспоненциальной функции. Его радиус сходимости ∞ и, следовательно, он сходится для всех значений х ∈ ℝ.

Радиус сходимости R для e ˣ равен R=∞. Это означает, что уравнение 3 — степенной ряд, сходящийся для всех значений x ∈ ℝ.

Рисунок 4: Эта анимация показывает, что по мере того, как мы включаем больше терминов в уравнение. 3 приближаемся к e ˣ.

Теперь, чтобы получить числа Бернулли, мы делаем два шага. Первый тривиален: мы вычитаем 1 из обеих частей уравнения. 3 и разделить на х. Получаем:

Уравнение 4: Ряд Тейлора для функции (e ˣ-1)/x получается после простой обработки уравнения. 3.

действительно для x ≠ 0. Числа Бернулли определяются путем инвертирования этого ряда следующим образом:

Уравнение 5: Как (косвенно) определяются числа Бернулли.

Чтобы найти B s, воспользуемся математическим приемом. Поскольку уравнение 4 и уравнение. 5 являются обратными друг другу (по построению), их произведение равно 1. Затем мы можем умножить правые части обоих уравнений, а затем умножить полученное произведение на н !.

После несложных алгебраических вычислений мы получаем красивое выражение, позволяющее сразу определить числа Бернулли:

Уравнение 6: Уравнения, из которых можно быстро вычислить число Бернулли.

В результате получаются первые числа Бернулли:

Уравнение 7: Первые числа Бернулли, полученные из уравнения. 6.

Приведем теперь вторую часть доказательства. В этом разделе нам нужно будет выразить тангенс x через числа Бернулли. Сначала рассмотрим следующее тождество:

что дает:

Уравнение 8: Степенной ряд в терминах чисел Бернулли.

Теперь мы выполняем два простых шага. Замените x в правой части уравнения 8 на 2 ix (где i — мнимая единица измерения), чтобы получить:

Теперь, сделав ту же замену в левой части уравнения. 8 получаем:

Уравнение 9: Степенной ряд для x cot x, записанный в терминах чисел Бернулли.

Затем мы используем тригонометрическое тождество

и уравнение. 9, чтобы прибыть в:

Уравнение 10: Степенной ряд для tan x, записанный в терминах чисел Бернулли.

Теперь к третьей и последней части доказательства. Используя неполные дроби, Эйлер пришел к следующему разложению:

Уравнение 11: Разложение x cot πx для нецелого числа x, также открытое Эйлером.

Теперь мы сравним уравнение. 9 и уравнение. 11 заменив x на πx в первом. После некоторых простых манипуляций мы приходим к этому чудесному выражению:

Уравнение 12: Результат, к которому мы стремились. Обратите внимание, что показатель степени всегда четный. Нет эквивалентного разложения для нечетных показателей.

Интересно, что аналогичной формулы для нечетных показателей степени нет (для k =1 сумма обратных величин кубов равна числу ~1,20, называемому константой Апери, но общей формулы, подобной уравнению 12, не существует). Может быть, кто-то, читающий это, узнает это!

На моем Github и личном веб-сайте www. marcotavora.me есть другие интересные материалы как по математике, так и по другим темам, таким как физика, наука о данных и финансы. Проверь их!

Обратная функция квадратного корня

Поиск

Чтобы найти обратную функцию квадратного корня, очень важно сначала набросать или построить график данной задачи, чтобы четко определить, каковы область и диапазон. Я буду использовать домен и диапазон исходной функции, чтобы описать домен и диапазон обратной функции, поменяв их местами. Если вам нужна дополнительная информация о том, что я имел в виду под «обменом доменов и диапазонов» между функцией и ее обратной функцией, см. мой предыдущий урок об этом.

Пример 1: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.

Каждый раз, когда я сталкиваюсь с функцией квадратного корня с линейным членом внутри подкоренного символа, я всегда думаю о ней как о «половине параболы», нарисованной сбоку. Поскольку это положительный случай функции извлечения квадратного корня, я уверен, что ее диапазон будет становиться все более положительным, проще говоря, взлетать до положительной бесконечности.

Эта конкретная функция квадратного корня имеет этот график с указанными доменом и диапазоном.

С этого момента мне придется решать обратное алгебраически, следуя предложенным шагам. По сути, замените \color{red}f\left( x \right) на \color{red}y, поменяйте местами x и y в уравнении, найдите y, который вскоре будет заменен соответствующим обратным обозначением, и, наконец, укажите домен и диапазон.

Не забудьте использовать методы решения радикальных уравнений, чтобы найти обратное. Возведение в квадрат или возведение во вторую степень члена квадратного корня должно устранить радикал. Тем не менее, вы должны сделать это для обеих сторон уравнения, чтобы сохранить его сбалансированным.

Убедитесь, что домен и диапазон обратной функции совпадают с исходной функцией. Они должны быть «напротив друг друга».

Размещение графиков исходной функции и ее обратной на одной оси координат.

Видите их симметрию по линии y = x? См. зеленую пунктирную линию.

Пример 2: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.

Эта функция является «нижней половиной» параболы, поскольку функция квадратного корня отрицательна. Этот отрицательный символ просто замаскирован -1. 92} = 1. Его домен и диапазон будут измененной «версией» исходной функции.

Пример 3: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.

Это график исходной функции, показывающий как ее домен, так и диапазон.

Определение диапазона обычно является сложной задачей. Лучший способ найти его — использовать график заданной функции с ее областью определения. Проанализируйте, как функция ведет себя вдоль оси y, рассматривая значения x из области.

Вот шаги, чтобы решить или найти обратную функцию квадратного корня.

Как видите, это очень просто. Убедитесь, что вы делаете это осторожно, чтобы избежать ненужных алгебраических ошибок.

Пример 4: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.

Эта функция представляет собой одну четвертую (четверть) круга с радиусом 3, расположенного в квадранте II. Другой способ его увидеть, это половина полукруга, расположенная над горизонтальной осью.

Я знаю, что он пройдет тест горизонтальной линии, потому что ни одна горизонтальная линия не пересекает его более одного раза. Это хороший кандидат на наличие обратной функции.

Опять же, я могу легко описать диапазон, потому что потратил время на его график. Что ж, я надеюсь, что вы осознаете важность наличия наглядного пособия, помогающего определить этот «неуловимый» диапазон.

Наличие в квадрате члена внутри подкоренного символа говорит мне, что я применю операцию извлечения квадратного корня к обеим частям уравнения, чтобы найти обратную. Таким образом, у меня будет плюс или минус случай. Это ситуация, когда я приму решение о том, какую из них выбрать в качестве правильной обратной функции. Помните, что обратная функция уникальна, поэтому я не могу допустить, чтобы у вас было два ответа.

Как мне решить, какой из них выбрать? Ключевым моментом является рассмотрение домена и диапазона исходной функции. Я поменяю их местами, чтобы получить домен и диапазон обратной функции. Используйте эту информацию, чтобы сопоставить, какая из двух функций-кандидатов удовлетворяет требуемым условиям.

Хотя у них один и тот же домен, диапазон здесь является решающим! Диапазон говорит нам о том, что обратная функция имеет минимальное значение y = -3 и максимальное значение y = 0.

Случай с положительным квадратным корнем не соответствует этому условию, поскольку он имеет минимум при y = 0 и максимум при y = 3. Отрицательный случай должен быть очевидным выбором даже при дальнейшем анализе.

Пример 5: Найдите обратную функцию, если она существует. Укажите его домен и диапазон.

Полезно увидеть график исходной функции, потому что мы можем легко определить ее домен и диапазон.

Отрицательный знак функции квадратного корня означает, что она находится ниже горизонтальной оси. Обратите внимание, что это похоже на пример 4. Это также четверть круга, но с радиусом 5. Домен заставляет четверть круга оставаться в квадранте IV.

Вот как мы алгебраически находим его обратное.

Вы выбрали правильную обратную функцию из двух возможных? Ответ – случай с положительным знаком.

Вас также может заинтересовать:

Обратная функция матрицы 2×2

Обратная функция абсолютного значения

Обратная функция постоянной Логарифмическая функция

Обратная квадратичная функция

Обратная рациональная функция

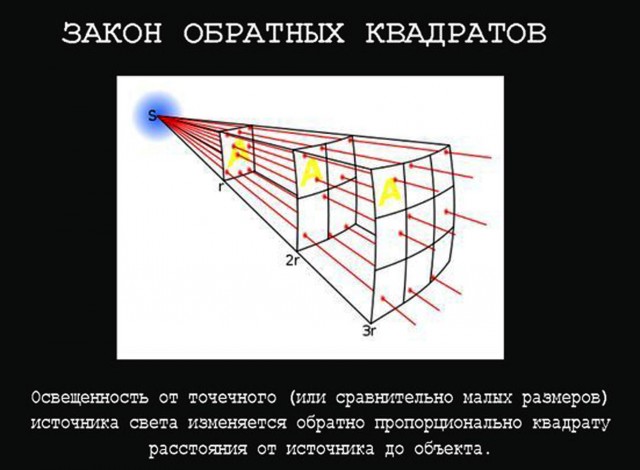
Закон обратных квадратов для чайников и практическое правило фотографии

Раскрытие информации: Этот пост может содержать партнерские ссылки. Я получаю небольшую комиссию от продажи продуктов, чтобы поддерживать работу этого сайта.

Я любил уроки физики в старшей школе. В колледже я получил несовершеннолетние по математике и технике. Но я почесал затылок, когда впервые прочитал о том, как объясняется закон обратных квадратов для фотографии со вспышкой. Это объяснение, график и калькулятор сделают это намного проще, чем многие другие объяснения.

Содержание

Объяснение закона обратных квадратов

Математик скажет вам, что закон обратных квадратов гласит, что интенсивность силы обратно пропорциональна квадрату расстояния до этой силы .

Вы скажете, что?

Затем математик попытается прояснить это, записав формулу закона обратных квадратов: Интенсивность = 1/D ² .

Самое простое фиктивное пещерное объяснение закона обратных квадратов заключается в том, что сила резко падает по мере удаления от источника, а затем ослабевает. это нет математики объяснение и вот как выглядит график пещерного человека по закону обратных квадратов:

Базовый калькулятор закона обратных квадратов

Поиграйте с ползунком, чтобы посмотреть, что произойдет. Обратите внимание, что первое снижение прочности происходит на 75%, а следующее только на 14%.

Как закон обратных квадратов применим к фотографии?

В фотографии, что буквально означает «писать светом», закон обратных квадратов описывает поведение света.

Несмотря на то, что он описывает поведение всех источников света, он наиболее полезен при съемке со вспышкой.

Для следующего калькулятора закона обратных квадратов мы рассмотрим флэш-память с ведущим числом 60. Ведущие числа — тема этой статьи. Сейчас это не важно, просто знайте, что для этого примера вы получите 100% силу на дистанции 60 метров.

Поэкспериментируйте с ползунком, чтобы увидеть, что происходит с мощностью вспышки на объекте при изменении расстояния с шагом 30 метров.

Крутые интерактивные ползунки, но какое практическое применение закона обратных квадратов для фотографии?

Представьте, что вы делаете групповой портрет с одной мощной вспышкой. Вам понадобится широкоугольный объектив, потому что они рассчитаны на пятнадцать человек. Они, конечно, с подсветкой, потому что ничто никогда не бывает легким. Вы уменьшаете головку вспышки и ставите перед ней зонт, чтобы обеспечить охват всех на фотографии.

Теперь вы размещаете вспышку как можно ближе к объектам съемки или отходите от них? Как вы аргументируете свой ответ?

Улучшите свои фотографии, ежемесячно получая дополнительные советы, подобные этому. Нажмите здесь (открывается в новом окне).

Посмотрите на следующие схемы.

В первом мы разместили вспышку в 10 футах от центра группы, которая имеет ширину 30 футов. Я проведу для вас тригонометрию, но люди на концах находятся в 18 футах от вспышки — почти вдвое больше, чем в центре.

Если люди в центре получают правильную экспозицию вспышки, то люди на концах получат примерно 25% этой мощности. Они будут темными, недоэкспонированными на целых два стопа.

На второй диаграмме мы перемещаем вспышку дальше от центра нашей группы. Тридцать футов. Тригонометрия говорит нам, что люди на концах находятся в 33 футах от вспышки — чуть больше центра.

Люди на концах получают 83% света, что и люди в центре. Это разница всего около трети стопа — разница незаметна для большинства людей.

Фактическая установка мощности вспышки не имеет ничего общего с отношения света, падающего на все ваши объекты.

Эмпирическое правило простого закона обратных квадратов

Если вы хотите, чтобы объекты были равномерно освещены с одной стороны на другую, увеличьте мощность и сделайте расстояние вспышки не менее ширины вашего тема . Чем дальше, тем лучше.

Если объект имеет ширину десять футов, поместите вспышку на расстоянии не менее десяти футов от центра.
Если объект шириной тридцать футов, поместите вспышку не менее тридцати футов.
И так далее.

Сделайте треугольник похожим на второй рисунок выше, а не на первый.

Если вы ищете резкое затемнение , например, если вы хотите просто осветить объект, но не фон, уменьшите мощность и поместите источник света как можно ближе к объекту . Чем он ближе, тем резче спад.

После того, как вы это сделаете (каламбур?), остается только отрегулировать мощность вспышки для правильной экспозиции.

Закон обратных квадратов касается расстояния, а не мощности вспышки.

Теперь все это имеет смысл?

Посмотрите это видео от Марка Уоллеса из AdoramaTV для ознакомления:

Понимание закона обратных квадратов света

связь между апертурой и законом обратных квадратов света, а также их влияние на ослабление света.

Содержание

Шкала диафрагмы (диафрагма)

Позвольте мне облегчить ваше знакомство с этой темой, объяснив сначала значение диафрагмы.

Переключение с максимальной диафрагмы на следующую меньшую уменьшает количество света, попадающего на объектив. Кроме того, диаметр апертуры каждый раз уменьшается в 1/√2 раза, что также сокращает поверхность линзы и, следовательно, количество света на вдвое меньше .

Благодаря этой градации мы просто адаптируем выдержку и диафрагму к существующему освещению: каждое число f (f-stop) является результатом предыдущего, умноженного на √2 (что равно 1,414). Мы округляем результат до 1,4, чтобы, например, апертура 4 — согласно расчету 4 x 1,4 — превратилась в следующее большее значение апертуры 5,6.

Вот отрывок из этой известной последовательности, которая выглядит следующим образом:

f/1 f/1.4 f/2 f/2.8 f/4 f/5.6 f/8 f/11 f/16 f/22 f /32

В редких случаях существуют макрообъективы с максимальным числом f 45. Поскольку макрообъективы часто располагаются очень близко к объекту, большое число f позволяет достичь хорошей глубины резкости. (несмотря на близость).

Закон обратных квадратов света

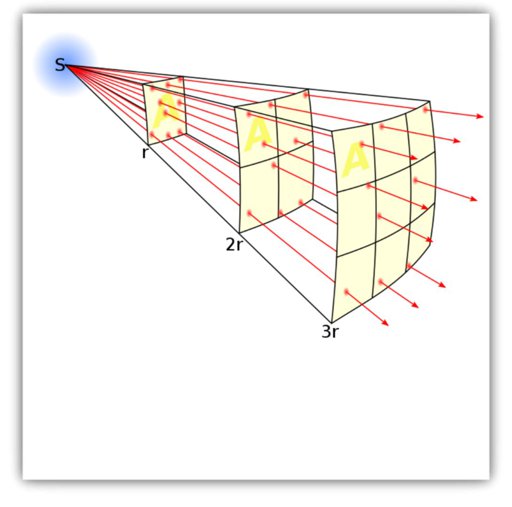
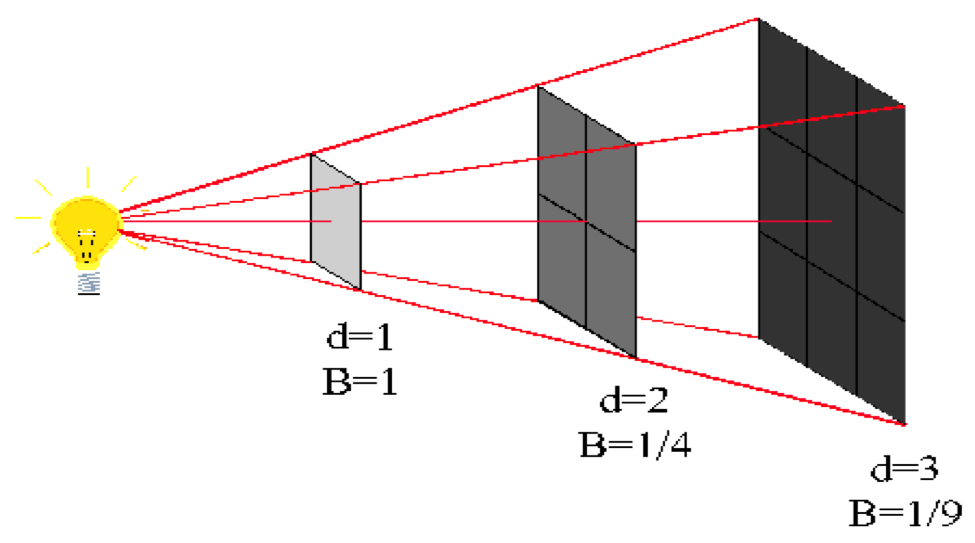
Мы создаем идеальное освещение для каждого сценария с помощью закона обратных квадратов. Закон обратных квадратов работает следующим образом: если вы удвоите расстояние между объектом и источником света, он освещает площадь поверхности, в четыре раза большую, чем предыдущая.

Обычно мы умножаем расстояние на себя, чтобы рассчитать увеличение площади этой поверхности. Однако большая площадь поверхности приводит к интенсивности света, которая обратно пропорциональна квадрату расстояния, поскольку такое же количество света должно быть распределено на большую площадь поверхности соответственно.

Таким образом, мы видим ослабление света, что означает уменьшение интенсивности света.

С технической точки зрения закон обратных квадратов выглядит следующим образом: Энергия (в нашем случае: интенсивность света) в месте А (области объекта) уменьшается обратно пропорционально квадрату расстояния А до источника энергии (например, нашей вспышки). глава).

Чтобы записать закон обратных квадратов (его формулу), потребуются лишь базовые математические знания. Однако физика, стоящая за этим, как правило, очень сложна. По этой причине мы собираемся подойти к этому закону только иллюстративно и с точки зрения фотографии. По этой причине мы имеем в виду экспозицию датчика изображения или пленки и освещение объекта. При использовании вспышки и прожектора закон обратных квадратов особенно удобен.

Интенсивность света, например, увеличивается в четыре раза (4) при уменьшении вдвое (1/2) расстояния до источника света и объекта. Соответственно, интенсивность света уменьшится до четверти, если мы удвоим расстояние. В соответствии с этим эти примерные пары цифр действительны (расстояние: 3-кратное; интенсивность: 1/9) и (4; 1/16), если мы умножим расстояние соответственно.

В общем, закон обратных квадратов объясняет непропорциональное падение света с увеличением расстояния от объекта до источника света. Эти знания помогают нам лучше понять, как соотнести свет и освещение с расстоянием до объекта и его яркостью.

Практическое применение

Из-за обратно-квадратичной зависимости описанного закона интенсивность света довольно сильно падает, когда объект сначала удаляется от источника света. После этого она непрерывно снижается на более слабом уровне. Например: если мы увеличим расстояние между источником света и объектом с 1 метра до 2 метров, 75 процентов интенсивности света будет потеряно на объекте. Но когда мы увеличиваем дистанцию с 4 до 10 метров, мы теряем всего 5 процентов.

Таким образом, интенсивность света вблизи источника света имеет особенно высокие значения. Но на расстоянии эта интенсивность достигает лишь крошечного значения. Вот как мы создаем соответствующее освещение: при постоянной выдержке значение f увеличивается, чем ближе объект находится к источнику света — чем меньше диафрагма, тем меньше света попадает в камеру.

И наоборот: значение f уменьшается по мере увеличения расстояния от объекта до источника света. В обоих случаях соответствующие снимки выглядят почти одинаково: просто потому, что через объектив проходит одинаковое количество света.

Так мы теоретически создаем правильное значение f для каждой комбинации расстояния, интенсивности света и скорости затвора.

Освещение только одного объекта

Для статических объектов достаточно одного фиксированного значения f. Однако для движущихся объектов требуются гибкие значения f, особенно когда они находятся очень близко к источнику света: из-за закона обратных квадратов небольшое изменение расстояния до источника света приводит к резкому изменению освещения. В свою очередь, одного фиксированного значения f достаточно для объекта, находящегося на большом расстоянии, даже если он перемещается в большем масштабе.

Освещение нескольких объектов

Иногда все объекты располагаются довольно близко к источнику света в виде прожектора или т.п. В таких случаях передний объект может быть переэкспонирован, тогда как тот, что сзади, останется недоэкспонированным.

Например, три объекта, расположенные друг за другом, пересекают значения f в диапазоне от f/22 до f/11. У этой проблемы есть простое решение, позволяющее равномерно осветить все объекты: просто расположите все объекты подальше от источника света. Таким образом, их относительные размеры по отношению друг к другу остаются одинаковыми, и всем им требуется только одно и то же значение f для хорошей экспозиции, например, f/4.

Вы можете очень хорошо увидеть различия в нашем примере ниже. Если освещение расположено на расстоянии 8 метров от первой модели, падение света до 4-й модели составляет всего около 2/3 ступеней. Однако, если бы вы разместили источник света всего в 2 метрах, разница в яркости между 1-й и 4-й моделями составила бы всего 2 1/3 ступени (например, f-stop 8 -> 3,5)!

Специальная проблема: Правильное освещение фона

Разумеется, в наших изображениях мы часто также хотим видеть контрасты вместо равномерной яркости: нам нужны более светлые и темные части изображения. Например, нам нужен достаточно темный фон, на котором наша привлекательная модель будет правильно и ярко освещена – близко к источнику света! Квадратичный спад света к более дальнему фону приводит к недоэкспонированному и, следовательно, темному фону. Вот как сильный контраст работает в нашу пользу благодаря закону обратных квадратов.

В свою очередь, мы также используем этот «закон обратных квадратов», когда хотим получить равномерное и хорошее освещение модели и фона: Затем мы размещаем источник света на значительном расстоянии как от модели, так и от фона — таким образом мы достигаем очень ровное освещение.

Как видно на примере ниже, уже достаточно разместить источник света на расстоянии 4 метров от модели, чтобы равномерно осветить и модель, и фон. Разница между моделью и фоном теперь составляет всего 2/2 стопа. Если бы модель была еще ближе к фону, падение света можно было бы уменьшить еще больше.

Кстати, если источник света расположить слишком близко к модели (всего 1 метр здесь), как видно на верхнем примере, падение света на корпусе модели уже настолько велико, что – в случае снимка в полный рост — ноги будут недоэкспонированы. Поэтому такое позиционирование стоит рассматривать только для портретного снимка.

Связь между головкой вспышки, мощностью, ISO и диафрагмой

Чтобы еще лучше увидеть зависимости, мы установили как можно больше значений относительно друг друга, как показано на графическом рисунке ниже.

Мы предполагаем головку вспышки мощностью 1000 Вт с гигантским диапазоном регулирования от 1 до 10. Значения диафрагмы и ISO были выбраны для отображения зависимости между этими цифрами. Значение ISO или диафрагмы (имеется в виду только одно из этих двух значений) необходимо установить в соответствии с таблицей, чтобы всегда получать одинаковое освещение (яркость) объекта при регулировке выходного контроллера головки вспышки.

Что сразу бросается в глаза, так это то, что выходная мощность головки вспышки (ватт/секунды) должна быть удвоена на каждую диафрагму. Таким образом, выход в верхнем диапазоне между 9и 10 увеличивается в общей сложности на 500 Вт, тогда как выходная мощность в нижнем диапазоне между 1 и 2 изменяется только прибл. 0,2 Вт. Теперь, взглянув на эти довольно экстремальные различия в мощности, вы поймете, какая большая работа по разработке потребовалась производителям головок вспышки, чтобы сделать все возможное с такой исключительно высокой точностью.

Заключение

Так что же вам обязательно следует помнить?

Относительно диафрагмы : Разница от одного диафрагменного числа к другому всегда приводит либо к удвоению, либо к уменьшению вдвое яркости. Для вспышки это также всегда означает удвоение или уменьшение вдвое мощности (Ws). Например, если мощность вспышки изменить с 5 на 6, то это в точности равно одному диафрагменному числу.

Относительно расстояния : Если объект расположен близко к источнику света, падение света на указанном объекте будет очень большим по сравнению с фоном. Легкий спад на площадь! При удвоении расстояния до объекта требуется в 4 раза больше световой энергии, чтобы сбалансировать разницу в яркости.

Удвоение/уменьшение вдвое расстояния всегда равно 2 ступеням диафрагмы относительно разницы яркости!

Большее расстояние между источником света и объектом приводит к более равномерному освещению как объекта, так и фона, так как с увеличением расстояния уменьшается ослабление света. Поэтому этот эффект оказывает огромное влияние на дизайн освещения.

P.S. Вы можете экспериментировать с расстояниями, апертурой и светоотдачей в set.a.light 3D, который был показан здесь еще в 2013 году. Это того стоит! Как только вы полностью поймете взаимосвязь между расстоянием, апертурой и ослаблением света, вы сможете легко использовать эти эффекты, чтобы улучшить дизайн освещения и выборочно управлять им.

Об авторе : Йоханнес Даунер является основателем и генеральным директором Elixxier, компании-разработчика программного обеспечения set.a.light 3D, которое позволяет фотографам планировать технические детали фотосессии в виртуальной среде. Эта статья также была опубликована здесь.

Обратные функции

Обратные функции работают в обратном направлении!

Начнем с примера:

Здесь у нас есть функция f(x) = 2x+3 , записанная в виде блок-схемы:

Таким образом, инверсия: 2x+3 равна: (y-3)/2

Инверсию обычно показывают, добавляя маленькую «-1» после имени функции, например:

f ^-1 (y)

Мы говорим « f обратное y»

Итак, обратное выражение f(x) = 2x+3 записывается:

f ^{-1 y) = (y-3)/2}

(я также использовал y вместо x , чтобы показать, что мы используем другое значение). заключается в том, что она должна вернуть нам исходное значение:

Когда функция f превращает яблоко в банан,
Затем обратная функция f ^-1 превращает банан обратно в яблоко

Пример:

Используя приведенные выше формулы, мы можем начать с x=4:

f(4) = 2×4 +3 = 11

Затем мы можем использовать обратное число 11:

f ^-1 (11) = (11-3)/2 = 4

И мы волшебным образом снова получаем 4 !

Мы можем записать это в одну строку:

f ^-1 ( f(4) ) = 4

0062

Таким образом, применение функции f, а затем обратной функции f ^-1 снова дает нам исходное значение:

f ^-1 ( f(x) ) = x

другой порядок, и он все еще работает:

f( f ^-1 (x)) = x

Пример:

Начните с:

f ^-1 (11) = (11-3)/2 = 4

И тогда:

f(4) = 2×4+3 = 11

Итак, мы можем сказать:

f( f ^-1 (11) ) = 11

«f от f, обратное 11, равно 11»

Решить с помощью алгебры

Мы можем решить обратное с помощью алгебры. Подставьте «y» вместо «f(x)» и найдите x:

Функция:	ф(х)	=	2x+3
Поставьте «y» вместо «f(x)»:	г	=	2x+3
Вычесть 3 с обеих сторон:	у-3	=	2x
Разделите обе стороны на 2:	(у-3)/2	=	х
Поменять стороны:	х	=	(у-3)/2

Решение (поместите «f ^-1 (y)» вместо «x»):	ж ^-1 (у)	=	(у-3)/2

Этот метод хорошо работает для более сложных инверсий.

Фаренгейты в Цельсии

Полезным примером является преобразование Фаренгейтов в Цельсий:

Чтобы преобразовать Фаренгейты в Цельсии: f(F) = (F — 32) × 5 9
4 Обратное (обратно по Цельсию в градусы Фаренгейта): f ^-1 (C) = (C × 9 5 ) + 32

Для вас: посмотрите, сможете ли вы выполнить шаги для создания этой инверсии!

Обратные общие функции

До сих пор это было легко, потому что мы знаем, что обратная функция умножения — это деление, а обратная функция сложения — вычитание, но как насчет других функций?

Вот список, который вам поможет:

Инверсия			Осторожно!
	<=>
	<=>		Не делить на ноль
1 х	<=>	1 г	x и y не равны нулю
x ²	<=>		х и у ≥ 0
x ^нет	<=>	или	n не ноль (разные правила когда n нечетное, четное, отрицательное или положительное)
е ^х	<=>	п(у)	г > 0
а ^х	<=>	журнал _a (у)	г и а > 0
sin(x)	<=>	грех ^-1 (у)	от -π/2 до +π/2
кос(х)	<=>	соз ^-1 (у)	от 0 до π
желтовато-коричневый(х)	<=>	рыжевато-коричневый ^-1 (у)	от -π/2 до +π/2

(Примечание: вы можете прочитать больше об арксинусе, косинусе и тангенсе. )

Осторожно!

Вы видели «Осторожно!» колонка выше? Это связано с тем, что некоторые инверсии работают только с определенными значениями .

Пример: Возведение в квадрат и квадратный корень

Когда мы возводим в квадрат отрицательное число , а затем делаем обратное, получается следующее:

Квадрат:(−2) ² = 4

Обратный (квадратный корень): √(4) = 2

Но мы не вернули исходное значение! Мы получили 2 вместо −2 . Наша вина, что мы не были осторожны!

Таким образом, функция квадрата (в ее нынешнем виде) не имеет обратной

Но мы можем это исправить!

Ограничить домен (значения, которые могут быть переданы в функцию).

Пример: (продолжение)

Просто убедитесь, что мы не используем отрицательные числа.

Другими словами, ограничьте его до 90 524 x ≥ 0 , и тогда мы получим обратное.

Итак, у нас есть такая ситуация:

x ² имеет ли , а не обратную
но {х ² | x ≥ 0 } (что говорит «x в квадрате, так что x больше или равен нулю», используя нотацию построителя наборов) имеет ли инверсию.

Нет обратного?

Давайте графически посмотрим, что здесь происходит:

Чтобы получить обратное значение, нам нужно уникальных значения .

Только подумайте… если есть два или более x-значения для одного y-значения , как мы узнаем, какое из них выбрать при возвращении?

Общая функция

Нет обратного

Представьте, что мы пришли к от x ₁ к определенному значению y, куда мы вернемся? х ₁ или х ₂ ?

В этом случае у нас не может быть обратного.

Но если мы можем иметь ровно один x для каждого y, мы можем получить обратное.

Это называется «однозначным соответствием» или Биективной функцией, например

Биективной функцией

Имеет обратный

Функция должна быть «биективной», чтобы иметь обратную.

Таким образом, биективная функция подчиняется более строгим правилам, чем общая функция, что позволяет нам иметь обратную функцию.

Домен и диапазон

Итак, о чем все эти разговоры о « Ограничение домена «?

В своей простейшей форме домен — это все значения, которые входят в функцию (а диапазон — это все значения, которые выходят).

В нынешнем виде приведенная выше функция имеет обратную функцию , а не , потому что некоторые значения y будут иметь более одного значения x.

Но мы могли бы ограничить домен, чтобы было уникальный x для каждого y …

… и теперь мы можем иметь обратное:

Обратите также внимание:

Функция f(x) переходит из домена в диапазон ,
Обратная функция f ^-1 (y) переходит из диапазона обратно в домен.

Давайте изобразим их обоих с точки зрения x . .. так что теперь f ^-1 (x) , а не f ^-1 (y) :

f(x) и f ^-1 (x) подобны зеркальным отражениям
(перевернуто по диагонали).

Другими словами:

График f(x) и f ^-1 (x) симметричен относительно прямой y=x

Пример:

)

Сначала , мы ограничиваем домен до x ≥ 0 :

{х ² | x ≥ 0 } «x в квадрате так, что x больше или равен нулю»
{√x | x ≥ 0 } «квадратный корень из x такой, что x больше или равен нулю»

И вы можете видеть, что они «зеркальные изображения»
относительно диагонали y=x.

Примечание: когда мы ограничиваем домен до x ≤ 0 (меньше или равно 0), обратное значение равно f ^-1 (x) = −√x :

{x ² | х ≤ 0 }
{−√x | х ≥ 0 }

Которые тоже обратные.

Ряд обратных квадратов: Ряд обратных квадратов — Вики

Содержание

История

Сходимость ряда

Второй метод Эйлера

Некоторые применения

Примечания

Литература

Ссылки

Здравствуйте

1. Базельская задача

3. Тождество Эйлера

4.

Правила форума

Кто сейчас на конференции

∑ Сумма ряда онлайн

Препод очень удивится увидев твоё верное решение😉

Введите данные для подсчета суммы ряда

Расходимость суммы обратных значений простых чисел

Частичные суммы

См. также

Примечания

Литература

Ссылки

Суммы квадратов, суммы кубов…

Литература

О суммах рядов обратных величин | Марко Тавора, доктор философии.

Обратная функция квадратного корня

Закон обратных квадратов для чайников и практическое правило фотографии

Объяснение закона обратных квадратов

Базовый калькулятор закона обратных квадратов

Как закон обратных квадратов применим к фотографии?

Крутые интерактивные ползунки, но какое практическое применение закона обратных квадратов для фотографии?

Эмпирическое правило простого закона обратных квадратов

Теперь все это имеет смысл?

Понимание закона обратных квадратов света

Содержание

Шкала диафрагмы (диафрагма)

Закон обратных квадратов света

Практическое применение

Освещение только одного объекта

Освещение нескольких объектов

Специальная проблема: Правильное освещение фона

Связь между головкой вспышки, мощностью, ISO и диафрагмой

Заключение

Обратные функции

Пример:

Пример:

Решить с помощью алгебры

Фаренгейты в Цельсии

Обратные общие функции

Осторожно!

Пример: Возведение в квадрат и квадратный корень

Но мы можем это исправить!

Пример: (продолжение)

Нет обратного?

Домен и диапазон

Пример:

)

Добавить комментарий Отменить ответ