Сравнить размер сенсора(матрицы) фотоаппарата
Дело в том, что измерения могут быть очень запутанными и неясными. Лично я, могу понять, насколько большой APS-C сенсор, по сравнению с полнокадровым сенсором, но у меня были проблемы в понимании того, в каком отношении находится небольшой 1/2.33 (или «1») датчик с другими сенсорами. Когда компания Nokia объявила о выпуске 808 PureView, мне действительно стало интересно, насколько большой, или маленький этот датчик. Теперь есть новый сайт, который называется «Датчик изображения камеры» (cameraimagesensor.com). Тут, вы можете сравнивать размеры и технические характеристики датчиков изображения различных фотокамер.
Сайт cameraimagesensor.com позволяет выбрать конкретный продукт из списка, будь то обычная цифровая камера, камера среднего формата, CSC, DSLR или мобильное устройство, например смартфоны. После того как объект был выбран, вы увидите, размер датчика на экране. Это не фотография в реальном размере, но она дает хорошее представление о том, как соотносятся разные датчики между собой.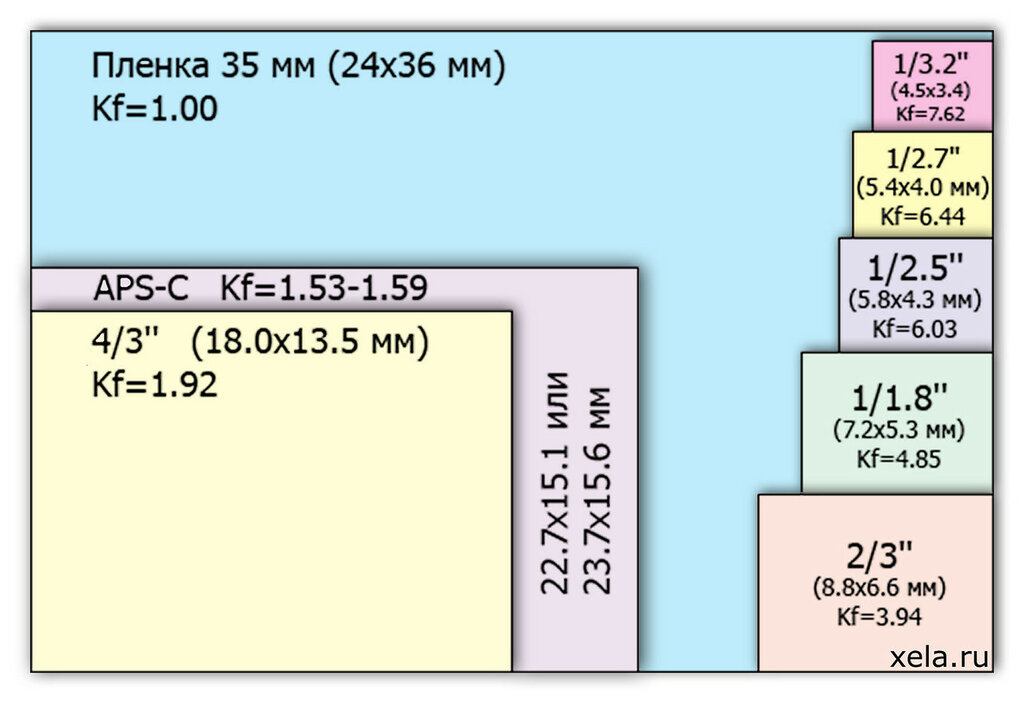
Так, что если вы хотите знать, насколько маленьким будет датчик 1/2.3-inch по сравнению с Micro Four Third, или с APS-C, то у вас есть такая возможность. Вы можете сделать это очень просто и наглядно, не вникая в странные цифры и обозначения.
То на сколько, качественным будет изображение, очень влияет размер датчика. Если вы хотите получить хорошее изображение, высокого качества, с минимальным количеством шума, при покупке камеры, вам необходимо остановить свой выбор на фотокамере с большим датчиком.
Таким образом, сайт cameraimagesensor.com, является замечательным мини-сайтом, с помощью которого вы можете получить визуальное представление о размере датчика изображения, и о других интересных технических характеристиках, таких как плотность пикселей, размер (высота) пикселя, размер сенсора в мм, и т.д.
Убедиться в интересных возможностях этого приложения вы можете прямо на нашем сайте, либо посетив сайт cameraimagesensor.com
какие лучше? CCD против CMOS
Недавно в нашей статье о выборе видеокамеры для семьи мы писали о матрицах.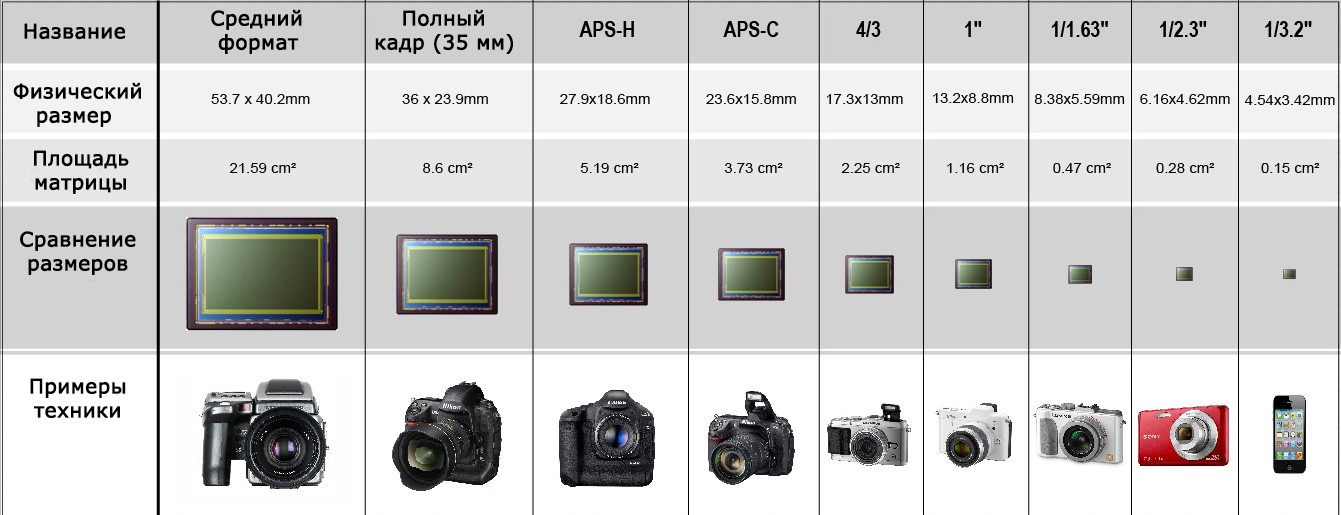 Там мы коснулись этого вопроса легко, однако сегодня постараемся более детально описать обе технологии.
Там мы коснулись этого вопроса легко, однако сегодня постараемся более детально описать обе технологии.
Что же такое матрица в видеокамере? Это микросхема, которая преобразовывает световой сигнал в электрический. На сегодняшний день существует 2 технологии, то есть 2 типа матриц – CCD (ПЗС) и CMOS (КМОП). Они отличаются друг от друга, каждая имеет свои плюсы и минусы. Нельзя точно сказать, какая из них лучше, а какая – хуже. Они развиваются параллельно. Вдаваться с технические детали мы не будем, т.к. они будут банально непонятны, но общими словами определим их главные плюсы и минусы.
Технология CMOS (КМОП)
CMOS-матрицы в первую очередь хвастаются низким энергопотреблением, что плюс. Видеокамера с этой технологией будет работать чуть дольше (зависит от емкости аккумулятора). Но это мелочи.
Главное отличие и достоинство – это произвольное считывание ячеек (в CCD считывание осуществляется одновременно), благодаря чему исключается размазывание картинки. Возможно, вы когда-нибудь видели «вертикальные столбы света» от точечных ярких объектов? Так вот CMOS-матрицы исключают возможность их появления. И еще камеры на их основе дешевле.
Возможно, вы когда-нибудь видели «вертикальные столбы света» от точечных ярких объектов? Так вот CMOS-матрицы исключают возможность их появления. И еще камеры на их основе дешевле.
Недостатки также есть. Первый из них – небольшой размер светочувствительного элемента (в соотношении к размеру пикселя). Здесь большая часть площади пикселя занята под электронику, поэтому и площадь светочувствительного элемента уменьшена. Следовательно, чувствительность матрицы уменьшается.
Т.к. электронная обработка осуществляется на пикселе, то и количество помех на картинке возрастает. Это также является недостатком, как и низкое время сканирования. Из-за этого возникает эффект «бегущего затвора»: при движении оператора возможно искажение объекта в кадре.
Технология CCD (ПЗС)
Видеокамеры с CCD-матрицами позволяют получить высококачественное изображение. Визуально легко заметить меньшее количество шумов на видео, отснятом с помощью видеокамеры на основе CCD-матрицы по сравнению с видео, отснятым на камеру CMOS. Это самое первое и важное преимущество. И еще: эффективность CCD-матриц просто потрясающая: коэффициент заполнения приближается к 100%, соотношение зарегистрированных фотонов равен 95%. Возьмите обычный человеческий глаз – здесь соотношение равно приблизительно 1%.
Высокая цена и большое энергопотребление – это недостатки данных матриц. Дело в том, что здесь процесс записи невероятно труден. Фиксация изображения осуществляется благодаря многим дополнительным механизмам, которых нет в CMOS-матрицах, поэтому технология CCD существенно дороже.
CCD-матрицы используются в устройствах, от которых требуется получение цветного и качественного изображения, и которыми, возможно, будут снимать динамические сцены. Это профессиональны видеокамеры в своем большинстве, хотя и бытовые тоже. Это также системы наблюдения, цифровые фотоаппараты и т.д.
CMOS-матрицам применяются там, где нет особо высоких требований к качестве картинки: датчики движения, недорогих смартфонах…Впрочем, так было ранее. Современные матрицы CMOS имеют разные модификации, что делает их весьма качественными и достойными с точки зрения составления конкуренции матрицам CCD.
Современные матрицы CMOS имеют разные модификации, что делает их весьма качественными и достойными с точки зрения составления конкуренции матрицам CCD.
Сейчас сложно судить о том, какая технология лучше, ведь обе демонстрируют прекрасные результаты. Поэтому ставить тип матрицы как единственный критерий выбора, как минимум, глупо. Важно учитывать многие характеристики.
Пожалуйста, оцените статью:
Какая матрица для фотоаппарата лучше: как выбрать
Покупая фотоаппарат, неважно какой: профессионального класса или рядовой бюджетный компакт для съемок друзей и семьи на природе, хочется, чтобы снимки получались качественными, а сам аппарат давал как можно больше свободы. Зная, какая матрица для фотоаппарата лучше, можно не впадать в ступор в магазине при виде двух моделей разных марок, которые выглядят одинаково, но стоят очень по-разному. Все дело в сенсоре, который и отвечает за то, какое изображение будет получаться и насколько гибкие рамки пользования фотоаппаратом будут у владельца.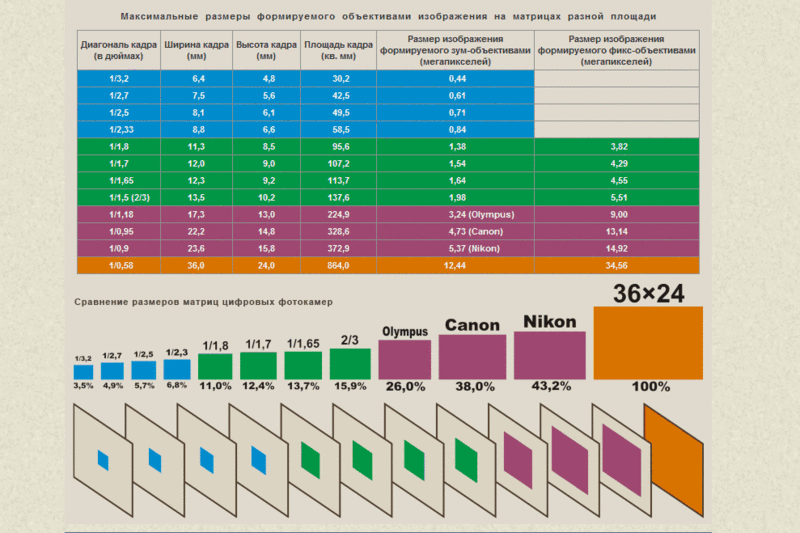
Немного технических сведений
Матрицы цифровых фотоаппаратов делятся на два основных типа по применяемым полупроводникам и технологии считывания информации.
- Тип матрицы ПЗС (CCD) — самый распространенный. Это достаточно дешевая технология, информация об изображении считывается последовательно с каждой ячейки.
- КМОП матрицы CMOS дороже, но эффективнее в плане скорости работы, поскольку позволяют считывать данные сразу со всех светочувствительных элементов. Такие сенсоры устанавливаются в дорогих камерах, поскольку ни один производитель не пройдет мимо шанса предоставить пользователю возможности съемки с очень малыми выдержками, что в свою очередь усложняет аппаратно-программный комплекс.
Большинство фотоаппаратов пользовательского класса оснащено ПЗС матрицами. При этом ставится вполне ожидаемое условие: для получения действительно качественных снимков при естественном освещении (или при недостаточном) лучше использовать штатив, поскольку время выдержки будет значительным.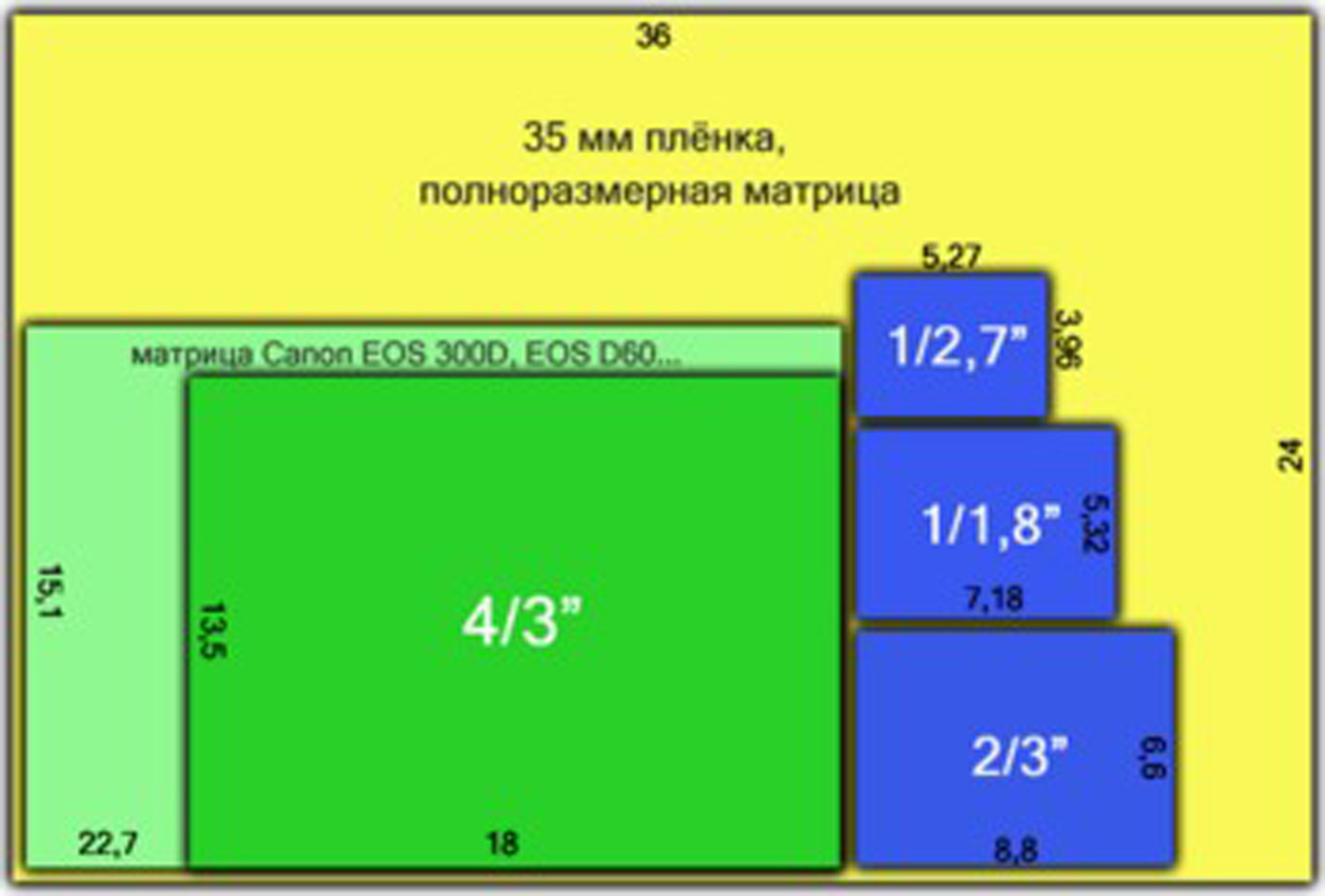 Аналогично — не получится делать снимки крайне быстро, поскольку нужно время на получение и обработку изображения.
Аналогично — не получится делать снимки крайне быстро, поскольку нужно время на получение и обработку изображения.
Некоторые производители решают последнюю проблему достаточно просто: оснащают фотоаппараты буфером памяти. Туда помещаются кадры до обработки, когда ведется съемка в так называемом спортивном режиме — серией за короткий промежуток времени.
Дорогие фотокамеры, оснащенные КМОП матрицами, позволяют делать снимки «с рук» с малой выдержкой, имеют высокую светочувствительность и низкий уровень шума. С помощью такого оборудования можно проводить экспонометрию, снижается время автофокусировки, естественно, легко сделать хороший кадр.
Еще одна технология, которая применяется в самой дорогой фототехнике — многослойные матрицы. Это не очередной пункт в списке «виды матриц». Светочувствительная зона таких аппаратов состоит из трех слоев ПЗС, каждый из которых считывает только один цвет. В результате качество изображения просто потрясает. Техника с данной технологией особо маркируется: 3CCD.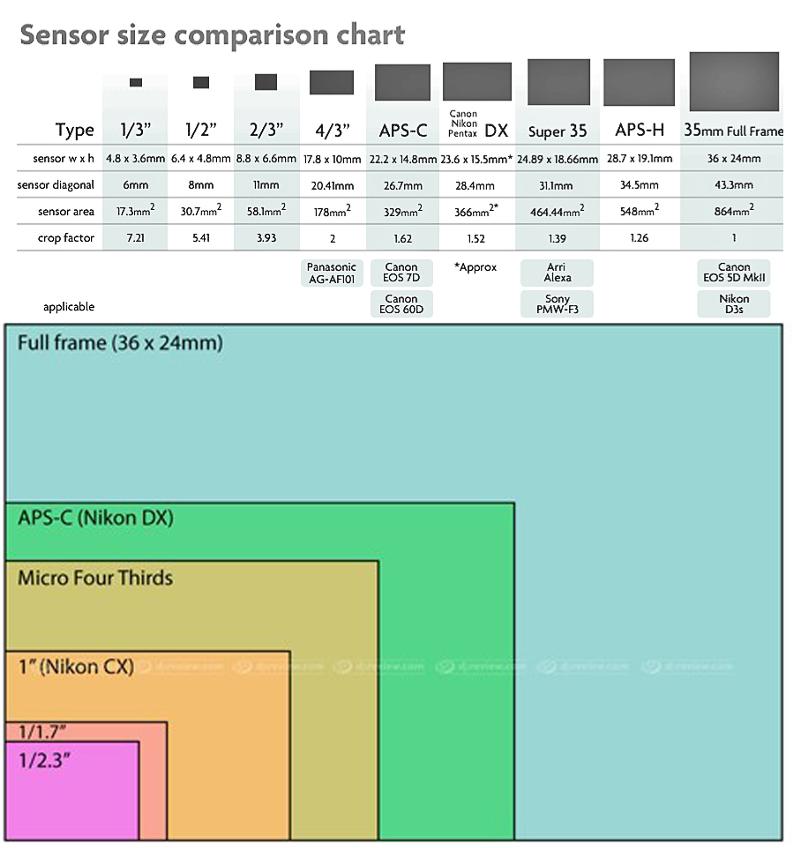
Последнее, что стоит упомянуть, – технологические размеры матриц. ПЗС сенсоры можно сделать маленькими, они построены на кремниевых элементах. А КМОП матрицы достаточно большие, что является еще одним рациональным доводом в пользу их применения в дорогой профессиональной технике.
Количественный показатель качества
Задавая себе вопрос, какая матрица фотоаппарата лучше,- можно достаточно быстро получить ответ без необходимости вникать в технологические особенности. Обратите внимание на следующие характеристики:
- заявленное количество мегапикселей в характеристике камеры;
- эффективное количество пикселей, которое ответственные производители указывают в документации к фотоаппарату;
- возможные размеры изображений, которые можно делать с помощью камеры.
Производители дешевых моделей фотоаппаратов часто лукавят, указывая, прежде всего, размерность картинки и выставляя огромные цифры как эффективный рекламный ход. Это не говорит о качестве получаемых снимков. Типы матриц фотоаппаратов могут быть разного класса. Однако если сенсор не имеет достаточной разрешающей способности, большие изображения на выходе будут иметь низкую детализацию и высокий уровень шума.
Типы матриц фотоаппаратов могут быть разного класса. Однако если сенсор не имеет достаточной разрешающей способности, большие изображения на выходе будут иметь низкую детализацию и высокий уровень шума.
Еще больше о качестве камеры скажет соотношение между заявленными мегапикселями матрицы и количеством эффективных точек. Это напрямую говорит о применяемой оптике. Если аппаратная часть выполнена ответственно, заявленное и эффективное количество пикселей будет почти одинаково, что не только положительно характеризует продажную цену, но и напрямую отвечает за качество снимков.
Светочувствительность и шумы
Светочувствительность матрицы — еще одна характеристика, которая описывает фотоаппарат. Покупать камеру стоит, ориентируясь на планируемые возможности применения. Сегодня в документации в графе светочувствительности можно встретить очень высокие цифры — до 51000 и больше. Однако это не говорит напрямую о возможности делать качественные снимки. Нет и рекомендаций, какой должна быть светочувствительность. Работает все следующим образом:
Однако это не говорит напрямую о возможности делать качественные снимки. Нет и рекомендаций, какой должна быть светочувствительность. Работает все следующим образом:
- для получения хорошего изображения требуется обеспечить выдержку, время которой зависит от уровня освещенности и светочувствительности матрицы;
- при среднем и низком освещении приходится применять штатив;
- если хочется продолжать снимать «с рук», можно программно поменять уровень светочувствительности матрицы в настройках фотоаппарата.
Однако высокая светочувствительность при малой установленной выдержке — это прямой путь к появлению шумов на снимке. Повышенная зернистость, появление мозаики — это те черты, которые раздражают и требуют тщательной вторичной обработки изображения.
Уровень светочувствительности является определяющим только при четком осознании того, в каких именно условиях будет использоваться камера. К примеру, при работе со штативом можно покупать фотоаппарат с высоким показателем, это даст широкие возможности съемки при самых разных освещениях без применения вспышки.
Физическая геометрия сенсора
Физический размер матрицы фотоаппарата в миллиметрах — еще один фактор, который не только напрямую отвечает за качество снимков, но и очень сильно формирует цену камеры. У самых лучших моделей соотношение размерности, которое основано на стандартном формате пленки 35 мм, близко к единице. Чем дешевле модель, тем выше показатель «кроп», обрезки, который сигнализирует о том, что матрица меньше по габаритам.
Чем меньше площадь сенсора, тем ниже охват визуального пространства перед объективом и:
- ниже общее количество света, которое падает на матрицу, следовательно, приходится повышать светочувствительность и увеличивать цифровой шум;
- больше теряется малых деталей, появляется размытие, это вызывают малые размеры, до которых преобразуется кадр.
Высокие значения кропа в фотоаппарате также означают, что разница в освещенности объектов в поле зрения фотоаппарата будет сглаживаться, что очень негативно сказывается на снимках, полученных в вечернее время без вспышки, например.
Коэффициент размерности указывается в документации к камере. Неважно, ориентируетесь ли на бюджетную или профессиональную модель — лучше будет купить аппарат с большой в геометрическом смысле матрицей.
Заключение
Невозможно сказать, какая матрица лучше. Выбирать фотоаппарат следует исходя из режимов, в которых он будет использоваться. Невозможно провести и всесторонне сравнение матриц фотоаппаратов – каждая проиграет в каком-то случае.
Правильно предсказанные условия съемок позволят камерам даже с относительно посредственными матрицами делать очень хорошие снимки. Главный фактор, который нужно учитывать обязательно — геометрические размеры матрицы. Тем, кто хочет получать действительно большие изображения в пикселях, также нужно обратить внимание на количество эффективных мегапикселей фотоаппарата.
Компактные фотоаппараты с большой матрицей / Гид покупателя
Большая матрица позволяет добиться высочайшей детализации, получить качественные кадры при недостаточном освещении, обеспечивает широкий динамический диапазон, возможность работать с боке. Поэтому все системные фотоаппараты (и зеркалки, и беззеркалки) оснащаются матрицами формата 1 дюйм и более. Однако они подразумевают покупку объективов, вспышек и другого оборудования.
Поэтому все системные фотоаппараты (и зеркалки, и беззеркалки) оснащаются матрицами формата 1 дюйм и более. Однако они подразумевают покупку объективов, вспышек и другого оборудования.
Альтернативный вариант — современные компактные фотоаппараты. Многие из них имеют крупные сенсоры, которые могут давать яркую и резкую картинку даже в условиях слабого освещения. Как выбрать компакт с большой матрицей? Мы подготовили подборку актуальных моделей 2017 года.
Canon PowerShot G9 X Mark II
Бюджетные фотоаппараты с большими матрицами — редкий класс фототехники, ведь чем больше сенсор, тем дороже камера. Обычно в компакты устанавливают дюймовые сенсоры. Они не так велики, но могут обеспечивать отличное качество снимков. Один из самых доступных фотоаппаратов с дюймовой матрицей — Canon PowerShot G9 X Mark II. В нём установлен 20-Мп CMOS-датчик.
Купить Canon PowerShot G9 X Mark II
Объектив обладает большой светосилой (F2 в широкоугольном положении) и трёхкратным оптическим зумом.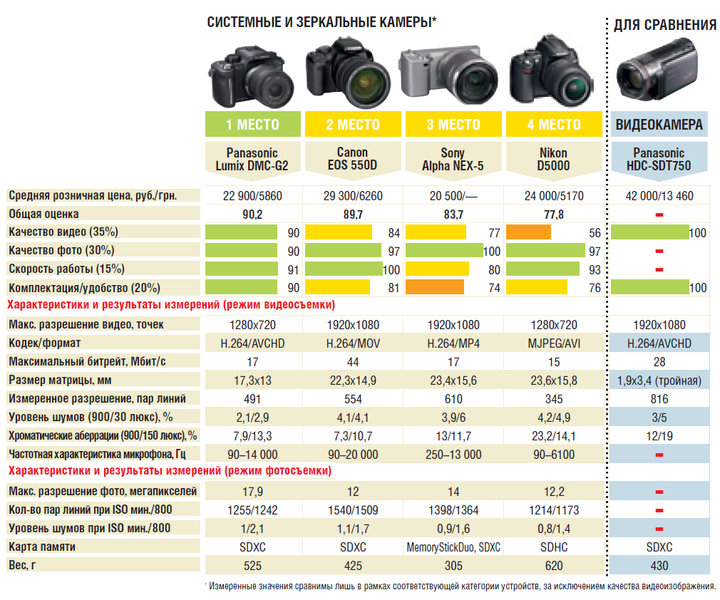 В широкоугольном положении угол его обзора эквивалентен 28 мм на полнокадровых аппаратах, и этого достаточно для большинства задач. Такой угол обзора приблизительно равен углу обзора объективов смартфонов.
В широкоугольном положении угол его обзора эквивалентен 28 мм на полнокадровых аппаратах, и этого достаточно для большинства задач. Такой угол обзора приблизительно равен углу обзора объективов смартфонов.
Экран сенсорный (можно фокусироваться и снимать одним касанием), но не поворотный. Впрочем, если вы не блогер и не увлекаетесь селфи, это не станет минусом.
Встроенный оптический стабилизатор эффективностью в 3,5 ступени экспозиции убережёт от смазанных кадров, а шустрый автофокус и быстрая серийная съёмка (8,2 кадра в секунду) позволят использовать камеру даже в динамичной репортажной съёмке.
Canon PowerShot G9 X Mark II / 10.2-30.6 mm УСТАНОВКИ: ISO 125, F6.3, 1/100 сУправление удобное, здесь реализованы все привычные автоматические и полуавтоматические режимы, ручной режим. В условные недостатки запишем отсутствие видоискателя. Однако экран неплохо справляется даже со съёмкой при ярком дневном свете. Плюс видоискатель увеличил бы габариты камеры. Её размер — 98×58×31 мм, вес — всего 206 граммов!
Canon PowerShot G9 X Mark II отлично подойдёт в качестве камеры на каждый день, а возможность зарядки батареи от USB позволит не носить с собой отдельное зарядное устройство.
Видеовозможности стандартные: Full HD с частотой до 60 кадров в секунду. Ролики записываются только в автоматическом режиме.
С помощью Wi-Fi с поддержкой NFC и Bluetooth аппарат соединяется со смартфоном, беспроводным принтером и облачным хранилищем CANON iMAGE GATEWAY.
Canon PowerShot G9 X Mark II можно смело рекомендовать как доступный и универсальный компакт с большой матрицей.
Canon PowerShot G7 X Mark II
Canon PowerShot G7 X Mark II — более продвинутая модель. Тут тоже используется дюймовый CMOS-сенсор на 20 Мп.
Купить Canon PowerShot G7X Mark II
Камера оснащена наклонным сенсорным дисплеем, который поворачивается даже в селфи-позицию.
Здесь есть необходимые автоматические функции, а в распоряжении продвинутого фотографа — ручные настройки.
Canon PowerShot G7 X Mark II / (65535) УСТАНОВКИ: ISO 125, F5.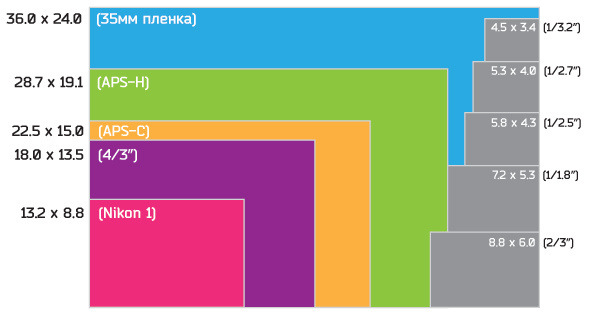 6, 1/100 с
6, 1/100 с
Ещё одно достоинство — широкоугольный светосильный объектив с 4,2-кратным зумом. В широкоугольном положении он даёт угол обзора, эквивалентный 24 мм, и имеет светосилу F1.8, а на максимальном зуме перед нами 100-мм объектив со светосилой F2.8. Встроенный нейтрально-серый фильтр ограничивает поток света, проходящий через объектив во время съёмки при ярком солнце и при работе с длинными выдержками.
Кроме того, объектив оснащён эффективной системой стабилизации изображения (до 4 ступеней экспозиции), которая пригодится во время съёмки при слабом освещении и видеозаписи.
По габаритам аппарат чуть толще и тяжелее Canon PowerShot G9 X Mark II: размер — 105,5×60,9×42 мм, вес — 319 граммов.
Аппарат позволяет снимать со скоростью 8 кадров в секунду, автофокус быстр и цепок.
Canon PowerShot G7 X Mark II УСТАНОВКИ: ISO 125, F3.2, 1/200 сЕсть Wi-Fi с поддержкой NFC и Bluetooth, доступна удалённая съёмка. Камеру можно подключить к другому фотоаппарату для обмена снимками, к беспроводному принтеру, ПК, облачному хранилищу.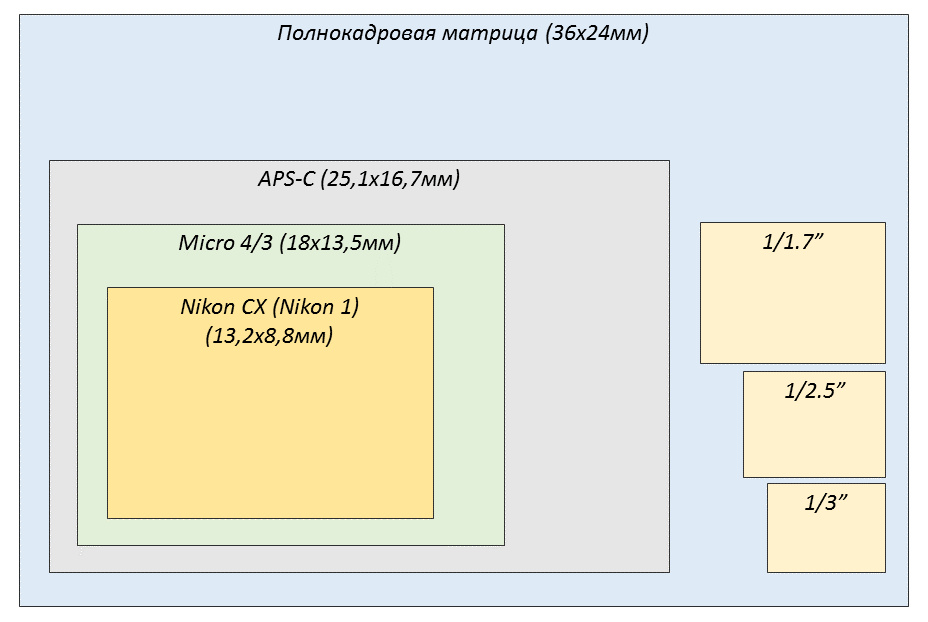
Видео записывается в формате Full HD с частотой 60 кадров в секунду. Доступны все ручные настройки экспозиции и баланса белого.
Canon PowerShot G7 X Mark II предоставляет максимум функций, поворотный экран, прекрасный светосильный объектив с разумной кратностью зума в компактном корпусе за относительно небольшие деньги. Камера порадует начинающего фотографа, блогера и даже профессионала, ищущего вторую камеру.
Canon PowerShot G3 X
Перед нами компакт с большой матрицей и зумом. Правда, компактом его можно назвать лишь условно. Такова классификация: раз на фотоаппарате установлен несъёмный объектив, значит это компакт. Canon PowerShot G3 X не из тех камер, которые способны потеряться в кармане. Она весит 745 граммов из-за универсального 25-кратного зум-объектива с диапазоном фокусных расстояний 24–600 мм (экв.).
Купить Canon PowerShot G3 X
На минимальном фокусном расстоянии это широкоугольник, который может запечатлеть пейзаж, сделать групповое фото или селфи с близкого расстояния. На максимальном фокусном это супертелеобъектив, способный показать крупным планом даже очень удалённые и мелкие предметы. Светосила для объектива такого класса тоже неплохая: от F2.8 на коротком конце до F5.6 при максимальном зуме. Эффективная оптическая стабилизация особенно важна при съёмке на больших фокусных расстояниях. Встроенный «стаб» гасит колебания камеры и экономит до 3,5 ступеней экспозиции.
На максимальном фокусном это супертелеобъектив, способный показать крупным планом даже очень удалённые и мелкие предметы. Светосила для объектива такого класса тоже неплохая: от F2.8 на коротком конце до F5.6 при максимальном зуме. Эффективная оптическая стабилизация особенно важна при съёмке на больших фокусных расстояниях. Встроенный «стаб» гасит колебания камеры и экономит до 3,5 ступеней экспозиции.
Съёмка на минимальном зуме, широкий угол обзора
Canon PowerShot G3 X / (65535) УСТАНОВКИ: ISO 125, F4, 1/1250 сСъёмка с той же позиции на максимальном зуме, деталь здания крупным планом
Canon PowerShot G3 X УСТАНОВКИ: ISO 200, F5.6, 1/1000 сБлагодаря большому фокусному расстоянию, можно добиться красивого боке.
Canon PowerShot G3 X / (65535) УСТАНОВКИ: ISO 160, F5.6, 1/200 сCanon PowerShot G3 X оснащён 20,2-Мп CMOS-сенсором.
Canon PowerShot G3 X / (65535) УСТАНОВКИ: ISO 125, F5.6, 1/500 сНаклонный сенсорный дисплей позволяет делать кадры в одно касание с нестандартных ракурсов.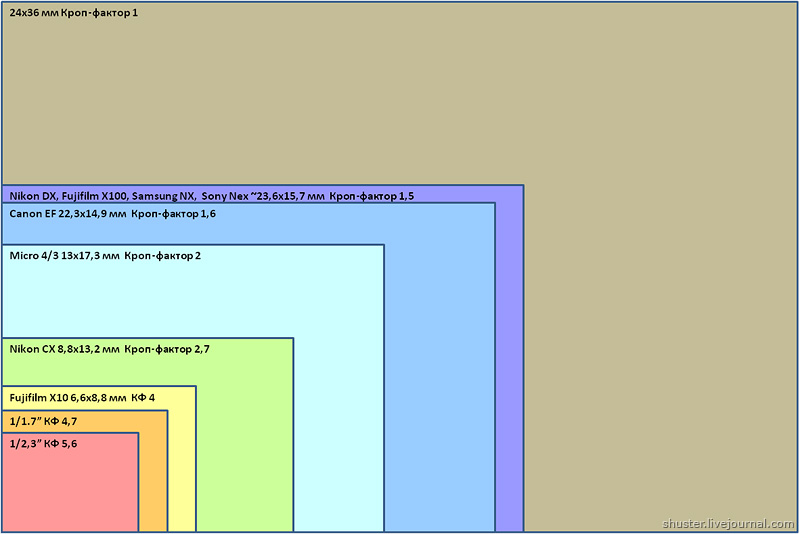 Жаль только, что он не поворачивается в селфи-позицию.
Жаль только, что он не поворачивается в селфи-позицию.
Canon PowerShot G3 X легко спутать с системной камерой. Он имеет ухватистую рукоятку, как у зеркалок. В ней размещена батарея. Её ресурса хватит на 335 кадров. Неплохой показатель автономности для этого класса камер!
Эргономика на высоте. Камера подойдёт как продвинутому фотографу, так и новичку. В отличие от предыдущих компактов, у Canon PowerShot G3 X есть горячий башмак, в который можно установить не только мощную внешнюю вспышку, но и электронный видоискатель (приобретается отдельно), который будет удобен при съёмке на ярком солнце.
Есть модуль Wi-Fi с поддержкой NFC и Bluetooth.
Canon PowerShot G3 X / (65535) УСТАНОВКИ: ISO 125, F3.2, 1/30 с Canon PowerShot G3 X / (65535) УСТАНОВКИ: ISO 800, F5, 1/60 сАппарат записывает видео в разрешении Full HD с частотой до 60 кадров в секунду. Поддерживается внесение ручных настроек при видеозаписи. Кстати, здесь имеется не только микрофонный вход, но и выход на наушники. Не хватает только 4К и «плоских» профилей для облегчения постобработки.
Не хватает только 4К и «плоских» профилей для облегчения постобработки.
Canon PowerShot G3 X — находка для тех, кому нужен мегазум с большой матрицей (необязательно компактный).
Sony Cyber-shot DSC-RX100 II
Компания Sony первой начала производить компактные камеры с большой матрицей. Серия RX-100 на сегодня насчитывает 5 фотоаппаратов. Sony Cyber-shot DSC-RX100 II не новинка, однако она вполне актуальна в 2017 году, производитель выпускает её параллельно с более новыми моделями, ведь она предлагает отличные возможности за относительно небольшие деньги.
Купить Sony Cyber-shot DSC-RX100 II
Как и во все компакты этой серии, в RX100 II установлена дюймовая 20,9-Мп матрица. Корпус металлический. Вес — 281 грамм. При сложенном объективе аппарат легко поместится в кармане.
Камера оснащена 3,6-кратным зумом с диапазоном фокусных расстояний 28–100 мм (экв.). То есть перед нами умеренный широкоугольник на минимальном зуме и неплохой телеобъектив, которым можно снимать на большой дистанции при максимальном зуме. На минимальном фокусном расстоянии объектив имеет завидную светосилу — F1.8. При зумировании она снижается вплоть до F4.9. Недостаток светосилы на большом зуме легко компенсируется эффективной оптической стабилизацией SteadyShot.
Максимальный угол обзора объектива
DSC-RX100M2 УСТАНОВКИ: ISO 160, F5, 1/30 с, 28.0 мм экв.Кадр сделан на максимальном фокусном расстоянии.
DSC-RX100M2 УСТАНОВКИ: ISO 800, F4.9, 1/125 с, 100.0 мм экв.Аппарат уверенно фокусируется даже при слабом освещении, а скорость серийной съёмки достигает 10 кадров в секунду.
Поворотный 3-дюймовый экран обеспечивает свободу в выборе точки съёмки. Повернуть его в положение для съёмки автопортретов не получится. Кстати, экран имеет очень высокое разрешение — 1228800 точек.
Среди прочих аппаратов серии Sony Cyber-shot DSC-RX100 II выделяет наличие мультиинтерфейсного разъёма, в который можно установить как мощные системные вспышки, так и дополнительные аксессуары (например, внешний микрофон).
Тут есть и полностью автоматический режим, и множество сюжетных программ, и ручной, и полуавтоматический режимы.
Возможности записи видео тоже на уровне: Full HD с частотой до 60 кадров в секунду.
Все беспроводные функции на месте. Благодаря Wi-Fi с поддержкой NFC, можно производить удалённую съёмку или скачивать изображения на мобильное устройство. Sony Cyber-shot DSC-RX100 II порадует фотографа прекрасным качеством фото и надёжной сборкой. Хороший баланс цены и возможностей делает её очень привлекательным приобретением!
Sony DSC-RX10 III
К компактным аппаратам Sony DSC-RX10 III можно отнести лишь формально. В распоряжении фотографа 25-кратный зум с фокусными расстояниями 24–600 мм (экв.), разработанный в сотрудничестве с Carl Zeiss. Радует и его светосила: F2.4 на минимальном фокусном и F4 на максимальном. Оптическая стабилизация работает эффективно, позволяя сэкономить целых 4,5 ступени экспозиции!
В сердце камеры — дюймовый сенсор EXMOR R с разрешением 20,2 Мп.
Купить Sony DSC-RX10 III
Съёмка на минимальном фокусном расстоянии
DSC-RX10M3 УСТАНОВКИ: ISO 100, F4, 1/30 с, 24.0 мм экв.Фото, сделанное с той же точки, на максимальном фокусном расстоянии
DSC-RX10M3 УСТАНОВКИ: ISO 640, F4, 1/250 с, 600.0 мм экв.Камера заряжена на уровне топовых зеркалок: продуманная эргономика, удобный хват, все режимы от авто до ручного, полезные функции типа брекетинга экспозиции. По скорости серийной съёмки она превосходит большинство зеркальных камер — 14 кадров в секунду! В режиме электронного затвора доступны сверхкороткие выдержки вплоть до 1/32000 с, которые позволят «остановить» даже самое быстрое движение. Есть наклонный дисплей разрешением 1228800 точек, качественный электронный видоискатель.
Sony DSC-RX10 III предоставляет уникальные в своём классе видеовозможности. Камера записывает видео в разрешении 4К при частоте 30 кадров в секунду. Аппарат готов и к профессиональному применению: в распоряжении пользователя S-Gamut/S-Log2, функция «Зебра», прямой вывод через HDMI, временной код/информационный бит, отображение данных гаммы, управление записью, режим двойной записи, маркер. Мультиинтерфейсный разъём позволяет установить внешний микрофон, видеосвет или фотовспышку. Доступна съёмка с эффектом замедления времени. В формате HD поддерживается съёмка со скоростью 960 кадров в секунду, а в Full HD — 280 кадров в секунду.
Мультиинтерфейсный разъём позволяет установить внешний микрофон, видеосвет или фотовспышку. Доступна съёмка с эффектом замедления времени. В формате HD поддерживается съёмка со скоростью 960 кадров в секунду, а в Full HD — 280 кадров в секунду.
Ценник может показаться чрезмерно высоким. Но много ли на рынке камер, способных записывать 4К-видео с профилем S-Log и имеющих все профессиональные возможности, да ещё и с 25-кратным светосильным зумом в комплекте? Получается, что Sony DSC-RX10 III — вполне бюджетное решение, например, для тележурналиста. Кстати, можно немного сэкономить, выбрав модель Sony DSC-RX10 II. Она отличается меньшей кратностью зума.
DSC-RX10M3 УСТАНОВКИ: ISO 2000, F4, 1/250 с, 361.0 мм экв.
Фотоаппараты с ультразумом и большой матрицей — довольно распространённый класс фототехники, но если вам нужен мощнейший инструмент для записи видео, обратите внимание на Sony DSC-RX10 III.
Sony Cyber-shot DSC-RX100M5
Перед нами самая актуальная компактная фотокамера с большой матрицей в серии аппаратов RX100. В ней реализованы лучшие наработки, а также есть возможность записи 4К-видео. Корпус металлический, весит 299 граммов.
Здесь установлена дюймовая 20,5-Мп матрица с обратной засветкой (BSI CMOS), что обеспечивает ещё более высокое качество снимков при высокой светочувствительности.
Купить Sony Cyber-shot DSC-RX100M5
Диапазон фокусных расстояний составляет 24–70 мм (экв.). Светосила объектива на минимальном фокусном расстоянии — F1.8, а на максимальном — F2.8. Широкий угол обзора позволит снимать красивые пейзажи, фотографировать в тесных помещениях и делать отличные групповые фото.
На верхней панели спрятаны удобная встроенная вспышка и видоискатель.
Экран не сенсорный, но имеет удобную наклонную конструкцию. Его можно повернуть и в селфи-позицию.
В авторежиме камерой может пользоваться даже новичок, но она имеет огромный потенциал. Sony Cyber-shot DSC-RX100M5 получила более совершенную систему гибридной фокусировки с 325 точками фокусировки.
Скорость серийной съёмки — 25 кадров в секунду. Такая скорость недоступна зеркальным фотоаппаратам. Благодаря большому буферу, камера может «стрелять» длинными очередями.
Камера записывает видео в 4К-разрешении (частота 30 кадров в секунду) в профилях S-Log2 и S-Log3. В ней реализованы все вспомогательные функции («Зебра», таймкод, раздельная запись видео). На сегодня Sony Cyber-shot DSC-RX100M5 — одна из самых доступных камер, предлагающих возможности видеозаписи такого уровня.
Есть у камеры и несколько ограничений. Первое — относительно непродолжительная работа от батареи. В среднем одного аккумулятора хватает на 220 кадров или 110 минут записи видео. Второе — при длительной записи 4К-видео возможны перегревы. Однако эти проблемы легко решить, взяв с собой дополнительные батареи и давая аппарату немного отдохнуть между записью видеороликов.
Второе — при длительной записи 4К-видео возможны перегревы. Однако эти проблемы легко решить, взяв с собой дополнительные батареи и давая аппарату немного отдохнуть между записью видеороликов.
Аппарат подойдёт всем, кому нужен компактный гаджет с профессиональными возможностями. Он может играть роль «записной книжки» фотографа, плюс это совершенный инструмент видеоблогера.
Sony Cyber-shot DSC-RX1RM2
Размер матрицы этой камеры равен кадру фотоплёнки, матрицы таких же размеров ставятся в топовые зеркальные и беззеркальные камеры. Sony — единственный производитель, который даёт возможность делать полнокадровые кадры компактом.
Купить Sony Cyber-shot DSC-RX1RM2
Для сравнения: матрица Sony Cyber-shot DSC-RX1RM2…
… и Sony Cyber-shot DSC-RX100 II.
Габариты — 113,3×65,4×72,0 мм, вес — 480 граммов. Аппарат оснащён 42,3-Мп CMOS-матрицей с обратной засветкой.
Здесь установлен фикс-объектив с фокусным расстоянием 35 мм и светосилой F2.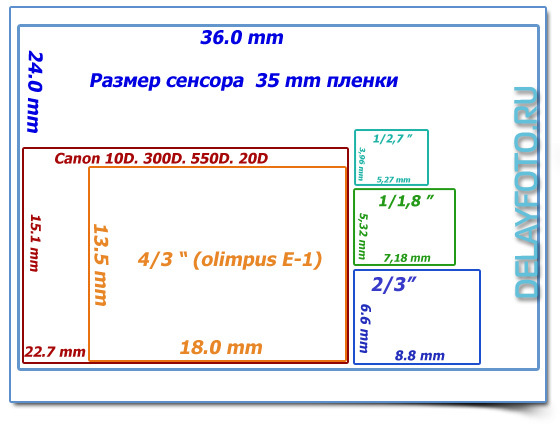
На матрице есть 399 датчиков фазовой фокусировки, которые обеспечивают быструю и точную наводку на резкость. Скорость серийной съёмки не столь высока и составляет 5 кадров в секунду.
У камеры продуманная эргономика, наклонный дисплей и удобный электронный видоискатель.
Через мультиинтерфейсный разъём к Sony Cyber-shot DSC-RX1RM2 подключается внешняя вспышка (встроенной нет) или другой аксессуар.
Конечно, не каждый сможет позволить себе такой премиальный компакт с большой матрицей. Однако если вы хотите иметь только самое лучшее, то выбор очевиден!
Если компания Canon делает ставку на компакты с дюймовой матрицей, то Fujifilm идут дальше и предлагают покупателю аппараты с матрицей формата APS-C. Она больше, поэтому обеспечивает лучшее качество изображения, более уверенную работу при слабом освещении. Впрочем, до Sony Cyber-shot DSC-RX1RM2 им все равно далековато…
Большая матрица влечёт за собой увеличение объектива. Чтобы сохранить компактность конструкции, инженерам пришлось оснастить камеры объективами с фиксированным фокусным расстоянием. Где-то мы это уже видели, да?
Где-то мы это уже видели, да?
Fujifilm X70
Не верится, что внутри этого малыша очень крупная матрица! Производитель постарался отсечь все необязательные опции. Следствие — впечатляющая компактность и относительно доступная цена. Здесь традиционный для Fujifilm ретродизайн, металлический корпус. Габариты — 112,5×64,4×44,4 мм, вес — 340 граммов. Fujifilm X70 оснащена широкоугольным фикс-объективом с фокусным расстоянием 18,5 мм (28 мм в экв.). Светосила F2.8 для фикса невелика, зато он очень лёгок.
Купить Fujifilm X70
Дисплей наклонный, сенсорный, его можно повернуть в позицию для селфи.
А вот снимать отдалённые объекты затруднительно: в распоряжении фотографа лишь трёхкратный цифровой зум. Отметим отсутствие оптической стабилизации объектива.
В камере установлен фирменный сенсор X-Trans CMOS II разрешением 16,3 Мп. Конёк камер Fujifilm — продвинутая работа с цветом.
Fujifilm X70 располагает всеми ручными настройками и фирменным автоматическим режимом Advanced SR AUTO, который распознаёт тип снимаемого сюжета и настраивает все параметры.
Модель имеет стандартный набор беспроводных возможностей: по Wi-Fi можно подключиться к мобильному устройству и передать на него снимки, снимать на расстоянии. Из дополнительных возможностей — печать фото на беспроводном принтере, автосохранение снимков на ПК, съёмка фото с геотегами посредством GPS-приёмника в смартфоне или планшете.
Возможности записи сюрпризов не сулят: Full HD с частотой до 60 кадров в секунду. Не помешала бы поддержка 4K-формата, ведь Fujifilm X70 потенциально будет интересен блогерам: хороший цвет фото и видео без обработки, удобный экран, потрясающая компактность.
Итак, это стильный и компактный фотоаппарат, способный обеспечить отличное качество фото благодаря большой матрице. Но функциональность камеры ограничена фикс-объективом. Однако она компактна и имеет относительно доступный ценник.
Fujifilm X100F
Fujifilm X100F — новая камера линейки. Её предшественники: X100, X100S и актуальная по сей день X100S. Перед нами премиальный компакт с большой матрицей. Камера привлекает взгляд своим ретродизайном.
Камера привлекает взгляд своим ретродизайном.
Купить Fujifilm X100F
Вряд ли все достоинства X100F оценят начинающие фотографы, хотя и они вполне справятся с управлением ею. Серия ориентирована на любителей плёночных дальномерных фотоаппаратов. Камера позволяет применять к фото и видео уникальные плёночные цветовые профили.
Здесь установлен уникальный гибридный видоискатель. Он может работать в режиме оптического или электронного видоискателя. Электронный видоискатель показывает картинку с той же яркостью и цветами, какие будут на фото, но в условиях слабого освещения может давать цифровой шум; оптический обеспечивает яркую и чёткую картинку в любых условиях, но правильность экспозиции и баланса белого по нему отследить нельзя.
Объектив без зума, его фокусное расстояние 35 мм (экв.). Он не обеспечивает привычного широкого угла обзора, зато передаёт перспективу почти так же, как человеческий глаз. Оптической стабилизации нет. Светосила составляет F2, поэтому можно рассчитывать не только на уверенную работу при слабом освещении, но и на красивое размытие фона.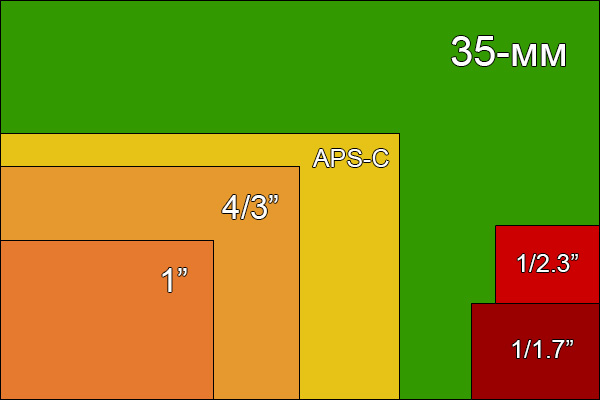
Из-за большой матрицы и продвинутого видоискателя вес камеры равен 469 граммам, габариты — 127×75×52 мм. Экран не поворотный и не сенсорный.
Что же нового в X100F по сравнению с предыдущими моделями сотой серии? Матрица X-Trans CMOS III разрешением 24 Мп и система гибридной фокусировки. На матрице расположены 49 датчиков фазовой детекции, а всего точек фокусировки 325! Для оперативного выбора нужной точки фокусировки есть джойстик.
Камера позволяет записывать видео в разрешении Full HD с частотой 60 кадров в секунду.
Цена соответствует премиальному статусу. Но если вы любите красивые и качественные вещи, Fujifilm X100F — отличный выбор!
Антимаркетинг: сравниваем камеры популярных смартфонов
Производители смартфонов прибегают к разным трюкам, показывая возможности встроенных камер и «забывая» сказать, почему вы вряд ли получите аналогичный результат. Мы попробуем подкинуть пищу для размышлений и помочь вам противостоять такой недобросовестной рекламе.
В этой статье сравниваются самые ходовые модели 2018 – 2019 года выпуска из среднего ценового сегмента. Формально в него же попадают и подешевевшие флагманы прошлых лет, но давайте ограничимся смартфонами одного исходного класса.
За снимками обратимся к специалистам из GSMArena. Они тестируют камеры смартфонов с 2010 года и накопили очень внушительную базу. Обычному покупателю будет сложно понять результат из тестовых таблиц, поэтому мы сделаем необходимые пояснения.
В сравнении принимают участие только основные (тыловые) камеры, работающие в автоматическом режиме при съёмке одиночных кадров цветных постеров и специальной тестовой карточки – фотографической миры PIMA/ISO 12233.
На всех смартфонах отключены бьюти-фильтры, искусственный недоинтеллект и прочие улучшалки, а где это возможно – установлен стиль изображения «точное». Смартфоны установлены на штатив. Делается серия кадров, из которой вручную выбирается самое резкое изображение. Для полноты картины съёмка повторяется в условиях нормальной и низкой освещённости. Значения ISO и выдержки, а также баланс белого устанавливаются камерами автоматически.
Для полноты картины съёмка повторяется в условиях нормальной и низкой освещённости. Значения ISO и выдержки, а также баланс белого устанавливаются камерами автоматически.
Матрицы и фокусные расстояния у всех разные, поэтому размер изображения тоже будет отличаться. Мы приводим идентичные фрагменты исходных кадров в формате PNG безо всякого масштабирования.
Оптическое разрешениеЕсли говорить о макро-режиме при ярком освещении, то здесь на разрешение больше всего влияет объектив. У всех смартфонов среднего уровня оптика одного класса, поэтому оно примерно одинаковое и находится в районе 12 – 16 линий на миллиметр. Вот как это выглядит на оказавшейся под рукой координатной сетке для цифровых микроскопов (100% кроп без обработки с 12 МП матрицы при ISO 100, съёмка со штатива).
Координатная сетка с шагом 0,1 мм (кликните, чтобы открыть на отдельной вкладке).Между рисками миллиметровой шкалы есть ещё девять тонких линий (цена деления 0,1 мм), и они чётко видны. 20 и более линий на миллиметр (lpmm) смартфон уже не покажет – они просто визуально сольются.
20 и более линий на миллиметр (lpmm) смартфон уже не покажет – они просто визуально сольются.
При обычной съёмке (с расстояния 40 см и более) широкоугольный объектив смартфона не способен передать мелкие детали из-за их малого углового размера. На общее восприятие картинки в большей степени влияет уже матрица, а она в любом смартфоне оставляет желать лучшего из-за очень низкого соотношения сигнал/шум. Алгоритмы шумоподавления всегда скрадывают детализацию. Теряется текстура, а эффективное разрешение падает до пары линий на миллиметр.
Вообще измерение оптического разрешения камеры – довольно сложная и дорогая задача. Мы возьмём профессиональные таблицы, но не будем вас мучить математикой. Просто скажем, что коэффициент пересчёта в lpmm для них составляет 0,075. То есть, если вы видите отдельные линии до маркера «20», а на промежуточной отметке «22» они уже слились, значит – разрешение составит полторы линии на миллиметр.
Насколько это много? Такая характеристика типична для цифромыльниц, которые сегодня вытеснили смартфоны. Системные камеры и зеркалки любительского уровня со съёмным объективом в комплекте обычно дают 20-30 lpmm (в самой резкой зоне по центру), а профессиональные – до 100 lpmm, но разглядеть это великолепие можно только при использовании полнокадровых и среднеформатных матриц. В смартфоне такие просто негде разместить.
Системные камеры и зеркалки любительского уровня со съёмным объективом в комплекте обычно дают 20-30 lpmm (в самой резкой зоне по центру), а профессиональные – до 100 lpmm, но разглядеть это великолепие можно только при использовании полнокадровых и среднеформатных матриц. В смартфоне такие просто негде разместить.
В верхнем ряду каждого снимка представлена пара фрагментов миры. Смотрим, где линии впервые видны по-отдельности. Настолько чётко, что их легко сосчитать. Чем левее (больше значение в подписи), тем выше реальная разрешающая способность камеры. Для наглядного сравнения относительных результатов этого достаточно, а определение точных частотно-контрастных характеристик оставим лабораториям, специализирующимся на оптике.
Второй ряд демонстрирует цветную вышивку на сером фоне. Он хорошо показывает степень детализации изображения и характер его огрубления при съёмке в полутьме.
Третий ряд показывает точность автофокуса на цветном фоне и качество цветопередачи в разных условиях освещения. Некоторые смартфоны искусственно усиливают яркость и/или насыщенность отдельных оттенков, делая цвета неестественными.
Huawei P Smart (2019)Характеристики камеры: 13 MP, f/1.8, PDAF (подробнее см. раздел «Краткий словарь терминов»).
(кликните для увеличения)У Huawei P Smart (2019) камера «мылит» вплоть до отметки «24». Действительно отдельными линии начинают восприниматься с промежуточного маркера 22 и далее (подробнее см. раздел «Оптическое разрешение»). Точнее трудно сказать из-за того, что изображение слегка не в фокусе (напомню, что это лучшая попытка в серии). Автофокус у P Smart явно оставляет желать лучшего.
Правый верхний угол снимка показывает диапазон яркости камеры. На нём видны провалы в тенях. Полутона после отметки 15 сливаются в сплошной чёрный. Впрочем, это совершенно типичный результат для смартфонов. Немного расширить диапазон яркости поможет съёмка в HDR (только статичных объектов со штатива) или в RAW (хотя у смартфонов это повышает разрядность каждого канала всего до 10-12 бит, а не до 14 бит, как у зеркалок).
Немного расширить диапазон яркости поможет съёмка в HDR (только статичных объектов со штатива) или в RAW (хотя у смартфонов это повышает разрядность каждого канала всего до 10-12 бит, а не до 14 бит, как у зеркалок).
Пара изображений посередине демонстрирует детализацию при минимальном ISO (слабое или выключенное шумоподавление) и высоком ISO (сильное шумоподавление). На левой картинке текстура вышивки сильно смазана (отчасти это объясняется и небольшой промашкой автофокуса), а на правой сглаживание затронуло даже крупные стежки. Также ожидаемо видим ухудшение цветопередачи – серые вертикальные линии теперь выглядят зелёными (цвета окружающего их фона).
Вообще с цветопередачей тёмных полутонов у Huawei P Smart (2019) дела обстоят неважно, особенно на высоких значениях ISO. Это видно и на картинке с цветными карандашами, где тёмно-зелёный и тёмно-синий грифель на ISO 64 ещё хоть как-то различимы, а при ISO 800 уже выглядят практически одинаково чёрными. Баланс белого также далёк от идеального. Серый фон миры в левом верхнем углу имеет зеленоватый оттенок.
Серый фон миры в левом верхнем углу имеет зеленоватый оттенок.
Камера: 16 MP, f/2.2, PDAF
(кликните для увеличения)У P20 lite лучше сработал автофокус (изображение более резкое), однако из-за мелких пикселей (1,0 мкм) видим сильные цветовые шумы. В результате их подавления итоговое разрешение снимка даже чуть ниже, чем у P Smart – до маркера «20» линии сливаются.
На высоких ISO ослик выглядит бледным и зернистым даже в районе гладкой серой вставки. Кстати, ISO пришлось поднимать до 1000 единиц – сказывается сравнительно низкая светосила объектива.
Зато баланс белого очень хорош, а вертикальные полоски седла в полутьме сохранили настоящий серый цвет – огрубление цветопередачи у P20 Lite не такое сильное. При хорошей освещённости картинка и вовсе радует – угадываются средние по размеру стежки, а на карандашах можно разглядеть текстуру.
Huawei Mate 20 liteКамера: 20 MP, f/1.8, PDAF.
(кликните для увеличения)Число мегапикселей растёт, а эффективная разрешающая способность в лучшем случае остаётся такой же. При ярком освещении все изображения выглядят презентабельно. Цвета не вызывают каких-то сомнений, хотя баланс белого слегка смещён в область более низкой цветовой температуры (серый выглядит желтоватым).
При ярком освещении все изображения выглядят презентабельно. Цвета не вызывают каких-то сомнений, хотя баланс белого слегка смещён в область более низкой цветовой температуры (серый выглядит желтоватым).
При слабом освещении автофокус промахнулся – вышивка получилась очень смазанной и бледной. Цвета поплыли: серый фон порозовел, а тёмно-зелёный стал более синим (бирюзовым). От текстуры дерева не осталось и следа. В полутьме таким смартфоном даже не стоит пытаться фотографировать.
Honor 8XКамера: 20 MP, f/1.8, PDAF
(кликните для увеличения)Казалось бы, имеем те же 20 мегапикселей при диафрагме 1.8 и то же разрешение, но в итоге получаем немного другой результат. Баланс белого смещён в противоположную сторону: занижен синий канал и слегка завышен зелёный. Провалы в тенях чуть глубже – уже с маркера «13» всё сливается в чёрный. Зато автофокус точнее сработал, из-за чего вышивка выглядит детальнее – очень чёткие края. На высоких ISO изображение такое же замыленное, а серые стежки на зелёном фоне опять стали зелёными.
Камера: 13 MP, f/1.8, PDAF.
(кликните для увеличения)Облегчённая версия десятого «Хонора» вытягивает разрешение до отметки «24» и даже чуть больше, но тёмные полутона сливаются как у всех. Баланс белого слегка смещён в сторону тёплых оттенков. Сами цвета выглядят естественно. Детализация средняя при хорошем освещении. Съёмка в темноте чуть лучше по сравнению с 8X – текстуры сглаживаются, но не пропадают. Тонкие серые полосы также стали зелёными, края объектов заметно размыты из-за сильного шумоподавления.
Motorola (Lenovo) Moto G6Камера: 12 MP, f/1.8, PDAF.
(кликните для увеличения)Отдельные линии видны от промежуточного маркера 22. При 12 Мп эффективное разрешение снимков почти такое же, как у Huawei Mate 20 lite с его 20 Мп сенсором. Сказывается увеличенный размер пикселей (1,4 мкм), дающий сравнительно низкие шумы.
Баланс белого плывёт в сторону низкой цветовой температуры (слегка желтит).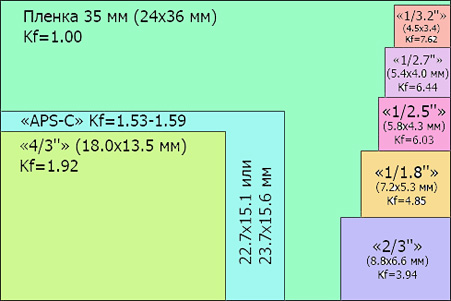 Провалы в тенях довольно глубокие (столбики градиентной заливки 14 – 19 сливаются). Текстура карандашей немного смазана, цвета естественные.
Провалы в тенях довольно глубокие (столбики градиентной заливки 14 – 19 сливаются). Текстура карандашей немного смазана, цвета естественные.
При ярком освещении вышивка выглядит очень детально: видно даже мелкие стежки. Это один из самых резких кадров в обзоре. На высоких ISO автофокус наводится точнее, чем у большинства смартфонов, но сглаживание и огрубление цветопередачи при этом сильнее заметны.
Nokia 7.1Камера: 12 MP, f/1.8, Dual Pixel PDAF
(кликните для увеличения)Главное отличие – технология улучшенного фазового автофокуса. Как плоские, таки и объёмные предметы на всех снимках очень чёткие. Эффективное разрешение аналогично Moto G6 – линии сливаются в районе маркера «22».
Алгоритм подавления яркостных шумов здесь менее агрессивный, поэтому сравнительно высокая детализация сохраняется даже на высоких значениях ISO. Цвета почти не бледнеют и слабо искажаются – серые полоски на зелёном фоне остаются серыми.
Samsung Galaxy A7 (2018)Камера: 24 МP, f/1. 7, PDAF
7, PDAF
Работу автофокуса трудно назвать образцовой – фотографии карандашей смазаны даже при съёмке в условиях яркого освещения. Оптическое разрешение камеры весьма радует: отдельные линии видны вплоть до маркера «28», хроматических аберраций невооружённым глазом не наблюдается.
Очень заметна светосильная оптика: в то время как другие смартфоны поднимают ISO до 800 – 1000 единиц, A7 в тех же условиях достаточно 400. Как результат – меньше яркостных шумов и чище картинка.
Однако алгоритмы цветового шумоподавления зачем-то сделали очень агрессивными – текстура карандашей пропала полностью даже при ISO50, вместо рисунка дерева видно только мутные пятна. Мелкие стежки на вышивке превратились в группу артефактов. Вот так на уровне софта можно угробить хорошую аппаратную платформу.
Xiaomi RedMi Note 7Камера: 48 MP, f/1.8, PDAF
(кликните для увеличения)С яркостным диапазоном у этой камеры всё как обычно, поэтому мы пропустим 50 оттенков серого, чтобы показать иллюзию 48 мегапикселей за счёт технологии Quad Bayer Array. Здесь её работа отчётливо видна в верхнем ряду.
Здесь её работа отчётливо видна в верхнем ряду.
Повышение количества пикселей матрицы в четыре раза никак не влияет на реальное оптическое разрешение: на обоих снимках линии сливаются за маркером 22. Более того, на них очень заметны хроматические аберрации – это кривая работа алгоритма интерполяции «тетрапикселей» (см. Краткий словарь терминов) на этапе дематризации.
Автофокус не смог точно навестись на резкость, поэтому даже при хорошем освещении мелкие детали смазываются. Текстура карандашей выглядит как артефакты пикселизации. С таким же успехом вы можете растянуть вчетверо картинку, снятую на Honor 8X, Moto G6 или Nokia 7.1.
Xiaomi Mi8 LiteКамера: 12 МP, f/1.9, Dual Pixel PDAF
(кликните для увеличения)Оптическое разрешение чуть выше среднего для группы прямых конкурентов – линии сливаются за маркером «22». Диапазон яркости максимальный для восьмибитной растровой картинки – различимы все градиентные столбики до маркера 16 (B) включительно.
Радуют щадящие алгоритмы шумоподавления. На всех снимках хорошо видна текстура и мелкие детали. Их можно разглядеть даже на ISO 800, что большая редкость.
Баланс белого смещён в сторону жёлто-зелёного оттенка. Автофокус Dual Pixel PDAF работает менее точно, чем аналогичный у Nokia 7.1.
Краткий словарь терминовPDAF – Phase Detection Auto Focus, фазовый автофокус. Для проверки автоматической фокусировки в нём определяется схождение лучей из нескольких точек с центра и краёв объектива. В «зеркалках» он работает шустро и довольно точно, а в телефонах – гораздо хуже из-за габаритных ограничений. В темноте часто промахивается, так как часть лучей просто не фиксируется и проверить их сходимость не удаётся.
Dual Pixel PDAF – улучшенный фазовый автофокус, в котором для оценки резкости используется почти вся площадь матрицы. Гораздо быстрее и точнее PDAF. Разница особенно заметна при низкой освещённости.
Laser AF – лазерный автофокус. Работает как лазерный дальномер. Объект съёмки подсвечивается ИК-лазером, после чего оценивается время получения отражённого от него света. По этим данным вычисляется расстояние до объекта, а блок линз быстро перемещается на заранее заданную величину. В целом работает быстрее PDAF и даёт меньше ошибок (особенно в темноте), но из-за низкой мощности лазера его заявленная дальность ограничена пятью метрами, а реально эффективная – двумя-тремя.
Работает как лазерный дальномер. Объект съёмки подсвечивается ИК-лазером, после чего оценивается время получения отражённого от него света. По этим данным вычисляется расстояние до объекта, а блок линз быстро перемещается на заранее заданную величину. В целом работает быстрее PDAF и даёт меньше ошибок (особенно в темноте), но из-за низкой мощности лазера его заявленная дальность ограничена пятью метрами, а реально эффективная – двумя-тремя.
f/x.y – диафрагменное число, или просто диафрагма. Показывает светопропускание объектива через отношение входного зрачка объектива (принимается за единицу) к заднему фокусному расстоянию. У смартфонов регулируемой диафрагмы нет, поэтому f принимается соответствующим её максимально открытому положению. Условно говоря, чем меньше знаменатель – тем лучше. Например, камера с f/1.8 пропускает за единицу времени больше света (обладает большей светосилой), чем с f/2.2. В одинаковых условиях первая будет снимать на более коротких выдержках и/или устанавливать меньшее значение ISO, что положительно скажется на качестве снимка.
ISO – светочувствительность матрицы, оцениваемая по стандарту ISO 12232:2006. Чем выше ISO, тем при более низкой освещённости можно снимать, но достигается это ценой повышения яркостных шумов. На ISO 50 – 200 эти шумы незначительны и картинка выглядит максимально чёткой. На ISO 800 и выше включаются алгоритмы агрессивного шумоподавления, из-за чего изображение становится блёклым и сильно сглаженным. Мелкие детали теряются полностью, цветопередача огрубляется.
1/x.y» – эквивалентный размер матрицы. Чем меньше число в знаменателе, тем крупнее матрица (см таблицу в начале статьи). Сами пиксели (при одинаковом разрешении) тоже крупнее, поэтому ниже уровень цветовых шумов. Проще говоря, в пределах одного поколения матрица 1/1.7″ даёт более детальное изображение, чем 1/2.7″.
X мм – фокусное расстояние в эквиваленте кадра 35-мм плёнки. Чем меньше это значение, тем более широкий угол обзора у камеры. Больше объектов влезает в кадр ценой усиления геометрических искажений.
MP – разрешение матрицы в мегапикселях (миллионах точек). Правило «чем больше, тем лучше» здесь работает только до определённого предела – пока размер пикселей не станет слишком мелким. Сейчас у лучших матриц для смартфонов пиксели от 1,2 мкм и более, но обратите внимание: 1,6 мкм обычно указывается как маркетинговый ход. У современных матриц 40 MP эквивалентны десяти «тетрапикселям» – квадрату из четырёх пикселей под общим светофильтром одного цвета (технология Quad Bayer Array). Здесь 1,6 мкм – сторона квадрата. Нетрудно подсчитать, что размер одного пикселя составляет 0,8 мкм.
ВыводыВ нашем кратком сравнении участвовали десять смартфонов с матрицами от 12 до 48 Мп. С лёгкой руки маркетологов большинство покупателей считают, что чем больше мегапикселей, тем лучше изображение. Возможно, это и было так на заре цифровой фотографии (разница между 0,3 и 3 Мп действительно не вызывает сомнений), но сейчас дальнейшая гонка за разрешением КМОП-сенсора у смартфонов потеряла смысл.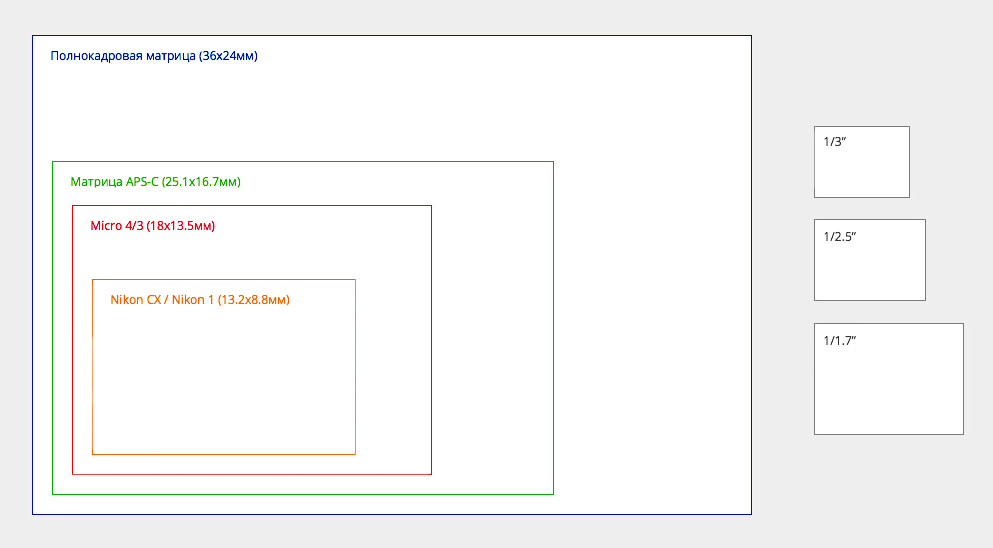 Картинка просто становится крупнее, а вот будет ли она детальнее – зависит совершенно от других факторов. Главные из них – свойства оптической системы, физические размеры матрицы и алгоритмы обработки.
Картинка просто становится крупнее, а вот будет ли она детальнее – зависит совершенно от других факторов. Главные из них – свойства оптической системы, физические размеры матрицы и алгоритмы обработки.
Каждый элемент объектива вносит свои оптические аберрации, а процессор обработки изображений ещё сильнее искажает картинку, пытаясь подавить цифровой шум. Особенно это заметно на крошечных матрицах смартфонов. В какой-то момент достигается предел разрешающей способности системы, и вы больше не увидите новых деталей, как бы сильно ни увеличивали фотографию. Первые «зеркалки» с матрицами 3 – 5 Мп и нормальным объективом до сих пор снимают лучше любого смартфона, будь в нём хоть 48 миллионов подслеповатых наноглаз.
Гораздо большее значение для смартфона имеет система автофокуса, светосила и настройка программных алгоритмов шумоподавления. Большинство кадров снимаются с рук, поэтому оптическая стабилизация очень выручит. Если же её нет, или она формальная – добавьте света (это укоротит выдержку и/или ISO, сделав снимок чётче и чище), либо воспользуйтесь штативом.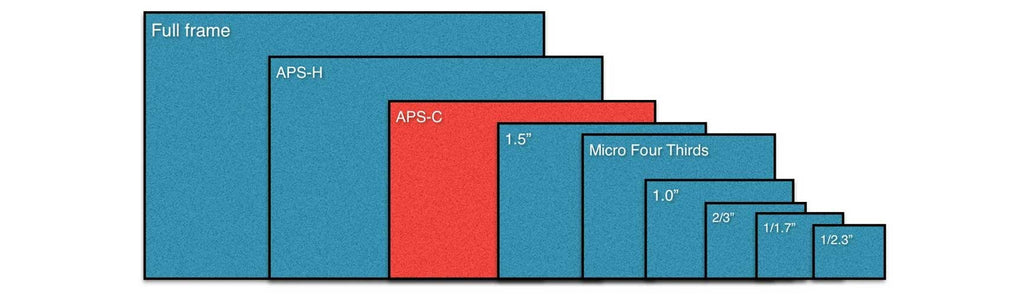
Баланс белого не совсем корректно определяется всеми смартфонами даже в идеальных условиях съёмки, поэтому по возможности снимайте в RAW. Тогда при постобработке вы просто укажите нужную цветовую температуру, и все полутона автоматически исправятся без потерь. Также этот формат позволит вам немного увеличить диапазон яркости и скорректировать свет/тень без появления заметных артефактов.
Матрицы фотоаппаратов Nikon
© 2017 Vasili-photo.com
В приведённой ниже таблице собраны некоторые сведения о матрицах, использующихся в цифровых зеркальных фотоаппаратах Nikon.
Каждая строка таблицы соответствует определённой матрице. Для каждой матрицы указаны производитель и модель (за исключением тех случаев, когда модель неизвестна). Далее перечислены фотоаппараты Nikon, в которых данный сенсор когда-либо использовался (камеры, выпускающиеся в настоящее время, выделены жирным шрифтом). Затем указан период, на протяжении которого матрица (точнее, оснащаемые ей камеры) находилась (или находится) в производстве, тип матрицы, её формат, число мегапикселей и общий рейтинг качества изображения по данным DxOMark.
| Производитель и модель матрицы | Камеры | Годы выпуска | Тип матрицы | Формат | Мп | Рейтинг DxOMark |
| Sony IMX309AQJ | D850 | с 2017 | КМОП | FX | 45,4 | 100 |
| Sony IMX321 | D500, D7500 | с 2016 | КМОП | DX | 20,9 | 84-86 |
| Sony T4K54 | D5 | с 2016 | КМОП | FX | 20,8 | 88 |
| Sony IMX193AQK | D5300, D3300, D5500, D3400, D5600 | с 2013 | КМОП | DX | 24,2 | 82-86 |
| Toshiba HEZ1 TOS-5105 |
D5200, D7100, D7200 | 2012-2017 | КМОП | DX | 24,2 | 83-87 |
| Sony IMX128AQP | D600, D610, D750 | с 2012 | КМОП | FX | 24,3 | 93-94 |
| Nikon NC81369R | D3200 | 2012-2014 | КМОП | DX | 24,2 | 81 |
| Sony IMX094AQP | D800, D810 | 2012-2017 | КМОП | FX | 36,3 | 95-97 |
| Nikon NC81366W | D4, D4s, Df | с 2012 | КМОП | FX | 16,2 | 89 |
| Sony IMX071 | D7000, D5100 | 2010-2013 | КМОП | DX | 16,2 | 80 |
| Nikon NC81362A | D3100 | 2010-2012 | КМОП | DX | 14,2 | 67 |
| Nikon NC81361A | D3s | 2009-2011 | КМОП | FX | 12,1 | 82 |
| Sony IMX028 (?) | D3X | 2008-2012 | КМОП | FX | 24,5 | 88 |
| Sony IMX038BQL | D90, D5000, D300s | 2008-2014 | КМОП | DX | 12,3 | 70-73 |
| Sony IMX038BQL | D300 | 2007-2009 | КМОП | DX | 12,3 | 67 |
| Nikon NC81338L | D3, D700 | 2007-2012 | КМОП | FX | 12,1 | 81 |
| Sony ICX493AQA | D80, D40x, D60, D3000 | 2006-2010 | ПЗС | DX | 10,2 | 61-65 |
| Sony ICX483AQA | D200 | 2005-2007 | ПЗС | DX | 10,2 | 64 |
| Sony IMX007AQ | D2X, D2Xs | 2004-2008 | КМОП | DX | 12,2 | 59 |
| Sony ICX453AK | D70, D70s, D50, D40 | 2004-2009 | ПЗС | DX | 6,1 | 50-56 |
| Nikon JFET-LBCAST | D2H, D2Нs | 2003-2007 | LBCAST | DX | 4,1 | 40 |
| Sony ICX413AQ | D100 | 2002-2005 | ПЗС | DX | 6,1 | — |
| Sony | D1X | 2001-2004 | ПЗС | DX | 5,3 | — |
| Sony | D1, D1H | 1999-2003 | ПЗС | DX | 2,7 | — |
Очевидно, что основным поставщиком сенсоров для фотоаппаратов Nikon является компания Sony, однако время от времени Nikon использует матрицы собственного производства.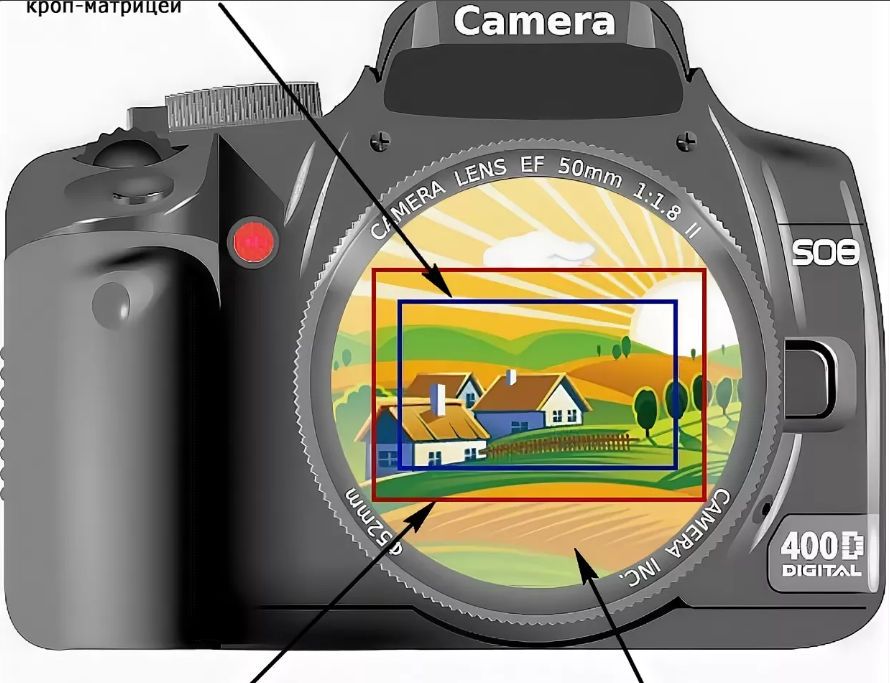
В фотокамерах D5200, D7100, D7200 установлен сенсор Toshiba. В 2015 году Sony скупила заводы Toshiba, занимающиеся производством фотоматриц, и потому в качестве производителя матрицы T4K54, используемой в фотоаппарате Nikon D5, указан нынешний владелец завода, на котором она выпускается, т.е. Sony, несмотря на то, что раньше этот завод принадлежал Toshiba.
Мне неизвестны модели сенсоров, использовавшихся в первых цифровых зеркальных фотоаппаратах Nikon – D1, D1H и D1X. Кроме того, я не вполне уверен: точно ли в Nikon D3X устанавливалась та же самая матрица Sony IMX028, что и в Sony α900.
Для некоторых сенсоров общий рейтинг матрицы DxOMark указан в виде диапазона. Это связано с тем, что качество изображения зависит не только от самой матрицы, но и от сопутствующей ей электроники (АЦП, процессор и пр. ), а также от алгоритмов первичного шумоподавления и оцифровки сигнала. Вследствие этого у разных фотокамер, оснащённых одним и тем же сенсором, качество изображения может незначительно различаться. Например, общий рейтинг DxOMark для Nikon D810 составляет 97 баллов, а для Sony A7R – 95 баллов, хотя матрица в обеих камерах одна и та же – Sony IMX094AQP. Иными словами, Nikon ухитряется добиваться от сенсоров Sony большей производительности, чем это получается у самой Sony.
), а также от алгоритмов первичного шумоподавления и оцифровки сигнала. Вследствие этого у разных фотокамер, оснащённых одним и тем же сенсором, качество изображения может незначительно различаться. Например, общий рейтинг DxOMark для Nikon D810 составляет 97 баллов, а для Sony A7R – 95 баллов, хотя матрица в обеих камерах одна и та же – Sony IMX094AQP. Иными словами, Nikon ухитряется добиваться от сенсоров Sony большей производительности, чем это получается у самой Sony.
Спасибо за внимание!
Василий А.
Post scriptum
Если статья оказалась для вас полезной и познавательной, вы можете любезно поддержать проект, внеся вклад в его развитие. Если же статья вам не понравилась, но у вас есть мысли о том, как сделать её лучше, ваша критика будет принята с не меньшей благодарностью.
Не забывайте о том, что данная статья является объектом авторского права. Перепечатка и цитирование допустимы при наличии действующей ссылки на первоисточник, причём используемый текст не должен ни коим образом искажаться или модифицироваться.
Желаю удачи!
|
Дата публикации: 14.01.2016 Последнее обновление: 27.09.2017 |
Вернуться к разделу «Фотооборудование»
Перейти к полному списку статей
| Добавить | |
| Характеристики | |
| Основные | |
| Класс | |
| Число мегапикселей матрицы | |
| Дисплей | |
| Видоискатель | |
| Тип объектива | |
| Матрица | |
| Тип матрицы | |
| Физический размер | |
| Число эффективных пикселов | |
| Разрешение матрицы | |
| Разрешение матрицы по Y | |
| Чувствительность ISO, мин | |
| Чувствительность ISO, макс | |
| Функция очистки матрицы | |
| Объектив | |
| Байонет | |
| Фокусное расстояние, мин | |
| Фокусное расстояние, макс | |
| Ручная фокусировка | |
| Стабилизатор изображения | |
| Светосила объектива | |
| Объектив в комплекте | |
| Дисплей и видоискатель | |
| Размер дисплея | |
| Тип дисплея | |
| Число точек дисплея | |
| Второй дисплей | |
| Поле зрения видоискателя | |
| Экспозиция и баланс белого | |
| Экспокоррекция | |
| Замер экспозиции | |
| Выдержка, макс | |
| Выдержка, мин | |
| Режимы экспозиции | |
| Брекетинг экспозиции | |
| Баланс белого | |
| Съемка | |
| Формат кадра | |
| Серийная съемка | |
| Число кадров в серии, JPEG | |
| Число кадров в серии, RAW | |
| Формат файла | |
| Автоспуск | |
| Видео и звук | |
| Формат записи видео | |
| Разрешение видео, макс | |
| Частота кадров, макс | |
| Запись звука | |
| Вспышка | |
| Встроенная вспышка | |
| Дальность действия | |
| Система замера вспышки | |
| Подавление «Красных глаз» | |
| Подсветка автофокуса | |
| Горячий башмак | |
| Брекетинг вспышки | |
| Синхроконтакт | |
| Память | |
| Поддержка карт памяти | |
Интерфейсы и доп. функции функции | |
| Интерфейсы | |
| Дистанционное управление | |
| Питание | |
| Аккумулятор | |
| Запас заряда | |
| Корпус | |
| Материал | |
| Габариты | |
| Вес |
Рассечение матрицы камеры, часть 2: Внешняя матрица ←
22 августа 2012 г.
Добро пожаловать в третий пост из серии «Камера перспективы — Интерактивный тур». В предыдущем посте мы узнали, как разложить матрицу камеры на произведение внутренней и внешней матриц. В следующих двух постах мы более подробно рассмотрим внешние и внутренние матрицы. Сначала мы рассмотрим различные способы взглянуть на внешнюю матрицу с интерактивной демонстрацией в конце.
Внешняя матрица камеры
Внешняя матрица камеры описывает местоположение камеры в мире и направление, в котором она направлена.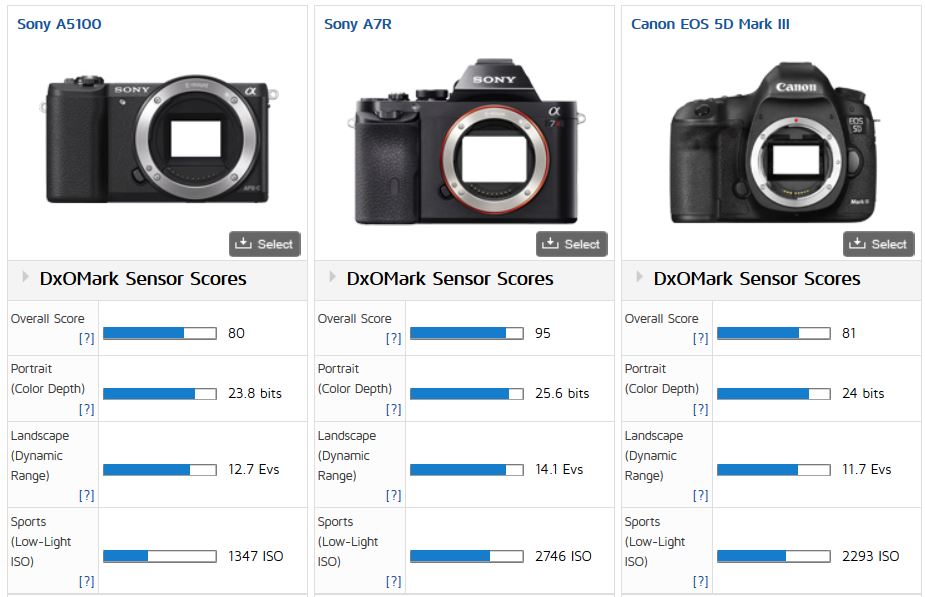 Те, кто знаком с OpenGL, знают это как «матрицу просмотра» (или свернутую в «матрицу просмотра модели»). Он состоит из двух компонентов: матрицы вращения R и вектора перемещения t , но, как мы скоро увидим, они не совсем соответствуют повороту и перемещению камеры. Сначала мы исследуем части внешней матрицы, а позже рассмотрим альтернативные способы описания позы камеры, которые более интуитивно понятны.
Те, кто знаком с OpenGL, знают это как «матрицу просмотра» (или свернутую в «матрицу просмотра модели»). Он состоит из двух компонентов: матрицы вращения R и вектора перемещения t , но, как мы скоро увидим, они не совсем соответствуют повороту и перемещению камеры. Сначала мы исследуем части внешней матрицы, а позже рассмотрим альтернативные способы описания позы камеры, которые более интуитивно понятны.
Внешняя матрица принимает форму жесткой матрицы преобразования: матрица вращения 3×3 в левом блоке и вектор-столбец переноса 3×1 справа:
\ [[R \, | \, \ boldsymbol {t}] = \ left [\ begin {array} {ccc | c} r_ {1,1} & r_ {1,2} & r_ {1,3} & t_1 \\ r_ {2,1} & r_ {2,2} & r_ {2,3} & t_2 \\ r_ {3,1} & r_ {3,2} & r_ {3,3} & t_3 \\ \ end {array} \ right] \]
Часто можно увидеть версию этой матрицы с дополнительной строкой (0,0,0,1), добавленной внизу.Это делает матрицу квадратной, что позволяет нам дополнительно разложить эту матрицу на поворот с последующим переводом на :
\ [ \ begin {align} \оставили [ \ begin {array} {c | c} R & \ boldsymbol {t} \\ \ hline \ boldsymbol {0} & 1 \ end {массив} \ right] & = \оставили [ \ begin {array} {c | c} Я & \ boldsymbol {t} \\ \ hline \ boldsymbol {0} & 1 \ end {массив} \верно ] \ раз \оставили [ \ begin {array} {c | c} R & \ boldsymbol {0} \\ \ hline \ boldsymbol {0} & 1 \ end {массив} \верно ] \\ знак равно \ left [\ begin {array} {ccc | c} 1 & 0 & 0 & t_1 \\ 0 & 1 & 0 & t_2 \\ 0 & 0 & 1 & t_3 \\ \ hline 0 & 0 & 0 & 1 \ end {array} \ right] \ times \ left [\ begin {array} {ccc | c} r_ {1,1} & r_ {1,2} & r_ {1,3} & 0 \\ r_ {2,1} & r_ {2,2} & r_ {2,3} & 0 \\ r_ {3,1} & r_ {3,2} & r_ {3,3} & 0 \\ \ hline 0 & 0 & 0 & 1 \ end {array} \ right] \ end {align} \]
Эта матрица описывает, как преобразовать точки в мировых координатах в координаты камеры. Вектор t можно интерпретировать как положение начала отсчета мира в координатах камеры, а столбцы R представляют направления мировых осей в координатах камеры.
Вектор t можно интерпретировать как положение начала отсчета мира в координатах камеры, а столбцы R представляют направления мировых осей в координатах камеры.
Важно помнить, что внешняя матрица описывает, как мир трансформируется относительно камеры . Это часто нелогично, потому что мы обычно хотим указать, как камера трансформируется относительно мира .Далее мы рассмотрим два альтернативных способа описания внешних параметров камеры, которые более интуитивно понятны, и способы их преобразования в форму внешней матрицы.
Построение внешней матрицы из позы камеры
Часто более естественно указать позу камеры напрямую, чем указывать, как точки мира должны преобразовываться в координаты камеры. К счастью, построить внешнюю матрицу камеры таким способом легко: просто создайте жесткую матрицу преобразования, которая описывает позу камеры, а затем возьмите ее обратную.
Пусть C — вектор-столбец, описывающий положение центра камеры в мировых координатах, и пусть \ (R_c \) — матрица вращения, описывающая ориентацию камеры относительно осей мировых координат.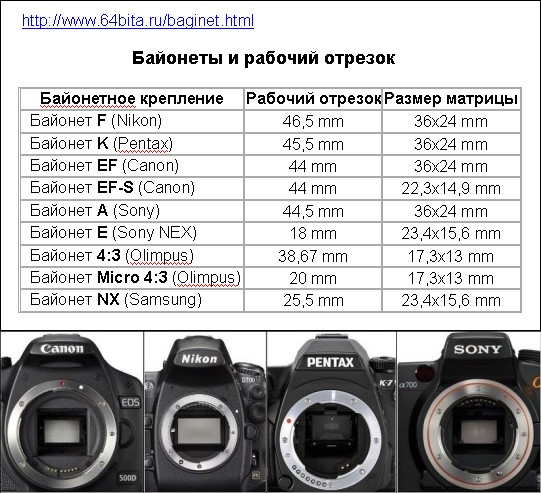 TC \\
\ hline
\ boldsymbol {0} & 1 \\
\ end {массив}
\ right] & \ text {(умножение матриц)}
\ end {align}
TC \\
\ hline
\ boldsymbol {0} & 1 \\
\ end {массив}
\ right] & \ text {(умножение матриц)}
\ end {align}
При применении инверсии мы используем тот факт, что инверсией матрицы вращения является ее транспонирование, а инвертирование матрицы переноса просто инвертирует вектор переноса.Т \\ \ boldsymbol {t} & = -RC \ end {align} \]
Некоторые тексты пишут внешнюю матрицу, заменяя -RC на t , что смешивает мировое преобразование ( R ) и нотацию преобразования камеры ( C ).
Обзорная камера
Читатели, знакомые с OpenGL, могут предпочесть третий способ определения позы камеры с использованием (a) положения камеры, (b) того, на что она смотрит, и (c) направления «вверх».В унаследованном OpenGL это выполняется функцией gluLookAt (), поэтому мы назовем ее «обзорной» камерой. Пусть C будет центром камеры, p будет целевой точкой, а u направлен вверх. Алгоритм вычисления матрицы вращения (перефразирован из документации OpenGL):
Алгоритм вычисления матрицы вращения (перефразирован из документации OpenGL):
- Вычислить L = p — C.
- Нормализовать L.
- Вычислить s = L x u. (перекрестное произведение)
- Нормализовать s.
- Вычислить u ‘= s x L.
Тогда матрица внешнего вращения имеет следующий вид:
\ [ R = \ left [ \ begin {array} {ccc} s_1 & s_2 & s_3 \\ u_1 ‘& u_2’ & u_3 ‘\\ -L_1 и -L_2 и -L_3 \ end {массив} \верно] \]
(обновлено 21 мая 2014 г. — транспонированная матрица)
Вы можете получить вектор трансляции так же, как и раньше: t = -RC .
Попробуйте!
Ниже представлена интерактивная демонстрация трех различных способов параметризации внешних параметров камеры.Обратите внимание на то, как камера по-разному перемещается при переключении между тремя параметрами.
Для этого требуется браузер с поддержкой WebGL и включенным Javascript.
Javascript требуется для этой демонстрации.
Слева : сцена с камерой и просмотром объема. Виртуальная плоскость изображения отображается желтым цветом. Справа : изображение камеры.
Настройте внешние параметры, указанные выше.
Это параметризация, ориентированная на мир. Эти параметры описывают, как мир изменяется относительно камеры . Эти параметры соответствуют непосредственно записям в матрице внешней камеры.
При настройке этих параметров обратите внимание на то, как камера перемещается в мире (левая панель), и контрастируйте с параметризацией «ориентированной на камеру»:
- Вращение влияет на положение камеры (синее поле).
- Направление движения камеры зависит от текущего поворота.
- Положительное вращение перемещает камеру по часовой стрелке (или, что эквивалентно, вращает мир против часовой стрелки).

Также обратите внимание, как изменяется изображение (правая панель):
- Вращение никогда не перемещает начало мира (красный шар).
- При изменении \ (t_x \) сферы всегда перемещаются по горизонтали, независимо от вращения.
- Увеличение \ (t_z \) всегда перемещает камеру ближе к началу координат мира.
Настройте внешние параметры, указанные выше.
Это параметризация, ориентированная на камеру, которая описывает, как камера изменяется относительно мира . Эти параметры соответствуют элементам матрицы внешней камеры inverse .
При настройке этих параметров обратите внимание на то, как камера перемещается в мире (левая панель), и контрастируйте с параметризацией «мир-центричность»:
- Вращение происходит относительно положения камеры (синий прямоугольник).

- Направление движения камеры не зависит от текущего поворота.
- Положительное вращение вращает камеру против часовой стрелки (или, что эквивалентно, вращает мир по часовой стрелке).
- Увеличение \ (C_y \) всегда перемещает камеру к небу, независимо от поворота.
Также обратите внимание, как изменяется изображение (правая панель):
- При вращении вокруг оси y обе сферы перемещаются по горизонтали.
- При разных поворотах изменение \ (C_x \) перемещает сферы в разных направлениях.
Настройте внешние параметры, указанные выше.
Это параметризация «взгляда», которая описывает ориентацию камеры с точки зрения того, на что она смотрит. Отрегулируйте \ (p_x \), \ (p_y \) и \ (p_z \), чтобы изменить направление взгляда камеры (оранжевая точка). Вектор вверх зафиксирован на (0,1,0) ‘. Обратите внимание, что перемещение центра камеры, * C *, заставляет камеру вращаться.
Вектор вверх зафиксирован на (0,1,0) ‘. Обратите внимание, что перемещение центра камеры, * C *, заставляет камеру вращаться.
Настройте внутренние параметры, указанные выше. При настройке этих параметров наблюдайте, как изменяется громкость просмотра на левой панели:
- При изменении фокусного расстояния желтая фокальная плоскость перемещается, что меняет угол поля зрения просматриваемого объема.
- Изменение главной точки влияет на то, где зеленая центральная линия пересекает фокальную плоскость.
- Установка наклона на ненулевое значение приводит к тому, что фокальная плоскость становится непрямоугольной
Внутренние параметры приводят только к двумерным преобразованиям; глубина объектов игнорируется. Чтобы убедиться в этом, посмотрите, как на изображение в правой панели влияет изменение внутренних параметров:
- Изменение фокусного расстояния одинаково масштабирует ближнюю и дальнюю сферу.

- Изменение главной точки не влияет на параллакс.
- Никакая комбинация внутренних параметров не покажет закрытые части объекта.
Заключение
Мы только что изучили три различных способа параметризации внешнего состояния камеры. Какую параметризацию вы предпочитаете использовать, зависит от вашего приложения. Если вы пишете FPS в стиле Wolfenstein, вам может понравиться параметризация, ориентированная на мир, потому что движение по (t_z) всегда соответствует движению вперед.Или вы можете интерполировать камеру через путевые точки в вашей сцене, и в этом случае предпочтительна параметризация, ориентированная на камеру, поскольку вы можете напрямую указать положение своей камеры. Если вы не уверены, что предпочитаете, поиграйте с указанным выше инструментом и решите, какой подход кажется наиболее естественным.
Присоединяйтесь к нам в следующий раз, когда мы исследуем внутреннюю матрицу, и мы узнаем, почему скрытые части вашей сцены никогда не могут быть обнаружены путем увеличения вашей камеры. Увидимся позже!
Увидимся позже!
% PDF-1.4
%
400 0 obj
>
эндобдж
xref
400 109
0000000016 00000 н.
0000003483 00000 н.
0000003712 00000 н.
0000003748 00000 н.
0000004227 00000 п.
0000004392 00000 п.
0000004535 00000 н.
0000004695 00000 н.
0000004839 00000 н.
0000004968 00000 н.
0000005111 00000 п.
0000005240 00000 п.
0000005383 00000 п.
0000005512 00000 н.
0000005655 00000 н.
0000005784 00000 н.
0000005927 00000 н.
0000006056 00000 н.
0000006199 00000 н.
0000006328 00000 н.
0000006471 00000 н.
0000006601 00000 п.
0000006744 00000 н.
0000006874 00000 н.
0000007017 00000 п.
0000007145 00000 н.
0000007288 00000 н.
0000007416 00000 н.
0000007560 00000 н.
0000007688 00000 н.
0000007832 00000 н.
0000007869 00000 н.
0000008225 00000 н. 0000008617 00000 н.
0000009177 00000 н.
0000009264 00000 н.
0000009367 00000 п.
0000009992 00000 н.
0000010142 00000 п.
0000010556 00000 п.
0000011223 00000 п.
0000012683 00000 п.
0000013991 00000 п.
0000014174 00000 п.
0000014232 00000 п.
0000014655 00000 п.
0000014877 00000 п.
0000015541 00000 п.
0000016841 00000 п.
0000017175 00000 п.
0000017458 00000 п.
0000018776 00000 п.
0000024044 00000 п.
0000024387 00000 п.
0000024994 00000 п.
0000026034 00000 п.
0000026702 00000 п.
0000027149 00000 н.
0000027246 00000 п.
0000027739 00000 п.
0000027993 00000 п.
0000028206 00000 п.
0000029544 00000 п.
0000030846 00000 п.
0000031983 00000 п.
0000032805 00000 п.
0000040421 00000 п.
0000426541 00000 н.
0000429274 00000 н.
0000436155 00000 п.
0000440319 00000 п.
0000440383 00000 п.
0000440769 00000 н.
0000440992 00000 н.
0000441064 00000 н.
0000441174 00000 н.
0000441279 00000 н.
0000441328 00000 н.
0000441450 00000 н.
0000441499 00000 н.
0000441630 00000 н.
0000008617 00000 н.
0000009177 00000 н.
0000009264 00000 н.
0000009367 00000 п.
0000009992 00000 н.
0000010142 00000 п.
0000010556 00000 п.
0000011223 00000 п.
0000012683 00000 п.
0000013991 00000 п.
0000014174 00000 п.
0000014232 00000 п.
0000014655 00000 п.
0000014877 00000 п.
0000015541 00000 п.
0000016841 00000 п.
0000017175 00000 п.
0000017458 00000 п.
0000018776 00000 п.
0000024044 00000 п.
0000024387 00000 п.
0000024994 00000 п.
0000026034 00000 п.
0000026702 00000 п.
0000027149 00000 н.
0000027246 00000 п.
0000027739 00000 п.
0000027993 00000 п.
0000028206 00000 п.
0000029544 00000 п.
0000030846 00000 п.
0000031983 00000 п.
0000032805 00000 п.
0000040421 00000 п.
0000426541 00000 н.
0000429274 00000 н.
0000436155 00000 п.
0000440319 00000 п.
0000440383 00000 п.
0000440769 00000 н.
0000440992 00000 н.
0000441064 00000 н.
0000441174 00000 н.
0000441279 00000 н.
0000441328 00000 н.
0000441450 00000 н.
0000441499 00000 н.
0000441630 00000 н. 0000441678 00000 н.
0000441841 00000 н.
0000441889 00000 н.
0000442010 00000 н.
0000442120 00000 н.
0000442301 00000 п.
0000442349 00000 н.
0000442486 00000 н.
0000442624 00000 н.
0000442772 00000 н.
0000442820 00000 н.
0000442942 00000 н.
0000443060 00000 н.
0000443108 00000 п.
0000443241 00000 н.
0000443289 00000 н.
0000443429 00000 н.
0000443477 00000 н.
0000443525 00000 н.
0000443573 00000 н.
0000443621 00000 н.
0000443669 00000 н.
0000443807 00000 н.
0000443855 00000 н.
0000443992 00000 н.
0000444040 00000 н.
0000444088 00000 н.
0000002476 00000 н.
трейлер
] / Назад 795936 >>
startxref
0
%% EOF
508 0 объект
> поток
h ޔ Smlu ~ X [lf \ h5۵] hFM (/ j * (_ P | a:
S8 $ & | 2f_> а $!% ~ W! =? TjPXP
T6b * 9) mѹzc99f} K?) 7 @ jG: ZZp {ܽ Y7u5n [z | # ʸ 鶨 / o
46zw {| `g, UL? 56Ch ‘؛ ku y
ҳ) = L!> j; H./{‘-RF5LTZr.25XTi%Ci ו * MUɓx% gg) ~; Żaxbx6BzD`
0000441678 00000 н.
0000441841 00000 н.
0000441889 00000 н.
0000442010 00000 н.
0000442120 00000 н.
0000442301 00000 п.
0000442349 00000 н.
0000442486 00000 н.
0000442624 00000 н.
0000442772 00000 н.
0000442820 00000 н.
0000442942 00000 н.
0000443060 00000 н.
0000443108 00000 п.
0000443241 00000 н.
0000443289 00000 н.
0000443429 00000 н.
0000443477 00000 н.
0000443525 00000 н.
0000443573 00000 н.
0000443621 00000 н.
0000443669 00000 н.
0000443807 00000 н.
0000443855 00000 н.
0000443992 00000 н.
0000444040 00000 н.
0000444088 00000 н.
0000002476 00000 н.
трейлер
] / Назад 795936 >>
startxref
0
%% EOF
508 0 объект
> поток
h ޔ Smlu ~ X [lf \ h5۵] hFM (/ j * (_ P | a:
S8 $ & | 2f_> а $!% ~ W! =? TjPXP
T6b * 9) mѹzc99f} K?) 7 @ jG: ZZp {ܽ Y7u5n [z | # ʸ 鶨 / o
46zw {| `g, UL? 56Ch ‘؛ ku y
ҳ) = L!> j; H./{‘-RF5LTZr.25XTi%Ci ו * MUɓx% gg) ~; Żaxbx6BzD`
Матрица камеры — обзор
3.2 Получение внутренних параметров камеры и трехмерных координат характерных точек
Предполагая, что координаты точки в трехмерном мире р в пространстве р ж ( х ш , у ш , г ж ) в опорном кадре камеры, и его соответствующие координаты изображение р ( x p , y p ). Согласно обычной модели камеры-обскуры и искажению объектива [11,12], они связаны следующими уравнениями проекции:
Согласно обычной модели камеры-обскуры и искажению объектива [11,12], они связаны следующими уравнениями проекции:
xn = xw / zwyw / zw = xy, r2 = x2 + y2,
xd = xd (1 ) xd (2) = (1 + k1r2 + k2r4) xn + 2p1xy + p2 (r2 + 2×2) p1 (r2 + 2y2) + 2p2xy,
(2) xpyp1 = Kxd (1) xd (2) 1withK = fxα · Fxu00fyv0001.
, где ( u 0 , v 0 ) — главная точка на плоскости изображения, x n и x d — идеальные и фактические координаты изображения p соответственно. f x и f y обозначают эффективное фокусное расстояние, k 1 , k 2 — коэффициенты радиального искажения, а p 1 , p 2 — коэффициенты тангенциального искажения. α — коэффициент перекоса, а K — матрица камеры. Все эти внутренние параметры могут быть получены заранее с помощью некоторых эффективных методов калибровки камеры [13,14], и они считаются фиксированными после калибровки камеры.
Учитывая, что интервал между характерными точками известен, можно получить трехмерные локальные координаты характерных точек в соответствующей системе координат камеры [9], которые обозначаются как aijl и bijr ( i = 1, 2, …, м , j = 1, 2,…, n ) соответственно. Взяв для иллюстрации позу 1 на рис. характерная точка b 11 , b 31 согласно RCCF соответственно.
Однако существует одна потенциальная проблема, заключающаяся в том, что выбросы, которые являются центрами характерных точек, извлеченных на изображении, выходят далеко за пределы их наземной истинности, могут не дать нам правильно вычислить трехмерные координаты характерной точки в пространстве. Хотя мы сделали характерные точки на наших мишенях светящимися, чтобы избежать этой проблемы в большинстве условий, все же существует вероятность того, что центры одной или двух характерных точек будут извлечены с большой ошибкой. В этом состоянии мы должны использовать алгоритм RANSAC [15], чтобы проверить центр всех характерных точек, извлеченных на одном изображении, с целью обнаружения и устранения возможных выбросов заранее, а затем использовать следы, характерные точки с допустимым шумом. , чтобы продолжить калибровку.И в этой статье мы предполагаем, что все извлеченные точки центра являются промежуточными и действительными.
Предположим, что в позиции j -е единичные направления цели a , b при LCCF и RCCF равны ajl, bjl и ajr, bjr, соответственно, поэтому их можно вычислить по следующему уравнению:
(3) ajl = amjl-a1jl / amjl-a1jl, bjr = bmjr-b1jr / bmjr-b1jr, (j∈ [1, n]).
Модель камеры с проектором| imatest
Устарело в текущей версии
Модель проекционной камеры описывает математику преобразования мировой точки в точку изображения.Это делается с помощью модели камеры с отверстиями. Вместе с моделью искажения, которая характеризует отклонение от модели точечного отверстия, этим методом можно моделировать большинство камер *.
Вместе с моделью искажения, которая характеризует отклонение от модели точечного отверстия, этим методом можно моделировать большинство камер *.
Модель проекционной камеры учитывает только взаимосвязь между мировыми координатами и координатами изображения. Он не учитывает другие факторы, такие как функция передачи модуляции (MTF), оптические аберрации (например, хроматические аберрации, кома и т. Д.), Линейность и воспроизведение цвета, которые могут повлиять на качество изображения.j \ left (\ mathbf {X} _ {i} \ right) \)
Есть три компонента для применения модели проективного преобразования: внешние элементы, модель камеры-точечного отверстия и искажение точек для учета разницы между встроенной камерой и моделью-крошечным отверстием.
Проекция трехмерных точек в модели камеры-обскуры.
Изображение проецируемых точек.
Внутренние функции камеры описывают свойства модели камеры-обскуры, которые связывают относительные мировые координаты камеры относительно камеры с координатами изображения. В модели крошечного отверстия лучи проходят по прямой линии от объекта в сцене через крошечное отверстие к фокальной плоскости. Его геометрия похожа на треугольники, связывающие мировые координаты с координатами изображения. Математическая модель для этого использует 5 параметров: фокусное расстояние в направлениях x и y, основная точка в направлениях x и y и перекос между направлениями x и y.
В модели крошечного отверстия лучи проходят по прямой линии от объекта в сцене через крошечное отверстие к фокальной плоскости. Его геометрия похожа на треугольники, связывающие мировые координаты с координатами изображения. Математическая модель для этого использует 5 параметров: фокусное расстояние в направлениях x и y, основная точка в направлениях x и y и перекос между направлениями x и y.
Параметры
Фокусное расстояние
В модели точечного отверстия фокусное расстояние \ (f \) — это расстояние от отверстия до фокальной плоскости вдоль оптической оси.Системы с большим фокусным расстоянием будут иметь большее увеличение в более узком поле зрения (FOV), тогда как меньшие фокусные расстояния будут иметь больший охват.
Возможно иметь разное фокусное расстояние вдоль каждого направления фокальной плоскости. В этом случае фокусное расстояние оси \ (y \) изменяется на \ (\ alpha \).
\ (f_y = \ alpha \ cdot f \)
Для настоящей камеры-обскуры \ (f_x = f_y \) (\ (\ alpha = 1 \)), однако на практике это может быть связано с факторами, включая производственные дефекты, искажение объектива и изображения, полученные от системы сканирования..jpg) Интерпретация неравных фокусных расстояний заключается в том, что эффективная форма пикселя не является квадратной.
Интерпретация неравных фокусных расстояний заключается в том, что эффективная форма пикселя не является квадратной.
Принцип действия
Точка \ ((pp_x, pp_y) \) является основной точкой, которая представляет собой пиксельную координату пересечения оптической оси с фокальной плоскостью. Функция сдвига наклона-сдвига перемещает фокальную плоскость (и главную точку) вокруг оптической оси.
Косой
Фактор перекоса \ (s \) вводит трансформацию сдвига изображения.Для многих камер это 0. Случаи, когда оно не равно нулю, включают в себя фотографирование изображения (введение гомографии) и несинхронизацию процесса выборки пикселей из фреймграббера. Ненулевой перекос означает, что оси x и y камеры не перпендикулярны друг другу.
Внутренняя матрица
Внутренняя матрица \ (\ mathbf {K} \) — это верхнетреугольная матрица, которая преобразует мировую координату относительно камеры в координату однородного изображения. Существует две общие и эквивалентные формы внутренней матрицы:
\ (\ mathbf {K} = \ begin {bmatrix} f & s & pp_x \\ 0 & f \ cdot \ alpha & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \)
\ (\ mathbf {K} = \ begin {bmatrix} f_x & s & pp_x \\ 0 & f_y & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \)
Многие камеры могут быть представлены с более простой внутренней матрицей.
\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ begin {bmatrix} f & 0 & pp_x \\ 0 & f & pp_y \\ 0 & 0 & 1 \ end {bmatrix} \ begin {bmatrix} X \\ Y \\ Z \ end {bmatrix} \)
\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ begin {bmatrix} f \ cdot X + pp_x \ cdot Z \\ f \ cdot Y + pp_y \ cdot Z \\ Z \ конец {bmatrix} \)
После преобразования в неоднородные координаты
\ (\ begin {bmatrix} x ‘\\ y’ \ end {bmatrix} = \ begin {bmatrix} \ displaystyle \ frac {f \ cdot X + pp_x \ cdot Z} {Z} \\ \ displaystyle \ frac { е \ cdot Y + pp_y \ cdot Z} {Z} \ end {bmatrix} = \ begin {bmatrix} f \ cdot \ displaystyle \ frac {X} {Z} + pp_x \\ f \ cdot \ displaystyle \ frac {Y } {Z} + pp_y \ end {bmatrix} \)
Проверка этого результата показывает, что расстояние от оптической оси (основной точки) пропорционально отношению расстояния мировых точек от оптической оси к расстоянию до камеры.Это означает, что точка, которая вдвое дальше от оптической оси и вдвое дальше от камеры, будет соответствовать той же точке изображения. Лучшая реконструкция точки с помощью одной камеры — это то, что точка находится где-то на линии.
Лучшая реконструкция точки с помощью одной камеры — это то, что точка находится где-то на линии.
Квартир
Все эти значения рассчитываются в единицах количества пикселей. Шаг пикселя \ (p \) используется для преобразования количества пикселей в физические единицы. Например:
\ (f [\ mathrm {mm}] = f [\ mathrm {пикселей}] \ cdot p \ left [\ frac {\ mu \ mathrm {m}} {\ mathrm {pixel}} \ right] \ cdot \ гидроразрыв {1 [\ mathrm {mm}]} {1000 [\ mu \ mathrm {m}]} \)
Обратный
Инверсия внутренней матрицы камеры используется для преобразования неискаженных точек изображения в линии от центра камеры.{-1} = \ displaystyle \ frac {1} {f} \ begin {bmatrix} 1 & 0 & -pp_x \\ 0 & 1 & -pp_y \\ 0 & 0 & f \ end {bmatrix} \)
Модель искажения камеры описывает отклонение физической камеры от модели проекционной камеры. Он преобразует неискаженные точки 2D-изображения в точки искаженного 2D-изображения (те, которые находятся за пределами камеры). Модель обратной дисторсии преобразует точки искаженного изображения в неискаженные.
Модель обратной дисторсии преобразует точки искаженного изображения в неискаженные.
Внешний вид камеры описывает положение и ориентацию камеры в мире.Существует два способа описания преобразования координат между мировыми координатами и координатами относительно камеры: преобразование точки и преобразование осей (поза). Они оба имеют одинаковую форму матрицы вращения / переноса и являются противоположными друг другу.
Центр камеры соответствует расположению входного зрачка камеры. В панорамной фотографии это часто называют точкой отсутствия параллакса. Камеры с большим полем зрения (например, камеры «рыбий глаз») будут иметь разные положения входного зрачка при разных углах поля зрения.Для этих камер используется осевое расположение входного зрачка.
Точечное преобразование
Описание преобразования точки преобразует мировую точку в точку относительно камеры. Его матрица вращения / переноса прямо умножается вправо на внутреннюю матрицу для формирования матрицы камеры. {\ top} \ mathbf {t} \\ &&& \ end {array} \ right] \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ end {bmatrix} \)
{\ top} \ mathbf {t} \\ &&& \ end {array} \ right] \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ end {bmatrix} \)
В обозначении позы камеры центр камеры расположен в \ (\ mathbf {t} \).
Матрица камеры \ (\ mathbf {P} \) представляет собой комбинацию внутренней матрицы камеры и точечного преобразования.
\ (\ mathbf {P} = \ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right] \ left [\ begin {array} { ccc | c} &&& \\ & \ mathbf {R} && \ mathbf {t} \\ &&& \ end {array} \ right] \)
Матрица камеры преобразует точки мира в координаты однородного изображения.
Мировые очки к точкам изображений
- Преобразование мировой координаты в координату относительно камеры путем умножения на мировую точку в преобразование точки изображения.Это преобразование является обратным позы.
- Примените внутреннюю матрицу камеры к относительной координате камеры, чтобы получить однородную координату изображения.
- Преобразует однородную координату изображения в неоднородную координату.
- Примените модель искажения, чтобы определить положение изображения мировой точки на фокальной плоскости.
Обозначение преобразования точек
\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ underbrace {\ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right]} _ {\ mathrm {intrinics}} \ underbrace {\ left [\ begin {array} {ccc | c} &&& \\ & \ mathbf {R} && \ mathbf {t} \\ &&& \ конец {массив} \ right]} _ {\ mathrm {обратная \ поза}} \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ end {bmatrix} \)
\ (\ begin {bmatrix} x ‘\\ y’ \ end {bmatrix} = \ begin {bmatrix} \ mathrm {distort} _ {x} \! \! \ Left (\ displaystyle \ frac {x} {w } \ right) \\\ mathrm {искажать} _ {y} \! \! \ left (\ displaystyle \ frac {y} {w} \ right) \ end {bmatrix} \)
Обозначение преобразования осей
\ (\ begin {bmatrix} x \\ y \\ w \ end {bmatrix} = \ underbrace {\ left [\ begin {array} {ccc} && \\ & \ mathbf {K} & \\ && \ end {array} \ right]} _ {\ mathrm {intrinics}} \ underbrace {\ left [\ begin {array} {ccc | c} &&& \\ & \ mathbf {R} ^ {\ top} && — \ mathbf { R} ^ {\ top} \ mathbf {t} \\ &&& \ end {array} \ right]} _ {\ mathrm {inverse \ pose}} \ begin {bmatrix} X \\ Y \\ Z \\ 1 \ конец {bmatrix} \)
\ (\ begin {bmatrix} x ‘\\ y’ \ end {bmatrix} = \ begin {bmatrix} \ mathrm {distort} _ {x} \! \! \ Left (\ displaystyle \ frac {x} {w } \ right) \\\ mathrm {искажать} _ {y} \! \! \ left (\ displaystyle \ frac {y} {w} \ right) \ end {bmatrix} \)
Изображение указывает на линии
- Примените модель обратного искажения, чтобы неискажать точки изображения.
 Это помещает их в геометрию камеры-обскуры.
Это помещает их в геометрию камеры-обскуры. - Преобразуйте координату изображения в однородную координату с весом \ (w \). Можно использовать любое действительное, отличное от нуля \ (w \), однако два общих из них — это 1 или расстояние от центра камеры до мировой точки.
- Умножьте координату однородного изображения на значение, обратное внутренней матрице камеры. Этот вектор является вектором направления линии между точкой и центром камеры в координатах относительно камеры.
- Примените поворот позы камеры (обратный матрице точечного преобразования) к вектору направления.\ top \ right | \ right | \) — расстояние от центра камеры (расположение входного зрачка) до мировой точки.
Что вам нужно знать в первую очередь)
Матрица перспективы и ортогональной проекции
Что вам нужно знать в первую очередь
Прежде чем мы начнем изучать, как построить базовую матрицу перспективной проекции, нам сначала нужно рассмотреть некоторые методы, на которых построены матрицы проекции.

Преобразование угла обзора в единичный куб
Рис. 1: P ‘- это проекция буквы P на холст.
Умножение точки P на нашу простую матрицу перспективной проекции даст точку P ‘, чьи:
- x’- и y’-координаты являются координатами P на плоскости изображения. Оба x ‘и y’ определены в пространстве NDC. Как упоминалось во введении, матрица перспективной проекции повторно отображает координаты трехмерной точки в ее «2D» положение на экране в пространстве NDC (в диапазоне [-1,1] в этом уроке). Обычно матрица гарантирует, что точки, видимые через камеру (содержащиеся в пирамиде), будут переназначены в диапазон [-1,1] (независимо от того, является ли холст квадратным — это не координаты экранного пространства, а координаты NDC).
-
Помимо переназначения трехмерной точки на ее двумерные координаты, нам также потребуется переназначить ее координату z. В предыдущем уроке по растеризации мы вообще не беспокоились о переназначении z ‘, но графические процессоры переназначают P’ z-координату в диапазон [0,1] или [-1,1] в зависимости от API.
 Когда P лежит на ближней плоскости отсечения, z ‘переназначается на 0 (или -1), а когда P лежит на дальней плоскости отсечения, z’ переназначается на 1.
Когда P лежит на ближней плоскости отсечения, z ‘переназначается на 0 (или -1), а когда P лежит на дальней плоскости отсечения, z’ переназначается на 1.
Рисунок 2: матрица проекции преобразует усеченную пирамиду обзора в единичный куб или канонический объем обзора.
Тот факт, что координаты x и y точки P ‘, а также ее координата z переназначены в диапазон [-1,1] и [0,1] (или [01,1]), по существу означает, что преобразование точки P матрицей проекции преобразует объем усеченной точки обзора в куб размером 2x2x1 (или 2x2x2). Этот куб часто называют единичным кубом (это не совсем куб, если он имеет размер 2x2x1, но вы поняли идею) или объем канонического представления . Вы также можете увидеть этот процесс, как если бы усеченная пирамида была нормализована.Это очень важная концепция в компьютерной графике, которую иногда трудно даже визуализировать, но усеченная зона обзора, определяемая ближней и дальней плоскостями отсечения, а также размерами экрана, который вовсе не является кубом, а имеет форму усеченной пирамиды.
 действительно «искривлен» в куб. По сути, это то, что делает матрица проекции. Когда пространство, определяемое усеченной пирамидой, «деформируется» в куб, становится легче работать с точками (куб — геометрическая форма, с которой работать намного проще, чем усеченная пирамида).Эта очень важная концепция — одна из вещей, которые вы должны помнить о матрицах проекций. Матрица проекции (по крайней мере, так, как она используется в компьютерной графике) преобразует пространство, определяемое усеченной пирамидой, в единичный куб.
действительно «искривлен» в куб. По сути, это то, что делает матрица проекции. Когда пространство, определяемое усеченной пирамидой, «деформируется» в куб, становится легче работать с точками (куб — геометрическая форма, с которой работать намного проще, чем усеченная пирамида).Эта очень важная концепция — одна из вещей, которые вы должны помнить о матрицах проекций. Матрица проекции (по крайней мере, так, как она используется в компьютерной графике) преобразует пространство, определяемое усеченной пирамидой, в единичный куб. Об вырезании
Рисунок 3: пример обрезки в 2D. На этапе отсечения новые треугольники могут быть сгенерированы везде, где исходная геометрия перекрывает границы усеченной области просмотра.
Рис. 4: точка, расположенная за камерой, будет проецироваться так же, как и точки впереди, но ее проецируемые координаты будут отражаться в обоих направлениях.
Давайте познакомимся с концепцией отсечения. По сути, он «обрезает» геометрию, пересекающую границы усеченной области обзора.
$$ \ begin {array} {l} x ‘= \ dfrac {2} {- 10} = -0,2, \\ y ‘= \ dfrac {5} {- 10} = -0,5, \\ \ end {array} $$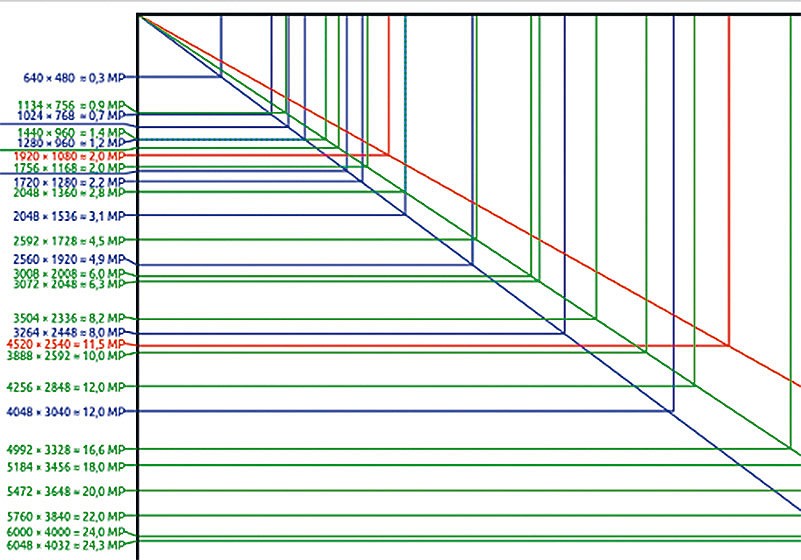 Другими словами, если некоторые треугольники или линии перекрывают просматриваемые плоскости усеченной вершины, геометрия «обрезается» таким образом, что части геометрии, содержащиеся в усеченной вершине, сохраняются, а части, которые находятся вне ее объема ( и, следовательно, не видны камере), выброшены (рис. 3). Отсечение может показаться только процессом оптимизации, хотя его основная цель — не выбрасывать части сцены, которые не видны, чтобы ускорить рендеринг.«К сожалению» перспективная проекция одинаково хорошо работает для объектов, которые находятся перед камерой или за ней. Рассмотрим точку, расположенную за «наблюдателем». Представим себе точку с координатами (2, 5, 10). Если применить к этому моменту правила перспективной проекции, то получится:
Другими словами, если некоторые треугольники или линии перекрывают просматриваемые плоскости усеченной вершины, геометрия «обрезается» таким образом, что части геометрии, содержащиеся в усеченной вершине, сохраняются, а части, которые находятся вне ее объема ( и, следовательно, не видны камере), выброшены (рис. 3). Отсечение может показаться только процессом оптимизации, хотя его основная цель — не выбрасывать части сцены, которые не видны, чтобы ускорить рендеринг.«К сожалению» перспективная проекция одинаково хорошо работает для объектов, которые находятся перед камерой или за ней. Рассмотрим точку, расположенную за «наблюдателем». Представим себе точку с координатами (2, 5, 10). Если применить к этому моменту правила перспективной проекции, то получится: Обратите внимание на то, что проецируемые координаты будут совершенно правильными, но также обратите внимание, что точка фактически зеркально отражается на холсте в обоих направлениях.
 Хотя координаты x и y точки в пространстве камеры положительны, в конечном итоге они оказываются отрицательными в пространстве экрана (рисунок 4).
Хотя координаты x и y точки в пространстве камеры положительны, в конечном итоге они оказываются отрицательными в пространстве экрана (рисунок 4). Урок, объясняющий один из наиболее распространенных алгоритмов отсечения, известный как алгоритм Коэна-Сазерленда, будет позже добавлен в раздел, посвященный расширенной растеризации, хотя мы поговорим больше об отсечении и пространстве отсечения в четвертой главе.
Теперь, когда мы понимаем концепцию отсечения, мы можем более легко объяснить, почему это преобразование из пирамиды просмотра в этот канонический объем просмотра выполняется.
Рис. 5: преобразование усеченной перспективы в единичный куб до отсечения.
- Основная причина, как мы упоминали ранее, заключается в том, что он преобразует довольно сложное для работы пространство (усеченную пирамиду усеченной пирамиды) в базовый блок. В этом пространстве легче выполнять такие операции, как, например, отсечение.
- После определения относительно этого канонического объема просмотра становится тривиальным преобразование трехмерных координат точек в двухмерные координаты на плоскости изображения.

Имейте в виду, что модель камеры, которую мы хотим смоделировать, — это камера-обскура , которая определяется ближней и дальней плоскостью отсечения, а также углом обзора (см. Урок по модели камеры-обскуры). Параметр угла обзора необходимо учитывать при переназначении точек из пространства экрана в пространство NDC.
Проецирование точек на экран
Прежде чем мы изучим, как создать перспективную матрицу, мы сначала еще раз рассмотрим, как проецировать трехмерные точки на экран (этот процесс подробно описан в уроке «Вычисление пиксельных координат трехмерной точки»).Обычно 3D-точки, проецируемые на плоскость изображения, сначала преобразуются в систему координат камеры. В этой системе координат положение глаза соответствует началу координат, оси x и y определяют плоскость, параллельную плоскости изображения, а ось z перпендикулярна этой плоскости xy. В нашей настройке плоскость изображения будет расположена ровно на одну единицу от начала системы координат камеры, то есть глаза.
 Это соглашение может вас смутить, если вы привыкли к системе, в которой расстояние до плоскости изображения произвольно, как в случае с OpenGL.В следующих главах мы узнаем, как расширить матрицу для обработки произвольных плоскостей отсечения. Но пока мы будем использовать это соглашение, чтобы упростить демонстрацию.
Это соглашение может вас смутить, если вы привыкли к системе, в которой расстояние до плоскости изображения произвольно, как в случае с OpenGL.В следующих главах мы узнаем, как расширить матрицу для обработки произвольных плоскостей отсечения. Но пока мы будем использовать это соглашение, чтобы упростить демонстрацию. Имейте в виду, что Scratchapixel использует правую систему координат, как и многие другие коммерческие приложения, такие как Maya. Чтобы узнать больше о правой и левой системах координат, ознакомьтесь с уроком по геометрии в разделе «Математика и физика для компьютерной графики». Поскольку мы используем правую систему координат, камера будет указывать в направлении, противоположном оси z.Это связано с тем, что, когда мы проецируем точки на плоскость изображения, мы хотим, чтобы ось x указывала вправо. С математической точки зрения, все точки, видимые камерой, имеют отрицательную z-компоненту, когда точки выражены в системе координат камеры. Это подробно объясняется в предыдущем уроке.

Давайте представим, что мы хотим спроецировать точку P на холст. Если мы проведем линию от P до глаза, мы увидим, что P проецируется на экран в точке P ‘. Как мы вычисляем P ‘?
Рисунок 6: Для проецирования P на плоскость изображения (в точке P ‘) мы задаем координаты xy точки P по координате z точки P.
На рисунке 6 вы можете видеть, что зеленый (\ (\ Delta ABC \)) и красный (\ (\ Delta DEF \)) треугольники имеют одинаковую форму, но не одинаковый размер. Такие треугольники называются подобными . Другими словами, красный треугольник можно рассматривать как уменьшенную версию зеленого треугольника. Подобные треугольники обладают полезным свойством: соотношение сторон между ними постоянно. Другими словами:
$$ \ dfrac {BC} {EF} = \ dfrac {AB} {DE}. $$Поскольку нас интересует сторона BC, т.е.е. положение P ‘на плоскости изображения, мы можем написать:
$$ BC = \ dfrac {AB * EF} {DE}. $$Учитывая, что B лежит на плоскости изображения, которая находится на расстоянии одной единицы от A (AB = 1), у нас есть окончательная формула для расчета длины BC:
$$ BC = \ dfrac {(AB = 1) * EF} {DE} = \ dfrac {EF} {DE}. $$
$$
Из этого уравнения мы можем найти координаты x и y точки P ‘. Все, что нам нужно сделать, это разделить координаты x и y точки P на ее координату z. В математической форме можно записать (уравнение 1):
$$ \ begin {array} {l} P’_x = \ dfrac {P_x} {- P_z}, \\ P’_y = \ dfrac {P_y} {- P_z}.\ end {массив} $$Обратите внимание, что мы разделили \ (P_x \) и \ (P_y \) на \ (- P_z \), а не на \ (P_z \), потому что z-компонента точек, видимых через камеру, всегда отрицательна, если определена в камере. система координат. Таким образом, очень просто вычислить координаты P ‘, которая является проекцией P на плоскость изображения. Обратите внимание, что на рисунке 6 показана только проекция координаты Y точки P на плоскость изображения. Если повернуть рисунок 5 на девяносто градусов по часовой стрелке и заменить ось y осью x, вы получите вид сверху, представляющий проекцию координаты x точки P на плоскость изображения.
Однородные координаты
Рисунок 7: чтобы умножить трехмерную точку на матрицу 4×4, нам нужно преобразовать декартовы координаты точки в однородные координаты.
 Поскольку все это преобразование требует установки однородной четвертой координаты на 1, это преобразование должно быть только неявным. В самой функции умножения точки на матрицу мы можем преобразовать точку из однородной обратно в декартовы координаты, разделив преобразованные координаты точки x ‘, y’ и z ‘на w’.
Поскольку все это преобразование требует установки однородной четвертой координаты на 1, это преобразование должно быть только неявным. В самой функции умножения точки на матрицу мы можем преобразовать точку из однородной обратно в декартовы координаты, разделив преобразованные координаты точки x ‘, y’ и z ‘на w’.Вы можете подумать, что на самом деле в перспективной проекции нет ничего особенно сложного. Сам принцип действительно довольно прост. Однако на этом история не заканчивается. На самом деле мы хотим закодировать этот процесс проецирования в матрицу, чтобы проецирование точки на плоскость изображения могло быть получено с помощью базового умножения матрицы точек. Давайте быстро рассмотрим, что мы знаем об этом процессе.
Если вы помните, что мы говорили в уроке по геометрии, две матрицы могут быть умножены друг на друга, если числа на каждой стороне знака умножения равны, или, иначе говоря, если количество столбцов левой матрицы и количество строк правой матрицы равно.
$$ \ begin {array} {l} {\ color {\ red} {\ text {no:}}} & [n \: m] * [q \: n] \\ {\ color {\ green} {\ text {yes:}}} & [m \: n] * [n \: q] \\ \ end {массив} $$
Помните, что точка может быть представлена матрицей с одной строкой (некоторые люди предпочитают запись с одним столбцом, но Scratchapixel использует запись с одной строкой). Но тогда наша точка представляет собой матрицу 1×3 (1 строка, 3 столбца) и, следовательно, не может быть умножена на матрицу 4×4 (матрицы 4×4 используются в CG для преобразования точек и векторов.Они кодируют вращение, масштаб и перенос). Что мы можем сделать? Чтобы решить эту проблему, мы используем трюк, который состоит в представлении точки с координатами не три на четыре. Говорят, что такие точки имеют однородные координаты и могут быть представлены в виде матрицы 1×4. Четвертая координата точки в ее однородном представлении обозначается буквой w . Когда мы переводим точку из декартовых координат в однородные, w устанавливается равным 1.
$$ \ begin {array} {l} [x \: y \: z] \ neq [x \: y \: z \: w = 1.2] \\ x = \ dfrac {x} {w}, y = \ dfrac {y} {w}, z = \ dfrac {z} {w}, w = \ dfrac {w} {w} = 1 \\ {[x \: y \: z] = [x \: y \: z \: w = 1]} \ end {массив} $$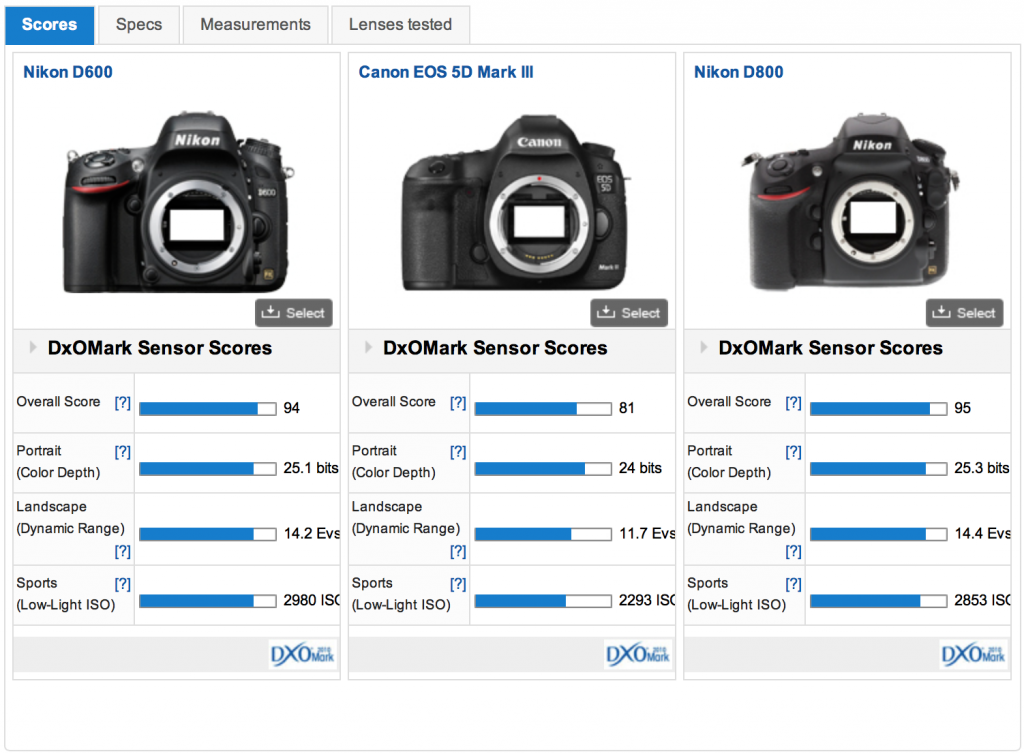 \ (P_c \) (точка в декартовых координатах) и \ (P_h \) (точка в однородных координатах) взаимозаменяемы, пока w равно 1.Когда w отличается от 1, мы должны разделить все четыре координаты точки [xyzw] на w, чтобы вернуть значение w равным 1 (если мы хотим снова использовать точку как трехмерную декартову точку) .
\ (P_c \) (точка в декартовых координатах) и \ (P_h \) (точка в однородных координатах) взаимозаменяемы, пока w равно 1.Когда w отличается от 1, мы должны разделить все четыре координаты точки [xyzw] на w, чтобы вернуть значение w равным 1 (если мы хотим снова использовать точку как трехмерную декартову точку) . Возможно более формальный способ определения этой идеи — сказать, что точка с однородными координатами [x, y, z, w] соответствует трехмерной декартовой точке [x / w, y / w, z / w] .
Вот как выглядит типичная матрица преобразования:
$$ \ begin {bmatrix} \ color {green} {m_ {00}} & \ color {green} {m_ {01}} & \ color {green} {m_ {02}} & \ color {blue} {0} \\ \ color {green} {m_ {10}} & \ color {green} {m_ {11}} & \ color {green} {m_ {12}} & \ color {blue} {0} \\ \ color {green} {m_ {20}} & \ color {green} {m_ {21}} & \ color {green} {m_ {22}} & \ color {blue} {0} \\ \ color {красный} {T_x} & \ color {красный} {T_y} & \ color {красный} {T_z} & \ color {синий} {1} \\ \ end {bmatrix} $$Внутренняя матрица [3×3] (зеленая) кодирует поворот и масштаб.
Помните, что матрицы преобразования 4×4 называются аффинными. Аффинное преобразование имеет два очень специфических свойства: Три коэффициента внизу матрицы (выделены красным) кодируют перевод.
Три коэффициента внизу матрицы (выделены красным) кодируют перевод. - Коллинеарность сохраняется: все точки, лежащие на линии, по-прежнему лежат на линии после применения преобразования.
- Соотношения расстояний сохраняются: середина линейного сегмента остается средней точкой после применения преобразования.
Мы знаем, что мы используем эти матрицы для преобразования трехмерных точек, однако, как мы только что сказали, на самом деле мы обрабатываем эти трехмерные точки так, как если бы они были точками с однородными координатами. Мы делаем это, «неявно» предполагая, что эти трехмерные точки на самом деле имеют четвертую координату, значение которой равно 1.
$$ P = \ {x, y, z, w = 1 \}. $$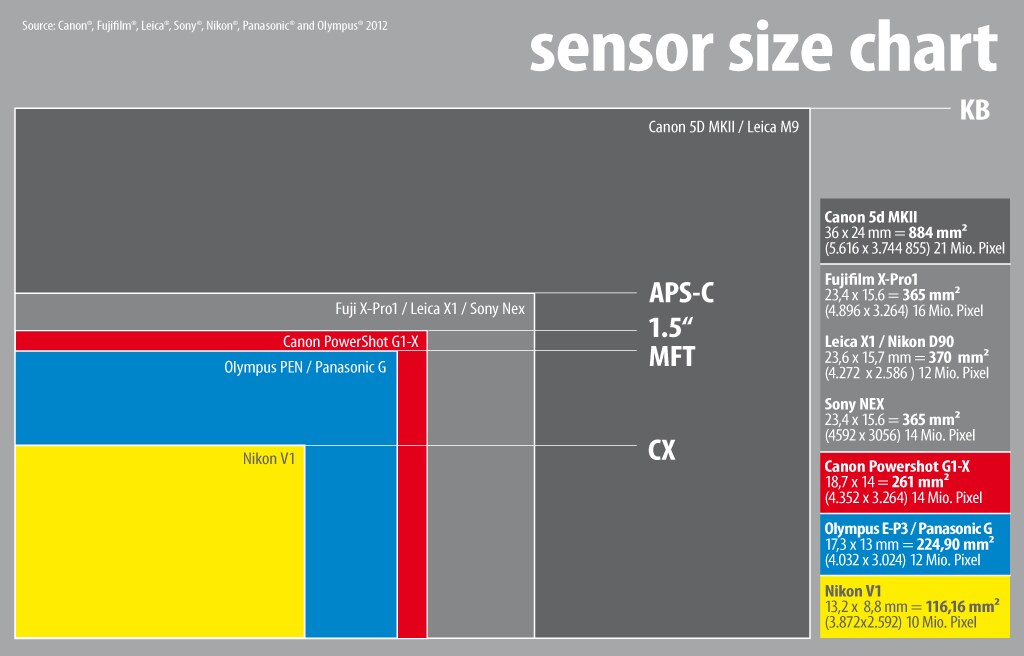 Помните, что трехмерная точка с координатами {x, y, z} и точка с однородными координатами {x, y, z, w } эквивалентны, пока w = 1.Трехмерную точку можно определить как точку с однородными координатами, если мы напишем:
Помните, что трехмерная точка с координатами {x, y, z} и точка с однородными координатами {x, y, z, w } эквивалентны, пока w = 1.Трехмерную точку можно определить как точку с однородными координатами, если мы напишем: Всегда имейте в виду, что если вы умножаете «трехмерную» точку на матрицу 4×4, ваша точка будет (по крайней мере, неявно, если вы явно не определяете эту точку с четырьмя координатами, как это делают некоторые программы) точкой с однородными координатами и чьей w-координата равна 1. Почему мы не определяем точки с четырьмя координатами «явно» в программировании, это просто для экономии памяти (на самом деле нет смысла использовать память для хранения координаты, значение которой всегда равно 1).Теперь давайте умножим эту точку 1×4 на нашу матрицу преобразования 4×4. Если мы умножим матрицу [1×4] (нашу точку) на матрицу [4×4], мы должны получить матрицу [1×4], другими словами, другую точку с однородными координатами. Чтобы преобразовать эту точку обратно в 3D, нам нужно будет разделить координаты точек {x, y, z} на w.
$$ \ begin {bmatrix} x ‘& z’ & y ‘& w’ \ end {bmatrix} знак равно \ begin {bmatrix} x & z & y & w = 1 \ end {bmatrix} * \ begin {bmatrix} \ color {green} {m_ {00}} & \ color {green} {m_ {01}} & \ color {green} {m_ {02}} & \ color {blue} {0} \\ \ color {green} {m_ {10}} & \ color {green} {m_ {11}} & \ color {green} {m_ {12}} & \ color {blue} {0} \\ \ color {green} {m_ {20}} & \ color {green} {m_ {21}} & \ color {green} {m_ {22}} & \ color {blue} {0} \\ \ color {красный} {T_x} & \ color {красный} {T_y} & \ color {красный} {T_z} & \ color {синий} {1} \\ \ end {bmatrix} $$ $$ \ begin {array} {l} x ‘= x * m_ {00} + y * m_ {10} + z * m_ {20} + (w = 1) * T_x, \\ y ‘= x * m_ {01} + y * m_ {11} + z * m_ {21} + (w = 1) * T_y, \\ z ‘= x * m_ {02} + y * m_ {12} + z * m_ {22} + (w = 1) * T_z, \\ \ color {purple} {w ‘= x * 0 + y * 0 + z * 0 + (w = 1) * 1 = 1}. Хотя четвертая строка матрицы преобразования 4×4 — это , всегда установлено на {0, 0, 0, 1}, что означает, что в результате способа точки и матрицы умножаются друг на друга, w ‘, четвертая координата преобразованная точка всегда равна 1.Посмотрим, почему так происходит:
Хотя четвертая строка матрицы преобразования 4×4 — это , всегда установлено на {0, 0, 0, 1}, что означает, что в результате способа точки и матрицы умножаются друг на друга, w ‘, четвертая координата преобразованная точка всегда равна 1.Посмотрим, почему так происходит:  \\
\ end {массив}
$$
\\
\ end {массив}
$$
Как видите, независимо от внутренней матрицы 3×3 и значений коэффициентов трансляции, w ‘всегда будет равно 1. Это потому, что w’ вычисляется из w, которое равно 1, а коэффициенты четвертого столбца матрицы, которые для матрицы преобразования всегда равны {0, 0, 0, 1} соответственно. Они постоянны. Они никогда не меняются, иначе это не была бы матрица преобразования (скорее, матрица проекции, как мы скоро увидим). На практике это также означает, что преобразование координат x ‘, y’ и z ‘обратно в декартовы координаты путем деления их на w’ не требуется, поскольку w ‘также всегда равно 1.
Трехмерная декартова точка P, преобразованная в точку с однородными координатами {x, y, z, w = 1} и умноженная на матрицу аффинного преобразования 4×4, всегда дает точку P ‘с однородными координатами и w-координатой w’ всегда равно 1. Таким образом, преобразование преобразованной точки P ‘с однородными координатами {x’, y ‘, z’, w ‘} обратно в трехмерную декартову координату {x’ / w ‘, y’ / w ‘, z ‘/ w’}, не требует явной нормировки преобразованной точки «однородные координаты на w».
Технически функция, реализующая точку, умноженную на матрицу 4×4, должна выглядеть так (версия 1):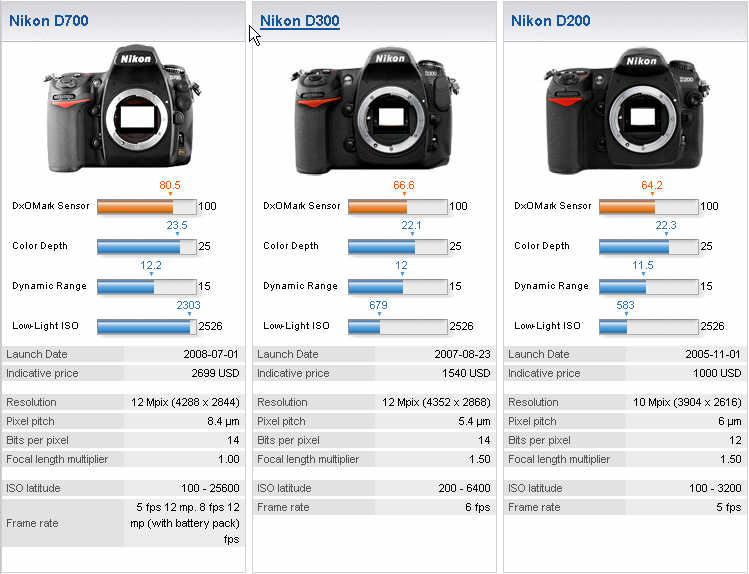
шаблон
Предполагается, что исходная точка является точкой с однородными координатами (отсюда и название Vec4), поскольку только точки с четырьмя координатами могут быть умножены на матрицы 4×4. В Vec4 координата w определена явно. Но поскольку src.w всегда предполагается равным 1 (это условие взаимозаменяемости точек с декартовыми координатами и точек с однородными координатами), код можно упростить до (версия 2):void multVecMatrix (const Vec4 & src, Vec3& dst) const { S a, b, c, w; // обратите внимание, что src.w = 1 a = src.x * x [0] [0] + src.y * x [1] [0] + src.z * x [2] [0] + src.w * x [3] [0]; b = src.x * x [0] [1] + src.y * x [1] [1] + src.z * x [2] [1] + src.w * x [3] [1]; c = src.x * x [0] [2] + src.y * x [1] [2] + src.z * x [2] [2] + src.w * x [3] [2]; w = src.x * x [0] [3] + src.y * x [1] [3] + src.z * x [2] [3] + src.w * x [3] [3]; dst.x = a / w; dst.y = ч / б; dst.z = c / w; }шаблон
В этой версии src по-прежнему является точкой с однородными координатами, но поскольку ее w-координата равна 1, нам действительно не нужно явно определять ее, поэтому src в этом случае определяется как Vec3.Кроме того, если матрица является матрицей аффинного преобразования, мы знаем, что w также всегда должно быть равно 1. Таким образом, w не нужно вычислять, и деление координат x, y и z на w может также можно пропустить. Это сокращает код до версии 3:void multVecMatrix (const Vec3 & src, Vec3& dst) const { S a, b, c, w; // поскольку src. Предполагается, что w всегда равно 1, его не нужно определять явно
a = src.x * x [0] [0] + src.y * x [1] [0] + src.z * x [2] [0] + x [3] [0];
b = src.x * x [0] [1] + src.y * x [1] [1] + src.z * x [2] [1] + x [3] [1];
c = src.x * x [0] [2] + src.y * x [1] [2] + src.z * x [2] [2] + x [3] [2];
w = src.x * x [0] [3] + src.y * x [1] [3] + src.z * x [2] [3] + x [3] [3];
dst.x = a / w;
dst.y = ч / б;
dst.z = c / w;
}
Предполагается, что w всегда равно 1, его не нужно определять явно
a = src.x * x [0] [0] + src.y * x [1] [0] + src.z * x [2] [0] + x [3] [0];
b = src.x * x [0] [1] + src.y * x [1] [1] + src.z * x [2] [1] + x [3] [1];
c = src.x * x [0] [2] + src.y * x [1] [2] + src.z * x [2] [2] + x [3] [2];
w = src.x * x [0] [3] + src.y * x [1] [3] + src.z * x [2] [3] + x [3] [3];
dst.x = a / w;
dst.y = ч / б;
dst.z = c / w;
} шаблон
Этот код обычно используется для преобразования точек с помощью матриц аффинного преобразования.void multVecMatrix (const Vec3 & src, Vec3& dst) const { S а, б, в; // поскольку предполагается, что src.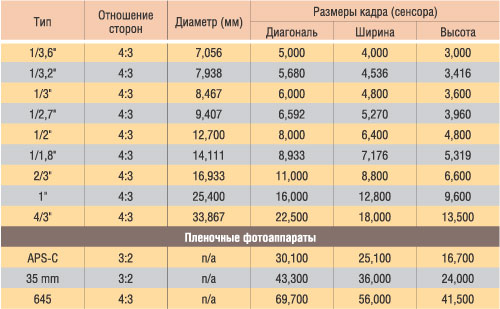 w всегда равняется 1, его не нужно определять явно
a = src.x * x [0] [0] + src.y * x [1] [0] + src.z * x [2] [0] + x [3] [0];
b = src.x * x [0] [1] + src.y * x [1] [1] + src.z * x [2] [1] + x [3] [1];
c = src.x * x [0] [2] + src.y * x [1] [2] + src.z * x [2] [2] + x [3] [2];
// нет необходимости вычислять w явно. Для аффинных преобразований он всегда равен 1
// w = src.x * 0 + src.y * 0 + src.z * 0 + 1 * 1 = 1;
// деление на w не нужно
dst.x = a;
dst.y = b;
dst.z = c;
}
w всегда равняется 1, его не нужно определять явно
a = src.x * x [0] [0] + src.y * x [1] [0] + src.z * x [2] [0] + x [3] [0];
b = src.x * x [0] [1] + src.y * x [1] [1] + src.z * x [2] [1] + x [3] [1];
c = src.x * x [0] [2] + src.y * x [1] [2] + src.z * x [2] [2] + x [3] [2];
// нет необходимости вычислять w явно. Для аффинных преобразований он всегда равен 1
// w = src.x * 0 + src.y * 0 + src.z * 0 + 1 * 1 = 1;
// деление на w не нужно
dst.x = a;
dst.y = b;
dst.z = c;
} Почему мы прошли это длинное объяснение? Во-первых, чтобы поближе познакомиться с концепцией однородных координат. В CG мы работаем в основном с двумя типами матриц: матрицами аффинного преобразования 4×4 и матрицами проекций 4×4. Матрицы аффинного преобразования сохраняют w-координату преобразованных точек равной 1, как мы только что видели, но матрицы проекций, которые мы будем изучать в этом уроке, этого не делают.
 Таким образом, точка, преобразованная матрицей проекции, потребует, чтобы координаты x ‘y’ и z ‘были нормализованы, что, как вы теперь знаете, не требуется, когда точки преобразуются матрицей аффинного преобразования.
Таким образом, точка, преобразованная матрицей проекции, потребует, чтобы координаты x ‘y’ и z ‘были нормализованы, что, как вы теперь знаете, не требуется, когда точки преобразуются матрицей аффинного преобразования.Матрица аффинного преобразования Матрица проекции
(перспективная или орфографическая)Входная трехмерная точка неявно преобразуется в однородные координаты {x, y, z, w = 1} Входная трехмерная точка неявно преобразуется в однородные координаты {x, y, z, w = 1} \ (m_ {30}, m_ {31}, m_ {32} \) и \ (m_ {33} \) всегда равны {0,0,0,1} соответственно. \ (m_ {30}, m_ {31}, m_ {32} \) и \ (m_ {33} \) принимают значения, специфичные для матриц проекции.Вскоре мы объясним, что это за ценности. w ‘всегда равно 1.
Нет необходимости вычислять w’. $$ \ begin {array} {l} w ‘& = & x * (m_ {30} = 0) + \\ && y * (m_ {31} = 0) + \\ && z * (m_ {32} = 0) + \\ && (w = 1) * 1 \\ & = & 1 \ end {array} $$w ‘может отличаться от 1 и требует явного вычисления: $$ \ begin {array} {l} w ‘& = & x * (m_ {30}! = 0) + \\ && y * (m_ {31}! = 0) + \\ && z * (m_ { 32}! = 0) + \\ && (w = 1) * (m_ {33}! = 1) \\ &! = & 1 \ end {array} $$ Нормализация никогда не нужна $$ \ begin {array} {l} P’_H = \ {x ‘, y’, z ‘, w’ = 1 \} \\ P’_C = \ {x ‘, y’, z ‘\} \ конец {массив} $$ Нормализация необходима, если \ (w ‘! = 1 \).  $$ \ begin {array} {l} P’_H = \ {x ‘, y’, z ‘, w’! = 1 \} \\ P’_C = \ {x ‘/ w’, y ‘/ w ‘, z’ / w ‘\} \ end {array} $$
$$ \ begin {array} {l} P’_H = \ {x ‘, y’, z ‘, w’! = 1 \} \\ P’_C = \ {x ‘/ w’, y ‘/ w ‘, z’ / w ‘\} \ end {array} $$
Почему важно знать разницу между аффинным преобразованием и матрицами проекции? Это очень важно. Во-первых, потому что, если вы умножаете точку на матрицу проекции, вам нужно будет использовать версию функции умножения точечной матрицы, которая явно вычисляет w, а затем нормализует координаты преобразованной точки. Что-то похожее на эту функцию (версия 2):
шаблон
Если вы не используете эту функцию с матрицей проекции, результат будет неверным.Конечно, по причинам оптимизации вы не хотите использовать эту функцию при использовании более распространенных матриц аффинного преобразования (w ‘не нужно вычислять, а преобразованные координаты не нужно нормализовать). Таким образом, вам нужно будет быть осторожным, чтобы в конечном итоге создать две функции и вызвать одну или другую в зависимости от типа используемой матрицы. Однако на практике этого почти никогда не происходит. Программисты часто не заморачиваются и просто используют что-то вроде этого (по крайней мере, избегает ненужного деления, когда w равно 1):void multVecMatrix (const Vec3 & src, Vec3& dst) const { S a, b, c, w; // поскольку src.Предполагается, что w всегда равно 1, его не нужно определять явно a = src.x * x [0] [0] + src.y * x [1] [0] + src.z * x [2] [0] + x [3] [0]; b = src.x * x [0] [1] + src.y * x [1] [1] + src.z * x [2] [1] + x [3] [1]; c = src.x * x [0] [2] + src.y * x [1] [2] + src.z * x [2] [2] + x [3] [2]; w = src.x * x [0] [3] + src.y * x [1] [3] + src. z * x [2] [3] + x [3] [3];
dst.x = a / w;
dst.y = ч / б;
dst.z = c / w;
}
z * x [2] [3] + x [3] [3];
dst.x = a / w;
dst.y = ч / б;
dst.z = c / w;
} шаблон
void multVecMatrix (const Vec3 & src, Vec3& dst) const { S a, b, c, w; // поскольку src.Предполагается, что w всегда равно 1, его не нужно определять явно a = src.x * x [0] [0] + src.y * x [1] [0] + src.z * x [2] [0] + x [3] [0]; b = src.x * x [0] [1] + src.y * x [1] [1] + src.z * x [2] [1] + x [3] [1]; c = src.x * x [0] [2] + src.y * x [1] [2] + src.z * x [2] [2] + x [3] [2]; w = src.x * x [0] [3] + src.y * x [1] [3] + src.z * x [2] [3] + x [3] [3]; if (w! = 1) { dst.x = a / w; dst.y = ч / б; dst.z = c / w; } еще { dst.х = а; dst.y = b; dst.z = c; } }
Этот код можно использовать как со стандартным аффинным преобразованием, так и с матрицами проекции. Хотя основная причина, по которой мы так много говорили об однородных координатах, заключается в том, что этап нормализации играет ключевую роль в работе матриц проекции, как мы увидим в следующей главе.
Датчики | Бесплатный полнотекстовый | Сравнение компьютерного зрения и фотограмметрических подходов к эпиполярной передискретизации последовательности изображений
1.Введение
Эпиполярная передискретизация — это процедура устранения параллакса Y или вертикального несоответствия между парой стереоизображений. Эта процедура важна как для обработки стереоизображений, так и для создания трехмерного (3D) контента. Для обработки стереоизображений это может преобразовать двумерные (2D) задачи поиска соответствий в одномерные (1D) и, следовательно, улучшить автоматическое создание карты глубины [1,2,3]. Для создания 3D-контента это может устранить зрительную усталость и обеспечить высокое качество 3D-восприятия [4].Кроме того, это может улучшить обработку различных систем стереозрения, таких как мобильные роботы или интеллектуальные транспортные средства. Эпиполярная передискретизация широко изучалась в областях компьютерного зрения и фотограмметрии. В компьютерном зрении эпиполярная передискретизация достигается гомографическим преобразованием для отправки эпиполей исходных изображений в бесконечность [5,6,7,8,9,10,11]. В зависимости от того, как оценивается гомография, методы эпиполярной повторной выборки можно разделить на два подхода: некалиброванные и откалиброванные случаи.Некалиброванный подход оценивает гомографию по фундаментальной матрице, которая определяется с помощью точек привязки между парой стереоизображений.
Эта процедура важна как для обработки стереоизображений, так и для создания трехмерного (3D) контента. Для обработки стереоизображений это может преобразовать двумерные (2D) задачи поиска соответствий в одномерные (1D) и, следовательно, улучшить автоматическое создание карты глубины [1,2,3]. Для создания 3D-контента это может устранить зрительную усталость и обеспечить высокое качество 3D-восприятия [4].Кроме того, это может улучшить обработку различных систем стереозрения, таких как мобильные роботы или интеллектуальные транспортные средства. Эпиполярная передискретизация широко изучалась в областях компьютерного зрения и фотограмметрии. В компьютерном зрении эпиполярная передискретизация достигается гомографическим преобразованием для отправки эпиполей исходных изображений в бесконечность [5,6,7,8,9,10,11]. В зависимости от того, как оценивается гомография, методы эпиполярной повторной выборки можно разделить на два подхода: некалиброванные и откалиброванные случаи.Некалиброванный подход оценивает гомографию по фундаментальной матрице, которая определяется с помощью точек привязки между парой стереоизображений.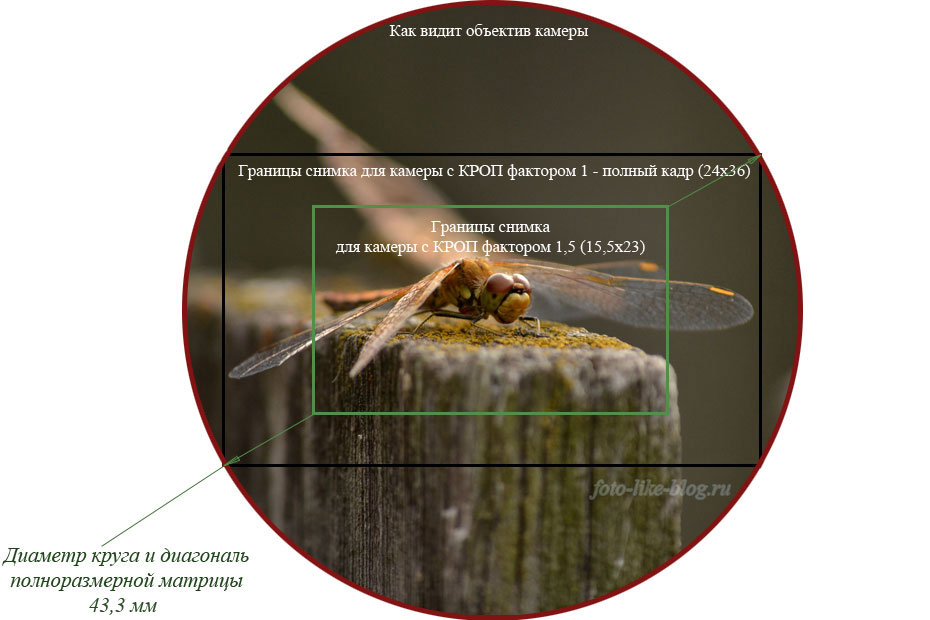 Калиброванный подход оценивает гомографию на основе известных внутренних и внешних параметров стереоизображений. Обычно эти параметры получают методом стереокалибровки с использованием калибровочных шаблонов [12,13]. В фотограмметрии эпиполярная передискретизация выполняется с помощью перспективного преобразования, которое выравнивает эпиполярные линии с горизонтальными линиями изображения.Это преобразование определяется параметрами относительной ориентации двух изображений. Коллинеарные или копланарные уравнения используются для математической оценки параметров [14,15,16,17]. В типичном фотограмметрическом приложении предполагается, что внутренние параметры известны. Параметры относительной ориентации, которые являются внешними параметрами правого изображения относительно левого кадра изображения, оцениваются связующими точками. Эпиполярная передискретизация, разработанная в каждом поле, служит своей цели и применению.В компьютерном зрении, например, эпиполярная передискретизация используется для зрения роботов и быстрой обработки изображений [18,19,20].
Калиброванный подход оценивает гомографию на основе известных внутренних и внешних параметров стереоизображений. Обычно эти параметры получают методом стереокалибровки с использованием калибровочных шаблонов [12,13]. В фотограмметрии эпиполярная передискретизация выполняется с помощью перспективного преобразования, которое выравнивает эпиполярные линии с горизонтальными линиями изображения.Это преобразование определяется параметрами относительной ориентации двух изображений. Коллинеарные или копланарные уравнения используются для математической оценки параметров [14,15,16,17]. В типичном фотограмметрическом приложении предполагается, что внутренние параметры известны. Параметры относительной ориентации, которые являются внешними параметрами правого изображения относительно левого кадра изображения, оцениваются связующими точками. Эпиполярная передискретизация, разработанная в каждом поле, служит своей цели и применению.В компьютерном зрении, например, эпиполярная передискретизация используется для зрения роботов и быстрой обработки изображений [18,19,20]. В фотограмметрии он в основном используется для точного исправления изображений для стереоплоттеров [14,21,22]. Для обслуживания новых и сложных приложений возрастает потребность в объединении методов, разработанных в области компьютерного зрения и фотограмметрии. Однако оценка методов эпиполярной передискретизации, разработанных в каждой области, с использованием общего набора данных, сравнение их характеристик и понимание их различий с теоретической и практической точек зрения, отсутствуют.
В фотограмметрии он в основном используется для точного исправления изображений для стереоплоттеров [14,21,22]. Для обслуживания новых и сложных приложений возрастает потребность в объединении методов, разработанных в области компьютерного зрения и фотограмметрии. Однако оценка методов эпиполярной передискретизации, разработанных в каждой области, с использованием общего набора данных, сравнение их характеристик и понимание их различий с теоретической и практической точек зрения, отсутствуют.В этой статье мы стремимся сравнить методы эпиполярной передискретизации, разработанные в компьютерном зрении и фотограмметрии. В частности, мы стремимся применить эпиполярную передискретизацию не для исправления одной стереопары, а для исправления последовательности стереоизображений. Мы утверждаем, что большинство предыдущих исследований проводилось для эпиполярной передискретизации одной пары изображений, и что эпиполярная передискретизация последовательностей изображений не была изучена досконально.
 Здесь мы фокусируемся на эпиполярной передискретизации последовательностей изображений с интенсивностью стерео приложений, где две камеры устанавливаются на разных платформах и перемещаются независимо.
Здесь мы фокусируемся на эпиполярной передискретизации последовательностей изображений с интенсивностью стерео приложений, где две камеры устанавливаются на разных платформах и перемещаются независимо.Сначала мы рассмотрим общие принципы и формулировки эпиполярной передискретизации, разработанные в области компьютерного зрения. Затем мы рассмотрим эпиполярную передискретизацию, разработанную в фотограмметрии. Мы еще раз подтвердим хорошо известный принцип, согласно которому методы эпиполярной передискретизации, разработанные в компьютерном зрении и фотограмметрии, математически идентичны. Мы также укажем на практические различия между ними. Затем мы объясним последовательности изображений и репрезентативные методы эпиполярной передискретизации, используемые для тестов.Наконец, мы сообщаем и сравниваем их эффективность по одной паре изображений и по последовательностям изображений.
2. Эпиполярная передискретизация в компьютерном зрении
Эпиполярная геометрия между стереопарой поясняется на рисунке 1. Два центра перспективы (C1 и C2 на рисунке) и точка заземления P определяют эпиполярную плоскость. Эпиполярные линии l1 и l2 являются пересечением между эпиполярной плоскостью и левой и правой плоскостями изображения соответственно. Эпиполи e1 и e2 — это точки пересечения линии, соединяющей два центра перспективы и левую и правую плоскости изображения.Для перспективных изображений любые соответствующие точки q1 и q2 левого и правого изображения удовлетворяют следующему матричному уравнению [23]:
где q1 (u1, v1,1) и q2 (u2, v2,1) — координаты однородного изображения левой и правой точек изображения (p1 и p2), а F — фундаментальная матрица. Эпиполярные линии l1 и l2 и эпиполи e1 и e2 можно найти с помощью F:
Два центра перспективы (C1 и C2 на рисунке) и точка заземления P определяют эпиполярную плоскость. Эпиполярные линии l1 и l2 являются пересечением между эпиполярной плоскостью и левой и правой плоскостями изображения соответственно. Эпиполи e1 и e2 — это точки пересечения линии, соединяющей два центра перспективы и левую и правую плоскости изображения.Для перспективных изображений любые соответствующие точки q1 и q2 левого и правого изображения удовлетворяют следующему матричному уравнению [23]:
где q1 (u1, v1,1) и q2 (u2, v2,1) — координаты однородного изображения левой и правой точек изображения (p1 и p2), а F — фундаментальная матрица. Эпиполярные линии l1 и l2 и эпиполи e1 и e2 можно найти с помощью F:
l1 = FTq2, l2 = Fq1, Fe1 = 0, FTe2 = 0
(2)
Эпиполярная передискретизация может быть достигнута путем гомографического преобразования отображения эпиполя исходного изображения в бесконечно удаленную точку.Гомография в случае некалиброванного подхода может быть определена из фундаментальной матрицы как где T — перенос, переводящий главную точку (cx, cy) изображения в начало системы координат, A — поворот вокруг начала координат, переводящий эпиполь в точку (k, 0,1) T на x- ось, а G — преобразование, переводящее перемещенный эпиполь в бесконечно удаленную точку (k, 0,0) T, как показано ниже [8].
T = [10 − cx01 − cy001], G = [100010−1 / k01]
(4)
После вычисления гомографии обычно выполняется оптимизация для выравнивания соответствующих эпиполярных линий между стереоизображениями [7,9,24].При некалиброванном подходе фундаментальная матрица может быть оценена по связующим точкам без какой-либо дополнительной информации. Таким образом, этот подход позволяет автоматизировать весь процесс и использовать изображения из неизвестного источника. Есть много исследований, касающихся надежной оценки фундаментальной матрицы и надежной реконструкции эпиполярной геометрии. Среди них были нормированный восьмиточечный алгоритм Хартли [25] и алгоритмы, которые применяют дополнительные ограничения, такие как алгебраическая минимизация [26], минимизация эпиполярного расстояния [8,24] и другие геометрические функции стоимости [27,28,29]. ].Однако некалиброванный подход может быть чувствительным к шуму связующих точек и склонным к искажению изображения, поскольку преобразование не основано на физической геометрии между двумя изображениями. Фузиелло и Ирсара [30] попытались преодолеть эти проблемы, предложив новый некалиброванный подход, названный квази-евклидовым эпиполярным выпрямлением. Они оценили стереогеометрию с помощью нелинейных уравнений путем минимизации геометрических ошибок повторного проецирования. В калиброванном подходе внутренние и внешние параметры для левого и правого изображений оцениваются отдельно методом стереокалибровки с использованием специальных калибровочных шаблонов [12,13,31 , 32].Внешние параметры используются для оценки относительной геометрической взаимосвязи между двумя изображениями. Затем гомография для эпиполярной передискретизации определяется относительной геометрической зависимостью. Предположим, что R1 и R2 представляют собой матрицы вращения 3 × 3, содержащие внешние параметры вращения левой и правой камер, а C1 и C2 — матрицы перемещения 3 × 1, содержащие внешние параметры, связанные с положение центра перспективы, относительное вращение R и перемещение B между двумя изображениями определены ниже [33]:
Фузиелло и Ирсара [30] попытались преодолеть эти проблемы, предложив новый некалиброванный подход, названный квази-евклидовым эпиполярным выпрямлением. Они оценили стереогеометрию с помощью нелинейных уравнений путем минимизации геометрических ошибок повторного проецирования. В калиброванном подходе внутренние и внешние параметры для левого и правого изображений оцениваются отдельно методом стереокалибровки с использованием специальных калибровочных шаблонов [12,13,31 , 32].Внешние параметры используются для оценки относительной геометрической взаимосвязи между двумя изображениями. Затем гомография для эпиполярной передискретизации определяется относительной геометрической зависимостью. Предположим, что R1 и R2 представляют собой матрицы вращения 3 × 3, содержащие внешние параметры вращения левой и правой камер, а C1 и C2 — матрицы перемещения 3 × 1, содержащие внешние параметры, связанные с положение центра перспективы, относительное вращение R и перемещение B между двумя изображениями определены ниже [33]:
R = R2R1T = [r11r12r13r21r22r23r31r32r33], B = R1 (C2 − C1) = [bxbybz]
(5)
Гомографию, h2 для левого и h3 для правого изображения, можно оценить двумя поворотами. Первое вращение, Rhalf1 и Rhalf2, распределяется из относительного вращения R, чтобы перекрытие между двумя изображениями достигло максимума. Второе вращение Rrect преобразует эпиполь в бесконечность с использованием вектора базовой линии B:
Первое вращение, Rhalf1 и Rhalf2, распределяется из относительного вращения R, чтобы перекрытие между двумя изображениями достигло максимума. Второе вращение Rrect преобразует эпиполь в бесконечность с использованием вектора базовой линии B:
h2 = RrectRhalf1, h3 = RrectRhalf2
(6)
где R = Rhalf1 (Rhalf2) T, Rrect = [m1Tm2Tm3T] T, а m1, m2 и m3 определяются какm1 = m || m ||, m2 = [- bybx0] Tbx2 + by2, m3 = m1 × m2
(7)
Как упоминалось выше, хотя калиброванный подход гарантирует минимальное искажение изображения и высокую точность, он требует предварительного процесса калибровки.Соответственно, этот подход потенциально связан с ограничением доступности.
3. Фотограмметрическая эпиполярная передискретизация
В этом разделе мы рассмотрим эпиполярную передискретизацию, разработанную в фотограмметрии. Хотя его математическая формулировка хорошо известна [17], мы переформулируем здесь фотограмметрические модели камеры, чтобы сравнить их более непосредственно с моделями, разработанными в области компьютерного зрения.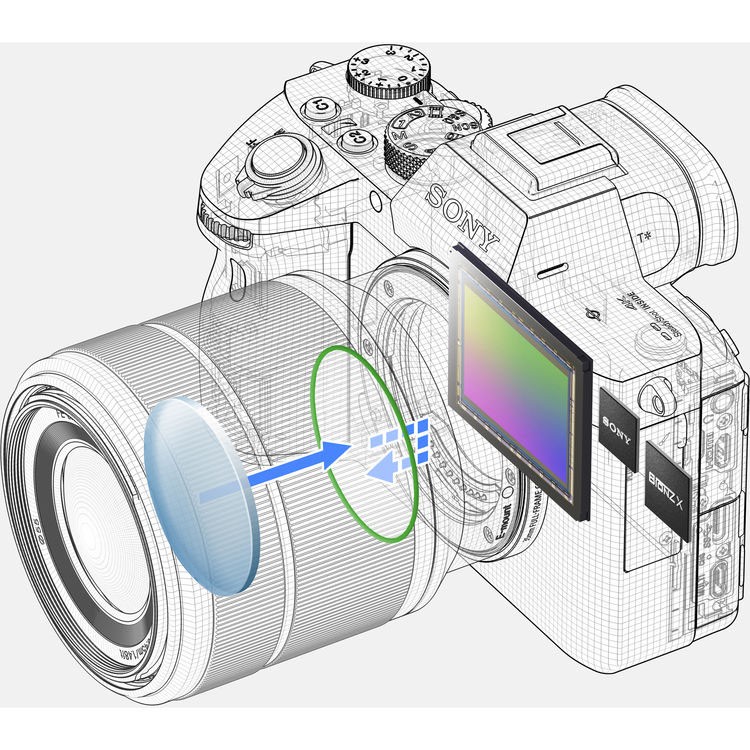 В фотограмметрии геометрическая связь между точкой земли P и ее левой и правой точками изображения, q1 и q2, объясняется коллинеарным уравнением ниже:
В фотограмметрии геометрическая связь между точкой земли P и ее левой и правой точками изображения, q1 и q2, объясняется коллинеарным уравнением ниже:
q1 = M1p1 = λ1M1R1P1, q2 = M2p2 = λ2M2R2P2
(8)
где λ — коэффициент масштабирования, R1 и R2 — матрицы вращения 3 × 3, определенные, как и раньше.P1 = C1P →, P2 = C2P →, а p1 (x1, y1, f1) и p2 (x2, y1, f2) — векторы взгляда левого и правого кадров камеры от центра перспективы до точки проекции. M1 и M2 — матрицы камер левого и правого изображений для преобразования координат камеры в координаты изображения следующим образом:M1 = [f10cx10f1cy1001], M2 = [f20cx20f2cy2001]
(9)
где cx и cy определены как уравнение (4), а f — фокусное расстояние камеры.Геометрическая взаимосвязь между стереоизображениями может быть объяснена условием, что вектор базовой линии S = C1C2 →, левый вектор обзора P1 и правый вектор обзора P2 компланарны.Это компланарное условие может быть выражено скалярным тройным произведением трех векторов, как показано ниже.
P2T · [S × P1] = P2T [S] × P1 = 0, [S] × = [0 − szsysz0 − sx − sysx0]
(10)
Принимая левую ось камеры в качестве опорного кадра, то есть, R1 = I3 × 3 и С1 = 03 × 1, приведенное выше уравнения в одной плоскости может быть переписано в виде фундаментальной матрицы, как показано ниже:P2T [S] × P1 = p2TR [B] × p1 = 0
(11)
q2T (M2−1) TR [B] × M1−1q1 = q2TFq1 = 0
(12)
где R и B — относительное вращение и перемещение правой камеры относительно левого кадра изображения [17].Как показано в уравнении (12), хорошо известно, что копланарное уравнение, используемое в фотограмметрии, математически идентично фундаментальному матричному уравнению, используемому в компьютерном зрении. Основное различие в некалиброванном и фотограмметрическом подходах состоит в том, что первый оценивает все восемь параметров фундаментальной матрицы по связующим точкам, тогда как второй оценивает относительные вращательные и поступательные параметры. Эпиполярная передискретизация выполняется двумя перспективными преобразованиями, полученными из внешних параметров. [17,34].Во-первых, правая плоскость изображения является повторно проецируются параллельно системе отсчета (левая камера осей) с использованием углов поворота правой камеры, как показано на рисунке 2а. Во-вторых, две плоскости изображения затем повторно проецируются для выравнивания с базовой линией, соединяющей два центра перспективы, и для удаления параллаксов Y, как показано на рисунке 2b. Эти два перспективных преобразования также могут быть выражены гомографией как
[17,34].Во-первых, правая плоскость изображения является повторно проецируются параллельно системе отсчета (левая камера осей) с использованием углов поворота правой камеры, как показано на рисунке 2а. Во-вторых, две плоскости изображения затем повторно проецируются для выравнивания с базовой линией, соединяющей два центра перспективы, и для удаления параллаксов Y, как показано на рисунке 2b. Эти два перспективных преобразования также могут быть выражены гомографией как
h2 = RbaseR1T, h3 = RbaseR2T
(13)
где Rbase — это второе перспективное преобразование для выравнивания относительно базовой линии и определяется из углов поворота базовой линии для осей X, Y и Z какRbase = RΩRΦRΚ = [1000cosΩsinΩ0 − sinΩcosΩ] [cosΦ0 − sinΦ010sinΦ0cosΦ] [cosΚsinΚ0 − sinΚcosΚ0001]
(14)
Ω = ω1 + ω22, Φ = −tan − 1bzbx2 + by2, Κ = tan − 1bybz
(15)
Как показано в уравнениях (13) — (15), фотограмметрическая эпиполярная передискретизация математически идентична таковой при калиброванном подходе.Основное различие калиброванного и фотограмметрического подходов состоит в том, что первый вычисляет параметры относительного ориентирования на основе левых и правых внешних параметров, которые оцениваются с помощью калибровочных шаблонов, тогда как последний оценивает параметры относительного ориентирования непосредственно по связующим точкам.
Фотограмметрический подход также может быть чувствительным к шуму связующих точек. Чтобы преодолеть проблему чувствительности при передискретизации эпиполярной выборки, можно применить байесовский подход. Байесовский подход — популярный метод оценки, который использует априорную и апостериорную статистику ошибок неизвестных параметров [35].При фотограмметрической эпиполярной передискретизации можно ограничить диапазон сходимости внешних параметров, задав для параметров априорную статистику ошибок. Можно также уменьшить влияние ошибок связующей точки на общую оценку, установив априорную статистику ошибок измерений связующей точки. Преимущества байесовского подхода заключаются в том, что он может накладывать ограничения как на уравнения наблюдения, так и на параметры оценки, и что эти ограничения способствуют определению неизвестных как весов.Если априорные ограничения для неизвестных определяются из фактических геометрических характеристик устройства камеры, этот подход должен работать более согласованно для последовательностей стереоизображений и более устойчиво для ошибок связующих точек. Для многих фотограмметрических приложений ограничения могут быть определены из технических характеристик сенсоров или из практики эксплуатации [36,37].4. Наборы данных и методология
Для сравнительного анализа методов эпиполярной передискретизации с помощью двух веб-камер (Microsoft Webcam Cinema) были получены четыре последовательности стереоизображений (TEST01, TEST02, TEST03 и TEST04).Четыре последовательности изображений были разработаны таким образом, чтобы коэффициенты ошибок были увеличены с TEST01 до TEST04. Две последовательности (TEST01 и TEST02) были получены в режиме низкого разрешения с размером изображения 320 × 240 пикселей и две (TEST03 и TEST04) в режиме высокого разрешения с 640 × 480 пикселей. Каждая последовательность была получена с разными базовыми расстояниями и разными углами наклона камеры (см. Таблицу 1). Это было сделано для того, чтобы проверить влияние более широкой базовой линии и большего угла наклона на производительность эпиполярной передискретизации.Для каждой последовательности 100 стереопар было получено без движения камеры для анализа согласованности оценки геометрии в отношении изменения связующих точек между различными парами. Для оценки эпиполярной геометрии связующие точки были извлечены с использованием масштабно-инвариантного преобразования признаков (SIFT). ) [38] и алгоритм удаления выбросов [39], основанный на консенсусе случайной выборки (RANSAC). Допуски на удаление выбросов были установлены на один пиксель для TEST01 и три пикселя для других наборов данных. Допуск в один пиксель был выбран, чтобы установить оптимальный случай, когда связующие точки имеют небольшую ошибку положения.Допуск в три пикселя был выбран для практического случая, поскольку это значение наиболее широко использовалось на практике. Это нацелено на анализ устойчивости к ошибкам связующих точек. Дополнительные связующие точки были извлечены вручную в 10 точках из отдельных последовательностей изображений. Эти точки использовались для проверки точности передискретизации эпиполярной выборки. На рисунке 3 показана одна стереопара из четырех последовательностей изображений и 10 связующих точек, извлеченных вручную. В экспериментах были протестированы пять существующих методов эпиполярной передискретизации: три разработаны в области компьютерного зрения и два — в фотограмметрии.В таблице 1 перечислены методы, использованные для экспериментов. Обратите внимание, что эти методы были выбраны в качестве репрезентативных методов различных подходов, упомянутых в Разделах 2 и 3. «Буге» указывает калиброванный подход, основанный на гомографиях в уравнении (6), разработанном Буге [40]. «Хартли» — это нормализованный восьмиточечный алгоритм с минимизацией геометрической ошибки, основанный на функции стоимости Сэмпсона, которая является одним из наиболее известных некалиброванных методов, разработанных в области компьютерного зрения [8].«Фузиелло» — это квази-евклидово эпиполярное выпрямление, разработанное Фузиелло и Ирсара [30]. Эти два метода относятся к неоткалиброванным подходам. «Ким» представляет собой фотограмметрический метод повторной выборки эпиполярных изображений, основанный на относительной ориентации, описанной в Разделе 3 [16]. «Байесовский» — это фотограмметрическая эпиполярная передискретизация с байесовским подходом для оценки параметров относительной ориентации, как описано в разделе 3.Для первых трех методов мы использовали общедоступное программное обеспечение, а для четвертого и пятого методов мы реализовали алгоритмы в -жилой дом.Метод Буге требует процесса калибровки, определяющего внутренние и внешние параметры. Для этого было использовано 10 пар рисунков на шахматной доске. Внутренние параметры, полученные в результате этого процесса, также использовались в методах Кима и Байеса.
Как упоминалось ранее, байесовский метод должен определять априорные ограничения для параметров оценки и измерений связующих точек. Эти ограничения будут способствовать правильному определению неизвестных параметров за счет ограничения диапазона их сходимости по методу наименьших квадратов.Мы устанавливаем априорные значения ковариации для связующих точек равными одному пикселю с учетом ожидаемой ошибки исправления и ожидаемой точности связующих точек, полученных с помощью алгоритмов SIFT и удаления выбросов. Мы устанавливаем априорные значения ковариации, связанные с параметрами ориентации, равными квадрату 30 ° с учетом ожидаемого отклонения углов камеры от идеального случая. Мы устанавливаем априорные значения ковариации для вектора базовой линии (by и bz) равными единице с учетом ожидаемого отклонения вектора базовой линии от идеального случая при принятии bx = 100.Для разных настроек эксперимента потребуются разные значения ковариации. В нашем случае мы устанавливаем относительно большие значения угловой ковариации и относительно небольшие значения позиционной ковариации. Это произошло потому, что мы установили две камеры на стереосистему и вращали их вручную.
Для количественного сравнения методов использовалось всего четыре показателя эффективности. Для оценки эпиполярной геометрии использовались ошибки исправления (Er) и флуктуация эпиполярной линии (Ev), а для оценки искажения изображения использовались ортогональность (Eo) и относительное изменение масштаба в результирующих изображениях (Ea) [11].Ошибки исправления относятся к остатку параллаксов Y в результирующем изображении и измеряются как разность преобразованных вертикальных координат связующих точек на левом и правом изображениях. Флуктуация эпиполярной линии измерялась в пикселях как стандартное отклонение координат преобразованного изображения по всей последовательности изображений. В идеальном случае ошибки выпрямления и флуктуации эпиполярной линии должны быть равны нулю. Ортогональность измерялась как углы осей x и y после эпиполярной передискретизации, которые в идеале должны составлять 90 °.Относительное изменение масштаба измерялось как отношение двух диагональных линий после эпиполярной передискретизации, которое в идеале должно составлять одну. Для получения дополнительных сведений о показателях производительности см. [11].5. Результаты оценки эффективности
Эксперименты проводились сначала с использованием одиночных пар, а затем с использованием последовательностей изображений. В двух экспериментах результаты метода Буге использовались как основополагающие, поскольку они были получены с помощью калибровочных шаблонов. В таблице 1 приведено сравнение производительности пяти методов, примененных к отдельным парам.Для других методов, кроме метода Буге, мы выбрали 10 последовательных кадров из каждой последовательности изображений, накопили связующие точки из 10 кадров и оценили единую матрицу преобразования. Обратите внимание, что из-за ограничения размера матрицы мы выбрали 10 вместо всех кадров. Среди четырех параметров точности флуктуация эпиполярной линии (Ev) не была включена, потому что она связана только с последовательностью изображений. Фактическое количество связующих точек из 10 кадров, используемых для эпиполярной передискретизации, также показано в таблице 1.Для лучшей интерпретации результатов эксперимента измерения искажений также были представлены в виде разностей (ΔEo и ΔEa) с таковыми по методу Буге. В результатах наборов данных TEST01 и TEST02 все методы показали удовлетворительные результаты с точки зрения ошибок исправления. Эти результаты демонстрируют, что, хотя несовпадающие связующие точки включены частично, приемлемая точность преобразования может быть получена, если конфигурация камеры благоприятна. Однако в случае наборов данных TEST03 и TEST04 ошибки исправления были увеличены для всех методов тестирования.В частности, значительное увеличение ошибки наблюдалось для некалиброванных методов повторной выборки эпиполярных данных, Хартли и Фузиелло. Это наблюдение хорошо согласуется с предыдущими исследованиями, показывающими, что некалиброванные методы были более подвержены ошибкам связующих точек в слабой стереогеометрии [10,11]. Некалиброванные методы также показывают большее искажение изображения. Это искажение наблюдалось для всех наборов данных по сравнению с результатами метода Буге. В этом эксперименте два фотограмметрических метода, Ким и Байесовский, показали почти идентичные результаты.Это можно интерпретировать как то, что влияние ошибок связующих точек было обработано лучше, чем в некалиброванных методах, путем непосредственной оценки параметров относительной ориентации. Небольшое увеличение ошибок исправления для Кима и Байеса наблюдалось с TEST04 из-за широкой базовой линии и большого угла наклона. Таблица 2 суммирует сравнение производительности методов эпиполярной передискретизации, примененных ко всем 100 стереопарам из четырех наборов тестовых данных. Обратите внимание, что Bouguet не использовался с последовательностями изображений, поскольку он использует идентичную гомографию для всех пар в одной и той же последовательности изображений.Для этого эксперимента мы не накапливали связующие точки последовательных изображений. Мы обрабатывали каждый кадр независимо, оценивая матрицу преобразования, создавая эпиполярную передискретизированную пару и вычисляя точность преобразования для каждого кадра. В таблице 2 показано среднее количество связующих точек, используемых для каждой последовательности изображений. Параметры точности в Таблице 2 были средним («Среднее» в Таблице) и стандартным отклонением (Stdev) параметров для 100 кадров. Во-первых, мы замечаем, что производительность для последовательности изображений отличается от производительности для отдельных пар.Для одной пары все протестированные методы показали небольшие различия между собой, тогда как для последовательностей изображений их эффективность существенно различалась. Все методы показали отклонения в последовательностях изображений в ошибках исправления, ошибках искажения изображения и флуктуациях эпиполярных линий. В частности, флуктуация эпиполярной линии была очень значительной для всех тестовых наборов данных, кроме байесовского метода. Эти результаты подразумевают несогласованную оценку геометрии в соответствии с изменением связующих точек между каждым кадром, и что эти методы могут не подходить для обработки эпиполярной повторной дискретизации последовательностей изображений.Среди протестированных байесовский метод показал наименьшие изменения последовательностей изображений. Этот результат демонстрирует, что за счет ограничения диапазонов сходимости параметров ориентации была достигнута стабильная оценка геометрии. Это свойство байесовского подхода может быть благоприятным для последовательностей изображений. На рисунке 4 показано колебание ошибок исправления для всех кадров изображения TEST02 для сравнения согласованности.Во-вторых, мы можем видеть тенденцию к ухудшению точности из-за слабой стереогеометрии, которая аналогична результату для эксперимента с одной парой.Сравнивая результаты TEST01 и TEST02, мы можем проверить, что точность ухудшилась из-за более крупных ошибок связующих точек. Тем не менее байесовский метод показал наименьшую деградацию. Сравнивая TEST02 и TEST03, мы можем заметить, что ошибки выпрямления и флуктуации эпиполярных линий увеличиваются с увеличением размера изображения и, следовательно, с меньшим размером пикселя в идентичной камере. Сравнивая TEST03 и TEST04, мы можем заметить, что ошибки также увеличиваются из-за большего несовпадения двух изображений.
В-третьих, все четыре ошибки в таблице 2 были увеличены по сравнению с ошибками в таблице 1 для всех протестированных методов. Это было ожидаемо, потому что количество связующих точек, используемых для эпиполярной повторной выборки в таблице 2, было меньше, чем в таблице 1. Однако байесовский метод дал наименьшее снижение точности. Это наблюдение может также налагать предпочтение байесовскому методу в случае меньшего количества связующих точек. Кроме того, мы проверили различия в производительности тестируемых методов путем визуального сравнения повторно дискретизированных последовательностей изображений.На рисунке 5 показана часть передискретизированных левого и правого изображений TEST02 для каждого метода. В каждом столбце показаны последовательные пары изображений, прошедшие повторную выборку из определенного метода. Белые горизонтальные линии представляют собой эпиполярные линии повторно дискретизированных изображений. Мы можем проверить эффекты искажения изображения и несогласованные оценки эпиполярной геометрии на полученных изображениях. Повторно дискретизированные последовательности с несовместимыми оценками эпиполярной геометрии не могут сформировать последовательность стереоскопических изображений из-за резких изменений сцены.Последний столбец показал, что байесовский метод может согласованно обрабатывать последовательность изображений. Явное сравнение времени выполнения не проводилось, потому что каждый тестируемый метод применялся в разных обстоятельствах. Методы Хартли и Ким были оптимизированы для быстрого выполнения (около 32 и 26 кадров / с соответственно на платформе с процессором i5-4460, тактовой частотой 3,20 ГГц и объемом памяти 8 ГБ). Методы Фузиелло и Байеса не были оптимизированы для скорости. Метод Fusiello был доступен только в исполняемых файлах Matlab и был очень медленным (около 2 кадров / с).Байесовский метод использовал матрицы очень большого размера без эффективного матричного разложения для оценки параметров, а также был медленным (около 13 кадров / с). Тем не менее, сокращение времени обработки для Fusiello или байесовского метода было сочтено выходящим за рамки данной статьи и не было опробовано.6. Выводы
В этой статье методы эпиполярной передискретизации, разработанные в области компьютерного зрения и фотограмметрии, были проанализированы с точки зрения ошибок исправления, искажения изображения и стабильности эпиполярной геометрии.Анализ был сосредоточен на повторной выборке последовательностей изображений.
Из теоретического обзора мы отметили, что хотя методы эпиполярной передискретизации, разработанные в двух областях, математически идентичны, их эффективность при оценке параметров может быть разной.
На основе анализа результатов эксперимента мы показали, что для эпиполярной передискретизации одной пары изображений можно использовать все некалиброванные и фотограмметрические методы, и, однако, для последовательностей изображений все протестированные методы, кроме байесовского метода, показали значительные различия в терминах. искажений изображения и флуктуации эпиполярных линий между парами изображений в одной и той же последовательности.Наши результаты показывают, что байесовский метод подходит для эпиполярной передискретизации последовательностей изображений. Эти результаты означают, что, хотя различия между методами передискретизации эпиполярной выборки могли быть незаметными при передискретизации одной пары, они могут не проявляться в последовательностях передискретизации изображений.
В качестве будущего исследования мы исследуем причины таких вариаций, способы их минимизации и способы устранения оставшихся небольших вариаций в байесовском методе. Также будет изучена оптимизация скорости обработки байесовского метода.В последнее время стремительная смена источников изображений и диверсификация соответствующих приложений требуют слияния технологий компьютерного зрения и фотограмметрии. Мы надеемся, что наше исследование может внести вклад в понимание технологий эпиполярной передискретизации, разработанных в обеих областях, и в разработку новых стереоприложений.
% PDF-1.4 % 230 0 объект > эндобдж xref 230 76 0000000016 00000 н. 0000002579 00000 н. 0000002759 00000 н. 0000002823 00000 н. 0000002859 00000 н. 0000002913 00000 н. 0000002971 00000 н. 0000003055 00000 н. 0000003092 00000 н. 0000003125 00000 н. 0000003160 00000 н. 0000003196 00000 п. 0000003254 00000 н. 0000003338 00000 н. 0000003375 00000 н. 0000003408 00000 н. 0000003443 00000 н. 0000003479 00000 п. 0000003610 00000 н. 0000003679 00000 н. 0000003749 00000 н. 0000003818 00000 н. 0000003888 00000 н. 0000004119 00000 н. 0000004285 00000 п. 0000004422 00000 н. 0000004558 00000 н. 0000004695 00000 н. 0000004838 00000 н. 0000004975 00000 н. 0000005113 00000 п. 0000005284 00000 п. 0000005416 00000 н. 0000005683 00000 п. 0000013636 00000 п. 0000014254 00000 п. 0000014416 00000 п. 0000014785 00000 п. 0000015147 00000 п. 0000029447 00000 п. 0000029795 00000 п. 0000029956 00000 н. 0000030459 00000 п. 0000049279 00000 п. 0000049850 00000 п.
Сравнение матриц фотоаппаратов: Сравнение шумов матриц лучших камер
