В поисках суперлинзы
Джон Пендри, Дэвид Смит
«В мире науки» №11, 2006
Построенная из метаматериала с удивительными оптическими свойствами, суперлинза может создавать изображения с деталями меньше длины волны используемого света.
Почти 40 лет назад советский ученый Виктор Веселаго выдвинул гипотезу о существовании материалов с отрицательным показателем преломления (УФН, 1967, т. 92, с. 517). Световые волны в них должны двигаться против направления распространения луча и вообще вести себя удивительным образом, линзы же из этих материалов — обладать волшебными свойствами и непревзойденными характеристиками. Однако у всех известных веществ показатель преломления положителен: за нескольких лет интенсивных поисков Веселаго не нашел ни одного материала с подходящими электромагнитными свойствами, и его гипотеза была забыта. О ней вспомнили лишь в начале XXI в. (см.: Теория и практика Виктора Веселаго).
Благодаря последним достижениям в области материаловедения идея Веселаго была возрождена. Электромагнитные свойства веществ определяются особенностями образующих их атомов и молекул, обладающих довольно узким диапазоном характеристик. Поэтому свойства миллионов известных нам материалов не так уж разнообразны. Однако в середине 1990-х гг. ученые из Центра технологии материалов им. Маркони в Англии занялись созданием метаматериалов, которые состоят из макроскопических элементов и рассеивают электромагнитные волны совсем не так, как любые известные вещества.
В 2000 г. Дэвид Смит вместе с коллегами из Калифорнийского университета в Сан-Диего изготовил метаматериал с отрицательным показателем преломления. Поведение света в нем оказалось настолько странным, что теоретикам пришлось переписать книги по электромагнитным свойствам веществ. Экспериментаторы уже занимаются разработкой технологий, в которых используются удивительные свойства метаматериалов, и создают суперлинзы, позволяющие получать изображения с деталями меньше длины волны используемого света. С их помощью можно было бы делать микросхемы с наноскопическими элементами и записывать на оптические диски огромные объемы информации.
Отрицательное преломление

Чтобы понять, как возникает отрицательное преломление, рассмотрим механизм взаимодействия электромагнитного излучения с веществом. Проходящая через него электромагнитная волна (например, луч света) заставляет двигаться электроны атомов или молекул. На это расходуется часть энергии волны, что влияет на ее свойства и характер распространения. Для получения требуемых электромагнитных характеристик исследователи подбирают химический состав материала.
Но как показывает пример метаматериалов, химия — не единственный путь получения интересных свойств вещества. Электромагнитный отклик материала можно «конструировать», создавая крошечные макроскопические структуры. Дело в том, что обычно длина электромагнитной волны на несколько порядков больше размеров атомов или молекул. Волна «видит» не отдельную молекулу или атом, а коллективную реакцию миллионов частиц. Это справедливо и для метаматериалов, элементы которых тоже значительно меньше длины волны.
Поле электромагнитных волн, что следует из их названия, имеет как электрическую, так и магнитную составляющую. Электроны в материале движутся вперед и назад под действием электрического поля и по кругу под действием магнитного. Степень взаимодействия определяется двумя характеристиками вещества: диэлектрической проницаемостью ε и магнитной проницаемостью μ. Первая показывает степень реакции электронов на электрическое поле, вторая — степень реакции на магнитное. У подавляющего большинства материалов ε и μ больше нуля.
Оптические свойства вещества характеризуются показателем преломления n, который связан с ε и μ простым соотношением: n = ± √(ε∙μ). Для всех известных материалов перед квадратным корнем должен стоять знак «+», и поэтому их показатель преломления положителен. Однако в 1968 г. Веселаго показал, что у вещества с отрицательными ε и μ показатель преломления n должен быть меньше нуля. Отрицательные ε или μ получаются в том случае, когда электроны в материале движутся в направлении, противоположном по отношению к силам, создаваемым электрическим и магнитным полями. Хотя такое поведение кажется парадоксальным, заставить электроны двигаться против сил электрического и магнитного полей не так уж сложно.
Если толкнуть маятник рукой, он послушно переместится в направлении толчка и начнет колебаться с так называемой резонансной частотой. Подталкивая маятник в такт с качанием, можно увеличить амплитуду колебаний. Если же толкать его с более высокой частотой, то толчки перестанут совпадать с колебаниями по фазе, и в какой-то момент руку ударит маятник, движущийся ей навстречу. Точно так же электроны в материале с отрицательным показателем преломления входят в противофазу и начинают сопротивляться «толчкам» электромагнитного поля.
Метаматериалы
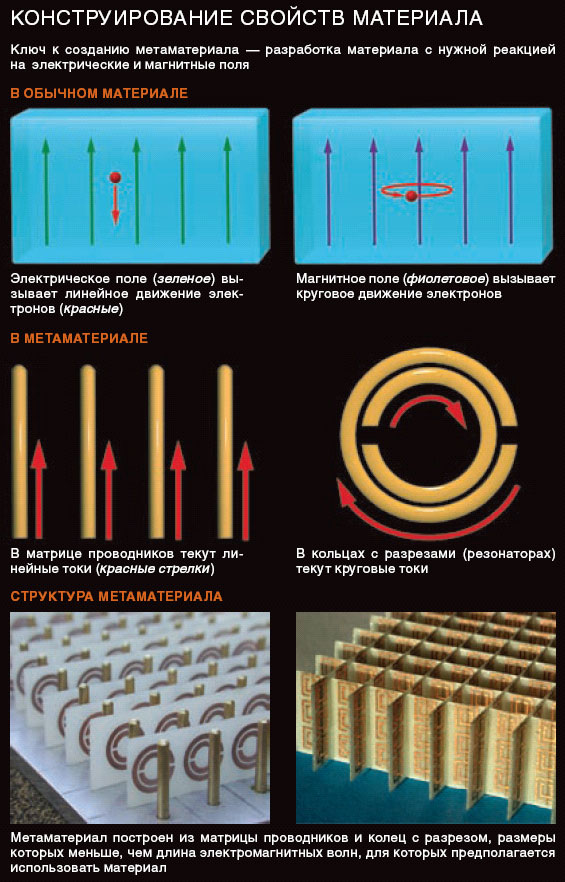
Ключ к такого рода отрицательной реакции — резонанс, то есть стремление колебаться со специфической частотой. Он создается в метаматериале искусственно с помощью крошечных резонансных контуров, имитирующих отклик вещества на магнитное или электрическое поле. Например, в разорванном кольцевом резонаторе (РКР) магнитный поток, проходящий через металлическое кольцо, наводит в нем круговые токи, аналогичные токам, обуславливающим магнетизм некоторых материалов. А в решетке из прямых металлических стержней электрическое поле создает направленные вдоль них токи.
Свободные электроны в таких контурах колеблются с резонансной частотой, зависящей от формы и размеров проводника. Если приложено поле с частотой ниже резонансной, будет наблюдаться нормальная положительная реакция. Однако с увеличением частоты отклик становится отрицательным, так же как в случае с маятником, движущимся навстречу, если толкать его с частотой выше резонансной. Таким образом, проводники в некотором диапазоне частот могут реагировать на электрическое поле как среда с отрицательной ε, а кольца с разрезами могут имитировать материал с отрицательной μ. Эти проводники и кольца с разрезами и есть элементарные блоки, необходимые для создания широкого ассортимента метаматериалов, в том числе таких, которые искал Веселаго.
Первое экспериментальное подтверждение возможности создания материала с отрицательным показателем преломления было получено в 2000 г. в Калифорнийском университете в Сан-Диего (
Калифорнийские ученые сконструировали метаматериал, состоящий из чередующихся проводников и РКР, собранных в виде призмы. Проводники обеспечивали отрицательную ε, а кольца с разрезами — отрицательную μ. В результате должен был получиться отрицательный показатель преломления. Для сравнения была изготовлена призма точно такой же формы из тефлона, у которого n = 1,4. Исследователи направили пучок СВЧ-излучения на грань призмы и измерили интенсивность волн, выходящих из нее разными углами. Как и ожидалось, пучок подвергся положительному преломлению на призме из тефлона и отрицательному на призме из метаматериала. Предположение Веселаго стало реальностью: материал с отрицательным показателем преломления был наконец получен. Или же нет?
Желаемое или действительное?
Эксперименты в UCSD наряду с замечательными новыми предсказаниями, которые физики делали о свойствах материалов с отрицательным показателем преломления, вызвали волну интереса среди других исследователей. Когда Веселаго высказал свою гипотезу, метаматериалов еще не было, и специалисты не стали тщательно исследовать феномен отрицательного преломления. Теперь они стали уделять ей гораздо больше внимания. Скептики спрашивали, не нарушают ли материалы с отрицательным показателем преломления фундаментальные законы физики. Если бы это оказалось так, то вся программа исследований была бы поставлена под сомнение.
Самые горячие споры вызвал вопрос о скорости волны в сложном материале. Свет распространяется в вакууме с максимальной скоростью c = 300 тыс. км/с. Скорость света в материале меньше: v =
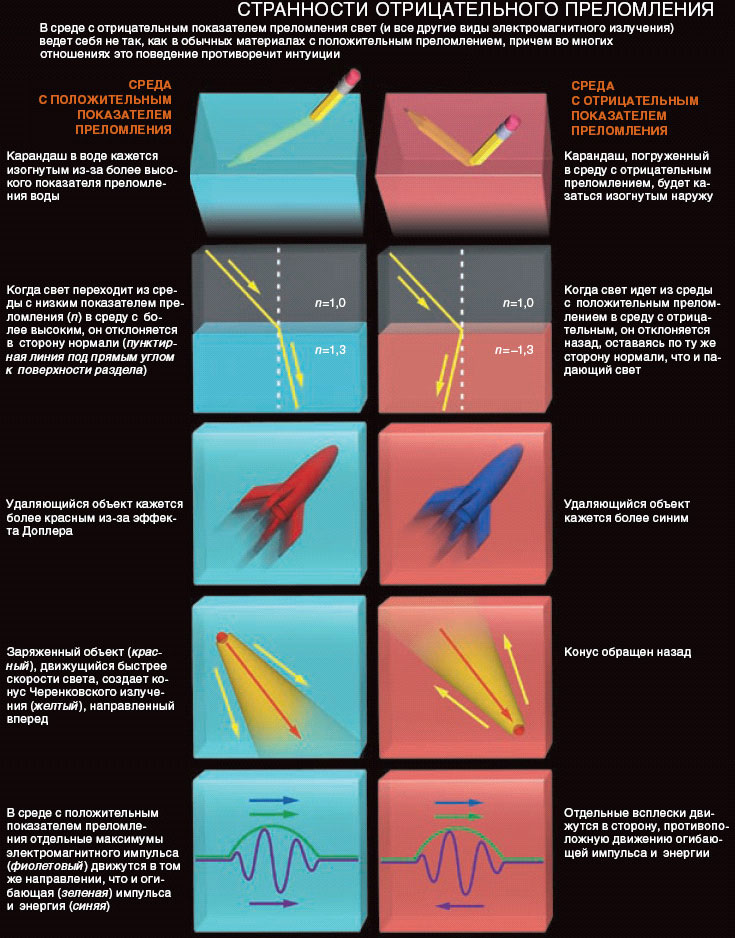
В более полном ответе учитывается, что волна имеет две скорости: фазовую и групповую. Чтобы понять их смысл, представьте себе импульс света, движущийся в среде. Он будет выглядеть примерно так: амплитуда волны возрастает до максимума в центре импульса, а затем снова спадает. Фазовая скорость — это скорость отдельных всплесков, а групповая скорость — это скорость, с которой движется огибающая импульса. Они не обязательно должны быть одинаковыми.
Веселаго обнаружил, что в материале с отрицательным показателем преломления групповая и фазовая скорости имеют противоположные направления: отдельные максимумы и минимумы движутся назад, тогда как весь импульс перемещается вперед. Интересно рассмотреть, как будет себя вести непрерывный пучок света от источника (например, прожектора), погруженного в материал с отрицательным показателем преломления. Если бы можно было наблюдать отдельные колебания световой волны, то мы бы увидели, что они появляются на объекте, освещенном лучом, движутся назад и, в конечном счете, исчезают в прожекторе. Однако энергия светового пучка движется вперед, удаляясь от источника света. Именно в этом направлении фактически распространяется луч, несмотря на удивительное обратное движение его отдельных колебаний.
Практически наблюдать отдельные колебания световой волны трудно, а форма импульса может быть очень сложной, так что физики, чтобы показать различие между фазовой и групповой скоростями, часто используют хитрый трюк. Когда две волны с немного разными длинами движутся в одном направлении, они интерферируют, и возникает картина биений, максимумы которых перемещаются с групповой скоростью.
Применив этот прием к эксперименту
Как же тогда объяснить результаты экспериментов в UCSD? Валанджу и многие другие исследователи приписывали наблюдаемое отрицательное преломление другим явлениям. Быть может, образец поглощал так много энергии, что волны выходили наружу только с узкой стороны призмы, имитируя отрицательное преломление? В конце концов, метаматериал UCSD действительно сильно поглощает излучение, а измерения проводились вблизи призмы. Поэтому гипотеза о поглощении выглядит вполне правдоподобно.
Полученные выводы вызвали большое беспокойство: они могли обесценить не только эксперименты UCSD, но и весь круг явлений, предсказанных Веселаго. Однако после некоторых размышлений мы поняли, что полагаться на картину биений как на показатель групповой скорости нельзя: для двух волн, движущихся в разных направлениях, интерференционная картина никак не связана с групповой скоростью.
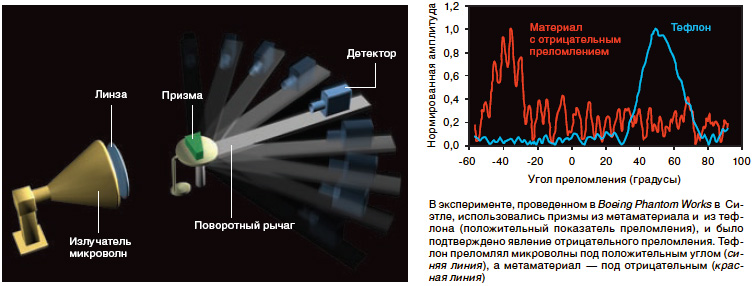
По мере того, как доводы критиков начали рушиться, появилось еще одно экспериментальное подтверждение отрицательного преломления. Группа Минаса Таниэлиана (Minas Tanielian) из компании Boeing Phantom Works в Сиэтле повторила эксперимент UCSD с призмой из метаматериала с очень низким поглощением. Кроме того, датчик был расположен намного дальше от призмы, чтобы поглощение в метаматериале нельзя было перепутать с отрицательным преломлением луча. Высочайшее качество новых данных положило конец сомнениям в существовании отрицательного преломления.
Продолжение следует
Когда дым сражения рассеялся, мы начали понимать, что замечательная история, которую рассказал Веселаго, была не последним словом о материалах с отрицательным показателем преломления. Советский ученый пользовался методом геометрического построения световых лучей с учетом отражения и преломления на границах различных материалов. Этот мощный прием помогает понять, например, почему объекты в бассейне кажутся нам ближе к поверхности, чем на самом деле, и почему наполовину погруженный в жидкость карандаш представляется изогнутым. Все дело в том, что коэффициент преломления воды (n = 1,3) больше, чем у воздуха, и лучи света на границе между воздухом и водой преломляются. Показатель преломления приблизительно равен отношению реальной глубины к кажущейся.
Веселаго использовал построение хода лучей, чтобы предсказать, что брус из материала с отрицательным показателем преломления n = −1 должен действовать как линза с уникальными свойствами. Большинство из нас знакомо с линзами из материалов с положительным преломлением — в камерах, лупах, микроскопах и телескопах. Они имеют фокусное расстояние, и место, где формируется изображение, зависит от сочетания фокусного расстояния и расстояния между объектом и линзой. Изображения обычно отличаются по размеру от объекта, и линзы работают лучше всего для объектов, лежащих на оси, проходящей через линзу. Линза Веселаго работает совершенно иначе, чем обычные: ее работа намного проще, она действует только на объекты, расположенные рядом с ней, и переносит все оптическое поле с одной стороны линзы на другую.
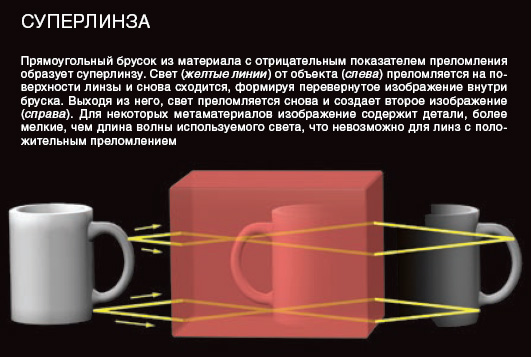
Линза Веселаго столь необычна, что Джону Пендри (John B. Pendry) пришлось задаться вопросом: насколько совершенно она может работать? И в частности, каково может быть предельное разрешение линзы Веселаго? Оптические элементы с положительным показателем преломления ограничены дифракционным пределом — они могут разрешать детали, размер которых равен или больше длины волны света, отраженного от объекта. Дифракция накладывает окончательный предел на все системы создания изображения, наподобие наименьшего объекта, который можно рассмотреть в микроскоп, или наименьшего расстояния между двумя звездами, которое может разрешить телескоп. Дифракция определяет также наименьшую деталь, которую можно создать в процессе оптической литографии при производстве микрочипов (микросхем). Подобным же образом дифракция ограничивает количество информации, которую можно сохранить или прочитать на оптическом цифровом видеодиске (DVD). Способ обойти дифракционный предел мог бы решительным образом изменить технологии, позволив оптической литографии проникнуть в диапазон наноразмеров и, возможно, в сотни раз увеличить количество данных, сохраняемых на оптических дисках.
Чтобы определить, действительно ли оптика с отрицательным преломлением могла бы превзойти обычную («положительную») оптику, нам следует продвинуться дальше, чем просто рассмотреть ход лучей. Прежний подход пренебрегает дифракцией, и таким образом его нельзя использовать, чтобы предсказать разрешение линз с отрицательным преломлением. Чтобы включить в рассмотрение дифракцию, нам пришлось использовать более точное описание электромагнитного поля.
Суперлинза
При более точном описании электромагнитные волны любых источников — излучающих атомов, радиоантенн или пучка света, — после прохождения через маленькое отверстие создают два разных типа полей: дальнее и ближнее поле. Дальнее поле, на что указывает его название, наблюдается вдали от объекта и улавливается линзой, формируя изображение объекта. К сожалению, это изображение содержит только грубую картину объекта, в которой дифракция ограничивает разрешение величиной длины волны. Ближнее поле содержит все мельчайшие детали объекта, но его интенсивность быстро падает с расстоянием. Линзы с положительным преломлением не дают никакого шанса на перехват чрезвычайно слабого ближнего поля и передачу его данных в изображение. Однако это не так для линз с отрицательным преломлением.
Подробно исследовав, как ближние и дальние поля источника взаимодействуют с линзой Веселаго, Пендри в 2000 г. к всеобщему удивлению пришел к заключению, что линза, в принципе, может фокусировать как ближние, так и дальние поля. Если бы это ошеломляющее предсказание оказалось верным, это означало бы, что линза Веселаго, в отличие от всей другой известной оптики, не подчиняется дифракционному пределу. Поэтому плоскую структуру с отрицательным преломлением назвали суперлинзой.
При последующем анализе мы и другие исследователи нашли, что разрешение суперлинзы ограничено качеством ее материала с отрицательным преломлением. Для лучшей работы требуется не только чтобы показатель преломления n был равен −1, но также чтобы ε и μ оба были равны −1. Линза, у которой эти условия не выполняются, имеет резко ухудшенное разрешение. Одновременное выполнение этих условий — очень серьезное требование. Но в 2004 г. Энтони Грбич (Anthony Grbic) и Джордж Элефтериадес (George V. Eleftheriades) из Университета Торонто экспериментально показали, что метаматериал, построенный так, чтобы иметь ε =−1, и μ =−1 в диапазоне радиочастот, действительно может разрешить объекты в масштабе меньшем, чем дифракционный предел. Их результат доказал, что суперлинзу можно построить, но можно ли ее создать для еще более коротких — оптических длин волн?
Сложность масштабирования метаматериалов в область оптических длин волн имеет две стороны. Прежде всего, металлические проводящие элементы, образующие микросхемы метаматериала, типа проводников и колец с разрезом, нужно уменьшить до масштаба нанометров, чтобы они были меньше, чем длина волны видимого света (400–700 нм). Во вторых, короткие длины волн соответствуют более высоким частотам, а металлы на таких частотах обладают худшей проводимостью, подавляя таким образом резонансы, на которых основаны свойства метаматериалов. В 2005 г. Костас Соуколис (Costas Soukoulis) из университета штата Айова и Мартин Вегенер (Martin Wegener) из университета Карлсруэ в Германии экспериментально продемонстрировали, что можно сделать кольца с разрезами, которые работают при длинах волн всего 1,5 мкм. Несмотря на то, что при столь малых длинах волн резонанс на магнитной компоненте поля становится весьма слабым, с такими элементами все еще можно сформировать интересные метаматериалы.

Но мы пока еще не можем изготовить материал, который при длинах волн видимого света приводит к μ =−1. К счастью, возможен компромисс. Когда расстояние между объектом и изображением намного меньше, чем длина волны, необходимо выполнить только условие ε =−1, а значением μ можно пренебречь. Как раз в прошлом году группа Ричарда Блэйки (Richard Blaikie) из университета Кентербери в Новой Зеландии и группа Ксианга Джанга (Xiang Zhang) из Калифорнийского университета в Беркли, следуя этим предписаниям, независимо продемонстрировали сверхразрешение в оптической системе. При оптических длинах волн собственные резонансы металла могут приводить к отрицательной диэлектрической постоянной (ε). Поэтому очень тонкий слой металла при длине волны, где ε =−1, может действовать как суперлинза. И Блэйки, и Джанг использовали слой серебра толщиной около 40 нм, чтобы получить изображение пучков света с длиной волны 365 нм, испускаемых сформированными отверстиями, меньшими, чем длина волны света. И хотя серебряная пленка далека от идеальной линзы, серебряная суперлинза существенно улучшала разрешение изображения, доказывая правильность основного принципа работы суперлинзы.
Взгляд в будущее
Демонстрация работы суперлинзы — лишь последнее из многих предсказаний свойств материалов с отрицательным преломлением, которые предстоит реализовать, а это признак быстрого прогресса, происходящего в этой все расширяющейся области. Возможность отрицательного преломления заставила физиков пересмотреть практически всю область электромагнетизма. И когда этот круг идей будет полностью понят, основные оптические явления, такие как преломление и дифракционный предел разрешения, придется пересмотреть с учетом новых неожиданных поворотов, связанных с материалами, дающими отрицательное преломление.
Волшебство метаматериалов и магию отрицательного преломления все-таки необходимо «конвертировать» в прикладную технологию. Такой шаг потребует совершенствования конструкции метаматериалов и производства их по разумной цене. Сейчас в этой области действует множество исследовательских групп, энергично разрабатывающих способы решения проблемы.
Литература:
1. Reversing Light with Negative Refraction. John B. Pendry and David R. Smith // Physics Today. Vol. 57. No. 6. P. 37–43. June 2004.
2. Negative-Refraction Metamaterials: Fundamental Principles and Applications. G. V. Eleftheriades and K. Balmain. Wiley-IEEE Press, 2005.
Дополнительная информация о метаматериалах и отрицательном преломлении имеется на сайтах:
Шаг к суперлинзе: За пределы дифракции
Снять с полки микроскоп и рассмотреть под ним — не комара или волос, и даже не крупные растительные клетки — а частицы вируса в капле крови… Или — крупные молекулы? Просто дух захватывает от возможностей убить время в компании с таким инструментом. Не говоря уж о перспективах для науки и электроники. Не хватает главного: суперлинзы.

Прямое и обратное преломление

Идея метаматериала, предложенного Дарду Гани: цвета демонстрируют магнитные поля, создаваемые плазмонами; черные стрелки — направление тока в слоях металла; цифры соответствуют петлям электромагнитного поля, за счет которых возникает отрицательный коэффициент преломления
В самом деле, чтобы рассмотреть предмет, длина волны излучения, которое от него отражается, должна быть заметно меньше самого предмета. К дифракционному пределу оптических линз (около 200 нм) мы уже давно подошли, а для самых мелких объектов приходится использовать более коротковолновое излучение, вплоть до рентгеновских и гамма-лучей. Для того же, чтобы рассмотреть нанометровые объекты, нередко требуется сканирующий туннельный микроскоп, работающий на совершенно иных принципах. И в любом случае — требуется сложнейшая и дорогая аппаратура, тонкая подготовка образцов и прочее, и прочее, что делает наблюдения за микромиром уделом специалистов, а никак не увлеченных «популярных механиков».
Однако еще несколько десятилетий назад Виктор Веселаго теоретически обосновал создание искусственных метаматериалов с отрицательным показателем преломления: микроструктура этих метаматериалов особым образом взаимодействует с проходящим сквозь нее излучением. На поверхности ее свет преломляется, лучи его сходятся и снова расходятся, а выходя из метаматериала, преломляются еще раз. При особым образом подобранной структуре изображение, составленное вышедшими из метаматериала лучами, содержит детали даже более мелкие, чем длина их волны.
Сегодня уже делаются первые шаги по практическому получению таких метаматериалов. Они обещают нам целый ряд удивительных новинок, включая «плащ-невидимку» и — ту же «суперлинзу», очередной шаг к обретению которой сделали недавно ученые из группы американского профессора Дарду Гани (Durdu Guney). По расчетам авторов, их материал позволит получать посредством лучей оптического спектра изображения объектов размерами до 100 нм — в тысячи раз меньше толщины человеческого волоса.
Главный секрет здесь — в плазмонах, условных частицах, «квантах колебания» свободного электронного газа, которые возникают на поверхности тонких металлических пленок в метаматериале, содержащем также сферические наноструктуры. Возбужденные внешним электромагнитным полем, они улавливают падающие на них фотоны излучения и отражают их так, как если бы метаматериал обладал отрицательным показателем преломления. В отличие от аналогичных работ, метаматериал, предложенный Гани и его коллегами, демонстрирует отрицательное преломление для всего видимого спектра.
Когда же дело дойдет до практики, производство метаматериалов нужной структуры, по общему мнению экспертов, будет совсем недорогим. Ну а получившиеся суперлинзы можно использовать не только в науке, но и в литографии для получения сложных объектов совсем крошечных размеров, а также в электронике, в цифровых фотоаппаратах — и, конечно, в домашних микроскопах. «С суперлинзой ученым сможет стать каждый», — говорит Гани.
По пресс-релизу Michigan Technological University
Профессора физики Ланкастерского университета (Lancaster University, Великобритания) Владимир Фалько (Vladimir I. Falko) и Вадим Чеянов и профессор физики Колумбийского университета (Columbia University, Нью-Йорк, США) Борис Альтшулер (Boris Altshuler), работающий также в американском подразделении Исследовательской лаборатории NEC (NEC Laboratories America), выполнили теоретические расчеты и компьютерное моделирование, из которых вытекает возможность использования графена в качестве материала для изготовления электронных линз. Эта работа 2 марта появилась в журнале Science.
Графен состоит в тесном родстве с обычным графитом. Как известно, графит сложен из атомов углерода, упакованных в параллельные листы, внутри которых они образуют плоские шестиугольники. Химические связи между соседними листами довольно слабы, поэтому от графита при трении легко отслаиваются чешуйки, что и позволяет делать из него карандашные грифели и использовать для смазки трущихся поверхностей. Недавно исследователи нашли способы получать изолированные одноатомные слои, сложенные из углеродных шестиугольников. Так был создан новый материал, который и назвали графеном.
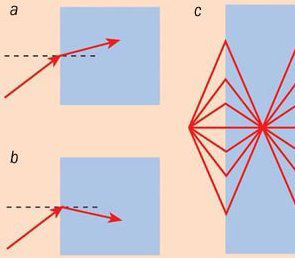
Графен — двумерная система с очень любопытными физическими свойствами. Эти свойства, в частности, проявляются при вхождении в графен пучка электронов. Согласно принципам квантовой механики, такой пучок, подобно световому импульсу, обладает как фазовой, так и групповой скоростью (первая определяет быстроту пространственного перемещения фазы волны, в данном случае электронной волновой функции, а вторая — скорость движения волнового пакета, которая в данном случае совпадает с классической скоростью электрона). В обычных веществах векторы обеих этих скоростей направлены в одну сторону. Однако симметрия электронных уровней графенового листа такова, что эти векторы при определенных условиях могут оказаться антипараллельными. В результате электронный луч при попадании в графен изменит не только величину угла с перпендикуляром к поверхности падения, как при нормальном преломлении, но и его знак. Такое преломление называется отрицательным (на рис. 1 нормальному преломлению соответствует рисунок a, отрицательному — рисунок b).
Сорок лет назад советский физик Виктор Веселаго теоретически продемонстрировал, что прямоугольный брусок (плоскопараллельная пластинка), изготовленный из материала с отрицательным преломлением, будет фокусировать свет подобно выпуклой стеклянной линзе (см. рис. 1 c). Через три с лишним десятка лет англичанин Джон Пендри доказал, что такая пластинка будет в состоянии превзойти самую лучшую линзу по точности фокусировки. Как известно, пределы возможностей обычной линзы или комбинации линз ограничены длиной световой волны. Линза Веселаго, как ее теперь называют, может, в принципе, фокусировать свет и на меньших расстояниях, если только изготовить ее достаточно тщательно.
Чеянов и его коллеги предложили реализовать электронный аналог линзы Веселаго в виде графенового листа, помещенного между плоскими электродами, на один из которых подается положительное напряжение, а на другой — отрицательное. Положительный электрод создает со своей стороны избыток электронов, отрицательный — недостаток. В результате со стороны анода возникает электронная проводимость, со стороны катода — дырочная. Граница между ними образует точный аналог электронно-дырочных переходов (p-n-переходов), которые возникают при легировании проводников — внесении в них донорных и акцепторных примесей (первые создают электронную проводимость, а вторые — дырочную). Расчеты показывают, что в области такого перехода создаются условия для того, чтобы пучок электронов испытал преломление с показателем, равным минус единице. Если со стороны анода расположить точечный источник электронов, то при прохождении через графеновый лист посылаемые им частицы сфокусируются в облачко очень малого размера.
Пока что это устройство существует только в теории. Сейчас его могли бы изготовить лишь в пяти-шести лабораториях, технические сложности слишком велики. Компьютерное моделирование показывает, что даже при сверхнизких температурах это устройство, в отличие от идеальной линзы Веселаго, всё же не сможет осуществлять фокусировку на дистанциях, уступающих квантовомеханической длине волны электронов. Однако характерные длины электронных волн неизмеримо меньше длин волн видимого света (например, длина волны электрона с энергией всего лишь в 1 электронвольт примерно равна одному нанометру), так что фокусировка всё равно может быть достаточно жесткой. Будет ли построена такая линза — это вопрос к экспериментаторам.
Источник: Vadim V. Cheianov, Vladimir Fal’ko, B. L. Altshuler. The Focusing of Electron Flow and a Veselago Lens in Graphene p-n Junctions // Science. 2007. V. 315. P. 1252–1255.
См. также:
1) Дж. Пендри, Д. Смит. В поисках суперлинзы («В мире науки» №11, 2006).
2) Суперлинзы становятся все реальнее, «Элементы», 20.10.2005.
Алексей Левин
Гиперлинза, разработанная авторами. Фотография сделана при помощи сканирующего электронного микроскопа
Изображение: University at Buffalo, The State University of New York
Физики из Университета Буффало разработали гиперлинзу, работающую в видимом диапазоне и способную обойти дифракционный предел. Для ее изготовления авторы прибегли к метаматериалам — классу материалов с необычными оптическими свойствами. Об этом сообщает пресс-релиз Университета, статья опубликована в открытом доступе в журнале Nature.
Метаматериалами называют класс материалов, свойства которых определяются скорее их микроструктурой, нежели веществом, из которых они созданы. К ним относятся, например, среды, обладающие отрицательным коэффициентом преломления. Впервые их теоретически описал советский физик Виктор Веселаго 1968 году. Это свойство приводит, например, к тому, что свет попадая в такую среду, преломляется в ту же сторону, откуда пришел пучок, а тонкая прямоугольная пластина ведет себя как линза. Как правило такие материалы состоят из многочисленных повторяющихся элементов, например, металлических колец или различных тонких слоев.
Слева устройство линзы, созданной авторами, справа — традиционной суперлинзы
Изображение: Jingbo Sun еt al. / Nature Communications, 2015
Гиперлинза в новой работе была изготовлена авторами из метаматериала на основе золота и полимера (ПММА). Она имеет веерообразную форму, что отличает ее от традиционных суперлинз, в которых тонкие слои расположены на манер концентрических окружностей. Для проверки работоспособности линзы физики разместили перед ней две узкие наноразмерные щели, отстоящие друг от друга на 250 нанометров. На них, с помощью оптического волновода, направили луч лазера с длиной волны 780 нанометров — щели разделили его на два отдельных луча.
Эксперимент с использованием гиперлинзы (сверху) и без. Во втором случае пучки света от двух щелей сливаются в одно пятно
Изображение: Jingbo Sun еt al. / Nature Communications, 2015
Если сразу после щели находились бы линзы из традиционных материалов, то любая их комбинация не позволила бы различить два образовавшихся пучка света. Однако гиперлинза смогла пространственно разделить их, что удалось зафиксировать исследователям. Веерообразная структура послужила одновременно преобразователем эванесцентных волн, порожденных щелями, в распространяющиеся, а также выполнила свою роль линзы.
Схема устройства, использованного авторами в эксперименте
Изображение: Jingbo Sun еt al. / Nature Communications, 2015
Авторы отмечают, что представленные ими линзы позволяют получать изображения малых объектов с меньшими потерями, чем у традиционных суперлинз.
Впервые идея линз, преодолевающих дифракционный предел появилась в 2000 году, когда английский физик Джо Пендри теоретически показал, что в отличие от классических сред с положительным коэффициентом преломления, в метаматериалах эванесцентные волны усиливаются, а не затухают. Создав метаматериал с определенными оптическими характеристиками (гиперболической дисперсией), преобразующий эванесцентные волны в распространяющиеся, физики смогли получить требуемые характеристики.
Главной особенностью гиперлинз, созданных авторами, является возможность конвертировать эванесцентные волны света в распространяющиеся. Эванесцентными, или затухающими, называют особый класс волн, распространяющихся вдоль границы раздела фаз. С удалением от поверхности амплитуда таких волн экспоненциально, затухает. Важной особенностью этих волн является значительно меньшее значение дифракционного предела — именно с помощью них реализована сканирующая оптическая ближнепольная микроскопия, один из первых методов позволивших увидеть наномир в цвете. Однако создать реальное изображение объекта (для чего и необходима линза) можно только с помощью обычных, распространяющихся волн.
Суперлинза сжала свет до наномасштаба
Российские и датские ученые впервые наблюдали в эксперименте плазмонную нанострую. Это явление позволяет сфокусировать свет на наномасштабе и в теории — обойти одно из фундаментальных ограничений обычной собирающей линзы. Подобное уплотнение световых волн необходимо, чтобы использовать их в качестве переносчика сигналов в компактных устройствах, которые будут работать быстрее электроники.
До изобретения лазерной указки герои любовных романов сообщали на энный этаж о своем присутствии, бросая камешек в окно. Один из недостатков камня как носителя сигнала — его масса, из-за которой отправка сообщения требует усилий и времени. Масса электрона мала, но тоже не равна нулю, поэтому и его нельзя мгновенно привести в движение. Если бы вместо электронов микросхемы оперировали фотонами — частицами света, техника работала бы намного быстрее.
Сегодня не представляется возможным заменить электронный микрочип фотонным аналогом, потому что такое устройство будет иметь огромные размеры. Миниатюризация потребует управления фотонами на столь маленьких масштабах, что световую волну придется локализовать в минимальном объеме. В идеале нужно собрать свет в пятно размером менее 50% длины волны, что невозможно сделать обычной линзой, — это фундаментальное ограничение называется дифракционным пределом.
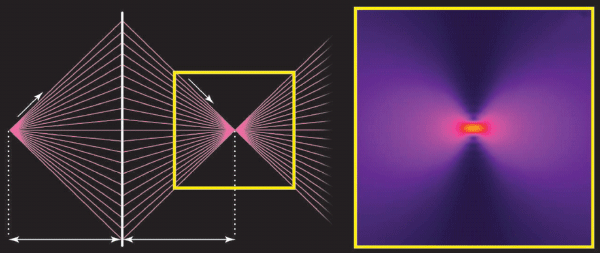
Ученые из России и Дании сконструировали фокусирующий элемент, который способен превратить свет в особый вид электромагнитных волн со сжатием до 60% длины исходного излучения и потенциалом преодолеть дифракционный предел. Изготовленная коллективом металинза представляет собой квадратный кусок диэлектрика размером 5 на 5 микрометров и толщиной 0,25 микрометра. Эта частица помещена на золотую пленку толщиной 0,1 микрометра, на обратной стороне которой нанесена рельефная решетка:
Дарья Сокол Схема металинзы Лазерный импульс, падающий на золотую пленку, преобразуется в поверхностные плазмоны-поляритоны — особые электромагнитные колебания, которые распространяются в плоскости металлической пленки и, проходя под квадратной диэлектрической частицей, фокусируются до 60% исходной длины волны. Чем сильнее фокусировка, тем миниатюрнее может быть техника
При облучении такой системы лазером в плоскости раздела между золотом и диэлектриком возникает возмущение в виде так называемого поверхностного плазмона-поляритона. Оно представляет собой коллективное колебание электронов в металле (плазмон), согласованное с распространением по поверхности световой волны (поляритона). Ценность этого превращения в том, что поверхностные плазмоны-поляритоны поддаются субволновой фокусировке, то есть их можно локализовать сильнее, чем породивший их лазерный импульс.

«Один из механизмов субволновой фокусировки основан на явлении плазмонной наноструи, которое нам удалось впервые экспериментально зафиксировать», — рассказывает инициатор работы, профессор Томского политехнического университета Игорь Минин. Статья опубликована в журнале Optics Letters.
Замдиректора ИСВЧПЭ РАН и ведущий научный сотрудник лаборатории двумерных материалов и наноустройств МФТИ Дмитрий Пономарёв поясняет принцип уплотнения волн в суперлинзе: «Мы использовали компьютерное моделирование, чтобы подобрать подходящие размеры диэлектрической частицы и характеристики дифракционной решетки на золоте. В результате поверхностная плазмонная волна имеет разную фазовую скорость на краях и в центре диэлектрика, из-за чего фронт волны изгибается и формируется плазмонная наноструя — область высокой плотности плазмонов-поляритонов».
Евгений Пелевин Один из авторов исследования, директор Центра фотоники и двумерных материалов МФТИ Валентин Волков, за ближнепольным микроскопом. Подобный инструмент использовался исследователями, чтобы впервые наблюдать плазмонную нанострую
Таким образом можно сильно локализовать излучение и манипулировать «сжатым светом» на наномасштабе, а это — необходимое условие для интеграции на чипе фотонных и плазмонных устройств, которые будут работать значительно быстрее своих электронных аналогов.
Директор Центра фотоники и двумерных материалов МФТИ Валентин Волков добавил: «Экспериментальное наблюдение плазмонных струй стало возможным благодаря объединению усилий ученых нашего центра и коллег из Москвы, Томска и Копенгагена. Наше сотрудничество будет продолжено — в ближайшем будущем мы продемонстрируем другие интересные эффекты, связанные с образованием, распространением и применением плазмонных струй».
Материал предоставлен пресс-службой МФТИ
Суперлинза сжала свет до наномасштаба — МФТИ
Иллюстрация. Суперлинза. Дизайнер: Дарья Сокол, пресс-служба МФТИ
Российские и датские ученые впервые наблюдали в эксперименте плазмонную нанострую. Это явление позволяет сфокусировать свет на наномасштабе и в теории — обойти одно из фундаментальных ограничений обычной собирающей линзы. Подобное уплотнение световых волн необходимо, чтобы использовать их в качестве переносчика сигналов в компактных устройствах, которые будут работать быстрее электроники. Статья опубликована в журнале Optics Letters.
До изобретения лазерной указки герои любовных романов сообщали на энный этаж о своем присутствии, бросая камешек в окно. Один из недостатков камня как носителя сигнала — его масса, из-за которой отправка сообщения требует усилий и времени. Масса электрона мала, но тоже не равна нулю, поэтому и его нельзя мгновенно привести в движение. Если бы вместо электронов микросхемы оперировали фотонами — частицами света, техника работала бы намного быстрее.
Сегодня не представляется возможным заменить электронный микрочип фотонным аналогом, потому что такое устройство будет иметь огромные размеры. Миниатюризация потребует управления фотонами на столь маленьких масштабах, что световую волну придется локализовать в минимальном объеме. В идеале нужно собрать свет в пятно размером менее 50% длины волны, что невозможно сделать обычной линзой, — это фундаментальное ограничение называется дифракционным пределом.
Ученые из России и Дании сконструировали фокусирующий элемент, который способен превратить свет в особый вид электромагнитных волн со сжатием до 60% длины исходного излучения и потенциалом преодолеть дифракционный предел. Изготовленная коллективом металинза представляет собой квадратный кусок диэлектрика размером 5 на 5 микрометров и толщиной 0,25 микрометра. Эта частица помещена на золотую пленку толщиной 0,1 микрометра, на обратной стороне которой нанесена рельефная решетка (рисунок 1).
Рисунок 1. Лазерный импульс, падающий на золотую пленку, преобразуется в поверхностные плазмоны-поляритоны — особые электромагнитные колебания, которые распространяются в плоскости металлической пленки и, проходя под квадратной диэлектрической частицей, фокусируются до 60% исходной длины волны. Чем сильнее фокусировка, тем миниатюрнее может быть техника. Дизайнер: Дарья Сокол, пресс-служба МФТИ
При облучении такой системы лазером в плоскости раздела между золотом и диэлектриком возникает возмущение в виде так называемого поверхностного плазмона-поляритона. Оно представляет собой коллективное колебание электронов в металле (плазмон), согласованное с распространением по поверхности световой волны (поляритона). Ценность этого превращения в том, что поверхностные плазмоны-поляритоны поддаются субволновой фокусировке, то есть их можно локализовать сильнее, чем породивший их лазерный импульс.
«Один из механизмов субволновой фокусировки основан на явлении плазмонной наноструи, которое нам удалось впервые экспериментально зафиксировать», — рассказывает инициатор работы, профессор Томского политехнического университета Игорь Минин.
Замдиректора ИСВЧПЭ РАН и ведущий научный сотрудник лаборатории двумерных материалов и наноустройств МФТИ Дмитрий Пономарёв поясняет принцип уплотнения волн в суперлинзе: «Мы использовали компьютерное моделирование, чтобы подобрать подходящие размеры диэлектрической частицы и характеристики дифракционной решетки на золоте. В результате поверхностная плазмонная волна имеет разную фазовую скорость на краях и в центре диэлектрика, из-за чего фронт волны изгибается и формируется плазмонная наноструя — область высокой плотности плазмонов-поляритонов».
Фото. Один из авторов исследования, директор Центра фотоники и двумерных материалов МФТИ Валентин Волков, за ближнепольным микроскопом. Подобный инструмент использовался исследователями, чтобы впервые наблюдать плазмонную нанострую. Источник: Евгений Пелевин, пресс-служба МФТИ
Таким образом можно сильно локализовать излучение и манипулировать «сжатым светом» на наномасштабе, а это — необходимое условие для интеграции на чипе фотонных и плазмонных устройств, которые будут работать значительно быстрее своих электронных аналогов.
Директор Центра фотоники и двумерных материалов МФТИ Валентин Волков добавил: «Экспериментальное наблюдение плазмонных струй стало возможным благодаря объединению усилий ученых нашего центра и коллег из Москвы, Томска и Копенгагена. Наше сотрудничество будет продолжено — в ближайшем будущем мы продемонстрируем другие интересные эффекты, связанные с образованием, распространением и применением плазмонных струй».
Работа была поддержана Российским научным фондом и Российским фондом фундаментальных исследований.
Российские и датские ученые впервые наблюдали в эксперименте плазмонную нанострую. Это явление позволяет сфокусировать свет на наномасштабе и в теории — обойти одно из фундаментальных ограничений обычной собирающей линзы. Подобное уплотнение световых волн необходимо, чтобы использовать их в качестве переносчика сигналов в компактных устройствах, которые будут работать быстрее электроники. Статья об итогах работы опубликована в журнале Optics Letters, кратко о них сообщается в пресс-релизе Московского физико-технического института.
До изобретения лазерной указки герои любовных романов сообщали о своем присутствии, бросая камешек в окно. Один из недостатков камня как носителя сигнала — его масса, из-за которой отправка сообщения требует усилий и времени. Масса электрона мала, но тоже не равна нулю, поэтому и его нельзя мгновенно привести в движение. Если бы вместо электронов микросхемы оперировали фотонами — частицами света, техника работала бы намного быстрее.
Сегодня не представляется возможным заменить электронный микрочип фотонным аналогом, потому что такое устройство будет иметь огромные размеры. Миниатюризация потребует управления фотонами на столь маленьких масштабах, что световую волну придется локализовать в минимальном объеме. В идеале нужно собрать свет в пятно размером менее 50 % длины волны, что невозможно сделать обычной линзой, — это фундаментальное ограничение называется дифракционным пределом.
Ученые из России и Дании сконструировали фокусирующий элемент, который способен превратить свет в особый вид электромагнитных волн со сжатием до 60 % длины исходного излучения и потенциалом преодолеть дифракционный предел. Изготовленная коллективом металинза представляет собой квадратный кусок диэлектрика размером 5 на 5 микрометров и толщиной 0,25 микрометра. Эта частица помещена на золотую пленку толщиной 0,1 микрометра, на обратной стороне которой нанесена рельефная решетка.

Лазерный импульс, падающий на золотую пленку, преобразуется в поверхностные плазмоны-поляритоны — особые электромагнитные колебания, которые распространяются в плоскости металлической пленки и, проходя под квадратной диэлектрической частицей, фокусируются до 60 % исходной длины волны. Чем сильнее фокусировка, тем миниатюрнее может быть техника. Дизайнер: Дарья Сокол, пресс-служба МФТИ
При облучении такой системы лазером в плоскости раздела между золотом и диэлектриком возникает возмущение в виде так называемого поверхностного плазмона-поляритона. Оно представляет собой коллективное колебание электронов в металле (плазмон), согласованное с распространением по поверхности световой волны (поляритона). Ценность этого превращения в том, что поверхностные плазмоны-поляритоны поддаются субволновой фокусировке, то есть их можно локализовать сильнее, чем породивший их лазерный импульс.
«Один из механизмов субволновой фокусировки основан на явлении плазмонной наноструи, которое нам удалось впервые экспериментально зафиксировать», — рассказывает инициатор работы, профессор Томского политехнического университета Игорь Минин.
Замдиректора Института сверхвысокочастотной полупроводниковой электроники РАН и ведущий научный сотрудник лаборатории двумерных материалов и наноустройств МФТИ Дмитрий Пономарёв поясняет принцип уплотнения волн в суперлинзе: «Мы использовали компьютерное моделирование, чтобы подобрать подходящие размеры диэлектрической частицы и характеристики дифракционной решетки на золоте. В результате поверхностная плазмонная волна имеет разную фазовую скорость на краях и в центре диэлектрика, из-за чего фронт волны изгибается и формируется плазмонная наноструя — область высокой плотности плазмонов-поляритонов».

Один из авторов исследования, директор Центра фотоники и двумерных материалов МФТИ Валентин Волков, за ближнепольным микроскопом. Подобный инструмент использовался исследователями, чтобы впервые наблюдать плазмонную нанострую. Источник: Евгений Пелевин, пресс-служба МФТИ
Таким образом можно сильно локализовать излучение и манипулировать «сжатым светом» на наномасштабе, а это необходимое условие для интеграции на чипе фотонных и плазмонных устройств, которые будут работать значительно быстрее своих электронных аналогов.
Директор Центра фотоники и двумерных материалов МФТИ Валентин Волков добавил: «Экспериментальное наблюдение плазмонных струй стало возможным благодаря объединению усилий ученых нашего центра и коллег из Москвы, Томска и Копенгагена. Наше сотрудничество будет продолжено — в ближайшем будущем мы продемонстрируем другие интересные эффекты, связанные с образованием, распространением и применением плазмонных струй».
Таблица гиперфокальных расстояний | PhotoPills
Как использовать таблицу гиперфокальных расстояний
Если вы хотите, чтобы все элементы на горизонте (горы, здания, звезды и т. Д.) Были четко сфокусированы на изображении, сфокусируйтесь на гиперфокальном расстоянии!
Вы знаете, что, когда объектив сфокусирован на гиперфокальном расстоянии, все, что падает на расстоянии от половины этого расстояния до бесконечности, будет приемлемо четким на изображении. Это делает расчет гиперфокальных расстояний необходимостью для пейзажных и ночных фотографов, когда цель состоит в том, чтобы максимизировать глубину резкости при коротких фокусных расстояниях (от 7 до 35 мм).
Диаграмма гиперфокального расстояния — это самый быстрый способ расчета гиперфокального расстояния для нужных вам настроек. Просто введите вашу камеру, фокусное расстояние и диафрагму и прочитайте значения на графике.
Обратите внимание, что гиперфокальное расстояние увеличивается при увеличении фокусного расстояния или диафрагмы (меньшие числа f: f / 2.8, f / 4), уменьшая глубину резкости.
Напротив, гиперфокальное расстояние уменьшается за счет уменьшения фокусного расстояния или диафрагмы (большее число f: f / 8, f / 11), увеличивая глубину резкости.
Поэтому, если вы делаете фокус на гиперфокальном расстоянии для самой широкой диафрагмы объектива, скажем, f / 2.8, когда вы решите закрыть диафрагму, вам не нужно будет фокусироваться на новом гиперфокальном расстоянии, потому что это короче предыдущего. В результате при закрытии диафрагмы при съемке с фокусировкой объектива на предыдущем гиперфокальном расстоянии все элементы на горизонте останутся в фокусе.
По этой причине говорят, что вам не нужно снова фокусироваться при закрытии диафрагмы, если ранее вы делали фокус на гиперфокальном расстоянии.

Как сфокусироваться на гиперфокальном расстоянии
Давайте представим на мгновение, что вы на месте съемки, готовые насладиться отличным ночным побегом. Вы хотите захватить как можно больше звезд, поэтому установите короткое фокусное расстояние (например, 14 мм), чтобы захватить как можно больше неба.
Вы вычислили гиперфокальное расстояние и готовитесь сфокусироваться на нем. Вы устанавливаете режим автоматической фокусировки и используете факел, чтобы осветить камень, расположенный на более или менее гиперфокальном расстоянии.
Вы измерили расстояние, пройдя «эквивалентное» количество шагов. Вы также дважды проверили его с помощью инструмента дополненной реальности PhotoPills DoF.
Это критический момент, вы должны быть уверены, что не упустите шанс. Если вы потерпите неудачу при фокусировке на гиперфокальном расстоянии, даже на один дюйм (2,5 см), вы не сможете сфокусировать элементы на горизонте. Вы получите, например, звезды не в фокусе.
Поскольку вы не собираетесь измерять гиперфокальное расстояние линейкой, убедитесь, что вы фокусируете объектив на расстоянии, которое немного больше (2 фута — 60 см), чем гиперфокальное расстояние.Таким образом, вы убедитесь, что все фоновые элементы находятся в фокусе. Так работает гиперфокальное расстояние, все дело в математике.
Следующим шагом является настройка фокуса в автоматическом режиме и установка фокуса на ручной, чтобы при съемке фокус не изменялся. Все, что вам нужно сделать сейчас, это наслаждаться звездами!
Нужно больше? Посмотрите следующее видео. Мы покажем вам, как сфокусироваться на гиперфокальном расстоянии:
Понимание глубины резкости
Также, если вы заинтересованы в овладении гиперфокальным расстоянием и глубиной резкости, в этой статье вы найдете все, что вам нужно знать, чтобы стать настоящим рассказчиком!
Глубина резкости: исчерпывающее руководство
В нем вы найдете множество примеров, которые вдохновят вас при съемке на большой глубине резкости…

… также есть множество советов и примеров, как снимать на малой глубине резкости.

Таблица гиперфокальных расстояний в приложении PhotoPills
Диаграмма гиперфокальных расстояний также доступна в приложении PhotoPills, дополненная представлением дополненной реальности, чтобы помочь вам визуализировать, куда фокусироваться.

Таблица гиперфокального расстояния PhotoPills — результаты в виде диаграммы.

Таблица гиперфокального расстояния PhotoPills — результаты на картинке.
Примечание: с учетом размера датчика вычисляется путаница, исходя из размера отпечатка 8 «× 10» (20 см × 25 см), расстояния просмотра 10 «(25 см) и стандартной остроты зрения производителей.
Наконец, если вы заинтересованы в улучшении вашей фотографии, ознакомьтесь с нашими подробными руководствами по фотографии:
, а также с основными документами по фотографии:
Как встроить таблицу гиперфокальных расстояний на свой веб-сайт
Воспользуйтесь возможностями Таблица гиперфокального расстояния PhotoPills с вами. Просто скопируйте следующие строки и вставьте их в код вашего веб-сайта прямо в том месте, где вы хотите его вставить:
