В поисках суперлинзы
Джон Пендри, Дэвид Смит
«В мире науки» №11, 2006
Построенная из метаматериала с удивительными оптическими свойствами, суперлинза может создавать изображения с деталями меньше длины волны используемого света.
Почти 40 лет назад советский ученый Виктор Веселаго выдвинул гипотезу о существовании материалов с отрицательным показателем преломления (УФН, 1967, т. 92, с. 517). Световые волны в них должны двигаться против направления распространения луча и вообще вести себя удивительным образом, линзы же из этих материалов — обладать волшебными свойствами и непревзойденными характеристиками. Однако у всех известных веществ показатель преломления положителен: за нескольких лет интенсивных поисков Веселаго не нашел ни одного материала с подходящими электромагнитными свойствами, и его гипотеза была забыта. О ней вспомнили лишь в начале XXI в. (см.: Теория и практика Виктора Веселаго).
Благодаря последним достижениям в области материаловедения идея Веселаго была возрождена. Электромагнитные свойства веществ определяются особенностями образующих их атомов и молекул, обладающих довольно узким диапазоном характеристик. Поэтому свойства миллионов известных нам материалов не так уж разнообразны. Однако в середине 1990-х гг. ученые из Центра технологии материалов им. Маркони в Англии занялись созданием метаматериалов, которые состоят из макроскопических элементов и рассеивают электромагнитные волны совсем не так, как любые известные вещества.
В 2000 г. Дэвид Смит вместе с коллегами из Калифорнийского университета в Сан-Диего изготовил метаматериал с отрицательным показателем преломления. Поведение света в нем оказалось настолько странным, что теоретикам пришлось переписать книги по электромагнитным свойствам веществ. Экспериментаторы уже занимаются разработкой технологий, в которых используются удивительные свойства метаматериалов, и создают суперлинзы, позволяющие получать изображения с деталями меньше длины волны используемого света. С их помощью можно было бы делать микросхемы с наноскопическими элементами и записывать на оптические диски огромные объемы информации.
Отрицательное преломление

Чтобы понять, как возникает отрицательное преломление, рассмотрим механизм взаимодействия электромагнитного излучения с веществом. Проходящая через него электромагнитная волна (например, луч света) заставляет двигаться электроны атомов или молекул. На это расходуется часть энергии волны, что влияет на ее свойства и характер распространения. Для получения требуемых электромагнитных характеристик исследователи подбирают химический состав материала.
Но как показывает пример метаматериалов, химия — не единственный путь получения интересных свойств вещества. Электромагнитный отклик материала можно «конструировать», создавая крошечные макроскопические структуры. Дело в том, что обычно длина электромагнитной волны на несколько порядков больше размеров атомов или молекул. Волна «видит» не отдельную молекулу или атом, а коллективную реакцию миллионов частиц. Это справедливо и для метаматериалов, элементы которых тоже значительно меньше длины волны.
Поле электромагнитных волн, что следует из их названия, имеет как электрическую, так и магнитную составляющую. Электроны в материале движутся вперед и назад под действием электрического поля и по кругу под действием магнитного. Степень взаимодействия определяется двумя характеристиками вещества: диэлектрической проницаемостью ε и магнитной проницаемостью μ. Первая показывает степень реакции электронов на электрическое поле, вторая — степень реакции на магнитное. У подавляющего большинства материалов ε и μ больше нуля.
Оптические свойства вещества характеризуются показателем преломления n, который связан с ε и μ простым соотношением: n = ± √(ε∙μ)
. Для всех известных материалов перед квадратным корнем должен стоять знак «+», и поэтому их показатель преломления положителен. Однако в 1968 г. Веселаго показал, что у вещества с отрицательными ε и μ показатель преломления n должен быть меньше нуля. Отрицательные ε или μ получаются в том случае, когда электроны в материале движутся в направлении, противоположном по отношению к силам, создаваемым электрическим и магнитным полями. Хотя такое поведение кажется парадоксальным, заставить электроны двигаться против сил электрического и магнитного полей не так уж сложно.Если толкнуть маятник рукой, он послушно переместится в направлении толчка и начнет колебаться с так называемой резонансной частотой. Подталкивая маятник в такт с качанием, можно увеличить амплитуду колебаний. Если же толкать его с более высокой частотой, то толчки перестанут совпадать с колебаниями по фазе, и в какой-то момент руку ударит маятник, движущийся ей навстречу. Точно так же электроны в материале с отрицательным показателем преломления входят в противофазу и начинают сопротивляться «толчкам» электромагнитного поля.
Метаматериалы
Ключ к такого рода отрицательной реакции — резонанс, то есть стремление колебаться со специфической частотой. Он создается в метаматериале искусственно с помощью крошечных резонансных контуров, имитирующих отклик вещества на магнитное или электрическое поле. Например, в разорванном кольцевом резонаторе (РКР) магнитный поток, проходящий через металлическое кольцо, наводит в нем круговые токи, аналогичные токам, обуславливающим магнетизм некоторых материалов. А в решетке из прямых металлических стержней электрическое поле создает направленные вдоль них токи.
Свободные электроны в таких контурах колеблются с резонансной частотой, зависящей от формы и размеров проводника. Если приложено поле с частотой ниже резонансной, будет наблюдаться нормальная положительная реакция. Однако с увеличением частоты отклик становится отрицательным, так же как в случае с маятником, движущимся навстречу, если толкать его с частотой выше резонансной. Таким образом, проводники в некотором диапазоне частот могут реагировать на электрическое поле как среда с отрицательной ε, а кольца с разрезами могут имитировать материал с отрицательной μ. Эти проводники и кольца с разрезами и есть элементарные блоки, необходимые для создания широкого ассортимента метаматериалов, в том числе таких, которые искал Веселаго.
Первое экспериментальное подтверждение возможности создания материала с отрицательным показателем преломления было получено в 2000 г. в Калифорнийском университете в Сан-Диего (UCSD). Поскольку элементарные кирпичики метаматериала должны быть значительно меньше длины волны, исследователи работали с излучением сантиметрового диапазона и использовали элементы размером в несколько миллиметров.
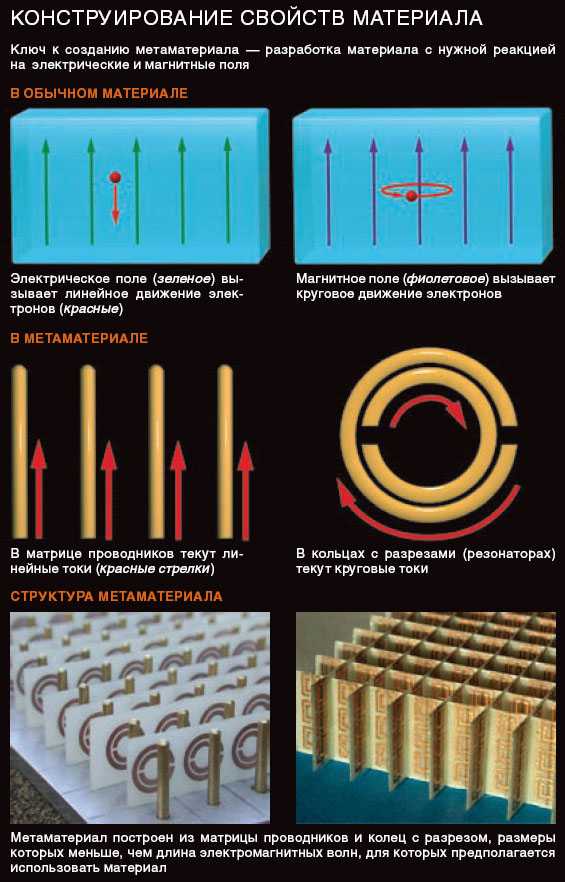
Калифорнийские ученые сконструировали метаматериал, состоящий из чередующихся проводников и РКР, собранных в виде призмы. Проводники обеспечивали отрицательную ε, а кольца с разрезами — отрицательную μ. В результате должен был получиться отрицательный показатель преломления. Для сравнения была изготовлена призма точно такой же формы из тефлона, у которого n = 1,4. Исследователи направили пучок СВЧ-излучения на грань призмы и измерили интенсивность волн, выходящих из нее разными углами. Как и ожидалось, пучок подвергся положительному преломлению на призме из тефлона и отрицательному на призме из метаматериала. Предположение Веселаго стало реальностью: материал с отрицательным показателем преломления был наконец получен. Или же нет?
Желаемое или действительное?
Эксперименты в UCSD наряду с замечательными новыми предсказаниями, которые физики делали о свойствах материалов с отрицательным показателем преломления, вызвали волну интереса среди других исследователей. Когда Веселаго высказал свою гипотезу, метаматериалов еще не было, и специалисты не стали тщательно исследовать феномен отрицательного преломления. Теперь они стали уделять ей гораздо больше внимания. Скептики спрашивали, не нарушают ли материалы с отрицательным показателем преломления фундаментальные законы физики. Если бы это оказалось так, то вся программа исследований была бы поставлена под сомнение.
Самые горячие споры вызвал вопрос о скорости волны в сложном материале. Свет распространяется в вакууме с максимальной скоростью c = 300 тыс. км/с. Скорость света в материале меньше: v = c/n. Но что будет, если n отрицателен? Простая интерпретация формулы для скорости света показывает, что свет распространяется в обратном направлении.

В более полном ответе учитывается, что волна имеет две скорости: фазовую и групповую. Чтобы понять их смысл, представьте себе импульс света, движущийся в среде. Он будет выглядеть примерно так: амплитуда волны возрастает до максимума в центре импульса, а затем снова спадает. Фазовая скорость — это скорость отдельных всплесков, а групповая скорость — это скорость, с которой движется огибающая импульса. Они не обязательно должны быть одинаковыми.
Веселаго обнаружил, что в материале с отрицательным показателем преломления групповая и фазовая скорости имеют противоположные направления: отдельные максимумы и минимумы движутся назад, тогда как весь импульс перемещается вперед. Интересно рассмотреть, как будет себя вести непрерывный пучок света от источника (например, прожектора), погруженного в материал с отрицательным показателем преломления. Если бы можно было наблюдать отдельные колебания световой волны, то мы бы увидели, что они появляются на объекте, освещенном лучом, движутся назад и, в конечном счете, исчезают в прожекторе. Однако энергия светового пучка движется вперед, удаляясь от источника света. Именно в этом направлении фактически распространяется луч, несмотря на удивительное обратное движение его отдельных колебаний.
Практически наблюдать отдельные колебания световой волны трудно, а форма импульса может быть очень сложной, так что физики, чтобы показать различие между фазовой и групповой скоростями, часто используют хитрый трюк. Когда две волны с немного разными длинами движутся в одном направлении, они интерферируют, и возникает картина биений, максимумы которых перемещаются с групповой скоростью.
Применив этот прием к эксперименту UCSD по преломлению в 2002 г., Прашант Валанджу (Prashant М. Valanju) и его коллеги из Техасского университета в Остине наблюдали нечто любопытное. Преломляясь на границе сред с отрицательным и положительным показателем преломления, две волны с разными длинами отклонялись на немного разные углы. Картина биений получалась не такой, как следовало бы для лучей при отрицательном преломлении, а такой, какой должна быть при положительном преломлении. Сопоставляя картину биений с групповой скоростью, исследователи из Техаса заключили, что любая физически осуществимая волна должна испытывать положительное преломление. И хотя материал с отрицательным показателем преломления мог бы существовать, отрицательное преломление получить невозможно.
Как же тогда объяснить результаты экспериментов в UCSD? Валанджу и многие другие исследователи приписывали наблюдаемое отрицательное преломление другим явлениям. Быть может, образец поглощал так много энергии, что волны выходили наружу только с узкой стороны призмы, имитируя отрицательное преломление? В конце концов, метаматериал UCSD действительно сильно поглощает излучение, а измерения проводились вблизи призмы. Поэтому гипотеза о поглощении выглядит вполне правдоподобно.
Полученные выводы вызвали большое беспокойство: они могли обесценить не только эксперименты UCSD, но и весь круг явлений, предсказанных Веселаго. Однако после некоторых размышлений мы поняли, что полагаться на картину биений как на показатель групповой скорости нельзя: для двух волн, движущихся в разных направлениях, интерференционная картина никак не связана с групповой скоростью.
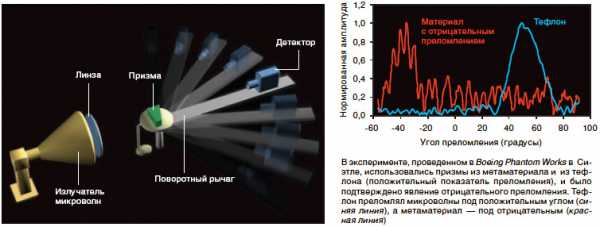
По мере того, как доводы критиков начали рушиться, появилось еще одно экспериментальное подтверждение отрицательного преломления. Группа Минаса Таниэлиана (Minas Tanielian) из компании Boeing Phantom Works в Сиэтле повторила эксперимент UCSD с призмой из метаматериала с очень низким поглощением. Кроме того, датчик был расположен намного дальше от призмы, чтобы поглощение в метаматериале нельзя было перепутать с отрицательным преломлением луча. Высочайшее качество новых данных положило конец сомнениям в существовании отрицательного преломления.
Продолжение следует
Когда дым сражения рассеялся, мы начали понимать, что замечательная история, которую рассказал Веселаго, была не последним словом о материалах с отрицательным показателем преломления. Советский ученый пользовался методом геометрического построения световых лучей с учетом отражения и преломления на границах различных материалов. Этот мощный прием помогает понять, например, почему объекты в бассейне кажутся нам ближе к поверхности, чем на самом деле, и почему наполовину погруженный в жидкость карандаш представляется изогнутым. Все дело в том, что коэффициент преломления воды (n = 1,3) больше, чем у воздуха, и лучи света на границе между воздухом и водой преломляются. Показатель преломления приблизительно равен отношению реальной глубины к кажущейся.
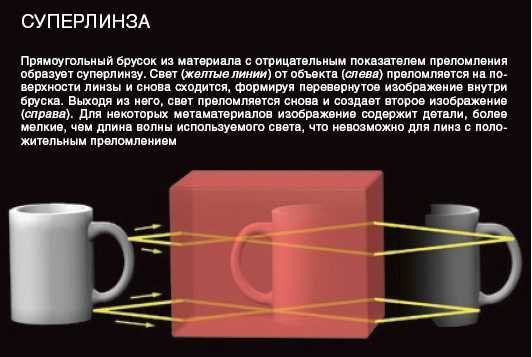
Веселаго использовал построение хода лучей, чтобы предсказать, что брус из материала с отрицательным показателем преломления n = −1 должен действовать как линза с уникальными свойствами. Большинство из нас знакомо с линзами из материалов с положительным преломлением — в камерах, лупах, микроскопах и телескопах. Они имеют фокусное расстояние, и место, где формируется изображение, зависит от сочетания фокусного расстояния и расстояния между объектом и линзой. Изображения обычно отличаются по размеру от объекта, и линзы работают лучше всего для объектов, лежащих на оси, проходящей через линзу. Линза Веселаго работает совершенно иначе, чем обычные: ее работа намного проще, она действует только на объекты, расположенные рядом с ней, и переносит все оптическое поле с одной стороны линзы на другую.
Линза Веселаго столь необычна, что Джону Пендри (John B. Pendry) пришлось задаться вопросом: насколько совершенно она может работать? И в частности, каково может быть предельное разрешение линзы Веселаго? Оптические элементы с положительным показателем преломления ограничены дифракционным пределом — они могут разрешать детали, размер которых равен или больше длины волны света, отраженного от объекта. Дифракция накладывает окончательный предел на все системы создания изображения, наподобие наименьшего объекта, который можно рассмотреть в микроскоп, или наименьшего расстояния между двумя звездами, которое может разрешить телескоп. Дифракция определяет также наименьшую деталь, которую можно создать в процессе оптической литографии при производстве микрочипов (микросхем). Подобным же образом дифракция ограничивает количество информации, которую можно сохранить или прочитать на оптическом цифровом видеодиске (DVD). Способ обойти дифракционный предел мог бы решительным образом изменить технологии, позволив оптической литографии проникнуть в диапазон наноразмеров и, возможно, в сотни раз увеличить количество данных, сохраняемых на оптических дисках.
Чтобы определить, действительно ли оптика с отрицательным преломлением могла бы превзойти обычную («положительную») оптику, нам следует продвинуться дальше, чем просто рассмотреть ход лучей. Прежний подход пренебрегает дифракцией, и таким образом его нельзя использовать, чтобы предсказать разрешение линз с отрицательным преломлением. Чтобы включить в рассмотрение дифракцию, нам пришлось использовать более точное описание электромагнитного поля.
Суперлинза
При более точном описании электромагнитные волны любых источников — излучающих атомов, радиоантенн или пучка света, — после прохождения через маленькое отверстие создают два разных типа полей: дальнее и ближнее поле. Дальнее поле, на что указывает его название, наблюдается вдали от объекта и улавливается линзой, формируя изображение объекта. К сожалению, это изображение содержит только грубую картину объекта, в которой дифракция ограничивает разрешение величиной длины волны. Ближнее поле содержит все мельчайшие детали объекта, но его интенсивность быстро падает с расстоянием. Линзы с положительным преломлением не дают никакого шанса на перехват чрезвычайно слабого ближнего поля и передачу его данных в изображение. Однако это не так для линз с отрицательным преломлением.
Подробно исследовав, как ближние и дальние поля источника взаимодействуют с линзой Веселаго, Пендри в 2000 г. к всеобщему удивлению пришел к заключению, что линза, в принципе, может фокусировать как ближние, так и дальние поля. Если бы это ошеломляющее предсказание оказалось верным, это означало бы, что линза Веселаго, в отличие от всей другой известной оптики, не подчиняется дифракционному пределу. Поэтому плоскую структуру с отрицательным преломлением назвали суперлинзой.
При последующем анализе мы и другие исследователи нашли, что разрешение суперлинзы ограничено качеством ее материала с отрицательным преломлением. Для лучшей работы требуется не только чтобы показатель преломления n был равен −1, но также чтобы ε и μ оба были равны −1. Линза, у которой эти условия не выполняются, имеет резко ухудшенное разрешение. Одновременное выполнение этих условий — очень серьезное требование. Но в 2004 г. Энтони Грбич (Anthony Grbic) и Джордж Элефтериадес (George V. Eleftheriades) из Университета Торонто экспериментально показали, что метаматериал, построенный так, чтобы иметь ε =−1, и μ =−1 в диапазоне радиочастот, действительно может разрешить объекты в масштабе меньшем, чем дифракционный предел. Их результат доказал, что суперлинзу можно построить, но можно ли ее создать для еще более коротких — оптических длин волн?
Сложность масштабирования метаматериалов в область оптических длин волн имеет две стороны. Прежде всего, металлические проводящие элементы, образующие микросхемы метаматериала, типа проводников и колец с разрезом, нужно уменьшить до масштаба нанометров, чтобы они были меньше, чем длина волны видимого света (400–700 нм). Во вторых, короткие длины волн соответствуют более высоким частотам, а металлы на таких частотах обладают худшей проводимостью, подавляя таким образом резонансы, на которых основаны свойства метаматериалов. В 2005 г. Костас Соуколис (Costas Soukoulis) из университета штата Айова и Мартин Вегенер (Martin Wegener) из университета Карлсруэ в Германии экспериментально продемонстрировали, что можно сделать кольца с разрезами, которые работают при длинах волн всего 1,5 мкм. Несмотря на то, что при столь малых длинах волн резонанс на магнитной компоненте поля становится весьма слабым, с такими элементами все еще можно сформировать интересные метаматериалы.
Но мы пока еще не можем изготовить материал, который при длинах волн видимого света приводит к μ =−1. К счастью, возможен компромисс. Когда расстояние между объектом и изображением намного меньше, чем длина волны, необходимо выполнить только условие ε =−1, а значением μ можно пренебречь. Как раз в прошлом году группа Ричарда Блэйки (Richard Blaikie) из университета Кентербери в Новой Зеландии и группа Ксианга Джанга (Xiang Zhang) из Калифорнийского университета в Беркли, следуя этим предписаниям, независимо продемонстрировали сверхразрешение в оптической системе. При оптических длинах волн собственные резонансы металла могут приводить к отрицательной диэлектрической постоянной (ε). Поэтому очень тонкий слой металла при длине волны, где ε =−1, может действовать как суперлинза. И Блэйки, и Джанг использовали слой серебра толщиной около 40 нм, чтобы получить изображение пучков света с длиной волны 365 нм, испускаемых сформированными отверстиями, меньшими, чем длина волны света. И хотя серебряная пленка далека от идеальной линзы, серебряная суперлинза существенно улучшала разрешение изображения, доказывая правильность основного принципа работы суперлинзы.
Взгляд в будущее
Демонстрация работы суперлинзы — лишь последнее из многих предсказаний свойств материалов с отрицательным преломлением, которые предстоит реализовать, а это признак быстрого прогресса, происходящего в этой все расширяющейся области. Возможность отрицательного преломления заставила физиков пересмотреть практически всю область электромагнетизма. И когда этот круг идей будет полностью понят, основные оптические явления, такие как преломление и дифракционный предел разрешения, придется пересмотреть с учетом новых неожиданных поворотов, связанных с материалами, дающими отрицательное преломление.
Волшебство метаматериалов и магию отрицательного преломления все-таки необходимо «конвертировать» в прикладную технологию. Такой шаг потребует совершенствования конструкции метаматериалов и производства их по разумной цене. Сейчас в этой области действует множество исследовательских групп, энергично разрабатывающих способы решения проблемы.
Литература:
1. Reversing Light with Negative Refraction. John B. Pendry and David R. Smith // Physics Today. Vol. 57. No. 6. P. 37–43. June 2004.
2. Negative-Refraction Metamaterials: Fundamental Principles and Applications. G. V. Eleftheriades and K. Balmain. Wiley-IEEE Press, 2005.
Дополнительная информация о метаматериалах и отрицательном преломлении имеется на сайтах:
elementy.ru
2. Метаматериалы
излучение на которых будет полностью отражаться от фотонного кристалла при любых углах падения в этой плоскости. В таком плане двумерный случай существенно отличается от одномерного. Фотонные запрещенные зоны для двумерных кристаллов более полные, чем для одномерных, но все же не до конца. Не будем забывать, что мы условились о падении света только в одной плоскости. Если изменить плоскость падения и пустить
свет, например, вдоль плоскости β (рис.1.13(б)), то те волны, которым было запрещено попасть внутрь кристалла, теперь смогут легко это сделать, зато под запрет попадут волны с другими частотами.
2.1.Отрицательное преломление
Метаматериалами, или, точнее, электромагнитными метаматериалами, называются вещества, обнаруживающие необычные электромагнитные свойства [3]. Греческая приставка мета означает выход за границу чего-либо. Таким образом, метаматериал — это вещество или искусственная структура, электромагнитные свойства которой выходят за рамки обычных представлений. Сам термин метаматериалы был предложен руководителем Центра электромагнитных материалов и устройств в Остине (штат Техас, США) Роджером Уолсером в 2000 году.
Примером метаматериала является изотропная среда с отрицательным показателем преломления. Такое вещество иногда называют средой Веселого по фамилии отечественного физика В.Г. Веселаго, исследовавшего электромагнитные свойства данной среды [4]. Рассмотрим простейший случай преломления света на плоской границе
раздела двух сред. Пусть угол падения электромагнитной волны равен | , а | ||||||
угол преломления равен | (рис. | 2.1). Связь между этими углами дается | |||||
известным законом Снеллиуса: |
|
|
|
| |||
|
|
|
| = | 1 , |
|
|
|
|
| (2.1) | ||||
|
|
|
| 2 |
|
| |
где |
| — коэффициенты преломления сред. В случае обычных | |||||
прозрачных | материалов | их | показатели преломления являются | ||||
| 1,2 |
|
|
|
|
|
|
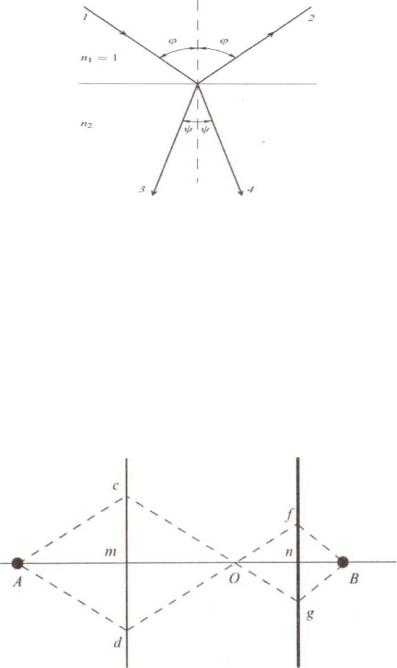
положительными величинами 1,2 | > 0 . Тогда преломленный | луч | (4) | ||||
отклоняется по другую сторону от нормали к границе раздела сред по сравнению с падающим лучом (1), как это видно на рис. 2.1.
Если же показатель преломления первой среды положителен, а второй среды отрицателен, то преломленный луч отклоняется в ту же сторону от нормали, что и падающий луч. Это соответствует изменению
23
знака угла преломления, вытекающему из равенства (2.1), если показатели преломления сред имеют разные знаки.
Преломление электромагнитной волны, изображенное на рис. 2.1 лучами 1—3, называется отрицательным преломлением, или аномальной
рефракцией.
Исторически впервые эффект отрицательного преломления электромагнитного излучения был рассмотрен советским физиком Л.И. Мандельштамом в 40-х годах XX века в одной из лекций, где был
представлен ход преломленного луча в среде с п < 0.
Рис. 2.1. Преломление и отражение света на границе раздела двух сред: лучи 1—4 — обычное преломление, лучи 1—3 — отрицательное преломление, лучи 1—2 — отражение
Отрицательное преломление используется в простом оптическом устройстве, предложенном отечественным физиком В.Г. Веселаго и получившем название линза Веселаго. Схематическое изображение линзы Веселаго представлено на рис. 2.2. Это устройство является плоскопараллельной пластиной, приготовленной из материала с отрицательным преломлением.
24
Рис. 2.2. Линза Веселаго
Если слева от пластины расположить источник света А на расстоянии, меньшем толщины пластины Ат < тп, то лучи от этого источника сойдутся справа от пластины в точке В. В этом легко убедиться с помощью простого геометрического построения и с учетом того, что при пересечении границ раздела cd и fg преломленные лучи отклоняются к оси АВ. Указанное построение= выполнено на рис. 2.2 для случая2 =, когда плоскопараллельная пла1 стина с показателем преломления — 1 помещена в вакуум 1, причем выполняется неравенство Ат < пт. Видно, что в этом случае геометрическая длина, пройденная лучом света от источника А в точку В по любому пути, вне пластины равна длине пути, пройденному светом в пластине:
| Ат + тВ = тп, Ас + gB = eg, Ad + fB = df. | (2.2) | |||
| Поскольку в рассматриваемом случае | 2 = −1 | , то из равенств (2.2) | ||
следует, что оптическая длина пути, |
|
|
| ||
∫ |
| пройденная светом из точки А в точку | |||
В, равна нулю. Напомним, что оптическая длина пути равна интегралу L = | |||||
| , где п — показатель преломления | вещества, dl — | дифференциал | ||
геометрической длины пути. Поскольку оптическая длина пути в рассматриваемом случае равна нулю для любой траектории распространения света, отвечающей закону Снеллиуса (2.1), то автоматически выполняется принцип Ферма, который формулируется в виде L = 0 и гласит, что свет распространяется по траекториям, на которых оптическая длина пути имеет экстремум.
Таким образом, с помощью линзы Веселаго можно получать изображение предметов, расположенных на расстоянии, меньшем толщины линзы, но нельзя получить изображение источника на большем расстоянии. В частности, линза Веселаго не фокусирует в точку плоскопараллельный пучок света и поэтому не является линзой в строгом смысле этого слова. Тем не менее, данное оптическое устройство позволяет получить идеальное изображение предмета в том смысле, что точечный предмет оно переводит в точечное изображение. Это характеристическое свойство линзы Веселаго связано с тем, что в основе формирования изображения лежит отрицательное преломление электромагнитного излучения, а не его дифракция.
25
studfiles.net
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОПТИЧЕСКОЙ ЛИНЗЫ ОТРИЦАТЕЛЬНОГО ПРЕЛОМЛЕНИЯ
Сеитбек Даулет Эсмухамедулы
студент 2 курса, кафедра математического и компьютерного моделирования, ВКГТУ, г. Усть—Каменогорск
Е-mail: [email protected]
Гарифуллина Жадыра Рифхатовна
научный руководитель, преподаватель, магистрант тех. наук, кафедра информационные системы, ВКГТУ, г. Усть—Каменогорск
Оптика является одной из областей научного исследования, где эффективно применяется математическое и компьютерное моделирование. Результаты исследования в области оптики в форме оптических приборов, устройств, находятся в большом требовании в почти всех областях деятельности человека.
В научной литературе [6, c. 176; 7, c. 231; 8, c. 211; 9, c. 166; 10, c. 177] рассматриваются собирающие линзы из левого материала, имеющие форму плоскопараллельной пластинки. Но у такой линзы есть недостаток: она фокусирует в одну точку только те лучи, угол падения которых близок к нулю. Все остальные лучи, исходящие из источника, теряются.
Цель работы: найти форму собирающей линзы из материала с отрицательным показателем преломления такую, чтобы она фокусировала в одну точку все лучи, исходящие от точечного источника, при всех углах падения.
Задачи:
1. Изучение хода световых лучей при преломлении на границе обычного вещества и вещества с отрицательным показателем преломлением. Обобщение принципа Ферма для левых сред.
2. Численное моделирование формы поверхности линзы из левого материала, фокусирующей в одну точку все лучи, исходящие от точечного источника.
3. Изучение свойств изображений, полученных в линзе из левого материала.
Изготовление линзы такой специальной формы открывает новые перспективы для развития технологий, что подтверждает актуальность и практическую значимость исследования.
В работе для построения формы линзы из материала с отрицательным показателем преломления, фокусирующей в одну точку все лучи точечного источника, применялся метод численного моделирования с применением языка программирования ФОРТРАН. Результаты обобщались и систематизировались. Для исследования хода лучей в «левых средах» применялись математический анализ и аналитическая геометрия.
Основные результаты:
1. Построен алгоритм и написана программа (на фортране), с помощью которых можно вычислять формы линз из левого материала, собирающей в одну точку все лучи, исходящие от точечного источника, при любом показателе преломления. Пример такой линзы показан на рис. 1.
Рисунок 1. Построение изображения в линзе из вещества с отрицательным показателем преломления п=–3
А — источник, Е — изображение. Синяя линия — поверхность линзы
3. Изучены свойства изображения и оптические свойства поверхности линзы из вещества с отрицательным показателем преломления.
4. В ходе исследования изучен ход лучей при преломлении на границе левых сред и обобщен принцип Ферма.
Все наши результаты новые и могут применяться на практике.
Ключевые слова: Принцип Ферма, суперлинзы, вещества с отрицательным показателем преломления, численное моделирование и язык программирования ФОРТРАН.
ВВЕДЕНИЕ
Оптика — один из старейших разделов физики — переживает в наши дни настоящее возрождение. В последние годы получены материалы со столь необычными оптическими свойствами, что свет в них может замедлиться в триллионы раз, в то время как скорость света в природных материалах замедляется максимум в два с половиной раза. Публикуются даже работы, описывающие принцип создания плаща-невидимки [4].
Поведение луча света зависит от среды, в которой он распространяется. Сейчас уже созданы искусственные среды с отрицательным показателем преломления, в которых свет преломлялся «в неправильную сторону». Поведение света в таких средах предсказал в 1960-е годы советский физик В.Г. Веселаго [1, с. 439].
Явление отрицательного преломления открывает замечательные перспективы для развития технологий. В частности, одной из главных целей исследователей является создание суперлинзы, которая бы фокусировала свет в область размером меньше, чем длина волны света, т. е. лучше, чем это в принципе способны сделать обычные линзы.
Для микроволнового излучения определенной частоты фотонный кристалл, используемый в этом эксперименте, выглядел как среда с отрицательным показателем преломления. Поместив такую пластинку перед источником излучения и просканировав поле позади нее, исследователи убедились, что она действительно фокусирует расходящееся излучение.
Этот впечатляющий эксперимент, демонстрирующий сверхвысокое разрешение линзы, заключался в следующем. Два точечных источника, расположенных на расстоянии 10 мм друг от друга, испускали микроволновое излучение с длиной волны 18 мм. В случае «обычной» линзы изображения от столь близких источников попросту слились бы в одно пятно. Новая же линза выдала изображение двух отдельных четко различимых пятнышек размером около 5 мм. Авторы работы выражают уверенность в том, что усовершенствование их методики в скором времени еще сильнее улучшит свойства суперлинз.
В другой недавней статье американские физики сообщают о создании нового метаматериала, обладающего отрицательным коэффициентом преломления в ближнем инфракрасном диапазоне. Отличие этой работы от предыдущих состоит в том, что типичный размер неоднородностей в этой структуре составляет сотни нанометров, что существенно меньше длины волны инфракрасного света. Из-за этого излучение «чувствует себя» не в решетке (фотонном кристалле), а в почти однородной среде, словно внутри материала совершенно нового типа (именно это и подразумевает слово «метаматериал»). Изюминкой этой работы является эффективная технология выращивания образца достаточно большого размера и микроскопической толщины.
Такие суперлинзы должны привести к прорыву в радио — и оптоэлектронике, оптических устройствах хранения данных, материаловедении, поэтому изучение возможностей, предоставляемых метаматериалами, является актуальной задачей.
Вещества, которые обладают отрицательным показателем преломления, были названы в [9, c. 166; 10, c. 177] “left-handed materials” («левые среды»). В русскоязычной научной литературе также применяется термин, предложенный академиком В.Г. Веселаго, «вещества с отрицательным преломлением» (сокращенно ВОП). Соответственно обычные вещества называют «вещества с положительным преломлением» (или ВПП) [2, c. 129].
В научной литературе рассматриваются собирающие линзы из левого материала, имеющие форму плоскопараллельной пластинки. Но у такой линзы есть недостаток: она фокусирует в одну точку только те лучи, угол падения которых близок к нулю. Все остальные лучи, исходящие из источника, теряются.
Весь набор законов геометрической оптики выводится из принципа экстремума. Но, очевидно, что для новых материалов с отрицательным показателем преломления принцип Ферма, а также основные законы геометрической оптики нуждаются в уточнении.
ЧАСТЬ 1
ОПТИЧЕСКИЕ СВОЙСТВА ЛЕВЫХ СРЕД. ПРИНЦИП ФЕРМА ДЛЯ СРЕД С ОТРИЦАТЕЛЬНЫМ ПОКАЗАТЕЛЕМ ПРЕЛОМЛЕНИЯ
Среды обладают дисперсионными свойствами — волны разных частот распространяются в средах с различными фазовыми скоростями. Это явление называют дисперсией.При распространении монохроматической волны в среде с дисперсией никаких особых явлений не наблюдается; волна распространяется со своей фазовой скоростью, которая определяется значением показателя преломления на частоте волны. Но если в диспергирующей среде одновременно распространяется группа волн разных частот, то по мере распространения волн возникают фазовые сдвиги между отдельными спектральными компонентами. При этом происходит деформация формы суммарного процесса. Если на входе в диспергирующую среду возмущение имело вид импульса (волнового пакета) определенной формы, то после прохождения некоторого слоя форма импульса может существенно измениться.
Рисунок 2. Преломление света на границе двух сред.
Рисунок 3. Прохождение света через плоскую границу двух сред с показателями преломления п1 и п2
Рассмотрим закон, точнее — принцип — принцип Ферма.
Формулировка этого принципа в литературе встречается в разных вариантах. Например:
Луч света всегда распространяется в пространстве между двумя точками по тому пути, вдоль которого время его прохождения меньше, чем вдоль любого другого пути, соединяющего эти точки [5, c. 144].
Проиллюстрируем это на рис. 3, на котором изображены возможные пути луча, пересекающего плоскую поверхность, разделяющую две среды, имеющие показатели преломления п1 и п2.
В том случае, если п1 и п2 оба положительны (т. е. обе среды состоят из ВПП), луч идет по пути АО1В , а углы и удовлетворяют закону Снеллиуса:
.
Оптическая длина этого пути равна:
L=n1· АО1+n2·О1В.
Далее мы докажем, что закон Снеллиуса будет выполняться, если производная оптического пути L будет равна нулю. При этом сама величина L для реального пути будет минимальна и положительна.
Если п1 и п2 оба отрицательны (т. е. обе среды состоят из ВОП), ход лучей будет такой же, как и в предыдущем случае, но с одним важным отличием. В первом случае волновой вектор в обоих средах направлен вдоль лучей, т. е. от А к В, а во втором случае волновой вектор направлен против направления лучей, т. е. от В к А. При этом оптическая длина L оказывается отрицательной и для реального пути АО1В будет максимальной.
Оба случая соответствуют положительному значению величины относительного показателя преломления второй среды относительно первой.
Положение существенно изменится, если величина будет отрицательной. Это произойдет, если по одну сторону границы находится ВПП, а по другую — ВОП. Тогда луч из первой среды во вторую пойдет по пути АО3В, для углов и по-прежнему будет выполняться закон Снеллиуса, но с отрицательным значением угла .
Подчеркнем, что в этом случае реальный путь от точки А до В не является самым коротким по времени распространения. Например, виртуальный путь АО2В свет пройдет за меньшее время, а путь АО4В — за большее время по сравнению со временем прохождения светом реального пути АО3В.
Поэтому формулировка принципа Ферма через время распространения не является корректной.
Для реального пути распространения света будет выполнено условие экстремума оптической длины пути с учетом знака относительного показателя преломления. Рассмотрим доказательство этого факта (рис. 4) для преломления лучей на границе ВПП и ВОП. Пусть сверху снова расположен материал с показателем преломления , а снизу — материал с показателем преломления . Пусть точка А — источник света, точка С — произвольная точка на границе веществ, точка В — некоторая точка преломленного луча.
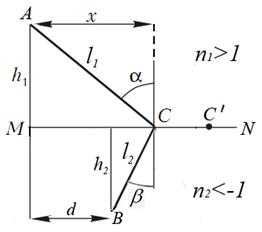
Рисунок 4. Преломления лучей на границе ВПП и ВОП
Оптическая длина пути АСВ равна:
.
Или: .
Найдем первую производную оптической длины пути по переменной х:
.
Очевидно, что производная равна нулю в том и только в том случае, если выполняется закон Снеллиуса:
=0
с учетом знака показателя преломления .
Отметим, что когда относительный показатель преломления двух сред отрицательный, нельзя заранее утверждать, что экстремум длины оптического пути будет обязательно максимумом или минимумом. Тип экстремума зависит от геометрии конкретной задачи и конкретных величин п1 и п2.
В этом можно убедиться, если найти вторую производную: если она положительна, то имеет место минимум, а если вторая производная отрицательна — то у функции имеется максимум. Найдем вторую производную от длины оптического пути:
.
Последнее выражение может принимать как положительные, так и отрицательные значения или равняться нулю, в зависимости от взаимного расположения точек А, В и С.
Все сказанное позволяет обобщить принцип Ферма для сред с отрицательным показателем преломления.
Мы предлагаем записать принцип Ферма через экстремум длины оптического пути:
Реальный путь распространения света в среде соответствует локальному экстремуму длины оптического пути.
Слово «локальный» указывает на тот факт, что в задаче могут быть несколько возможных оптических путей. Отметим, что в такой формулировке принцип Ферма справедлив и для материалов с положительным показателем преломления.
Длина оптического пути L между точками А и В в общем случае, когда коэффициент преломления меняется от точки к точке, задается интегралом:
.
Т. к. величина п, входящая в эту формулу, может быть и отрицательной, то и длина оптического пути может иметь любой знак и любую величину. Если свет проходит через ВОП, то эта длина будет отрицательной.
ЧАСТЬ 2
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ФОРМЫ ПОВЕРХНОСТИ ЛИНЗЫ ИЗ ЛЕВОГО МАТЕРИАЛА
В некоторых случаях длина оптического пути может равняться нулю. Именно такова длина оптического пути между объектом и его изображением в линзе, сделанной из ВОП и изображенной на рис. 5. Здесь изображена плоскопараллельная пластинка из левого материала, которая действует как собирающая линза.
Очевидно, что расстояние от источника до его изображения равно удвоенной толщине пластинки. Если источник расположен на расстоянии от пластинки, превышающем ее толщину, то изображение получится мнимое.
Рассмотрим формирование изображения при преломлении лучей на границе ВПП и ВОП. (рис. 6) Пусть сверху расположен материал с показателем преломления , а снизу — материал с показателем преломления . Пусть точка А — источник света, точка С — произвольная точка на границе веществ, точка В — лежит на продолжении перпендикуляра, опущенного из А на границу раздела.
Рисунок 5. Прохождение света от объекта А к изображению В сквозь плоскопараллельную линзу, изготовленную из ВОП с коэффициентом преломления .
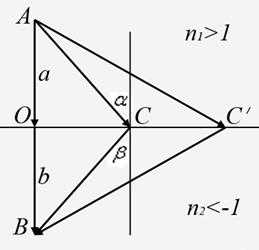
Рисунок 6. Формирование изображения при преломлении лучей на границе ВПП и ВОП.
Обозначим расстояние от источника до границы , расстояние от границы до изображения .
Из закона Снеллиуса:
следует, что:
, или .
Тогда, , где относительный показатель преломления равен по модулю: . Найдем отношение:
,
. (1)
Чаще всего теоретически рассматривают ВОП такие, что , тогда из формулы (1) следует, что , все лучи от точечного источника А собираются в точке В, расположенной симметрично относительно границы раздела сред.
Эту ситуацию иллюстрирует рис 5, на котором в качестве линзы используется плоскопараллельная пластинка из ВОП. Линза из идеальной левой среды (ВОП), у которой ε = μ = –1, создает действительное изображение всех точек предмета, расположенных в слое, ширина которого равна толщине пластины (рис 7).

Рисунок 7. Объемное изображение, получаемое из плоскопараллельной пластины из левого материала.
В работе [8, c. 211] доказано, что разрешающая способность такой плоской линзы превышает предел, обусловленный волновой природой света.
Английский физик Джон Пендри показал, что такая «суперлинза» будет фокусировать свет в точку, размером в сотни раз меньшую, чем длина волны падающего света. В то же время в «правой» оптике, как известно, нельзя получить изображение такого же качества, что и исходное, прошедшее через обычную линзу, т. к. нельзя сфокусировать луч в точку, размерами меньше длины волны (умноженной на константу). Для «левой» оптики такого ограничения не существует!
Как следует из (1), для достаточно малых углов все лучи, исходящие из точки А, приблизительно пересекаются в точке В для любых . Т. е. и в случае произвольного отрицательного относительного показателя преломления граница раздела правой и левой сред может служить линзой, но только для малых углов падения.
Если угол мал, то , , поэтому из (1) следует, что:
. (2)
Действительный график функции расстояния изображения от границы как функции угла падения луча на границу раздела сред для значения представлении на рисунке 8. При этом расстояния источника мы положили равным :
.
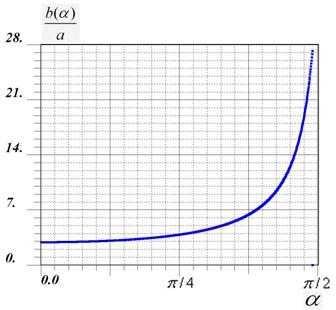
Рисунок 8. Действительный график функции расстояния изображения

Рисунок 9. Отсутствие изображения, при значении функции
Как видно из графика, при значение функции . Изображение при этом не существует, что иллюстрирует рис 9:
Для небольших углов падения (приблизительно ) преломленные лучи практически пересекаются в одной точке. При увеличении угла падения расстояние до пересечения преломленнго луча с прямой АВ резко возрастает, и изображения нет.
Чтобы получить изображение для отрицательного значения коэффициента преломления можно «искривить» поверхность раздела сред на некоторый угол, свой для каждого угла падения. Таким образом, плоская пластинка превратится в некоторую «закругленную» поверхность строго определенной формы.
В нашей работе с помощью численного моделирования решена задача построения такой поверхности раздела сред, для которой все лучи, исходящие из точки А, после преломления пересекутся в одной точке (рис. 10). При этом предполагается, что относительный показатель преломления сред . В соответствии с формулой (2) расстояние до изображения В равно: или
. (3)
Здесь АО — перпендикуляр к поверхности, ограниченной отрезком ОС1, угол падения , — перпендикуляр к поверхности раздела сред в точке падения луча.
Найдем угол , на который нужно повернуть поверхность раздела, чтобы преломленный луч пошел по пути .

Рисунок 10. Нахождение угла
На рисунке 10 обозначено: — положение элемента поверхности после поворота на угол , отрезок — нормаль к этой новой поверхности в точке .
Из треугольников АОС1 и ВОС1 получим:
, ,
откуда с учетом (3) следует, что:
. (4)
Закон преломления Снеллиуса:
, (5)
где угол преломления есть .
Систему уравнений (4), (5) для неизвестных величин и мы решали численно следующим образом.
1. Зная координаты точек и О, с помощью скалярного произведения векторов определяем угол :
2.
3. Рассматриваем последовательные значения угла такие: , , — достаточно малый угол (в нашей программе он равнялся ). Для каждого из уравнения (5) находим угол :
. (6)
4. В соответствии с уравнением (4) проверяем равенство нулю выражения:
. (7)
Если выражение в левой части (7) дает ноль с некоторой заданной точностью (в нашей программе она составила ), то угол принимается за искомый угол поворота поверхности в точке .
Расчеты показали, что выражение в левой части (7) монотонно возрастает: пока угол мал, оно отрицательно, начиная с некоторого значения это выражение становится положительным. Уменьшая интервал, в котором заключен корень уравнения (7), можно определить угол поворота поверхности с любой наперед заданной точностью.
ЗАКЛЮЧЕНИЕ
Изучая ВОП, мы показали, что обычная формулировка принципа Ферма (через время прохождения луча от источника до изображения) не применима для левых сред. Мы предложили и обосновали обобщенную формулировку этого принципа, верную для любых сред (и правых, и левых): Реальный путь распространения света в среде соответствует локальному экстремуму длины оптического пути.
Теоретически обычно рассматривают левые вещества с относительным показателем преломления , т. к. это наиболее простой случай, позволяющий изучить основные особенности плоскопараллельной пластинки, выполняющей роль линзы.
Практически же изготавливаются метаматериалы с показателем , для которых до сих пор не были найдены и не объяснены: оптимальная форма линзы, ее свойства, а также свойства получаемого с ее помощью изображения.
В нашей работе восполняется этот пробел.
В ходе численных экспериментов и программирования на языке FORTRAN мы нашли такую форму линзы из левого материала, которая бы могла давать четкое изображение при значении относительного показателя преломления .
Мы установили свойства этого изображения.
Список литературы:
1.Блиох К.Ю., Блиох Ю.П. Что такое левые среды и чем они интересны? УФН, т. 174, 2004 — 439 с.
2.Веселаго В.Г. УФН 172 (2002) — 129 c.
3.Жувикин Г. Лабиринты фотонных кристаллов. — Журнал «Компьютера» 2001, № 30 — 231 c.
4.Иванова И. Материалы с сайта — [Электронный ресурс] — Режим доступа — URL: http://elementy.ru/news/430422 — октярбрь 2009 года.
5.Физический энциклопедический словарь. — М.: Сов Энциклопедия, 1983 — 144 c.
6.Fang N. et al., Science, 308, 534 (22 April 2005) — 176 c.
7.Lu Zh. Et al., Physical Review Letters, 95, 153901 (4 October 2005) — 231 c.
8.Pendry J.B. Negative refraction makes a perfect lens. Phys. Rev. Letters. 85 3966 (2000) — 211 c.
9.Shelby R.A., Smith D.R., Schultz S. Science 292—77 (2001) — 166 c.
10.Smith D.R. et al. Phys. Rev. Lett. 84—4184 (2000) — 177 c.
sibac.info
Электронную линзу Веселаго можно изготовить из графена
Профессора физики Ланкастерского университета (Lancaster University, Великобритания) Владимир Фалько (Vladimir I. Falko) и Вадим Чеянов и профессор физики Колумбийского университета (Columbia University, Нью-Йорк, США) Борис Альтшулер (Boris Altshuler), работающий также в американском подразделении Исследовательской лаборатории NEC (NEC Laboratories America), выполнили теоретические расчеты и компьютерное моделирование, из которых вытекает возможность использования графена в качестве материала для изготовления электронных линз. Эта работа 2 марта появилась в журнале Science.
Графен состоит в тесном родстве с обычным графитом. Как известно, графит сложен из атомов углерода, упакованных в параллельные листы, внутри которых они образуют плоские шестиугольники. Химические связи между соседними листами довольно слабы, поэтому от графита при трении легко отслаиваются чешуйки, что и позволяет делать из него карандашные грифели и использовать для смазки трущихся поверхностей. Недавно исследователи нашли способы получать изолированные одноатомные слои, сложенные из углеродных шестиугольников. Так был создан новый материал, который и назвали графеном.
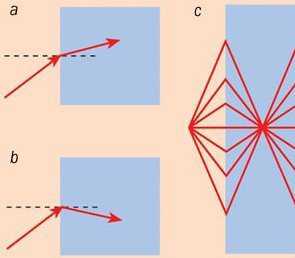
Графен — двумерная система с очень любопытными физическими свойствами. Эти свойства, в частности, проявляются при вхождении в графен пучка электронов. Согласно принципам квантовой механики, такой пучок, подобно световому импульсу, обладает как фазовой, так и групповой скоростью (первая определяет быстроту пространственного перемещения фазы волны, в данном случае электронной волновой функции, а вторая — скорость движения волнового пакета, которая в данном случае совпадает с классической скоростью электрона). В обычных веществах векторы обеих этих скоростей направлены в одну сторону. Однако симметрия электронных уровней графенового листа такова, что эти векторы при определенных условиях могут оказаться антипараллельными. В результате электронный луч при попадании в графен изменит не только величину угла с перпендикуляром к поверхности падения, как при нормальном преломлении, но и его знак. Такое преломление называется отрицательным (на рис. 1 нормальному преломлению соответствует рисунок a, отрицательному — рисунок b).
Сорок лет назад советский физик Виктор Веселаго теоретически продемонстрировал, что прямоугольный брусок (плоскопараллельная пластинка), изготовленный из материала с отрицательным преломлением, будет фокусировать свет подобно выпуклой стеклянной линзе (см. рис. 1 c). Через три с лишним десятка лет англичанин Джон Пендри доказал, что такая пластинка будет в состоянии превзойти самую лучшую линзу по точности фокусировки. Как известно, пределы возможностей обычной линзы или комбинации линз ограничены длиной световой волны. Линза Веселаго, как ее теперь называют, может, в принципе, фокусировать свет и на меньших расстояниях, если только изготовить ее достаточно тщательно.

Чеянов и его коллеги предложили реализовать электронный аналог линзы Веселаго в виде графенового листа, помещенного между плоскими электродами, на один из которых подается положительное напряжение, а на другой — отрицательное. Положительный электрод создает со своей стороны избыток электронов, отрицательный — недостаток. В результате со стороны анода возникает электронная проводимость, со стороны катода — дырочная. Граница между ними образует точный аналог электронно-дырочных переходов (p-n-переходов), которые возникают при легировании проводников — внесении в них донорных и акцепторных примесей (первые создают электронную проводимость, а вторые — дырочную). Расчеты показывают, что в области такого перехода создаются условия для того, чтобы пучок электронов испытал преломление с показателем, равным минус единице. Если со стороны анода расположить точечный источник электронов, то при прохождении через графеновый лист посылаемые им частицы сфокусируются в облачко очень малого размера.
Пока что это устройство существует только в теории. Сейчас его могли бы изготовить лишь в пяти-шести лабораториях, технические сложности слишком велики. Компьютерное моделирование показывает, что даже при сверхнизких температурах это устройство, в отличие от идеальной линзы Веселаго, всё же не сможет осуществлять фокусировку на дистанциях, уступающих квантовомеханической длине волны электронов. Однако характерные длины электронных волн неизмеримо меньше длин волн видимого света (например, длина волны электрона с энергией всего лишь в 1 электронвольт примерно равна одному нанометру), так что фокусировка всё равно может быть достаточно жесткой. Будет ли построена такая линза — это вопрос к экспериментаторам.
Источник: Vadim V. Cheianov, Vladimir Fal’ko, B. L. Altshuler. The Focusing of Electron Flow and a Veselago Lens in Graphene p-n Junctions // Science. 2007. V. 315. P. 1252–1255.
См. также:
1) Дж. Пендри, Д. Смит. В поисках суперлинзы («В мире науки» №11, 2006).
2) Суперлинзы становятся все реальнее, «Элементы», 20.10.2005.
Алексей Левин
elementy.ru
Суперлинза: дифракционный предел преодолен — CNews
Ученым удалось создать линзу с разрешением, превосходящим дифракционный предел. Новый инструмент, разрешение которого достигает одной шести длины волны, позволяет получать изображения объектов микронных размеров и сможет найти применение, в частности, в области нанотехнологий. Традиционный метод увеличения изображений основан на искривлении и последующем фокусировании отраженных от предмета световых лучей каким-либо материалом с положительным коэффициентом преломления. Еще недавно считалось, что предел возможному в оптике ставит фундаментальный рэлеевский критерий разрешения оптических приборов. Он заключается в том, что минимальный размер различимого объекта принципиально ограничен дифракцией излучения. Критерий Рэлея является одной из иллюстраций принципа неопределенности Гейзенберга, согласно которому любая попытка повысить степень локализации положения источника света приводит к возрастанию неопределенности импульса фотонов. При рассеянии фотонов в максимальном диапазоне углов точность определения положения не может быть больше, чем половина длины волны отраженного света.
Тем не менее, фундаментальное ограничение удалось преодолеть. Как сообщает PhysicsWeb, американским ученым удалось создать линзу с отрицательным коэффициентом преломления, которая имеет разрешение, равное одной шестой длины волны. Это стало возможным, поскольку законы обычной оптики применимы только для дальней зоны взаимодействия света с объектом – той, которая превышает длину волны падающего излучения. Однако эти ограничения не относятся к так называемому «ближнему световому полю». Оно локализовано на расстояниях много меньших, чем длина оптических волн и ассоциируется с областью, в которой существует излучение нерадиационной природы, амплитуда которого экспоненциально уменьшается по мере увеличения расстояния от границы раздела сред. Нанометровая оптика основана на регистрации в дальней зоне чрезвычайно слабых следов взаимодействия света с микрообъектом, находящимся в именно ближнем световом поле. Для этого используются экзотические материалы с отрицательным показателем преломления.
Потенциальная возможность изготовления искусственно структурированных на нанометровом уровне материалов, обладающих такими необычными свойствами, была предсказана российским физиком Виктором Веселаго еще в 1968 г, почти за сорок лет до реализации на практике. В апрельском выпуске журнала Science физик из университета штата Калифорния Сян Чжан (Xiang Zhang) описал изготовленную его группой «суперлинзу», представляющую собой серебряную пленку толщиной всего 35 нм, которая, как маска, накладывается на исследуемый объект. Слабые электромагнитные волны от ближнего поля объекта, достигающие поверхности пленки, возбуждают электрические осцилляции на субволновом уровне, известные специалистам как «поверхностные плазмоны», которые затем усиливаются и регистрируются. Такая линза впервые оказалась способной «разглядеть» объекты размером 40 нм, в то время как самые мощные оптические микроскопы имеют разрешающую способность около 400 нм (одна десятая размера красных кровяных телец).
#gallery#
«Наше изобретение имеет громадный потенциал, оно способно оказать революционное воздействие многие прикладные области как, например, биомедицину или оптическую литографию», — полагает г-н Чжан. Джон Пендри (John Pendry) из Имперского колледжа Лондона и Дэвид Смит (David Smith) из Графского университета в США, ведущие специалисты в этой области, согласны со своим коллегой и считают, что это поистине выдающее достижение современной прикладной науки.Другие материалы рубрики
www.cnews.ru
Шаг к суперлинзе: За пределы дифракции
Снять с полки микроскоп и рассмотреть под ним — не комара или волос, и даже не крупные растительные клетки — а частицы вируса в капле крови… Или — крупные молекулы? Просто дух захватывает от возможностей убить время в компании с таким инструментом. Не говоря уж о перспективах для науки и электроники. Не хватает главного: суперлинзы.

Прямое и обратное преломление
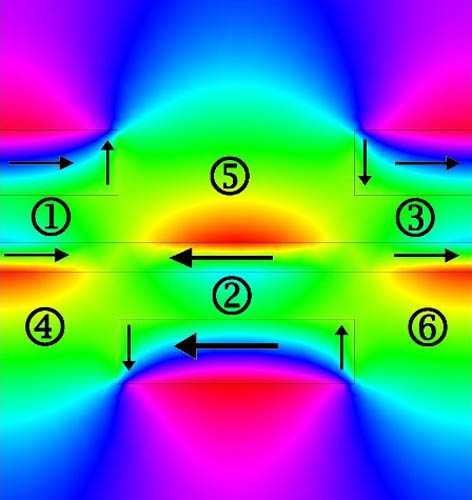
Идея метаматериала, предложенного Дарду Гани: цвета демонстрируют магнитные поля, создаваемые плазмонами; черные стрелки — направление тока в слоях металла; цифры соответствуют петлям электромагнитного поля, за счет которых возникает отрицательный коэффициент преломления
В самом деле, чтобы рассмотреть предмет, длина волны излучения, которое от него отражается, должна быть заметно меньше самого предмета. К дифракционному пределу оптических линз (около 200 нм) мы уже давно подошли, а для самых мелких объектов приходится использовать более коротковолновое излучение, вплоть до рентгеновских и гамма-лучей. Для того же, чтобы рассмотреть нанометровые объекты, нередко требуется сканирующий туннельный микроскоп, работающий на совершенно иных принципах. И в любом случае — требуется сложнейшая и дорогая аппаратура, тонкая подготовка образцов и прочее, и прочее, что делает наблюдения за микромиром уделом специалистов, а никак не увлеченных «популярных механиков».
Однако еще несколько десятилетий назад Виктор Веселаго теоретически обосновал создание искусственных метаматериалов с отрицательным показателем преломления: микроструктура этих метаматериалов особым образом взаимодействует с проходящим сквозь нее излучением. На поверхности ее свет преломляется, лучи его сходятся и снова расходятся, а выходя из метаматериала, преломляются еще раз. При особым образом подобранной структуре изображение, составленное вышедшими из метаматериала лучами, содержит детали даже более мелкие, чем длина их волны.
Сегодня уже делаются первые шаги по практическому получению таких метаматериалов. Они обещают нам целый ряд удивительных новинок, включая «плащ-невидимку» и — ту же «суперлинзу», очередной шаг к обретению которой сделали недавно ученые из группы американского профессора Дарду Гани (Durdu Guney). По расчетам авторов, их материал позволит получать посредством лучей оптического спектра изображения объектов размерами до 100 нм — в тысячи раз меньше толщины человеческого волоса.
Главный секрет здесь — в плазмонах, условных частицах, «квантах колебания» свободного электронного газа, которые возникают на поверхности тонких металлических пленок в метаматериале, содержащем также сферические наноструктуры. Возбужденные внешним электромагнитным полем, они улавливают падающие на них фотоны излучения и отражают их так, как если бы метаматериал обладал отрицательным показателем преломления. В отличие от аналогичных работ, метаматериал, предложенный Гани и его коллегами, демонстрирует отрицательное преломление для всего видимого спектра.
Когда же дело дойдет до практики, производство метаматериалов нужной структуры, по общему мнению экспертов, будет совсем недорогим. Ну а получившиеся суперлинзы можно использовать не только в науке, но и в литографии для получения сложных объектов совсем крошечных размеров, а также в электронике, в цифровых фотоаппаратах — и, конечно, в домашних микроскопах. «С суперлинзой ученым сможет стать каждый», — говорит Гани.
По пресс-релизу Michigan Technological University
www.popmech.ru
Как вычислить расстояние до объекта по фотографии
В связи с известным событием по всему интернету развернулись бурные дискуссии, участники которых обвиняют своих оппонентов то в незнании программы средней школы, то в непонимании того очевидного факта, что в военное время косинус угла может достигать четырёх.Не желая в эти дискуссии ввязываться, я лучше на наглядном примере покажу вам, как, имея на руках фотографию какого-либо известного объекта и немного вспомогательной информации, можно с большой точностью по совсем не сложным формулам рассчитать, на каком расстоянии этот объект находился от фотографа в момент съёмки. По возможности я постараюсь каждый шаг сопровождать иллюстрацией, расчётом или ссылкой на источник. Итак, приступим.

Как известно, простейший объектив для фотоаппарата можно сделать из одной двояковыпуклой линзы. Конечно, существуют фотоаппараты вообще без объектива (так называемые пинхол-камеры, предок которых — камера-обскура), но в данном случае они нам не слишком интересны. Для начала мы рассмотрим, как строится изображение в простейшем однолинзовом объективе, а затем я покажу, что те же методы хорошо подходят и для сложных объективов, сочетающих в себе более десятка последовательно расположенных линз.
Напомню вам схему хода лучей в тонкой линзе из школьного курса геометрической оптики:

На этой схеме d — расстояние от линзы до объекта, D — расстояние от линзы до изображения объекта (на матрице или плёнке), а f — фокусное расстояние линзы.
Формула тонкой линзы из того же курса связывает эти три расстояния:
Теперь ещё раз посмотрим на оптическую схему: h — это линейный размер объекта съёмки, а H — размер его уменьшенного изображения. Нетрудно заметить, что h = d tan α, а H = D tan α (это следует из свойств прямоугольного треугольника). Подставив эти величины в формулу тонкой линзы, увидим, что tan α сокращается, и в результате получим следующее уравнение:
«Неудобная» величина D ушла, а остальные мы знаем или можем легко вычислить. На основе этого уравнения получаем вот такую формулу расстояния до объекта: d = (f(H + h)) / H. Ну а теперь давайте проверим её на практике.
Вот фотография, которую я сделал из своего окна:

На ней запечатлён дом 1 по 3-му Дорожному проезду, что в Москве. Это 22-этажная башня серии И-700А.
Какую полезную информацию можно извлечь из данной фотографии? Напомню, для расчёта нам нужны неизвестные пока величины h, H и f. h — это реальная высота дома (в метрах). Сходу я её не нагуглил, зато выяснил вот что: высота потолков в этом доме — 2,64 м, а толщина перекрытий — 0,22 м. Наверняка при измерении высоты потолков не учитывалась толщина напольного покрытия. Точно она мне не известна, так что, немного округлив, примем высоту одного этажа равной 2,9 м. Хорошо видны 23 панели, таким образом, высота видимого участка составляет примерно 66,7 м. Запомним эту величину и приступим к анализу фотографии.
H — это размер изображения дома на матрице фотоаппарата. По фотографии мы можем подсчитать его в пикселях, но, как известно, размер пикселя — это всё равно что размер ангела: точных данных ни у кого нет. Но здесь нужно вспомнить, что конкретные физические размеры имеет матрица фотоаппарата. Лезем в поисковик и узнаём, что для камеры Nikon D90 размер матрицы составляет 2,36 × 1,58 см, а разрешение — 4288 × 2848 пикс. Наша фотография не была кадрирована или повёрнута, поэтому мы можем узнать точный линейный размер изображения дома на матрице, составив пропорцию. Но чтобы делать это не вручную, воспользуемся программой Adobe Photoshop, где есть масса полезных инструментов.
По умолчанию Photoshop, конечно, не знает, какого размера должна быть наша фотография, и указывает ей разрешение 300 пикс./дюйм, или 118,11 пикс./см:
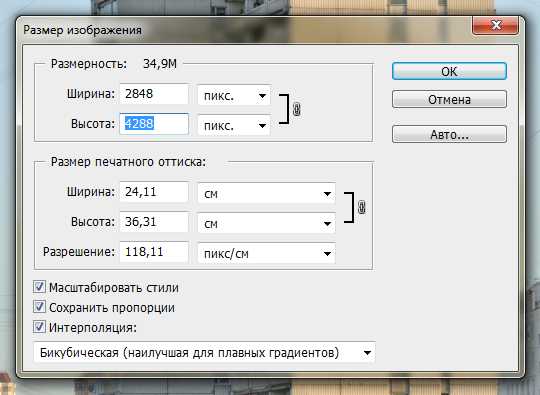
Но мы, зная физический размер матрицы и количество пикселей по длинной стороне снимка, делаем такой расчёт: 4288 / 2,36 (размер матрицы в сантиметрах), и получаем правильное разрешение — 1817 пикс./см. Вписываем его в соответствующее окошко и, чтобы не изменились реальные размеры фотографии, а лишь были пересчитаны её длина и ширина в см, указываем в верхних полях «100 проц»:
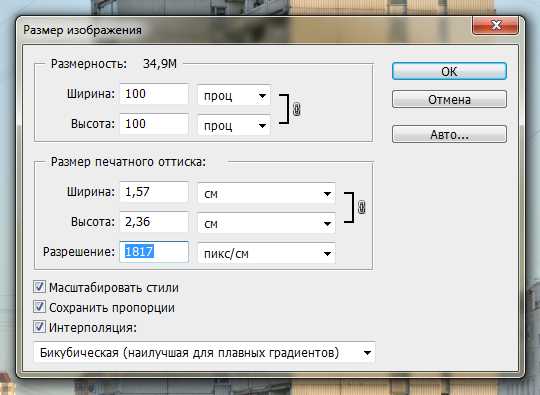
Как видите, при этом в поле «Размер печатного оттиска» появились уже известные нам размеры матрицы: 2,36 × 1,57 см. Точнее, в спецификации было указано 1,58 см, но это несущественная погрешность.
Теперь при помощи инструмента «Линейка» измерим высоту видимого участка дома (23 панели) на фотографии (смотрите в правый верхний угол):
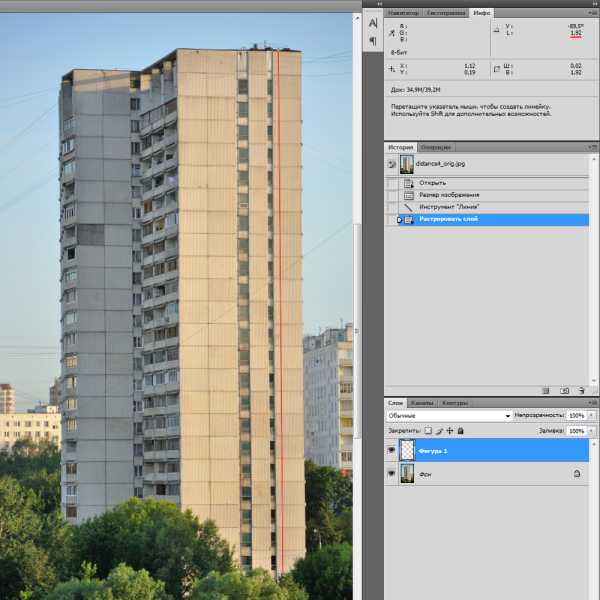
Получается, что высота изображения дома на матрице составляет 1,92 см, или 0,0192 м.
Осталось только выяснить фокусное расстояние, но для этого, к счастью, ничего считать не нужно: оно сразу прописывается при съёмке в метаданных фотографии (EXIF). Открываем их в фоторедакторе и видим:
Фокусное расстояние при съёмке составляло 105 мм, или 0,105 м, то есть я снимал дом с максимально возможным для этого объектива приближением.
Ну что ж, теперь у нас есть все данные для расчёта. Подставляем их в формулу d = (f(H + h)) / H и получаем: d = (0,105(0,0192 + 66,7)) / 0,0192 = 364,9 м. Внимательный читатель наверняка заметил, сколь ничтожно мала величина H в сравнении с h, поэтому нашу формулу смело можно упростить до вида d = fh / H. Для любых фотографий относительно крупных объектов, сделанных с расстояния больше 10 м, она будет давать практически тот же результат.
Ну а теперь самое интересное — нужно проверить, верна ли была использованная нами формула? Ведь в начале я говорил, что мы рассматриваем упрощённую конструкцию объектива, а не реальную. Может быть, наши расчёты не имеют ничего общего с действительностью? К счастью, это легко выяснить. Заходим на Яндекс.Карты и переходим в точку с координатами 55.604364, 37.611455. Затем активируем инструмент «Линейка» и ставим на карте две точки: одну — возле окна, из которого было сделано фото, а другую — возле стены дома, на которой мы считали панели:
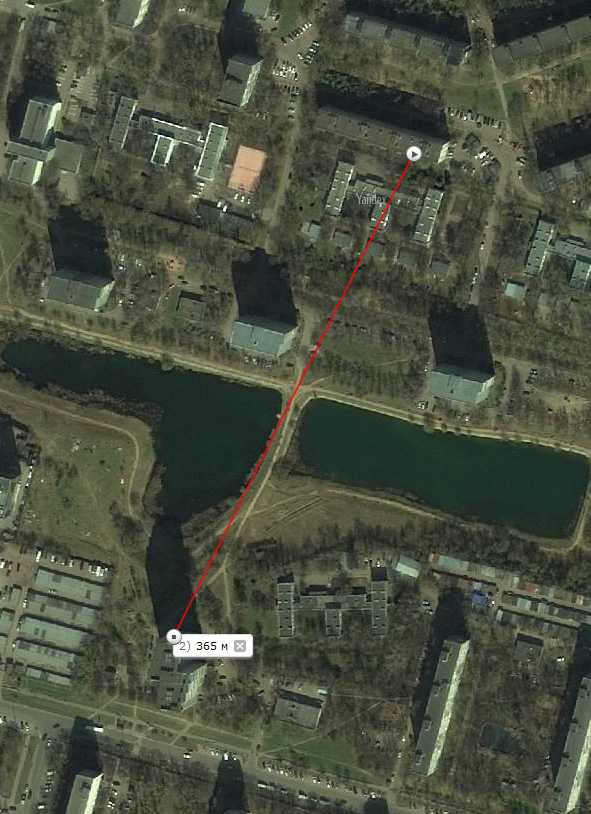
Получаем 365 м. Ну не красота, а? Величины совпали с точностью до 0,1 м! Конечно, такая точность в известной мере является результатом везения, потому что и при измерении размеров изображения, и при подсчёте высоты этажей, и при расстановке точек на карте я вполне мог допускать погрешности в 1–3%. Но, как бы то ни было, в конечном итоге расчётная и измеренная величины сошлись.
Скептически настроенный читатель может подумать, что я подгонял цифры, и что для другой фотографии всё будет по-другому. Что ж, у меня есть ещё одно фото того же дома, сделанное с аналогичной точки, но совсем с другим фокусным расстоянием:

Проделаем для него те же измерения и расчёты. У меня получилось, что размер изображения дома составляет 0,39 см, а фокусное расстояние — 21 мм. Подставляем эти числа в упрощённую формулу и получаем d = (0,021 × 66,7) / 0,0039 = 359,2 м. Результат немного отличается, но всё равно в рамках погрешности совпадает с измеренным по карте. Расхождение несложно объяснить: камера указывает фокусное расстояние как целое число, то есть и 20,51, и 21,49 мм она покажет как 21 мм. А это уже даёт погрешность 2,4%.
Впрочем, самых въедливых скептиков наверняка не убедил и этот пример. Ведь в обоих случаях я использовал один и тот же объектив — а что, если формула работает для него чисто по совпадению? Справедливое замечание. Чтобы проверить, так ли это, я возьму кадр, сделанный не только другим объективом, но и другим фотоаппаратом, причём не цифровым, а плёночным.
Вот фотография, которую мы будем анализировать:

Её много лет назад сделал мой отец на свой «Зенит-Е» с объективом Гелиос-44-2. Фокусное расстояние этого объектива составляет 58 мм. Определить физический размер изображения дома очень просто: у меня есть слайд, который я оцифровал с определённым разрешением, и сканер прописал его в свойствах файла. Тут даже пересчитывать ничего не нужно, достаточно воспользоваться линейкой.
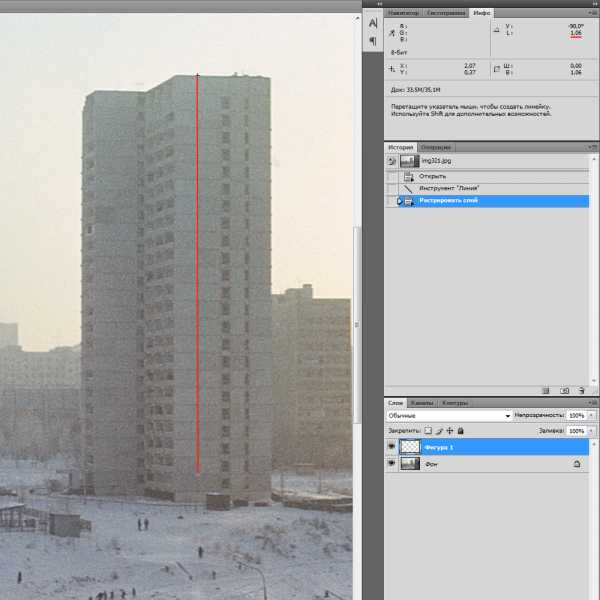
Участок из тех же 23-х панелей имеет на слайде высоту 1,06 см. Подставляем значения в формулу: d = (0,058 × 66,7) / 0,0106 = 365 м. Полное совпадение!
Что ж, мы получили интересные результаты: выходит, простая формула для тонкой линзы позволяет получать весьма точные (и легко проверяемые) результаты при анализе реальных фотографий, а не «сферических коней в вакууме». Почему же так происходит, если реальный объектив представляет собой не одну линзу, а целый бутерброд из линз? Ответ на этот вопрос поможет дать статья Википедии. Для сложного объектива при расчёте вводят не одну, а две главные плоскости. Фактически, расстояния d и D, которые вы видели на схеме в самом начале этого поста, в этом случае отсчитываются от разных (хотя и не слишком удалённых друг от друга) точек. Но расстояние D, даже небольшое изменение которого могло бы существенно повлиять на результат просто в силу небольших размеров этого плеча оптической системы, нам, к счастью, знать не нужно, потому что производитель объектива уже рассчитал и нанёс на его корпус фокусное расстояние, через которое величину D, как было показано выше, легко выразить. А что касается изменения расстояния от передней главной плоскости до объекта, то какими бы толстыми ни были линзы и каким бы длинным ни был объектив (мы, конечно, говорим о реальных конструкциях, а не воображаемых объективах размером с дом), при расстоянии до объекта съёмки в несколько сотен метров, как в нашем случае, величиной в десяток-другой сантиметров можно смело пренебречь.
На основании вышеизложенного легко вывести формулу для соотношения расстояний до объектов, запечатлённых на одной и той же фотографии. Причём знать фокусное расстояние объектива и размер матрицы в этом случае уже будет не нужно, поскольку они сократятся при составлении пропорции.
Как видите, даже знаний из программы средней школы достаточно, чтобы убедиться в полной некомпетентности отдельных «экспертов». Любите математику и не давайте себя обмануть!
bootsector.livejournal.com
