Оптика: очки и контактные линзы
Оптические системы, предназначенные для наблюдения сильно удаленных предметов, называются телескопическими. Их отличительным оптическим свойством является то, что в систему лучи поступают в виде параллельных пучков и выходят из системы также в виде параллельных пучков. Эти системы применяются для визуального наблюдения предметов. Предметы наблюдаются в виде изображений, образованных оптической системой, под знаительно большими углами, чем при рассмотрении их невооруженным глазом. Вследствие этого происходит искажение перспективы. Все предметы представляются приближенными к наблюдателю, а пространство предметов сжатым по направлению наблюдения.
Простейшая телескопическая система состоит из двух элементов: объектива и окуляра. Чтобы удовлетворить условию параллельности сопряженных пучков лучей в пространстве предметов и в пространстве изображений, необходимо, чтобы задний фокус объектива совпадал с передним фокусом окуляра. Оптическая длина такой системы равна сумме фокусных расстояний объектива и окуляра.
Если в качестве окуляра применена положительная оптическая система (например, симметричный окуляр), то такая оптическая система, дающая обратное изображение, называется системой Кеплера. К таким системам относятся зрительные трубы геодезических и астрономических инструментов. Ход лучей в такой системе показан на рис. 83. Объектив является входным зрачком. Он образует изображение величиной 21′ в передней фокальной плоскости окуляра. Выходной зрачок системы расположен за окуляром. Глаз наблюдателя, помещенный в выходном зрачке, сможет рассмотреть все изображение, так как через выходной зрачок проходят все пучки лучей. Если в качестве окуляра применена отрицательная оптическая система, то такая система называется системой Галилея. Она имеет применение в театральных биноклях. Ход лучей в тонкой системе Галилея показан на рис. 84. Такая система дает прямое изображение, отличается малым полем зрения и имеет вследствие этого ограниченное применение.
Ее преимуществом является сокращение длины, что наглядно показано на рис. 85. При одинаковых фокусных расстояниях объектива и окуляра система Галилея короче системы Кеплера на два фокусных расстояния окуляра.
85. При одинаковых фокусных расстояниях объектива и окуляра система Галилея короче системы Кеплера на два фокусных расстояния окуляра.
Главными оптическими характеристиками телескопической системы являются: 1) видимое увеличение Г; 2) поле зрения 2w; 3) диаметр выходного зрачка D’.
Обычно знак минус в формуле видимого увеличения опускается. Видимым увеличением телескопической системы называется отношение диаметра входного зрачка к диаметру выходного зрачка.
Обычно знак минус в формуле видимого увеличения опускается.Видимым увеличением телескопической системы называется отношение диаметра входного зрачка к диаметру выходного зрачка.
Диаметр входного зрачка выбирается из условия разрешающей способности (40,2), а диаметр выходного зрачка — из условия видимого увеличения (54,2). Поле зрения телескопической системы ограничивается полем зрения окуляра. Принимая за наибольшее угловое поле зрения окуляра 2w’=100°, получим возможный угол поля зрения системы
tg wмакс = tg 50°/Г.
Однако следует иметь в виду, что в некоторых случаях, поступаясь качеством изображения, применяют окуляры и с полем зрения до 2w’= 140°.
При рассмотрении необходимой разрешающей способности зрительных труб надо учитывать разрешающую способность глаза. За разрешающую способность глаза обычно принимают 60″, хотя исследования указывают на значительно большие возможности глаза. Так, например, глаз различает черные штрихи на белом фоне даже в том случае, когда их угловая величина достигает 6″. Исходя из формулы (23,1), запишем необходимую разрешающую способность зрительной трубы (в секундах)
Ψ = 60/Г (54,4)
Учитывая формулу (51,3), получаем зависимость между диаметром входного зрачка и видимым увеличением зрительной трубы, т. е. формулу полезного увеличения зрительной трубы
Гп = 0,5D. (54,5)
Полезным увеличением называется то наименьшее увеличение
зрительной трубы, при котором разрешающая сила объектива может быть полностью использована глазом наблюдателя.
В действительности для геодезических зрительных труб, для которых особенно важно полное использование разрешающей способности глаза, между диаметром входного зрачка и видимым увеличением существует в среднем зависимость (по данным зрительных труб СССР и Германии)
Гп = 0,74D. (54,6)
Оценку разрешающей способности телескопических систем всегда производят в угловой мере. На рис. 86 показана характеристическая кривая разрешающей способности главной трубы триангуляционного теодолита, измеренная при наблюдении без фильтра. Асимметрия кривой разрешающей способности является показателем нарушения центрированности оптической системы.
В табл. 7 указывается разрешающая способность некоторых отечественных приборов в центре поля.
Длина простой зрительной трубы равна
L=f’о6 + f’ок. (54,7)
Если оптическая система должна быть длинной (цистоскоп, перископ, смотровые трубки и т. п.), то между объективом и окуляром помещают оборачивающие системы. Они предназначаются для поворота изображения на 180° вокруг оптической оси и удлинения хода лучей в приборе. Применяются линзовые оборачивающиеся системы двух типов, однообъективные и двухобъективные (рис. 87). В двухобъективной системе между объективами лучи идут в виде параллельных пучков. Длина однообъективной системы равна
Они предназначаются для поворота изображения на 180° вокруг оптической оси и удлинения хода лучей в приборе. Применяются линзовые оборачивающиеся системы двух типов, однообъективные и двухобъективные (рис. 87). В двухобъективной системе между объективами лучи идут в виде параллельных пучков. Длина однообъективной системы равна
Loc = —a + a’.
Длина двухобъективной системы равна
Loc=-f1 + d + f2.
Таким образом, общая длина телескопической системы, включающей оборачивающие системы, определяется уравнением
L =f’об+Σ Lос+f’ок (54,8)
Каждую оборачивающую систему можно характеризовать линейным увеличением. Оборачивающие системы влияют на видимое увеличение всего прибора. Если β1, β2, β3, βk — линейные увеличения оборачивающих систем, то видимое увеличение может быть найдено по формуле
Сложные зрительные трубы вместо оборачивающих линзовых систем (рис.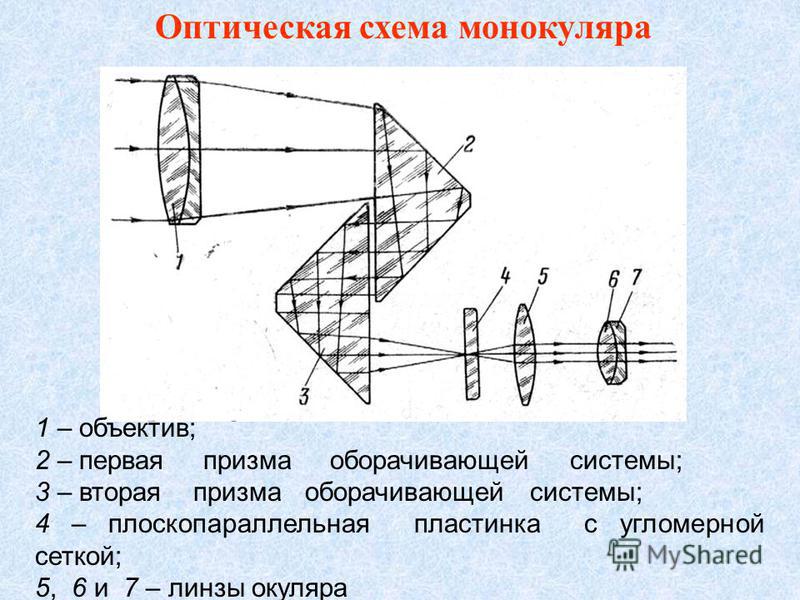 88) могут иметь и призменные оборачивающие системы (например, призменный бинокль).
88) могут иметь и призменные оборачивающие системы (например, призменный бинокль).
Габариты телескопической системы определяются длиной и диаметром. Длина системы зависит от фокусных расстояний объектива, окуляра, объективов оборачивающих систем и расстоянии между объективами оборачивающих систем. Диаметр системы зависит от относительных отверстий, углов поля зрения, коэффициента виньетирования и положения зрачков.
Расчету габарита предшествует составление технических условий на систему. Кроме основных характеристик в технические условия включаются требования к виду изображеиия (прямое или обратное), длине системы, наличию качающихся или вращающихся деталей и т. п.
Расчет габарита разделяется на две части: 1) определение фокусных расстояний компонентов и расстояний между ними; 2) расчет диаметров деталей и узлов.
Первоначально определяются фокусные расстояния всех компонентов, составляющих систему, и расстояния между ними. При расчете габарита толщины всех линзовых деталей и узлов принимаются равными нулю, тогда все линзы, объективы и окуляр изображаются в виде главных плоскостей, а отражающие призмы и пластины редуцируются к воздуху.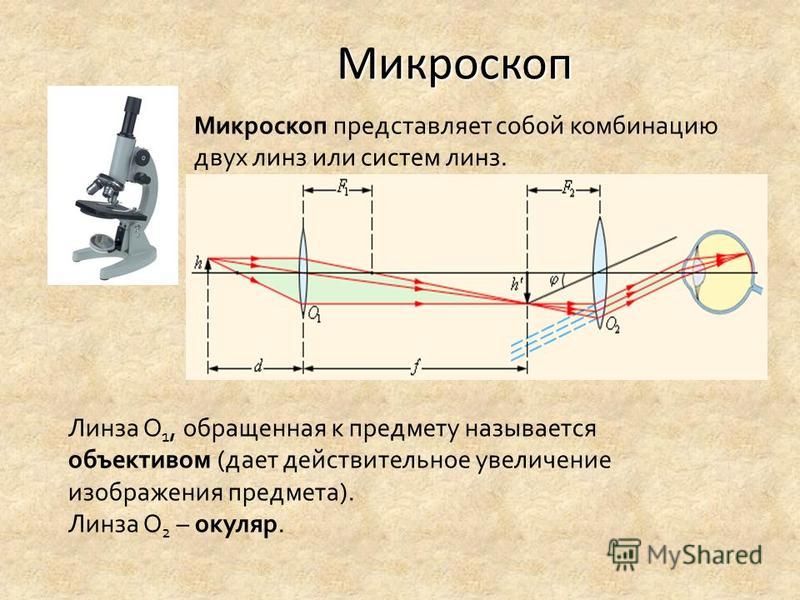
Покажем основы расчета габарита сложной телескопической системы, имеющей двухобъективную оборачивающую систему (рис 88). Для внесения определенности в расчет положим известным фокусное расстояние окуляра. Выбор его обусловливается соображениями удобного размещения глаза наблюдателя (например, f’ s=20 мм, 25 мм, 30 мм или 40 мм)
Заданными характеристиками являются 1) видимое увеличение Г, 2) поле зрения 2w, 3) диаметр выходного зрачка D’, 4) длина оптической системы от объектива до окуляра L, 5) коэффициент виньетирования kw, 6) фокусное расстояние окуляра f’s, 7) поло жение входного зрачка от объектива t, 8) лилейное увеличение β оборачивающей системы, равное отношению f’4 к f’3 (обычно β=-1)
Если вычисленный диаметр объектива D1 меньше диаметра входного зрачка D, то за световой диаметр объектива принимается диаметр входного зрачка D. Диаметр окуляра определяется наибольшими высотами действительного луча, проходящего через окуляр под наибольшим углом поля зрения Определение диаметров компонентов, составляющих оптическую систему, дублируется вычислением высот и углов осевого и наклонных лучей по формулам (48,3) и (48,4) При вычислении осевого луча начальными параметрами служат
u1=0 и h2=D/2.
В результате получается uпосл=0, что является проверкой правильности выполненных вычислений (проверка телескопичности).
При определении хода наклонного пучка лучей выполняют вычисление трех лучей, верхнего, главного и нижнего, по тем же формулам. При вычислении главного луча начальными параметрами служат
tg u1 = tg w, h1 = t*tg w,
где t—расстояние от первого компонента системы (объектива) до входного зрачка. Вычисление главного луча позволяет найти расстояние от последнего компонента системы (окуляра) до выходного зрачка:
В результате вычислений всех трех последних лучей uпосл
должны быть одинаковыми. Наибольшие высоты на каждом компоненте системы определяют световые диаметры (Ф=2h).Телескопические приборы охватывают большую группу оптических приборов. В различных отраслях техники эти приборы получили свое самостоятельное развитие, обусловленное условиями эксплуатации и точностями определения тех или иных параметров.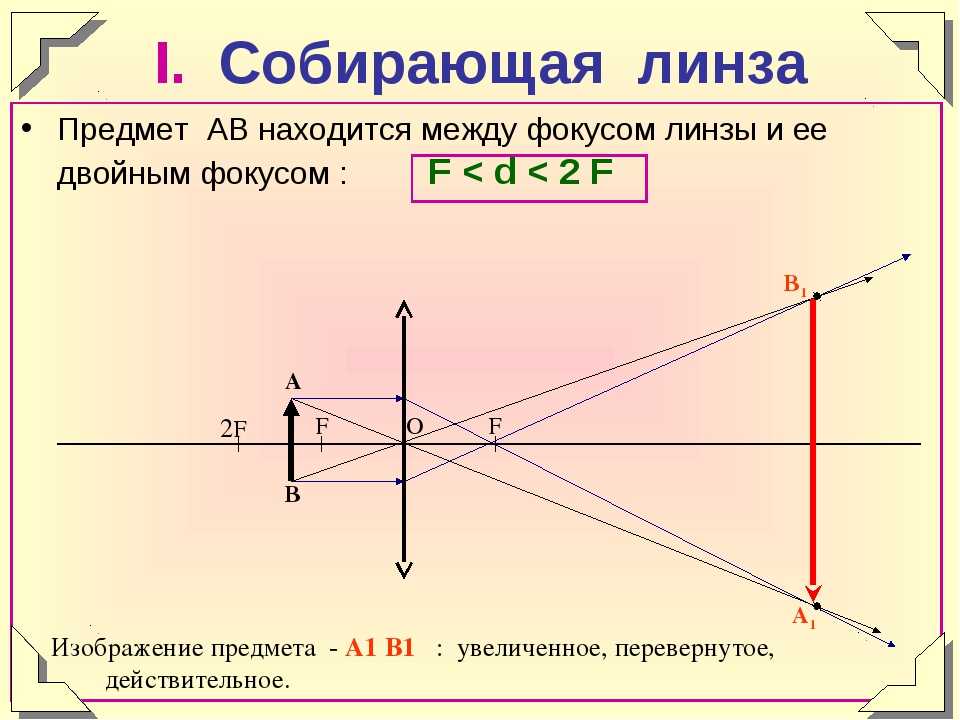
Основными группами приборов являются: 1) астрономические, 2) геодезические, 3) зрительные трубы, 4) бинокли, 5) перископы, 6) прицелы винтовочные, 7) прицелы пулеметно-минометные, 8) прицелы танковые, 9) прицелы артиллерийские, 10) прицелы авиационные, 11) дальномеры.
Некоторые из оптических приборов настолько хорошо конструктивно отработаны, что сохраняют оптическое устройство и конструкцию на протяжении многих десятилетий. К таким оптическим приборам относится стереотруба (рис. 89), предназначенная для стереоскопического рассмотрения из-за укрытий. Подобные бинокулярные оптические приборы состоят из двух однотипных половинок для левого и правого глаза. Зрительные трубы являются составной частью многих приборов в пирометрии, фотограмметрии, гравиометрии, спектроскопии, фотометрии, гониометрии, микроскопии и т. д. Данные об окулярах некоторых зрительных труб приведены в табл. III в приложении.
Простая физика — EASY-PHYSIC
Предлагаю разбор первой тренировочной работы по физике, Статград, 18 сентября 2018 года.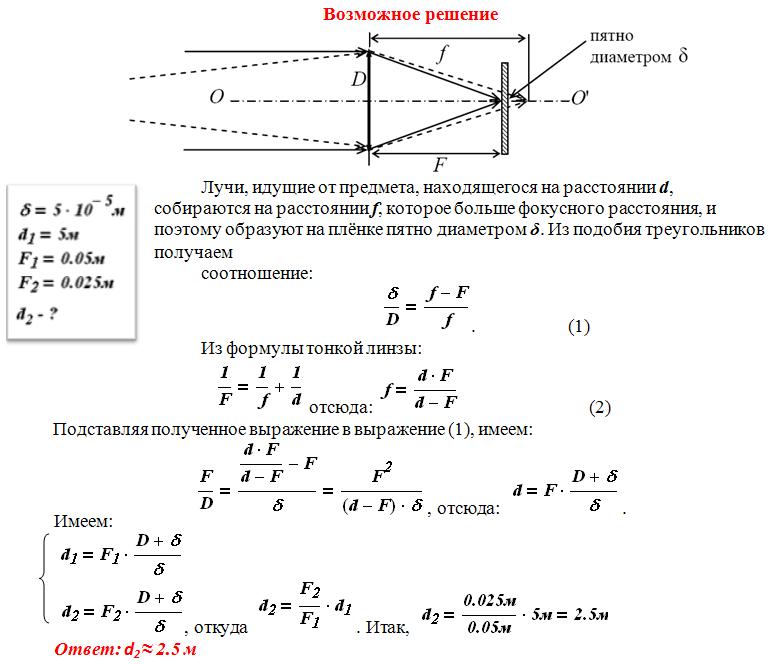 Задачи 25-32.
Задачи 25-32.
Задача 25.
Брусок равномерно двигают по горизонтальной поверхности. В процессе движения по этой поверхности он проходит два участка одинаковой длины с различными коэффициентами трения. Известно, что на первом участке модуль работы силы трения 2,5 Дж, а на втором участке модуль работы силы трения 7,5 Дж. При этом на втором участке коэффициент трения на 0,4 больше, чем на первом. Определите, чему равен коэффициент трения на втором участке.
Так как длины участков равны, то очевидно, что величины работ будут относиться так же, как и силы трения. Модули работ равны:
Поделим эти уравнения друг на друга:
Также известно, что
Тогда
Откуда
А
Ответ: 0,6
Задача 26.
Высокий вертикальный цилиндр закрыт тонким поршнем массой 1 кг и площадью 100 см. Под поршнем находится идеальный газ. Атмосферное давление над поршнем равно 101 кПа, расстояние между дном цилиндра и поршнем 50 см. Цилиндр перевернули так, что поршень оказался снизу, но не выпал из цилиндра. На сколько увеличилось расстояние между дном цилиндра и поршнем в состоянии равновесия? Температура газа в исходном и конечном состоянии одинакова.
Цилиндр перевернули так, что поршень оказался снизу, но не выпал из цилиндра. На сколько увеличилось расстояние между дном цилиндра и поршнем в состоянии равновесия? Температура газа в исходном и конечном состоянии одинакова.
Сначала на газ сверху давит атмосфера и вес поршня, распределенный по его площади. Следовательно, давление газа равно
Затем сосуд переворачивают, и сила давления газа складывается с весом поршня, а вверх направлена сила давления атмосферы.
Объем газа в цилиндре изменился при переворачивании, и это произошло изотермически:
Если расписать объемы как произведения площади поршня на его высоту над дном, получим (площади сократим)
Или
Ответ: увеличилось на 1 см.
Задача 27.
Маленький шарик, несущий заряд 2 мкКл, подвешенный в вакууме на нити длиной 50 см, вращается в однородном вертикальном магнитном поле. При этом шарик движется в горизонтальной плоскости по окружности с постоянной угловой скоростью 20 рад/с, а нить всегда составляет с вертикалью угол . Модуль силы Лоренца, действующей на этот шарик, равен 20 мкН. Определите модуль индукции магнитного поля.
Модуль силы Лоренца, действующей на этот шарик, равен 20 мкН. Определите модуль индукции магнитного поля.
Сила Лоренца равна
Тогда индукция
Где .
Ответ: 2 Тл.
Задача 28.
Бабочки летают, быстро хлопая крыльями. Объясните с точки зрения физических законов и закономерностей, за счёт чего им удаётся удерживаться в воздухе. Оцените, с какой частотой ν бабочке-монарху надо махать крыльями в воздухе плотностью кг/м, чтобы не упасть, если масса бабочки г, площадь крыльев см, максимальная вертикальная скорость концов крыльев в полёте м/c. Считайте, что бабочка опускает крылья вниз плашмя, а поднимает их вверх ребром.
Заметим сразу же, что скорость концов крыльев дана, но скорость любой другой точки крыла (не на конце крыла) – меньше. Эта скорость по мере приближения к точкам прикрепления крыльев уменьшается вплоть до нуля. Поэтому будем считать, что все крыло двигается вниз со скоростью — это будет средняя скорость. Если крыло двигается вниз плашмя с такой скоростью, то оно «заметает» порцию воздуха объемом . Масса этого воздуха равна
Если крыло двигается вниз плашмя с такой скоростью, то оно «заметает» порцию воздуха объемом . Масса этого воздуха равна
Крыло толкает воздух, сообщает ему импульс, равный
По закону сохранения импульса такой же импульс будет передан и бабочке.
Мы уже учли, что крыльев 2 штуки: дана площадь обоих. Но не учли, что бабочка делает много взмахов. Пусть частота взмахов , то есть
Тогда
Тогда, так как
То можно найти частоту:
Ответ: 4 Гц.
Задача 29.
Гоночный автомобиль едет по треку, имеющему на повороте радиусом м угол наклона полотна дороги к горизонту внутрь поворота. С какой максимальной скоростью может двигаться автомобиль, чтобы не заскользить и не вылететь с трека? Коэффициент трения колёс автомобиля о дорогу . Ответ выразите в км/ч.
Задача 29.
«Честно» расставим силы и запишем уравнение по второму закону Ньютона в проекциях на оси. Оси направим так: Ох вдоль плоскости вниз и Оу перпендикулярно плоскости вверх.
Тогда по оси :
Откуда
Теперь для оси :
Следовательно,
Сократим массу, подставим :
Выразим в км/ч:
Ответ: 129 км/ч.
Задача 30.
В тепловом двигателе в качестве рабочего тела используется идеальный газ, а цикл состоит из двух изохор 1–2 и 3–4 и двух адиабат 2–3 и 4–1 (см. рисунок). Известно, что в адиабатических процессах температура газа изменяется в раза (растёт в процессе 4–1 и падает в процессе 2–3). Найдите КПД цикла.
Задача 30.
Так как в адиабатных процессах газ не обменивается теплотой с внешней средой, то передача тепла газу и обратно происходит только на изохорах. А в изохорном процессе, как известно, работа равна нулю. Поэтому полученное газом количество теплоты на изохоре 1-2 равно изменению его внутренней энергии:
А отданное количество теплоты равно изменению внутренней энергии газа в процессе 3-4:
Тогда КПД цикла равен
Но по условию и , поэтому
Ответ: 50%
Задача 31.
В электрической цепи, схема которой изображена на рисунке, конденсатор ёмкостью мкФ в начальный момент заряжен до напряжения В, а оба ключа разомкнуты. Замкнув ключ К1, к конденсатору подключили цепочку из двух последовательно соединённых катушек с одинаковой индуктивностью мГн, в результате чего в цепи возникли гармонические колебания. В момент, когда сила тока в цепи при этих колебаниях обратилась в ноль, замкнули ключ К2. Как и на сколько изменилась после этого амплитуда колебаний силы тока в цепи?
Задача 31.
Итак, в конденсаторе сосредоточен заряд
Поэтому при возникновении колебаний заряд будет меняться по закону косинуса:
Где
Здесь при вычислениях мы сложили индуктивности последовательно соединенных катушек.
Ток в цепи, как производная заряда, будет меняться по закону синуса:
Максимальное значение тока равно А.
При замыкании ключа 2 в цепи останется только одна катушка, и изменится угловая частота колебаний.
Поэтому изменится и амплитуда тока, которая прямо зависит от угловой частоты:
То есть амплитуда тока возрастет на 0,41 А.
Ответ: 0,41 А.
Задача 32.
Телескопические устройства состоят обычно из двух линз – длиннофокусного объектива и короткофокусного окуляра. В трубе системы Кеплера окуляр – лупа, т. е. собирающая линза, а в трубе системы Галилея окуляр – это рассеивающая линза. В обеих трубах фокальные плоскости объектива и окуляра совпадают, так что параллельный пучок света на входе в систему преобразуется в параллельный же пучок на её выходе. Рассмотрим две такие трубы с одинаковым угловым увеличением , с одинаковыми фокусными расстояниями объективов см и одинаковыми по модулю фокусными расстояниями окуляров. Какая труба короче и на сколько?
Трубы Кеплера и Галилея отличаются вот чем: для трубы Кеплера
Схема телескопа Кеплера
А для трубы Галилея
Схема телескопа Галилея
Увеличение телескопа определяется выражением:
Тогда
Следовательно, если длины отличаются на , то они отличаются на 5 см.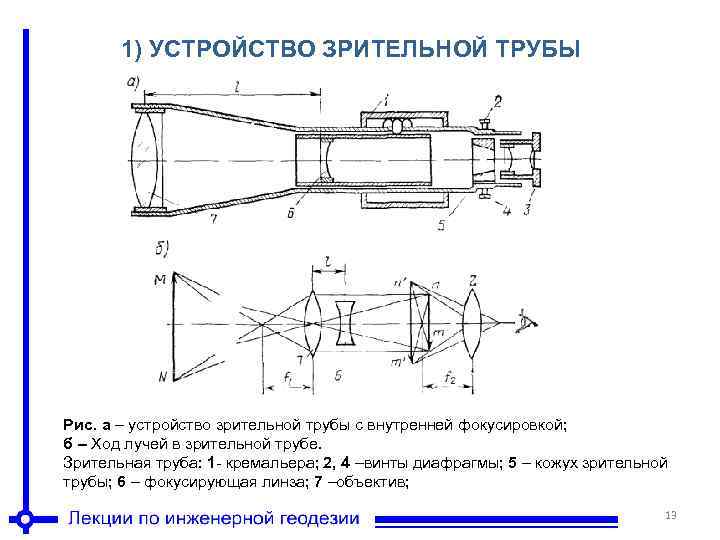 Вот когда на помощь пришла астрономия и задачи на устройство телескопов — кстати, статья на эту тему выйдет 1 ноября.
Вот когда на помощь пришла астрономия и задачи на устройство телескопов — кстати, статья на эту тему выйдет 1 ноября.
Ответ: 5 см.
Телескопы | Физика
Цели обучения
К концу этого раздела вы сможете:
- Описать изобретение телескопа.
- Описать работу телескопа.
Телескопы предназначены для наблюдения за удаленными объектами, создавая изображение, превышающее изображение, видимое невооруженным глазом. Телескопы собирают гораздо больше света, чем глаз, что позволяет наблюдать за тусклыми объектами с большим увеличением и лучшим разрешением. Хотя Галилею часто приписывают изобретение телескопа, на самом деле это не так. То, что он сделал, было важнее. Он сконструировал несколько первых телескопов, первым исследовал с их помощью небо и сделал с их помощью монументальные открытия. Среди них спутники Юпитера, кратеры и горы на Луне, детали солнечных пятен и тот факт, что Млечный Путь состоит из огромного количества отдельных звезд.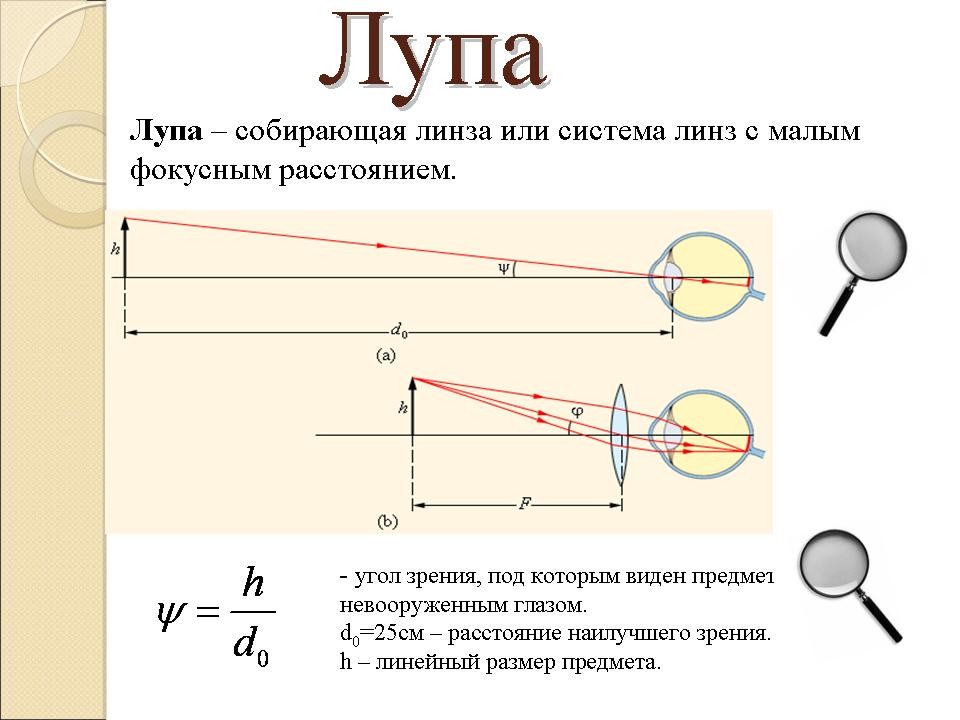
На рис. 1а показан телескоп, состоящий из двух линз, выпуклого объектива и вогнутого окуляра. Такая же конструкция использовалась Галилеем. Такое расположение дает вертикальное изображение и используется в подзорных трубах и оперных биноклях.
Рис. 1. (а) Галилей изготовил телескопы с выпуклым объективом и вогнутым окуляром. Они создают вертикальное изображение и используются в подзорных трубах. (b) Большинство простых телескопов имеют две выпуклые линзы. Объектив формирует изображение случая 1, которое является объектом для окуляра. Окуляр формирует конечное изображение случая 2, которое увеличивается.
Наиболее распространенный двухлинзовый телескоп, как и простой микроскоп, использует две выпуклые линзы и показан на рис. 1b. Объект находится так далеко от телескопа, что практически находится на бесконечности по сравнению с фокусными расстояниями линз ( d o ≈ ∞). Таким образом, первое изображение получается в точке d i = f o , как показано на рисунке. Чтобы доказать это, обратите внимание, что
Чтобы доказать это, обратите внимание, что
[латекс]\displaystyle\frac{1}{d_{\text{i}}}=\frac{1}{f_{\text{o}}}-\frac{1} {d_{\text{o}}}=\frac{1}{f_{\text{o}}}-\frac{1}{\infty}\\[/latex]
Поскольку [латекс]\frac{1}{\infty}=0\\[/latex], это упрощается до [латекс]\frac{1}{d_{\text{i}}}=\frac{1 }{f_{\text{o}}}\\[/latex], что означает, что d i = f o , как заявлено. Это правда, что для любого удаленного объекта и любой линзы или зеркала изображение находится на фокусном расстоянии.
Первое изображение, сформированное объективом телескопа, как показано на рисунке 1b, не будет большим по сравнению с тем, что вы могли бы увидеть, глядя на объект напрямую. Например, пятно, образованное солнечным светом, сфокусированным на листе бумаги с помощью увеличительного стекла, является изображением Солнца, и оно небольшого размера. Окуляр телескопа (как и окуляр микроскопа) увеличивает это первое изображение. Расстояние между окуляром и объективом делают немного меньше суммы их фокусных расстояний так, чтобы первое изображение было ближе к окуляру, чем его фокусное расстояние. то есть 9{\prime}}{\theta}=-\frac{f_{\text{o}}}{f_{\text{e}}}\\[/latex]
то есть 9{\prime}}{\theta}=-\frac{f_{\text{o}}}{f_{\text{e}}}\\[/latex]
Знак минус указывает, что изображение перевернуто. Для получения наибольшего углового увеличения лучше всего иметь объектив с большим фокусным расстоянием и окуляр с коротким фокусным расстоянием. Чем больше угловое увеличение M , тем больше объект будет казаться при просмотре в телескоп, что позволит увидеть больше деталей. Ограничения наблюдаемых деталей накладываются многими факторами, в том числе качеством линз и атмосферными возмущениями.
Изображение в большинстве телескопов перевернуто, что неважно для наблюдения за звездами, но представляет реальную проблему для других применений, таких как телескопы на кораблях или оптические прицелы. Если необходимо вертикальное изображение, можно использовать схему Галилея на рис. 1а. Но чаще используется третья выпуклая линза в качестве окуляра, увеличивая расстояние между первыми двумя и снова инвертируя изображение, как показано на рис. 2.
рис.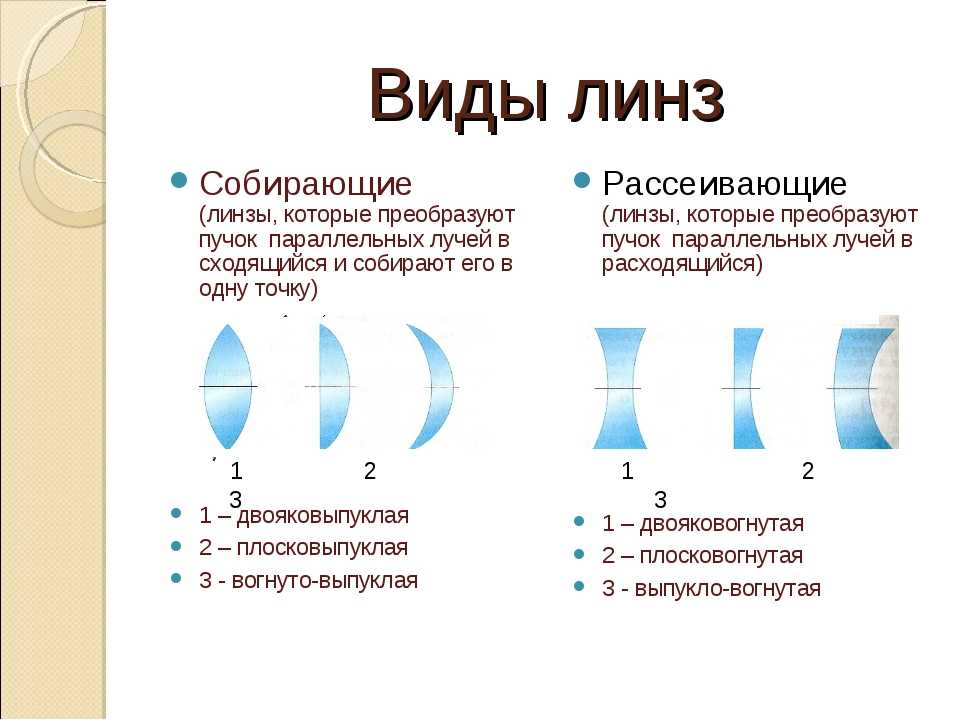 2. Такое расположение трех линз в телескопе дает вертикальное окончательное изображение. Первые две линзы находятся достаточно далеко друг от друга, чтобы вторая линза еще раз инвертировала изображение первой. Третья линза действует как лупа и удерживает изображение в вертикальном положении в удобном для просмотра месте.
2. Такое расположение трех линз в телескопе дает вертикальное окончательное изображение. Первые две линзы находятся достаточно далеко друг от друга, чтобы вторая линза еще раз инвертировала изображение первой. Третья линза действует как лупа и удерживает изображение в вертикальном положении в удобном для просмотра месте.
Рис. 3. Показан двухэлементный телескоп, состоящий из зеркала в качестве объектива и линзы в качестве окуляра. Этот телескоп формирует изображение так же, как и уже рассмотренный двухвыпуклый телескоп, но он не страдает хроматическими аберрациями. Такие телескопы могут собирать больше света, поскольку можно построить зеркала большего размера, чем линзы.
Телескоп также может быть изготовлен с вогнутым зеркалом в качестве его первого элемента или объектива, поскольку вогнутое зеркало действует как выпуклая линза, как показано на рис. 3. Плоские зеркала часто используются в оптических приборах, чтобы сделать их более компактными или направить свет к камерам и другим сенсорным устройствам. Есть много преимуществ в использовании зеркал, а не линз для объективов телескопа. Зеркала могут быть сконструированы намного больше, чем линзы, и, таким образом, могут собирать большое количество света, необходимое, например, для наблюдения за далекими галактиками. Большие и относительно плоские зеркала имеют очень большое фокусное расстояние, поэтому возможно большое угловое увеличение.
Есть много преимуществ в использовании зеркал, а не линз для объективов телескопа. Зеркала могут быть сконструированы намного больше, чем линзы, и, таким образом, могут собирать большое количество света, необходимое, например, для наблюдения за далекими галактиками. Большие и относительно плоские зеркала имеют очень большое фокусное расстояние, поэтому возможно большое угловое увеличение.
Телескопы, как и микроскопы, могут использовать диапазон частот электромагнитного спектра. На рис. 4а показан компактный массив австралийских телескопов, в котором используются шесть 22-метровых антенн для картографирования южного неба с помощью радиоволн. На рис. 4b показана фокусировка рентгеновских лучей на рентгеновской обсерватории Чандра — спутнике, вращающемся вокруг Земли с 1999 года и наблюдающем за высокотемпературными явлениями в виде взрывающихся звезд, квазаров и черных дыр. Рентгеновские лучи, обладающие гораздо большей энергией и меньшей длиной волны, чем РЧ и свет, в основном поглощаются и не отражаются при падении перпендикулярно среде. Но они могут отражаться при падении под небольшими углами взгляда, так же как камень будет прыгать по озеру, если его бросить под небольшим углом. Зеркала для Чандры состоят из длинного ствола и 4 пар зеркал, фокусирующих лучи в точке на расстоянии 10 метров от входа. Зеркала чрезвычайно гладкие и состоят из стеклокерамической основы с тонким покрытием из металла (иридия). Четыре пары изготовленных с высокой точностью зеркал имеют изысканную форму и выровнены таким образом, что рентгеновские лучи рикошетят от зеркал, как пули от стены, фокусируясь на определенном месте.
Но они могут отражаться при падении под небольшими углами взгляда, так же как камень будет прыгать по озеру, если его бросить под небольшим углом. Зеркала для Чандры состоят из длинного ствола и 4 пар зеркал, фокусирующих лучи в точке на расстоянии 10 метров от входа. Зеркала чрезвычайно гладкие и состоят из стеклокерамической основы с тонким покрытием из металла (иридия). Четыре пары изготовленных с высокой точностью зеркал имеют изысканную форму и выровнены таким образом, что рентгеновские лучи рикошетят от зеркал, как пули от стены, фокусируясь на определенном месте.
Рис. 4. (a) Компактный массив австралийских телескопов в Наррабри (500 км к северо-западу от Сиднея). (кредит: Ян Бейли) (b) Фокусировка рентгеновских лучей на обсерватории Чандра, спутнике, вращающемся вокруг Земли. Рентгеновские лучи рикошетят от 4 пар зеркал, образуя бочкообразный путь, ведущий к точке фокусировки. (кредит: НАСА)
Текущая захватывающая разработка — это совместные усилия с участием 17 стран по строительству массива телескопов в квадратном километре (SKA), способных охватывать диапазон частот от 80 МГц до 2 ГГц. Начальным этапом проекта является строительство Австралийского массива квадратных километров Pathfinder в Западной Австралии (см. рис. 5). В проекте будут использованы передовые технологии, такие как адаптивная оптика , в которой линза или зеркало состоят из множества тщательно выровненных крошечных линз и зеркал, которыми можно управлять с помощью компьютеров. Ряд быстро меняющихся искажений можно свести к минимуму, деформируя или наклоняя крошечные линзы и зеркала. Использование адаптивной оптики в коррекции зрения является актуальной областью исследований.
Начальным этапом проекта является строительство Австралийского массива квадратных километров Pathfinder в Западной Австралии (см. рис. 5). В проекте будут использованы передовые технологии, такие как адаптивная оптика , в которой линза или зеркало состоят из множества тщательно выровненных крошечных линз и зеркал, которыми можно управлять с помощью компьютеров. Ряд быстро меняющихся искажений можно свести к минимуму, деформируя или наклоняя крошечные линзы и зеркала. Использование адаптивной оптики в коррекции зрения является актуальной областью исследований.
Рис. 5. Изображение австралийского следопыта в квадратном километре в Западной Австралии, сделанное художником. (кредит: SPDO, XILOSTUDIOS) 9{\prime}}{\theta}=-\frac{{f}_{\text{o}}}{{f}_{\text{e}}}\\[/latex], где θ угол, образуемый объектом, видимым невооруженным глазом, θ ′ — угол, образуемый увеличенным изображением, а f o и f e — фокусные расстояния объектива и окуляра .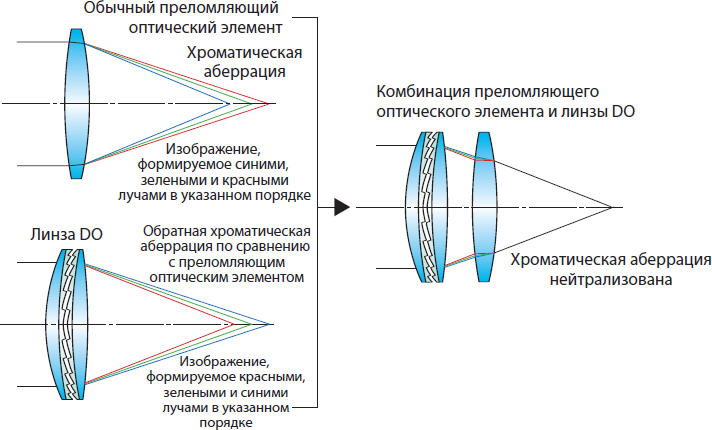
Концептуальные вопросы
- Если вы хотите, чтобы ваш микроскоп или телескоп проецировали реальное изображение на экран, как бы вы изменили положение окуляра относительно объектива?
Задачи и упражнения
Если не указано иное, расстояние от линзы до сетчатки составляет 2,00 см.
- Каково угловое увеличение телескопа с объективом с фокусным расстоянием 100 см и окуляром с фокусным расстоянием 2,50 см?
- Найдите расстояние между линзами объектива и окуляра в телескопе в приведенной выше задаче, необходимое для получения конечного изображения очень далеко от наблюдателя, где зрение наиболее расслаблено. Обратите внимание, что телескоп обычно используется для наблюдения за очень удаленными объектами.
- Большой телескоп-рефлектор имеет зеркало объектива с радиусом кривизны 10,0 м. Какое угловое увеличение он дает при использовании окуляра с фокусным расстоянием 3,00 м?
- Небольшой телескоп имеет вогнутое зеркало с радиусом кривизны 2,00 м в качестве объектива.
 Его окуляр представляет собой линзу с фокусным расстоянием 4,00 см. а) Каково угловое увеличение телескопа? б) Под каким углом слагается солнечное пятно диаметром 25 000 км? в) Каков угол его телескопического изображения?
Его окуляр представляет собой линзу с фокусным расстоянием 4,00 см. а) Каково угловое увеличение телескопа? б) Под каким углом слагается солнечное пятно диаметром 25 000 км? в) Каков угол его телескопического изображения? - Бинокль 7,5x дает угловое увеличение -7,50, действуя как телескоп. (Зеркала используются, чтобы сделать изображение вертикальным.) Если у бинокля есть линзы объектива с фокусным расстоянием 75,0 см, каково фокусное расстояние линз окуляра?
- Создайте свою собственную задачу. Рассмотрите телескоп того типа, который использовал Галилео, с выпуклым объективом и вогнутым окуляром, как показано на рисунке 1а. Постройте задачу, в которой вы вычисляете местоположение и размер полученного изображения. Среди вещей, которые следует учитывать, — фокусные расстояния линз и их взаимное расположение, а также размер и расположение объекта. Убедитесь, что угловое увеличение больше единицы. То есть угол, образуемый изображением в глазу, больше, чем угол, образуемый объектом.

Глоссарий
адаптивная оптика: оптическая технология, при которой компьютеры настраивают линзы и зеркала в устройстве для коррекции искажений изображения [latex]M=-\frac{{f}_{\text{o}}}{{f}_{\text{e}}}\\[/latex]
Избранные решения задач и упражнений
1. –40,0
3. –1,67
5. +10,0 см
9.5 Телескопы | Texas Gateway
Цели обучения
К концу этого раздела вы сможете делать следующее:
- Схема изобретения телескопа
- Описать работу телескопа
Информация, представленная в этом разделе, поддерживает следующие цели обучения и научные практики AP®:
- 6.E.4.1 Учащийся может планировать стратегии сбора данных и выполнять анализ данных оценка данных о формировании изображений за счет отражения света от изогнутых сферических зеркал. (СП 3.2, 4.1, 5.1, 5.
 2, 5.3)
2, 5.3) - 6.E.5.1 Учащийся может использовать количественные и качественные представления и модели для анализа ситуаций и решения задач, связанных с формированием изображения, происходящим из-за преломления света через тонкие линзы. (Ст. 1.4, 2.2)
Телескопы предназначены для наблюдения за удаленными объектами, создавая изображение, превышающее изображение, видимое невооруженным глазом. Телескопы собирают гораздо больше света, чем глаз, что позволяет наблюдать за тусклыми объектами с большим увеличением и лучшим разрешением. Хотя Галилею часто приписывают изобретение телескопа, на самом деле это не так. То, что он сделал, было важнее. Он сконструировал несколько первых телескопов, первым исследовал с их помощью небо и сделал с их помощью монументальные открытия. Среди них спутники Юпитера, кратеры и горы на Луне, детали солнечных пятен и тот факт, что Млечный Путь состоит из огромного количества отдельных звезд.
На рис. 9.23(а) показан телескоп, состоящий из двух линз, выпуклого объектива и вогнутого окуляра, такой же конструкции, как у Галилея. Такое расположение дает вертикальное изображение и используется в подзорных трубах и оперных биноклях.
Рис. 9.23 (а) Галилей изготовил телескопы с выпуклым объективом и вогнутым окуляром. Они создают вертикальное изображение и используются в подзорных трубах. (b) Большинство простых телескопов имеют две выпуклые линзы. Объектив формирует изображение случая 1, которое является объектом для окуляра. Окуляр формирует конечное изображение случая 2, которое увеличивается.
Наиболее распространенный двухлинзовый телескоп, как и простой микроскоп, использует две выпуклые линзы и показан на рис. 9.23(b). Объект находится так далеко от телескопа, что практически находится на бесконечности по сравнению с фокусными расстояниями линз (do≈∞).(do≈∞). Таким образом, первое изображение получается при di=fo,di=fo, как показано на рисунке. Чтобы доказать это, заметим, что
9,25 1di=1fo-1do=1fo-1∞. 1di=1fo-1do=1fo-1∞. size 12{ { {1} over {d rSub { size 8 {i} } } } = { {1} over {f rSub { size 8 {o} } } } — { {1} over {d rSub { size 8 {o} } } } = { {1} над {f rSub { размер 8 {o} } } } — { {1} над { бесконечность } } } {}
1di=1fo-1do=1fo-1∞. size 12{ { {1} over {d rSub { size 8 {i} } } } = { {1} over {f rSub { size 8 {o} } } } — { {1} over {d rSub { size 8 {o} } } } = { {1} над {f rSub { размер 8 {o} } } } — { {1} над { бесконечность } } } {}
Поскольку 1/∞=0,1/∞=0, размер 12{ {1} косая черта { бесконечность =0} } {} это упрощается до
9.26 1di=1fo,1di=1fo, размер 12{ { {1 } over {d rSub { size 8{i} } } } = { {1} over {f rSub { size 8{o} } } } } {}
, что означает, что di=fo,di=fo, как заявлено . Это правда, что для любого удаленного объекта и любой линзы или зеркала изображение находится на фокусном расстоянии.
Первое изображение, сформированное объективом телескопа, как показано на рис. 9.23(b), не будет большим по сравнению с тем, что вы могли бы увидеть, глядя прямо на объект. Например, пятно, образованное солнечным светом, сфокусированным на листе бумаги с помощью увеличительного стекла, является изображением Солнца, и оно небольшого размера. Окуляр телескопа, как и окуляр микроскопа, увеличивает это первое изображение. Расстояние между окуляром и объективом делают немного меньше суммы их фокусных расстояний так, чтобы первое изображение было ближе к окуляру, чем его фокусное расстояние. То есть,
до’до’ меньше, чем
fe, fe, и поэтому окуляр формирует изображение случая 2, большое и смещенное влево для удобства просмотра. Если угол, образуемый объектом при наблюдении невооруженным глазом, равен
θ, θ, а угол, образуемый изображением телескопа, равен
θ′,θ′, то угловое увеличение
ММ определяется как их отношение. То есть,
М=θ’/θ. М=θ’/θ. Можно показать, что угловое увеличение телескопа связано с фокусными расстояниями объектива и окуляра; и дается
Расстояние между окуляром и объективом делают немного меньше суммы их фокусных расстояний так, чтобы первое изображение было ближе к окуляру, чем его фокусное расстояние. То есть,
до’до’ меньше, чем
fe, fe, и поэтому окуляр формирует изображение случая 2, большое и смещенное влево для удобства просмотра. Если угол, образуемый объектом при наблюдении невооруженным глазом, равен
θ, θ, а угол, образуемый изображением телескопа, равен
θ′,θ′, то угловое увеличение
ММ определяется как их отношение. То есть,
М=θ’/θ. М=θ’/θ. Можно показать, что угловое увеличение телескопа связано с фокусными расстояниями объектива и окуляра; и дается
9,27 M=θ′θ=-fofe.M=θ′θ=-fofe.
Знак минус указывает, что изображение перевернуто. Для получения наибольшего углового увеличения лучше всего иметь объектив с большим фокусным расстоянием и окуляр с коротким фокусным расстоянием. Чем больше угловое увеличение 90 201 M,M, размер 12{M} {} 90 020, тем больше объект будет казаться при просмотре в телескоп, что позволит увидеть больше деталей.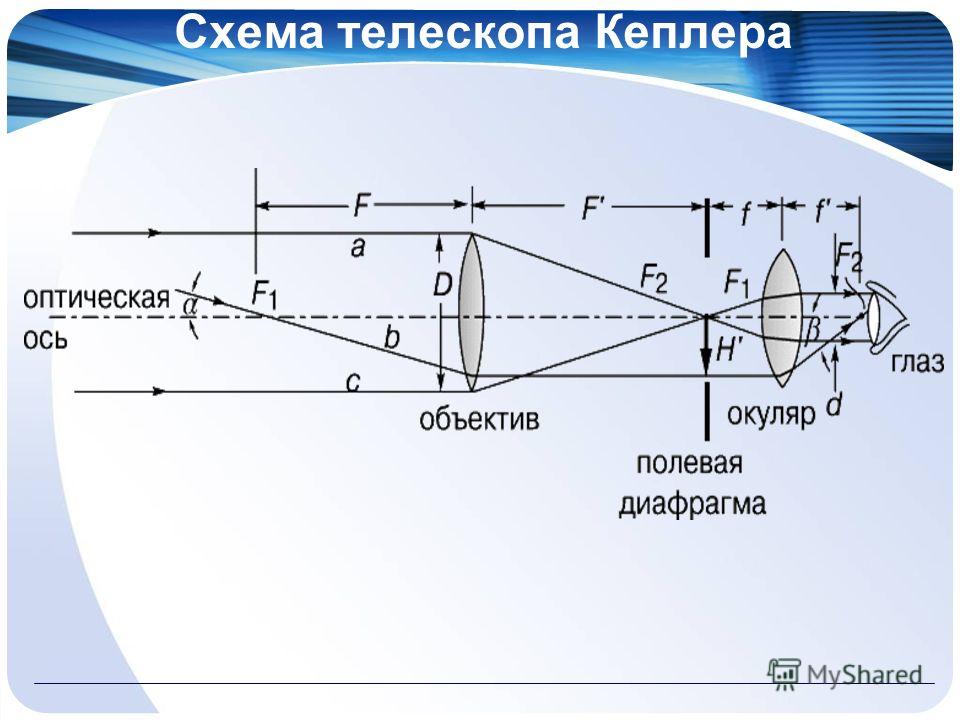 Ограничения наблюдаемых деталей накладываются многими факторами, в том числе качеством линз и атмосферными возмущениями.
Ограничения наблюдаемых деталей накладываются многими факторами, в том числе качеством линз и атмосферными возмущениями.
Изображение в большинстве телескопов перевернуто, что неважно для наблюдения за звездами, но представляет реальную проблему для других применений, таких как телескопы на кораблях или оптические прицелы. Если необходимо вертикальное изображение, можно использовать схему Галилея на рис. 9.23(а). Но чаще используется третья выпуклая линза в качестве окуляра, увеличивающая расстояние между первыми двумя и снова инвертирующая изображение, как показано на рис. 9.24.
Рис. 9.24 Такое расположение трех линз в телескопе дает вертикальное окончательное изображение. Первые две линзы находятся достаточно далеко друг от друга, чтобы вторая линза еще раз инвертировала изображение первой. Третья линза действует как лупа и удерживает изображение в вертикальном положении в удобном для просмотра месте.
Телескоп также может быть изготовлен с вогнутым зеркалом в качестве первого элемента или объектива, поскольку вогнутое зеркало действует как выпуклая линза, как показано на рис. 9.25. Плоские зеркала часто используются в оптических приборах, чтобы сделать их более компактными или направлять свет на камеры и другие сенсорные устройства. Есть много преимуществ в использовании зеркал, а не линз для объективов телескопа. Зеркала могут быть сконструированы намного больше, чем линзы, и, таким образом, могут собирать большое количество света, необходимое, например, для наблюдения за далекими галактиками. Большие и относительно плоские зеркала имеют очень большое фокусное расстояние, поэтому возможно большое угловое увеличение.
9.25. Плоские зеркала часто используются в оптических приборах, чтобы сделать их более компактными или направлять свет на камеры и другие сенсорные устройства. Есть много преимуществ в использовании зеркал, а не линз для объективов телескопа. Зеркала могут быть сконструированы намного больше, чем линзы, и, таким образом, могут собирать большое количество света, необходимое, например, для наблюдения за далекими галактиками. Большие и относительно плоские зеркала имеют очень большое фокусное расстояние, поэтому возможно большое угловое увеличение.
Рис. 9.25 Показан двухэлементный телескоп, состоящий из зеркала в качестве объектива и линзы в качестве окуляра. Этот телескоп формирует изображение так же, как и уже рассмотренный двухвыпуклый телескоп, но он не страдает хроматическими аберрациями. Такие телескопы могут собирать больше света, поскольку можно построить зеркала большего размера, чем линзы.
Телескопы, как и микроскопы, могут использовать диапазон частот электромагнитного спектра. На рис. 9.26(а) показан компактный массив Австралийского телескопа, который использует шесть 22-метровых антенн для картографирования южного неба с помощью радиоволн. Рисунок 9.26(b) показана фокусировка рентгеновских лучей на рентгеновской обсерватории Чандра — спутнике, вращающемся вокруг Земли с 1999 года и рассматривающем высокотемпературные явления в виде взрывающихся звезд, квазаров и черных дыр. Рентгеновские лучи, обладающие гораздо большей энергией и меньшей длиной волны, чем РЧ и свет, в основном поглощаются и не отражаются при падении перпендикулярно среде. Но они могут отражаться при падении под небольшими углами взгляда, так же как камень будет прыгать по озеру, если его бросить под небольшим углом. Зеркала для Чандры состоят из длинного бочкообразного пути и четырех пар зеркал, фокусирующих лучи в точке на расстоянии 10 м от входа. Зеркала чрезвычайно гладкие и состоят из стеклокерамической основы с тонким покрытием из металла — иридия. Четыре пары изготовленных с высокой точностью зеркал имеют изысканную форму и выровнены таким образом, что рентгеновские лучи рикошетят от зеркал, как пули от стены, фокусируясь на определенном месте.
На рис. 9.26(а) показан компактный массив Австралийского телескопа, который использует шесть 22-метровых антенн для картографирования южного неба с помощью радиоволн. Рисунок 9.26(b) показана фокусировка рентгеновских лучей на рентгеновской обсерватории Чандра — спутнике, вращающемся вокруг Земли с 1999 года и рассматривающем высокотемпературные явления в виде взрывающихся звезд, квазаров и черных дыр. Рентгеновские лучи, обладающие гораздо большей энергией и меньшей длиной волны, чем РЧ и свет, в основном поглощаются и не отражаются при падении перпендикулярно среде. Но они могут отражаться при падении под небольшими углами взгляда, так же как камень будет прыгать по озеру, если его бросить под небольшим углом. Зеркала для Чандры состоят из длинного бочкообразного пути и четырех пар зеркал, фокусирующих лучи в точке на расстоянии 10 м от входа. Зеркала чрезвычайно гладкие и состоят из стеклокерамической основы с тонким покрытием из металла — иридия. Четыре пары изготовленных с высокой точностью зеркал имеют изысканную форму и выровнены таким образом, что рентгеновские лучи рикошетят от зеркал, как пули от стены, фокусируясь на определенном месте.
Рис. 9.26 (a) Компактная антенная решетка Австралийского телескопа в Наррабри (500 км к северо-западу от Сиднея). (Ян Бейли) (b) Фокусировка рентгеновских лучей на обсерватории Чандра , спутнике на орбите Земли. Рентгеновские лучи рикошетят от четырех пар зеркал, образуя бочкообразный путь, ведущий к точке фокусировки. (NASA)
В настоящее время интересной разработкой является совместная работа с участием 17 стран по строительству массива телескопов в квадратных километрах, способных работать в диапазоне частот от 80 МГц до 2 ГГц. Начальным этапом проекта является строительство Австралийского массива квадратных километров Pathfinder в Западной Австралии (см. рис. 9)..27). В проекте будут использоваться передовые технологии, такие как адаптивная оптика, в которой линза или зеркало состоят из множества тщательно выровненных крошечных линз и зеркал, которыми можно управлять с помощью компьютеров. Ряд быстро меняющихся искажений можно свести к минимуму, деформируя или наклоняя крошечные линзы и зеркала.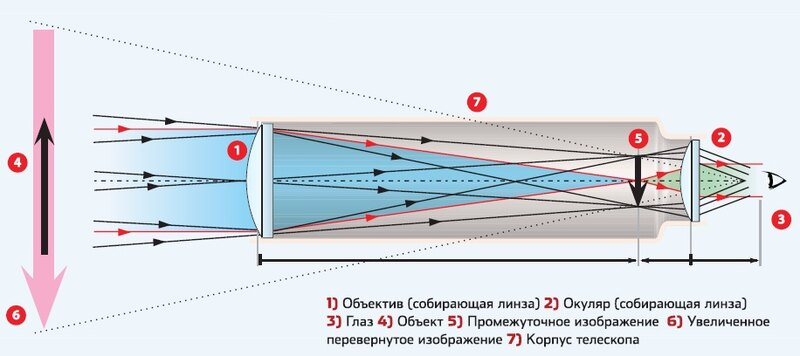

 Его окуляр представляет собой линзу с фокусным расстоянием 4,00 см. а) Каково угловое увеличение телескопа? б) Под каким углом слагается солнечное пятно диаметром 25 000 км? в) Каков угол его телескопического изображения?
Его окуляр представляет собой линзу с фокусным расстоянием 4,00 см. а) Каково угловое увеличение телескопа? б) Под каким углом слагается солнечное пятно диаметром 25 000 км? в) Каков угол его телескопического изображения?
 2, 5.3)
2, 5.3)