Угол рисунок – определение угла, измерение углов, обозначения и примеры

Луч и угол — урок. Геометрия, 7 класс.

Точка, которая лежит на прямой, разделяет прямую на две части, каждая из которых называется лучом, исходящим из этой точки, а саму точку называют началом каждого из лучей.

Точка \(A\) разделяет прямую \(a\) на два луча. Так как в задании важно понять, который из лучей рассматривать,

поставим на прямой ещё две точки \(B\) и \(C\) и назовём лучи:

луч \(AB\) и луч \(AC\).

 

Обрати внимание!

Первой точкой всегда называют начальную точку луча.

На этом рисунке любая из точек может быть начальной точкой некоторого луча, который нарисован. Из каждой точки исходят два луча в противоположных направлениях и так же, как прямая, продолжаются бесконечно.

 

Обрати внимание!

Луч \(BC\) — тот же луч \(BA\), но луч \(BC\) oтличается от луча \(AC\). Эти лучи имеют некоторую общую часть.

Угол — геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Эти лучи называют сторонами  угла, а их общее начало  — вершиной угла.

 

 

Угол обозначают большими латинскими буквами ∡KMN или малыми греческими буквами, например, α.

 

Обрати внимание!

Угол ∡KMN можно назвать также ∡NMK, но буква вершины всегда пишется посередине.

Иногда угол можно обозначить только одной большой латинской буквой вершины,

цифрой или названиями лучей — малыми латинскими буквами, например, ∡M, ∡1 или ∡mn.

Лучи \(n\) и \(m\) с общим началом в точке \(M\) делят плоскость на две части — внутренняя область угла и внешняя область угла.

Углом можно называть также лучи с общим началом вместе с внутренней областью. Тогда точки \(A\) и \(B\) не принадлежат углу ∡M, а точки \(C\), \(D\) и \(E\) принадлежат углу ∡M.

Если нарисовать два луча, исходящих из одной точки, то внутренняя область образует один угол, а внешняя область образует другой угол.

 

Если обе стороны угла лежат на одной прямой, угол называют развёрнутым.

У развёрнутого угла любую из двух частей, на которые он разделяет плоскость, можно считать внутренней областью.

 

Если во внутренней области угла провести луч с началом в вершине данного угла, то этот луч делит данный угол на два угла.

В таком случае очень важно следить за названиями углов, так как мы имеем данный угол и две его части. Например, не совсем понятно, какой угол мы подразумеваем, если пишем ∡A. Лучше использовать три большие буквы, тогда названия углов будут понятны: ∡CAB, ∡CAD, ∡DAB.

www.yaklass.ru

Прямой, тупой, острый и развернутый угол

Давайте начнем с определения того, что такое угол. Во-первых, он является геометрической фигурой. Во-вторых, он образован двумя лучами, которые называются сторонами угла. В-третьих, последние выходят из одной точки, которую называют вершиной угла. Исходя из этих признаков, мы можем составить определение: угол — геометрическая фигура, которая состоит из двух лучей (сторон), выходящих из одной точки (вершины).

Их классифицируют по градусной величине, по расположению относительно друг друга и относительно окружности. Начнем с видов углов по их величине.

Существует несколько их разновидностей. Рассмотрим подробнее каждый вид.

Основных типов углов всего четыре — прямой, тупой, острый и развернутый угол.

Прямой

Он выглядит так:

Его градусная мера всегда составляет 90^о, иначе говоря, прямой угол — это угол 90 градусов. Только они есть у таких четырехугольников, как квадрат и прямоугольник.

Тупой

Он имеет такой вид:

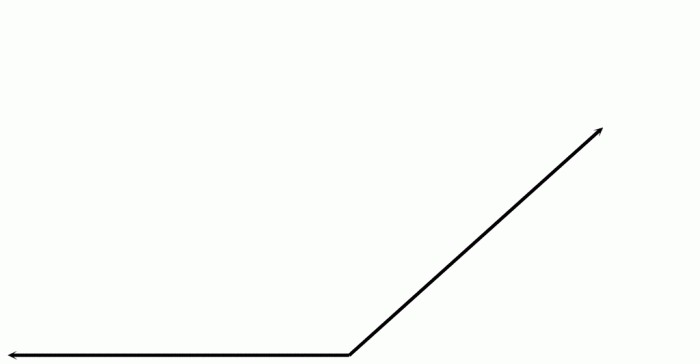
Градусная мера тупого угла всегда больше 90^о, но меньше 180^о. Он может встречаться в таких четырехугольниках, как ромб, произвольный параллелограмм, во многоугольниках.

Острый

Он выглядит так:

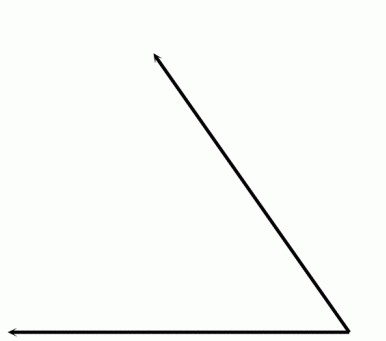
Градусная мера острого угла всегда меньше 90^о. Он встречается во всех четырехугольниках, кроме квадрата и произвольного параллелограмма.

Развернутый

Развернутый угол имеет такой вид:

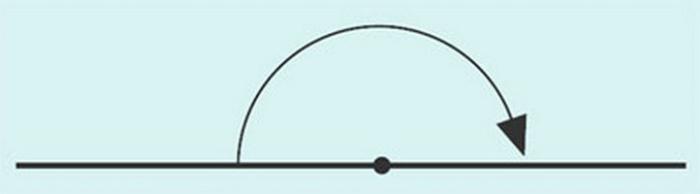
В многоугольниках он не встречается, но не менее важен, чем все остальные. Развернутый угол — это геометрическая фигура, градусная мера которой всегда равняется 180º. На нем можно построить смежные углы, проведя из его вершины один или несколько лучей в любых направлениях.

Есть еще несколько второстепенных видов углов. Их не изучают в школах, но знать хотя бы об их существовании необходимо. Второстепенных видов углов всего пять:

1. Нулевой

Он выглядит так:

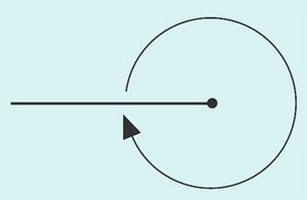
Само название угла уже говорит о его величине. Его внутренняя область равняется 0^о, а стороны лежат друг на друге так, как показано на рисунке.

2. Косой

Косым может быть и прямой, и тупой, и острый, и развернутый угол. Главное его условие — он не должен равняться 0^о, 90^о, 180^о, 270^о.

3. Выпуклый

Выпуклыми являются нулевой, прямой, тупой, острый и развернутый углы. Как вы уже поняли, градусная мера выпуклого угла — от 0^о до 180^о.

4. Невыпуклый

Невыпуклыми являются углы с градусной мерой от 181^о до 359^о включительно.

5. Полный

Полным является угол с градусной мерой 360^о.

Это все типы углов по их величине. Теперь рассмотрим их виды по расположению на плоскости относительно друг друга.

1. Дополнительные

Это два острых угла, образовывающие один прямой, т.е. их сумма 90^о.

2. Смежные

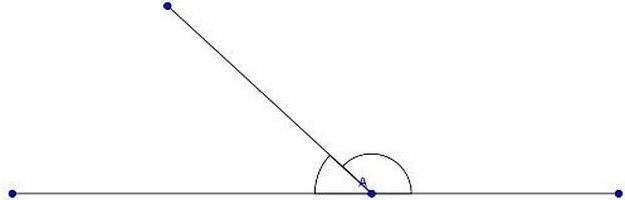
Смежные углы образуются, если через развернутый, точнее, через его вершину, провести луч в любом направлении. Их сумма равна 180^о.

3. Вертикальные

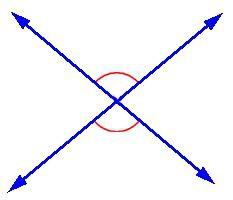
Вертикальные углы образуются при пересечении двух прямых. Их градусные меры равны.

Теперь перейдем к видам углов, расположенным относительно окружности. Их всего два: центральный и вписанный.

1. Центральный

Центральным является угол с вершиной в центре окружности. Его градусная мера равна градусной мере меньшей дуги, стянутой сторонами.

2. Вписанный

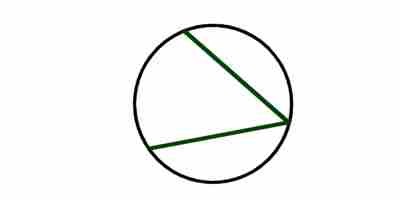
Вписанным называется угол, вершина которого лежит на окружности, и стороны которого ее пересекают. Его градусная мера равна половине дуги, на которую он опирается.

Это все, что касается углов. Теперь вы знаете, что помимо наиболее известных — острого, тупого, прямого и развернутого — в геометрии существует много других их видов.

fb.ru

Конспект «Угол. Смежные и вертикальные углы»

«Угол. Смежные и вертикальные углы»

Ключевые слова конспекта: углы, биссектриса, виды углов, измерение углов, смежные и вертикальные углы, свойства смежных и вертикальных углов, углы при пересечении двух прямых секущей.

---

---

Угол — фигура, образованная двумя лучами, которые выходят из одной точки (вершины).

Биссектриса — луч, который выходит из вершины угла и делит его пополам.

Виды углов. Измерение углов

• Развернутый угол — угoл, стороны которого лежат на одной прямой.
• Прямой угoл — угoл, который равен половине развернутого угла.
• Острый угол — угoл меньше прямого угла.
• Тупой угoл — угoл больше прямого, но меньше развернутого.

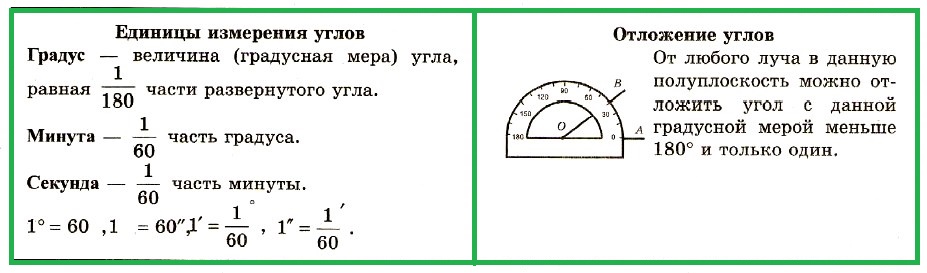
Единицы измерения углов:
Градус — величина (градусная мера) угла, равная части развернутого угла.
Минута — часть градуса.
Секунда — часть минуты.

Смежные и вертикальные углы

Смежные углы — два угла, у которых одна сторона общая,а две другие стороны являются дополняющими лучами.
Вертикальные углы — два угла, стороны одного из которых являются дополняющими лучами сторон другого.

Теорема. Сумма смежных углов равна 180°.

Теорема. Вертикальные углы равны.

---

Свойства смежных и вертикальных углов

 

Углы при пересечении двух прямых секущей

---

Это конспект по теме «Смежные и вертикальные углы». Выберите дальнейшие действия:

uchitel.pro

понятие, определение и виды углов на рисунках

 

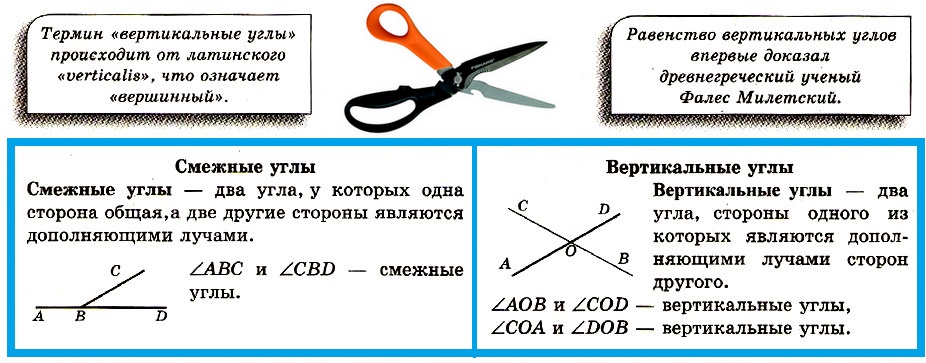
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О, и сторонами k и m.

На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.

Развернутый и неразвернутый угол

Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.

Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла.  На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.

В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).

На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.

Измерение углов

Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус. Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля. 

В зависимости от градусной меры углы делятся на несколько групп.

1. Острый угол — градусная мера от 0 до 90 градусов.

2. Прямой угол — градусная мера 90 градусов.

3. Тупой угол — градусная мера больше 90 градусов.

Нужна помощь в учебе?

Предыдущая тема: Луч: понятие, сущность, примеры и задача
Следующая тема:&nbsp&nbsp&nbspРавенство геометрических фигур: определение и примеры

Все неприличные комментарии будут удаляться.

www.nado5.ru

Угол. Измерение угла — урок. Математика, 5 класс.

Геометрическая фигура угол образуется из двух лучей с общей начальной точкой.

Общая точка называется вершиной угла, а лучи — сторонами угла.

Если угол образован дополнительными (или противоположными) лучами, то он называется развёрнутым.

 

Для названия угла часто используют три большие латинские буквы, название вершины угла пишется посередине.

Иногда угол можно назвать только одной буквой, которая находится у вершины.

Можно также познакомиться с греческим алфавитом и использовать маленькие буквы для названий углов.

Чаще используют: α,β,γ,δ,ϵ,η,ϕ,ω — и другие.

 

Попытаемся представить точку как что-то бесконечно маленькое, а прямую — как что-то бесконечно простирающееся в обе стороны.

 

 

Пример:

описание рисункa:

1. на рисунке показан угол ∡ABC, ∡B или ∡α;

2. также нарисован развёрнутый угол ∡KLM.

Так же как каждый отрезок имеет длину, которую можно измерить линейкой и выразить в единицах измерения, так и каждый угол имеет величину.

 

За единицу измерения углов принимают градус, что является 1180 частью развёрнутого угла.

Величина развёрнутого угла — \(180°\).

Углы измеряют транспортиром.

 

 

Особый угол, половина развёрнутого угла — прямой угол.

Прямой угол обозначают маленьким квадратиком внутри угла.

Величина прямого угла равна \(90°\).

 

Углы, величина которых меньше \(90°\), называются острыми.

 

Углы, величина которых больше \(90°\), называются тупыми.

www.yaklass.ru

Угол / Начальные геометрические сведения / Справочник по геометрии 7-9 класс

1. Главная
2. Справочники
3. Справочник по геометрии 7-9 класс
4. Начальные геометрические сведения
5. Угол

Угол — геометрическая фигура

Мы знаем, что углом называется геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки.

Лучи — это сто­роны угла, а точка (их общее начало) — вершина угла

---

Изображать угол можно и так (не отмечаем точкой общее начало, считаем, что точка есть)

 

Обозначения угла

1)

На сторонах угла не отмечены точки (только обозначены большими латинскими буквами

А и В)

Считается, что буква А обозначает любую точку на верхней стороне угла (по данному рисунку)

Точка В обозначает любую точку на нижней стороне угла (по данному рисунку)

Читаем: угол АОВ

Пишем: 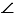АОВ

---

2)

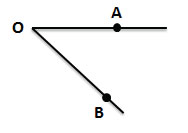
На сторонах угла отмечены и обозначены произвольные точки А и В 

Читаем: угол АОВ

Пишем: 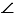 АОВ

---

3)

Стороны угла (лучи) обозначены малыми латинскими буквами k и m

Читаем: угол km

Пишем:  km

---

4)

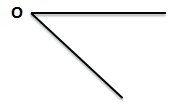
Обозначена только вершина угла

Читаем: угол О

Пишем: 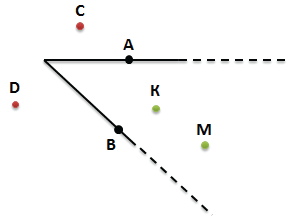О

 

Развернутый угол

Построим прямую АВ и отметим на этой прямой точку О

Лучи ОА и ОВ лежат на одной прямой (являются дополнительными)

Угол АОВ называется развернутым

 

Угол на плоскости

Изобразим часть плоскости

(так как плоскость бесконечна, мы не можем изобразить ее всю, только часть ее)

Построим на этой плоскости неразвернутый угол

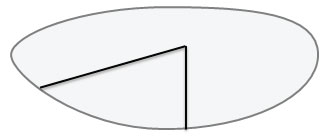
Этот угол делит плоскость на две части (области) — внешнюю и внутреннюю

---

Замечание

Любой угол разделяет плоскость на две ча­сти. Названия этих частей ( внутренняя область и внешняя область) применяется для неразвернутого угла.

Если угол развёрнутый, то любую из двух частей, на которые он разделяет плоскость, мож­но считать внутренней областью угла.

---

 

Расположение точек относительно угла

По рисунку определим положение отмеченных точек A, B, C, D, K, M

Точки А и В лежат на сторонах угла

Точки D и C лежат вне угла (во внешней об­ласти угла)

Точки К и М, лежат внутри угла (во внутренней об­ласти угла)

---

При необходимости мы можем продолжить стороны угла, например, чтобы уточнить положение точки М

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Точки, прямые, отрезки

Провешивание прямой на местности

Луч

Равенство геометрических фигур

Сравнение отрезков

Сравнение углов

Длина отрезка

Единицы измерения длины, расстояний

Градусная мера угла

Измерение углов на местности

Смежные углы

Вертикальные углы

Перпендикулярные прямые

Построение прямых углов на местности

Начальные геометрические сведения

Правило встречается в следующих упражнениях:

7 класс

Задание 6, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 21, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 8, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 266, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 300, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 664, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 9, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 11, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 811, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 875, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

---

© budu5.com, 2019

Пользовательское соглашение

Copyright

budu5.com

Геометрия. Урок 2. Углы — ЁП

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!

Содержание страницы:

 

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB  или ∠BOA,  но ни в коем случае не ∠OAB,∠OBA,∠ABO,∠BAO.

Величину угла измеряют в градусах. ∠AOB=24°.

 

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Или

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.

∠AOD=∠BOD=∠AOB2

Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.

Свойство: сумма смежных углов равна 180°.

Пример:

Пары углов

(1) и (3)
(2) и (4)

называются вертикальными.

По свойству вертикальных углов:

∠COD=∠AOB
∠BOD=∠AOC

Пары углов

(1) и (2)
(2) и (3)
(3) и (4)
(4) и (1)

называются смежными.

По свойству смежных углов:

∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°

 

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

Пары углов:

(1) и (5)
(2) и (6)
(3) и (7)
(4) и (8)

называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).

Пары углов:

(3) и (5)
(4) и (6)

называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).

Пары углов:

(1) и (7)
(2) и (8)

называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).

Пары углов:

(3) и (6)
(4) и (5)

называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).

Пары углов:

(1) и (8)
(2) и (7)

называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).

Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:

• Соответственные углы равны.
• Внутренние накрест лежащие углы равны.
• Внешние накрест лежащие углы равны.
• Сумма внутренних односторонних углов равна 180°.
• Сумма внешних односторонних углов равна 180°.

 

Сумма углов произвольного n-угольника вычисляется по формуле:

Sn=180°⋅(n−2)

где n – это количество углов в n-угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.

Сумма углов треугольника: S3=180°⋅(3−2)=180°

Сумма углов четырехугольника: S4=180°⋅(4−2)=360°

Сумма углов пятиугольника: S5=180°⋅(5−2)=540°

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.

αn=180°⋅(n−2)n

 

Модуль геометрия: задания, связанные с углами

 

Скачать домашнее задание к уроку 2.

 

epmat.ru