Закон квадрата-куба | это… Что такое Закон квадрата-куба?
Закон квадрата — куба представляет собой принцип, применяемый в технике и биомеханике, и базируется на математическом пересчете размеров. Он был впервые продемонстрирован в 1638 г. Галилео Галилеем в «Discorsi e Dimostrazioni Matematiche, intorno a due nuove scienze («Беседы и математические доказательства двух новых наук»), 1638»;. Он гласит
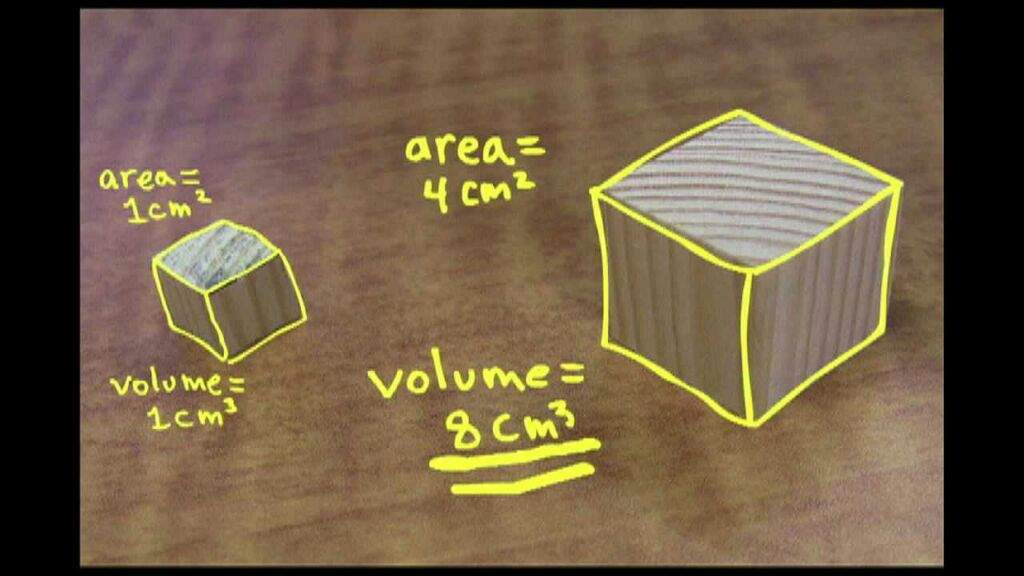
Когда объект подвергается пропорциональному увеличению размеров, его новый объем будет пропорционален кубу множителя, а новая площадь его поверхности пропорциональна квадрату множителя.
где v1 — объем исходного объекта, v2 — новый объем, — линейный размер исходного объекта, а — новый линейный размер. Заметьте, что не имеет значения, какой линейный размер используется.
где A1 — площадь поверхности исходного объекта, а A2 — новая площадь поверхности.
Например, куб с длиной стороны 1 метр имеет плошадь поверхности 6 м² и объем 1 м³. Если длину стороны удвоить, площадь его поверхности увеличится до 24 м², а его объем увеличится до 8 м³. Этот принцип применим ко всем телам.
Содержание
|
Применения
Техника
Если физический объект увеличить в размерах при сохранении неизменной плотности материала, из которого он изготовлен, его масса увеличится в третьей степени, в то время как площадь его поверхности — только в квадрате масштабного множителя. Это должно означать, что в том случае, если увеличенному в размерах объекту сообщить то же ускорение, что и оригиналу, на поверхность увеличившегося объекта будет действовать большее давление
Давайте рассмотрим простой пример — тело массой = M имеет ускорение = a и площадь поверхности = A , на которую действует ускоряющая сила.
Сила, вызванная ускорением: F = M*a, а давление на поверхность T = F/A = M*a/A
Теперь рассмотрим объект, размеры которого умножены на коэффициент = x так, чтобы его новая масса M’ = x3*M, а поверхность, на которую действует сила, имеет новую площадь, A’ = x2*A.
Новая сила, вызванная ускорением F’ = x³*M*a и
Результирующее давление на поверхность
T' = F'/A'
= x3*M*a/(x2*A)
= x*(M*a/A)
= x*T
Таким образом, при простом увеличении размеров объекта с сохранением того же самого материала конструкции (плотности), и при же самом ускорении, давление, производимое им на повехность, увеличится во столько же раз. Это показывает, что способность сопротивляться напряжению у объекта снизится и он станет более склонен к разрушению в процессе ускорения.
Это и есть объяснение тому, почему большие транспортные средства плохо выдерживают испытания на разрушения при столкновениях и почему есть пределы высоты строительства высотных зданий.
Аналогично, чем больше размер объекта, тем меньше другие объекты окажут сопротивление движению, вызывая его замедление
Биомеханика
Если размеры животного значительно увеличить, его мускульная сила серьезно уменьшится, так как поперечное сечение его мускулов увеличится пропорционально площади коэффициента масштабирования, в то время как его масса увеличится пропорционально кубу коэффициента масштабирования. В результате этого сердечно-сосудистые функции сильно ограничатся. Для летающих животных, если их увеличить в размерах, их нагрузка на крылья должна возрасти, и поэтому им, чтобы совершать такой же взлет, придется лететь быстрее,. Это будет нелегко ввиду того, что сила мускулов станет меньше. Это также объясняет, почему шмель может иметь большой размер тела относительно размаха его крыльев, что невозможно для большего летающего животного. Для животных малых размеров сопротивление воздуха на единицу массы также выше, что объясняет, отчего маленькое насекомое, такое, как муравей не погибнет, падая с любой высоты, а экипаж танка, также как и слон, не сможет выжить при падении с высоты в одну милю
По этой причине гигантские насекомые, пауки и другие животные, показываемые в фильмах ужасов — нереальны, поскольку такие крутые размеры вызвали бы их разрушение.
Исключением являются гигантские водные животные, поскольку вода способна поддерживать такие огромные существа.
Данная статья статья представляет собой несколько доработанный перевод статьи из английской Википедии
Square-Cube Law
См. также
Биомеханика
Allometric law (англ.)
On Being the Right Size (англ.)
Ссылки
Wayne Throop. «Sauropods, Elephants, Weightlifters: Miscellaneous Issues» (англ.).
«World Builders: The Limits to Animal Size — Size to Volume Ratio». (англ.)
Michael C. LaBarbera. «The Biology of B-Movie Monsters»(англ.)
Закон квадрата | это… Что такое Закон квадрата?
Закон квадрата — куба представляет собой принцип, применяемый в технике и биомеханике, и базируется на математическом пересчете размеров. Он был впервые продемонстрирован в 1638 г. Галилео Галилеем в «Discorsi e Dimostrazioni Matematiche, intorno a due nuove scienze («Беседы и математические доказательства двух новых наук»), 1638»;.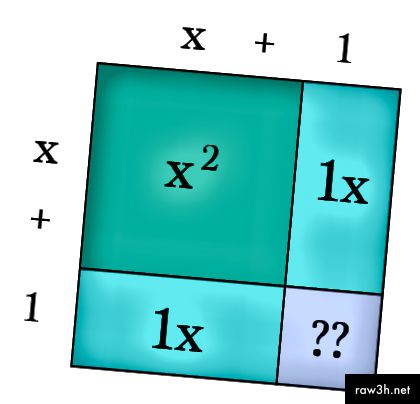
Он гласит
Когда объект подвергается пропорциональному увеличению размеров, его новый объем будет пропорционален кубу множителя, а новая площадь его поверхности пропорциональна квадрату множителя.
где — объём исходного объекта, — новый объём, — линейный размер исходного объекта, а — новый линейный размер. Заметьте, что не имеет значения, какой линейный размер используется.
где — площадь поверхности исходного объекта, а — новая площадь поверхности.
Например, куб с длиной стороны 1 метр имеет площадь поверхности 6 м² и объём 1 м³. Если длину стороны удвоить, площадь его поверхности увеличится до 24 м², а его объём увеличится до 8 м³. Этот принцип применим ко всем телам.
Содержание
|
Техника
Если физический объект увеличить в размерах при сохранении неизменной плотности материала, из которого он изготовлен, его масса увеличится пропорционально произведению массы и коэффициента увеличения в третьей степени, в то время как площадь его поверхности — только в квадрате масштабного множителя.
Давайте рассмотрим простой пример — тело массой = M имеет ускорение = a и площадь поверхности = A , на которую действует ускоряющая сила.
Сила, вызванная ускорением: F = M*a, а давление на поверхность T = F/A = M*a/A
Теперь рассмотрим объект, размеры которого умножены на коэффициент = x так, чтобы его новая масса M’ = x3*M, а поверхность, на которую действует сила, имеет новую площадь, A’ = x2*A.
Новая сила, вызванная ускорением F’ = x³*M*a и
Результирующее давление на поверхность
T' = F'/A'
= x3 *M*a/(x2*A)
= x*(M*a/A)
= x*T
Таким образом, при простом увеличении размеров объекта с сохранением того же самого материала конструкции (плотности), и при том же самом ускорении, давление, производимое им на поверхность, увеличится во столько же раз.
Это показывает, что способность сопротивляться напряжению у объекта снизится и он станет более склонен к разрушению в процессе ускорения.
Это и есть объяснение тому, почему большие транспортные средства плохо выдерживают испытания на разрушения при столкновениях и почему есть пределы высоты строительства высотных зданий. Аналогично, чем больше размер объекта, тем меньше другие объекты окажут сопротивление движению, вызывая его замедление
Биомеханика
Если размеры животного значительно увеличить, его мускульная сила серьёзно уменьшится, так как поперечное сечение его мускулов увеличится пропорционально квадрату коэффициента масштабирования, в то время как его масса увеличится пропорционально кубу коэффициента масштабирования. В результате этого сердечно-сосудистые функции сильно ограничатся. Для летающих животных, если их увеличить в размерах, их нагрузка на крылья должна возрасти, и поэтому им, чтобы сохранять ту же подъемную силу, придется лететь быстрее,. Это будет нелегко ввиду того, что сила мускулов станет меньше.
По этой причине гигантские насекомые, пауки и другие животные, показываемые в фильмах ужасов — нереальны, поскольку такие крупные размеры вызвали бы их разрушение. Исключением являются гигантские водные животные, поскольку вода способна поддерживать такие огромные существа.
Тепловые процессы
Закон квадрата-куба применим также и к тепловым процессам. Поверхность теплообмена возрастает пропорционально квадрату размера, а объём, содержащий или генерирующий теплоту — пропорционально кубу. Следовательно, теплопотери в расчёте на единицу объёма объекта уменьшаются при увеличении его размеров и, наоборот, увеличиваются при уменьшении размеров. Поэтому, например, энергия, необходимая для обогрева или охлаждения единицы объёма склада, уменьшается с ростом размеров склада.
В технике
Закон имеет очень широкое применение в технике. К примеру, он является единственной причиной того, что для создания самолетов вдвое бОльшей грузоподъемности было бессмысленно (и никогда не применялось) удвоение всех размеров на всех чертежах самолета — запрет на прямое масштабирование наложен законом квадрата-куба.
Интересным примером непонимания данного закона уже в наше время является история создания двигателя для а/м «Запорожец». Данный двигатель был скопирован удвоением всех основных размеров небольшого двухцилиндрового пускового двигателя с немецких бомбардировщиков времен II Мировой войны. Это безграмотное решение привело к целой лавине негативных эффектов, от несоответствия массы балансиров шатунов требуемой, до большой избыточной толщины стенок цилиндров, впоследствии растачивавшихся любителями до фантастических диаметров.
В живых существах
Данная статья представляет собой несколько доработанный перевод статьи из английской Википедии Square-Cube Law с добавлением текста о тепловых процессах
См.
такжеБиомеханика
Allometric law (англ.)
On Being the Right Size (англ.)
Ссылки
Wayne Throop. «Sauropods, Elephants, Weightlifters: Miscellaneous Issues» (англ.).
«World Builders: The Limits to Animal Size — Size to Volume Ratio». (англ.)
Michael C. LaBarbera. «The Biology of B-Movie Monsters»(англ.)
Закон обратных квадратов
Закон обратных квадратов Любой точечный источник, распространяющий свое влияние одинаково во всех направлениях без ограничения радиуса действия, будет подчиняться закону обратных квадратов. Это следует из строго геометрических соображений. Интенсивность воздействия на любом заданном радиусе r есть сила источника
разделить на площадь шара. Будучи строго геометрическим по своему происхождению, закон обратных квадратов применим к разнообразным явлениям. Точечные источники гравитационной силы, электрического поля, света, звука или излучения подчиняются закону обратных квадратов. Применение закона обратных квадратов:
| Индекс | |||||
| Назад |
Это предмет продолжающихся споров с таким источником, как скунс на вершине флагштока; исчезнет ли его запах по закону обратных квадратов?Как одно из полей, которые подчиняются общему закону обратных квадратов, гравитационное поле можно представить в форме, показанной ниже, показывающей, что ускорение свободного падения g является выражением интенсивности гравитационного поля.
| Индекс Концепции гравитации | |||||
| Вернуться назад |
Как одно из полей, подчиняющихся общему закону обратных квадратов, электрическое поле точечного заряда можно представить в виде, показанном ниже
где точечный заряд Q — источник поля.
| Индекс Концепции гравитации | ||||||||||||||||||||||||||||||||||
«Квадратный закон»
Кривые вентилятора и насоса представляют собой характеристику вентилятора или насоса с точки зрения расхода и напора или давления, которые будут создаваться данным элементом оборудования с заданной конструкцией рабочего колеса и заданным диаметром рабочего колеса при заданная скорость. Системные кривые — это характеристика трубопроводной сети с точки зрения напора, необходимого для создания заданного расхода. Их форма сильно зависит от физических характеристик трубопроводной сети; расстояния, диаметр трубы, количество и тип фитингов и т. д. Форма кривой немного более предсказуема, поскольку она выпадает из фундаментального физического соотношения, называемого уравнением Дарси-Вейсбаха. Выглядит немного пугающе, но, к счастью, вытекающий из него квадратичный закон гораздо менее страшен. Если вы работаете с насосами или вентиляторами, очень полезно понимать, что если вы нанесете кривую системы для вашей системы на вентилятор или кривую насоса для вентилятора или насоса, который его обслуживает, точка, где эти две пересекающиеся линии являются рабочей точкой для вентилятора или насоса, обслуживающего эту конкретную систему в этой конкретной конфигурации. Например, на левом рисунке показана системная кривая для вентилятора Greenheck 40-AFDW-41, работающего при 37 500 кубических футов в минуту и 4 дюйма водяного столба. статического давления. На правом рисунке показана системная кривая для Bell and Gossett Series e-1510 6G, работающего со скоростью 1100 галлонов в минуту и 40 футов вод. точно не соответствует ни одной из линий стандартных размеров крыльчатки. (Вы можете использовать закон подобия насоса, чтобы предсказать размер рабочего колеса, который вам нужен, что является отдельным обсуждением. Квадратичный закон применим к стационарной системеПри применении квадратичного закона есть несколько вещей, которые вы должны принять во внимание, чтобы использовать его правильно. Во-первых, квадратичный закон применяется к тому, что называется «фиксированной системой»; то есть система, в которой все заслонки и клапаны находятся в фиксированном положении, а вентилятор или насос работают с фиксированной скоростью. Если что-то изменилось в системе, например:
, то эти действия создают новую системную кривую. На практике это означает, что система водоснабжения с трехходовыми регулирующими клапанами, обслуживающая нагрузки или печь в вашем доме, будет работать как стационарная система.
тогда различные условия, создаваемые движением клапана или скоплением пыли в печном фильтре, приведут к немного другой рабочей точке и слегка другая системная кривая Квадратичный закон и уравнение Дарси Вейсбаха Квадратный закон берет свое начало в уравнении Дарси Вейсбаха, как упоминалось ранее. Это соотношение предполагает полностью развитое турбулентное течение. В то время как это обычноверно для наших систем, это не всегда верно.
, представляет собой другой тип потока, называемый потоком «открытого канала», и его нельзя предсказать с помощью уравнения Дарси Вейсбаха. С учетом того, что даже в полностью заполненных трубах и воздуховодах, находящихся под давлением в системах HVAC, могут быть некоторые места и/или рабочие условия, при которых поток не будет полностью развиваться турбулентным потоком. Например, в фильтре или сетчатом фильтре, где площадь поперечного сечения может увеличиваться по сравнению с воздуховодом или трубой, обслуживающей его, поток может фактически быть ламинарным или переходным от турбулентного к ламинарному, даже при проектных условиях. Или в трубе в змеевике или в воздуховоде, где поток изменяется, может быть условие нагрузки, ниже которого поток переходит от полностью развитого турбулентного потока к ламинарному потоку. Открытые и закрытые системы
Напротив, вода в системе охлажденной воды обычно видит только сжимаемый газ, такой как воздух в расширительном баке. Это не означает, что не существует закрытых систем водяного конденсатора и открытых систем охлажденной воды. Например, есть градирни, в которых на самом деле есть змеевик, содержащий воду конденсатора, а затем отдельный контур трубопровода, который используется для распыления воды над змеевиком и ее охлаждения, в основном за счет испарения. В этом случае фактический водяной контур конденсатора представляет собой замкнутый контур, а насос, распыляющий воду на змеевик, представляет собой разомкнутый контур.
Перепад высот между уровнем воды в бассейне градирни и выпускным отверстием в верхней части системы трубопроводов называется «подъемом» градирни, потому что если вы хотите, чтобы вода циркулировала в контуре, то в В дополнение к напору, достаточному для преодоления сопротивления потока, которое возникнет при движении воды по трубе, насос также должен иметь достаточную напорную способность для подъема воды через перепад высот между выпускным отверстием в верхней части трубы. Напротив, насосу в закрытой системе достаточно давления, достаточного для преодоления сопротивления потока в контуре трубопровода, даже если здание высотой в сотни футов. Это связано с тем, что вес воды на одной стороне контура трубопровода толкает воду вверх по другой стороне. Квадратичный закон и открытые системы Если вы провели небольшой мысленный эксперимент, в котором использовалась открытая система с насосом, оснащенным каким-либо приводом с регулируемой скоростью, и вы начинаете с насоса при нулевой скорости вращения и постепенно увеличиваете скорости насоса, вы, вероятно, можете видеть, что до тех пор, пока насос не будет вращаться достаточно быстро, чтобы создать давление нагнетания, равное весу воды в части трубы над резервуаром башни, потока не будет. Это означает, что для открытых систем системная кривая не проходит через нуль галлонов в минуту при нулевом напоре. Скорее, он проходит через точку нуля галлонов в минуту при давлении, равном подъемной силе башни. Например, если подъем на башне составляет 10 футов водяного столба, то кривая системы будет начинаться с 0 галлонов в минуту при 10 футах водяного столба. И если вы повторите небольшой мысленный эксперимент в начале этого раздела, вы, вероятно, увидите, что в этой системе не будет потока, поскольку вы увеличиваете скорость насоса до тех пор, пока скорость вращения не будет составлять 10 футов вод. ст. давления. Тогда начнет возникать поток, и связь между потоком и давлением, необходимым для его создания, будет предсказуема по квадратичному закону. Это означает, что если вы хотите рассчитать кривую системы для открытой системы, вам нужно выполнить расчет только для той части напора, которая приведет к циркуляции воды. Итак, если в нашем примере системе требуется 10 футов водяного столба. чтобы поднять воду над башней и еще 20 ft.w.c. для циркуляции воды нам понадобится насос, рассчитанный на расчетный расход при 30 футах водяного столба. Но мы бы рассчитали системную кривую только на основе 20 футов водяного столба. Квадратичный закон и замкнутые системыСистемы зданий обычно управляются либо для поддержания фиксированного давления в некоторой точке системы, либо для фиксированного расхода. Например, насосные системы с переменным расходом и системы вентиляторов могут управляться для фиксированного давления в некоторой точке ниже по потоку от насоса или вентилятора, поскольку регулирующие клапаны или заслонки открываются и закрываются в ответ на изменения нагрузок, с которыми они связаны. Точно так же можно управлять вентилятором постоянного объема или насосной системой, чтобы поддерживать постоянный объем, даже если фильтры накапливают мусор и требуют большего давления для поддержания постоянной скорости потока. Существует ряд различных стратегий управления, которые используются для достижения рабочих профилей системы этого типа, и результатом может быть условие, при котором система развивает определенное давление, даже если их поток не создается. Напротив, все ситуации, описанные в начале этого раздела, связаны с системами, которые не являются стационарными системами;
Для любой из заданных системных кривых, полученных в результате изменений в системе, описанных выше, если вы замедлите работу насоса или вентилятора без каких-либо других изменений, рабочая точка будет следовать системной кривой, проходящей через нуль расход при нулевом напоре. Но, поскольку системы контролируются для обеспечения требуемого уровня производительности, будь то устойчивый поток при изменении условий или фиксированное давление при изменении условий, то, если вы нанесете на график точки, связанные с каждым рабочим состоянием, вы получите либо прямую вертикальная линия с постоянным расходом для систем, контролирующих постоянный расход, как показано на изображении слева ниже, или семейство кривых, которые не являются чистыми параболами (название кривой, которая создается с помощью y, является функцией квадрата x отношение типа), которое будет проходить через ноль кубических футов в минуту при целевом фиксированном рабочем давлении, как показано на изображении справа. Для системы с переменным расходом (правая иллюстрация) принято считать, что рабочая кривая представляет собой параболу, проходящую через нулевой расход при фиксированной заданной точке рабочего давления. Хотя в целом это верно, это не совсем так, как видно из иллюстрации. Но для большинства рабочих условий принятие параболы через ноль кубических футов в минуту при фиксированном рабочем давлении является разумным предположением. Это то, что вы могли бы спроектировать, если бы использовали версию квадратичного закона, связанную с открытой системой, которая была представлена в конце предыдущего раздела. Применение квадратичного закона для понимания производительности насосов и вентиляторов В полевых условиях или при проектировании знание квадратичного закона и способов его применения может оказаться очень полезным. Например, если вы столкнулись с насосом, у которого был дросселирован нагнетательный клапан, вполне вероятно, что подрядчик по балансировке сделал это, чтобы вернуть насос в расчетную рабочую точку, потому что оказалось, что он имеет больший напор, чем необходимо для достижения расчетного расхода в » как установленная система». Но есть и хорошие новости. оказывается, что вы можете использовать кривую насоса, квадратичный закон и полевые испытания, чтобы получить информацию, необходимую для оценки вариантов. На рисунке ниже и слева показаны рабочая точка и кривая системы для проектных условий, а также размер рабочего колеса, необходимый для их обеспечения. Так как насос оказался негабаритным, его пришлось дросселировать, чтобы вернуть его в проектную точку. На рисунке ниже и справа показана новая рабочая точка (красный кружок), которая была создана, когда клапан был полностью открыт. В отличие от стационарных систем (которые, как правило, являются системами с постоянным расходом), системы с переменным расходом (например, водяные системы с двухходовыми клапанами на потребителях или воздушные системы с оборудованием для регулирования расхода на оконечных устройствах) фактически работать с семейством системных кривых, поскольку при каждом движении клапана или заслонки создается новая рабочая точка и системная кривая. Например, на рисунке слева показано, как будет меняться кривая системы для вентилятора Greenheck по мере того, как фильтры переходят от перепада давления, который они имеют, когда они чистые, к перепаду давления, который они имеют, когда они загрязнены. На правом рисунке показана новая системная кривая, созданная для примера с насосом Белла и Госсета после открытия дроссельного клапана на нагнетании насоса. Новая системная кривая позволяет оценить различные варианты оптимизации насоса, чтобы он обеспечивал расчетный расход при широко открытом клапане, например, изменение размера рабочего колеса, как показано ниже, или изменение скорости насоса, как показано на рисунке. выше. Суть в том, что, используя квадратичный закон для проектирования кривой системы для различных условий работы в наших системах, а затем нанося результаты на кривую вентилятора или насоса для обслуживающего их оборудования, мы можем получить представление о том, как системы будут работать и какие стратегии мы могли бы использовать для оптимизации их работы. Загрузка ниже даст вам файлы .wmf для уравнения Дарси Вейсбаха и уравнения квадратного закона, которые я проиллюстрировал ранее в посте. Вам также будет полезна соответствующая информация на веб-сайте:
|
| ||||||||||||||||||||||||||||||||||
Электрическая сила в законе Кулона подчиняется закону обратных квадратов.
д. Для любого такого описания источника, если вы определили количество излучения на единицу площади, достигающее 1 метра, то оно будет вчетверо больше на 2 метра.
Форма кривой очень специфична для физических характеристик вентилятора или насоса и деталей их конструкции. И хотя конструктор, вероятно, предвидит форму кривой для вентилятора или насоса, которые он проектирует, опубликованные кривые основаны на заводских испытаниях в условиях, определяемых отраслевыми стандартами. Изображение слева — это пример кривой вентилятора, а изображение справа — пример кривой насоса. Обе они представляют собой диаграммы в Excel, созданные из изображения кривой производителя с помощью Plot Digitizer. Изображения, которые были оцифрованы для их создания, также показаны ниже оцифрованных версий для сравнения.
)
Я использовал фразу «будет стремиться к работе, потому что, если:
Например: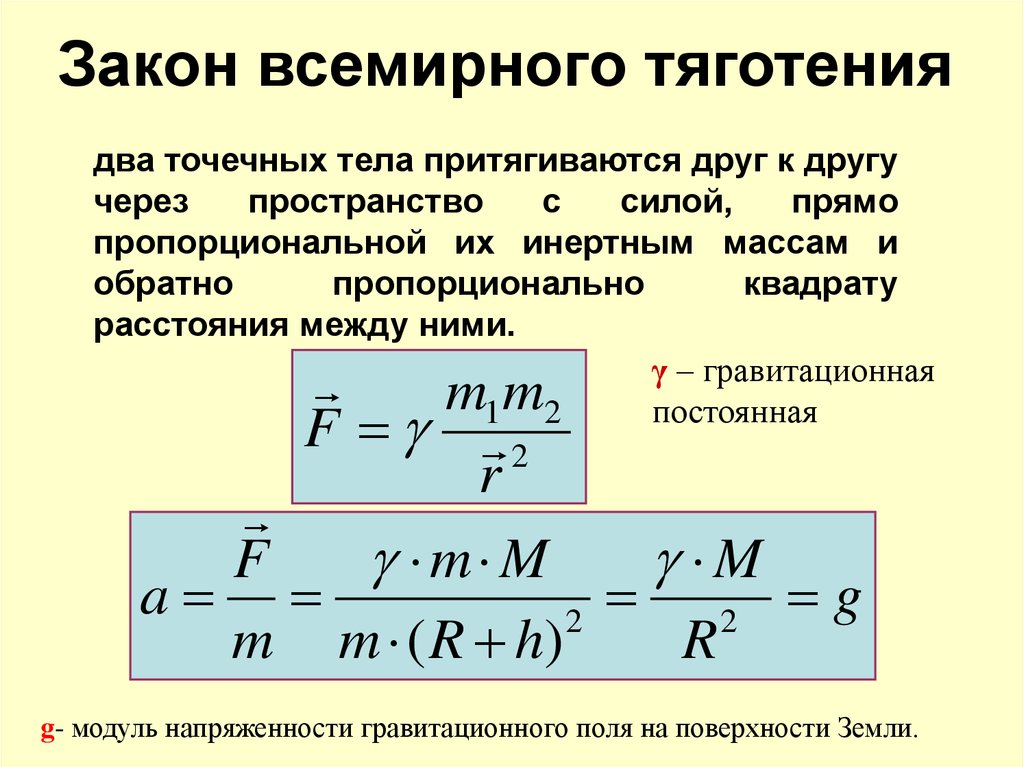
Сам расширительный бак обычно закрыт и находится под давлением, но на некоторых объектах это может быть открытый бак, расположенный в верхней точке системы.
Воздухоочистители, в которых охлажденная вода распыляется в воздушный поток для его охлаждения и осушения, также являются примерами открытых систем охлажденной воды. 
башня и уровень воды в бассейне.
который произвел поток, с формулой, похожей на то, что показано ниже.
Но важно понимать, что, несмотря на сходство с описанным выше явлением, есть тонкая, но существенная разница. Для явления, описанного для открытой системы, сначала не было потока и, следовательно, не было падения давления из-за потока, условие, которое сохранялось до тех пор, пока насос не создавал достаточное давление, чтобы поднять воду над градирней и запустить поток, после чего давление, необходимое для производимый поток был функцией квадрата расхода. В системе не было никаких изменений, которые привели бы к прекращению потока, когда давление упало ниже подъемной силы башни, а система трубопроводов была стационарной.
Хорошей новостью является то, что процесс дросселирования, вероятно, сэкономил немного энергии по сравнению с тем, чтобы ничего не делать. Но плохая новость заключается в том, что падение давления, которое происходит через дроссельный клапан, на самом деле представляет собой потраченную впустую энергию по сравнению с тем, что потребовалось бы, если бы вы могли достичь расчетного расхода с широко открытым клапаном.
Затем квадратичный закон был использован для проецирования системной кривой для новой рабочей точки на кривой насоса, что затем позволяет вам оценить варианты оптимизации насоса, такие как обрезка рабочего колеса (показано на изображениях после следующего раздела текста) или изменение скорости насоса (показано ниже).
Выполнение этого анализа позволяет предсказать, как мощность вентилятора системы будет меняться в зависимости от загруженных фильтров.
