Зависимость фокусного расстояния от расстояния до объекта: Зависимость угла обзора от фокусного расстояния

Как вычислить расстояние до объекта по фотографии

В связи с известным событием по всему интернету развернулись бурные дискуссии, участники которых обвиняют своих оппонентов то в незнании программы средней школы, то в непонимании того очевидного факта, что в военное время косинус угла может достигать четырёх.

Не желая в эти дискуссии ввязываться, я лучше на наглядном примере покажу вам, как, имея на руках фотографию какого-либо известного объекта и немного вспомогательной информации, можно с большой точностью по совсем не сложным формулам рассчитать, на каком расстоянии этот объект находился от фотографа в момент съёмки. По возможности я постараюсь каждый шаг сопровождать иллюстрацией, расчётом или ссылкой на источник. Итак, приступим.

Как известно, простейший объектив для фотоаппарата можно сделать из одной двояковыпуклой линзы. Конечно, существуют фотоаппараты вообще без объектива (так называемые пинхол-камеры, предок которых — камера-обскура), но в данном случае они нам не слишком интересны. Для начала мы рассмотрим, как строится изображение в простейшем однолинзовом объективе, а затем я покажу, что те же методы хорошо подходят и для сложных объективов, сочетающих в себе более десятка последовательно расположенных линз.

Напомню вам схему хода лучей в тонкой линзе из школьного курса геометрической оптики:

На этой схеме d — расстояние от линзы до объекта, D — расстояние от линзы до изображения объекта (на матрице или плёнке), а f — фокусное расстояние линзы.

Формула тонкой линзы из того же курса связывает эти три расстояния:

Теперь ещё раз посмотрим на оптическую схему: h — это линейный размер объекта съёмки, а H — размер его уменьшенного изображения. Нетрудно заметить, что h = d tan α, а H = D tan α (это следует из свойств прямоугольного треугольника). Подставив эти величины в формулу тонкой линзы, увидим, что tan α сокращается, и в результате получим следующее уравнение:

«Неудобная» величина D ушла, а остальные мы знаем или можем легко вычислить. На основе этого уравнения получаем вот такую формулу расстояния до объекта:

Ну а теперь давайте проверим её на практике.

Вот фотография, которую я сделал из своего окна:

На ней запечатлён дом 1 по 3-му Дорожному проезду, что в Москве. Это 22-этажная башня серии И-700А.

Какую полезную информацию можно извлечь из данной фотографии? Напомню, для расчёта нам нужны неизвестные пока величины h, H и f. h — это реальная высота дома (в метрах). Сходу я её не нагуглил, зато выяснил вот что: высота потолков в этом доме — 2,64 м, а толщина перекрытий — 0,22 м. Наверняка при измерении высоты потолков не учитывалась толщина напольного покрытия. Точно она мне не известна, так что, немного округлив, примем высоту одного этажа равной 2,9 м. Хорошо видны 23 панели, таким образом, высота видимого участка составляет примерно 66,7 м. Запомним эту величину и приступим к анализу фотографии.

H — это размер изображения дома на матрице фотоаппарата.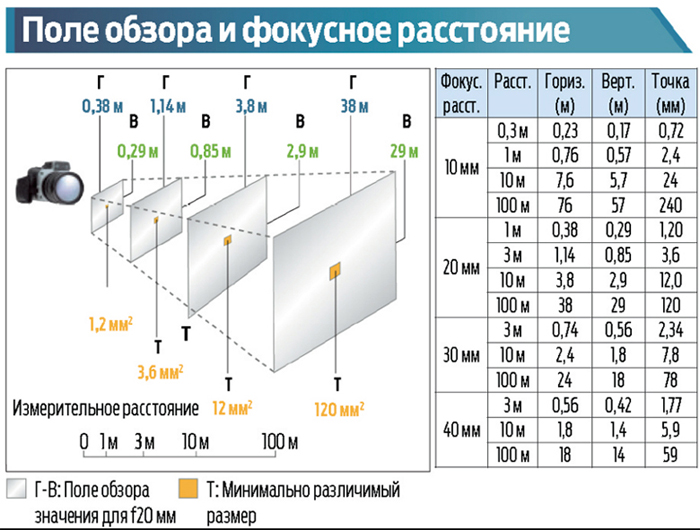 По фотографии мы можем подсчитать его в пикселях, но, как известно, размер пикселя — это всё равно что размер ангела: точных данных ни у кого нет. Но здесь нужно вспомнить, что конкретные физические размеры имеет матрица фотоаппарата. Лезем в поисковик и узнаём, что для камеры Nikon D90 размер матрицы составляет 2,36 × 1,58 см, а разрешение — 4288 × 2848 пикс. Наша фотография не была кадрирована или повёрнута, поэтому мы можем узнать точный линейный размер изображения дома на матрице, составив пропорцию. Но чтобы делать это не вручную, воспользуемся программой Adobe Photoshop, где есть масса полезных инструментов.

По умолчанию Photoshop, конечно, не знает, какого размера должна быть наша фотография, и указывает ей разрешение 300 пикс./дюйм, или 118,11 пикс./см:

Но мы, зная физический размер матрицы и количество пикселей по длинной стороне снимка, делаем такой расчёт: 4288 / 2,36 (размер матрицы в сантиметрах), и получаем правильное разрешение — 1817 пикс./см. Вписываем его в соответствующее окошко и, чтобы не изменились реальные размеры фотографии, а лишь были пересчитаны её длина и ширина в см, указываем в верхних полях «100 проц»:

Как видите, при этом в поле «Размер печатного оттиска» появились уже известные нам размеры матрицы: 2,36 × 1,57 см.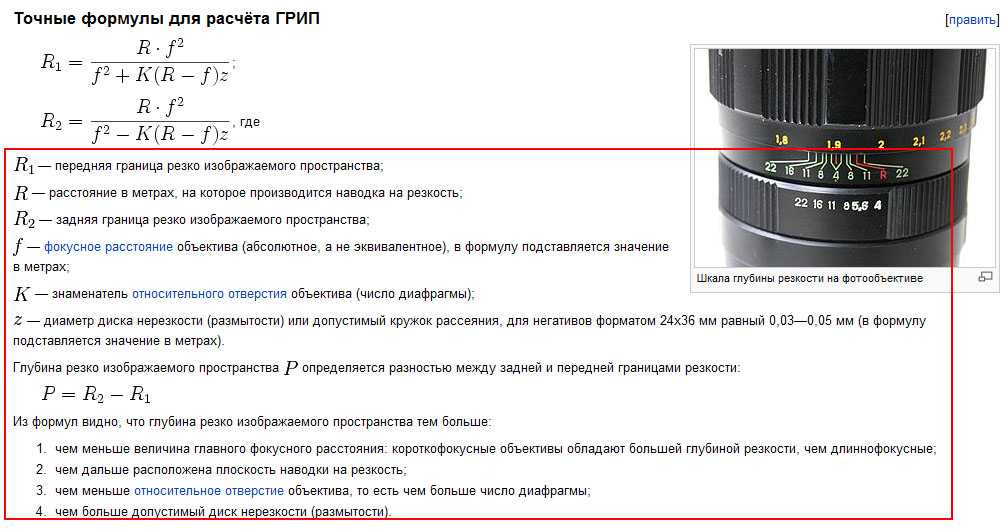 Точнее, в спецификации было указано 1,58 см, но это несущественная погрешность.

Теперь при помощи инструмента «Линейка» измерим высоту видимого участка дома (23 панели) на фотографии (смотрите в правый верхний угол):

Получается, что высота изображения дома на матрице составляет 1,92 см, или 0,0192 м.

Осталось только выяснить фокусное расстояние, но для этого, к счастью, ничего считать не нужно: оно сразу прописывается при съёмке в метаданных фотографии (EXIF). Открываем их в фоторедакторе и видим:

Фокусное расстояние при съёмке составляло 105 мм, или 0,105 м, то есть я снимал дом с максимально возможным для этого объектива приближением.

Ну что ж, теперь у нас есть все данные для расчёта. Подставляем их в формулу

и получаем: d = (0,105(0,0192 + 66,7)) / 0,0192 = 364,9 м. Внимательный читатель наверняка заметил, сколь ничтожно мала величина H в сравнении с h, поэтому нашу формулу смело можно упростить до вида

Для любых фотографий относительно крупных объектов, сделанных с расстояния больше 10 м, она будет давать практически тот же результат.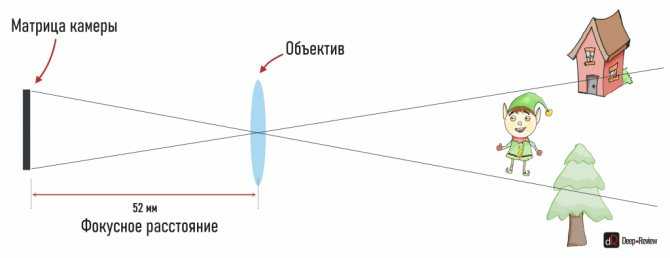

Ну а теперь самое интересное — нужно проверить, верна ли была использованная нами формула? Ведь в начале я говорил, что мы рассматриваем упрощённую конструкцию объектива, а не реальную. Может быть, наши расчёты не имеют ничего общего с действительностью? К счастью, это легко выяснить. Заходим на Яндекс.Карты и переходим в точку с координатами 55.604364, 37.611455. Затем активируем инструмент «Линейка» и ставим на карте две точки: одну — возле окна, из которого было сделано фото, а другую — возле стены дома, на которой мы считали панели:

Получаем 365 м. Ну не красота, а? Величины совпали с точностью до 0,1 м! Конечно, такая точность в известной мере является результатом везения, потому что и при измерении размеров изображения, и при подсчёте высоты этажей, и при расстановке точек на карте я вполне мог допускать погрешности в 1–3%. Но, как бы то ни было, в конечном итоге расчётная и измеренная величины сошлись.

Скептически настроенный читатель может подумать, что я подгонял цифры, и что для другой фотографии всё будет по-другому.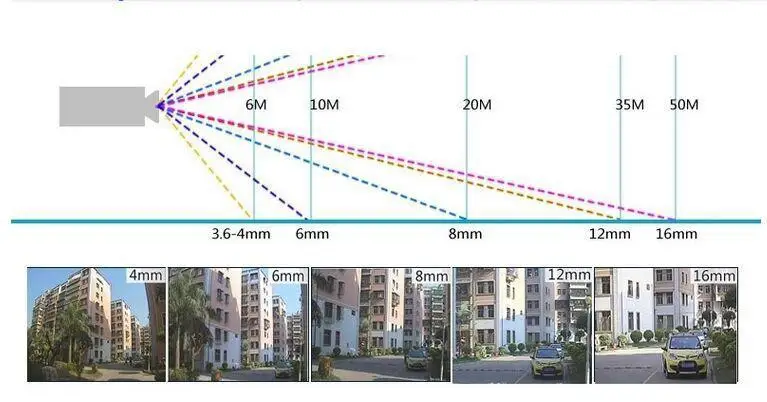 Что ж, у меня есть ещё одно фото того же дома, сделанное с аналогичной точки, но совсем с другим фокусным расстоянием:

Проделаем для него те же измерения и расчёты. У меня получилось, что размер изображения дома составляет 0,39 см, а фокусное расстояние — 21 мм. Подставляем эти числа в упрощённую формулу и получаем d = (0,021 × 66,7) / 0,0039 = 359,2 м. Результат немного отличается, но всё равно в рамках погрешности совпадает с измеренным по карте. Расхождение несложно объяснить: камера указывает фокусное расстояние как целое число, то есть и 20,51, и 21,49 мм она покажет как 21 мм. А это уже даёт погрешность 2,4%.

Впрочем, самых въедливых скептиков наверняка не убедил и этот пример. Ведь в обоих случаях я использовал один и тот же объектив — а что, если формула работает для него чисто по совпадению? Справедливое замечание. Чтобы проверить, так ли это, я возьму кадр, сделанный не только другим объективом, но и другим фотоаппаратом, причём не цифровым, а плёночным.

Вот фотография, которую мы будем анализировать:

Её много лет назад сделал мой отец на свой «Зенит-Е» с объективом Гелиос-44-2. Фокусное расстояние этого объектива составляет 58 мм. Определить физический размер изображения дома очень просто: у меня есть слайд, который я оцифровал с определённым разрешением, и сканер прописал его в свойствах файла. Тут даже пересчитывать ничего не нужно, достаточно воспользоваться линейкой.

Участок из тех же 23-х панелей имеет на слайде высоту 1,06 см. Подставляем значения в формулу: d = (0,058 × 66,7) / 0,0106 = 365 м. Полное совпадение!

Что ж, мы получили интересные результаты: выходит, простая формула для тонкой линзы позволяет получать весьма точные (и легко проверяемые) результаты при анализе реальных фотографий, а не «сферических коней в вакууме». Почему же так происходит, если реальный объектив представляет собой не одну линзу, а целый бутерброд из линз? Ответ на этот вопрос поможет дать статья Википедии.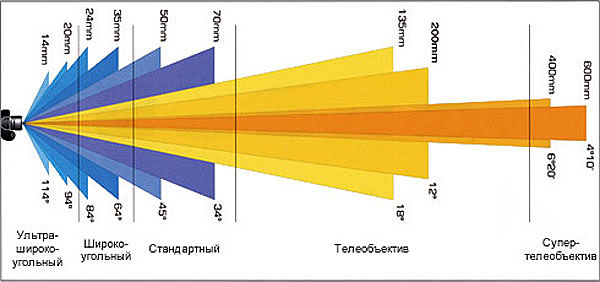 Для сложного объектива при расчёте вводят не одну, а две главные плоскости. Фактически, расстояния d и D, которые вы видели на схеме в самом начале этого поста, в этом случае отсчитываются от разных (хотя и не слишком удалённых друг от друга) точек. Но расстояние D, даже небольшое изменение которого могло бы существенно повлиять на результат просто в силу небольших размеров этого плеча оптической системы, нам, к счастью, знать не нужно, потому что производитель объектива уже рассчитал и нанёс на его корпус фокусное расстояние, через которое величину D, как было показано выше, легко выразить. А что касается изменения расстояния от передней главной плоскости до объекта, то какими бы толстыми ни были линзы и каким бы длинным ни был объектив (мы, конечно, говорим о реальных конструкциях, а не воображаемых объективах размером с дом), при расстоянии до объекта съёмки в несколько сотен метров, как в нашем случае, величиной в десяток-другой сантиметров можно смело пренебречь.

На основании вышеизложенного легко вывести формулу для соотношения расстояний до объектов, запечатлённых на одной и той же фотографии. Причём знать фокусное расстояние объектива и размер матрицы в этом случае уже будет не нужно, поскольку они сократятся при составлении пропорции.

Как видите, даже знаний из программы средней школы достаточно, чтобы убедиться в полной некомпетентности отдельных «экспертов». Любите математику и не давайте себя обмануть!

Tags: наука и техника, развенчание мифов

kapankov.ru — Фокусные расстояния

Мы уже затронули при рассмотрении объективов такое понятие как фокусное расстояние. Чтобы более детально разобраться с ним, необходимо вспомнить школьный курс геометрической оптики. Я напомню некоторые базовые понятия, необходимые нам. Взгляните на изображение. Мы имеем объект съемки (1) — свечу и линзу объектива (2). Согласно законам физики двояковыпуклая линза переворачивает изображение объекта (3). Теперь определим плоскости: 4 — плоскость объекта съемки, 5 — плоскость, проходящая через центр линзы. Линия 8 называется главной оптической осью, она проходит строго перпендикулярно через центр линзы и относительно неё получается перевернутое изображение (3) на плоскости изображения (7). Линия 9 представляет собой световой поток, или другими словами луч, исходящий от объекта (излучаемый или отражаемый, который преломляется в линзе на границе сопряжения двух сред (воздуха и стекла) дважды (при входе в линзу и при выходе).

Плоскость 7, также называется Фокальной плоскостью и она является особенно важной для получения изображения. Именно на этой плоскости устанавливается матрица или пленка. На самой камере эта плоскость помечается специальным значком, для того, чтобы можно было оценить расстояния при макросъемке.

Теперь еще немного физики. Все параллельные главной оптической оси лучи света, исходящие от бесконечно удаленного объекта и входящие в линзу собираются в точке фокуса, т.е. на фокальной плоскости.

Я не упомянул плоскость 6. Её иногда путают с фокальной плоскостью из-за пересечения света и главной оптической оси. Однако, это пересечение конкретного луча света 9, входящего под конкретным углом в линзу от объекта, находящегося на конкретном расстоянии от линзы. Для луча света от объекта, находящемся на другом расстоянии, пересечение будет в соответствующей другой точке. Эту схему мы еще изучим при рассмотрении темы ГРИП. При фокусировке на более удаленном объекте (левее от линзы на изображении) нам придется передвинуть линзу также влево, для того, чтобы получить четкое изображение на фокальной плоскости, при этом плоскость 6 также сдвинется немного вправо. Здесь может возникнуть вопрос: при фокусировке, т.е. при сдвиге линз относительно фокальной плоскости должно меняться и фокусное расстояние? Ответ: да. В современных объективах механизм внутренней фокусировки фактически меняет оптическую схему. Пусть на некоторых дорогих объективах это и не сильно незаметно, но это происходит. Метки фокусных расстояний на объективе наносятся исходя от фокусировки на бесконечности. При фокусировке на ближайших объектах фокусное расстояние может и не соответствовать этим меткам и тогда говорят об эффективном или действительном фокусном расстоянии (которое, как правило, уменьшается при фокусировании на более ближних объектах). Как именно изменяется ЭФР при фокусировке — вопрос сложный, так как надо понимать работу конкретной оптической схемы и уж точно на пальцах при помощи простой формулы не посчитать.

Фокусное расстояние — это расстояние от задней (или второй) главной точки объектива до его фокуса при вхождении в объектив пучка света, параллельного его оптической оси. Задняя главная точка в случае идеальной двояковыпуклой линзы размещается ровно в центре линзы. Задняя главная плоскость в этом случае совпадает с передней и проходит ровно через центр. Поэтому фокусное расстояние в этом случае будет от центра линзы (а не от поверхности её!) до фокуса. Но вы, возможно, уже знаете, что реальные объективы состоят из набора линз, а зум-объективы эти линзы объединяют в группы, которые перемещаются относительно друг друга. Взгляните на изображение объектива в разрезе.

Так вот в зависимости от конструкции объектива, точнее от его оптической схемы задняя главная плоскость (и соответственно задняя главная точка на ней) может находиться как внутри объектива, так и вне его. Используя различные виды линз, производители добиваются смещения этой плоскости и решения задачи создания объективов с различными фокусными расстояниями. Взгляните на изображения (взято из журнала «Наука и жизнь», №10, 1999 г.) Здесь представлены некоторые оптические схемы объективов:

а — нормальный объектив (f — фокусное расстояние примерно от диафрагмы до фокальной плоскости)
б — длиннофокусный объектив (f — главная задняя точка находится перед объективом!)
в — широкоугольный объектив (f — главная задняя точка находится за объективом!)
б — зеркально-линзовый телеобъектив (f — главная задняя точка находится также перед объективом!)

Поэтому ОШИБОЧНЫ следующие утверждения (иногда случается слышу от разных фотолюбителей):
1 — фокусное расстояние это расстояние от поверхности последней линзы, до матрицы
2 — фокусное расстояние это расстояние от поверхности передней линзы, до матрицы
3 — фокусное расстояние это расстояние от поверхности передней линзы, до байонета (конструкция крепления съемного объектива к камере)
4 — фокусное расстояние это расстояние от диафрагмы, до матрицы
и т. д. возможны различные сочетания. Конечно, в каких-то конкретных случаях оптических схем некоторые утверждения возможно и верны, но это частные случаи и никак не могут отражать определение понятия фокусного расстояния. Например, для нормальных объективов типа «полтинник» главная задняя точка действительно располагается приблизительно в области диафрагмы.

Фокусное расстояние — это расстояние от задней (второй) главной точки (плоскости) объектива до фокальной точки (плоскости).

Разберемся на что влияет фокусное расстояние и почему невозможно иметь только один фикс-объектив на все случаи жизни (хотя, говорят, Картье-Брессон обходился всю жизнь полтинником).

Легче всего это понять на зум-объективе, на котором мы можем изменять фокусное расстояние. Визуально мы видим приближение и удаление изображаемой картинки. Если попытаться понять из-за чего это происходит, то мы придем к выводу, что мы в сущности меняем угол обзора в объективе вытягивая его и наоборот (в некоторых герметичных объективах «вытягивание» происходит незаметно внутри корпуса)! Фокусное расстояние объектива в зависимости от размера матрицы и определяет угол поля зрения объектива — максимально возможный угол между двумя лучами света, прошедшими через объектив и ограниченный диагональю кадра. Почему диагональю? Да потому, что объектив — круглый, а матрица аккуратно вписывается в этот круг. На просторах интернета нашел изображение неизвестного мне автора, которое очень хорошо отражает изменение угла обзора в зависимости от используемого объектива. Чем больше фокусное расстояние — тем меньше угол обзора.

Тут важно еще отметить, что условное разделение на широкоугольные, длиннофокусные и т.д. объективы для разных камер происходит с учетом Эквивалентного фокусного расстояния (об этом чуть ниже)

Существует формула определения угла обзора, в зависимости от фокусного расстояния объектива:

Зум-объективы, как уже не раз было сказано, позволяют менять фокусное расстояние. И вроде бы это очень удобно, т.к. нет необходимости бегать назад и вперед, чтобы найти нужную композицию, да в сумке таскать несколько объективов и менять их для каждого случая съемки. Но, нужно помнить при этом, что использование конкретных фокусных расстояний должно в большинстве случаев соответствовать расстоянию до объекта. Почему? Потому, что расстояние влияет на перспективу! Очень популярно приводить в качестве иллюстрации следующее изображение.

В зависимости от расстояния до объекта мы по разному видим перспективу. А угол обзора определяется этим расстоянием.

Важное замечание: изменение фокусного расстояния не изменяет перспективу, но изменяет угол обзора и, соответственно, изменяет масштаб кадра. Перспектива меняется с изменением расстояния до объекта. То есть, необходимо изменять расстояние до объекта, чтобы скомпенсировать изменение фокусного расстояния. Взгляните на следующие фотографии. Они сделаны с разными фокусными расстояниями (подписаны снизу), но при этом фотограф отодвигался назад, для чтобы не менять пропорции объекта съемки в кадре. Теперь оцените первую (10 мм) и последнюю (300 мм) фотографии, по-моему это два разных человека :).

Очень часто вижу, когда люди пытаются фотографировать портреты с очень близкого расстояния в широкоугольном положении объектива (18, например, на Canon EF-S 18-55 IS), при этом лицо на фотографии получается немного смешным, т. к. нос (ближайшая точка к камере) становится большим, а задняя часть головы как бы сдавленная. И самое печальное, что многих такие фото устраивают. Не стоит думать, что чем больше ФР — тем лучше, вовсе нет! При длинных ФР портрет, к примеру, становится «плоским».

Взгляните на следующий фотосет, на котором наилучшим образом показана зависимость изменения перспективы от фокусного расстояния и расстояния до объекта, при неизменном масштабе объекта в кадре.

Человеческий глаз имеет угол обзора в районе 46 градусов, поэтому говорят, что ФР 50 является «нормальной» величиной для объектива. Согласитесь, что наиболее естественным является кадр, снятый с ФР = 50 мм. С другой стороны кадры с ФР 135 и 200 выглядят необычно и, может быть, даже выигрышно с художественной точки зрения и мне лично они больше нравятся.

Иногда можно услышать почти магическое выражение (в программе многих фотокурсов можно прочитать такое): эффект схождения вертикальных линий при наклоне камеры. Под наклоном понимается именно наклон или поворот относительно плоскости матрицы (вверх, вниз, вправо, влево), а не вращательный поворот относительно оптической оси. Это явление тоже относится к определению перспективы. Если мы будем снимать параллельные линии, нанесенные на плоскости строго перпендикулярной главной оптической оси, мы увидим их параллельными на готовой фотографии. Если камеру наклонить, линии начнут сходиться, поскольку часть линий будет удалена от камеры, а часть наоборот приближена. Если мы рассматриваем картину, на которой изображено, например, поле и уходящая вдаль дорога, мы видим, что дорога чем дальше от нас, тем уже. То есть линии, которые в природе вроде бы параллельны, отдаляясь от камеры сходятся. Я думаю, что это совершенно очевидные вещи для любого хоть сколько-нибудь образованного человека.

Говоря о зеркальных камерах нужно разделять их на полнокадровые и «кропнутые» (обрезанные). На полнокадровых камерах размер матрицы эквивалентен кадру 35-мм пленки, а на кропнутых используются уменьшенные (обрезанные) матрицы. Из-за этого камеры имеют столь разительную разницу в цене. Для камер Canon кропнутые матрицы в 1,6 раза меньше своих полноформатных собратьев, поэтому говорят, что их кроп-фактор равен 1,6. Взгляните на изображение. Красная рамка очень условно обозначает границы кадра полнокадровой камеры, а синяя рамка — кадр кроп-камеры.

На что же влияет этот кроп-фактор? Из-за того, что мы фактически вырезали центральную часть кадра, мы фактически уменьшили угол обзора и как бы увеличили фокусное расстояние. На самом деле ФР не меняется никак. Поэтому придумали такое понятие как Эквивалентное Фокусное Расстояние (ЭФР), которое позволяет определить, какое фокусное расстояние будет иметь объектив с таким же углом обзора на полнокадровой камере. Через ЭФР можно сравнивать объективы разных камер и понимать их угол обзора. То есть, «нормальный» 50 mm объектив для полноформатной камеры на кроп-камере превращается в 50*1,6=80 мм. Сразу уточню, что на EF-S объективах Canon, которые специально проектируются только для кроп-камер пишутся обычные нормальные ФР, а не ЭФР. То есть если мы видим 15-85, мы мысленно теперь должны понимать, что это эквивалентно 21-136.

Обратите внимание, что эффективное или действительное фокусное расстояние не то же самое, что и эквивалентное фокусное расстояние. Это разные понятия.

Можно иногда услышать, что кроп-камеры крайне удобны для использования с телеобъективами для съемки спортивных состязаний, из-за увеличения фокусного расстояния. Например, накрутив объектив 70-200, мы получаем ЭФР в 200*1,6=320мм! Да, в определенных условиях такой подход оправдан.

Из этой статьи важно усвоить три вещи. Во-первых, необходимо использовать подходящие фокусные расстояния для каждого случая: очень грубо, ландшафты снимаем на широкоугольник, портрет на полтинник, удаленные объекты — на телевик. Во-вторых, необходимо правильно оценить получаемую перспективу в кадре и выбрать нужное расстояние до объекта, а не просто крутить зум-объектив как вздумается. И в-третьих, чем больше фокусное расстояние, тем сильнее размытие вне зоны фокусировки и это важное свойство используется для формирования нужной глубины резкости (ГРИП), но это мы рассмотрим в отдельной статье.

Дополнительные материалы:

КОРОТКО ОБ ОБЪЕКТИВАХ

Домашнее задание

Сделайте самостоятельно серию портретов с разными ФР, как показано на выше на фотографиях с девушками. Диафрагму держите открытой, ISO можно выставить в режим auto. Соблюдайте точно размер портретируемого в кадре. Для этого придется двигаться вперед-назад. Оцените перспективу и размытие фона.

Твитнуть

BSP Security — Объективы камер наблюдения

Варифокальные и фиксированные объективы.

 

В фиксированных объективах фокусное расстояние, а значит, и угол обзора жестко зафиксированы. Эти линзы, как правило, имеют фокусное расстояние в 3.6мм, 4.3мм, 8мм, 12мм, 16мм, 25мм и т.д. Чем выше число фокусного расстояния, тем больше теле эффект, и более узкий угол обзора. Важно понимать, что характеристики фокусного расстояния не имеют ничего общего с фактическим размером самого объектива. Как правило, объективы 3,6мм или даже 6мм используются для широких зон просмотра, объективы с большим фокусным расстоянием дадут более сконцентрированную вдаль картинку. Объектив 3,6мм обеспечит угол обзора порядка 90 градусов. 12мм объектив охватывает лишь около 25 градусов, поэтому до приобретения камеры или объектива важно заранее спланировать место монтажа и необходимую зону просмотра.

 

Широкоугольные (двойная дистанция до объекта)	2.8мм и менее
Стандартные (без искажений)	3.6мм – 4мм
Узкоугольные (половина и менее дистанции до объекта)	8мм и более

 

 

Варифокальные объективы немного дороже фиксированных, в связи с тем, что вы получаете гибкую систему настройки положения линз. Объективы переменного фокуса (или варифокальные линзы) камер наблюдения позволяют пользователю изменять угол обзора в зависимости от потребностей и задач. Некоторые линзы обеспечивают переменное фокусное расстояние в пределах 4-8мм (широчайший угол обзора на 4 мм и наиболее узкий при 8 мм фокусного расстояния), другие могут обеспечить 5-50мм (50мм для фиксирования удаленного изображения). Наиболее востребованными сегодня варифокальными линзами являются линзы с фокусным расстоянием 2,8-12мм, покрывающие наиболее стандартные потребности специалистов видеонаблюдения и конечных потребителей.

 

Важно понимать, что требуется высокая точность при ручной настройке варифокальных объективов, в то время как объективы с фиксированным фокусом изначально оптимальным образом откалиброваны на получение максимально четкой картинки.

 

Настройки варифокальных объективов.

Следующий момент, на который необходимо обратить внимание при приобретении камер с варифокальными объективами – это легкость настройки фокусного расстояния и диафрагмы. Во многих камерах настройки линзы вынесены наружу корпуса, что удобно при монтаже. Но в этом случае нужно оценивать вероятность случайного стороннего воздействия на элементы настройки линзы (сбой настройки посторонним человеком, погодными явлениями, проч. ).

• объективы с внутренней ручной настройкой – в камерах с таких подходом к настройке объектива необходимо снять лицевую часть корпуса (или открыть ее) и вручную настроить зум и фокус объектива. Существует мнение, что такой порядок несколько снижает удобство настройки камеры при монтаже. Однако, такой подход дает и свои преимущества: гибкость настройки, невозможность сбить уже поставленные настройки). 
• камеры в ручной внешней настройкой – в камерах реализован простой механизм настройки все того же объектива через набор шестеренок. При этом настройки зума и фокуса выведены наружу камеры, т.е. для настройки нет необходимости снимать лицевую часть корпуса. Однако, набор шестеренок в механизме настройки имеет небольшую дискретность хода, что иногда чувствуется.
• камеры с роботизированной настройкой – такие камеры содержат внутри автоматизированный механизм, работающий через IP или RS485 протоколы, позволяющий настраивать объектив камеры удаленно (не вручную) через ПО или WEB-interface. Однако, такой подход тоже имеет незначительную дискретность хода настройки и, соответственно, более высокую стоимость камер. Реализуется чаще всего в Буллет камерах из соображений свободного пространства в корпусе:

1. настройка через ПО зума и фокуса – в таких камерах удаленно настраивается и зум, и фокус независимо друг от друга.
2. настройка через ПО только зума, фокус автоматически подстраивается под зум – в таких камерах достаточно настроить необходимый зум, фокус подстраивается автоматически.

 

Средние углы обзора линз

При выборе той или иной линзы чаще всего возникает вопрос угла обзора. Упрощенно зависимость угла обзора линзы от фокусного расстояния можно представить таким образом:

 

Средние углы обзора линз
Линза / фокусное расстояние	Угол обзора	Пример
2,5мм	120°
3,6мм	92°
4,3мм	78°
6,0мм	53°
12мм	25°
25мм	18°

 

А некоторое понимание о зависимости изображени от фокусного расстояния объектива и фактического расстояния до объекта съемки можно получить из следующего изображения:

 

Зависимость угла обзора от фокусного расстояния

Для выбора объектива под конкретную задачу необходимы следующие данные

: 
 

 1. Место установки видеокамеры (улица / помещение). 
Для уличных видеокамер используются объективы с автоматической диафрагмой (изменение диаметра входного отверстия объектива/регулировка входящего потока света) с управлением Video Drive или Direct Drive. Объективы Video Drive несколько дороже и уже практически не применяются, но предпочтительнее, т.к. быстрее отрабатывают изменения освещенности. Для видеокамер, устанавливаемых в помещении используются объективы с ручной диафрагмой или без диафрагмы. 

 2. Размер зоны наблюдения, 
т.е. размеры и расстояние до объекта наблюдения. Если эти данные известны, то необходимое фокусное расстояние вычисляется по следующим формулам: 
f=v*S/V или f=h*S/H, 

где f- фокусное расстояние 
 v- вертикальный размер матрицы 
 V- вертикальный размер объекта 
 S- расстояние до объекта 
 h- горизонтальный размер матрицы 
 H- горизонтальный размер объекта.

Размер матрицы

Формат матрицы	1/3″	1/4″
вертикальный размер, мм	3,6	2,4
горизонтальный размер, мм	4,8	3,2

 

Пример.   Необходимо с расстояния 25 м наблюдать за фасадом здания длинной 15 м.   Тогда для видеокамеры с матрицей 1/3″ получим,   f= 4,8*25/15=7,99 мм.    Следовательно, выбираем объектив с фокусным расстоянием 8 мм.

 3. Формат матрицы видеокамеры. 
Видеокамеры с матрицей 1/3″ могут работать с объективами 1/2″ и 1/3″. Видеокамеры 1/2″, только с объективами 1/2″.

 4. Необходимость изменения угла поля зрения в процессе работы.

 
В этом случае используются ручные Manual Zoom или так называемые Вариофокальные объективы или Motor Zoom — это объективы с дистанционным управлением фокусным расстоянием. 

Углы обзора 1/3″ видеокамер. 
Все приведенные в таблице данные приблизительные и даны в качестве начальной справки.

Объектив (фокусное расстояние), мм	Угол обзора по вертикали, град	Угол обзора по горизонтали, град	Угол обзора по диагонали, град	Дистанция распознавания, м	Дистанция наилучшего качества
2,5	90	120	150	2	0,7
2,9	78	104	130	3	1,2
3,4	70	94	110	3,4	1,4
3,5	63	79	98
3,6	54	72	92	3,5	1,5
3,7	52	70	90	3,8	1,6
4,0	48	65	75
4,3	47	62	73	4	1,8
5,5	40	55	70	5	2
6,0	32	42	53	6	2,3
8,0	24	32	40	8	3
12,0	17	22	28	12	4
16,0	12	17	21	16	6
25,0	8	11	14	25	10
50,0	4	5,5	7	50	20
75	2,8	3,7	4,6	70	30

 

Зависимость угла зрения (гор. ) объектива от его фокусного расстояния

f (mm) / ПЗС	2,45	2,96	3,6	4,0	6,0	8,0	12,0	16,0	36,0	72,0
1/3	93º	86º	72º	62º	43,5º	35,6º	22º	18º	7,8º	3,6º

 

Зависимость размера видимого объекта (в метрах) от фокусного расстояния (для ПЗС — 1/3″)

f (mm) Дист.	2,45	2,96	3,6	4,0	6,0	8,0	12,0	16,0	36,0	72,0
3 м	6×4,5	5×3,75	4×3	3,8×2,85	2,4×1,8	1,8×1,35	1,2×0,9	0,9×0,67
5 м	10×7,5	8,4×6,3	6,6×4,5	6×4,5	4×3	3×2,25	2×1,5	1,5×1,12	0,66×0,5
10 м	20×15	17×12,8	13×10	12×9	8×6	6×4,5	4×3	3×2,2	1,3×0,97	0,66×0,5
20 м	40×30	34×25	26×20	22×16,5	16×12	12×9	8×6	6×4,5	2,7×2	1,3×0,97
30 м	60×45	50×37	40×30	36×16,5	24×18	18×13,5	12×9	9×6,7	4×3	2×1,5
40 м	80×60	65×49	53×40	48×36	34×25	24×18	16×12	12×9	5,4×4,1	2,7×2
50 м				95×71	40×30	30×22	20×15	15×11,2	6,6×4,9	3,4×2,5
80 м					64×48	48×36	32×24	24×18	11×8,2	5,4×4
100 м						60×45	40×30	30×22	13,5×10	6,6×4,9
150 м							60×45	45×34	20×15	9,5×7,1

Как выбрать объектив камеры видеонаблюдения

Многие при выборе камеры видеонаблюдения замечают, что есть одна и та же модель камеры, но с разными объективами. Почти все задаются вопросом — как правильно выбрать объектив камеры видеонаблюдения, который будет выполнять поставленные задачи? Давайте разберемся в вопросе.

Виды объективов по типу регулировки:

• Монофокальные (с постоянным фокусным расстоянием)
• Вариофокальные (с переменным фокусным расстоянием)
• Трансфокальные (моторизированные зум объективы)

Монофокальные объективы — самые простые в техническом плане и самые бюджетные в финансовом. Имеют постоянное фокусное расстояние и фиксированный угол обзора. Самые популярный тип объективов ввиду низкой стоимости

Вариофокальные — второй по популярности тип объективов. Имеет гораздо больше плюсов, так как сочетает в одной камере сразу много возможностей. Может выступать в качестве широкоугольной камеры высокого разрешения или камеры дальнего действия для определенных целей — таких как идентификация номеров, распознавание лиц в ночное время с большого расстояния и прочее. Из минусов возможная расфокусировка, только ручная регулировка фокусного расстояния и высокая стоимость. 

Трансфокальные объективы — максимально универсальны, поскольку позволяют управлять фокусным расстоянием дистанционно. Особенно это востребовано в видеонаблюдении на производстве, когда камеры видеонаблюдения располагаются на существенной высоте  и частая регулировка фокусного расстояния требует дополнительных расходов, потому что, как правило, в штате нет ответственного сотрудника за выполнение данной задачи. Требуется привлечение специалистов по обслуживанию систем видеонаблюдения. Дистанционная регулировка реализованная в трансфокальных объективах позволяет производить оперативное изменение фокусного расстояния в конкретный момент времени (увеличение объекта). 

Критерии выбора и основные характеристики объектива

1. Фокусное расстояние

Основным параметром объектива является понятие «Фокусное расстояние».
Фокусное расстояние — расстояние в миллиметрах от матрицы камеры до объектива.  От него напрямую зависит какой угол обзора будет иметь камера видеонаблюдения и какое расстояние выбрать от камеры видеонаблюдения до объекта. Существует таблица взаимосвязи угла обзора камеры и расстояния до объекта от фокусного расстояния объектива:

В случае если Вам необходимо максимально точно определить необходимое фокусное расстояние, то можете воспользоваться формулами для самостоятельного просчета:

F = v*S/V,
где F – фокусное расстояние, S – расстояние до предмета, V – вертикальный размер предмета, v – вертикальный размер матрицы;

F = h*S/H,
где h – горизонтальный размер матрицы, S — расстояние до объекта, H – ширина предмета.

Значение фокусного расстояния необходимо округлить в большую сторону до ближайшего значения. Угол обзора должен быть максимально широким, чтобы в поле зрения был не только сам объект, но и прилегающая территория.

Соответствие дюймов и фактических размеров матрицы можно взять из таблицы:

Формат	1”	½”	1/3”	¼”
Высота, мм	9,6	4,8	3,6	2,4
Ширина, мм	12,8	6,4	4,8	3,2

Задача 1: 
Рассчитать необходимое фокусное расстояние.
Видеонаблюдение за КПП шириной 10м. Матрица видеокамеры 1/3”. Видеокамеру монтируют на расстоянии 20м.

F = h*S/H=4,8*20/10=9,6

Задача 2: 
Рассчитать расстояние до объекта
КПП шириной 10м. Матрица видеокамеры 1/3”. Фокусное расстояние камеры 12мм.
Воспользуемся формулой:
F = h*S/H.
Из нее путем выведения неизвестного получаем:
S=F*H/h=12*10/4,8=25м

2. Угол обзора
Угол обзора определяет ширину/высоту объекта или иными словами площадь участка, который попадет в поле зрения объектива камеры видеонаблюдения. Широкоугольные камеры с маленьким значением фокусного расстояния позволяют производить общий обзор большой площади с низким качеством детализации. Если стоит задача производить детализированное видеонаблюдение за объектами попадающими в определенную зону, то рекомендуем использовать узкоугольные камеры видеонаблюдения. 

Полезные советы:

• Для видеонаблюдения в коридорах, лестницах, вдоль ограждений и зданий используют камеры с узкоугольными объективами от 3° до 30°
• Для видеонаблюдения в офисе, на парковке и дома используют камеры видеонаблюдения с средними значениями угла обзора от 30° до 70°
• Для видеонаблюдения за воротами, входными группами, большими площадками используют камеры видеонаблюдения с широкоугольными объективами от 70° до 95°

Взаимосвязь фокусного расстояния, угла обзора и размер матрицы:

Фокусное расстояние	матрицы 1/3″		матрицы 1/4“
	Угол обзора по	Угол обзора по	Угол обзора по	Угол обзора по
	горизонтали	вертикали	горизонтали	вертикали
2. 8 мм	82	65	65	52
2.9 мм	80	63	63	50
3 мм	77	62	62	48
3.5 мм	69	55	55	42
3.6 мм	67	53	53	41
3.7 мм	66	52	52	40
3. 8 мм	65	51	51	38
4 мм	62	48	48	37
4.2 мм	60	46	46	36
4.4 ММ	57	45	45	34
4.5 ММ	56	44	44	33
5 мм	51	40	39	30
6 мм	43	33	33	25
7 мм	38	29	29	22
8 мм	34	25	25	19
8. 8 мм	31	23	23	17.5
10 мм	27	20	20.5	15.4
12 мм	22.6	17	17	12.8
15 мм	18.2	13.7	13.7	10.3
16 мм	17.1	12.8	12.8	9.6
25 мм	8	11	7. 3	5.5
50 мм	4	5.5	2.7	2.8

3. Значение диафрагмы 

Регулирует объем светового потока, проходящий через объектив к матрице. Диафрагмы различают фиксированные и автоматические. Если в течение суток степень освещенности объекта кардинально изменяется, то стоит применять объективы с автоматической регулировкой диафрагмы. Иначе в светлое время суток Вы получите солнечные засветы, а в темное — неразличимую детализацию объектов. 

При выборе объектива камеры видеонаблюдения учитывают значение параметра диафрагмы — светочувствительность. Единица измерения светочувствительности — 1 Люкс (Лк) или иными словами производная одного Люмена (единица измерения светового потока) на единицу измерения площади (квадратный метр). Простыми словами Люмен — минимальное количество света, необходимое для четкого и качественного изображения. Существует зависимость: чем меньше значение светочувствительности, тем позднее камера переходит в черно-белый режим. Чем меньше значение светочувствительности объектива, тем шире будут открываться створки в условиях недостаточной освещенности и тем больше света будет получать матрица, что позволит получить качественное изображение лишенное шумов.

4. Материал линз и корпуса объектива
Материал корпуса на начальном этапе не влияет на качество изображения, но с течением времени пластиковый корпус наиболее сильно подвергается механическим воздействиям окружающей среды. Корпус объектива из пластика с годами может дать такой эффект как помутнение или изменение цветовых параметров объектов. Аналогично происходит и с пластиковыми линзами объектива камеры видеонаблюдения.

Мегапиксельные объективы
Данная категория объективов была разработана благодаря развитию новых технологий и появлением на рынке IP-камер видеонаблюдения. Если Вам необходим объектив с высокой контрастностью и разрешением, то склоните свой выбор в пользу именно мегапиксельных объективов. 

Достоинства мегапиксельного объектива:

• Высокое разрешение и контрастность
• Высококачественные стеклянные линзы с тонкой шлифовкой
• Сверхпрочный корпус
• Встроенная функция ИК-коррекции
• Повышенная разрешающая способность
• Хорошее качество изображения без искажений даже в углах кадра

ВЫВОД:
Сегодня мы помогли Вам познакомиться с пониятием объектив камер видеонаблюдения и узнать его основные параметры, по которым стоит производить выбор. Но помните, что помимо объектива в камере видеонаблюдения еще много составляющих: матрица, процессор и прочее. И стоит понимать, что для правильного выбора камеры видеонаблюдения под конкретные задачи надо довериться специализированной компании, имеющей в штате высококвалифицированных специалистов. Не стоит экономить на безопасности объекта, особенно это касается стратегических объектов специального назначения. 

Вернуться к списку

Камера и объектив здравого смысла

1. Фокусное расстояние (фокусное расстояние)

Фокусное расстояние — это расстояние от центральной точки объектива до четкого изображения, сформированного на пластиковой плоскости. Размер фокусного расстояния определяет размер угла обзора.Значение фокусного расстояния мало, угол обзора велик, и диапазон наблюдения также велик; В зависимости от того, можно ли отрегулировать фокусное расстояние, его можно разделить на две категории: объектив с фиксированным фокусом и зум-объектив.

2. Диафрагма (Ирис)

Представленный F, измеренный отношением фокусного расстояния объектива f и чистой диафрагмы D. Каждая линза помечена максимальным значением F, например, 8 мм / F 1,4 означает, что максимальная диафрагма составляет 5,7 мм. Чем меньше значение F, тем больше апертура и чем больше значение F, тем меньше апертура.

3. Максимальный размер CCD (SensorSize)

Самый большой размер ПЗС-матрицы, который может охватывать диаметр объектива. В основном: 1/2 ″, 2/3 ″, 1 ″ и выше 1 ″.

4. Интерфейс (крепление)

Как подключить объектив к камере. Обычно используемые включают C, CS, F, V, T2, Leica, M42x1, M75x0,75 и так далее.

5. Глубина резкости (DOF)

Глубина резкости относится к диапазону, в котором изображение остается четким на определенном расстоянии до и после объекта после того, как объект находится в фокусе. Глубина резкости зависит от величины диафрагмы объектива, фокусного расстояния и расстояния съемки.Чем больше апертура, тем меньше глубина резкости, чем меньше апертура, тем больше глубина резкости. Чем длиннее фокусное расстояние, тем меньше глубина резкости, чем короче фокусное расстояние, тем больше глубина резкости. Чем ближе расстояние до объекта, тем меньше глубина резкости, чем дальше от объекта, тем больше глубина резкости. (Не забудьте контролировать одну переменную. Если расстояние до объекта и фокусное расстояние изменяются вместе, глубина резкости в целом становится больше, потому что увеличение расстояния до объекта больше, чем замедление фокусного расстояния)　　

6. Резолюция (Резолюция)

Разрешение представляет собой способность объектива записывать детали объекта. Единица измерения — это количество линий, которые могут различать черные и белые линии на миллиметр: «пары линий / мм» (lp / mm). Чем выше разрешение, тем чище объектив.

7. Рабочее расстояние (WD)

Расстояние от первой рабочей поверхности линзы до измеряемого объекта.

8. Поле зрения (FOV)

Размер области, фактически захваченной камерой.

9. Оптическое увеличение (Увеличение, ß) // Это обычно более важно для телецентрических объективов. Когда камера используется в качестве микроскопа, чем больше увеличение, тем лучше.

CCD / FOV, размер чипа, разделенный на поле зрения.

10. Числовая апертура (NA)

Числовая апертура равна произведению показателя преломления n среды между объектом и линзой объектива и синусоидальной величины половины угла апертуры линзы объектива (a \ 2). Формула расчета равна N.A = n * sina / 2. Числовая апертура тесно связана с другими оптическими параметрами, пропорциональна разрешающей способности и пропорциональна увеличению. То есть числовая апертура напрямую определяет разрешение объектива: чем больше числовая апертура, тем выше разрешение, в противном случае верно обратное.

11, задний фокус (Flangedistance)

Чтобы быть точным, обратная мощность является параметром камеры, который относится к расстоянию от плоскости интерфейса камеры до чипа. Тем не менее, при выборе объектива для онлайн-сканирования или камеры с большой областью фокусировки задний фокус является очень важным параметром, поскольку он напрямую влияет на конфигурацию объектива. Камеры разных производителей могут иметь разную тыловую мощность, даже если интерфейс одинаковый.

Во-вторых, выбор объектива

1. Выберите интерфейс объектива и максимальный размер ПЗС

Интерфейс объектива может быть установлен при условии, что он совпадает с интерфейсом камеры или может соответствовать дополнительному порту преобразования. Общий интерфейс — это порт C и порт CS. Основное различие между ними — это расстояние между датчиком изображения и объективом. Тип интерфейса не подразделяется, и размер порта C одинаков, максимальный размер CCD, поддерживаемый объективом, должен быть больше или равен размеру дополнительного CCD-чипа камеры.

1.

CS-mount: расстояние между датчиком изображения и объективом должно быть 12,5 мм

 

С-крепление: расстояние между датчиком изображения и объективом должно составлять 17,5 мм. Шайба 5 мм (соединительное кольцо C / CS) может использоваться для преобразования объектива с креплением C в объектив с креплением CS

Резьба порта C и резьба порта CS имеют одинаковый диаметр один дюйм, резьба in32, их разность составляет фокусное расстояние, фокусное расстояние порта C составляет 17,5 мм. Порт CS составляет 12,5 мм.

　　

На самом деле, это не сложное условие, но некоторые изображения, сделанные таким образом, становятся черными, потому что они не могут взорваться. Поэтому существует три основных условия выбора подходящего промышленного объектива:

В соответствии с формулой расчета фокусного расстояния, приведенной ниже в блоге, рассчитайте фокусное расстояние, подходящее для экспериментальной среды.

Чтобы в полной мере использовать пиксели камеры, размер объектива должен быть больше или равен размеру поверхности изображения камеры.

c. Для высокоточных промышленных вычислений третий пункт очень важен, это выбрать объектив, который больше или равен разрешению камеры (фактически связан с размером пикселя, а не с количеством пикселей), это разрешение объектива, как правило, При покупке объектива указывается, какое разрешение имеет объектив. ¡Для элементов зрения, которые не являются высокоточными, выбранное разрешение объектива может быть ниже, чем разрешение камеры. Чем выше разрешение камеры, тем она дороже и только умеренная.

Примечание. Вычислительная формула, приведенная выше, подходит только для выбора промышленных объективов, поскольку она соответствует принципу получения изображений с маленькими отверстиями, не нужно учитывать ее оптическое увеличение, поскольку промышленные объективы с одинаковым фокусным расстоянием и размером изображения имеют фиксированное оптическое увеличение на фиксированном расстоянии. Это то же самое: если это широкоугольный объектив типа «скопа», вы должны выбрать другой способ, то есть «оптическое увеличение» объектива, то есть CCD / FOV, потому что они не соответствуют строгому принципу формирования изображений с небольшими отверстиями, но есть и более Великолепная преломляющая сила.

 

Характеристики качества объектива:искажениеКак правило, хорошее искажение объектива очень мало, но для многих хороших объективов, если разрешение камеры особенно велико, в кадре изображения все равно будут присутствовать искажения. Следовательно, коэффициент искажения также является характеристикой измерения качества объектива. Проектам, чувствительным к искажению, следует обратить особое внимание на этот момент. Разрешение, как правило, выбор разрешения камеры и объектива должен совпадать. Вот некоторые сведения о разрешении объектива:

Как правило, при выборе камеры и объектива с точки зрения согласования разрешения, чтобы упростить память соотношения соответствия между объективом и камерой, люди часто используют соответствующее разрешение камеры для обозначения объектива. Этот метод именования на самом деле не является научным, и он также приносит много недоразумений людям, которые плохо знакомы с визуальной системой. Часто камера с мегапиксельным разрешением механически применяется к мегапиксельной линзе, а камера с разрешением в два мегапикселя соответствует 200. Мегапиксельная линза и 5-мегапиксельная камера соответствуют 5-мегапиксельной линзе. Фактически, объектив соответствует камере не по разрешению в пикселях (количеству пикселей) самой камеры, а по соответствующему предельному пространственному разрешению (то есть частоте отсечки в пространстве, соответствующей передаточной функции MTF).
Согласно опубликованным в настоящее время показателям производительности, предельное пространственное разрешение, соответствующее мегапиксельной линзе, составляет 90 пар пар / мм, а предельное пространственное разрешение, соответствующее двухпиксельной линзе, составляет 110 линий. Пар / мм, предельное пространственное разрешение, соответствующее 5-мегапиксельной линзе, составляет 160 пар линий / мм. Согласно принципу согласования объектива камеры, предельное разрешение объектива должно быть больше или равно предельному разрешению камеры, тогда предельное разрешение камеры с мегапиксельной линзой должно быть менее 90 пар пар / мм, двух мегапиксельной линзы и 500 Принцип работы камер с мегапиксельными объективами такой же.
Итак, откуда вы знаете предельное пространственное разрешение камеры? Предельное пространственное разрешение камеры определяется не собственным разрешением камеры, а размером одного пикселя чипа камеры. Конкретная формула расчета выглядит следующим образом:
1 / (размер одного пикселя * 2), единица измерения: пара / мм
Например, наша широко используемая камера AVT GUPPY Pro серии F125B с 1,3-миллиметровой ПЗС-матрицей с разрешением 1,3 миллиона пикселей и размером 3,75 мкм * 3,75 мкм. Чем больше разрешение, тем меньше размер пикселя. Тогда предел пространственного разрешения этой камеры:
1 мм / (3,75 * 2) = 133,33 пары / мм
Это видно из того факта, что предельное пространственное разрешение объектива больше, чем предельное пространственное разрешение камеры, более уместно выбрать объектив на 5 миллионов пикселей.

Содержание линзы введение:

2. Выберите фокусное расстояние объектива

Как показано на рисунке, когда размер ПЗС камеры, рабочее расстояние (WD) и поле зрения (FOV) известны, можно рассчитать фокусное расстояние (f) требуемого объектива.

　 　

　 　

3. Выберите диафрагму объектива

Диафрагма объектива определяет яркость изображения.При съемке высокоскоростных движущихся объектов и короткого времени экспозиции следует использовать объектив с большой апертурой для увеличения яркости изображения.

4. Выберите телецентрический объектив

Телецентрическая линза — это линза, специально разработанная для коррекции параллакса традиционной линзы, которая может находиться в пределах определенного расстояния до объекта, поэтому результирующее увеличение изображения не изменится при изменении расстояния до объекта. Сравнение между телецентрическим объективом и традиционным объективом, как показано на рисунке:

　

 

 

Телецентрические линзы делятся на два типа: телецентрические на стороне объекта и двусторонние телецентрические, как показано на рисунке:

 

 

1.       Выберите угол источника света

В зависимости от желаемого эффекта изображения выбирайте источники света с разными углами падения. Освещение под большим углом, в целом изображение более яркое, подходит для неотражающих объектов на поверхности, освещение под низким углом, фон изображения черный, а характеристика белая, что позволяет выделить контур измеряемого объекта и неровности поверхности, многоугольная подсветка, общий эффект изображения более мягкий, подходящий Обнаружение изогнутых объектов, подсветка, эффект изображения — это чёрно-белый отчетливый контур объекта, часто используемый для измерения размера, коаксиальная подсветка, эффект изображения — это черная функция на ярком фоне, используемая для обнаружения плоских объектов с сильным отражением. Принципиальная схема различных угловых источников света выглядит следующим образом:

 

1. Выберите цвет источника света

Принимая во внимание цвет источника света и цвет фона, использование света той же цветовой системы, что и измеряемый объект, сделает изображение ярче (например, красный свет делает красный объект ярче), а использование света противоположной цветовой системы относительно измеряемого объекта сделает изображение темнее (например, : Красный свет делает синие объекты темнее).

 

Примеры различных цветовых световых эффектов:

 

Цветная карта	Эффект красного света	Эффект зеленого света	Blu-Ray эффект

　
 

Чем длиннее длина волны, тем сильнее проникающая способность, чем короче длина волны, тем сильнее диффузионная способность. Инфракрасное проникновение является сильным, подходящим для обнаружения объектов с плохим пропусканием света, таких как коричневое устное жидкое загрязнение ротовой полости. Ультрафиолет чувствителен к тонким поверхностям и подходит для обнаружения мест, где контраст не очевиден, таких как обнаружение текста на бутылках с пищевыми маслами.

      　　

1. Выберите форму и размер источника света

В основном делятся на круглые, квадратные и полосовые. Обычно выбирается источник света той же формы, что и измеряемый объект, и окончательная форма источника света подвергается испытательному эффекту. Выбор размера источника света требует, чтобы свет во всем поле зрения был равномерным, и лучше быть немного больше, чем поле зрения. 🔥 👍 👍

                     　　

2. Выберите, использовать ли рассеянный источник света

Если поверхность измеряемого объекта отражает свет, лучше всего использовать рассеянный источник света. Многоугловое рассеянное освещение делает общую яркость поверхности измеряемого объекта равномерной, фон изображения — мягким, а особенности обнаружения не нарушаются фоном

Преломление и лучевая модель света

В то время как вся поверхность сетчатки содержит нервные клетки, есть небольшой участок диаметром примерно 0,25 мм, где концентрация колбочек наибольшая. Эта область, известная как центральная ямка , является оптимальным местом для формирования изображения. Глаз обычно вращается в своей глазнице, чтобы сфокусировать изображения объектов в этом месте. Расстояние от внешней поверхности роговицы (где свет преломляется больше всего) до центральной части ямки на сетчатке составляет примерно 2,4 см. Свет, попадая на роговицу, должен давать изображение на расстоянии 2,4 см от ее внешнего края. В отличие от фотоаппарата, который имеет возможность изменять расстояние между пленкой (детектором) и объективом, расстояние между сетчаткой (9Детектор 0005 ) и роговица (рефрактор ) фиксируется. Расстояние до изображения не меняется. Следовательно, глаз должен иметь возможность изменять фокусное расстояние, чтобы сфокусировать изображения как близких, так и удаленных объектов на поверхности сетчатки. При изменении расстояния до объекта необходимо изменить фокусное расстояние, чтобы расстояние до изображения оставалось постоянным.

Аккомодация

Способность глаза регулировать свое фокусное расстояние известна как размещение . Поскольку близлежащий объект (маленький объект d _{) обычно фокусируется на более дальнем расстоянии (большое изображение} d _{), глаз приспосабливается, принимая форму линзы с более коротким фокусным расстоянием. Это уменьшение фокусного расстояния приведет к большему преломлению света и приблизит изображение к системе роговица/хрусталик и к поверхности сетчатки. Таким образом, для близлежащих объектов цилиарные мышцы сокращаются и сжимают хрусталик, придавая ему более выпуклую форму. Это увеличение кривизны линзы соответствует более короткому фокусному расстоянию. С другой стороны, удаленный объект (большой d объект ) обычно фокусируется на более близком расстоянии (маленькое изображение} d _{). Глаз приспосабливается, принимая форму линзы с большим фокусным расстоянием. Поэтому при взгляде на удаленные объекты цилиарные мышцы расслабляются, и хрусталик принимает более плоскую форму. Это уменьшение кривизны линзы соответствует большему фокусному расстоянию. В приведенной ниже таблице данных показано, как может потребоваться изменение фокусного расстояния для поддержания постоянного расстояния до изображения 1,80 см.}

Зависимость f от d объекта (d изображение фиксируется на 1,80 см) Расстояние до объекта Фокусное расстояние 0,25 м 1,68 см 1 м 1,77 см 3 м 1,79 см 100 м 1,80 см Бесконечность 1,80 см (Приведенные выше значения были рассчитаны с использованием уравнения линзы. Уравнение линзы представляет собой упрощенную математическую модель глаза.)

Способность глаза к аккомодации является автоматической. Более того, это происходит мгновенно. Сосредоточьтесь на удаленном объекте и быстро переключите внимание на ближайший объект; обратите внимание, что нет заметной задержки в способности глаза сфокусировать близлежащий объект. Проживание — это выдающийся подвиг!

 

Диоптрия

Оптика измеряет силу линзы в единице, известной как диоптрия. диоптрии обратны фокусному расстоянию.

диоптрии = 1/(фокусное расстояние)

Система линз с фокусным расстоянием 1,8 см (0,018 м) представляет собой линзу с 56 диоптриями. Линзовая система с фокусным расстоянием 1,68 см представляет собой линзу с оптической силой 60 диоптрий. Здоровый глаз способен сфокусировать как удаленные, так и близлежащие объекты без необходимости использования корректирующих линз. То есть здоровый глаз способен принимать как малое, так и большое фокусное расстояние; у него будет возможность просматривать объекты с большим изменением расстояния. Максимальная вариация силы глаза называется 9.0003 Сила размещения . Если глаз способен принять фокусное расстояние 1,80 см (56 диоптрий) для наблюдения за объектами, находящимися за много миль, а также способность принять фокусное расстояние 1,68 см для наблюдения за объектом на расстоянии 0,25 метра (60 диоптрий), то его Сила аккомодации будет измеряться как 4 диоптрии (60 диоптрий — 56 диоптрий).

Здоровый глаз молодого человека имеет способность аккомодации приблизительно 4 диоптрии. По мере того, как человек становится старше, сила аккомодации обычно снижается, поскольку человек становится менее способен видеть близлежащие объекты. Эта неспособность видеть близлежащие объекты приводит к необходимости использования корректирующих линз. В следующих двух разделах Урока 6 мы обсудим два наиболее распространенных дефекта зрения — близорукость и дальнозоркость.

 

Вы когда-нибудь задумывались, как бы выглядела офтальмологическая карта в кабинете врача, если бы у вас было плохое зрение? Теперь вы можете узнать. Используйте виджет «Несовершенное зрение» и виджет «Таблица зрения », чтобы увидеть, как будет выглядеть таблица Снеллена при несовершенном зрении.

Следующий раздел:

Как расстояние до объекта и фокусное расстояние влияют на глубину резкости? « Physics Soup

Примечание: это вторая часть серии статей о глубине резкости. Щелкните здесь, чтобы перейти к части 1, в которой объясняется взаимосвязь между размером апертуры и глубиной резкости.)

Помимо размера диафрагмы, фотографы также могут управлять глубиной резкости, изменяя расстояние от камеры до объекта или фокусное расстояние объектива. В частности:

• При фиксированном фокусном расстоянии и размере диафрагмы увеличение расстояния до объекта увеличивает глубину резкости.
• При фиксированном расстоянии до объекта и размере диафрагмы увеличение фокусного расстояния приведет к уменьшению глубины резкости.

Эти два эффекта тесно связаны между собой, и стремление понять их представляет собой отличный пример того, как мы можем использовать уравнения для расширения нашей интуиции при решении относительно сложных задач. Читайте дальше, если хотите узнать больше!

Прежде чем мы перейдем к сути этого поста, нам нужно быстро просмотреть факторы, определяющие глубину резкости. В моем предыдущем посте о размере диафрагмы и глубине резкости мы видели, что точечный объект создает круг (круг нерезкости ) на датчике камеры, когда датчик не точно расположен в положении изображения. Когда кружок нерезкости «достаточно мал», мы говорим, что объект находится в приближенном фокусе . Существует ряд положений изображения, окружающих датчик, которые создают круги, которые достаточно малы, чтобы быть в приблизительном фокусе. Мы можем обозначить ширину этого диапазона как Δd _{i, приемлемо} . Точно так же существует соответствующий диапазон положений объекта, которые создают изображения в этом диапазоне. Ширина диапазона положений объекта называется глубиной резкости (ГРИП). Эти идеи проиллюстрированы на рисунке ниже:

Давайте сначала рассмотрим взаимосвязь между глубиной резкости и расстоянием до объекта. Для начала давайте взглянем на некоторые диаграммы лучей, иллюстрирующие, что происходит, когда мы увеличиваем расстояние между объектом и линзой при фиксированном фокусном расстоянии. Мы переместим объект дважды (каждый раз на одну и ту же величину) и посмотрим, как изменится изображение:

На основании этих диаграмм мы можем сделать два важных наблюдения:

1. По мере удаления объекта от линзы изображение приближается к линзе и уменьшается в размерах. В результате увеличивается угловой размер искривленного светового конуса. В моем предыдущем посте мы видели, что более широкий изогнутый световой конус уменьшает Δd _{i, допустимое} . Назовем это угловым эффектом .
2. Несмотря на то, что первый и второй сдвиги объекта имеют одинаковый размер, второй смещение изображения меньше, чем смещение первого изображения. Другими словами, положение изображения менее чувствительно к положению объекта, когда объект находится дальше от объектива. При этом конкретный Δd _{i, допустимый} должен соответствовать большему диапазону положений объекта. Назовем это эффектом чувствительности .

Что это значит для ФО? Ответ на этот вопрос не очень однозначен, потому что у нас есть две конкурирующие силы. По мере удаления объекта от линзы угловой эффект уменьшается Δd _{i,допустимо} на меньшее значение. Однако эффект чувствительности означает, что это меньшее значение Δd _{i,допустимое} соответствует большей глубине резкости, чем она была бы в исходном положении объекта. В зависимости от относительной силы угловых эффектов и эффектов чувствительности ГРИП может уменьшаться или увеличиваться!

Чтобы двигаться дальше, нам потребуется количественно определить глубину резкости для различных расстояний до объекта. Для объектива с заданным фокусным расстоянием общая процедура будет следующей:

1. Выберите центральное положение объекта.
2. Определите соответствующую позицию изображения.
3. Предположим, что датчик камеры расположен в этом месте.
4. Выберите другое положение объекта, найдите соответствующее изображение и определите размер круга нерезкости, который он создает.
5. Повторите шаг 4 несколько раз, чтобы найти положение объекта на крайних границах приблизительного диапазона фокусировки. Это определит глубину резкости в этом центральном положении объекта.
6. Повторите шаги 2-5 много раз для разных положений центрального объекта.

Это можно сделать графически, нарисовав миллионы диаграмм лучей. Однако гораздо проще рассчитать глубину резкости численно, используя уравнения, описывающие простую модель объектива. Давайте сделаем это вместо этого!

Уравнение тонкой линзы является ключом к численному определению глубины резкости. Если вы раньше посещали уроки физики, вы, вероятно, хорошо с ней знакомы. Для объекта размером с точку, который излучает свет в сторону линзы, уравнение связывает расстояние от объекта до линзы (d _o ), расстояние от изображения до объектива (обозначается d _i ) и фокусное расстояние объектива (обозначается f ) следующим образом:

.

Строго говоря, это уравнение применимо только к идеализированным линзам с нулевой толщиной. Разумеется, таких объективов в реальной жизни не существует. Однако объективы фотоаппаратов тщательно разработаны таким образом, чтобы они функционировали почти так же, как идеальные тонкие линзы. Мы не сможем полностью доверять точным значениям чисел, которые мы получаем из этого уравнения, но мы должны быть в состоянии поверить в выявленные нами общие тенденции.

Обратите внимание, что уравнение тонкой линзы содержит всю информацию, которую мы узнали из диаграмм лучей, которые я нарисовал выше. В частности, мы можем использовать уравнение тонкой линзы для обнаружения угловых эффектов и эффектов чувствительности. Для этого мы можем решить уравнение для расстояния до изображения, а затем построить график зависимости d _i от d _o для определенного фокусного расстояния, скажем, 50 мм:

. положение изображения уменьшается по направлению к фокальной точке. Из этого мы можем сделать вывод об угловом эффекте. Кроме того, мы можем видеть, что кривая становится более плоской при больших позициях объекта. Отсюда мы можем сделать вывод об эффекте чувствительности. Я явно проиллюстрировал это, показав, как один и тот же Δd _{i, приемлемо} может привести к увеличению глубины резкости на больших расстояниях до объектов (меньших расстояниях до изображений).

Прежде чем мы сможем численно рассчитать глубину резкости, нам нужно определить диаметр кружка нерезкости (C) в зависимости от положения объекта, фокусного расстояния, радиуса апертуры (A) и положения сенсора (S). На следующей диаграмме показано, как связаны эти величины, а также высота объекта (h _o ) и высота изображения (h _i ):

Прежде всего, мы можем найти диаметр кружка нерезкости, используя θ ₁ , θ ₂ , d _i и S:

Затем мы можем найти углы, используя A и h _i :

Когда мы объединяем эти три уравнения, высота изображения фактически сокращается:

.

В качестве последнего алгебраического шага мы можем найти расстояние до изображения, используя уравнение тонкой линзы. Когда мы объединим все вместе, мы можем получить большое уродливое уравнение для C. Не волнуйтесь, я хотел только наметить, как это сделать — я не буду утомлять вас подробностями алгебры!

Теперь, когда мы знаем, как найти C, мы можем выбрать S, A и f и вычислить C для различных положений объекта. Например, мы могли бы представить себе использование объектива 55 мм, чтобы сделать снимок объекта, расположенного в 10 футах от объектива камеры. Типичный радиус апертуры составляет около 1 дюйма. На следующем графике показан диаметр кружка нерезкости для различных положений близлежащих объектов:

Я использую камеру Pentax K10D. Его сенсор имеет 10,75 млн пикселей, расположенных на прямоугольнике размером 23,5 х 15,7 мм. Таким образом, мы можем оценить, что каждый пиксель составляет около 5,9мкм в поперечнике. Если мы выберем 6 мкм в качестве порогового значения для максимального диаметра круга, мы можем обнаружить, что глубина резкости составляет около 1,7 дюйма в поперечнике.

Наконец, мы можем повторять этот процесс много раз для разных расстояний до объекта, чтобы увидеть, как изменяется глубина резкости:

В итоге мы видим, что глубина резкости увеличивается при увеличении расстояния до объекта. Но на самом деле, если мы вспомним наш предыдущий анализ, мы узнали кое-что еще: это означает, что эффект чувствительности более важен, чем угловой эффект для определения глубины резкости на разных расстояниях до объекта.

Мы можем повторно использовать некоторые из тех же идей, чтобы понять, как фокусное расстояние влияет на глубину резкости. В частности, давайте воспользуемся уравнением тонкой линзы, чтобы построить график зависимости d _i от d _o для различных фокусных расстояний:

Из этого графика видно, что при больших фокусных расстояниях расстояние до изображения изменяется быстрее с расстоянием до объекта. . Другими словами, положение изображения становится более чувствительным к положению объекта при увеличении фокусного расстояния. Из нашего предыдущего анализа мы знаем, что эффект чувствительности определяет глубину резкости, и что увеличение чувствительности должно приводить к уменьшению глубины резкости. Мы можем проверить это предсказание, используя нашу простую модель для расчета глубины резкости для разных фокусных расстояний. Опять же, давайте представим, что вы используете камеру, чтобы сфотографировать объект, который находится на расстоянии 10 футов. Предположим, что радиус апертуры составляет 1 дюйм, а порог фокусировки — 6 мкм.

Наш первоначальный вывод был верным — с увеличением фокусного расстояния глубина резкости уменьшается!

Повторим, что мы сделали:

• Мы начали с рисования нескольких диаграмм лучей для объектов на разных расстояниях. Это позволило выявить два конкурирующих эффекта: угловой эффект и эффект чувствительности.
• Затем мы использовали уравнение тонкой линзы для создания численной модели, которая позволила нам рассчитать глубину резкости для любой комбинации положения объекта и фокусного расстояния.
• Сравнивая эти численные результаты с интуицией, которую мы получили из диаграмм лучей, мы обнаружили, что эффект чувствительности определяет общее поведение глубины резкости при изменении расстояния до объекта и фокусного расстояния.

Обратите внимание: если бы мы сразу перешли к численной модели, мы бы не поняли, что эффект чувствительности является основной причиной поведения! Этот пример иллюстрирует важность сочетания интуиции с расчетами при попытке понять сложные проблемы.

Итак, теперь мы определили три правила для управления глубиной резкости:

• Для фиксированного фокусного расстояния и положения объекта увеличение размера диафрагмы уменьшит глубину резкости.
• При фиксированном фокусном расстоянии и размере диафрагмы увеличение расстояния до объекта увеличивает глубину резкости.
• При фиксированном расстоянии до объекта и размере диафрагмы увеличение фокусного расстояния приведет к уменьшению глубины резкости.

Конечно, трудно предсказать, как изменится глубина резкости, если мы одновременно изменяем фокусное расстояние, положение объекта и размер диафрагмы. Тем не менее, эти отношения полезно знать. Я надеюсь, что вы сможете использовать их в своих собственных фотографических начинаниях!

Нравится:

Нравится Загрузка…

Устранение путаницы с глубиной резкости

Устранение путаницы с глубиной резкости

Устранить Путаница с глубиной резкости: Фотографический доказательство того, что глубина резкости не зависит от фокусного расстояния… вроде, как бы, что-то вроде.

Пока пытаясь узнать, что означает термин глубина резкости (DOF), я наткнулся на веб-страницу http://www.dpreview.com/learn/?/key=depth+of+field . На этой странице объясняется термин и предоставляется онлайн-калькулятор. где вы вводите фокусное расстояние, расстояние до объекта (хотя это не поясняется, если это расстояние от объекта до первого элемент на объективе или в фокальной плоскости камеры), диафрагмы, и он сообщает вам, какая глубина резкости (расстояние в перед и за точкой фокусировки, над которой будет находиться изображение фокус) есть. Казалось, на все мои вопросы были даны ответы.

затем просматривая другую страницу на ту же тему, я прочитал, что «некоторые специалисты сейчас думают, что ГРИП не зависит от фокусного длины.» Меня это шокировало, потому что я полагал, что люди фотографировать так долго, что все эти вопросы были решены. Потом мой брат рассказал мне о сайте под названием Luminous. Пейзаж на http://luminous-landscape.com. На странице ДОФ на этом сайте автор однозначно утверждает, что ГРИП не является функцией фокусное расстояние и доказывает это серией фотографий чучела животного.

После чтение через сложный, по крайней мере для меня, математический анализ ГРИП на странице http://normankoren.com/Tutorials/MTF6.html, я Думаю, я понял, что происходит и как может быть путаница в чем-то, что кажется легко разрешимым. проблема не в физике или математике, которые определяют глубину резкости, а скорее в семантике формулировок утверждений о степени свободы. я считаю, что Luminous Landscape предлагает наиболее четкие и полные уточнение: ГРИП не зависит от фокусного расстояния, когда размер изображение на сенсоре остается постоянным.

какая это означает, что глубина резкости не зависит от фокусного расстояния, если , когда вы меняя фокусное расстояние, вы также меняете расстояние от камеры до объект по нужное количество, чтобы сохранить постоянный масштаб изображения. Изменяя как фокусное расстояние, так и расстояние, эти два изменения компенсируются. влияние друг друга на DOF. Люди, претендующие на степень свободы зависит от по фокусному расстоянию работают при совершенно правильном предположении, что расстояние остается постоянным. Их заявление о степени свободы будет таким: Сохранение расстояние диафрагма постоянна, глубина резкости уменьшается по мере увеличения фокусного расстояния.

Пока фотографии чучела животных на сайте Luminous Landscape предназначен для доказательства того, что глубина резкости не является функцией фокусного расстояния, когда масштаб изображения сохраняется постоянным, я не нашел их убедительными и решил проверить это предположение на себе.

Ниже Я сделал две фотографии, из которых, как я полагаю, становится очевидным, что когда размер изображения на датчике поддерживается постоянным, глубина резкости не зависит от изменения фокусного расстояния.

Снято с объективом 50 мм

Снято с объективом 200 мм

на верхнем фото изображена сетка, расположенная под углом 45 градусов к плоскости камеры. объектив. Объектив был установлен на 50мм и F11. (вертикальные линии сетки равны 0,20 дюймов друг от друга.)

я затем сделал второе фото с объективом, установленным на 200 мм и F11, но переместил камеру назад так, чтобы сетка проецировалась на датчик в том же размере, что и на первой фотографии. Обработка велась до минимума и применяется к обоим изображениям в равной степени. Очевидно, что глубина резкости у обоих одинакова, несмотря на то, что стреляли в верхнюю 50мм и нижний на 200мм.

Так, какое определение более применимо? Я считаю, что это зависит от того, что человек пытается сделать в то время. Если кто-то принимает пейзаж, они скорее переключат фокусные расстояния, чем подберут все свое снаряжение и переехать на новое место. Так как они обычно будет оставаться на месте при изменении фокусных расстояний, определение, которое ГРИП , зависит ли от фокусного расстояния, будет иметь больше смысла. Кому-то вроде меня, который много работает с макросами и для данного объект всегда старайтесь заполнить им датчик, двигаясь вперед и назад, определение, что ГРИП не зависит от фокусного расстояния будет кажутся более правильными. (И более удручающе. Имеется в виду, например, что когда я фотографирую колибри и стараюсь заполнить кадр с птицей, я всегда буду ограничиваться одной и той же глубиной поле: всего около 4 дюймов даже при F18.)

Другая способ переформулировать утверждение, что ГРИП не зависит от фокусного длина до тех пор, пока расстояние изменяется для сохранения того же масштаба изображения 90 350 заключается в том, что ГРИП не зависит от расстояния до тех пор, пока фокусное длина изменяется, чтобы сохранить изображение того же размера. Двое высказывания взаимно обратны друг другу.

Так, каковы общие рекомендации для DOF?

1. Глубина резкости увеличивается по мере уменьшения диафрагмы. (это примерно линейная эффект: уменьшение диафрагмы на два шага диафрагмы увеличивает глубину резкости на коэффициент 2.)

(Примечание: Уменьшение диафрагмы работает примерно до F18. Помимо этого апертура настолько мала, что дифракционные эффекты могут размыть изображение больше, чем расширенная глубина резкости помогает повысить резкость.)

2. ГРИП увеличивается с увеличением расстояния, если фокусное расстояние остается такой же. (Это квадратичная зависимость: удвоение расстояние увеличивает глубину резкости примерно в 4 раза.)

3. ГРИП увеличивается по мере уменьшения фокусного расстояния, если расстояние до объект постоянный. (Это отношение обратных квадратов: уменьшение фокусного расстояния в 2 раза увеличивает глубину резкости на примерно 4. )

( приведенные выше соотношения были получены из упомянутого калькулятора степеней свободы ранее на этой странице. Приблизительное отношение, которое DOF пропорциональна квадрату расстояния, умноженному на апертуру, деленному на квадрат фокусного расстояния примерно соответствует анализ на http://normankoren.com/Tutorials/MTF6.html.)

4. Глубина резкости постоянна, если диафрагма постоянна, а фокусное расстояние и расстояния изменяются таким образом, чтобы размер изображения объект, проецируемый на датчик, является постоянным.

Возврат на главную страницу и просмотреть 90 других предметы, включая несколько других страниц, связанных с камерами, объективами и фотографией.

Молекулярные выражения: физика света и цвета

Для получения дополнительной информации о производителях микроскопов

используйте кнопки ниже для перехода на их веб-сайты:

jpg»> Праймер для микроскопии Свет и цвет Основы микроскопа Специальные методы Цифровая визуализация Конфокальная микроскопия Визуализация живых клеток Микрофотография Музей микроскопии Виртуальная микроскопия Флуоресценция Веб-ресурсы Информация о лицензии Использование изображения Пользовательские фотографии Партнеры Информация о сайте Свяжитесь с нами Публикации Дом Галереи: gif»> Фотогалерея Кремниевый зоопарк Фармацевтика Чип-шоты Фитохимикаты Галерея ДНК Микроскейпы Витамины Аминокислоты Камни Религиозная коллекция Пестициды пивные шоты Коктейльная коллекция Заставки Выиграть обои Обои для Mac Киногалерея	Интерактивные учебные пособия по Java Радиус и показатель преломления Влияние на работу объектива Действие простой двояковыпуклой тонкой линзы определяется принципами преломления (которые зависят от радиуса кривизны линзы и показателя преломления) и может быть понято с помощью нескольких простых правил, касающихся геометрии, используемой для отслеживания световые лучи через линзу. В этом интерактивном учебном пособии показано, как изменения показателя преломления и радиуса двояковыпуклой линзы влияют на взаимосвязь между объектом и изображением, создаваемым линзой. Учебник инициализируется симметричной двояковыпуклой тонкой линзой с показателем преломления по умолчанию 1,6 и радиусом 80 миллиметров, создающей изображение объекта (стрелка), расположенного на расстоянии 135 миллиметров от линзы. Для работы с учебным пособием используйте ползунок Lens Radius , чтобы отрегулировать это значение в диапазоне от 60 до 100 миллиметров. По мере увеличения радиуса линзы линза становится тоньше (менее округлой), а фокусное расстояние также увеличивается. Обратите внимание, что синие сферические маркеры фокальной точки (обозначенные F для пространства объекта и F’ для пространства изображения) перемещаются вперед и назад вдоль оптической оси при перемещении ползунка Lens Radius . Увеличение или уменьшение радиуса линзы влияет на размер и положение изображения, формируемого линзой. Изображение Увеличение и идентичность ( Реальное или Виртуальное ) представлены над фокальной точкой пространства изображения и постоянно обновляются по мере изменения размера и положения изображения. Показатель преломления виртуальной двояковыпуклой линзы можно изменять в пределах от 1,4 до 1,8 путем перемещения ползунка Показатель преломления . По мере увеличения показателя преломления фокусные точки (синие сферы) приближаются к линзе, и наоборот. Подобно изменению радиуса линзы, изменения показателя преломления влияют на размер и положение изображения. Фокусное расстояние , Высота объекта , Положение изображения и Высота изображения представлены в пространстве слева от объектива, под фокусом пространства объекта. По мере перевода ползунков эти значения постоянно обновляются учебником. Ползунок Object Position (переменное значение от 45 до 145 миллиметров) можно использовать для регулировки отношения между объектом и линзой при изменении значений радиуса и показателя преломления. Объект (или образец), отображаемый объективом, расположен в предметная плоскость , условно расположенная с левой стороны линзы и представленная серой стрелкой, идущей вверх от осевой линии или оптической оси , проходящей через центр линзы перпендикулярно главной самолеты. Следы лучей через линзу (красные и серые линии) исходят от объекта и проходят слева направо через линзу, образуя реальное изображение (перевернутая серая стрелка) в плоскости изображения с правой стороны линзы. Характеристические трассировки лучей , включая основной луч , представлены в учебнике красными линиями, а другие лучи показаны серыми трассами. Расстояние между передней главной плоскостью линзы и образцом называется расстоянием до объекта , а расстояние от задней главной плоскости до изображения называется расстоянием до изображения. Эти параметры являются фундаментальными элементами, определяющими геометрическую оптику простой линзы, и могут использоваться для расчета важных свойств линзы, включая фокусное расстояние и коэффициент увеличения. Двояковыпуклые линзы являются простейшими увеличительными линзами, их точка фокусировки и коэффициент увеличения зависят от угла кривизны поверхностей. Более высокие углы кривизны приводят к более коротким фокусным расстояниям из-за того, что световые волны преломляются под большим углом по отношению к оптической оси линзы. Симметричный характер двояковыпуклых линз сводит к минимуму сферическую аберрацию в приложениях, где изображение и объект расположены симметрично. Когда двояковыпуклая оптическая система полностью симметрична (по сути, увеличение 1:1), сферическая аберрация минимальна, а кома и дисторсия в равной степени сведены к минимуму или устранены. Как правило, двояковыпуклые линзы работают с минимальными аберрациями при коэффициентах увеличения от 0,2x до 5x. Выпуклые линзы обычно используются для фокусировки и увеличения изображения. Линза работает, преломляя входящие световые волновые фронты в точках, где они входят и выходят из поверхности линзы. Угол преломления и, следовательно, фокусное расстояние будут зависеть от геометрии поверхности линзы, а также от материала, из которого изготовлена ​​линза. Материалы с высоким показателем преломления будут иметь меньшее фокусное расстояние, чем материалы с более низким показателем преломления. Например, линзы из синтетических полимеров, таких как Lucite (показатель преломления 1,47), имеют более низкий показатель преломления, чем стекло (1,51), что приводит к несколько большему фокусному расстоянию. К счастью, показатели преломления люцита и стекла настолько близки, что люцит можно использовать вместо стекла во многих объективах, в том числе в популярных фотокамерах типа «пленка в коробке», которые в настоящее время широко используются потребителями. Линза из чистого алмаза (показатель преломления 2,42) будет иметь фокусное расстояние значительно меньшее, чем у стекла или люцита, хотя высокая стоимость чистого алмаза будет непомерно высокой для изготовления линзы. Соавторы Мэтью Дж. Парри-Хилл , Роберт Т. Саттер и Майкл В. Дэвидсон — Национальная лаборатория сильного магнитного поля, 1800 Ист Пол Дирак Доктор, Университет штата Флорида, Таллахасси, Флорида, 32310. НАЗАД СВЕТ И ЦВЕТ ВЕРНУТЬСЯ К ОБЪЕКТИВАМ И ГЕОМЕТРИЧЕСКОЙ ОПТИКЕ Вопросы или комментарии? Отправить нам письмо. © 1998-2022 автор Майкл В. Дэвидсон и Государственный университет Флориды. Все права защищены. Никакие изображения, графика, сценарии или апплеты не могут быть воспроизведены или использованы каким-либо образом без разрешения владельцев авторских прав. Использование этого веб-сайта означает, что вы соглашаетесь со всеми правовыми положениями и условиями, изложенными владельцами. Этот веб-сайт поддерживается нашими Группа графического и веб-программирования в сотрудничестве с Optical Microscopy в Национальной лаборатории сильного магнитного поля. Последнее изменение: понедельник, 18 сентября 2017 г., 14:47 Число обращений с 14 августа 2002 г.:

Полное руководство по обучению фотографии: диафрагма и глубина резкости

— Фото: Георг Кревенка, студент

но в то же время задайтесь вопросом, как добавить другой вид размытия. Размытие фона. Размытие фона фотографии при сохранении резкости объекта придает изображению глубину и устраняет отвлекающие факторы.

Размытие фона? Это называется глубиной резкости (DOF). Глубина резкости фотографии указывает на то, резко ли сфокусирована вся сцена или все, кроме небольшой части, размыто и забыто.

Диафрагма и глубина резкости напрямую связаны, но есть ряд других факторов, которые также играют роль в этом размытом фоне. Вот что нужно знать начинающим фотографам об диафрагме и глубине резкости.

Что такое глубина резкости?

— Фото: Аарон Ван Сверинген, студент

Понимание глубины резкости (ГРИП) немного упрощается, если вы немного понимаете, как работает камера и объектив камеры. Объектив перенаправляет свет на датчик камеры. Различные кусочки стекла внутри объектива регулируют световые лучи так, что они собираются вместе на датчике изображения. Когда точки света встречаются на датчике, изображение находится в фокусе. Точки света, которые встречаются до или после датчика изображения, не в фокусе.

Фокус зависит от расстояния. Эти различные кусочки стекла внутри объектива регулируются таким образом, что свет, отражающийся от объекта, попадает на датчик, создавая сфокусированное изображение. Объектив камеры с большим фокусным расстоянием приведет к узкому углу обзора, при этом фокус изображения будет находиться дальше на расстоянии. Любой объектив с малым фокусным расстоянием можно считать широкоугольным объективом. Широкоугольный объектив захватывает более широкое поле зрения, но не может передать много деталей.

А как насчет других объектов на изображении? Поскольку эти объекты находятся на другом расстоянии от камеры, чем объект, световые лучи не будут встречаться на датчике, а это означает, что эти объекты не в фокусе.

Но как далеко должны быть эти другие объекты, чтобы быть не в фокусе? Будет ли объект в футе от вас в фокусе? А дюйм? Миллиметр?

Глубина резкости определяет диапазон расстояний, на котором объекты остаются четкими. Например, при определенных настройках камеры (о которых мы поговорим далее) объекты, находящиеся в футе или даже в нескольких футах от объекта, все равно будут оставаться приемлемо резкими. Но если вы доведете эту настройку камеры до другой крайности, объекты в дюйме от объекта будут казаться размытыми.

Небольшая глубина резкости означает, что диапазон расстояний, на котором объекты кажутся резкими, очень мал. Например, малая глубина резкости может означать, что объекты, которые находятся дальше, чем в дюйме от объекта, размыты. На изображениях с таким узким диапазоном фон выглядит очень не в фокусе.

С другой стороны, большая глубина резкости означает широкий диапазон. При большой глубине резкости даже объекты, находящиеся на расстоянии нескольких футов от объекта, все равно будут четкими. Конечно, один дюйм и несколько футов — это просто примеры — точный диапазон варьируется, но короткие диапазоны называются узкими, а длинные — широкой глубиной резкости.

Глубина резкости также действует в обоих направлениях — если объект, находящийся в шести дюймах позади объекта, находится в фокусе, объект, находящийся в шести дюймах перед объектом, также будет в фокусе. Если вы делаете снимок трех объектов на трех разных расстояниях — например, групповое фото с тремя рядами — фокусировка на среднем объекте поможет вам использовать весь этот диапазон фокусировки. Глубина резкости влияет на передний план или переднюю часть изображения так же сильно, как и на фон.

Диафрагма и глубина резкости (ГРИП)

— Фото: Mar Washburn, Student

Диафрагма позволяет фотографу контролировать, насколько велик (или мал) этот диапазон расстояний. Как одна из трех различных настроек экспозиции, диафрагма влияет на количество света, попадающего в изображение, путем изменения размера отверстия в объективе. Большее отверстие в объективе создает более яркое изображение и наоборот.

Но чем шире апертура или отверстие объектива, тем короче становится расстояние, на котором появляется резкий объект. Очень широкая диафрагма, такая как f/1.8, создает изображение с очень малой глубиной резкости, где даже объекты, находящиеся на расстоянии одного дюйма, немного размыты. На портрете, сделанном с фокусировкой на глазах объекта при f/1.8, нос объекта — и, возможно, даже кончики его ресниц — будут не в фокусе.

По мере того как апертура объектива уменьшается, диапазон расстояний, при котором изображение получается четким, становится шире. При меньшей диафрагме в фокус попадают объекты, находящиеся дальше от объекта. Диафрагма f/22 пропускает очень мало света, но при этом большая часть сцены остается в фокусе. Объекты в нескольких футах от объекта будут выглядеть такими же резкими.

F/1.8 и f/22 являются крайними примерами — между ними также много значений диафрагмы. Если вы снова снимаете этот портрет и хотите, чтобы глаза и нос были четкими, вы можете немного сузить диафрагму, чтобы сфокусировать все лицо и при этом получить приличное размытие фона.

Что еще влияет на глубину резкости?

Aperture — один из крупнейших игроков, когда дело доходит до глубины резкости, но хотя Aperture может быть самым ценным игроком, это не единственный игрок на площадке.

Фокусное расстояние также влияет на глубину резкости изображения. Чем ближе вы находитесь к объекту, тем уже становится ваша глубина резкости. Макрофотографы часто используют очень узкую диафрагму, потому что они находятся очень близко к объекту. Диафрагма f/2.8, использованная при съемке крупного плана шмеля, может сделать его глаза резкими, но его жало потеряется в размытии. Это потому, что чем ближе вы к объекту, тем уже ваша глубина резкости.

Чем дальше от объекта, тем глубина резкости снова сужается — если вы используете то же фокусное расстояние. Использование зум-объектива имеет тот же эффект, что и приближение к объекту: он сужает глубину резкости, оставляя фон размытым.

Распространенное заблуждение состоит в том, что именно зум-объектив на самом деле создает размытие фона, но если вы сделали снимок крупным планом, а затем использовали зум-объектив для создания той же композиции издалека, изображения будут иметь почти одинаковую глубину. поля. Зум-объективы не увеличивают размытие фона, но они создают такой же уровень размытия, как если бы вы снимали близко к объекту. Таким образом, хотя диафрагму f/1,8 невозможно найти на 300-миллиметровом зум-объективе, f/4 часто бывает достаточно, потому что качество зума объектива уже создаст узкий эффект глубины резкости — просто знайте, что это из-за расстояния. , а не сам объектив.

Поскольку объекты в пределах этого диапазона глубины резкости являются четкими, чем дальше объект от объекта, тем более размытым он будет выглядеть. Если вы сфотографируете птицу во дворе, но ближайшие деревья находятся в 50 ярдах от вас, эти деревья будут размыты просто потому, что они находятся слишком далеко от объекта. Хотя более широкая диафрагма сильнее размывает эти деревья, расстояние также влияет на уровень размытия фона.

Есть еще один фактор, влияющий на глубину резкости, но он находится вне вашего контроля, если вы не обновите камеру: размер сенсора. Датчик является цифровым эквивалентом куска пленки. Чем больше сенсор, тем уже глубина резкости или размытее фон. Вот почему легче получить фотографию с размытым фоном с зеркальной камеры и намного сложнее сделать с iPhone. В то время как у iPhone довольно широкий объектив с фиксированной диафрагмой f/2.8, у него маленький датчик, что затрудняет достижение размытия фона. Точно так же камера Micro Four Thirds будет иметь меньшее размытие фона, чем датчик размера APS-C, и даже меньше, чем полнокадровый датчик.

Применение и устранение неполадок

Понимание диафрагмы и глубины резкости позволяет фотографам проявлять творческий подход к размытию — например, сохранять нетронутыми детали потрясающего пейзажа с узкой апертурой или стирать отвлекающие факторы на портрете с широкой апертурой.

Но знание того, как диафрагма и расстояние влияют на глубину резкости, является отличным инструментом для устранения неполадок. Хитрое групповое фото — прекрасный пример. Допустим, у вас есть три ряда людей (это означает, что они находятся на разном расстоянии от камеры), и передний ряд находится в фокусе, а задний ряд размыт.

Во-первых, вы можете убедиться, что ваша точка автофокуса находится в среднем ряду. Если вы фокусируетесь на первом ряду, вы тратите половину глубины резкости, потому что он находится перед всеми вашими объектами.

Если вы фокусируетесь на этом среднем ряду и все еще получаете размытие фона, используйте более узкую диафрагму. Для групповых фотографий часто требуется f/8 или выше.

Теперь представьте, что у вас гораздо меньшая группа — всего два человека. Если вы не хотите использовать узкую диафрагму, возможно, потому, что вы снимаете с ограниченным освещением, например, внутри церкви, вы можете разместить этих двух людей на одинаковом расстоянии от камеры, чтобы они оба оказались в фокусе с узкой диафрагмой. Поскольку миллиметры играют роль при диафрагме такой ширины, как f/1,8, не стоит использовать сверхширокую диафрагму, иначе одна из них может быть просто не в фокусе, но вам не нужна та же самая диафрагма f/8, которую вы использовали, когда стояли ряды людей на разном расстоянии.

Узкие отверстия также облегчают фокусировку. Если вы заметили, что ваши динамичные снимки получаются немного мягкими, попробуйте сузить диафрагму. Поместив в фокус большую часть изображения, у вас будет больше шансов сфокусироваться, даже если у вас очень мало времени, чтобы сфокусировать снимок.

Понимание того, как расстояние влияет на глубину резкости, позволяет фотографам работать в рамках ограничений собственного оборудования. Скажем, вы снимаете портрет на фоне кирпичной стены, но у вас есть только штатный объектив, и вы не можете получить шире, чем f/3,6. Если вас не устраивает резкость этой кирпичной стены, просто отодвиньте объект от стены.

Поскольку расстояние между камерой и объектом также играет роль, вместо этого вы можете приблизиться к объекту или использовать зум-объектив. Конечно, приближение изменит вашу композицию, поэтому наличие такой широкой апертуры — хороший вариант.

Диафрагма и покупка объективов

Объективы в вашей фотосумке могут быть не такими широкими, как f/1,8, или такими узкими, как f/22. Большинство китовых объективов имеют максимальную диафрагму f/3,6 — вы не можете снимать шире, потому что физических частей, необходимых для получения такой широкой диафрагмы, просто нет.

Переход на объектив с диафрагмой f/1,8 позволит добиться большего размытия фона, а также улучшить качество съемки при слабом освещении, особенно по сравнению с комплектным объективом. Но чем шире становится объектив, тем больше становится ценник.

Объективы с фиксированным фокусным расстоянием или объективы с фиксированным фокусным расстоянием без возможности масштабирования часто являются хорошей альтернативой, поскольку они имеют широкий диапазон диафрагмы и не слишком дорого стоят. Фикс-объективы не так удобны, как зумы, но для приложений без быстро движущихся объектов, таких как портретная работа, они предлагают большую гибкость диафрагмы по цене.

По мере увеличения зума объектива также становится все труднее найти широкое отверстие — физически невозможно уменьшить диафрагму настолько сильно. Помните, что зум-объективы имитируют эффект приближения к объекту, поэтому отсутствие доступа к диафрагме f/1.8 на телеобъективе не такая уж большая проблема.

Aperture: что нужно помнить

Aperture может быть запутанным понятием для начинающих. Если есть что-то, что новички должны помнить об диафрагме, так это следующее:

Широкая апертура = узкая глубина резкости = фон не в фокусе
Узкая апертура = широкая глубина резкости = резкий фон в фокусе. Широкие диафрагмы имеют очень маленький диапазон расстояний в фокусе, в то время как малые диафрагмы имеют большой диапазон расстояний в фокусе.

Точно так же, как изучение выдержки или ISO, отправляясь с камерой и пробуя различные настройки диафрагмы, все эти детали, касающиеся диафрагмы и глубины резкости, станут вашей второй натурой. Поэкспериментируйте с использованием разных расстояний, чтобы отрегулировать уровень размытия фона.

Еще один способ запомнить диафрагму и глубину резкости? Добавьте это руководство в закладки, закрепите или поделитесь им, чтобы потом легко обращаться к нему.

16.3 Линзы — Физика | ОпенСтакс

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

• Описывать и прогнозировать формирование и увеличение изображения в результате преломления через выпуклые и вогнутые линзы, использовать диаграммы лучей для подтверждения формирования изображения и обсуждать, как эти свойства линз определяют их применение
• Объясните, как работает человеческий глаз с точки зрения геометрической оптики
• Выполнение расчетов на основе уравнения тонкой линзы для определения расстояний до изображения и объекта, фокусного расстояния и увеличения изображения, а также использование этих расчетов для подтверждения значений, определенных по лучевым диаграммам

Основные термины раздела

аберрация	хроматическая аберрация	вогнутая линза	собирающая линза	выпуклая линза
рассеивающая линза	окуляр	цель	окуляр	парфокальный

Характеристики линз

Поддержка учителей

Поддержка учителей

[BL][OL][AL]Прочитайте уравнение линзы/зеркала из раздела «Отражение». Просмотрите термины «фокальная точка», «фокусное расстояние», «расстояние до объекта», «расстояние до изображения», «вогнутость», «выпуклость», «схождение» и «расхождение» в разделе «Отражение».

Линзы

можно найти в огромном количестве оптических инструментов, начиная от простого увеличительного стекла и заканчивая зум-объективом камеры. В этом разделе мы используем закон преломления для изучения свойств линз и того, как они формируют изображения.

Кое-что из того, что мы узнали из предыдущего обсуждения изогнутых зеркал, применимо и к изучению линз. Вогнутая, выпуклая, фокусная точка F и фокусное расстояние f имеют те же значения, что и раньше, за исключением того, что каждое измерение производится от центра линзы, а не от поверхности зеркала. Выпуклая линза, показанная на рис. 16.25, имеет такую ​​форму, что все лучи света, входящие в нее параллельно ее центральной оси, пересекаются друг с другом в одной точке на противоположной стороне линзы. Центральная ось или ось определяется как линия, перпендикулярная линзе в ее центре. Такая линза называется собирающей линзой из-за собирающего эффекта, который она оказывает на световые лучи. На рис. 16.25 показано увеличенное изображение пути одного луча через линзу, чтобы проиллюстрировать, как луч меняет направление как при входе, так и при выходе из линзы. Поскольку показатель преломления линзы больше, чем у воздуха, луч движется к перпендикуляру при входе и от перпендикуляра при выходе. (Это соответствует закону преломления.) Из-за формы линзы свет отклоняется к оси на обеих поверхностях.

Рисунок 16.25 Лучи света, входящие в выпуклую, или собирающую, линзу параллельно ее оси, сходятся в ее фокусе F. Луч 2 лежит на оси линзы. Расстояние от центра линзы до фокальной точки равно фокусному расстоянию ƒ линзы. Расширенный вид пути, по которому проходит луч 1, показывает перпендикуляры и углы падения и преломления на обеих поверхностях.

Обратите внимание, что лучи от источника света, помещенного в фокус собирающей линзы, выходят параллельно с другой стороны линзы. Возможно, вы слышали об уловке использования собирающей линзы для фокусировки солнечных лучей в точку. Такая концентрация световой энергии может произвести достаточно тепла, чтобы зажечь бумагу.

На рис. 16.26 показана вогнутая линза и влияние, которое она оказывает на лучи света, входящие в нее параллельно ее оси (путь, пройденный лучом 2 на рисунке, является осью линзы). Вогнутая линза является рассеивающей линзой, потому что она заставляет световые лучи отклоняться (расходиться) от своей оси. В этом случае линза имеет такую ​​форму, что все световые лучи, входящие в нее параллельно ее оси, исходят из одной и той же точки F, определяемой как фокус рассеивающей линзы. Расстояние от центра линзы до точки фокуса снова называется фокусное расстояние или « ƒ » объектива. Обратите внимание, что фокусное расстояние рассеивающей линзы считается отрицательным. Увеличенный вид пути одного луча через линзу показан на рис. 16.26, чтобы показать, как форма линзы вместе с законом преломления заставляет луч следовать своей конкретной траектории и расходиться.

Рисунок 16.26 Лучи света входят в вогнутую или рассеивающую линзу, параллельную ее оси, расходятся и, таким образом, кажется, что они исходят из ее фокуса F. Пунктирные линии не являются лучами; они указывают направления, откуда исходят лучи. Фокусное расстояние, ƒ , рассеивающей линзы отрицательный. Расширенный вид пути, по которому проходит луч 1, показывает перпендикуляры и углы падения и преломления на обеих поверхностях.

Оптическая сила P линзы вычисляется очень легко. Это просто величина, обратная фокусному расстоянию, выраженному в метрах

.

P=1f.P=1f.

16.15

Единицами силы являются диоптрии, Д, которые выражаются в обратных метрах. Если фокусное расстояние отрицательно, как для рассеивающей линзы на рис. 16.26, то и оптическая сила также отрицательна.

Поддержка учителей

Поддержка учителей

[BL][OL]Объясните, что для трассировки лучей необходим фокус. Можно рассчитать положение фокальной точки, используя закон преломления (закон Снеллиуса) и показатель преломления материала линзы, но этот процесс требует много времени и его трудно выполнить точно. Повторите определения реального, виртуального, прямого и перевернутого, поскольку они применимы к изображениям.

Предупреждение о заблуждении

К сожалению, слово мощность используется для двух совершенно разных концепций. Если вы изучаете рецепт на очки, оптическая сила линз указывается в диоптриях. Если вы изучите этикетку на двигателе, уровень энергопотребления указан в виде мощности в ваттах.

В некоторых случаях линза формирует изображение в очевидном месте, например, когда кинопроектор проецирует изображение на экран. В других случаях расположение изображения менее очевидно. Где, например, изображение формируется очками? Мы используем трассировку лучей для тонких линз, чтобы проиллюстрировать, как они формируют изображения, и разрабатываем уравнения для количественного описания формирования изображения. Вот правила трассировки лучей:

1. Луч, входящий в собирающую линзу параллельно ее оси, проходит через фокус F линзы с другой стороны
2. Луч, входящий в рассеивающую линзу параллельно ее оси, кажется, исходит из точки фокусировки F со стороны входящего луча
3. Луч, проходящий через центр собирающей или рассеивающей линзы, не меняет направления
4. Луч, входящий в собирающую линзу через ее фокус, выходит параллельно ее оси
5. Луч, который входит в рассеивающую линзу, направляясь к фокусу на противоположной стороне, выходит параллельно оси

Рассмотрим объект на некотором расстоянии от собирающей линзы, как показано на рис. 16.27. Чтобы найти положение и размер формируемого изображения, мы прослеживаем пути избранных световых лучей, исходящих из одной точки на объекте. В этом примере исходной точкой является макушка головы женщины. На рис. 16.27 показаны три луча от вершины объекта, которые можно трассировать с помощью только что перечисленных правил трассировки лучей. Лучи покидают эту точку, путешествуя во многих направлениях, но мы сосредоточимся только на нескольких, траектории которых легко проследить. Первый луч — это тот, который входит в линзу параллельно ее оси и проходит через фокальную точку с другой стороны (правило 1). Второй луч проходит через центр линзы, не меняя направления (правило 3). Третий луч проходит через ближайший фокус на пути в линзу и выходит из линзы параллельно ее оси (правило 4). Все лучи, исходящие из одной и той же точки на макушке человека, преломляются таким образом, что пересекаются в одной и той же точке по другую сторону линзы. В этой точке расположено изображение макушки головы человека. Лучи из другой точки объекта, например пряжки ремня, также пересекаются в другой общей точке, образуя законченное изображение, как показано на рисунке. Хотя на рис. 16.27 прослеживаются три луча, для локализации изображения необходимы только два. Лучше всего трассировать лучи, для которых существуют простые правила трассировки лучей. Прежде чем применять трассировку лучей к другим ситуациям, давайте более подробно рассмотрим пример, показанный на рис. 16.27.

Рисунок 16.27 Трассировка лучей используется для определения местоположения изображения, сформированного линзой. Трассируются лучи, исходящие из одной и той же точки объекта. Каждый из трех выбранных лучей следует одному из правил трассировки лучей, поэтому их пути легко определить. Изображение находится в точке пересечения лучей. При этом формируется реальное изображение, которое можно спроецировать на экран.

Изображение, сформированное на рис. 16.27, является реальным изображением, то есть его можно проецировать. То есть световые лучи из одной точки объекта фактически пересекаются в месте расположения изображения и могут быть спроецированы на экран, кусок пленки или сетчатку глаза.

На рис. 16.27 расстояние до объекта d _o больше, чем f. Теперь рассмотрим лучевую диаграмму для выпуклой линзы, где d _o < f , и другую диаграмму для вогнутой линзы.

Виртуальная физика

Геометрическая оптика

Эта анимация показывает, как изображение, формируемое выпуклой линзой, изменяется при изменении расстояния до объекта, радиуса кривизны, показателя преломления и диаметра линзы. Для начала выберите Principal Rays в верхнем левом меню, а затем попробуйте изменить некоторые параметры, указанные вверху по центру. Show Help предоставляет несколько полезных меток.

PhET Исследования: геометрическая оптика Как линза формирует изображение? Посмотрите, как световые лучи преломляются линзой. Посмотрите, как меняется изображение, когда вы регулируете фокусное расстояние объектива, перемещаете объект, перемещаете объектив или перемещаете экран.

Как изменяется фокусное расстояние f при увеличении радиуса кривизны? Как изменяется f с увеличением показателя преломления?

1. Фокусное расстояние увеличивается в обоих случаях: при увеличении радиуса кривизны и показателя преломления.

2. Фокусное расстояние уменьшается в обоих случаях: при увеличении радиуса кривизны и показателя преломления.

3. Фокусное расстояние увеличивается при увеличении радиуса кривизны; она уменьшается, когда показатель преломления увеличивается.

4. Фокусное расстояние уменьшается при увеличении радиуса кривизны; она увеличивается с увеличением показателя преломления.

Поддержка учителей

Поддержка учителей

После того, как учащиеся ознакомятся с работой анимации, попросите их выбрать параметр 2-я точка в левом нижнем углу меню. Этот параметр обеспечивает лучи из второй точки объекта. Эту точку можно настроить таким образом, чтобы можно было изучать лучи как сверху, так и, например, от центра объекта.

Тип	Образовано, когда	Тип изображения	д и	М
Чемодан 1	f положительный, d o > f	Реальный	Положительный	Отрицательный м >, < или = –1
Чемодан 2	f положительный, d o < f	Виртуальный	Отрицательный	Положительный м > 1
Чемодан 3	f отрицательный	Виртуальный	Отрицательный	Положительный м < 1

Стол 16,3 Три типа изображений, формируемых линзами

Примеры на рис. 16.27 и рис. 16.28 представляют три возможных случая — случай 1, случай 2 и случай 3 — в таблице 16.3. В таблице м — увеличение; остальные символы имеют то же значение, что и для изогнутых зеркал.

Рисунок 16.28 (а) Изображение виртуальное и больше, чем объект. (b) Изображение виртуальное и меньше объекта.

Снап Лаборатория

Фокусное расстояние

• Экстремальные температуры — в этой лаборатории встречаются очень высокие или очень низкие температуры, которые могут вызвать ожоги. Используйте защитные рукавицы, очки и одежду при работе с очень горячими или очень холодными предметами. Немедленно сообщите своему учителю о любых ожогах.
• БЕЗОПАСНОСТЬ ДЛЯ ГЛАЗ — прямой взгляд на солнце может привести к необратимому повреждению глаз. Не смотрите на Солнце ни через какую линзу.

• Несколько линз
• Лист белой бумаги
• Линейка или рулетка

Инструкции

Процедура

1. Найдите несколько линз и определите, собирающие они или рассеивающие. В общем, те, что толще по краям, расходятся, а те, что толще ближе к центру, сходятся.
2. В яркий солнечный день вынесите собирающие линзы на улицу и попробуйте сфокусировать солнечный свет на листе белой бумаги.
3. Определите фокусные расстояния линз. Попросите одного из партнеров медленно перемещать линзу к бумаге и от нее, пока вы не найдете расстояние, на котором световое пятно будет самым ярким. Попросите другого партнера измерить расстояние от линзы до яркого пятна. Будьте осторожны, поскольку в зависимости от типа объектива бумага может начать гореть.

Поддержка учителей

Поддержка учителей

Убедитесь, что рядом с местом проведения эксперимента нет легковоспламеняющихся материалов. Например, голый бетонный тротуар приемлем, а сухая коричневая трава или листья — нет. Не смотрите на Солнце ни через какую линзу ! Это может привести к необратимому повреждению глаз!

Правда или ложь — яркое пятно, которое появляется в фокусе на бумаге, является изображением Солнца.

1. Правда
2. Ложь

Поддержка учителей

Поддержка учителей

[BL]Попросите учащихся назвать как можно больше инструментов и приспособлений, в состав которых входит одна или несколько линз. Заполните те, которые они пропустили, с помощью увеличительного стекла, камеры, глаза, телескопа, микроскопа, а также кино- и слайд-проекторов.

[OL]Объясните, чем человеческий глаз аналогичен фотокамере. Обсудите, где в каждом из них находится объектив, диафрагма и фокус. Обсудите, как камера фокусирует объекты на разных расстояниях, перемещая линзу, тогда как глаз делает это, изменяя форму линзы.

[AL]Попросите учащихся определить показатель преломления и объяснить, как он влияет на путь световых лучей, проходящих через линзу. Как изменится путь при изменении показателя преломления материала линзы? С изменениями длин волн, составляющих световой луч?

Формирование изображения линзами также можно рассчитать с помощью простых уравнений. Мы узнаем, как эти расчеты выполняются ближе к концу этого раздела.

Некоторыми распространенными применениями линз, с которыми мы все знакомы, являются увеличительные стекла, очки, фотоаппараты, микроскопы и телескопы. Мы рассмотрим последние два примера, которые являются наиболее сложными. Мы уже видели конструкцию телескопа, в котором используются только зеркала, на рис. 16.12. На рис. 16.29 показана конструкция телескопа с двумя линзами. Часть (а) рисунка показывает конструкцию телескопа, используемого Галилеем. Он создает вертикальное изображение, что более удобно для многих приложений. Часть (b) показывает расположение линз, используемых во многих астрономических телескопах. Эта конструкция создает перевернутое изображение, что не создает проблем при просмотре небесных объектов.

Поддержка учителей

Поддержка учителей

[OL][AL]Объясните, почему не имеет значения, перевернуто ли изображение небесного объекта. Спросите своих учеников, согласны ли они с утверждением: в космосе нет ни верха, ни низа.

Предупреждение о заблуждении

Мы не осознаем, что световые лучи исходят из каждой части объекта и проходят через каждую часть линзы; все они используются для формирования конечного изображения. В общем, мы чувствуем, что вся линза или зеркало необходимы для формирования изображения. На самом деле половина линзы формирует такое же, хотя и более тусклое изображение.

Рисунок 16.29 (а) Галилей сделал телескопы с выпуклым объективом и вогнутым окуляром. Они создают вертикальное изображение и используются в подзорных трубах. (b) Большинство простых телескопов имеют две выпуклые линзы. Объектив формирует изображение случая 1, которое является объектом для окуляра. Окуляр формирует конечное изображение случая 2, которое увеличивается.

На рис. 16.30 показан путь света через обычный микроскоп. Микроскопы были впервые разработаны в начале 1600-х годов производителями очков в Нидерландах и Дании. Простейший составной микроскоп состоит из двух выпуклых линз, как схематично показано на рис. 16.30. Первая линза называется 9объектив 1160 ; он имеет типичные значения увеличения от 5 × × до 100 × ×. В стандартных микроскопах объективы устанавливаются таким образом, что при переключении между ними образец остается в фокусе. Объективы, расположенные таким образом, описываются как парфокальные . Вторая линза, окуляр, также называемая окуляром , имеет несколько линз, которые скользят внутри цилиндрического корпуса. Возможность фокусировки обеспечивается движением как объектива, так и окуляра. Задача микроскопа — увеличивать мелкие объекты, и обе линзы способствуют конечному увеличению. Кроме того, конечное увеличенное изображение создается в месте, достаточно далеком от наблюдателя, чтобы его можно было легко рассмотреть, потому что глаз не может сфокусироваться на объектах или изображениях, которые находятся слишком близко.

Рисунок 16.30 Составной микроскоп, состоящий из двух линз, объектива и окуляра. Объектив формирует изображение случая 1, которое больше, чем объект. Это первое изображение является объектом для окуляра. Окуляр формирует окончательное изображение случая 2, которое увеличивается еще больше.

Реальные линзы ведут себя несколько иначе, чем то, как они моделируются с помощью диаграмм лучей или уравнений тонкой линзы. Настоящие линзы дают аберрации. Аберрация – это искажение изображения. Существует множество аберраций, которые возникают из-за размера линзы, материала, толщины и положения объекта. Одним из распространенных типов аберраций является хроматическая аберрация, связанная с цветом. Поскольку показатель преломления линз зависит от цвета или длины волны, изображения создаются в разных местах и ​​с разным увеличением для разных цветов. Закон отражения не зависит от длины волны, поэтому зеркала не имеют этой проблемы. Этот результат является еще одним преимуществом использования зеркал в оптических системах, таких как телескопы.

На рис. 16.31(а) показаны хроматические аберрации для одной выпуклой линзы и ее частичная коррекция с помощью системы из двух линз. Показатель преломления хрусталика увеличивается с уменьшением длины волны, поэтому фиолетовые лучи преломляются сильнее, чем красные, и поэтому фокусируются ближе к хрусталику. Рассеивающая линза частично исправляет это, хотя обычно это невозможно сделать полностью. Можно использовать линзы из разных материалов и с разной дисперсией. Например, ахроматический дублет, состоящий из собирающей линзы из кронового стекла, находящейся в контакте с рассеивающей линзой из бесцветного стекла, может значительно уменьшить хроматическую аберрацию (рис. 16.31(b)).

Рисунок 16.31 (а) Хроматическая аберрация вызвана зависимостью показателя преломления линзы от цвета (длины волны). Линза более мощная для фиолетового (V), чем для красного (R), создавая изображения с разными цветами, положениями и увеличением. (b) Системы с несколькими линзами могут частично корректировать хроматические аберрации, но для них могут потребоваться линзы из разных материалов, что увеличивает стоимость оптических систем, таких как камеры.

Физика глаза

Поддержка учителей

Поддержка учителей

[BL]Рассмотрите искривление света за счет преломления на границе между средами с разными показателями преломления. Обратите внимание, что чем больше разница в показателях преломления, тем сильнее искривляется свет.

[ПР]Покажите учащимся фотоаппарат и укажите части фотоаппарата, выполняющие ту же функцию, что и аналогичные части глаза: апертура (радужная оболочка), линза (линза), пленка или светочувствительный экран (сетчатка) и память (мозг).

[AL]Попросите учащихся в очках сравнить их. Спросите, знают ли они, корректируют ли их очки близорукость или дальнозоркость. Объясните, почему очки, корректирующие близорукость, являются рассеивающими (вогнутыми) и почему очки, корректирующие дальнозоркость, являются сужающимися (выпуклыми).

Глаз, пожалуй, самый интересный из всех оптических инструментов. Он замечателен тем, как формирует изображения, и богатством деталей и цветов, которые может обнаружить глаз. Тем не менее, наши глаза обычно нуждаются в некоторой коррекции, чтобы достичь того, что называется нормальным зрением , но вместо этого его следует называть идеальным зрением . Формирование изображения нашими глазами и обычная коррекция зрения легко анализируются с помощью геометрической оптики. На рис. 16.32 показана основная анатомия глаза. Роговица и хрусталик образуют систему, которая в хорошем приближении действует как единая тонкая линза. Для четкого зрения реальное изображение должно проецироваться на светочувствительную сетчатку, которая находится на фиксированном расстоянии от хрусталика. Хрусталик глаза регулирует свою силу для создания на сетчатке изображения объектов, находящихся на разном расстоянии. Центр изображения приходится на ямку, имеющую наибольшую плотность светорецепторов и наибольшую остроту (резкость) в поле зрения. В месте соприкосновения зрительного нерва с глазом, называемом 9-м, рецепторов нет. 1160 слепое пятно . Изображение, падающее на это место, невозможно увидеть. Переменное отверстие (или зрачок) глаза наряду с химической адаптацией позволяет глазу обнаруживать интенсивность света от самой низкой наблюдаемой до 10 ¹⁰ раз большей (без повреждений). Десять порядков — это невероятный диапазон обнаружения. Наши глаза выполняют огромное количество функций, таких как определение направления, движения, сложных цветов и расстояния. Обработка импульсов зрительного нерва начинается с взаимосвязей в сетчатке и продолжается в головном мозге. Зрительный нерв передает сигналы, полученные глазом, в мозг.

Рисунок 16.32 Роговица и хрусталик глаза действуют вместе, чтобы сформировать реальное изображение на светочувствительной сетчатке, которая имеет самую плотную концентрацию рецепторов в центральной ямке и слепое пятно над зрительным нервом. Сила хрусталика глаза регулируется, чтобы обеспечить изображение на сетчатке для различных расстояний до объекта.

Показатели преломления имеют решающее значение для формирования изображения с помощью линз. В таблице 16.4 показаны показатели преломления, относящиеся к глазу. Наибольшее изменение показателя преломления — и то, которое вызывает наибольшее искривление лучей — происходит в роговице, а не в хрусталике. Лучевая диаграмма на рис. 16.33 показывает формирование изображения роговицей и хрусталиком глаза. Лучи преломляются в соответствии с показателями преломления, указанными в таблице 16.4. Роговица обеспечивает около двух третей увеличения глаза, потому что скорость света значительно меняется при переходе из воздуха в роговицу. Линза обеспечивает оставшееся увеличение, необходимое для создания изображения на сетчатке. Роговицу и хрусталик можно рассматривать как единую тонкую линзу, хотя световые лучи проходят через несколько слоев материала (например, роговицу, водянистую влагу, несколько слоев хрусталика и стекловидное тело), ​​меняя направление на каждой поверхности раздела. Формируемое изображение очень похоже на изображение, создаваемое одной выпуклой линзой. Этот результат представляет собой изображение случая 1. Образы, сформированные в глазу, переворачиваются, но мозг переворачивает их еще раз, чтобы они казались прямыми.

Материал	Показатель преломления
* Показатель преломления различен по всей линзе и максимален в ее центре.
Вода	1,33
Воздух	1,00
Роговица	1,38
Водянистая влага	1,34
Линза	1,41 среднее *
Стекловидное тело	1,34

Стол 16,4 Показатели преломления, относящиеся к глазу

Рисунок 16.33 На сетчатке формируется изображение, при этом лучи света больше всего сходятся у роговицы, а также при входе и выходе из хрусталика. Лучи сверху и снизу объекта прослеживаются и создают на сетчатке перевернутое реальное изображение. Расстояние до объекта рисуется меньше масштаба.

Как уже отмечалось, изображение должно падать точно на сетчатку, чтобы обеспечить четкое зрение, т. е. расстояние до изображения, d _i , должно равняться расстоянию от линзы до сетчатки. Поскольку расстояние от линзы до сетчатки не меняется, d _i должны быть одинаковыми для объектов на всех расстояниях. Глазу удается изменять расстояние, изменяя силу (и фокусное расстояние) линзы, чтобы приспособиться к объектам на разных расстояниях. На рис. 16.33 вы можете видеть маленькие цилиарные мышцы над и под хрусталиком, которые изменяют форму хрусталика и, таким образом, фокусное расстояние.

Потребность в какой-либо коррекции зрения очень распространена. Обычные дефекты зрения легко понять, а некоторые просто исправить. На рис. 16.34 показаны два распространенных дефекта зрения. Близорукость, или близорукость, — это неспособность четко видеть удаленные объекты, в то время как близкие объекты находятся в фокусе. Близорукий глаз сверхсходится почти параллельных лучей от удаленного объекта, и лучи пересекаются перед сетчаткой. Более расходящиеся лучи от близкого объекта сходятся на сетчатке, создавая четкое изображение. Дальнозоркость или дальнозоркость — это неспособность четко видеть близкие предметы, в то время как удаленные предметы могут быть в фокусе. Дальнозоркий глаз не собирает лучи от близкого предмета в достаточной степени, чтобы лучи встретились на сетчатке. Менее расходящиеся лучи от удаленного объекта могут быть сведены для получения четкого изображения.

Рисунок 16.34 а) близорукий (миопический) глаз сводит лучи от удаленного предмета перед сетчаткой; таким образом, они расходятся, когда ударяются о сетчатку, и создают размытое изображение. Это расхождение может быть вызвано слишком мощной линзой глаза (другими словами, слишком коротким фокусным расстоянием) или слишком большой длиной глаза. (б) Глаз с дальнозоркостью (гиперметропический) не может собрать лучи от близкого объекта к тому моменту, когда они попадают на сетчатку и вызывают… размытое зрение вблизи. Эта плохая конвергенция может быть вызвана недостаточной оптической силой (другими словами, слишком большим фокусным расстоянием) линзы или слишком коротким глазом.

Поскольку близорукий глаз чрезмерно сводит световые лучи, коррекция близорукости заключается в размещении перед глазом рассеивающей очковой линзы. Эта линза уменьшает силу глаза со слишком коротким фокусным расстоянием (рис. 16.35, а). Поскольку дальнозоркий глаз не сводит световых лучей, коррекция дальнозоркости заключается в размещении перед глазом собирающей очковой линзы. Эта линза увеличивает силу глаза со слишком большим фокусным расстоянием (рис. 16.35, б).

Рисунок 16.35 (а) Для коррекции близорукости требуется рассеивающая линза, которая компенсирует чрезмерную конвергенцию глаза. Рассеивающая линза создает изображение ближе к глазу, чем предмет, так что близорукий человек может ясно его видеть. (b) Для коррекции дальнозоркости используется собирающая линза, которая компенсирует недостаточное схождение глазом. Собирающая линза формирует изображение дальше от глаза, чем предмет, так что дальнозоркий человек может ясно его видеть. Как в (а), так и в (б) лучи, которые встречаются на сетчатке, представляют собой скорректированное зрение, а другие лучи представляют собой нечеткое зрение без корректирующих линз.

Расчеты с использованием уравнений линзы

Как и было обещано, новых уравнений для запоминания не требуется. Мы можем использовать уже представленные уравнения для решения задач, связанных с изогнутыми зеркалами. Тщательный анализ позволяет применить эти уравнения к линзам. Вот уравнения, которые вам нужны

П=1ф,П=1ф,

, где P — сила, выраженная в обратных метрах (m ^–1 ), а не в диоптриях (D), а f — фокусное расстояние, выраженное в метрах (м). Вам также нужно

1f=1di+1do, 1f=1di+1do,

, где, как и прежде, d _o и d _i — расстояние до объекта и расстояние до изображения соответственно. Помните, что это уравнение обычно более полезно, если его изменить для решения одной из переменных. Например,

ди=фдодо-ф.ди=фдодо-ф.

Уравнения для увеличения, м , такие же, как и для зеркал

м=хихо=-дидо, м=хихо=-дидо,

где ч _i и h _o — высота изображения и высота объекта соответственно. Помните также, что отрицательное значение d _i указывает на виртуальное изображение, а отрицательное значение h _i указывает на перевернутое изображение.

Вот шаги, которые необходимо выполнить при решении проблемы с объективом:

• Шаг 1. Изучите ситуацию, чтобы определить, участвует ли в этом процесс формирования изображения линзой.
• Шаг 2. Определите, следует ли использовать трассировку лучей, уравнения тонкой линзы или и то, и другое. Эскиз очень полезен, даже если трассировка лучей специально не требуется для решения задачи. Напишите на эскизе полезные символы и значения.
• Шаг 3. Определите, что именно нужно определить в задаче (выявите неизвестные).
• Шаг 4. Составьте список того, что дано или может быть выведено из сформулированной проблемы (укажите известное). Полезно определить, относится ли ситуация к изображению случая 1, 2 или 3. Хотя это всего лишь названия типов изображений, они обладают определенными характеристиками (приведенными в табл. 16.3), которые могут оказаться очень полезными при решении задач.
• Шаг 5. Если требуется трассировка лучей, используйте правила трассировки лучей, перечисленные ранее в этом разделе.
• Шаг 6. Большинство количественных задач требуют использования уравнений тонкой линзы. Эти уравнения решаются обычным образом путем замены известных и решения неизвестных. Несколько проработанных примеров были включены ранее и могут служить руководством.
• Шаг 7. Проверьте правильность ответа. Имеет ли смысл ? Если вы правильно определили тип изображения (случай 1, 2 или 3), вам следует оценить, соответствует ли ваш ответ типу изображения, увеличению и т. д.

Все задачи будут решаться с помощью одного или нескольких только что представленных уравнений, а трассировка лучей используется только для общего анализа задачи. Затем шаги упрощаются до следующего:

1. Определите неизвестное.
2. Определить известные.
3. Выберите уравнение, подставьте известные и решите неизвестное.

Вот несколько примеров работы:

Рабочий пример

Сила увеличительного стекла

Стратегия

Солнце так далеко, что его лучи почти параллельны, когда достигают Земли. Лупа представляет собой выпуклую (или собирающую) линзу, фокусирующую почти параллельные лучи солнечного света. Таким образом, фокусное расстояние линзы — это расстояние от линзы до пятна, а ее сила в диоптриях (D) — величина, обратная этому расстоянию (в обратных метрах).

Решение

Фокусное расстояние линзы — это расстояние от центра линзы до пятна, которое, как мы знаем, равно 8,00 см. Таким образом,

f=8,00см.f=8,00см.

16,16

Чтобы найти силу линзы, мы должны сначала перевести фокусное расстояние в метры; затем подставляем это значение в уравнение для мощности.

P=1f=10,0800 m=12,5 DP=1f=10,0800 m=12,5 D

16,17

Обсуждение

Этот результат демонстрирует относительно мощный объектив. Помните, что силу линзы в диоптриях не следует путать с привычным понятием мощности в ваттах.

Рабочий пример

Формирование изображения выпуклой линзой.

Лампа из прозрачного стекла расположена на расстоянии 0,75 м от выпуклой линзы с фокусным расстоянием 0,50 м, как показано на рис. 16.36. Используйте трассировку лучей, чтобы получить приблизительное местоположение изображения. Затем используйте уравнения зеркала/линзы, чтобы вычислить (а) положение изображения и (б) его увеличение. Убедитесь, что трассировка лучей и уравнения тонкой линзы и увеличения дают согласованные результаты.

Рисунок 16.36 Лампочка, помещенная на расстоянии 0,75 м от линзы с фокусным расстоянием 0,50 м, дает реальное изображение на доске для плакатов, как обсуждалось в предыдущем примере. Трассировка лучей предсказывает расположение и размер изображения.

Стратегия

Поскольку объект расположен дальше от собирающей линзы, чем фокусное расстояние линзы, эта ситуация аналогична ситуации, показанной на предыдущем рисунке серии рисунков, изображающих женщину, стоящую слева от линзы. Трассировка лучей в масштабе должна дать аналогичные результаты для d _i . Численные решения для d _i и m могут быть получены с использованием уравнений тонкой линзы и увеличения, учитывая, что d _o = 0,75 м и f = 0,50 м.

Решение

Трассировка лучей в масштабе на рис. 16.36 показывает два луча из точки на нити накаливания лампы, пересекающие примерно 1,50 м на дальней стороне линзы. Таким образом, расстояние изображения d _i составляет около 1,50 м. Точно так же высота изображения на основе трассировки лучей больше высоты объекта примерно в два раза, и изображение инвертируется. Таким образом, м составляет около –2. Знак минус указывает, что изображение перевернуто. Уравнение линзы можно изменить, чтобы решить для d _i из предоставленной информации.

di=fdodo-f=(0,50)(0,75)0,75–0,50=1,5 mdi=fdodo-f=(0,50)(0,75)0,75–0,50=1,5 м м . Обсуждение . Трассировка лучей и использование уравнения линзы дают согласованные результаты. Уравнение тонкой линзы дает наиболее точные результаты и ограничивается только точностью данной информации. Трассировка лучей ограничена точностью, с которой вы рисуете, но она очень полезна как концептуально, так и визуально.

Рабочий пример

Формирование изображения вогнутой линзой

Предположим, что объект, например страница книги, находится на расстоянии 6,50 см от вогнутой линзы с фокусным расстоянием –10,0 см. Такая линза может быть использована в очках для коррекции ярко выраженной близорукости. Какое увеличение получается?

Стратегия

Этот пример идентичен предыдущему, за исключением того, что фокусное расстояние отрицательно для вогнутой или рассеивающей линзы. Таким образом, метод решения один и тот же, но результаты существенно различаются.

Раствор

di=fdodo-f=(-10,0)(6,50)6,50-(-10,0)=-3,94 cmdi=fdodo-f=(-10,0)(6,50)6,50-(-10,0)=-3,94 см

16,20

Теперь можно использовать уравнение увеличения, чтобы найти увеличение, m , потому что оба d _i и d _o известны. Ввод их значений дает

м=-дидо=—3,946,50=0,606.м=-дидо=—3,946,50=0,606.

16.21

Обсуждение

Ряд результатов в этом примере верен для всех изображений случая 3. Увеличение положительное (рассчитанное), то есть изображение прямое. Увеличение также меньше единицы, что означает, что изображение меньше объекта — в данном случае чуть больше половины его размера. Расстояние до изображения отрицательное, то есть изображение находится на той же стороне линзы, что и объект. Образ виртуальный. Изображение ближе к линзе, чем объект, потому что расстояние до изображения меньше по величине, чем расстояние до объекта. Расположение изображения неочевидно, если смотреть через вогнутую линзу. На самом деле, поскольку изображение меньше объекта, вы можете подумать, что он находится дальше; однако изображение находится ближе, чем объект — факт, который полезен при коррекции близорукости.

Смотреть физику

Уравнение линзы и решение задач

На видео показаны расчеты как для вогнутых, так и для выпуклых линз. Он также объясняет реальные и виртуальные изображения, прямые и перевернутые изображения, а также значение отрицательных и положительных знаков для задействованных переменных.

Физика часов: уравнение тонкой линзы и решение задач В этом видео приведены примеры использования уравнения тонкой линзы.

Нажмите, чтобы просмотреть содержимое

Если линза имеет увеличение –\frac{1}{2}, как изображение соотносится с объектом по высоте и ориентации?

1. Изображение прямое и вдвое меньше объекта.

2. Изображение вертикальное и вдвое выше объекта.

3. Изображение инвертировано и вдвое меньше объекта.

4. Изображение перевернуто и в два раза выше объекта.

Практические задачи

11.

Линза имеет фокусное расстояние 12,5\,\text{см}. Какова мощность линзы?

1. Оптическая сила линзы 0,0400\,\text{D}.

2. Оптическая сила линзы 0,0800\,\text{D}.

3. Оптическая сила линзы 4.00\,\text{D}.

4. Оптическая сила линзы 8. 00\,\text{D}.

12.

Если линза дает изображение высотой 5,00 см объекта высотой 8,00 см, когда она находится на расстоянии 10,0 см от линзы, каково видимое расстояние до изображения? Постройте лучевую диаграмму, используя бумагу, карандаш и линейку, чтобы подтвердить свои расчеты.

1. −3,12 см
2. −6,25 см
3. 3,12 см
4. 6,25 см

Проверьте свое понимание

Поддержка учителей

Поддержка учителей

Используйте эти вопросы, чтобы оценить достижение учащимися учебных целей раздела. Если учащимся не удается выполнить конкретную задачу, эти вопросы помогут определить, какая именно, а затем вы сможете направить учащихся к соответствующему содержанию.

13.

Линза имеет отрицательное увеличение. Какова ориентация изображения?

1. Отрицательное увеличение означает, что изображение прямое и настоящее.

2. Отрицательное увеличение означает, что изображение прямое и мнимое.

3. Отрицательное увеличение означает, что изображение инвертировано и виртуально.

4. Отрицательное увеличение означает, что изображение инвертировано и является реальным.

14.

Какая часть глаза контролирует количество попадающего света?

1. ученик
2. ирис
3. роговица
4. сетчатка

15.

Объект помещается между фокальной точкой и выпуклой линзой. Опишите образующееся изображение с точки зрения его ориентации и того, является ли изображение реальным или виртуальным.

1. Изображение настоящее и вертикальное.

2. Изображение реальное и перевернутое.

3. Изображение виртуальное и вертикальное.

4. Изображение виртуальное и перевернутое.

16.

Дальнозоркий человек покупает очки, чтобы скорректировать свою дальнозоркость. Опишите основной симптом дальнозоркости и тип линзы, которая его корректирует.

1. Люди с дальнозоркостью не могут сфокусироваться на предметах, которые находятся далеко, но они могут легко видеть близлежащие предметы. Для исправления этого используется выпуклая линза.

2. Люди с дальнозоркостью не могут сфокусироваться на предметах, находящихся близко, но они могут легко видеть предметы вдали. Для исправления этого используется вогнутая линза.

3. Люди с дальнозоркостью не могут сфокусироваться на близко расположенных объектах, но они легко видят удаленные объекты. Для исправления этого используется выпуклая линза.

4. Люди с дальнозоркостью не могут сфокусировать взгляд на предметах, находящихся либо близко, либо далеко. Для исправления этого используется вогнутая линза.

Поддержка учителей

Поддержка учителей

Эта задача производительности поддерживает следующее:

NGSS HS-PS4-1: использование математических представлений для обоснования утверждений о соотношениях между частотой, длиной волны и скоростью волн, распространяющихся в различных средах; и

NGSS HS-PS4-5: передача технической информации о том, как некоторые технологические устройства используют принципы поведения волн и взаимодействия волн с материей для передачи и захвата информации и энергии.

• Пустая бутылка искажает зрение, но не имеет эффекта линзы.
  Зависимость фокусного расстояния от расстояния до объекта: Зависимость угла обзора от фокусного расстояния