Главная — Фотошкола ЮУрГУ

Золотая спираль фибоначчи: взаимосвязь. Семя внутри семени» сферы

Содержание

«Золотая спираль»

«Тот, кто придерживается золотой середины, избежит и нищеты лачуг, и зависти дворцов»

(Цитата древнеримского поэта)

Форма «Золотой спирали»

Структура «Золотой спирали» символизирует две хорошо известные в сакральной геометрии фигуры: спираль Золотого сечения (фи) и спираль Фибоначчи. Она основана на форме круга на поле, известного как “Hackpen Hill Formation” («Образование у Хэкпен-Хилл»), который появился на пшеничном поле в Англии в 1999 году.

Фи (золотое сечение) – «ключ к физике космоса» (Платон)

Фи – это постоянная, влияние которой даже более глубоко и загадочно, чем пи. Как и число пи, фи – это число, не имеющее математического решения. Знаки после запятой просто продолжаются до бесконечности, не повторяясь. Особенность этого числа в том, что его можно найти во всех известных органических структурах.

Пропорция фи есть везде, от строения костей человека до спирального расположения семян подсолнуха и завитков раковин моллюсков, она лежит в основе всех биологических структур и кажется геометрической схемой самой жизни.

Платон называл пропорцию фи «ключом к физике космоса». Число фи – 1,6180339+, и, хотя у него нет арифметического решения, его можно легко получить при помощи циркуля и угольника.



Как найти золотое сечение

Вот два простых метода вычисления золотого сечения.
Первый метод
Если взять два одинаковых квадрата и поставить сторона к стороне, получится прямоугольник 1х2. Разделите один из квадратов пополам и проведите диагональ в полученном прямоугольнике (с соотношением сторон 1х0.5). Сумма длины этой диагонали и короткой стороны малого прямоугольника будет равна фи, 1,6180339+, если принять сторону квадрата за 1. (Эта формула точно описывает пол Камеры Царя в Великой пирамиде).


Второй метод
Второй метод нахождения золотого сечения – разделение отрезка АВ в точке С так, чтобы весь отрезок целиком был длиннее его первой части в той же пропорции, в какой первая часть длиннее остатка. АВ/АС=АС/СВ=1,6180339+ (обратите внимание на фрактальную и голографическую природу этого соотношения…)

Золотое сечение в архитектуре

Пропорция фи присутствует в архитектуре Великой пирамиды, в треугольнике, возникающем из высоты, половины основания и апофемы, то есть диагонали. Другими словами, основное сечение пирамиды дает нам золотое сечение. Если принять длину половины основания за 1, длина апофемы даст нам фи, а высота – квадратный корень из фи. Золотое сечение снова и снова встречается в Гизе и часто оказывается сложным и сбивающим с толку (о геометрии постройки Великой пирамиды написаны целые тома).

Ряд Фибоначчи и золотое сечение

Существует математическая прогрессия, известная как ряд Фибоначчи, и она имеет особое отношение к числу фи и пирамидам в Гизе. Принципы этого ряда впервые изложил средневековый математик Леонардо Фибоначчи. Этот ряд использовали для описания роста растений. Вот эта последовательность: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и так далее. Для того, чтобы получить каждое следующее число в этом ряду, надо сложить два предыдущих: 1+1=2, 1+2=3, 2+3=5, 3+5=8, 5+8=13 и так далее. 

У этой последовательности очень интересное соотношение с числом фи: если разделить каждый член этого ряда на предыдущий, полученные результаты будут стремиться к трансцендентному числу 1,6180339+. (Я не заставлю вас проводить эти расчеты. Просто смотрите…)

1/1=1 2/1=2 3/2=1.5 5/3=1.66 13/8=1.625 21/13=1.615 34/21=1.619 55/34=1.617 89/55=1.6181
Чем дальше вы будете продолжать считать, тем ближе будете подходить к числу фи. Конечно, вы никогда не дойдете до него, потому что у него нет арифметического решения, но вы будете бесконечно приближаться к нему.
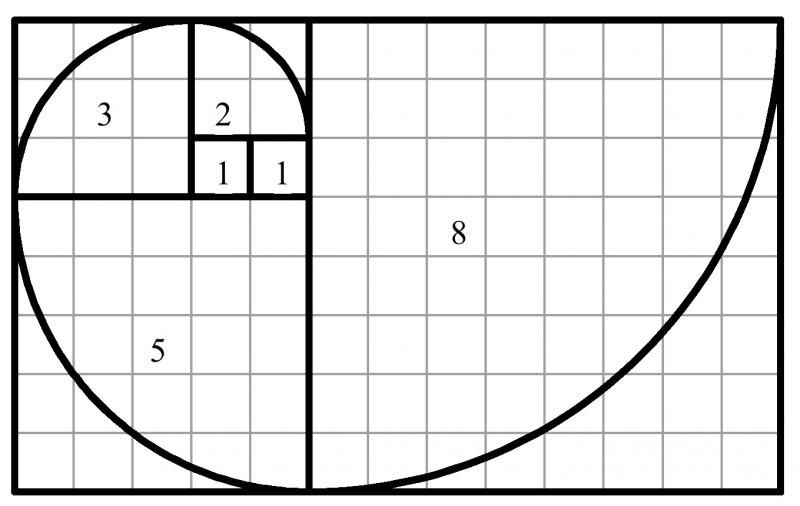
Эту последовательность можно изобразить графически, в виде так называемой спирали Фибоначчи. Эта спираль почти идентична логарифмической спирали фи, известной как спираль золотого сечения. Разница заключается в том, что спираль Фибоначчи – это интерпретация (при помощи целых чисел) арифметически невозможной спирали золотого сечения, у которой нет ни конца, ни начала. У спирали Фибоначчи есть определенное начало.

Спираль Фибоначчи и пирамиды в Гизе

Фотосъемка с воздуха показывает, что пирамиды в Гизе расположены на линии, четко соответствующей спирали Фибоначчи. Эта спираль проходит прямо через середину каждой из пирамид.


Ювелир – Давид Вейцман

David Weitzman is the force behind Ka Gold Jewelry. David has a vast knowledge in the fields of Kabbalah, Sacred Geometry, Ancient Egyptian wisdom, Jewish tradition, Tibetan Buddhism and other sacred concepts. David’s work harnesses the power of spiritual symbols to bring those wearing them happiness, vitality, excitement, success, and love.

Золотая спираль

Золотые спирали самоподобный. Форма бесконечно повторяется при увеличении.

В геометрия, а золотая спираль это логарифмическая спираль чей фактор роста φ, то Золотое сечение.[1] То есть золотая спираль становится шире (или удаляется от своего начала) в раз. φ за каждую четверть оборота.

Содержание

  • 1 Приближения золотой спирали
  • 2 Спирали в природе
  • 3 Математика
    • 3.1 Полярный склон
  • 4 Смотрите также
  • 5 Рекомендации

Приближения золотой спирали

Примерные и настоящие золотые спирали: зеленый спираль состоит из четверти окружностей, касающихся внутренней части каждого квадрата, а красный спираль — это золотая спираль, особый вид логарифмическая спираль. Появляются перекрывающиеся части желтый. Длина стороны большего квадрата до следующего меньшего квадрата находится в Золотое сечение.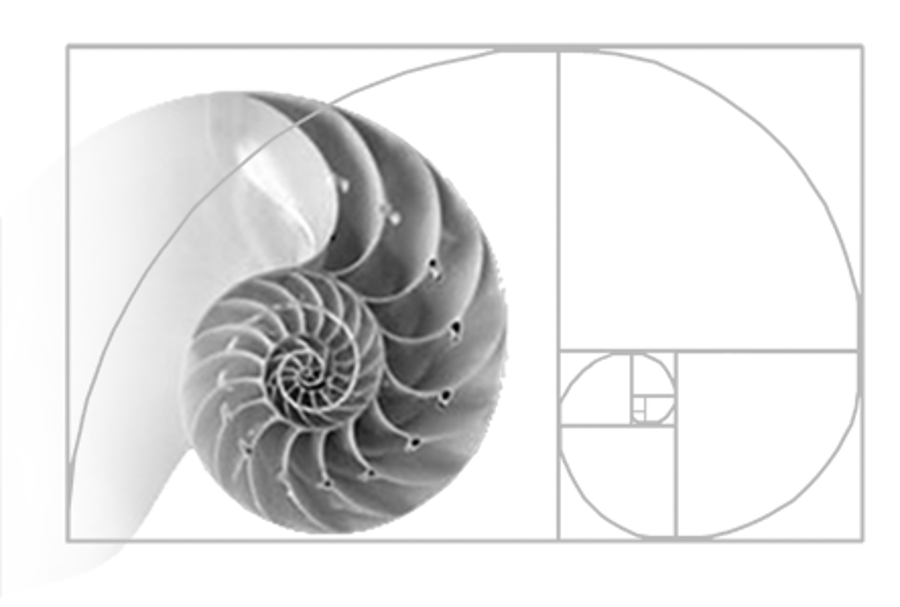 Для квадрата с длиной стороны 1, следующий меньший квадрат 1 / φ широкий. Следующая ширина 1 / φ², тогда 1 / φ³, и так далее.

Есть несколько сопоставимых спиралей, которые приблизительно равны золотой спирали, но не равны ей.[2]

Например, золотую спираль можно аппроксимировать, начав с прямоугольника, для которого соотношение между его длиной и шириной является золотым сечением. Затем этот прямоугольник можно разделить на квадрат и аналогичный прямоугольник, а затем таким же образом можно разделить этот новейший прямоугольник. После продолжения этого процесса для произвольного количества шагов результатом будет почти полное разбиение прямоугольника на квадраты. Углы этих квадратов можно соединить четвертью окружностей. Результат, хотя и не является истинной логарифмической спиралью, очень похож на золотую спираль.[2]

Другое приближение — это Спираль Фибоначчи, который построен несколько иначе. Спираль Фибоначчи начинается с прямоугольника, разделенного на 2 квадрата. На каждом шаге к прямоугольнику добавляется квадрат, равный длине самой длинной стороны прямоугольника. Поскольку соотношение между последовательными числами Фибоначчи приближается к Золотое сечение поскольку числа Фибоначчи приближаются к бесконечности, эта спираль становится все более похожей на предыдущее приближение, чем больше добавляется квадратов, как показано на рисунке.

Спирали в природе

Приблизительно логарифмические спирали может встречаться в природе, например, руки спиральные галактики[3] — золотые спирали являются частным случаем этих логарифмических спиралей, хотя нет никаких свидетельств того, что существует какая-либо общая тенденция к появлению этого случая. Филлотаксис связано с золотым сечением, потому что оно включает в себя следующие друг за другом листья или лепестки, разделенные золотой угол; это также приводит к появлению спиралей, хотя опять же ни одна из них (обязательно) не является золотой спиралью. Иногда говорят, что спиральные галактики и наутилус ракушки становятся шире в форме золотой спирали и, следовательно, связаны с обоими φ и ряд Фибоначчи. {б тета _ { mathrm {right}}} , = varphi}

Следовательно, б дан кем-то

б=пер⁡φθряграммчаст.{ displaystyle b = { ln { varphi} over theta _ { mathrm {right}}}.}

В Лукас спираль приближается к золотой спирали, когда ее члены большие, но не когда они маленькие. Включены 10 терминов, от 2 до 76.

Числовое значение б зависит от того, измеряется ли прямой угол как 90 градусов или как π2{ displaystyle textstyle { frac { pi} {2}}} радианы; и поскольку угол может быть в любом направлении, проще всего написать формулу для абсолютного значения б{ displaystyle b} (то есть, б также может быть отрицательным значением этого значения):

|б|=пер⁡φ90≐0.0053468{ displaystyle | b | = { ln { varphi} более 90} doteq 0,0053468 ,} за θ в градусах;
|б|=пер⁡φπ/2≐0.3063489{ displaystyle | b | = { ln { varphi} over pi / 2} doteq 0.3063489 ,} за θ в радианах. OEIS: A212225

Альтернативная формула для логарифмической и золотой спирали:[9]

р=аcθ{ Displaystyle г = ак ^ { тета} ,}

где постоянная c дан кем-то:

c=еб{ Displaystyle с = е ^ {Ь} ,}

что для золотой спирали дает c значения:

c=φ190≐1. {b theta} ,}

параметр б связано с полярным углом наклона α{ displaystyle alpha} :

загар⁡α=б{ Displaystyle загар альфа = Ь}.

В золотой спирали, будучи б{ displaystyle b} постоянный и равный |б|=пер⁡φπ/2{ displaystyle | b | = { ln { varphi} over pi / 2}} (за θ в радианах, как определено выше), угол наклона α{ displaystyle alpha} является:

α=арктан⁡(|б|)=арктан⁡(пер⁡φπ/2){ Displaystyle альфа = arctan (| b |) = arctan left ({ ln { varphi} over pi / 2} right)}, следовательно:
α≐17.03239113{ displaystyle alpha doteq 17.03239113} если измеряется в градусах, или
α≐0.2972713047{ displaystyle alpha doteq 0.2972713047} если измерять в радианах. OEIS: A335605

Его дополнительный угол

β=π/2−α≐1.273525022{ Displaystyle бета = пи / 2- альфа doteq 1.273525022} (в радианах) или
β=90−α≐73{ Displaystyle бета = 90- альфа doteq 73} (в градусах)

— угол между золотыми спиральными рукавами и линией из центра спирали. Клаус Майнцер (1996). Симметрии природы: Справочник по философии природы и науки. Вальтер де Грюйтер. С. 45, 199–200. ISBN  3-11-012990-6.

Спираль Фибоначчи: фото, построение спирали Фибоначчи

Природа всегда решает задачи самым простым и элегантным путем, какой только можно придумать. Золотое сечение, или, по-другому, спираль Фибоначчи, является наглядным отражением гениальности этих решений.

Следы этой пропорции обнаруживают в древних строениях и великих картинах, человеческом теле и небесных объектах. Вот уже несколько веков Золотое сечение и коэффициент Фи находятся под пристальным вниманием ученых различных областей.

«Сын счастливчика»

Именно так, по мнению ученых, можно назвать Леонардо Пизанского по прозвищу Фибоначчи. Это прозвище означает, что он — сын Боначчи («Боначчи» переводится как «счастливчик»). Весьма забавный факт, учитывая, скольких людей он сделал счастливыми косвенно, способствуя развитию математики, экономики и других областей знаний, в которых сейчас широко используется его открытие.

Этот средневековый итальянец внес настолько большой вклад в развитие современной науки, что переоценить его очень сложно. Ежедневно все большее количество научных исследований только подтверждает принцип, который он наглядно показал всему миру в виде цифр.

Леонардо Пизанский знаменит тем, что представил свой последовательный ряд чисел, который постоянно стремится к золотому сечению.

Золотое сечение

Это пропорция, которую можно графически изобразить в качестве отрезка, разделенного точкой на две части. Самое главное правило деления: весь отрезок относится к его большей части так же, как большая часть относится к меньшей.

То есть точка разделит отрезок таким образом, что если разделить всю длину (сумму частей) на величину большей части, получим то же число, что и при делении большей части на меньшую.

В результате деления всегда получается один и тот же результат — 1,618. Он получил название коэффициента Фи.

Числа Фибоначчи

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 и далее — именно эти цифры играют огромную роль в науке вот уже несколько веков.

Их назвали «ряд Фибоначчи» или «числа Фибоначчи». Самым главным свойством последовательности является то, что каждое новое число равно сумме двух предыдущих. Отражением именно этой последовательности стала так называемая золотая спираль Фибоначчи. Это она принесла ему большую известность.

Но мало кто знает, что на одной лишь спирали Фибоначчи вклад ученого не завершился. Этот средневековый математик научил Европу использовать в математике арабские цифры, что значительно ускорило развитие науки. Удивительно, но до написания им трактата об арабских цифрах вся Европа пользовалась исключительно римской системой.

Кто знает, как развивалась бы наука, если бы не его светлый ум.

Коэффициент «Фи»

Самое главное число в золотом сечении — 1,618. Присутствует оно и в последовательности Фибоначчи. Именно к этому коэффициенту стремится отношение каждого следующего числа к предыдущему. Вот почему открытие ряда Фибоначчи так повлияло на все научное сообщество. С появлением математического точного выражения человечество получило способ применять один из самых важных законов окружающего мира в новых изобретениях и исследованиях.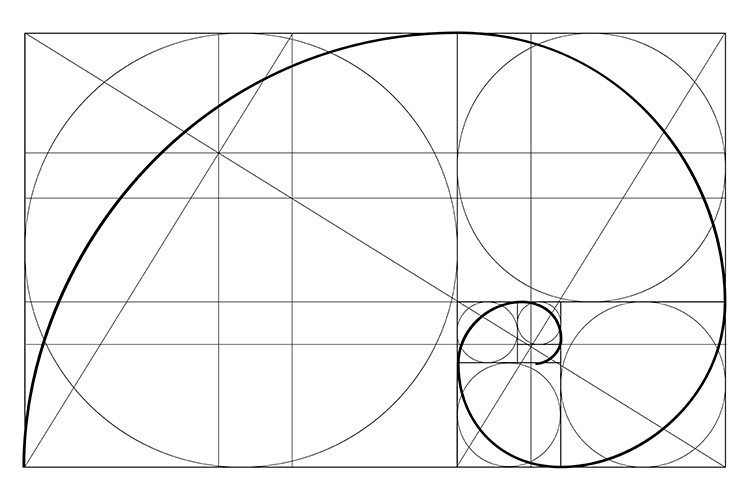

Это совершенное число, золотая середина и гениальное решение, которое повсеместно использует сама природа.

Популярность сквозь века

Первое упоминание принципа золотого сечения появилось еще во времена Пифагора. С тех пор ученые всегда наблюдали за этой пропорцией, изучали ее и строили разного рода догадки и предположения.

В современном мире это явление получило широкую огласку после выхода на экран фильма «Код да Винчи». В этой картине создатели фильма обратили внимание широкой аудитории на то, что золотое сечение используется и встречается повсюду. Там было упомянуто, что пропорция соблюдается везде, даже в человеческом теле. И естественно, множество людей тут же заинтересовалось этой темой. Интерес к золотому сечению, возникший благодаря этому фильму, не стихает до сих пор. Интернет заполнило огромное количество «живых» спиралей Фибоначчи на фото: волны, циклоны, растения, моллюски… Все эти снимки раз за разом показывают красоту одного из самых главных законов природы.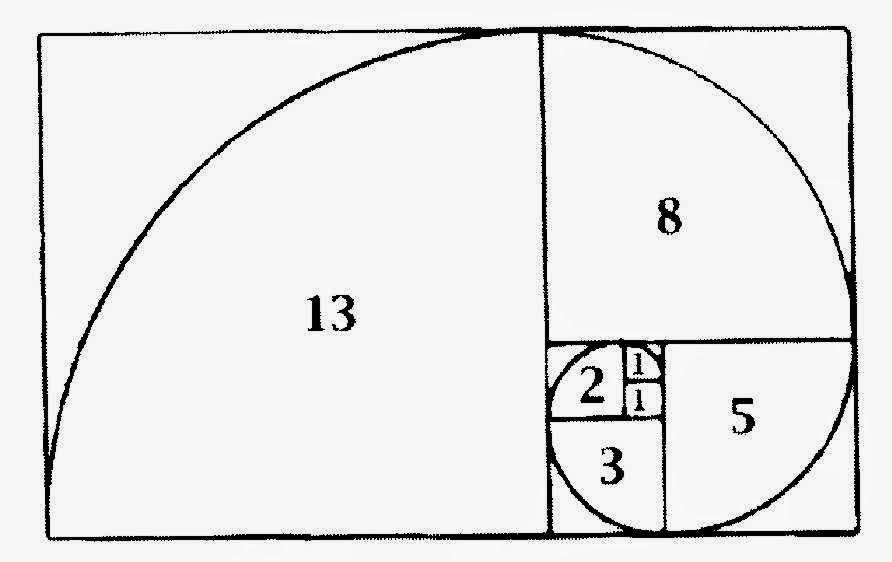

Как построить спираль Фибоначчи

Вполне логично, что узнав так много про этот замечательный «завиток», кому-то наверняка захочется собственноручно создать его аналог.

Сделать это достаточно просто. Достаточно иметь под рукой циркуль и тетрадь в клеточку или миллиметровую бумагу (либо линейку, которая поможет построить симметричные, аккуратные квадраты).

Начать построение спирали Фибоначчи нужно с изображения двух одинаковых квадратов с длиной стороны в одну единицу длины. Дуга, соединяющая два противоположных угла первого квадрата, и станет началом золотой спирали. По мере раскручивания последней к ней присоединяется все большее количество пропорциональных фигур, до тех пор, пока не будет достигнут нужный размер спирали. Самое важное – соблюдать правило, где длина стороны каждого следующего квадрата всегда равна сумме длин сторон двух предыдущих.

Золотой прямоугольник

Идеальный, с точки зрения спирали Фибоначчи, прямоугольник имеет стороны, длина которых пропорциональна друг к другу именно по коэффициенту фи. Иными словами, при делении одной стороны на другую обязательно должно получиться 1,618 либо 0,618 (число, обратное коэффициенту фи).

Такие прямоугольники довольно распространены в архитектуре и композиции. Интересно также то,что именно их большинство людей считают «идеальными» или «правильными» с визуальной точки зрения. Иными словами, человек интуитивно воспринимает эти пропорции более красивыми и естественными, приятным глазу. Даже если дело касается геометрических фигур.

В искусстве

Если отметить точками или линиями основные элементы в картинах и поделить полотно на множество мелких прямоугольников Фибоначчи, то можно заметить интересный факт. На огромном количестве произведений искусства фигуры размещены таким образом, что явные контрасты и важные элементы непременно будут находиться на гранях прямоугольников или располагаться непосредственно на самой спирали Фибоначчи.

Более того, уважающие себя современные архитекторы и дизайнеры тоже верны этому принципу.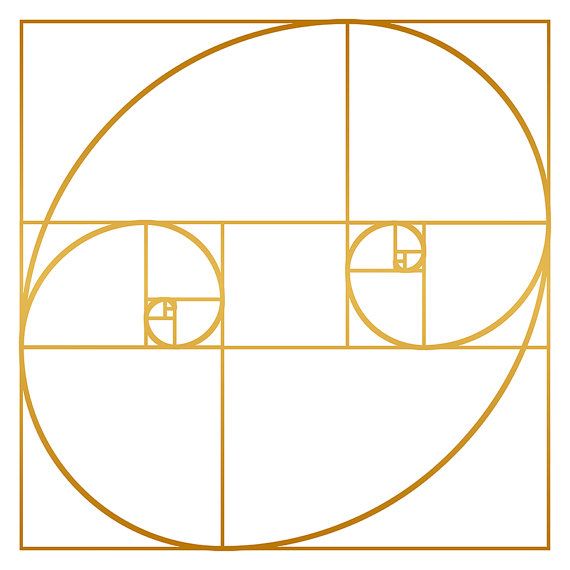 И в этом нет ничего удивительного. Спираль отражает закон самой природы, а она – гениальный творец.

Несколько поразительных и интересных фактов

  • Совсем недавно в социальных сетях даже была определенного рода мода на снимки девушек, которые откидывают волосы в воде, получая множество красивых брызг в форме спирали Фибоначчи.
  • Многие трейдеры считают принцип очень значимым, основывая на числах ряда Фибоначчи стратегии по продаже и покупке валюты.
  • Соотношение пиков кардиограммы также попадает под действие золотого сечения.
  • В металлургии давно известен факт, что сплавы различных металлов обладают лучшими свойствами стойкости, если удельный вес элементов относится друг к другу согласно коэффициенту Фи.
  • Пропорции различных веществ в гемоглобине подчинены этому закону.
  • Существует даже официально зарегистрированный Институт золотого сечения.
  • Помимо прямого коэффициента фи, существует еще обратно пропорциональное ему число 0,618, которое тоже часто используется в различных расчетах.

Все основополагающие знания человечество получило, наблюдая за миром вокруг. Раз за разом люди отмечали закономерности в смене сезонов, находили взаимосвязь между громом и молнией, изучали звезды и создавали календари.

Закон золотого сечения находится совсем на поверхности. И спирали Фибоначчи в природе, как отражение принципа, которому соответствует все живое, встречаются в огромном количестве явлений, в растительном и животном мирах.

Именно так, по принципу золотого сечения, наиболее гармонично развиваются живые организмы. Каждый следующий шаг — лишь сумма двух предыдущих. Каждый следующий виток спирали нарастает постепенно, раскрываясь все больше, но повторяя общее направление.

Это один из самых великих законов мироздания.

золотая спираль свободный вектор | Загрузите это сейчас!

Этот сайт использует куки. Продолжая просматривать, вы соглашаетесь на использование нами файлов cookie и других технологий отслеживания. Узнайте больше здесь.

    org/BreadcrumbList»>
  • Главная
  • Вектор

Пожаловаться

Скачать (1,6 КБ)

  • Рамка Золотая спираль

  • спираль фибоначчи

  • фибоначчи прямоугольник

  • спираль

  • спираль

  • Шаблоны векторных 62

  • Векторная модель 57

  • Золотая бабочка узор вектор материала

  • Золотой меч картинки

Золотая спираль — Вики

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 4 апреля 2022 года; проверки требует 1 правка.

Перейти к навигацииПерейти к поиску

Спираль Дюрера и золотая спираль, вписанные в последовательность вложенных друг в друга золотых прямоугольников: зелёная спираль — спираль Дюрера — составлена из четвертинок окружностей внутри квадратов, в то время как красная спираль является золотой спиралью, особым видом логарифмической спирали. Перекрывающиеся секции показаны жёлтым цветом. Длина части спирали внутри большего квадрата находится к длине спирали внутри следующего квадрата в золотой пропорции

Золотая спираль или спираль Фибоначчи — логарифмическая спираль, коэффициент роста которой равен φ4, где φ — золотое сечение. Коэффициент роста логарифмической спирали показывает, во сколько раз изменился полярный радиус спирали при повороте на угол 360°[1]. Своё название эта спираль получила из-за связи с последовательностью вложенных друг в друга прямоугольников с отношением сторон, равным φ, которые принято называть золотыми.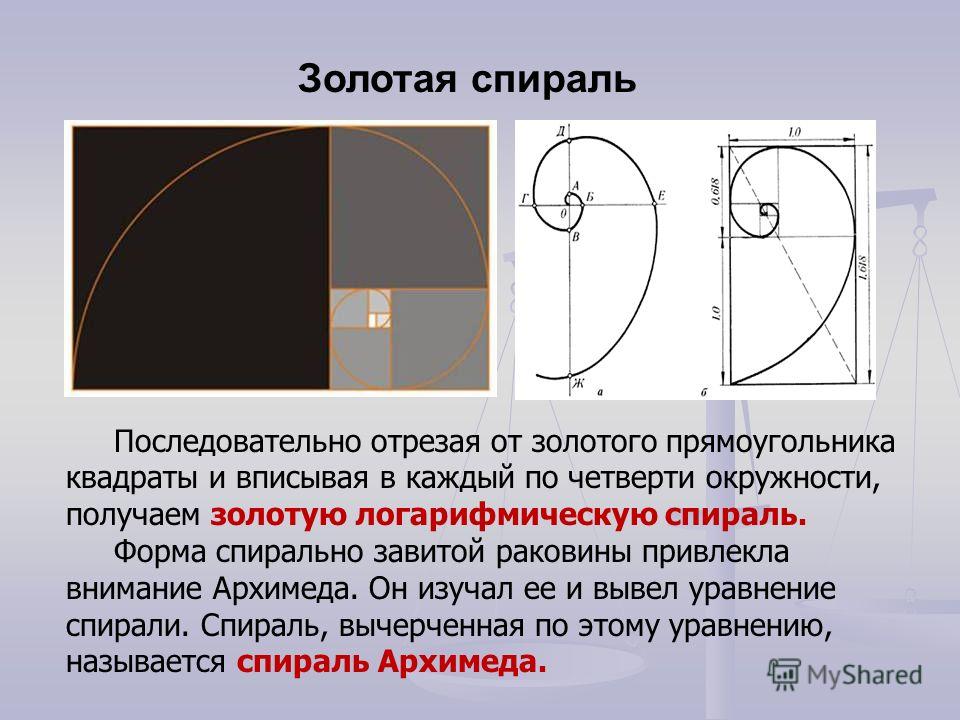 Золотую спираль можно как вписать в систему таких прямоугольников, так и описать вокруг неё. Популярность золотая спираль приобрела из-за того, что известная с начала XVI века и применяющаяся в искусстве[2] спираль, построенная по методу Дюрера[3][4], оказалась хорошей аппроксимацией для золотой спирали (см. рисунок).

Содержание

  • 1 Формула
  • 2 Приближения золотой спирали
  • 3 Спирали в природе
  • 4 См. также
  • 5 Примечания
  • 6 Литература

Формула

Спираль Фибоначчи аппроксимирует золотую спираль с использованием четвертинок окружности в квадратах с размерами квадратов, равных числам Фибоначчи. На рисунке показаны квадраты с размерами 1, 1, 2, 3, 5, 8, 13, 21.

Уравнение для золотой спирали в полярной системе координат то же самое, что и для других логарифмических спиралей, но со специальным значением коэффициента роста — φ4:

r=aφ±2θπ{\displaystyle r=a\varphi ^{\pm {\frac {2\theta }{\pi }}}},

где a — произвольная положительная вещественная константа, а φ=5+12{\displaystyle \varphi ={\frac {{\sqrt {5}}+1}{2}}} — золотое сечение. {\circ }}.



Приближения золотой спирали

Литовская монета

Существует несколько похожих спиралей, которые близки, но не совпадают в точности с золотой спиралью[5], с которой их часто путают.

Как уже было написано выше, при вписывании золотой спирали в последовательность вложенных друг в друга золотых прямоугольников, она аппроксимируется спиралью, построенной по методу Дюрера. Золотой прямоугольник можно разделить на квадрат и подобный ему прямоугольник, его, в свою очередь, разделить тем же образом, и продолжать этот процесс произвольное число раз. Если в эти квадраты вписать соединённые между собой четвертинки окружностей, то получается спираль, изображенная на первом рисунке.

Ещё одной аппроксимацией является спираль Фибоначчи, которая строится подобно вышеописанной спирали, за исключением того, что начинают с прямоугольника из двух квадратов и добавляют потом к большей стороне прямоугольника квадрат такой же длины.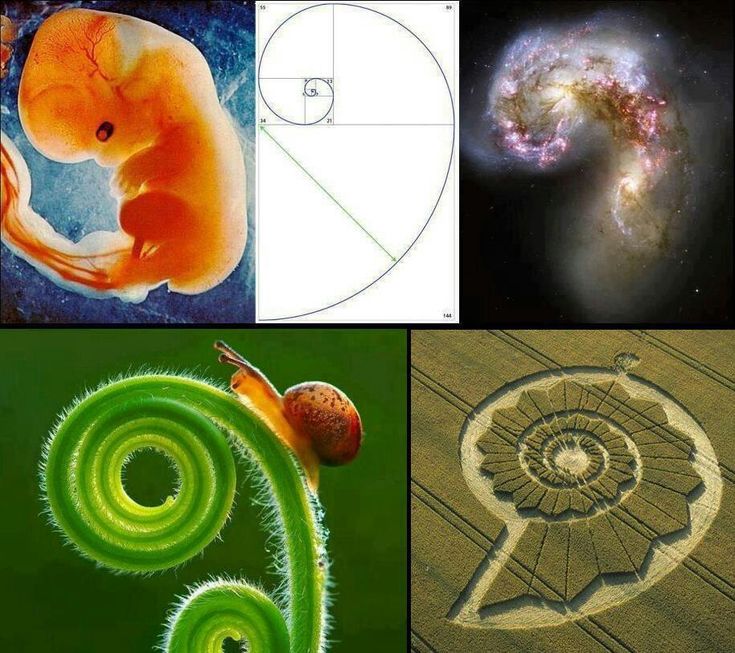 Поскольку отношение между соседними числами Фибоначчи стремится к золотой пропорции, спираль всё больше приближается к золотой спирали по мере добавления квадратов (см. второй рисунок).



Спирали в природе

В природе встречаются приближения к логарифмическим спиралям с коэффициентом роста равным φk. Так раковины моллюсков Nautilus pompilius и окаменелых аммонитов хорошо описываются при k = 2, а раковины некоторых улиток при k = 1.[6] Отношение длин трёх витков спирали уха у человека равно φ[7], что соответствует спирали с k = 1. Рукава спиральных галактик, несмотря на существующие утверждения[8], если и описываются логарифмической, то не золотой спиралью. В данном случае, описание ею является проявлением случайной близости. Недавний анализ спиралей, встречающихся в роговичном эпителии мышей, показал, что там встречаются как золотая, так и другие логарифмические спирали.[9]

См. также

  • Геликоид
  • Золотой угол
  • Золотой прямоугольник
  • Синусоидальная спираль
  • Спираль

Примечания

  1. ↑ Выгодский М. Я. Справочник по высшей математике. М.: Наука, 1977, с. 884.
  2. ↑ Прохоров А. Золотая спираль, Квант, 1984, №9.
  3. ↑ Аракелян. Г. Математика и история золотого сечения, М.: Логос, 2014, с. 50.
  4. ↑ Albrecht Durer (1525): Unterweysung der Messung mit dem Zirkel und Richtscheyt, in Linien Ebnen und gantzen Corporen. Verlag Dr. Alfons Uhl (Reprint 2000), Nordlingen, ISBN 3 921503 65 5 (Engl. Transl.: The Painter’s Manual, Abaris Books, New York 1977).
  5. ↑ Madden, 1999, с. 14–16.
  6. ↑ А.Н. Ковалев, Еще раз о золотых спиралях // Академия Тринитаризма, М., Эл № 77-6567, публ.23545, 13.07.2017 http://www.trinitas.ru/rus/doc/0016/001f/3352-kv.pdf Архивная копия от 13 октября 2017 на Wayback Machine
  7. ↑ Петухов С. В. Матричная генетика, алгебры генетического кода, помехоустойчивость. — Москва: Регулярная и хаотическая динамика, 2008. — С. 107.
  8. ↑ Gazale, 1999, с. 3.
  9. ↑ Rhee, 2015, с. 22–38.

Литература

  • David Darling. The Universal Book of Mathematics: From Abracadabra to Zeno’s Paradoxes. — John Wiley & Sons, 2004. — ISBN 9780471270478.
  • Ivars Peterson. Sea Shell Spirals. — Society for Science & the Public, 2005-04-01.
  • Keith Devlin. The myth that will not go away. — May 2007.
  • Jerry Rhee, Talisa Mohammad Nejad , Olivier Comets, Sean Flannery, Eine Begum Gulsoy, Philip Iannaccone , Craig Foster. Promoting convergence: The Phi spiral in abduction of mouse corneal behaviors // Complexity. — 2015. — Т. 20, вып. 3. — С. 22–38. — doi:10.1002/cplx.21562.
  • Midhat Gazale. Gnomon: From Pharaohs to Fractals. — Princeton University Press, 1999. — ISBN 9780691005140.
  • Charles B. Madden. Fractals in Music: introductory mathematics for musical analysis. — High Art Press, 1999. — ISBN 0-9671727-6-4.
  • Klaus Mainzer. Symmetries of Nature: A Handbook for Philosophy of Nature and Science. — Walter de Gruyter, 1996. — ISBN 3-11-012990-6.
  • Priya Hemenway. Divine Proportion: Φ Phi in Art, Nature, and Science. — Sterling Publishing Co, 2005. — ISBN 1-4027-3522-7.

Свойства принципа самонормирования и закон золотого сечения в спортивных уроках Текст научной статьи по специальности «Науки о Земле и смежные экологические науки»

УДК 796. 422. 091: 796. 015

СВОЙСТВА ПРИНЦИПА САМОНОРМИРОВАНИЯ И ЗАКОН ЗОЛОТОГО

СЕЧЕНИЯ В СПОРТИВНЫХ УРОКАХ

Головко Н.Г., кандидат педагогических наук, доцент Белгородский государственный аграрный университет

им. В.Я. Горина, Белгород, Россия Крамской С.И., кандидат социологических наук, профессор Белгородский государственный технологический университет

им. В. Г. Шухова, Белгород, Россия

PROPERTIES OF THE PRINCIPLE OF CONTROLLING ITSELF AND THE LAW OF THE GOLDEN SECTION IN SPORTS LESSONS

Golovko N. G., сandidate of Pedagogy science, associate professor Belgorod State Agrariаn University V. Y. Gorin, Belgorod, Russia Kramskoi S. I., сandidate of Sociological science, professor Belgorod State Technological University V. G. Shukhov, Belgorod, Russia

Аннотация. Закон золотого сечения (ЗЗС) обладает удивительным свойством принципа самонормирования (ПСН). Золотая спираль (ЗСп) ЗЗС идеальна. Она соответствует первоисточнику гармонии и не имеет ни начала, ни конца — бесконечна. Спираль Фибоначчи имеет начало, от которого она начинает свою ««раскрутку», что позволяет Природе после очередного замкнутого цикла осуществлять строительство и повторение новой спирали с «<нуля», где каждый последующий член этого ряда равен сумме двух предыдущих членов.

Summary. The law of the golden section (LGS) has the principle of the controlling itself (PCI), which is the remarkable property of this law. The golden spiral (GS) of the LGS is ideal. The golden spiral corresponds to the primary source of harmony and has no beginning and no end, it is infinite. The Fibonacci spiral has its beginning from which it starts «to untwist», this makes possible for the Nature after one closed cycle to make and repeat the new spiral from the beginning, in this case each following term of this series equals to the sum of two preceding terms.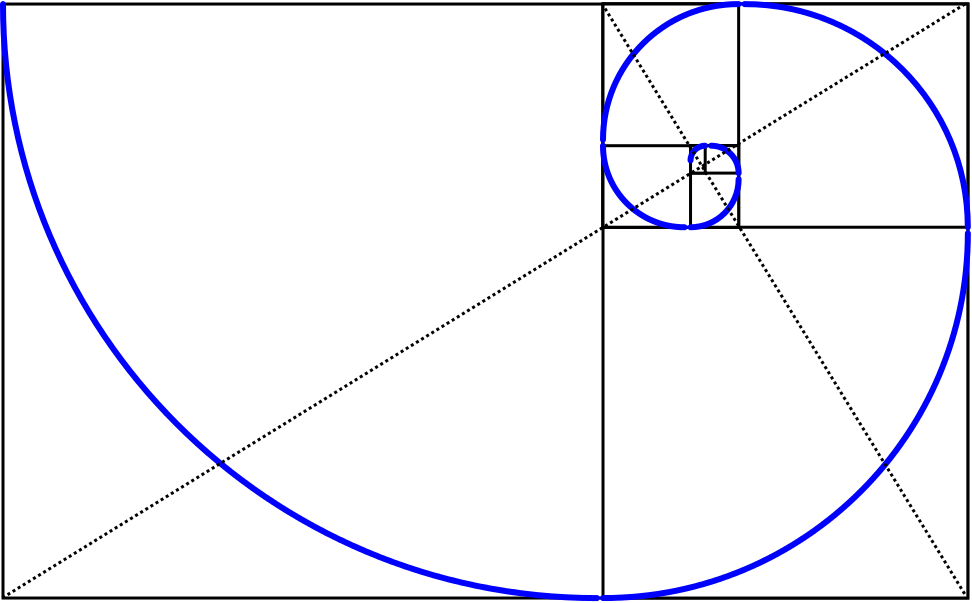

Ключевые слова: закон, принцип, этапы, нагрузка, предел, исход, максимум.

Keywords: law, principle, stages, load, limit, result, upper limit.

Введение. Актуальность, новизна, результативность, значимость. Закон золотого сечения (ЗЗС) обладает удивительным свойством принципа самонормирования (ПСН). Золотая спираль (ЗСп) ЗЗС идеальна. Она соответствует первоисточнику гармонии и не имеет ни начала, ни конца -бесконечна [1, с. 35-36; 2, с. 12-45, 56-89,126-189; 9, с. 4-7].

Цель. Задачи исследования. Цель — моделирование и разработка программы управления уравнением спортивного результата на основе цифровых отношений и величин чисел золотой пропорции и спирали Фибоначчи.

Методика, методы и результаты исследования и их обсуждение.

Спираль Фибоначчи имеет начало, от которого она начинает «раскрутку», что позволяет Природе после очередного замкнутого цикла (на примере тренировочных циклов: тренировочного микроцикла (ТМЦ), этапов отдаленной, непосредственной и соревновательной подготовки к соревнованиям (ЭОПС, ЭНПС, ЭС), мезоциклов (МЗ) спортивной нагрузки (СП), годичных тренировочных циклов (ГТЦ) и т.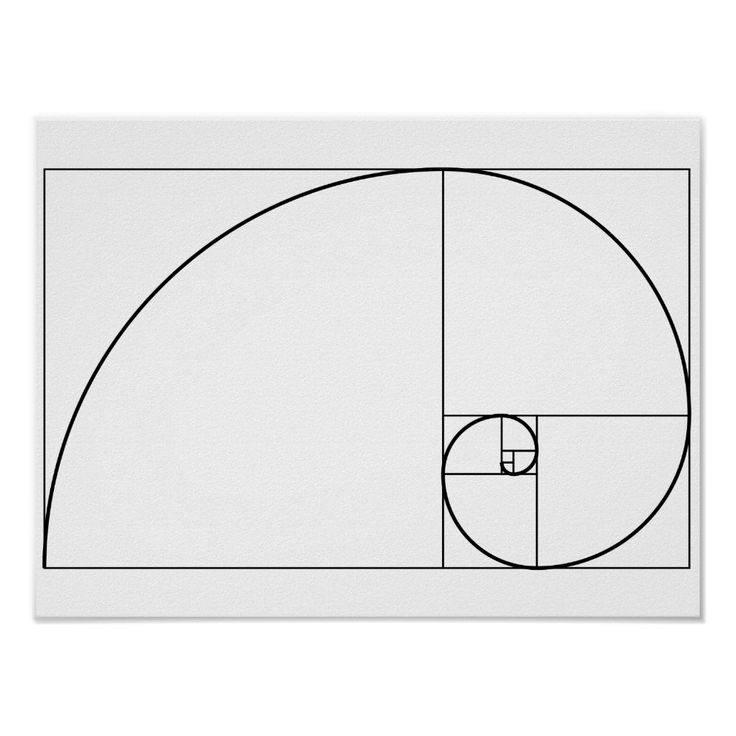 д.) осуществлять строительство и повторение новой спирали с «нуля», где каждый последующий член этого ряда равен сумме двух предыдущих членов [3, с. том 1. — с. 123-186; том 2. — с. 27-178; 4, с. 27-134; том 2. — с. 12-89; 10, с. 7375; 9, с. 2-7]:

ВП (- 21; -13;) [-8; -5; -3; -2; (-1; -1;) ||| (1; 1;) 2; 3; 5; 8;] (13; 21)

ВП -2,62; -1,62; -1; -0,62; -0,38;

ВИ 0,38; 0,62; 1; 1,62; 2,62;

где: ВП — великий предел

ВИ — великий исход

Данные отношения чисел золотой пропорции (ЗП), золотого коэффициента (ЗК) и золотой середины ЗЗС мы использовали при разработке построения программы управления уравнением спортивного результата и тренировочных принципов: принципа разнонаправленного варьирования и скорости преодоления отрезков дистанций и принципа раскачивания «маятника» (ПРВДС и ПРМ), а также отдельных частей и фрагментов спортивной нагрузки (СН): тренировочных и технико-тактических заданий (ТЗ и ТТЗ), интенсивности (И), процентного уровня реализации максимального рекордного результата (% УРМРР), повторного максимума (ПМ), объема нагрузки (V), константного времени текущей реакции приспособления организма (КВТРПО) спортсмена и т.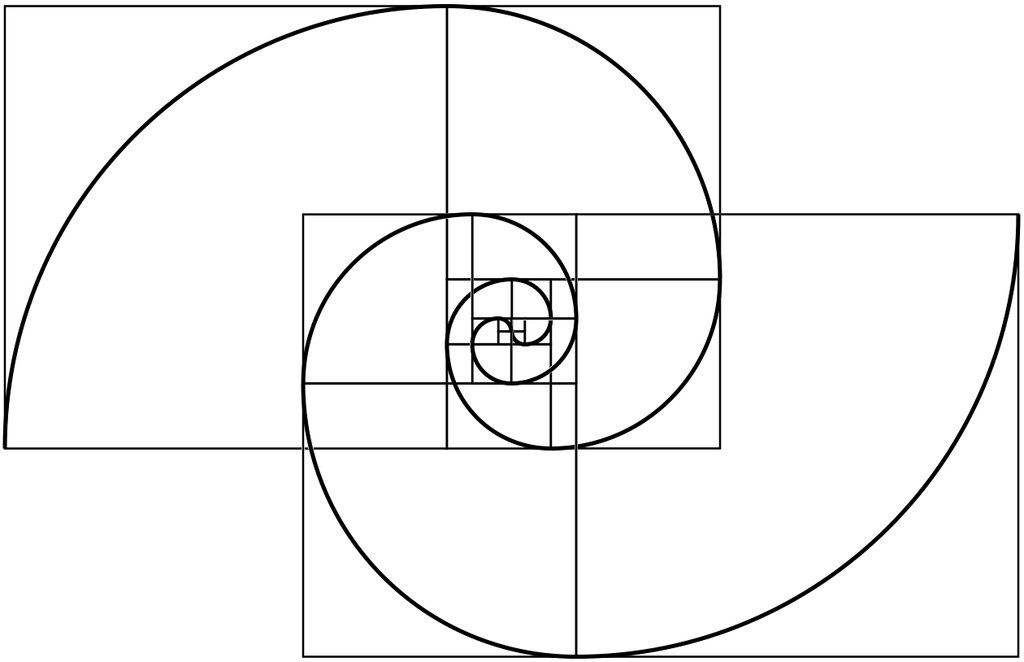 д. [10, с. 74-76; 5, с. 129- 311; 7, с. 34-89; 8. с. 7-28].

Выводы и практические рекомендации. Академик Толмачев В.К. в своей книге «Роскошь системного мышления» пишет: согласно Клавдию Птолемею, если в целом отрезке, состоящему из 21 равных частей выделить большую (мажор), состоящую из 13-и отрезков, и меньшую (минор) — из 8-и отрезков, то отношение целого отрезка (21) к мажору (13) равно отношению мажора (13) — к минору (8), то есть (мажор + минор)/мажор = мажор/минор, или (13+8)/13 = 13/8 = Ф =1,62.. Интересно, что хроматическая гамма связана и с числом 13 и числом 8, саму пропорцию 13/8 (как любую и ЗЗС) можно представить как 8/8+5/8=1+0,62 =1,62.. (или например: 13/13+8/13=1+0,62 = 1,62.. и т.д.) [2, с. 4-58]. Далее утверждается, что с этими пропорциями связывают многие духовные знания, но и разлад в гармонии здоровья и проявление различных нарушений и заболеваний в генетическом коде человека.

Итак, если мажор + минор =1, то решение задачи в виде корней уравнения х2-х-1= 0, дает цифровое значение: Х1= — 0,62. .., Х2=1,62…, или Ф-1 = 0,62., Ф =1,62.

Другое уравнение х2- у = ху, превращает тождество в Золотой крест ЗЗС, при следующих численных значениях: Х1= +0,62 ., У1= -1,62 ., Х2= -1,62 ., У2 =+ 0,62 .,

Подставив корни в уравнения Ф2-Ф=1 (1,62.-0,62 = 1) и в х (х-1) =1, имеем: Ф1(Ф1-1) =1,62.х 1,62.-1,62.= 2,62.-1,62.= 1 Ф-2- (- Ф-1) = 0,38.+ 0,62.=1

Эти уравнения ЗЗС отражают не только принцип самонормирования (ПСН) Единого закона (ЕЗ) двойственного отношения (монады), но и связь ЗЗС с биномом Ньютона (с монадой), утверждая и доказывая справедливость следующих тождеств [1, с. 33-36; 2, с. 168-190; 8, с. 23-35; 9, с. 4-7]:

А) Ф-3 = 0,24..; Б) Ф1 =1,62..;

Ф2 = 2,62; 2,62-1,62 = 1; Ф-2 = 0,38..; 0,62+0,38 = 1;

Фз = 3,62..; (3,62-1,62) -1 = 1; Ф-1 = 0,62..; (0,38 + 0,24) + 038 =1;

Резюме. Таким образом, этот ряд может быть продолжен и как вправо, так и влево, как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд). Ряды закона золотого сечения формируют не только натуральный ряд чисел, но и великие пределы (ВП) двойственных «золотых монад», триад (числа 5, 8, 13.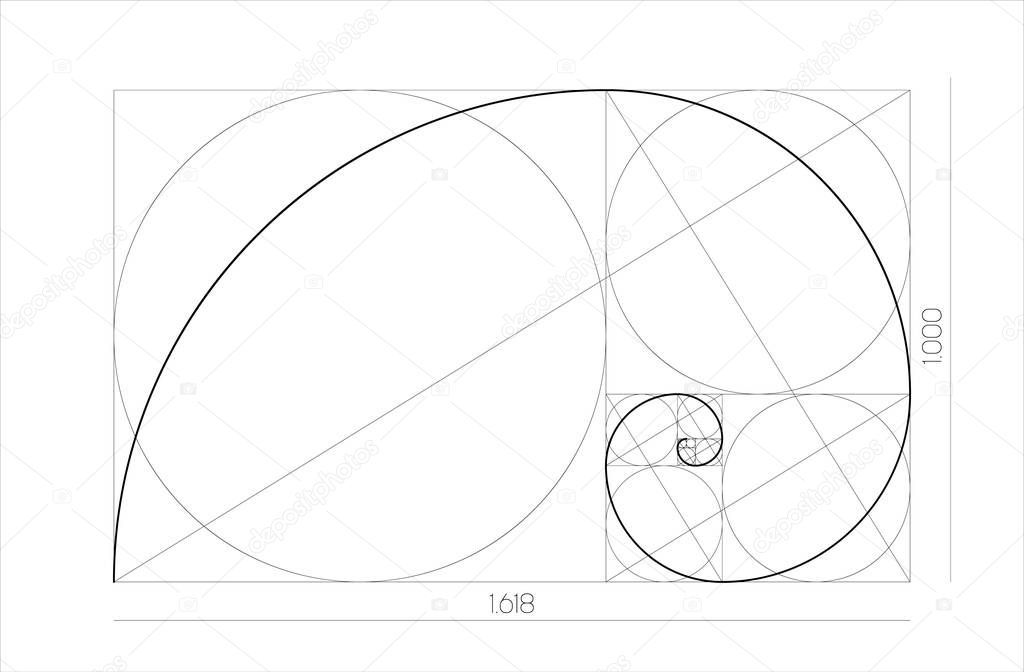 ..) и золотой крест (число 9), отражая одно из важнейших свойств мироздания — нормированной единицы, вскрывающей сущность динамики периодичности и свойства двойственного отношения (монады) и их норму самодостаточности (НСД):

0,38; 0,62;.. = (ВП 8/13|||ВС-П; 5/8;3/5;2/3; 1/2;1/1)

(ВИ 1>ВС-П =и = ВС-П>1 ВИ)

(1/1; 2/1; 3/2;5/3; 8/5;ВС-П |||13/8 (ВП) = 1,62; 2,62.,

где: ВП — великий предел,

ВИ — великий исход,

ВС-П — великая стена — «пустоты»

[1, с. 33-36; 3, том 1. — с. 12-34; том 2. — с. 16-78; 6. Том 1. — с. 57-148; том 2. — с. 67-183; 9, с. 2-7].

Q

Список литературы

а

w

1. Бендукидзе А.Д. Золотое сечение / А.Д. Бендукидзе // Квант. — 1973. -№8. — С. 33-36.

2. Васютинский Н.Д. Золотая пропорция / Н.Д. Васютинский — М.: Молодая гвардия, 1990. — 238 с.

3. Головко Н.Г. Управление уравнением спортивного результата: сборник научно-методических консультаций для студентов-легкоатлетов: в 2-х томах /БелГСХА им. В.Я. Горина; под ред.: Н.Г. Головко. — Белгород: Изд-во БелГСХА им. В.Я. Горина, 2012- а. — Том 1. — 223 с; Том 2.- 208 с.

4. Головко Н.Г. Уравнение спортивного рекорда: сборник научно-методических указаний: в 2-х томах / БелГСХА им. В.Я. Горина; под ред.: Н.Г. Головко. — Белгород: Изд-во БелГСХА им. В.Я. Горина, 2012-6. — Том 1. -268 с.; Том 2. — 273 с.

5. Головко Н.Г. Структура модели-гармонии рекордного результата: сборник научно-методических материалов для студентов ВУЗов РФ / БелГСХА им. В.Я. Горина; под ред.: Н.Г. Головко. — Белгород: Изд-во БелГСХА, 2012-а. — 370 с.

6. Головко Н.Г. Развитие выносливости бегуна: Монография. — в 3- х томах / Н.Г. Головко. — БелГСХА им. В.Я. Горина; под ред.: Н.Г. Головко. 3-е изд.: переработанное, дополненное, исправленное. — Белгород: Изд-во БелГСХА им. В.Я. Горина, 2013. — Том 1. — 228 с.; Том 2. — 242 с.; Том 3. — 256 с.

7. Петровский В. В. Организация спортивной тренировки / В. В. Петровский. — Киев: «<Здоров’ я», 1978.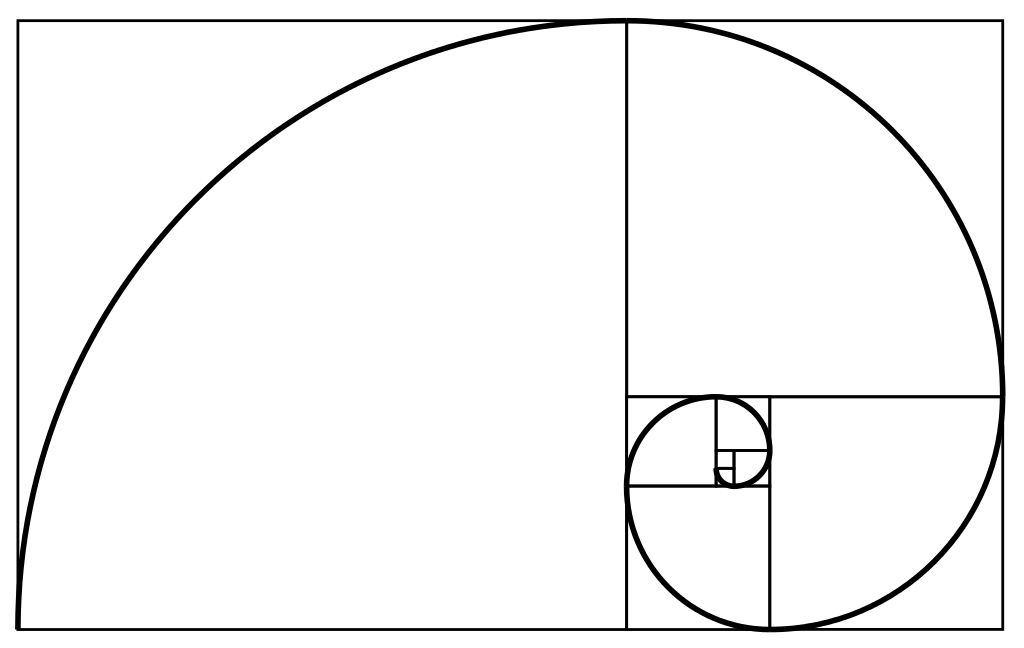 — 91 с.

8. Кеплер И. О шестиугольных снежинках / И. Кеплер. — М. : Наука. — 1982. — 37 с.

9. Шлиховский Н.В. Формула совершенства / Н.В. Шлиховский. — 2010. №4. — С. 2-7.

10.Энгвер Н.Н. Уравнение спортивного результата /Н.Н. Энгвер. — В сб.: «(Подготовка предупреждающей информации». — Рига, 1970. — С. 73-76.

_Q

Ш

References

1. Bendukidze A.D. Golden section /A.D. Bendukidze //Kvant. — 1973. — Na 8. -P. 33-36.

2. Vasyutinsky N.D. Golden proportion / N.D. Vasyutinsky — M.: Molodaja Gvardia, 1990. — 238 p.

3. Golovko N.G. Control of the sports results’ equation: collected scientific and methodological consultations for students-athletes: in 2 volumes / V.Y. Gorin

Belgorod State Agricultural Academy; ed. by N.G. Golovko. — Belgorod: Publishing House of V.Y. Gorin Belgorod State Agricultural Academy, 2012-a. -Volume 1. — 223 p.; Volume 2. — 208 p.

4. Golovko N.G. Equation of sports records: collected scientific and methodological instructions: in 2 volumes /V. Y. Gorin Belgorod State Agricultural Academy; ed. by N.G. Golovko. — Belgorod: Publishing House of V.Y. Gorin Belgorod State Agricultural Academy, 2012-b. — Volume 1. — 268 p., Volume 2. -273 p.

5. Golovko N.G. Structure of the model-harmony of the record result: collected scientific and methodological materials for students of higher educational institutions of Russia / V.Y. Gorin Belgorod State Agricultural Academy; ed. by N.G. Golovko. — Belgorod: Publishing House of Belgorod State Agricultural Academy, 2012-a. — 370 p.

6. Golovko N.G. Development of a runner’s endurance: Monograph. — in 3 volumes / N.G. Golovko. — V.Y. Gorin Belgorod State Agricultural Academy; ed. by N.G. Golovko. 3rd ed.: reprocessed, supplemented, corrected. — Belgorod: Publishing House of V.Y. Gorin Belgorod State Agricultural Academy, 2013. -Volume 1. — 228 p.; Volume 2. — 242 p.; Volume 3. — 256 p.

7. Petrovsky V. V. Organization of a sports training / V. V. Petrovsky. — Kiev: «Healthy’l», 1978. — 91 p.

8. Kepler I. About hexagonal snowflakes /1. Kepler. — M. : Nauka. — 1982. — 37 p.

9. Shlihovsky N. V. Formula of perfection / N. V. Shlihovsky. — 2010. № 4. — P. 2-7.

10.Engver N.N. Equation of the sports result / N.N. Engver. — In the collect. «Preparation of precautionary information». — Riga, 1970. — P. 73-76.

Что такое Золотая спираль? Чтобы узнать, давайте нарисуем один.

Пол Мироча

Это обсуждение представляет собой отрывок из семинара, организованного The Desert Lab 30 января 2021 года: «Фибоначчи и агавы», часть серии Seeing Math in Nature .

Как странная последовательность чисел, случайно открытая Фибоначчи около 1200 года, является ключом к золотой пропорции, золотому прямоугольнику, золотой спирали — и жизни, вселенной и всему остальному.
Эти геометрические спирали встречаются в природе. Как только вы нарисуете один, вы будете видеть их повсюду.

Что такое Фибоначчи на самом деле?

Леонардо Пизанский, которого звали Фибоначчи, был средневековым математиком  (1170 – ок.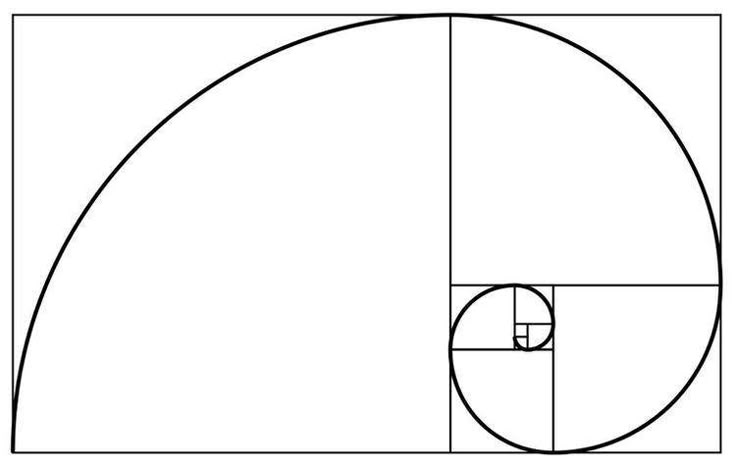  1240). Он не проектировал падающую башню, но, скорее всего, вы слышали, как кто-то произносил имя Фибоначчи, возможно, в художественной галерее или на коктейльной вечеринке. Вы, наверное, слышали, что это часть сакральной геометрии, лежащей в основе Жизни, Вселенной и Всего Всего. Но произвело ли на вас впечатление само знание этого? И я нет.

Фраза, которую я люблю использовать в начале урока рисования или мастер-класса: «Вы не поймете что-то по-настоящему, пока не попытаетесь это нарисовать». Давайте сделаем это.

Эта числовая последовательность действительно образует закономерности и геометрию, встречающиеся повсюду в природе. Почему Вселенной так нравятся эти числа? Может быть, это потому, что природа всегда меняется и растет, и это геометрия роста и формы.

Но сначала займемся цифрами.

Числа Фибоначчи

Знаменитая числовая последовательность Фибоначчи была проста: чтобы получить следующее число в последовательности, нужно сложить два предыдущих числа. Это был его ответ на популярную загадку чисел: предположим, что пара кроликов, самец и самка, способны спариваться, и каждый месяц их потомство производит пару кроликов мужского и женского пола. Сколько кроликов будет через год?

Ответ: 144, число Фибоначчи. Как мы увидим, эту последовательность и геометрию, которую она образует, можно найти повсюду в мире природы.

Странный факт: Количество лепестков на цветке обычно равно числу Фибоначчи. Что с этим?
Об этом мы поговорим в другом посте.

Затем есть еще один номер


, называемый Phi

Вот где это становится странным. Что математики обнаружили в последовательности Фибоначчи, так это то, что отношения последовательных чисел в последовательности Фибоначчи, то есть деление одного числа в последовательности на предыдущее, становятся все ближе и ближе к особому числу, 1,618…

8\5= 1,6  


377/233= 1,61802575…

1,618… для краткости называется Фи. Я поставил многоточие после него, потому что десятичные дроби идут до бесконечности). Поскольку фи — иррациональное число, оно стремится к бесконечности, никогда не повторяясь, приближаясь к фи, но никогда не достигая точной, поддающейся определению величины. Для вашего взгляда на этот кусочек бесконечности я вычислил Фи до 100 000 разрядов.

1,618, одно из самых известных иррациональных чисел, также называемое золотым сечением, 1:1,618…. Эта пропорция на протяжении всей истории так восхищала архитекторов, художников и математиков, что ее называли «золотой» и даже «священной». Некоторые называют эти числа и их результирующую геометрию основой нашего восприятия красоты.

Чтобы доказать это, я представлю следующий 5-секундный видеоролик.

Одной из причин такого восхищения этим отношением является то, что оно находится в золотом прямоугольнике. Пропорции сторон этого прямоугольника равны 1 к 1,618 . И почему эта пропорция вызывает такое восхищение?

Открыв его в природе, художники, философы, математики и архитекторы использовали это соотношение в своей работе. Они передали эту секретную формулу через века, чтобы создать то, что считается наиболее гармоничным соотношением между визуальными элементами. Просто в этом что-то есть. Это динамическая форма — мозг пытается, но не может точно отобразить этот прямоугольник с помощью простых чисел. Это потому, что он основан на иррациональном числе.

Это золотой прямоугольник: отношение его длинной стороны к короткой равно 1,618…

До сих пор речь шла о прямых пропорциях. Но самое интересное заключается в том, как числа Фибоначчи, Золотая пропорция и Золотой прямоугольник содержатся в Золотой спирали.

Швейцарский математик Якоб Бернулли был настолько впечатлен этой спиралью, что придал ей мистический смысл. Когда он умер в 1705 году, Бернулли попросил вырезать эту спираль на его надгробии вместе с латинской фразой «9».0036 eadem mutata resurgo ”, («Хоть и изменился, но воскресаю прежним».)

Рисование золотой спирали

Я собираюсь нарисовать это от руки карандашом по двум причинам:
1. рисование только рукой и мозг создает более глубокое обучение. Рука – это продолжение вашего мозга.
2. Это помогает нашим навыкам рисования практиковаться в оценке основных форм. Он не должен быть идеальным или прямым. Грубые формы будут работать так же хорошо или даже лучше, чем использование линейки и циркуля.

Вот быстрый 1,5-минутный предварительный просмотр того, как я рисую спираль. Тогда мы сделаем это вместе. Нарисовав это, некоторые люди сообщают о кратковременной искре просветления.

Ускоренное видео рисования спирали

1. Нарисуйте один крошечный квадрат в нижней правой четверти страницы. I лист бумаги для принтера подойдет. Это семя фрактальной модели.

2. Нарисуйте еще один квадрат того же размера от руки выше и разделите верхнюю сторону первого.

3. Нарисуйте еще один квадрат справа, той же высоты, что и два сложенных квадрата. (Подсказка: это неуловимый золотой прямоугольник)

4. Нарисуйте еще один квадрат поверх предыдущего прямоугольника. Это делает еще один золотой прямоугольник. Когда мы добавляем квадраты, результирующая общая форма всегда будет золотым прямоугольником. Это называется «самоподобием» и представляет собой простую фрактальную геометрию. Каждый прямоугольник, который мы создадим таким образом, будет точно таким же — изменится только размер.

5. Нарисуйте еще один квадрат той же высоты, что и предыдущая стопка, но ниже нее. (Да, еще один золотой прямоугольник) Получается однобоко, но это не имеет значения.

6. Нарисуйте еще один квадрат ниже предыдущей группы с одной стороной такой же ширины, как предыдущий золотой прямоугольник.

6. Нарисуйте еще один квадрат ниже предыдущей группы с одной стороной такой же ширины, как предыдущий золотой прямоугольник.

9. Теперь, если вы разметите квадраты по их размеру, исходя из того, что первый квадрат равен 1 единице, вы получите: ЧИСЛА ФИБОНАЧЧИ! По мере добавления квадратов длина каждой стороны будет основываться на том, что первый квадрат равен единице. Длина сторон каждого нового квадрата всегда будет соответствовать последовательности Фибоначчи.

10. Если начертить диагональ каждого квадрата, то можно начать видеть каркас спирали.

Обратите внимание, что мы рисуем диагонали квадратов, создавая еще одно значимое иррациональное число, встречающееся в природе: квадратный корень из двух, 1,414 … Это также гипотенуза прямоугольного треугольника, центральное понятие для пифагорейцев. Итак, оба этих загадочных числа присутствуют в Золотой Спирали.

Открытие того, что диагональ квадрата является иррациональным, не поддающимся определению числом, вызвало сдвиг парадигмы среди древнегреческих философов. Основной принцип их мировоззрения заключался в том, что Вселенная исчисляема, определяема целыми числами и дробями. Открытие иррационального свело их с ума.

Легенда гласит, что около 500 г. до н. э. пифагорейцы выбросили Гиппаса из Метапонта за борт за то, что он опубликовал свое доказательство того, что квадратный корень из двух — длина диагонали квадрата или гипотенуза прямоугольного треугольника — является бесконечным несчетным десятичным числом. Может быть, с тех пор культура научных кругов изменилась — или у академиков теперь есть более изощренные, но не менее эффективные средства разрешения споров.

В конце концов, пифагорейцы приняли это доказательство, и иррациональная природа гипотенузы стала дверью в тайный мистицизм, основанный на Культе Чисел.

Чтобы закончить этот рисунок, я нарисовал спираль оранжевым маркером.

Чтобы увидеть одну из причин, по которым Золотая спираль произвела такое впечатление на Якоба Бернулли, обратите внимание ниже на то, что это фрактал, другими словами, «самоподобный». Когда он становится больше, он всегда одинаков. Это верно, будь то раковина улитки или спиральная галактика.

Двухчасовой семинар UA Tumamoc «Фибоначчи и агавы» прошел онлайн 30 января 2021 года. Вы все еще можете приобрести билет с доступом к записи на это и другие мероприятия из серии онлайн-семинаров Desert Lab.

Символ золотой спирали – что это значит?

Раскрытие информации о партнерских программах

Содержание

От ураганов до цветов и сосновых шишек — спиральные узоры изобилуют в природе. Математика — это наука о закономерностях, поэтому неудивительно, что спирали веками вдохновляли математиков. Одной из таких спиралей является золотая спираль, которая считается своего рода кодом, управляющим архитектурой Вселенной. Золотая спираль — обширный, увлекательный предмет, сыгравший заметную роль в истории и произведениях искусства.

Взгляните на золотую спираль — ее происхождение, значения и значение.

Что такое символ золотой спирали?

Золотая спираль — это узор, созданный на основе концепции золотого сечения — универсального закона, представляющего «идеал» во всех формах жизни и материи. На самом деле его часто приводят в качестве примера связи между законами математики и строением живых существ. Чем больше мы понимаем математику, стоящую за символом, тем больше мы ценим его появление в природе и искусстве.

В математике золотое сечение — это особое число, приблизительно равное 1,618 и представленное греческой буквой Φ (Фи). Вы можете задаться вопросом, откуда взялась эта золотая спираль, и ответ на этот вопрос лежит внутри золотого прямоугольника. В геометрии золотую спираль можно нарисовать из золотого прямоугольника, стороны которого пропорциональны золотому сечению.

В 1800-х годах немецкий математик Мартин Ом назвал специальное число 1,618 золотым , вероятно, потому, что оно всегда существовало в математике. Еще раньше его даже описывали как 9.0003 божественный из-за его частоты в естественном мире. Спиральный узор, созданный из золотого сечения, также называют золотой спиралью .

Золотая спираль против спирали Фибоначчи

Золотое сечение встречается во многих математических контекстах. Вот почему золотую спираль часто связывают с последовательностью Фибоначчи — рядом чисел, тесно связанных с Фи. Технически последовательность начинается с 0 и 1 и продолжается бесконечно, и если вы разделите каждое число на его предшественник, результат будет сходиться к золотому сечению, примерно 1,618.

В математике есть несколько спиралей, и их можно измерить. Золотая спираль и спираль Фибоначчи очень похожи по форме, и многие используют их взаимозаменяемо, но это не одно и то же. Все можно объяснить математическими расчетами, и при измерении они не будут иметь одинаковой точной закономерности.

Говорят, что спираль Фибоначчи соответствует золотой спирали только в определенной точке, когда первая приближается к золотому сечению или 1,618. На самом деле, чем выше числа Фибоначчи, тем ближе их отношение к фи. Только имейте в виду, что не каждая спираль, встречающаяся в природе, основана на числах Фибоначчи или золотом сечении.

Значение и символизм Золотой спирали

Символ золотой спирали вдохновлял бесчисленное количество людей на протяжении всей истории. Это было связано с основами жизни, духовности и творчества.

  • Жизнь и творение

Золотая спираль уникальна по своим математическим свойствам и доказывает, что мы живем во вселенной, управляемой математическими законами. В то время как другие считают, что это просто очень странное совпадение, многие ученые и исследователи рассматривают его как свидетельство Великого Математика или Творца. В конце концов, разумный замысел в природе сложен, и некоторым может показаться нелогичным думать, что он возник случайно.

  • Баланс и гармония

Золотая спираль покорила своей красотой воображение математиков, дизайнеров и художников. Это отражено в некоторых из величайших произведений искусства и архитектуры. Он также ассоциируется с красотой, поскольку многие считают, что красота основана на его уникальных свойствах в математике и геометрии. Некоторые мистики считают, что этот символ также принесет в жизнь баланс и гармонию.

Символ золотой спирали в истории

Увлечение символом золотой спирали побудило многих художников использовать его в своих шедеврах. Есть большая вероятность, что вы уже видели этот символ в виде наложений на различные формы искусства, от Парфенона до Моны Лизы. К сожалению, существует много запутанных утверждений по этому вопросу, поэтому мы поможем вам решить, основаны ли они на мифах или математике.

  • Парфенон

Построенный между 447 и 438 годами до нашей эры, Парфенон в Афинах, Греция, является одним из самых эстетически привлекательных сооружений, когда-либо созданных. Многие предполагают, что он был построен на основе золотого сечения. Вы даже увидите несколько изображений парадного фасада храма с золотой спиралью и золотым прямоугольником на нем.

Нет никаких сомнений в том, что древние греки использовали математику и геометрию в своей архитектуре, но ученые не могут найти конкретных доказательств того, что они использовали золотое сечение при строительстве Парфенона. Многие считают это мифом, потому что большинство математических теорем были разработаны только после постройки храма.

Более того, необходимы точные измерения, чтобы сделать вывод, что в дизайне использовались золотое сечение и золотая спираль. По мнению экспертов, золотой прямоугольник должен быть обрамлен у основания ступеней, ведущих к Парфенону, а не у основания его колонн, как это обычно показано на нескольких иллюстрациях. Кроме того, строение находится в руинах, что делает его точные размеры предметом некоторой оценки.

  • Картины Леонардо да Винчи

Леонардо да Винчи уже давно называют «божественным» художником, связанным с золотым сечением. Эта ассоциация была даже поддержана романом Код да Винчи , так как в сюжете задействовано золотое сечение и числа Фибоначчи. Хотя все подлежит интерпретации, многие предполагают, что художник намеренно использовал золотую спираль в своих работах для достижения баланса и красоты.

Использование Да Винчи золотого сечения очевидно в Тайная вечеря и Благовещение , но Мона Лиза или Джоконда все еще обсуждаются. Говорят, что здесь мало архитектурных элементов и прямых линий, которые можно использовать в качестве ориентиров по сравнению с двумя другими картинами. Тем не менее, вы можете найти несколько интерпретаций золотых сечений на Моне Лизе с золотой спиралью в качестве наложений.

Вероятно, мы никогда не узнаем намерений Да Винчи в отношении своих шедевров, но многие находят это странное совпадение убедительным. Учитывая предыдущее использование художника, для него не было бы неожиданностью использовать его и на указанной картине. Только имейте в виду, что не на каждой картине Да Винчи есть явные свидетельства включения золотого сечения и золотой спирали, поэтому сложно сделать вывод, что все его шедевры основаны на них.

Символ золотой спирали в наше время

Золотая спираль способствует нашему пониманию жизни и Вселенной. Вот некоторые из недавних открытий, касающихся символа:

.
  • В математике

Золотая спираль играет роль в геометрии фракталов, сложном узоре, который повторяется вечно. Американский математик Эдмунд Харрис стал популярен благодаря своей фрактальной кривой, основанной на золотой спирали, ныне известной как спираль Харриса. Говорят, что он стремился нарисовать разветвляющиеся спирали, которые выглядели бы эстетически привлекательными, но в итоге получил уникальную спираль, используя математический процесс.

  • В биомеханике

Считается, что золотая спираль оказывает завораживающее влияние на движения человеческой руки. По словам анатома, движения человеческих пальцев повторяют узор золотой спирали. Вы даже найдете изображения сжатого кулака со спиральным символом в качестве наложения.

  • В дизайне и композиции

В настоящее время многие дизайнеры накладывают символ золотой спирали на изображение, чтобы проиллюстрировать пропорции золотого сечения в надежде достичь визуальной гармонии в своих работах. На их основе основаны некоторые современные логотипы и иконки, где дизайнеры применяют так называемую концепцию «соотношений внутри соотношений».

  • В природе

Природа полна спиралевидных узоров, но настоящая золотая спираль в природе встречается редко. Интересно, что ученые обнаружили, что соколы летят по золотой спирали, когда приближаются к своей добыче, вероятно, потому, что это энергоэффективный путь полета.

Вопреки распространенному мнению, раковина наутилуса не является золотой спиралью. При измерении они не будут совпадать, независимо от того, как они были выровнены или масштабированы. Кроме того, не все раковины наутилуса созданы одинаковыми, так как каждая из них имеет вариации и несовершенства формы.

Спирали подсолнухов и сосновых шишек красивы, но это не золотые спирали. На самом деле их спирали даже не закручиваются вокруг центра, в отличие от золотой спирали. Хотя у некоторых цветов количество лепестков соответствует числам Фибоначчи, есть несколько исключений.

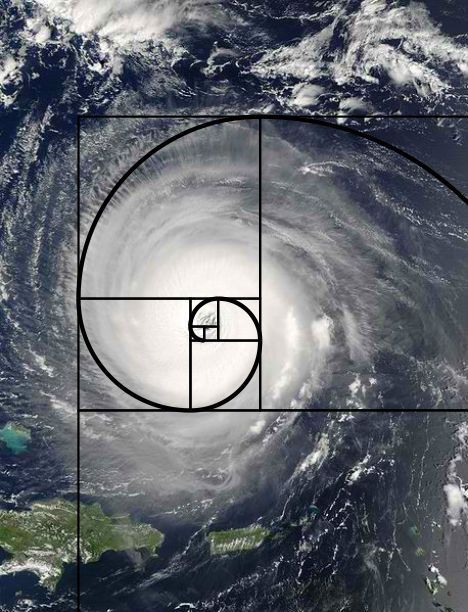
Эксперты также говорят, что галактика или случайное грозовое облако, которое соответствует части золотой спирали, не должно быть выводом о том, что все галактики и ураганы основаны на золотом сечении.

Кратко

Наша Вселенная заполнена спиралями, поэтому неудивительно, что многие заинтересовались математикой, стоящей за ними, и их значением. Художники давно признали золотую спираль самой приятной для глаз. Это действительно один из самых вдохновляющих узоров в природе, который можно воплотить в творческом художественном выражении.

Золотая спираль

Золотая спираль
следующая кривая предыдущая кривая 2D-кривые Трехмерные кривые поверхности фракталы многогранники

ЗОЛОТАЯ СПИРАЛЬ, СПИРАЛЬ ФИБОНАЧЧИ
и натуральные спирали

Фигура начинается с золотого прямоугольника ABCD , с АВ = 1 и = золотое сечение; рисуем квадрат ABA’D ‘ и получаем золотой прямоугольник А’Б’С’Д’ длина сторон которого и 1.
Этот процесс повторяется для получения прямоугольника A»B»C»D» и так далее и тому подобное, а также внешние квадраты; золотой спираль состоит из последовательных четвертей кругов, вписанных в каждый квадрат.

Диагонали пунктирные BD и CD’ пересекаются в точке O , являющейся асимптотической точкой спирали, называемой «глаз Бога» (золотое сечение также называют «божественной пропорцией»!)

Линии АА» и A’A»’ перпендикулярны и пересекаются в точке O .

Указанные числа являются длинами сторон квадратов.


Золотая спираль обладает частичным «eadem mutata resurgo» свойство, а именно инвариантность относительно подобия с центром O , соотношение и угол ;
, поэтому оно приближается к истинному логарифму спираль, где м определяется , следовательно с полярным уравнением, проходя по точкам А , А ‘, А » и т. д…

С каждым ходом радиус золотой спирали умножается на ; постоянный полярный тангенциальный угол равен

 


Золотая спираль (красная) и истинная логарифмическая спираль (зеленая)


Если вместо золотого прямоугольника начать с прямоугольником Фибоначчи, с AB = F n-1 и до н.э. = F n , где F n-1 и F n два последовательных числа Фибоначчи. чисел, мы получаем спираль, состоящую из четверти кругов, называемую Фибоначчи. спираль , которая приближается к золотой спирали, но не имеет Свойство «eadem mutata resurgo».

Мы также можем начать с золотого треугольника (равнобедренный треугольник с углом при вершине, равным ). Получаем спираль, которую можно назвать треугольная золотая спираль ; когда эта спираль вращается, увеличивается в j раз; следовательно, это является приближением логарифмической спирали ; коэффициент расширения на каждом повороте равен и полярный тангенциальный угол составляет около 76°.

См. также Падован спираль, коэффициент расширения на каждом витке которой равен шестой степени числа Падована, т.е. около 5,4.


На этом сайте, можно найти объяснение тому, что оболочка наутилус предположительно напоминает золотую спираль, но это явно противоречит прямому наблюдению: спираль наутилуса намного более плотное, и экспериментальные измерения показывают, что его коэффициент увеличения составляет около 3, что явно меньше, чем 6,9 золотой спирали. ..

Аммонит: значительно меньший коэффициент увеличения….

Усик зеленой фасоли предположительно приближается треугольная золотая спираль…

Сравните конструкцию золотой спирали с той спирали с n центров, что приближается к архимедовой спирали.


Швейцарская марка 1987 г.



следующая кривая предыдущая кривая 2D-кривые Трехмерные кривые поверхности фракталы многогранники

© Роберт ФЕРРЕОЛ 2017

Последовательность Фибоначчи

Последовательность Фибоначчи

Числа Фибоначчи

Математика лежит в основе многих закономерностей, которые мы наблюдаем в природе. Вот интересный пример, называемый рядом Фибоначчи, названный в честь итальянского математика Средневековья, хотя греки явно знали все об этом намного раньше, о чем свидетельствует дизайн классической архитектуры, такой как Парфенон. Одним из распространенных природных примеров является количество лепестков на цветах, хотя, конечно, есть и исключения.

Серия   Отношение
0 + 1 = 1                               1 / 0 = ?
    1 + 1 = 2                           1 / 1 = 1
        1 + 2 = 3                       2 / 1 = 2
            2 + 3 = 5                   3 / 2 = 1,5
                3 + 5 = 8               5 / 3 = 1,67
                    5 + 8 = 13           8 / 5 = 1,6
                        8 + 13 = 21       13 / 8 = 1,625
                            13 + 21 = 34   21 / 13 = 1,615
                                      и так далее. ..          

Если мы продлим ряд до бесконечности, отношение приблизится к ~1,618:1, константе, которую мы называем фи, которая представлена ​​греческой буквой φ

3 лепестка 5 лепестков 8 лепестков 13 лепестков 21 лепесток

Видео : Посмотрите следующее видео для хорошего объяснения. В то время как ведущая немного увлекается каким-то магическим мышлением, мне нравится ее энтузиазм.

Золотое сечение

Упражнение : Возьмите ананас и коробку цветных канцелярских кнопок. Как показано на видео выше, вставьте канцелярские кнопки одинакового цвета в каждую ячейку ананаса, следуя за завитками, с разным цветом для каждой линии. Сфотографируйте получившийся узор.

Золотая спираль представляет собой геометрический способ представления последовательности Фибоначчи и представлена ​​в природе, хотя и не всегда идеально, в сосновых шишках, раковинах наутилуса и улиток, ананасах и многом другом.

Ананас Сочный Сосновая шишка Раковина Наутилуса Подсолнечник

Чтобы нарисовать золотую спираль, вам понадобится циркуль и миллиметровка или линейка.


Посмотрите это видео, чтобы узнать, как это сделать.

 

Моделирование с помощью Excel : Загрузите этот файл Excel, чтобы создавать спирали, подобные Золотой спирали.

  

Узнайте, как изменение переменных влияет на кривые.

 

Дальнейшее чтение :

https://www.nationalgeographic.org/media/golden-ratio/

http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/phi2DGeomTrig.html

 

ЧАСТОТА ВСЕЛЕННОЙ И САКРАЛЬНАЯ ГЕОМЕТРИЯ – Modern ŌM

БЕСПЛАТНАЯ стандартная доставка по США и возврат при заказе на сумму более 99 долларов США

31 марта 2022 г.

И мистики, и ученые веками были очарованы священной формой, которая присутствует почти во всех живых существах — людях, растениях и животных.

Его знакомую форму можно узнать в нашей собственной ДНК, отпечатках пальцев, цветах, деревьях, раковинах, а на универсальном уровне — в ураганах и галактиках.

Что это за древний символ красоты, совершенства и пропорции?

Это священная форма

спирали .

 

На протяжении веков спираль олицетворяла бесконечное расширение, символизируя расширение природы и Вселенной, отражая волшебную взаимосвязь нашего микро- и макрокосмоса. На протяжении веков это знание считалось священным, способом постижения более глубокой красоты и духовности жизни.

Позже в этом посте мы расскажем, как вы можете носить этот священный секретный код во вселенной, чтобы вы тоже могли получить доступ к его магическим свойствам!

 

СВЯЗЬ МЕЖДУ ЗОЛОТОЙ СПИРАЛЬЮ И ЗОЛОТЫМ СООТНОШЕНИЕМ

Модель

Golden Spiral основана на концепции под названием GOLDEN RATIO , которая формировала наше понимание баланса и пропорции на протяжении тысячелетий.

ЗОЛОТОЕ СООТНОШЕНИЕ , равное 1,618, на протяжении всей истории называлось многими именами: Золотое сечение, Золотое сечение, Магическое сечение, Божественная пропорция.

Одна из самых известных математических формул, которую можно найти практически везде, включая природу, геометрию, человеческое тело и солнечную систему. Вы можете сказать, что это своего рода встроенная система нумерации космоса, и именно поэтому ее часто называют «секретным кодом природы » .

Люди знали о ЗОЛОТОМ СООТНОШЕНИИ

по крайней мере 4000 лет, а некоторые говорят, что даже дольше! Последние исследования показывают, что он использовался в дизайне иероглифов, найденных на стенах гробниц, а также при строительстве египетских пирамид и других древних сооружений по всему миру.

 

ЗОЛОТОЕ СООТНОШЕНИЕ И ПОСЛЕДОВАТЕЛЬНОСТЬ ФИБОНАЧЧИ

ЗОЛОТОЕ СООТНОШЕНИЕ

было подробно описано индийскими математиками примерно в 6 веке нашей эры и представлено на Западе в 1202 году Леонардо Фибоначчи из Пизы, тем самым парнем, который принес нам арабскую десятичную систему вместо неудобной римской, которая использовалась. в это время.

Принцип

Последовательности Фибоначчи прост — начиная с 0 и 1, каждое новое число в последовательности является суммой двух предыдущих.

0, 1, 1, 2, 3, 5, 8, 13 … — Последовательность продолжает разворачиваться в бесконечном порядке.

Эта формула окружает нас повсюду в нашей повседневной жизни, хотя мы редко замечаем ее.

Посмотрите, замечали ли вы когда-нибудь формулу Фибоначчи в этих знакомых вещах:

  • Цветы, листья и ветки многих растений расположены по схеме 1-3-5-8

  • Лепестки сосновой шишки расположены спиралями, пересекающимися в обоих направлениях: 8 спиралей в одном направлении и 13 в другом

  • Гигантские многоножки, гусеницы монархов, улитки и панголины имеют это соотношение в строении тела


  • Наиболее привлекательными для нас являются лица, основные черты которых имеют пропорции, наиболее близкие к золотому сечению

А вот и связь:


Если взять любые два последовательных числа Фибоначчи, их отношение очень близко к золотому сечению (1,618).

 

ЗОЛОТОЕ СООТНОШЕНИЕ В ДИЗАЙНЕ

ЗОЛОТОЕ СООТНОШЕНИЕ очень давно очаровывало западный мир — на протяжении всей истории архитекторы, музыканты, художники и скульпторы использовали его в качестве основы для своих творений.

Возможно, самым известным примером

ЗОЛОТОГО СООТНОШЕНИЯ в искусстве является ВИТРУВИАНСКИЙ ЧЕЛОВЕК Леонардо да Винчи, а также его шедевры МОНА ЛИЗА и ТАЙНАЯ УЖИНА. Многие известные художники, в том числе Микеланджело, Рафаэль, Рембрандт, Сера и Дали, использовали эту формулу в своем искусстве.

Вероятно, справедливо будет сказать, что на протяжении многих веков ЗОЛОТОЕ СООТНОШЕНИЕ формировало наше представление и понимание красоты.

ЗАЧЕМ НОСИТЬ ЗОЛОТОЕ СООТНОШЕНИЕ УКРАШЕНИЯ

Мы используем ЗОЛОТОЕ СООТНОШЕНИЕ

в дизайне Modern OM, чтобы усилить нашу энергетическую связь с прекрасным миром вокруг нас.

Наша ювелирная линия

GOLDEN RATIO включает малы и браслеты, созданные для настройки частот тела на энергетическую вибрацию Божественной Пропорции.

Все изделия этой линии также предназначены для работы с системой чакр, чтобы помочь вам оставаться в гармонии с присущими

RATIO свойствами баланса, выравнивания, красоты и неограниченного расширения.

Ношение наших украшений

GOLDEN RATIO — это постоянное напоминание о том, что все во Вселенной существует в совершенной гармонии. Это заставит вас больше улыбаться, дышать глубже, ценить и принимать всех людей и события, которые посылает вам Вселенная!

Марина Лихова