Золотое правило сечения: Правило третей и золотое сечение — как это работает | Статьи | Фото, видео, оптика

Золотое Сечение в Дизайне (Правило + Принципы + Применение)

Содержание статьи

1. Правило золотого сечения
2. Спираль золотого сечения
3. Применение в дизайне

Понятие «золотое сечение», о котором многие слышат впервые, на самом деле известно с незапамятных времён. О нём упоминает ещё Евклид в своих «Началах», написанных примерно за 300 лет до н. э. Сегодня правило находит применение как в точных науках, так и в искусстве. Широко распространено золотое сечение в дизайне. Причём в различных его областях. Оформление интерьеров, ландшафтов садов и парков, а также интернет-сайтов и логотипов компаний выполняется в соответствии со строгими правилами.

Правило золотого сечения

Почему дизайнеры взяли на вооружение это правило? Чем ближе к идеалу пропорции каждого предмета и расположение предметов относительно друг друга, тем лучше воспринимает картину в целом – человеческий мозг. «Золотая пропорция» предполагает деление целого на 2 части, меньшую и большую. Меньшая относится к большей, а большая – к целому, как 0,618 к 1. Если обратиться к математике, можно дать более точное определение.

Золотое сечение (пропорция) – это соотношение величин b и a, a > b, при этом a/b = (a+b)/a. Число, равное отношению a/b, обозначается греческой буквой Φ в честь древнегреческого скульптора и архитектора Фидия. На практике Ф=1,618. Если обратиться к процентам, золотое сечение – это деление величины на две, которые соотносятся как 62% и 38%.

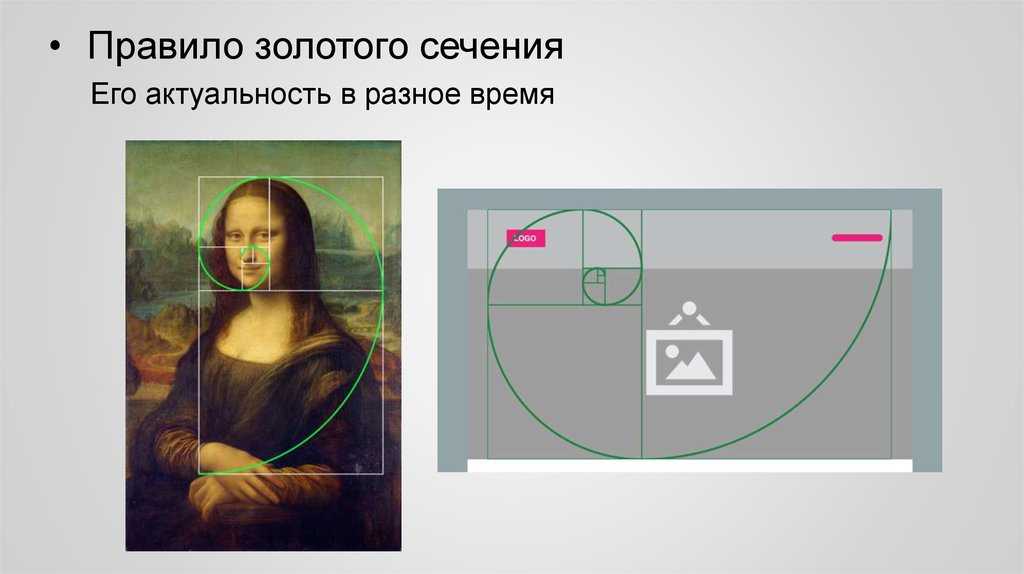
Исчерпывающее описание этому принципу дал Леонардо да Винчи. Известно, что представители различных сфер искусства, например, художники и музыканты, не ставя целью подогнать свои произведения под «золотую пропорцию», всё же инстинктивно её придерживались. Ведь именно так достигается гармония. Такую пропорцию именовали даже «божественной». Меньшая часть – Бог-Сын, большая – Бог-Отец, а целое – Дух Святой. Ещё один пример золотой пропорции представляет собой правило третей. Оно связано с особенностями зрительного восприятия человека. Если зритель смотрит на рисунок, который поделён на 9 равных фрагментов, он в первую очередь выделяет 4 точки, образованные в местах, где вертикальные линии пересекаются с горизонтальными.

Спираль золотого сечения

Говоря о «золотой пропорции», нельзя не упомянуть и ряд (спираль) Фибоначчи. Математик Леонардо Пизанский (Фибоначчи) жил в эпоху средневековья. Он составил последовательность чисел 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 и т. д. Сумма каждых 2 чисел, которые следуют друг за другом, равна третьему числу, идущему за ними. В качестве примера можно рассмотреть фаланги человеческих пальцев. А именно – соотношение 1-й фаланги ко 2-й и 3-й. В природе много примеров, заставляющих нас вспомнить о спирали Фибоначчи. Это ананасы и шишки, рога животных, раковины моллюсков.

Применение в дизайне

Повсеместно используется правило золотого сечения в дизайне интерьеров. Лёгкая асимметрия неожиданно дарит нам ощущение гармонии и покоя. Какое помещение можно назвать идеальным по форме? То, в котором ширина и длина соотносятся как 5 к 8, или 1 к 1,62. В помощь архитекторам Ле Корбюзье ещё в начале прошлого века разработал систему антропометрических пропорций. В основе её – фигура человека с идеальными пропорциями, с поднятой рукой. Изначально этой системой (ещё одно её название «модулор») пользовались при создании проектов многоквартирных домов.

 

Когда ещё только рассчитывается планировка квартиры, работа ведётся по принципу золотого сечения в дизайне. Зонирование территории осуществляется в соответствии с точками пересечения горизонтальных и вертикальных линий. Здесь можно поставить перегородки и ширмы, мебель или крупную бытовую технику. Если же это не типовая квартира, а дом, который вы строите, свой рост можно использовать как модуль. И в буквальном смысле слова подогнать пространство под себя. Расставляя мебель, можно руководствоваться теми же принципами. Так, диван должен занимать на более 2/3 стены, вдоль которой его поставили. Если рядом вы поместите журнальный столик – его длина не должна превышать 2/3 длины дивана. Принцип можно отнести к кровати. Рядом с постелью мы часто видим тумбочки. Их высота не должна быть больше 2/3 стены.

 

Чтобы в помещении вы испытывали чувство покоя, тёмные вещи лучше разместить внизу, ближе к полу, в светлые – на самом верху стены. Учитывайте размеры и цвет  картин и фотографий, которые вешаете на стену. Композиционно их следует размещать правильно – как в отношении стены, так и соотносительно друг к другу. Правило золотого сечения работает и тогда, когда речь идёт о выборе цветов. Лучше всего, если в помещении около 68% площади окрашено в один цвет, а оставшиеся 38% – в другой, второстепенный. Это касается выбора обоев и краски. Цветовым акцентам можно уделить не более 10%. Научившись применять на практике «золотую пропорцию», вы сможете стать настоящим профессионалом в области дизайна.

 

*Фотографии, используемые в статье, взяты из свободного доступа в интернете и используются на сайте в учебно-образовательных целях.

Золотое сечение

Давайте проверим, правда ли в природе часто встречаются объекты с соотношениями, близкими к золотому сечению, или это заблуждение.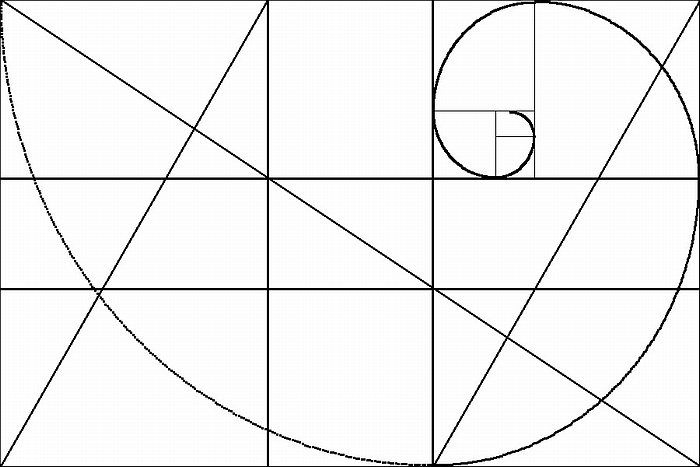

В этом проекте нам предстоит подтвердить или опровергнуть известное утверждение, что в природе часто встречаются объекты с пропорциями золотого сечения.

Что такое золотое сечение? Если взять отрезок длины С и разбить его на две части длинами А и В так, что отношение длины большей части к длине меньшей будет равно отношению длины всего отрезка к большей части

\[\frac{A}{B}=\frac{C}{A},\]

то такое разбиение и будет называться золотым сечением.

Для такого разбиения

\[\frac{A}{B}=\frac{C}{A}=1.6180339887…\]

А если рассчитать обратное отношение (разделить меньшую величину на большую), то получится

\[\frac{B}{A}=\frac{A}{C}=0.6180339887…\]

Если обобщить, то золотым сечением можно считать любое отношение двух величин А и В, если оно равно 1.6180339887.

Вопрос о том, есть ли в основе этого интересного соотношения какой-то важный смысл, с древних времен волновал человечество. На него пытались найти ответ представители совершенно разных профессий – математики и биологи, художники и архитекторы. Некоторые из них даже приписывали золотому сечению разные мистические свойства!

Многие предполагают, что золотое сечение играет в нашем мире особенную роль, и в качестве подтверждения приводят примеры золотого сечения в природе. Классические примеры – это отношение длины хвоста ящерицы к длине её туловища, соотношение длин побегов некоторых растений, многие пропорции человеческого тела.

Есть гипотеза о том, что пропорции золотого сечения лежат в основе нашего представления о гармонии. В искусстве иногда используется «правило золотого сечения» – в соответствии с ним самыми эстетичными нам кажутся композиции с пропорциями, близкими к золотому сечению.

В этом проекте мы попытаемся проверить, действительно ли в природе часто встречаются объекты с соотношениями, близкими к золотому сечению, или это заблуждение. Для этого мы будем измерять соотношений размеров разных объектов в окружающей нас живой природе – это могут быть части тела людей или животных, растения или грибы.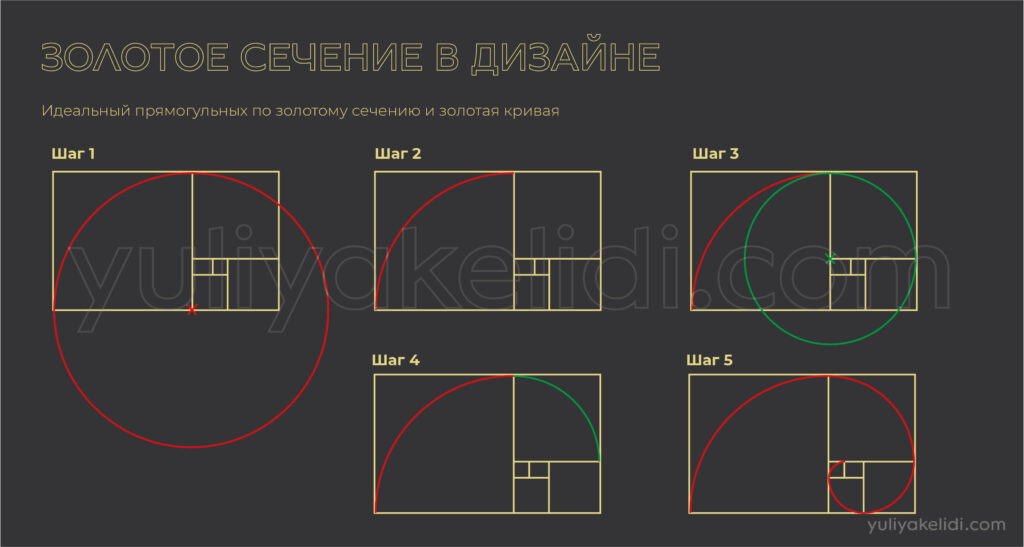

Выберем объект и начнём исследование: мы будем вычислять отношения разных частей этого объекта, которые нам удастся измерить (специально искать пропорции, близкие к золотому сечению, не стоит, нам нужно рассмотреть разные отношения величин). Например, если мы хотим вычислить пропорции рук человека, мы можем рассчитать отношение длины предплечья, то есть руки от локтевого сустава до запястья (A на рисунке), к длине кисти (E), отношение длины кисти (E) к ширине запястья (H), отношения длин разных пальцев или, например, отношение обхвата запястья (D) к ширине большого пальца (J).

Стоит иметь в виду, что можно измерять не только продольные и поперечные размеры, но и обхваты. При этом важно, что одно и то же измерение (длина ладони, например) может быть использовано при расчете разных отношений. Фантазировать и придумывать новые параметры и их сочетания здесь не только можно, но и нужно!

Собрав статистику, мы или убедимся в том, что соотношение 1,6 встречается в природе чаще, чем, например, 1,5 или 1,7, или сможем с уверенностью сказать, что это миф!

Золотое сечение — определение, формула, примеры

Золотое сечение, которое часто называют золотым сечением, божественной пропорцией или золотым сечением, представляет собой особый атрибут, обозначаемый символом ϕ, и примерно равен 1,618.

Изучение многих специальных формаций может быть выполнено с использованием специальных последовательностей, таких как последовательность Фибоначчи, и атрибутов, таких как золотое сечение.

Это соотношение встречается в различных искусствах, архитектуре и дизайне. Многие замечательные архитектурные сооружения, такие как Великая пирамида Египта, Парфенон, были частично или полностью спроектированы так, чтобы отражать в своей структуре золотое сечение. Великие художники, такие как Леонардо да Винчи, использовали золотое сечение в нескольких своих шедеврах, и в 1500-х годах оно было известно как «Божественная пропорция». Давайте узнаем больше о золотом сечении в этом уроке.

1.	Что такое золотое сечение?
2.	Формула золотого сечения
3.	Как рассчитать золотое сечение?
4.	Что такое золотой прямоугольник?
5.	Что такое последовательность Фибоначчи?
6.	Часто задаваемые вопросы о золотом сечении

Что такое золотое сечение?

Золотое сечение, также называемое золотым сечением, божественной пропорцией или золотым сечением, существует между двумя величинами, если их отношение равно отношению их суммы к большей величине между ними. Со ссылкой на это определение, если мы разделим линию на две части, части будут в золотом сечении, если:

Отношение длины более длинной части, скажем, «а», к длине более короткой части, скажем, «b» равно отношению их суммы «(a + b)» к большей длине.

Обратитесь к следующей диаграмме для лучшего понимания вышеуказанной концепции:

Обозначается греческой буквой ϕ, произносимой как «фи». Приблизительное значение ϕ равно 1,61803398875 . Оно находит применение в геометрии, искусстве, архитектуре и других областях. Таким образом, следующее уравнение устанавливает соотношение для расчета золотого сечения: два.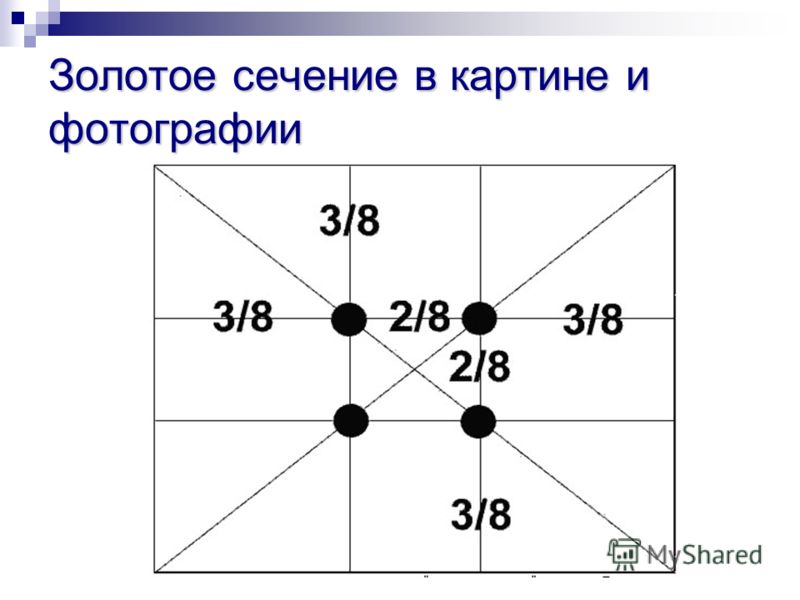

Определение золотого сечения

Когда линия делится на две части, длинная часть, которая делится на короткую часть, равна всей длине, деленной на длинную часть, определяется как золотое сечение. Ниже приведены примеры золотого сечения в архитектуре и искусстве.

Существует множество применений золотого сечения в области архитектуры. Многие архитектурные чудеса, такие как Великая мечеть Кайруана, были построены с учетом золотого сечения в их структуре. Такие художники, как Леонардо да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сера, использовали это как атрибут в своих работах.

Формула золотого сечения

Формулу золотого сечения можно использовать для расчета значения золотого сечения. Уравнение золотого сечения выведено, чтобы найти общую формулу для расчета золотого сечения.

Уравнение золотого сечения

Из определения золотого сечения

a/b = (a + b)/a = ϕ

Из этого уравнения получаем два уравнения:

a/b = ϕ → ( 1)

(а + b)/а = ϕ → (2)

Из уравнения (1)

a/b = ϕ

⇒ a = b

Подставить это в уравнение (2):

(bϕ + b)/bϕ = ϕ

b( ϕ + 1)/ bϕ = ϕ

(ϕ + 1)/ϕ = ϕ

1 + 1/ϕ = ϕ

1 + 1/ϕ = ϕ

Как рассчитать золотое сечение?

Значение золотого сечения можно рассчитать разными методами. Начнем с основного.

Метод проб и ошибок

Мы угадаем произвольное значение константы, а затем выполним следующие шаги, чтобы вычислить более близкое значение на каждой итерации.

• Вычислите мультипликативную обратную величину угаданного вами значения, т. е. 1/значение. Это значение будет нашим первым термином.
• Вычислите другой член, добавив 1 к мультипликативному, обратному этому значению.
• Оба условия, полученные на предыдущих шагах, должны быть равны. Если нет, мы будем повторять процесс, пока не получим примерно равное значение для обоих членов.
• Для второй итерации мы будем использовать предполагаемое значение, равное члену 2, полученному на шаге 2, и так далее.

Например,

Поскольку ϕ = 1 + 1/ϕ, оно должно быть больше 1. Начнем со значения 1,5 в качестве нашего первого предположения.

• Член 1 = Мультипликативное обратное 1,5 = 1/1,5 = 0,6666… ​​
• Член 2 = мультипликативный, обратный 1,5 + 1 = 0,6666. 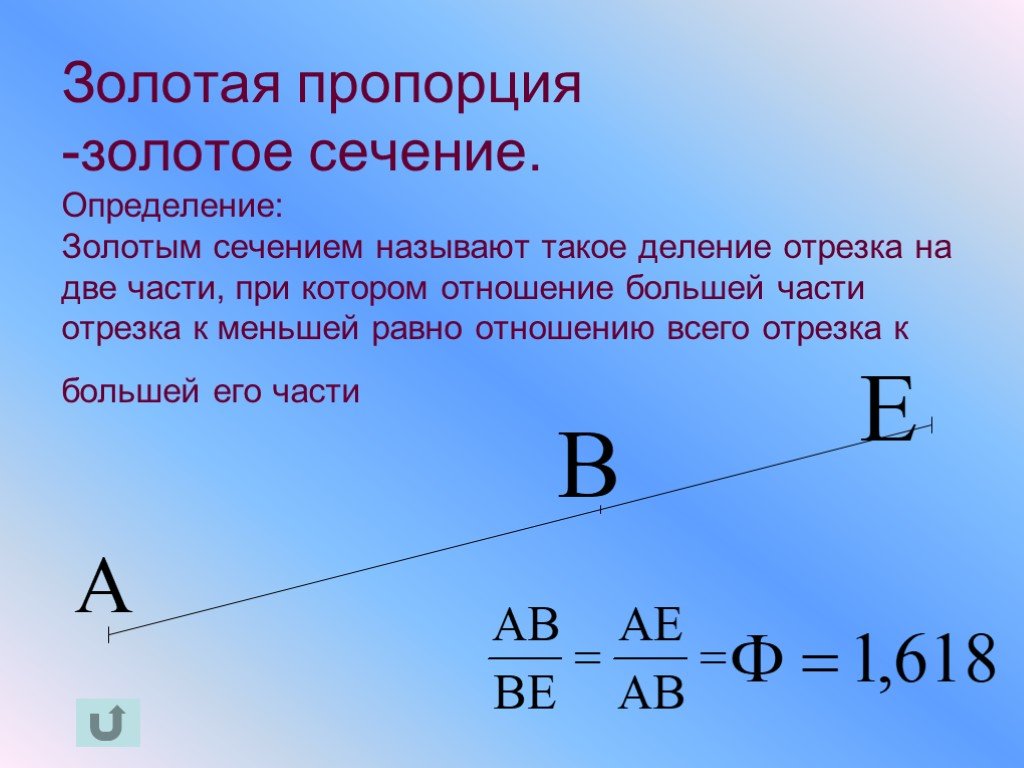. + 1 = 1,6666… ​​

Поскольку оба термина не равны, мы повторим этот процесс снова, используя предполагаемое значение, равное

термину 2 .

В следующей таблице приведены данные расчетов для всех принятых значений, пока мы не получим желаемые равные условия:

Итерация	Предполагаемое значение	Термин 1 (1/значение)	Термин 2 (1/значение + 1)
1.	1,5	11,511,5 = 0,6666..	0,6666.. + 1 = 1,6666..
2.	1.6666..	11,666..11,666.. = 0,6	0,6 + 1 = 1,6
3.	1,6	11,611,6 = 0,625	0,625 + 1 = 1,625
4.	1,625	11,62511,625 = 0,61538..	0,61538.. + 1 = 1,61538..
5.	1. 61538..	..	.. и так далее

Чем больше итераций вы выполните, тем ближе приблизительное значение будет к точному. Другие методы обеспечивают более эффективный способ вычисления точного значения. 92 — 4ac}}{2a}\)

Подставляя значения a = 1, b = -1 и c = -1, получаем

ϕ = \(\frac{1 \pm \sqrt{( 1 + 4 )}}{2}\)

Решение можно упростить до положительного значения, что даст:

ϕ = 1/2 + √5/2

Обратите внимание, что мы не рассматриваем отрицательное значение, так как \( \phi\) — это отношение длин, и оно не может быть отрицательным.

Следовательно, ϕ = 1/2 + √5/2

Что такое золотой прямоугольник?

В геометрии золотой прямоугольник определяется как прямоугольник, длины сторон которого находятся в золотом сечении. Золотой прямоугольник демонстрирует совершенно особую форму самоподобия. Все прямоугольники, созданные путем добавления или удаления квадрата, также являются золотыми прямоугольниками.

Построение золотого прямоугольника

Мы можем построить золотой прямоугольник, выполнив следующие шаги:

• Шаг 1: Сначала мы нарисуем квадрат со стороной 1 единица. На одной из его сторон нарисуйте точку посередине. Теперь мы проведем линию от этой точки до угла другой стороны.

• Шаг 2: Используя эту линию в качестве радиуса и точку, проведенную посередине, в качестве центра, нарисуйте дугу, идущую вдоль стороны квадрата. Длину этой дуги можно рассчитать с помощью теоремы Пифагора: √(1/2) ² + (1) ² = √5/2 шт.
• Шаг 3: Используйте пересечение этой дуги и стороны квадрата, чтобы нарисовать прямоугольник, как показано на рисунке ниже:

Это золотой прямоугольник, потому что его размеры находятся в золотом сечении. т. е. ϕ = (√5/2 + 1/2)/1 = 1,61803

Что такое последовательность Фибоначчи?

Последовательность Фибоначчи — это особый ряд чисел, в котором каждый член (начиная с третьего члена) является суммой двух предыдущих членов. Для нахождения последовательности Фибоначчи можно использовать следующие шаги:

• Начнем с того, что возьмем 0 и 1 в качестве первых двух членов.
• Таким образом, третий член 1 вычисляется путем сложения 0 и 1.
• Точно так же следующий член = 1 + 2 = 3 и так далее.

Последовательность Фибоначчи задается как 0, 1, 1, 2, 3, 5, 8, 13, 21,… и так далее. Последовательность Фибоначчи и золотое сечение имеют между собой особую связь. Когда мы начинаем вычислять отношения двух последовательных членов ряда Фибоначчи, значение каждого последующего отношения становится ближе к точному значению ϕ.

Например,

В следующей таблице показаны значения соотношений, максимально приближающиеся к значению ϕ. В следующей таблице показаны значения соотношений, максимально приближающиеся к значению ϕ.

Срок 1	Срок 2	Соотношение = Клемма 2 / Клемма 1
2	3	1,5
3	5	1. 6666..
5	8	1,6
8	13	1,625
13	21	1.61538

☛Связанные темы 

Ниже приведен список тем, тесно связанных с золотым сечением. Эти темы также дадут вам представление о том, как такие понятия рассматриваются в Cuemath.

• Среднее
• Соотношение
• Числа Фибоначчи
• Квадратные уравнения
• Соотношение, доля, процентные формулы

Часто задаваемые вопросы о золотом сечении

Что такое золотое сечение простыми словами?

Золотое сечение — это математическое отношение, которое существует между двумя величинами, если их отношение равно отношению их суммы к большей из них величин. Другими словами, когда линия разделена на две части и более длинная часть «а», разделенная на меньшую часть «b», равна сумме (а + b), деленной на «а», это означает, что линия отражая золотое сечение, которое равно 1,618.

Что вы подразумеваете под золотым прямоугольником?

В геометрии золотой прямоугольник определяется как прямоугольник, длины сторон которого находятся в золотом сечении. Золотой прямоугольник демонстрирует совершенно особую форму самоподобия. Все прямоугольники, созданные путем добавления или удаления квадрата, также являются золотыми прямоугольниками.

Почему золотое сечение красиво?

Золотое сечение — это соотношение, которое при использовании в различных областях для проектирования объектов делает объекты эстетически привлекательными и приятными на вид. Поэтому золотое сечение называют красивым атрибутом. Его можно заметить в различных узорах природы, например, в спиралевидном расположении цветов и листьев. Есть много применений золотого сечения в области архитектуры. Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в своей структуре, например, Великая пирамида Египта и Великая мечеть Кайруана.

Почему золотое сечение важно?

Золотое сечение — это математическое соотношение, которое часто встречается в природе и используется в различных областях. Он используется в нашей повседневной жизни, искусстве и архитектуре. Объекты, созданные с учетом золотого сечения в своей структуре и дизайне, более приятны и эстетичны для глаз. Это можно заметить по спиралевидному расположению цветков и листьев.

Где в реальной жизни используется золотое сечение?

Существует множество применений золотого сечения в области искусства и архитектуры. Многие архитектурные чудеса были построены, чтобы отразить золотое сечение в своей структуре. Такие художники, как Лео да Винчи, Рафаэль, Сандро Боттичелли и Жорж Сера, использовали это как атрибут в своих работах. Его можно использовать для изучения структуры многих объектов в нашей повседневной жизни, которые напоминают определенный узор.

Кто открыл золотое сечение?

Древнегреческие математики первыми упомянули о золотом сечении в своих работах. Математики V века до нашей эры Гиппакус и Евклид внесли большой вклад в свои исследования по этому вопросу.

Что такое формула золотого сечения?

Формулу золотого сечения можно использовать для расчета значения золотого сечения.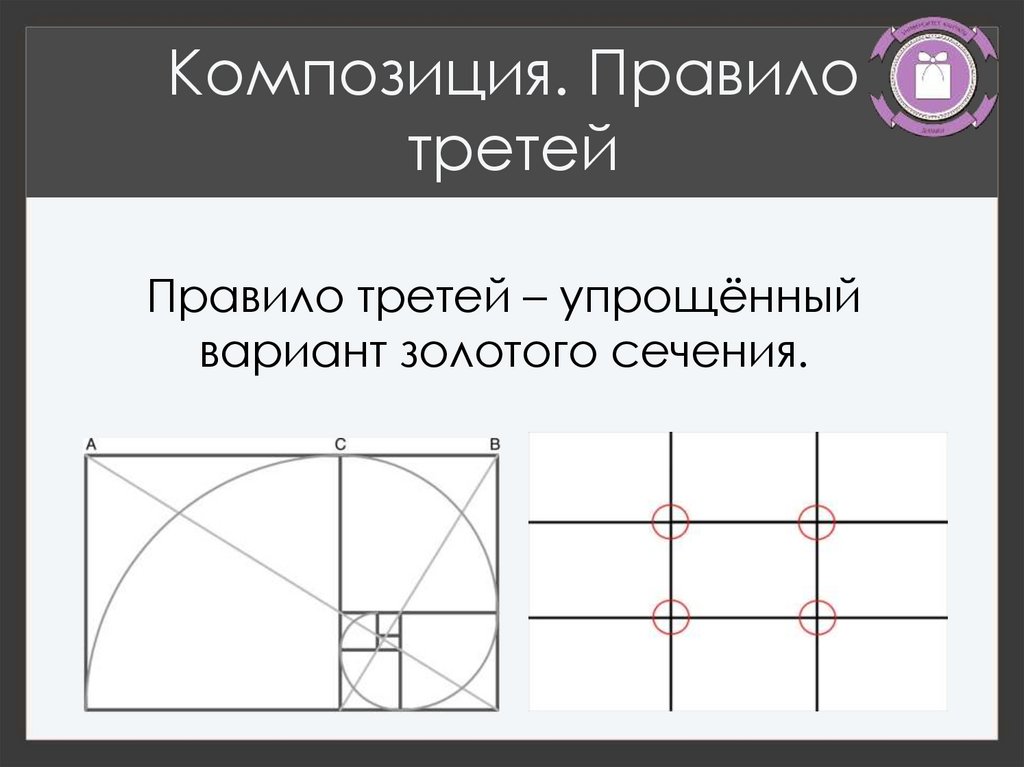 Формула для расчета золотого сечения дается как

1 + 1/ϕ = ϕ

, где ϕ обозначает золотое сечение.

Что такое золотое сечение?

Распаковка концепции последовательности Фибоначчи в дизайне.

Art by @tubik

Вдохновение окружает нас повсюду, и каждый в мире всегда черпает разные идеи из окружающего его искусства. Поэтому может показаться удивительным, что есть одно правило природы, которое так часто встречается вокруг нас, что оно было изображено в самых печально известных произведениях искусства.

Что общего у Моны Лизы, Великих пирамид Гизы, Парфенона и логотипа Apple? Все они либо демонстрируют золотое сечение, либо были разработаны с учетом золотого сечения.

Золотое сечение — это математическое отношение и соотношение, открытое и часто встречающееся в природе, но проявляющееся почти везде, например, в архитектуре, музыке, живописи, современном дизайне и т. д. При эффективном использовании он создает дизайн, который естественно и эстетически привлекателен для глаз благодаря своей художественной композиции.

Так в чем же секрет этого волшебного соотношения? Давайте еще немного разберемся в этом математическом чуде. И давайте посмотрим, как вы можете использовать его для улучшения своих проектов.

Ряд Фибоначчи

Итак, что такое золотое сечение?

Проще говоря, золотое сечение (также известное как отношение золотого сечения, божественная пропорция или золотая середина) — это математическое соотношение, которое дает число 1,618 . Представьте себе прямоугольник, в котором, если вы отрежете квадрат, оставшийся прямоугольник будет иметь те же пропорции, что и исходный прямоугольник. Продолжая этот шаблон, вы получите диаграмму золотого сечения.

Это число и само отношение получены из последовательности Фибоначчи, которая представляет собой последовательность чисел, которые естественным образом встречаются в нашей среде. Но это число также является решением квадратной формулы, в которую нам сейчас не нужно вдаваться. Но вы, возможно, помните числа Фибоначчи из средней школы. Или из блокбастера середины 2000-х, который свел всех с ума от святого Грааля, «Код да Винчи».

Помимо фантастики, золотое сечение можно найти и в природе. Вот почему ее также называют «божественной пропорцией». Из-за его частоты в естественном мире. Количество лепестков на цветке часто является числом Фибоначчи.

Семена сосновых шишек закручиваются в логарифмическую спираль чисел Фибоначчи. Даже количество сторон неочищенного банана обычно является числом Фибоначчи. Даже молекула ДНК внутри нашего тела является примером этой формы логарифмической спирали.

Теперь, когда мы освоились с этой концепцией, я уверен, что вы, ребята, не будете возражать против более подробной информации. Давайте спустимся в кроличью нору Фибоначчи.

Числа Фибоначчи представляют собой последовательность, начинающуюся с 0 и 1 и продолжающуюся добавлением двух предыдущих чисел до бесконечности. Следовательно, последовательность выглядит следующим образом: 0, 1, 1, 2, 3, 5, 8, 13, 21 и так далее.
Это потому, что 0 + 1 = 1, 1 + 1 = 2, 1 + 2 = 3, 2 + 3 = 5 и т. д. Отношения соседних чисел Фибоначчи (2/1, 3/2, 5/3 и т. д.) не совсем равны золотому сечению, но приближаются к нему. Это означает, что чем выше число Фибоначчи, тем ближе их отношение к 1,618. Дробь 5/3 уже довольно близка к 1,666666… ​​

Поскольку все мы дизайнеры, вероятно, легче понять эту концепцию визуально. Золотое сечение можно объяснить с помощью так называемого золотого прямоугольника. Прямоугольник с соотношением сторон 1:618. Теперь представьте себе квадрат, высота и ширина которого равны размеру меньшей части золотого прямоугольника. Если вы удалите этот квадрат, результирующая фигура будет иметь те же пропорции, что и исходный прямоугольник.

Таким образом, у вас остался еще один золотой прямоугольник меньшего размера. Продолжая этот шаблон, вы получите диаграмму золотого сечения. Точно так же вы можете просто добавить квадрат рядом с золотым прямоугольником с длиной, равной высоте прямоугольника, и вы добьетесь того же эффекта.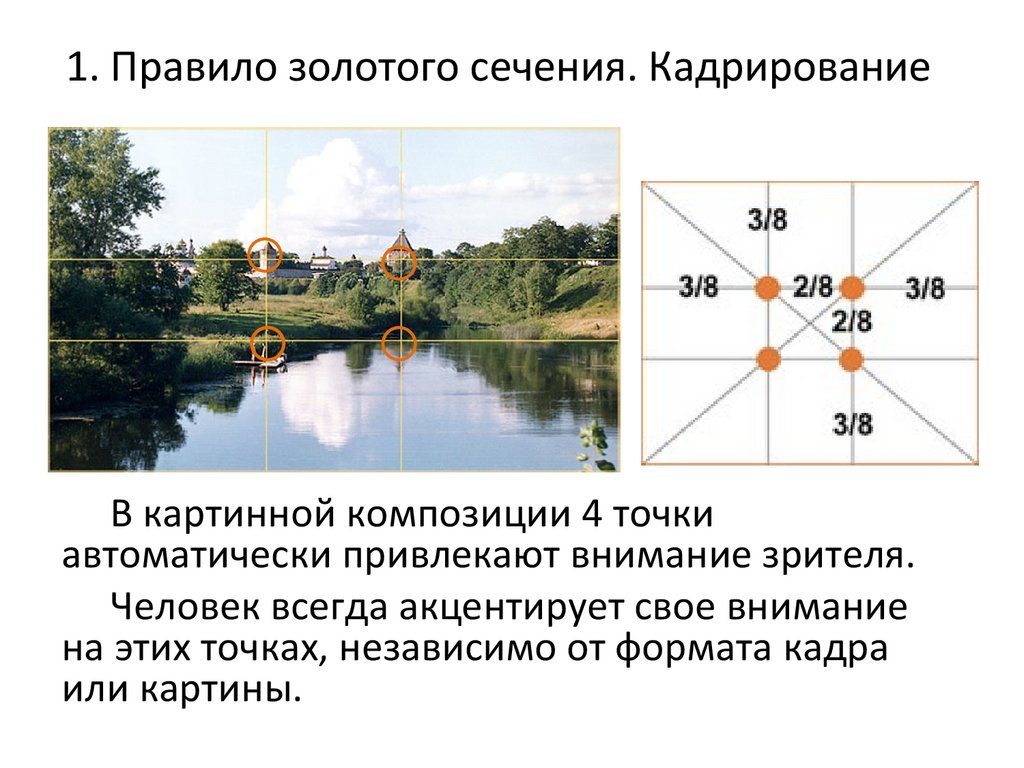

Проведя дугу окружности в каждом квадрате, мы получим Золотую Спираль (также известную как Спираль Дюрера). Другое естественное явление вытекает из самого отношения.

Золотое сечение, как и правило третей, можно использовать для создания красивых форм и сильной композиции. Это правило действует в архитектуре, дизайне и искусстве. Астроном 17-го века Иоганн Кеплер назвал золотое сечение «драгоценным камнем». Мы думаем, что астроном XVII века был прав, это бесценный инструмент.

Греческое происхождение золотого сечения

Известный греческий математик, которого называют «основателем геометрии», Евклид впервые упоминает это конкретное соотношение в своей работе «Элементы». или делящее) свойство этого иррационального числа.

Источник: Unsplash Фото, обработано в Vectornator.

Но только 2000 лет спустя немецкий математик Мартин Ом присвоил ему «золотую» характеристику. И только в 20 веке греческая буква фи была фактически принята американским математиком Марком Барром в качестве символа золотого сечения.

Барр выбрал именно эту букву, чтобы почтить память греческого скульптора Фидия, который, по признанию ряда искусствоведов, использовал золотое сечение во многих своих работах. Альтернативное обозначение — «тау», аббревиатура греческого слова «том», что означает «резать». И это ссылка на «разделяющую» приличность, упомянутую выше.

Греки тоже заметили красоту этого соотношения. Они поняли, что «божественная пропорция» обеспечивает наиболее эстетически приятную композицию. Это понятие было дополнено в эпоху Возрождения работами известного итальянского математика Леонардо да Винчи.

Он проиллюстрировал известную книгу «De divina ratione» («Божественная пропорция»), написанную Лукой Пачоли, монахом-францисканцем. В этой книге Пачоли пишет о математической взаимосвязи и художественной пропорции Золотого сечения и знаменитого Витрувианского человека Леонардо да Винчи, чтобы проиллюстрировать, как даже человеческое тело соблюдает золотое сечение.

Но работа Леонардо да Винчи не единственный пример. Золотая пропорция встречается во многих других контекстах. Хотя он получил свою известность в 16 веке, он использовался (сознательно или нет) задолго до этого. Возьмем, к примеру, Великую пирамиду в Гизе.

Соотношение его длины и высоты соответствует золотому сечению. Его гармоничные пропорции также создают так называемый Золотой треугольник (также известный как равносторонний треугольник или равнобедренный треугольник). Хотя это не доказано, некоторые утверждают, что греческая архитектура была построена с использованием числа фи, включая Парфенон.

Фото Маркуса Списке на Unsplash.

Как вы используете золотое сечение в дизайне?

Конечно, это краткое пособие по математике бесполезно, если вы не сможете успешно применять его в своей работе по графическому дизайну. Причина, по которой вы хотите применить это соотношение в своей работе, сводится к общей эстетике, которую вы хотите достичь.

Это соотношение позволяет создать ощущение естественной красоты, используя природную гармонию и пропорции окружающего мира. Даже наши лица следуют этому же соотношению. Нас настолько притягивает это соотношение, что благодаря нашей эволюции человеческое восприятие естественным образом склонно желать вещей, подсознательно демонстрирующих эту пропорцию Золотого сечения. Анализ некоторых из самых желанных людей в шоу-бизнесе показал, что пропорции лица, наиболее близкие к этому соотношению, оцениваются выше по внешнему виду среди зрителей!

Логотип Pepsi.

Когда дело доходит до драки, это соотношение дает базовые знания, которые вам необходимо знать при создании красивой композиции. Потому что это одна из ключевых целей дизайнера, верно? Для создания четких и понятных макетов, сбалансированных страниц и плавного дизайна иллюстраций.

Использование этих принципов естественным образом приведет к гораздо более целостному дизайну. Или, если вы думаете об этом с точки зрения UX, это приводит к лучшему опыту для ваших пользователей.

Золотую спираль можно использовать с помощью нескольких инструментов в вашем дизайне, таких как сетки, линейки интервалов, столбцы и желоба.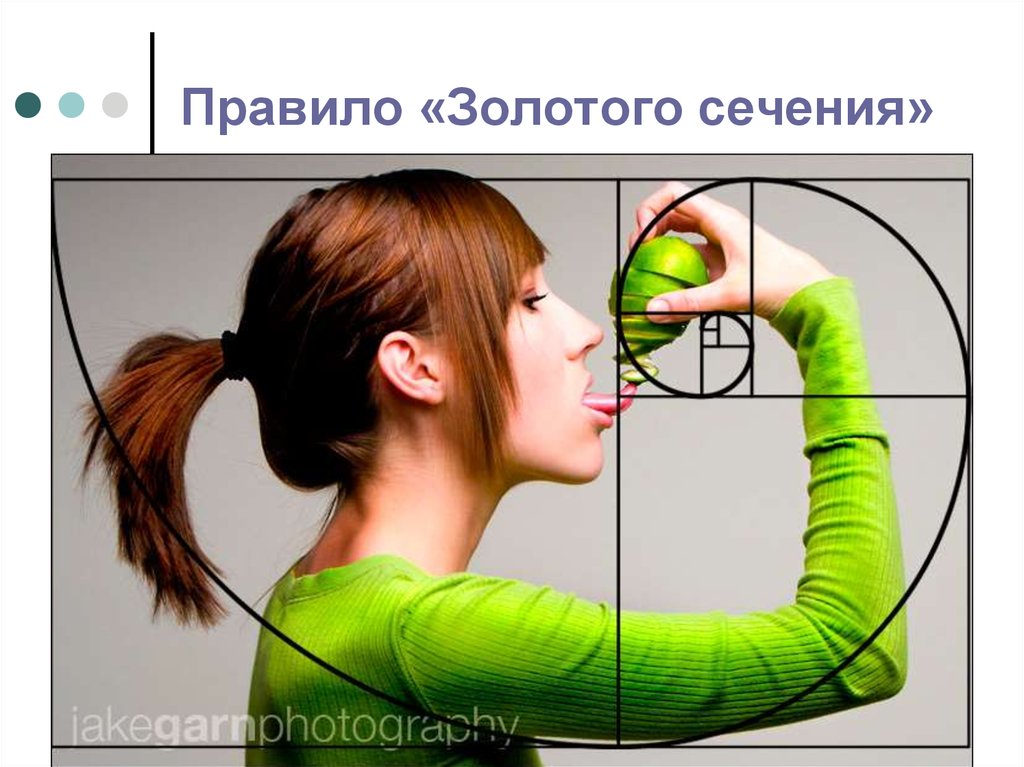 Если вы иллюстрируете, попробуйте изучить фигуры известных природных элементов, которые представляют собой последовательность Фибоначчи, таких как волны, рога, сосновые шишки или даже форму нашей галактики.

Если вы научитесь ею пользоваться, Золотая спираль может выглядеть в вашей работе особенно изящно, элегантно и даже драматично; поскольку его путь переносит взгляд зрителя на важные части вашей графики.

В частности, вот несколько способов, которыми вы можете использовать пропорцию Золотого сечения и Золотую спираль в своих интересах.

1 — Типографика и общая иерархия дизайна

На первый взгляд может показаться, что типографика и математика никак не связаны друг с другом. Ведь типографика состоит из букв, а математика — из цифр. Несколько противоположны друг другу.

Но дело в том, что типографика — это сочетание художественных форм букв и рациональных пропорций. Красивое сочетание формы и функциональности. Когда пропорции вашей типографики сбалансированы, вы действительно можете заставить ее петь в гармонии с вашим дизайном.

Вам необходимо учитывать три параметра текста: размер шрифта, высоту строки и ширину строки. Вместе эти измерения, которые мы воспринимаем как по горизонтали, так и по вертикали, отвечают за то, как мы воспринимаем типографику. Между всеми тремя существуют особые отношения.

Точнее, если ваша строка текста увеличивается в ширину, высота между строками также должна увеличиваться, чтобы улучшить ее читаемость. И как называется эта связь? Соотношение.

Если вы используете любое соотношение, почему бы не сделать его золотым? Снова и снова было доказано, что он улучшает эстетику всего, к чему прикасается.

Это соотношение может помочь вам определить размеры заголовков, основного текста и вспомогательного текста в дизайне.

Например, если ваш основной текст имеет размер 14 пикселей. Умножьте это на 1,618, и вы получите 22,652. Это означает, что ваш текст заголовка должен быть примерно 22px/23px в соответствии с соотношением, чтобы естественным образом сбалансировать текст в теле ниже. Вы даже можете использовать противоположный метод, чтобы определить размер основного текста, если вы зафиксировали размер заголовка.

2 — Редактирование и изменение размера изображений

Хотя легко понять, от какого пробела нужно избавиться при кадрировании и изменении размера ваших изображений, не забывайте, что впоследствии это потребует балансировки.

Обрезка во многом зависит от композиции вашего изображения. Сначала вам нужно подумать о некоторых ключевых вещах. Что является предметом визуального? Какие еще элементы вы можете включить в сцену? Есть ли на изображении линии или кривые, которые естественным образом появляются на изображении? Каким должен быть окончательный размер вашего холста?

Как только вы узнаете все ответы, у вас появится еще один вопрос. Вы хотите использовать фи-сетку или золотую спираль?

Phi Grid — это способ рассмотрения размерных отношений между элементами фотографии. Это похоже на правило третей, но не так просто. Вы не делите кадр на 3 равных сегмента.

Вместо этого сетка имеет соотношение 1:0,618:1, так как центральные линии расположены ближе друг к другу. Линии фи-решетки создают визуально приятные пропорции, которые люди почти автоматически воспринимают как красивые. Если вы решите обрезать с помощью Phi Grid, ваш объект будет расположен близко к центру изображения.

Со спиралью Фибоначчи структура вашей композиции совершенно другая. Если вы представите наложение спирали поверх вашего изображения, область с наибольшим количеством деталей будет находиться в самом маленьком прямоугольнике катушки. Но это не обязательно должно быть в углу. Это может быть где угодно в вашей композиции. Некоторые говорят, что лицо Моны Лизы также находится в этой важной области.

3 — Макет в дизайне пользовательского интерфейса

Использование этого соотношения также может помочь в разработке естественно привлекательного и успокаивающего пользовательского интерфейса, правильно привлекая внимание к важным вещам.

Кроме того, использование золотого сечения в ваших дизайнерских работах проще, чем вы думаете. Поскольку дизайн пользовательского интерфейса основан на логической композиции, вы можете использовать формулу в качестве инструмента для создания столбцов и пропорциональных макетов.

Предположим, вы хотите создать макет с боковой панелью шириной 1080 пикселей. Чтобы рассчитать ширину основного столбца, просто разделите 1080 пикселей на 1,618. Это создаст основной столбец шириной 667 пикселей. Вы хотите повторить тот же процесс для основного столбца, чтобы получить ширину боковой панели. Разделите 667 на 1,618, чтобы получить 412,5 пикселей.

Golden Canon Grid — Adrián Somoza для Bont™ в халяве

Но, конечно, эти размеры не всегда должны использоваться. Формула Золотого сечения просто дает рекомендации по наиболее приятному балансу между областями вашего дизайна.

На самом деле, теперь, когда вы это понимаете, вы можете увидеть этот хак в действии на многих веб-сайтах.

‍4 — Дизайн логотипа

Twitter, Pepsi и Apple. Эти бренды и их логотипы в значительной степени вдохновлены золотым сечением, и некоторые использовали это соотношение во всем дизайне своего логотипа!

Любовь Apple к золотому сечению хорошо известна среди ее поклонников и в мире дизайна. Многие из их логотипов приложений вдохновлены этим соотношением, и логотип iCloud является ярким примером этого.

Отличным способом использования золотого сечения является определение высоты и ширины логотипа, а также пропорций внутренних элементов во всем дизайне.

Золотой прямоугольник также можно использовать для размещения объектов и определения наилучшей композиции, наиболее приятной для глаз. Используя его простую формулу, вы убедитесь, что все части вашего логотипа расположены гармонично.

Или разобрать Золотую Спираль на части! Вы можете использовать круги, которые определяют Золотую спираль, в качестве основы вашего логотипа.

Итак, в следующий раз, когда вы будете стремиться к прорыву в логотипе, почему бы не попробовать это удобное соотношение, встречающееся в природе? Это откроет двери для удивительных дизайнерских впечатлений и обострит вашу дизайнерскую чувствительность, чтобы применять простые дроби и пропорции в вашем творческом процессе.

5 — Архитектура

Золотое сечение применяется в архитектуре так же, как и в искусстве, и математическая связь между известными архитектурными проектами и золотым сечением неотразима.

Источник изображения: Кимон Мариц

Древнегреческая архитектура часто использовала золотое сечение для проектирования и определения формы великих архитектурных подвигов, которыми славятся греки. Это соотношение определяет решающую взаимосвязь между архитектурными проектами и математикой.

Используя пропорции золотого сечения, архитекторы могут найти соответствующие пропорции относительно высоты и ширины зданий. В результате получается здание, которое является архитектурно прочным и эстетичным.

Этот принцип можно также применить к домашнему декору и дизайну интерьера. Например, золотое сечение окраски комнаты требует, чтобы 60 процентов вашей комнаты были окрашены в один оттенок, 30 процентов — во второй оттенок и 10 процентов — в третий оттенок.

6 — Полиграфический дизайн

Золотое сечение также может улучшить художественную композицию полиграфического дизайна. Все, от дизайна журнала и книги до маркетинговых материалов, может использовать золотое соотношение сторон для создания сильной композиции.

Существует средний коэффициент, который используют большинство дизайнеров при создании своих проектов. Однако настоящие художники будут учитывать пропорции поля по отношению к золотому сечению. Дизайнеры журналов, например, должны идеально сочетать изображение центрального прямоугольника с краями обложки.

Источник изображения: Сара Дорвейлер

Независимо от того, разрабатываете ли вы искусство для своего университетского издательства или для следующего великого романиста 21-го века, вам необходимо учитывать это математическое соотношение. Важнейшие отношения между пространством и контентом трудно идеально сбалансировать.

Золотое сечение может использоваться дизайнерами для определения надлежащего размера и расположения каждого элемента для создания обложки с идеальными пропорциями. Выравнивание угловых прямоугольников с угловыми прямоугольниками других изображений и обеспечение надлежащего интервала — наиболее положительное решение этой задачи.

7 — Фотография

Художественная композиция имеет решающее значение для любого изображения, картины или иллюстрации. Независимо от формата, золотое сечение можно использовать для улучшения ваших пропорций и обеспечения того, чтобы ваше изображение и пропорции полей были приятны для глаз.

Используя это математическое соотношение, вы можете незаметно привлечь внимание зрителя к тому месту на фотографии, которое вам нужно. Для этого разделите изображение на три части и используйте эти линии для настройки фотографии. Звучит знакомо? Это потому, что это также известно как правило третей.