16 бит hex в 14 бит со знаком int python?
Я получаю 16-битное число Hex (то есть 4 цифры) от датчика и хочу преобразовать его в целое число со знаком, чтобы действительно использовать его. В интернете есть множество кодов,которые выполняют эту работу, но с этим датчиком все немного сложнее.
На самом деле число имеет только 14 бит, первые два (слева) не имеют значения. Я пытался это сделать (в Python 3), но довольно сильно потерпел неудачу. Есть какие-нибудь предложения, как «cut» первые две цифры числа, а затем сделать rest целым числом со знаком? В таблице данных говорится, что E002 должен быть -8190 ane 1FFE должен быть +8190.
Большое спасибо!
python cut bits data-conversionПоделиться Источник Alex 17 сентября 2016 в 23:04
2 ответа
- Целое число со знаком на 5 бит?
Я все еще борюсь с побитовыми операторами, использующими Ruby.

- 16 бит hex и переменные
Я пытаюсь отправить следующий hex в NSOutputstream 0x0000000e000000010000001000003014 Я могу отправить hex, то есть 8 бит со следующим кодом: long myhex = 0x0000000e00000001; NSData *data = [[NSData alloc] initWithBytes:&myhex length: sizeof(myhex)]; [outputStream write:[data bytes]…
2
Давайте определим функцию преобразования:
>>> def f(x):
... r = int(x, 16)
... return r if r < 2**15 else r - 2**16
...
Теперь давайте проверим функцию на соответствие значениям, предоставленным таблицей данных:
>>> f('1FFE')
8190
>>> f('E002')
-8190
Обычное Соглашение для подписанных чисел состоит в том, что число отрицательно, если установлен старший бит, и положительно, если это не так. Следуя этому условию, ‘0000’ равно нулю, а ‘FFFF’ равно -1. Проблема в том, что
Следуя этому условию, ‘0000’ равно нулю, а ‘FFFF’ равно -1. Проблема в том, что int предполагает, что число положительное, и мы должны исправить это:
Для любого числа, равного или меньшего
0x7FFF, старший бит не установлен, и число является положительным. Таким образом, мы возвращаемr=int(x,16), если r<2**15.Для любого числа
r-int(x,16), которое равно или больше0x8000, мы возвращаемr - 2**16.Хотя ваш датчик может выдавать только 14-битные данные, производитель придерживается стандартного соглашения для 16-битных целых чисел.
Альтернатива
Вместо преобразования x в r и проверки значения r мы можем непосредственно проверить, установлен ли старший бит в x :
>>> def g(x):
... return int(x, 16) if x[0] in '01234567' else int(x, 16) - 2**16
. ..
>>> g('1FFE')
8190
>>> g('E002')
-8190
..
>>> g('1FFE')
8190
>>> g('E002')
-8190
Игнорирование верхних битов
Давайте предположим, что производитель не следует стандартным соглашениям и что верхние 2 бита ненадежны. В этом случае мы можем использовать модуль, %, чтобы удалить их, и после корректировки других констант в соответствии с 14-битными целыми числами мы имеем:
>>> def h(x):
... r = int(x, 16) % 2**14
... return r if r < 2**13 else r - 2**14
...
>>> h('1FFE')
8190
>>> h('E002')
-8190
Поделиться John1024 17 сентября 2016 в 23:23
1
Существует общий алгоритм расширения знака целочисленного значения val с двумя дополнениями, число битов которого равно nbits (так что самый верхний из этих битов-знаковый бит).
Этот алгоритм таков:
- рассматривайте значение как неотрицательное число и при необходимости маскируйте дополнительные биты
- инвертируйте знаковый бит, по-прежнему рассматривая результат как неотрицательное число
- вычтите числовое значение знакового бита, рассматриваемого как неотрицательное число, и получите в результате знаковое число.
 signbit) — signbit if __name__ == ‘__main__’:
print(‘sext(0xe002, 14) =’, sext(0xe002, 14))
print(‘sext(0x1ffe, 14) =’, sext(0x1ffe, 14))
signbit) — signbit if __name__ == ‘__main__’:
print(‘sext(0xe002, 14) =’, sext(0xe002, 14))
print(‘sext(0x1ffe, 14) =’, sext(0x1ffe, 14)) который при запуске показывает желаемые результаты:
sext(0xe002, 14) = -8190 sext(0x1ffe, 14) = 8190Поделиться torek 17 сентября 2016 в 23:12
Похожие вопросы:
получение нижних 16 бит Java int в виде 16-битного значения со знакомХммм. Рассмотрим эту программу, цель которой состоит в том, чтобы найти наилучший способ получить нижние 16 бит целого числа в виде целого числа со знаком. public class SignExtend16 { public static…
первый 16 бит из 32 бит hexПожалуйста, извините меня за отсутствие знаний здесь, но не мог бы кто-нибудь дать мне знать, как я могу получить первые 16 бит 32-битного числа hex.
Считывание 14 и 16 бит изображения Я пытаюсь прочитать (в BufferedImage ) 14-или 16-битное изображение по 1 или 3 каналам (оттенки серого или RGB). Я уточняю, что каждый цветовой компонент этого изображения хранится на 14 или 16…
Я уточняю, что каждый цветовой компонент этого изображения хранится на 14 или 16…
Целое число со знаком на 5 бит?Я все еще борюсь с побитовыми операторами, использующими Ruby. Получая значение 11100 (28 в базе 10) (из битового потока), я хотел бы видеть его как -4, то есть целое число со знаком на 5 бит. Как…
16 бит hex и переменныеЯ пытаюсь отправить следующий hex в NSOutputstream 0x0000000e000000010000001000003014 Я могу отправить hex, то есть 8 бит со следующим кодом: long myhex = 0x0000000e00000001; NSData *data = [[NSData…
Имя 16 и 32 бит8 бит называется byte. Как называется 16 бит? Short? Word? А как насчет 32 бит? Я знаю, что int зависит от CPU, меня интересуют универсально применимые имена.
8 бит hex строка со знаком целое числоУ меня есть 8-битное значение Hex, например: FB (-5). Теперь мне нужно целое число со знаком для этого hex. NSScanner не работает на этом месте, потому что вам нужно 4-байтовое значение hex, чтобы.
 ..
..
Конвертировать дополнять сырыми 14 бит два подписанных 16 разрядное целое числоЯ выполняю некоторую работу в embedded C с акселерометром, который возвращает данные в виде 14-битного числа дополнения 2. Я сохраняю этот результат непосредственно в uint16_t . Позже в моем коде я…
Читать OpenCV коврик 16 бит для QImage 8 бит оттенки серогоЧто я хочу сделать Файл : TIFF, 2 страницы, оттенки серого, 16 бит OpenCV : 2x мат, оттенки серого, 16 бит (CV_16UC1) Qt : 2x QImage, оттенки серого, 8 бит (Format_Greyscale8) Я хочу прочитать…
Преобразуйте бит Hash в Hex, а затем обратно в бит HashЯ создаю инструмент, который помогает находить дубликаты изображений. Чтобы использовать bktrees, мне нужно использовать бит hash, однако было бы неплохо сжать этот больший бит hash в меньший hex…
12 значное 16 разрядное число
На чтение 6 мин. Просмотров 70 Опубликовано
Коммутатор я хз пробывал ip менять.
Запустите командную строку и введите команду ipconfigЕсли в результате, который выдаст команда Вы увидите в графе IP-адрес или основной шлюз адрес вида 169.254.x.x, то очень вероятно, что проблема именно в DHCP. Вот что можно попробовать сделать в данном случае:
Зайдите в диспетчер устройств Windows 7
Кликните правой кнопкой мыши по значку Вашего сетевого адаптера, нажмите «Свойства»
Выберите пункт «Сетевой адрес» и введите в него значение из 12-значное 16-разрядное число (т. е. можно использовать цифры от 0 до 9 и буквы от A до F).
Нажмите ОК.
После этого в командной строке введите по порядку команды:Ipconfig /release
Ipconfig /renew когда ввёл эту команду выдало что типо тунгул не может что то там и перегрузил не помогло
Перезагрузите компьютер и, если проблема была вызвана именно этой причиной — скорее всего, все будет работать.
А теперь нормально поясни, что случилось, в чем дело и что ты натворил.
Коммутатор я хз пробывал ip менять.
Запустите командную строку и введите команду ipconfigЕсли в результате, который выдаст команда Вы увидите в графе IP-адрес или основной шлюз адрес вида 169.254.x.x, то очень вероятно, что проблема именно в DHCP. Вот что можно попробовать сделать в данном случае:
Зайдите в диспетчер устройств Windows 7
Кликните правой кнопкой мыши по значку Вашего сетевого адаптера, нажмите «Свойства»
Нажмите вкладку «Дополнительно»
Выберите пункт «Сетевой адрес» и введите в него значение из 12-значное 16-разрядное число (т. е. можно использовать цифры от 0 до 9 и буквы от A до F).
Нажмите ОК.
После этого в командной строке введите по порядку команды:Ipconfig /release
Ipconfig /renew когда ввёл эту команду выдало что типо тунгул не может что то там и перегрузил не помогло
Перезагрузите компьютер и, если проблема была вызвана именно этой причиной — скорее всего, все будет работать.
А теперь нормально поясни, что случилось, в чем дело и что ты натворил.
Что делать, если в Windows 7 пишет «Неопознанная сеть» — один из наиболее распространенных вопросов, возникающих у пользователей при настройке Интернета или Wi-Fi роутера, а также после переустановки Windows и в некоторых других случаях. Новая инструкция: Неопознанная сеть Windows 10 — как исправить.
Причина появления сообщения о неопознанной сети без доступа к интернету могут быть различными, постараемся рассмотреть все варианты в этой инструкции и подробно разберем как это исправить.
Если проблема возникает при подключении через роутер, то Вам подойдет инструкция Wi-Fi подключение без доступа к Интернету, данное руководство написано для тех, у кого ошибка возникает при прямом подключении по локальной сети.
Вариант первый и самый простой — неопознанная сеть по вине провайдера
Как показывает собственный опыт работы мастером, которого вызывают люди, если им потребовался ремонт компьютеров — почти в половине случаев, компьютер пишет «неопознанная сеть» без доступа к интернету в случае проблем на стороне Интернет-провайдера или при проблемах с интернет-кабелем.

Этот вариант наиболее вероятен в ситуации, когда еще сегодня утром или вчера вечером Интернет работал и все было в порядке, Вы не переустанавливали Windows 7 и не обновляли никакие драйвера, а компьютер вдруг стал сообщать о том, что локальная сеть является неопознанной. Что делать в этом случае? — просто ждать, когда проблема будет исправлена.
Способы проверить что доступ к интернету отсутствует именно по этой причине:
- Позвонить в справочную службу провайдера.
- Попробовать подключить интернет-кабель к другому компьютеру или ноутбуку, если такой имеется, независимо от установленной операционной системы — если он тоже пишет неопознанная сеть, значит дело действительно в этом.
Неверные настройки подключения по локальной сети
Еще одна распространенная проблема — наличие неверных записей в параметрах протокола IPv4 Вашего подключения по локальной сети. При этом, вы можете и не изменять ничего — иногда виной этому бывают вирусы и другое вредоносное программное обеспечение.

- Зайдите в панель управления — Центр управления сетями и общим доступом, слева выберите «Изменение параметров адаптера»
- Кликните правой кнопкой мыши по значку подключения по локальной сети и выберите в контекстном меню «Свойства»
- В открывшемся диалоговом окне свойств подключения по локальной сети вы увидите список компонентов подключения, выберите среди них «Протокол Интернета версии 4 TCP/IPv4» и нажмите кнопку «Свойства», располагающуюся тут же рядом.
- Убедитесь, что все параметры выставлены в «Автоматически» (в большинстве случаев должно быть так), или указаны правильные параметры, если Ваш провайдер требует четкого указания IP, шлюза и адреса DNS сервера.
Сохраните сделанные изменения, если они были сделаны и посмотрите, будет ли при подключении вновь появляться надпись о неопознанной сети.
Проблемы TCP/IP в Windows 7
Еще одна причина, почему появляется «неопознанная сеть» — внутренние ошибки протокола Интернета в Windows 7, в данном случае поможет сброс TCP/IP.
 Для того, чтобы сбросить настройки протокола, проделайте следующее:
Для того, чтобы сбросить настройки протокола, проделайте следующее:- Запустите командную строку от имени администратора.
- Введите команду netshintipresetresetlog.txt и нажмите Enter.
- Перезагрузите компьютер.
При выполнении этой команды переписываются два ключа реестра Windows 7, отвечающие за настройки DHCP и TCP/IP:
Драйвера для сетевой карты и появление неопознанной сети
Эта проблема обычно возникает, если вы переустановили Windows 7 и он теперь пишет «неопознанная сеть», при этом в диспетчере устройств вы видите, что все драйвера установлены (Windows установила автоматически или вы воспользовались драйвер-паком). Особенно это характерно и часто возникает после переустановки Windows на ноутбуке, ввиду некоторой специфичности оборудования портативных компьютеров.
В данном случае, убрать неопознанную сеть и пользоваться Интернетом Вам поможет установка драйверов с официального сайта производителя ноутбука или сетевой карты компьютера.

Проблемы с DHCP в Windows 7 (вы впервые подключаете интернет-кабель или кабель локальной сети и возникает сообщение неопознанная сеть)
В некоторых случаях в Windows 7 возникает проблема, когда компьютер не может получить сетевой адрес автоматически и пишет о разбираемой нами сегодня ошибке. При этом, бывает так, что до этого все работало хорошо.
Запустите командную строку и введите команду ipconfig
Если в результате, который выдаст команда Вы увидите в графе IP-адрес или основной шлюз адрес вида 169.254.x.x, то очень вероятно, что проблема именно в DHCP. Вот что можно попробовать сделать в данном случае:
- Зайдите в диспетчер устройств Windows 7
- Кликните правой кнопкой мыши по значку Вашего сетевого адаптера, нажмите «Свойства»
- Нажмите вкладку «Дополнительно»
- Выберите пункт «Сетевой адрес» и введите в него значение из 12-значное 16-разрядное число (т.е. можно использовать цифры от 0 до 9 и буквы от A до F).
- Нажмите ОК.

После этого в командной строке введите по порядку команды:
Перезагрузите компьютер и, если проблема была вызвана именно этой причиной — скорее всего, все будет работать.
Как разбить 16-разрядное целое число без знака на массив байтов в python? Ru Python
(используя python 3 здесь, есть некоторые различия в номенклатуре в 2)
Во-первых, вы можете просто оставить все как
bytes. Это совершенно верно:reg_val_msb, reg_val_lsb = struct.pack('<H', 0xABCD)bytesдопускают «распаковку кортежа» (не связанные сstruct.unpack, распаковка кортежа используется по всемуstruct.unpack). Иbytes– это массив байтов, к которым можно получить доступ по индексу, как вы хотели.b = struct.pack('<H',0xABCD) b[0],b[1] Out[52]: (205, 171)Если вы действительно хотели получить его в
array.array('B'), это все еще довольно просто:ary = array('B',struct. pack('<H',0xABCD)) # ary = array('B', [205, 171]) print("0x%X" % ary[0]) # 0xCD
pack('<H',0xABCD)) # ary = array('B', [205, 171]) print("0x%X" % ary[0]) # 0xCDДля некомплексных чисел вы можете использовать
divmod(a, b), который возвращает кортеж частного и оставшегося аргументов.В следующем примере используется
map()для демонстрационных целей. В обоих примерах мы просто говорим divmod, чтобы вернуть кортеж(a/b, a%b), where a=0xABCD and b=256.>>> map(hex, divmod(0xABCD, 1<<8)) # Add a list() call here if your working with python 3.x ['0xab', '0xcd'] # Or if the bit shift notation is distrubing: >>> map(hex, divmod(0xABCD, 256))Или вы можете просто поместить их в массив:
>>> arr = array.array('B') >>> arr.extend(divmod(0xABCD, 256)) >>> arr array('B', [171, 205])Вы можете написать свою собственную функцию следующим образом.
def binarray(i): while i: yield i & 0xff i = i >> 8 print list(binarray(0xABCD)) #[205, 171]Представление чисел в памяти компьютера
-32768Выход результатов вычислений за границы допустимого диапазона называется переполнением.
 Переполнение при вычислениях с фиксированной точкой не
вызывает
прерывания работы процессора. Машина продолжает считать, но результаты могут
оказаться неправильными.
Переполнение при вычислениях с фиксированной точкой не
вызывает
прерывания работы процессора. Машина продолжает считать, но результаты могут
оказаться неправильными.Вещественные числа. Числовые величины, которые могут принимать любые значения (целые и дробные) называются вещественными числами. В математике также используется термин «действительные числа». Решение большинства математических задач сводится к вычислениям с веществен-ными числами. Как же такие числа представляются в памяти компьютера?
Вещественные числа в памяти компьютера представляются в форме с плавающей точкой.
Форма с плавающей точкой использует представление вещественного числа R в виде произведения мантиссы m на основание системы счисления р в некоторой целой степени n, которую называют порядком:
R = m * рnНапример, число 25,324 можно записать в таком виде: 0.25324х102.
 Здесь
m=0.25324 — мантисса, n=2 — порядок. Порядок указывает, на какое количество
позиций и в
каком направлении должна «переплыть», т.е. сместиться десятичная точка в
мантиссе. Отсюда название «плавающая точка».
Здесь
m=0.25324 — мантисса, n=2 — порядок. Порядок указывает, на какое количество
позиций и в
каком направлении должна «переплыть», т.е. сместиться десятичная точка в
мантиссе. Отсюда название «плавающая точка».Однако справедливы и следующие равенства:
25,324 = 2,5324*101 = 0,0025324*104 = 2532,4*102 и т.п.Получается, что представление числа в форме с плавающей точкой неоднозначно? Чтобы не было неоднозначности, в ЭВМ используют нормализованное представление числа в форме с плавающей точкой. Мантисса в нормализован-ном представлении должна удовлетворять условию:
0,1pp.Иначе говоря, мантисса меньше единицы и первая значащая цифра — не ноль. Значит для рассмотренного числа нормализованным представлением будет: 0.25324 * 102. В разных типах ЭВМ применяются различные варианты представления чисел в форме с плавающей точкой. Для примера рассмотрим один из возможных.
 Пусть в памяти компьютера вещественное число представляется в форме с плавающей
точкой в двоичной системе счисления (р=2) и занимает ячейку размером 4 байта. В
ячейке должна содержаться следующая информация о числе: знак числа, порядок и
значащие цифры мантиссы. Вот как эта информация располагается в ячейке:
Пусть в памяти компьютера вещественное число представляется в форме с плавающей
точкой в двоичной системе счисления (р=2) и занимает ячейку размером 4 байта. В
ячейке должна содержаться следующая информация о числе: знак числа, порядок и
значащие цифры мантиссы. Вот как эта информация располагается в ячейке:
     1-й байт                    2-й байт    3-й байт   4-й байт  ± машинный порядок         М А Н Т И С С А      В старшем бите 1-го байта хранится знак числа. В этом разряде 0 обозначает плюс, 1 — минус. Оставшиеся 7 бит первого байта содержат машинный порядок.
 В
следующих
трех байтах хранятся значащие цифры мантиссы.
В
следующих
трех байтах хранятся значащие цифры мантиссы.Что такое машинный порядок? В семи двоичных разрядах помещаются двоичные числа в диапазоне от 0000000 до 1111111. В десятичной системе это соответствует диапазону от 0 до 127. Всего 128 значений. Знак порядка в ячейке не хранится. Но порядок, очевидно, может быть как положительным так и отрицательным. Разумно эти 128 значений разделить поровну между положительными и отрицательными значениями порядка. В таком случае между машинным порядком и истинным (назовем его математическим) устанавливается следующее соответствие:
Машинный порядок 0 1 2 3 … 64 65 … 125 126 127 Математический порядок -64 -63 -62 -61 … 0 1 … 61 62 63 Если обозначить машинный порядок Мр, а математический — р, то связь между ними ыразится такой формулой:
Мр = р + 64.
Итак, машинный порядок смещен относительно математического на 64 единицы и имеет только положительные значения. При выполнении вычислений с плавающей точкой процессор это смещение учитывает.
Полученная формула записана в десятичной системе. Поскольку 6410=4016 (проверьте!), то в шестнадцатеричной системе формула примет вид:
Мр16 = р16 + 4016И, наконец, в двоичной системе:
Мр2 = р2+100 00002- Теперь мы можем записать внутреннее представление числа 25,324 в форме с
плавающей точкой.
- Переведем его в двоичную систему счисления с 24 значащими цифрами. 25,32410= 11001,01010010111100011012
-
Запишем в форме нормализованного двоичного числа с плавающей точкой:
0,110010101001011110001101*10101
Здесь мантисса, основание системы счисления (210=102) и порядок
(510=1012)записаны в двоичной системе.

- Вычислим машинный порядок. Мр2 = 101 + 100 0000 = 100 0101
-
Запишем представление числа в ячейке памяти.
01000101 11001010 10010111 10001101
Это и есть искомый результат. Его можно переписать в более компактной шестнадцатеричной форме:
Для того, чтобы получить внутреннее представление отрицательного числа -25,324,достаточно в полученном выше коде заменить в разряде знака числа 0 на 1.
Получим:
11000101 11001010 10010111 10001101 А в шестнадцатеричной форме:
Никакого инвертирования, как для отрицательных чисел с фиксированной точкой, здесь не происходит.
Рассмотрим, наконец, вопрос о диапазоне чисел, представимых в форме с плавающей точкой. Очевидно, положительные и отрицательные числа расположены симметрично относительно нуля.
0,111111111111111111111111*1021111111 Следовательно, максимальное и минимальное числа равны между
собой по модулю: Rmax = |Rmin|. Наименьшее по абсолютной величине число равно
нулю. Чему же равно Rmax? Это число с самой большой мантиссой и самым большим
порядком:
Следовательно, максимальное и минимальное числа равны между
собой по модулю: Rmax = |Rmin|. Наименьшее по абсолютной величине число равно
нулю. Чему же равно Rmax? Это число с самой большой мантиссой и самым большим
порядком:Если перевести в десятичную систему, то получится
Rmax = (1 — 2-24) * 264 = 1019Очевидно, что диапазон вещественных чисел значительно шире диапазона целых чисел. Если в результате вычислений получается число по модулю большее, чем Rmax, то происходит прерывание работы процессора. Такая ситуация называется переполнением при вычислениях с плавающей точкой. Наименьшее по модулю ненулевое значение равно:
(1/2) * 2-64=2-66.Любые значения, меньшие данного по абсолютной величине, воспринимаются процессором как нулевые.
Как известно из математики, множество действительных чисел бесконечно и непрерывно.
N = 2t * ( U — L+ 1) + 1. Множество же вещественных чисел, представимых в памяти ЭВМ в форме с
плавающей точкой, является ограниченным и дискретным. Каждое следующее значение
получается прибавлением к мантиссе предыдущего единицы в последнем (24-м)
разряде. Количество вещественных чисел, точно представимых в па-мяти машины,
вычисляется по формуле:
Множество же вещественных чисел, представимых в памяти ЭВМ в форме с
плавающей точкой, является ограниченным и дискретным. Каждое следующее значение
получается прибавлением к мантиссе предыдущего единицы в последнем (24-м)
разряде. Количество вещественных чисел, точно представимых в па-мяти машины,
вычисляется по формуле:Здесь t — количество двоичных разрядов мантиссы; U — максимальное значение математического порядка; L — минимальное значение порядка. Для рассмотренного нами варианта (t = 24, U = 63, L = -64) получается:
N = 2 146 683 548.Все же остальные числа, не попадающие в это множество, но находящиеся в диапазоне допустимых значений, представляются в памяти приближенно (мантисса обрезается на 24-м разряде). А поскольку числа имеют погрешности, то и результаты вычислений с этими числами также будут содержать погрешность. Из сказанного следует вывод: вычисления с вещественными числами в компьютере выполняются приближенно.

Вопросы и задания
- Что такое форма с фиксированной точкой? Для представления каких чисел в компьютере она используется?
- Как в форме с фиксированной точкой представляются целые положительные и отрицательные числа?
1. Способы представления чисел в ЭВМ — Теория — 1.4 Кодирование чисел в ЭВМ
«Числа в прямом коде»
Вопрос о кодировании чисел возникает по той причине, что в машину нельзя либо нерационально вводить числа в том виде, в котором они изображаются человеком на бумаге. Во-первых, нужно кодировать знак числа. во-вторых, по различным причинам, которые будут рассмотрены ниже, приходится иногда кодировать и остальную часть числа.
Представление знаковых чисел
Для того, чтобы компьютер оперировал как положительными, так и отрицательными числами, в PC машинного представления числа необходимо ввести знаковую часть.

В двоичной СС знак представляется одним битом, принимающим значение «0» в случае положительного числа, и «1» — в случае отрицательного.
Обычно это крайний левый бит в представлении числа. Остальные — информационные разряды — представляют код модуля числа.
Т.о. компьютер имеет возможность манипулировать как знаковыми, так и беззнаковыми числами.
Для хранения числовых данных в КС используются устройства, называемые регистрами.
С учётом рассматриваемых ранее структур единиц информации вводят понятие формата данных.
Фактически регистр является аппаратной базой для представления числовых данных.
В компьютерах IBM PC AT машинное слово является 16-разрядным. Числовые данные могут иметь длину слова (16 бит) (word), полуслова (8 бит=байт) (byte), 32 бита — 2 слова (double word) — короткое целое (short integer).

Существует также 64 бита — учетверённое слово (guard word) — длинное целое (long int.).
В связи с тем, что алгоритмы выполнения компьютерных операций в КС имеют свою специфику, возникает проблема представления отрицательных чисел. Её решают за счёт особых способов кодирования модуля числа.
Замечание! Положение точки никогда явно не указывается, а только подразумевается.
Простейшим машинным кодом является прямой код, который получается при кодировании в числе только знаковой информации.
Прямым кодом отрицательного числа называется его изображение в естественной форме, у которого в знаковом разряде проставляется единица. Прямой код положительного числа совпадает с его обычным изображением в естественной форме.
Данное определение позволяет дать прямому коду такую интерпретацию:
Приведенное выше аналитическое выражение показывает, что прямой код дробного числа (J = 0) формируется как сумма абсолютной величины исходного числа и единицы.
 Прямой код целого числа (J = n — 1, причем знаковым является крайний левый разряд) формируется как сумма 10 n-1 + | X |.
Прямой код целого числа (J = n — 1, причем знаковым является крайний левый разряд) формируется как сумма 10 n-1 + | X |.Пример. В прямом коде дробные двоичные числа X1 = +0.1100112 и X2 = -0.1100112 будут иметь вид [X1]пр = 0.110011; [X2]пр = 1.110011. Используя 8-разрядную сетку (J = 7), иными словами имея 8 разрядов для представления числа, в прямом коде целые числа X1 = +1100112 и X2 = -1100112 будут иметь вид [X1]пр = 00110011; [X2]пр = 10110011.
Прямой код получил широкое распространение в ЭВМ вследствие своей простоты. В нем удобно хранить числа в памяти, перемножать числа. Но он также обладает некоторыми недостатками. Во-первых при использовании прямого кода появляется возможность получения +0 и -0. Во-вторых, как оказалось, он плохо приспособлен для сложения чисел.
 Действительно, при алгебраическом сложении чисел в прямом коде требуется выполнить четыре действия:
Действительно, при алгебраическом сложении чисел в прямом коде требуется выполнить четыре действия:1. Сравнить знаки слагаемых.
2. Сравнить слагаемые по модулю при неравенстве их знаков.
3. Выполнить соответствующую арифметическую операцию: сложение при равенстве знаков и вычитание из большего по модулю слагаемого меньшего при неравенстве их знаков.
4. Присвоить алгебраической сумме знак большего по модулю слагаемого.
Так как операция сложения значительно проще вычитания, то возникает вопрос: нельзя ли каким-то образом алгебраическое сложение свести к арифметическому? Оказывается, это возможно за счет несколько более сложного кодирования.
«Числа в обратном коде»
При замене операции вычитания сложением, помимо дополнения, можно использовать и другое вспомогательное число — инверсию отрицательного операнда, возникающую в результате замены его цифр взаимно обратными.
 Поскольку инверсия меньше дополнения на единицу младшего разряда, то для получения правильной разности необходимо производить соответствующую коррекцию суммы вспомогательных чисел.
Поскольку инверсия меньше дополнения на единицу младшего разряда, то для получения правильной разности необходимо производить соответствующую коррекцию суммы вспомогательных чисел.Таким образом, обратным кодом отрицательного двоичного числа будем называть его дополнение по модулю до Xmax, получаемое по следующему правилу: в знаковом разряде проставляется единица, а во всех остальных разрядах цифры заменяются на взаимно обратные.
Обратный код положительного числа совпадает с его прямым кодом. Аналитически обратный код определяется следующим соотношением:
С учетом цифры Хmax = 10J+1 — 10—F. Основное достоинство обратного кода по сравнению с дополнительным состоит в простоте процесса его формирования.
Пример. В обратном коде дробные двоичные числа X1 = +0.
 1100112 и X2 = -0.1100112 будут иметь вид [X1]обр = 0.110011; [X2]обр = 1.001100. Используя 8-разрядную сетку (J = 7) в дополнительном коде целые числа X1 = +1100112 и X2 = -1100112 будут иметь вид [X1]обр = 00110011; [X2]обр = 11001100.
1100112 и X2 = -0.1100112 будут иметь вид [X1]обр = 0.110011; [X2]обр = 1.001100. Используя 8-разрядную сетку (J = 7) в дополнительном коде целые числа X1 = +1100112 и X2 = -1100112 будут иметь вид [X1]обр = 00110011; [X2]обр = 11001100.«Числа в дополнительном коде»
Идея замены вычитания сложением основана на применении некоторых вспомогательных чисел, однозначно связанных с исходными отрицательными числами. Эти вспомогательные числа находятся как дополнение модулей заданных отрицательных операндов до некоторого граничного числа
Проиллюстрируем сказанное на простейшем примере с использованием десятичной системы счисления. Пусть имеется некоторая вычислительная машина, которая оперирует двухразрядными целыми числами, меньшими сотни: 0 ≤ Xмаш≤ Xmax = 99.
 Граничное число определяется как Xгр = 99 + 1 = 100 = 102 . Далее требуется алгебраически сложить числа Х1 = 84 и Х2 = -63. В соответствии с вышеизложенным, второе слагаемое поскольку оно отрицательно, заменится дополнением до Хгр = 102, т. е. положительным числом [X2]доп = 37. Далее выполняется арифметическое сложение чисел Х1 и [X2]доп:
Граничное число определяется как Xгр = 99 + 1 = 100 = 102 . Далее требуется алгебраически сложить числа Х1 = 84 и Х2 = -63. В соответствии с вышеизложенным, второе слагаемое поскольку оно отрицательно, заменится дополнением до Хгр = 102, т. е. положительным числом [X2]доп = 37. Далее выполняется арифметическое сложение чисел Х1 и [X2]доп:Поскольку числа не могут быть более сотни, то цифра в разряде сотен в сумме автоматически пропадает. Оставшуюся часть суммы можно считать результатом алгебраического сложения исходных чисел Х1 и Х2. Действительно, прямое вычитание подтверждает правильность конечного результата: 84 — 63 = 21. Другого исхода не могло и быть, так как вначале в соответствии с приведенной выше формулой мы добавили ко второму слагаемому сотню, чтобы получить нужное дополнение
а затем лишнюю сотню вычли из результата простым отбрасыванием появившейся и недопустимой в данной машине единицы в разряде сотен.

На первый взгляд кажется, что рассмотренный код не дает желаемого эффекта, так как нахождение дополнения отрицательного числа по приведенной выше формуле все равно происходит при помощи вычитания. Но это не так. Тот факт, что вычитание производится всегда из одного и того же и, главное, «круглого» числа, дает возможность избежать трудностей обычного вычитания.
Для дальнейшего изложения метода необходимо ввести некоторые новые понятия. Так взаимно обратными будем называть цифры, которые являются друг для друга дополнением до числа, на единицу меньшего, чем основание системы счисления. Чтобы проиллюстрировать сказанное, запишем в ряд все цифры используемой системы счисления, а затем под этим рядом запишем эти же цифры, но в обратном порядке, как это показано ниже:
Заметим одно замечательное свойство каждой пары цифр, расположенных относительно друг друга по вертикали при такой записи.
 Оказывается, что сумма любой из этих пар равна старшей цифре системы счисления. Поскольку такие пары образуются при записи всех цифр сначала в прямом, а затем в обратном порядке, будем называть цифры, дающие в сумме старшую цифру, взаимно обратными. Замена в некотором отрицательном числе всех цифр на взаимно обратные равносильна сложению исходного числа с |Xmax|. Используя понятие взаимно обратных цифр, можно дать правило нахождения дополнения отрицательных чисел без использования вычитания: для получения дополнения отрицательного числа следует все цифры исходного числа заменить на взаимно обратные и к полученному таким образом «обратному» числу (инверсному изображению) добавить единицу младшего разряда.
Оказывается, что сумма любой из этих пар равна старшей цифре системы счисления. Поскольку такие пары образуются при записи всех цифр сначала в прямом, а затем в обратном порядке, будем называть цифры, дающие в сумме старшую цифру, взаимно обратными. Замена в некотором отрицательном числе всех цифр на взаимно обратные равносильна сложению исходного числа с |Xmax|. Используя понятие взаимно обратных цифр, можно дать правило нахождения дополнения отрицательных чисел без использования вычитания: для получения дополнения отрицательного числа следует все цифры исходного числа заменить на взаимно обратные и к полученному таким образом «обратному» числу (инверсному изображению) добавить единицу младшего разряда.Справедливость правила можно проиллюстрировать на рассмотренном выше примере. Действительно,
что и требовалось получить. Таким образом, в десятичной машине для образования дополнения любого числа достаточно иметь в памяти пять пар ВОЦ и уметь производить соответствующую замену в отрицательных числах.

Аналогично, вместе с тем значительно проще, эта процедура выполняется в машинах, использующих двоичную систему счисления. В этом случае нужна только одна пара ВОЦ: 0 и 1. Очевидно, что граничным числом в случае дробных чисел будет единица. Учитывая цифру знакового разряда, которая для отрицательных чисел всегда равна 1, следует считать Хгр равным двум. В случае целых чисел граничное число всегда равно целой степени двух, равной весу не существующего в данном числе разряда, расположенного слева от знаковой цифры.
Поскольку вспомогательные числа (дополнения) связанны с исходными отрицательными числами однозначным способом, то можно считать их заданными исходными числами, но некоторым образом закодированными. Таким образом, можно говорить о дополнительном коде машинных чисел и дать следующее его определение: дополнительным кодом отрицательного двоичного числа называется его дополнение до граничного числа. Оно получается по следующему правилу: в знаковом разряде записывается единица, а во всех других разрядах цифры заменяются на взаимно обратные, после чего ко младшему разряду числа добавляется единица.

Дополнительный код положительного числа совпадает с его прямым кодом.
Аналитически дополнительный код определяется следующим выражением:
Пример. В дополнительном коде дробные двоичные числа X1 = +0.1100112 и X2 = -0.1100112 будут иметь вид [X1]доп = 0.110011; [X2]доп = 1.001100 + 0.000001 = 1.001101. Используя 8-разрядную сетку (J = 7) в дополнительном коде целые числа X1 = +1100112 и X2 = -1100112 будут иметь вид [X1]доп = 00110011; [X2]доп = 11001101.
Переход от дополнительного кода отрицательного числа к его прямому коду никаких трудностей не вызывает: нужно из исходного кода вычесть единицу младшего разряда, после чего во всех разрядах, за исключением знакового, заменить цифры на взаимно обратные.
 Однако практически производить такой переход легче по другому правилу: вначале заменить все цифры, за исключением знаковой, на взаимно обратные, после чего добавить единицу к младшему разряду.
Однако практически производить такой переход легче по другому правилу: вначале заменить все цифры, за исключением знаковой, на взаимно обратные, после чего добавить единицу к младшему разряду.Ниже представлена диаграмма, демонстрирующая на примере числа, записанные в дополнительном и прямом коде. Первые шестнадцать чисел начиная с нижней части диаграммы против часовой стрелки (0 : 15) кодируют идентичные числа в прямом и обратном коде. Если продолжать двигаться в том же направлении до нижней части диаграммы, то изображенные числа будут кодировать возрастающие числа в прямом коде (16 : 31). Если же двигаться от нижней части диаграммы по часовой стрелке до верхней части диаграммы, то проходимые таким образом двоичные числа будут кодировать в дополнительном коде уменьшающиеся числа (-1 : -16).
«5-разрядные числа в дополнительном коде»
Рисунок 1.4. Модифицированные коды.

Модифицированные коды (МК) — коды, в которых знак изображается двумя одинаковыми цифрами. МК используются только в процессе выполнения операции. Знаковые разряды обрабатываются так же, как и обычные числовые разряды. Появление в знаковых разрядах МК разных цифр (01 — при сложении положительных чисел, 10 — при сложении отрицательных чисел) свидетельствует о ПРС.
МК позволяет формировать правильный знак результата даже в случае ПРС.
A = 00.1112 = +710
B = 00.1112 = +710
C = A + B
(Правила сложения смотрите в разделе 3.1)
01 — это показатель некорректного выполнения операции, переполнения разрядной сетки.
Правильный вариант:
где 00 = +
1110 = 14 ⇒ полчен верный результат.

MATLAB — Числа — CoderLessons.com
MATLAB поддерживает различные числовые классы, которые включают целые числа со знаком и без знака, а также числа с плавающей запятой одинарной и двойной точности. По умолчанию MATLAB сохраняет все числовые значения как числа с плавающей запятой двойной точности.
Вы можете сохранить любое число или массив чисел в виде целых чисел или чисел одинарной точности.
Все числовые типы поддерживают базовые операции с массивами и математические операции.
Преобразование в различные числовые типы данных
MATLAB предоставляет следующие функции для преобразования в различные числовые типы данных —
функция Цель двойной Преобразует в число с двойной точностью не замужем Преобразует в число с одинарной точностью int8 Преобразует в 8-разрядное целое число со знаком int16 Преобразует в 16-разрядное целое число со знаком int32 Преобразует в 32-разрядное целое число со знаком int64 Преобразует в 64-разрядное целое число со знаком uint8 Преобразует в 8-разрядное целое число без знака uint16 Преобразует в 16-разрядное целое число без знака uint32 Преобразует в 32-разрядное целое число без знака uint64 Преобразует в 64-разрядное целое число без знака пример
Создайте файл сценария и введите следующий код —
Live Demo
x = single([5.
 32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5Когда вы запускаете файл, он показывает следующий результат —
x = 39.900 26.025 47.100 x = 39.900 26.025 47.100 x = 38 23 45 x = 38 23 45 x = 38 23 45 x = 38 23 45
пример
Давайте расширим предыдущий пример немного подробнее. Создайте файл сценария и введите следующий код —
Live Demo
x = int32([5.32 3.47 6.28]) .* 7.5 x = int64([5.32 3.47 6.28]) .* 7.5 x = num2cell(x)
Когда вы запускаете файл, он показывает следующий результат —
x = 38 23 45 x = 38 23 45 x = { [1,1] = 38 [1,2] = 23 [1,3] = 45 }Самые маленькие и самые большие целые числа
Функции intmax () и intmin () возвращают максимальное и минимальное значения, которые могут быть представлены всеми типами целых чисел.

Обе функции принимают в качестве аргумента целочисленный тип данных, например, intmax (int8) или intmin (int64), и возвращают максимальное и минимальное значения, которые вы можете представить в целочисленном типе данных.
пример
В следующем примере показано, как получить наименьшее и наибольшее значения целых чисел. Создайте файл сценария и напишите в нем следующий код —
Live Demo
% displaying the smallest and largest signed integer data str = 'The range for int8 is:\n\t%d to %d '; sprintf(str, intmin('int8'), intmax('int8')) str = 'The range for int16 is:\n\t%d to %d '; sprintf(str, intmin('int16'), intmax('int16')) str = 'The range for int32 is:\n\t%d to %d '; sprintf(str, intmin('int32'), intmax('int32')) str = 'The range for int64 is:\n\t%d to %d '; sprintf(str, intmin('int64'), intmax('int64')) % displaying the smallest and largest unsigned integer data str = 'The range for uint8 is:\n\t%d to %d '; sprintf(str, intmin('uint8'), intmax('uint8')) str = 'The range for uint16 is:\n\t%d to %d '; sprintf(str, intmin('uint16'), intmax('uint16')) str = 'The range for uint32 is:\n\t%d to %d '; sprintf(str, intmin('uint32'), intmax('uint32')) str = 'The range for uint64 is:\n\t%d to %d '; sprintf(str, intmin('uint64'), intmax('uint64'))Когда вы запускаете файл, он показывает следующий результат —
ans = The range for int8 is: -128 to 127 ans = The range for int16 is: -32768 to 32767 ans = The range for int32 is: -2147483648 to 2147483647 ans = The range for int64 is: 0 to 0 ans = The range for uint8 is: 0 to 255 ans = The range for uint16 is: 0 to 65535 ans = The range for uint32 is: 0 to -1 ans = The range for uint64 is: 0 to 18446744073709551616
Самые маленькие и самые большие числа с плавающей точкой
Функции realmax () и realmin () возвращают максимальное и минимальное значения, которые могут быть представлены числами с плавающей запятой.

Обе функции при вызове с аргументом ‘single’ возвращают максимальное и минимальное значения, которые вы можете представить с помощью типа данных с одинарной точностью, а при вызове с аргументом ‘double’ возвращают максимальное и минимальное значения, которые вы можете представить с помощью тип данных двойной точности.
пример
В следующем примере показано, как получить наименьшее и наибольшее числа с плавающей запятой. Создайте файл сценария и напишите в нем следующий код —
Live Demo
% displaying the smallest and largest single-precision % floating point number str = 'The range for single is:\n\t%g to %g and\n\t %g to %g'; sprintf(str, -realmax('single'), -realmin('single'), ... realmin('single'), realmax('single')) % displaying the smallest and largest double-precision % floating point number str = 'The range for double is:\n\t%g to %g and\n\t %g to %g'; sprintf(str, -realmax('double'), -realmin('double'), ... realmin('double'), realmax('double'))Когда вы запускаете файл, он показывает следующий результат —
AVR — как избавиться от чисел с плавающей точкой | avr
Одно из сильных ограничений AVR (на платформе MCS51 это сказывается не так) — быстрый расход памяти при написании программ на Си.

Что поделаешь, за удобства Си и скорость RISC надо платить. Еще больший соблазн — использование для вычислений (например, при измерении напряжений с помощью ADC) чисел float (числа с плавающей запятой). Несмотря на то, что эти вычисления не точны, их слишком просто и удобно применять — можно делить и умножать, не задумываясь о переполнении, и легко представлять результаты вычисления в формате, понятном человеку.
Но плата за float слишком высока — линкер добавляет код библиотек математики, и память программ кончается очень быстро. Другое ограничение — вычисления с float выполняются слишком медленно (если конечно не используется аппаратный перемножитель типа [1]). Если нет возможности реализовать алгоритм программы с применением чисел float (из-за вышеуказанных ограничений по объему кода и скорости), одним из вариантов решения проблемы является переход на числа с фиксированной запятой. Их математические операции (вычитание, сложение, деление, умножение) ничем не отличаются от математических операций с простыми целыми числами, код получается компактный и быстрый.

Число с фиксированной запятой (обычно байт или слово из двух байт) состоит из целой части (находится в старших битах 8 или 16-разрядного числа) и дробной части (находится в младших битах). Пример числа с фиксированной запятой указан на рисунке, с разрядностью в 8 бит (1 байт).
Перед использованием чисел с фиксированной запятой главное — выбрать разрядность числа (байт или слово), и также выбрать положение запятой. С разрядностью вроде все понятно — если возьмем слово (16 бит), вычисления будут точнее, но скорость упадет и объем кода вырастет (и то и другое не меньше чем в 2 раза), а если возьмем байт (8 бит), то получим максимальное быстродействие и самый маленький код, но ухудшится точность. Как обычно, нужен компромисс, и Ваша задача — принять верное решение. Положение запятой никак не влияет на объем кода и быстродействие при математических операциях. Она просто распределяет соотношение точности между целой и дробной частью.
 5 = 30/32). Значение байта при этом будет 100.11110b или 0x9E.
5 = 30/32). Значение байта при этом будет 100.11110b или 0x9E.При вычислениях с фиксированной запятой (как и с простыми вычислениями на целых числах) нужно применять особые правила:
1. В результате сложения двух чисел возможно появление дополнительного разряда. Это происходит, если произошло переполнение. Если возможность переполнения нужно учитывать, то дополнительный 1 бит числа надо где-то хранить.
2. Результат умножения двух 8-битных чисел хранить в 16-разрядном числе, двух 16-битных в 32-разрядном, и т. п. (разрядность при умножении складывается).
3. При делении (малого числа на большое особенно) нужно предварительно делимое умножить на константу. Самое простое — сдвинуть число влево на нужное число раз (каждый сдвиг умножает на 2), поместить сдвинутый результат в число вдвое большей разрядности, и потом уже спокойно делить. В результате получим число с фиксированной запятой. Например, если делим 8-разрядное целое делимое, сдвинутое влево на 5 разрядов (получили 16-разрядное делимое), на целый делитель, то получаем дробное 16-битное число с фиксированной запятой, где запятая находится между 5 и 4 разрядами.

4. Лучше как можно больше пользоваться предварительно вычисленными на этапе компилирования константами, чтобы убрать код, который будет их генерировать. Например, если мы должны сравнить напряжение на аккумуляторе с напряжением 1.05 вольт, то это напряжение 1.05 вольт лучше сразу представить в нужном формате и определить директивой #define.
Когда нужно отобразить число с фиксированной запятой как набор десятичных цифр, действуют по простому алгоритму:
— сначала берут целую часть, и преобразуют её в символьный вид обычным образом.
— за целой частью рисуют запятую (или точку).
— берут дробную часть, приводят её к десятичной дроби, просто домножая и числитель, и знаменатель дробной части на дробное число (при этом значение дроби, как мы знаем, не изменится) — константу. Эта константа выбирается так, чтобы знаменатель стал числом — степенью десятки, а не двойки — при этом получится десятичная дробь. Фраза «домножая на дробное число» означает набор целочисленных операций (сначала умножить на целую константу, а потом разделить на целую константу), результат которых и будет это умножение на дробное число. При операциях умножения и деления либо множитель будет четным, либо делитель, либо они оба — и множитель, и делитель, будут нечетными (мы ведь формируем таким образом умножение на нецелое число). В качестве четной удобно использовать константу, являющуюся степенью двойки (2, 4, 8 и т. д.), потому что умножение и деление на эту константу заменяется простым сдвигом влево и вправо соответственно.
— после этого полученное значение числителя переводим в набор десятичных цифр и приписываем их после запятой.Чтобы пояснить эти «премудрости» возьмем все тот же пример — переведем дробное число с фиксированной запятой 100.11110b (== 0x9E, наши 4.9375 вольта) в символьное представление:
— целая часть у нас равна 100b, т. е. 4, рисуем цифру 4
— рисуем за целой частью дробную точку: 4.
— берем дробную часть 11110b. Она равна 30, т. е. наша дробь — числитель 30, а знаменатель 32. Наша задача — подобрать такое дробное число, чтобы при его умножении на знаменатель 32 получилось число, которое можно представить степенью десятки, причем какая была степень десятки, столько десятичных знаков после запятой и получим. Пусть надо получить 3 десятичных знака после запятой, т. е. знаменатель 32 приводим к 1000. Число, на которое нужно домножить и числитель, и знаменатель, равно 1000/32 = 31.25. Отлично, но как умножить на дробное число, имея в распоряжении только целочисленную арифметику? Все просто — умножаем сначала на 125, а потом делим на 4 (т. к. 125/4 равно 31.25). Именно в таком порядке — сначала умножение (понадобится временное 16-битное число для хранения результата умножения), а потом деление, чтобы не потерять точность при отбрасывании остатка деления. На 125 умножаем как обычно, а делим на 4, сдвигая число на 2 бита вправо. Итак, 30 * 31.25 = (30 * 125) / 4 = 3750 / 4 = 937.5, округляем до 938. Таким образом, дробь 30/32 превратилась в дробь 938/1000.
— числитель 938 дописываем после запятой, получаем 4.938.При подборе констант для умножения/деления удобно использовать смекалку и старые добрые электронные таблицы Microsoft Excel.
[Ссылки]
1. AVR201: использование аппаратного перемножителя AVR.
Двоичное слово — обзор
III Коды постоянного веса
A Код постоянного веса (CW) с параметрами n , d , w — это набор C двоичных слов длиной n все имеют вес w , так что расстояние между любыми двумя кодовыми словами составляет не менее d . Все нетривиальные ( n , d , w ) коды CW имеют d ≤ 2 w . Пусть A ( n , d , w ) будет наибольшим количеством кодовых слов в любом коде CW с этими параметрами.Тогда классическая проблема состоит в том, чтобы определить это число или найти наилучшие верхние и нижние границы для A ( n , d , w ).
Двоичные коды CW нашли применение в задачах синхронизации, в таких областях, как системы связи с оптическим кодированием и множественным доступом (CDMA), связь с расширенным спектром со скачкообразной перестройкой частоты, модельное радио, проектирование сигналов радаров и гидролокаторов, а также построение последовательностей протоколов. для многопользовательского канала коллизий без обратной связи.Коды с постоянным весом по сравнению с другими алфавитами привлекли некоторое внимание, но пока что было немного приложений. Мы будем обсуждать только двоичные коды CW.
Коды с постоянным весом были тщательно изучены, и хорошей ссылкой на них является MacWilliams and Sloane (1977). Эрик Рейнс и Нил Слоан ведут таблицу наиболее известных нижних границ для A ( n , d , w ) на веб-сайте: http://www.research.att.com/njas/ коды / Andw /. Мы представим обзор этой темы с акцентом на связи с дизайном.
Поскольку сумма любых двух двоичных слов с одинаковым весом всегда имеет четный вес, мы имеем A ( n , 2δ — 1, w ) = A ( n , 2δ, w ). С этого момента мы будем предполагать, что расстояние d четное. У нас также есть A ( n , d , w ) = A ( n , d , n — w ), поскольку когда два слова находятся на расстоянии d отдельно, так же их дополнения.Это означает, что нужно рассматривать только случай w ≤ n /2.
Связь между кодами CW и проектами очевидна. С точки зрения наборов, код CW — это просто набор из w подмножеств из набора n , где пересечение любых двух подмножеств w содержит не более t = w − d2 элементов. Эквивалентно, CW-код — это частичная система Штейнера Sw − d2 + 1, w, n. Тогда мы имеем
A (n, d, w) ≤n (n − 1)… (n − w + d / 2) w (w − 1)… (d / 2)
с равенством тогда и только тогда, когда система Штейнера S (w − d2 + 1, w, n) существует.
Интерес к кодам CW также связан с проблемой поиска линейных (или нелинейных) кодов ( n , M , d ) максимального размера M . Очевидно, что A ( n , d , w ) является верхней границей количества слов данного веса в таком максимальном коде. И наоборот, такие коды (или их смежные классы) могут давать нижние границы для A ( n , d , w ). В частности, более сильная версия границы Хэмминга (приведенная в разделе о совершенных кодах) была первоначально доказана с использованием A ( n , 2 t + 2,2 t + 1).
A ( n , 2 t + 2,2 t + 1) — это просто количество блоков в максимальном частичном S ( t + 1,2 t + 1 , n ) конструкция или упаковка. Если C — это код с исправлением ошибок t , то для любого c ∈ C количество блоков в соседней упаковке ∣ NS ( c ) ∣ ≤ A ( n , 2 т + 2,2 т + 1).Количество слов, которые находятся на расстоянии t + 1 от c , но не на расстоянии t от любого другого кодового слова, равно
(nt + 1) — (2t + 1t + 1) | NS (c) | ≥ ( nt + 1) — (2t + 1t + 1) A (2t + 2,2t + 1).
Каждое такое слово находится на расстоянии t + 1 от не более ⌊ n / t + 1⌋ других кодовых слов. Таким образом, суммируя все c ∈ C , каждое такое слово считается не более указанного количества раз. Это дает более сильную версию границы Хэмминга:
| C | ((∑i = 0t (ni)) + (nt + 1) — (2t + 1t + 1) A (n, 2t + 2,2t + 1 ) ⌊N / (t + 1) ⌋) ≤2n.
Коды с постоянным весом не могут быть линейными, поскольку это означало бы, что нулевой вектор был в коде, но можно иметь код, в котором все ненулевые слова имеют одинаковый вес. Эти коды иногда называют линейными эквидистантными кодами . Двойник кода Хэмминга (также называемый симплексным кодом ) является примером такого кода. Фактически было доказано, что единственные такие коды формируются путем взятия нескольких копий симплексного кода. Доказательства того, что все такие коды являются обобщенными симплексными кодами, явно вытекают из теории кодирования (Bonisoli, 1983), а также неявно из результатов по планам и системам множеств (Teirlinck, 1980).Существует тесная связь между линейными эквидистантными кодами и конечной геометрией. Слова симплексного кода соответствуют гиперплоскостям проективного пространства [более GF (2)] так же, как слова веса 3 в коде Хэмминга соответствуют строкам в этом проективном пространстве. [О связях между кодами и конечной геометрией см. Black and Mullin (1976).]
Другой вариант кодов CW — это оптические ортогональные коды (OOC), которые были применены в оптических системах связи CDMA.Вкратце, ( n , w , t a , t b ) OOC — это код CW, C , длиной n и весом w . такое, что для любого c = ( c 0 , c 1 ,…, c n −1 ) ∈ C , и каждое y ∈ C , c ≠ y и каждый i ≢ 0 (mod n ),
(1) ∑j = 0n − 1cjcj + i≤ta,
и
(2) ∑j = 0n −1cjyj + i≤tc.
Уравнение (1) является свойством автокорреляции, а уравнение. (2) — свойство взаимной корреляции. Большинство исследований было сосредоточено на случае, когда t a = t c = t , и в этом случае мы ссылаемся на ( n , w , t ) OOC. Опять же, можно изменить эти свойства в терминах (частичных) конструкций или упаковок. В этом случае OOC представляет собой набор из w подмножеств целых чисел (mod n ), так что для подмножеств c , b ∈ C ,
(3) c + i∩c + j≤tai ≠ j,
и
(4) c + i∩b + j≤tc.
Здесь c + i = { x + i (mod n ) ∣ x ∈ c }.
Код OOC эквивалентен циклическому расчету или упаковке. Код или упаковка называется циклической, если каждый циклический сдвиг кодового слова (или блока) является другим кодовым словом. Набор всех циклических сдвигов кодового слова называется орбитой . Представителя с этой орбиты часто называют базовым блоком. OOC ( n , w , t ) представляет собой набор базовых блоков для циклической (частичной) конструкции или упаковки S ( t + 1, w , n ) (при условии т < т ).И наоборот, при таком циклическом частичном S ( t + 1, w , n ) дизайн или упаковка, можно сформировать ( n , w , t ) OOC, взяв один репрезентативный блок или кодовое слово с каждой орбиты.
Что означает 12- или 16-битное разрешение?
Что такое разрешение?
Разрешение в этом контексте относится к преобразованию аналогового напряжения в цифровое значение в компьютере (и наоборот).Компьютер — это цифровая машина, поэтому число хранится в виде последовательности нулей и единиц. Если вы сохраняете цифровое 2-битное число, вы можете хранить 4 разных значения: 00, 01, 10 или 11. Теперь предположим, что у вас есть устройство, которое преобразует аналоговое напряжение от 0 до 10 вольт в 2-битное цифровое значение. для хранения в компьютере. Это устройство выдаст следующие цифровые значения:
Напряжение 2-битное цифровое представление от 0 до 2.5
от 2,5 до 5
от 5 до 7,5
от 7,5 до 1000
01
10
11Таким образом, в этом примере 2-битное цифровое значение может представлять 4 разных числа, а диапазон входного напряжения от 0 до 10 вольт разделен на 4 части, что дает разрешение по напряжению 2,5 вольта на бит. 3-битное цифровое значение может представлять 8 (2 3 ) различных чисел. 12-битное цифровое значение может представлять 4096 (2 12 ) различных чисел.16-битное цифровое значение может представлять 65536 (2 16 ) различных чисел. В этот момент вам может прийти в голову, что цифровой вход можно рассматривать как 1-битный аналого-цифровой преобразователь. Низкое напряжение дает 0, высокое — 1.
В случае LabJack U12, несимметричный аналоговый вход имеет диапазон напряжения от -10 вольт до +10 вольт (общий диапазон 20 вольт) и возвращает 12-битное значение. Это дает разрешение по напряжению 20/4096 или 0,00488 вольт на бит (4,88 мВ / бит).
Что значит сказать, что устройство является 12-битным, 16-битным или 24-битным?
Когда вы видите устройства сбора аналогового ввода от различных производителей, называемые 12-битными, 16-битными или 24-битными, это обычно означает, что у них есть АЦП (аналого-цифровой преобразователь), который возвращает такое количество бит. Когда микросхема АЦП возвращает 16 бит, это, вероятно, лучше, чем 12-битный преобразователь, но не всегда. Тот простой факт, что преобразователь возвращает 16 бит, мало говорит о качестве этих бит.
Трудно просто указать «разрешение» данного устройства. Что нам нравится делать, так это предоставлять фактические данные измерений, которые говорят вам о разрешении устройства, включая типичный собственный шум.
Если вы посмотрите на устройство под названием «24-битное» только потому, что оно имеет преобразователь, который возвращает 24 бита данных на выборку, вы обнаружите, что оно обычно обеспечивает 20 эффективных бит или 18 бит без шума (например, UE9 -Pro). U6-Pro и T7-Pro обеспечивают одни из лучших характеристик среди 24-битных АЦП, при этом они работают с эффективностью около 22 бит или без шума на 20 бит.Вы увидите, что с этими устройствами мы можем упомянуть, что у них есть 24-битный АЦП (это то, что люди ищут и ищут), но мы стараемся не называть их «24-битными» и стараемся придерживаться эффективного разрешения.
Еще одна интересная особенность вашего типичного 24-битного сигма-дельта преобразователя заключается в том, что вы можете рассматривать его как имеющий внутри только 1-битный АЦП, но с синхронизацией и математикой они могут выдавать 24-битные показания:
http: //www.maxim-ic.com/appnotes.cfm/appnote_number/1870/
Аппаратное обеспечение с 24-битным АЦП
22-битное эффективное разрешение
22-битное эффективное разрешение20-битное эффективное разрешение
Оборудование с 16-разрядным АЦП или менее
19-битное эффективное разрешение
12-битное эффективное разрешение
19-битное эффективное разрешение
16-битное эффективное разрешение
12-битное эффективное разрешение
12-битное эффективное разрешение
8085 программа для сложения двух 16-разрядных чисел
8085 программа для сложения двух 16-разрядных чисел
Проблема — Напишите программу на языке ассемблера для сложения двух 16-разрядных чисел с помощью:
- (a) 8-разрядная операция
- (b) 16-битная операция
Пример —
(a) Сложение 16-битных чисел с использованием 8-битной операции — Это длительный метод и требует больше памяти по сравнению с 16-битной операцией.
Алгоритм —
- Загрузить младшую часть первого числа в регистр B
- Загрузить младшую часть второго числа в A (аккумулятор)
- Сложить оба числа и сохранить
- Загрузить старшую часть первое число в регистре B
- Загрузить старшую часть второго числа в A (аккумулятор)
- Сложить оба числа с переносом из младших байтов (если есть) и сохранить в следующем месте
Программа —
АДРЕС ПАМЯТИ МНЕМОНИКА КОММЕНТАРИИ 2000 LDA 2050 A ← 2050 A ← 2050 9037 B LDA 2052 A ← 2052 2007 ADD B A ← A + B 2008 STA 3050 A → 3050 200B LDA 2051 A ← 2051 200E MOV B, A B ← A 200F LDA 2053 ADC B A ← A + B + CY 2013 STA 3051 A → 3051 2016 HLT Останавливает выполнение1 - MOV B, A сохраняет значение A в регистре B
- LDA 2052 сохраняет значение 2052 в A
- ADD B сложение содержимое B и A и сохранить в A
- STA 3050 сохраняет результат в ячейке памяти 3050
- LDA 2051 сохраняет значение 2051 в A
- MOV B, A сохраняет значение A в регистре B
- LDA 2053 сохраняет значение 2053 в A
- ADC B добавляет содержимое B, A и переносит из младшего бита сложение и сохраняет в A
- STA 3051 сохраняет результат в ячейке памяти 3051
- HLT останавливает выполнение
(b) Сложение 16-битных чисел с использованием 16-битной операции — Это очень короткий метод, и требуется меньше памяти по сравнению с 8-битным операция.
Алгоритм —
- Загрузить младшие и старшие биты первого числа сразу
- Скопировать первое число в другую регистровую пару
- Загрузить младшие и старшие биты второго числа сразу
- Добавить обе пары регистров и сохраняют результат в ячейке памяти
Программа —
АДРЕС ПАМЯТИ МНЕМОНИКА КОММЕНТАРИИ 2000 LH6 2003 XCHG DH & EL 2004 LHLD 2052 HL ← 2052 2007 DAD D H ← H + E 2008 SHLD 3050 A → 3050 200B HLT Останавливает выполнение Пояснение —
- LHLD 2050 загружает значение 2050 в регистр L и значение 2051 в регистре H (первое число)
- XCHG копирует содержимое регистра H в регистр D и регистр L в регистр S
- LHLD 2052 загружает значение 2052 в регистр L и значение 2053 в регистр H (второе число)
- DAD D добавляет значение H с D и L с E и сохраняет результат в H и L
- SHLD 3050 сохраняет результат в ячейке памяти 3050
- HLT останавливает выполнение
Понимание 4-байтовых номеров автономных систем
Несмотря на все мои трепы, которые я делаю в этом блоге об истощении IPv4-адресов и необходимости подготовиться к IPv6, есть еще один числовой ресурс, который также быстро истощается, и о котором я раньше не писал: 2-байтовый автономный системные номера (ASN).
16-битное числовое пространство дает вам 65 536 возможных чисел (номера AS от 0 до 65535). Из них IANA резервирует 1026 из них: 64512 — 65534 для частных многоразовых ASN (аналогично частным IPv4-адресам RFC1918) и несколько других, таких как 0 и 65535 и один важный для этой статьи, 23456. В настоящее время 49 150 ASN. были выделены из общего пула, поэтому осталось 15360 доступных ASN: около 23,8 процента от общего пула.
Анализ скорости выделения 2-байтовых ASN показывает, что доступный пул закончится в середине 2011 года.Очень близко к дате, когда у нас закончатся адреса IPv4.
К счастью, причин для беспокойства по поводу исчерпания ASN гораздо меньше, чем по поводу исчерпания IPv4, по двум причинам:
В отличие от IP-адресов, которые необходимы любому, кто хочет подключиться к IP-сети, номера автономных систем имеют значение только для сети, использующие BGP.
- Так же, как IPv6 был создан для решения проблемы IPv4, предлагая размер адреса в четыре раза больше, были созданы 4-байтовые ASN для решения проблемы истощения 2-байтовых ASN.Но там, где переход на IPv6 может быть затруднен из-за отсутствия взаимодействия между IPv4 и IPv6, переход на 4-байтовые ASN намного проще.
В этом посте описывается формат 4-байтового ASN, как он взаимодействует с 2-байтовыми ASN и что вам нужно сделать (если что-нибудь), чтобы подготовить вашу сеть к ним.
4-байтовый формат ASN
4-байтовые ASN предоставляют 2 32 или 4294967296 номеров автономных систем в диапазоне от 0 до 4294967295.Первое, на что следует обратить внимание в отношении этих чисел, это то, что они включают все старые 2-байтовые ASN, от 0 до 65 535. Это очень помогает в обеспечении взаимодействия между автономными системами, использующими 2-байтовые ASN, и системами, использующими 4-байтовые ASN. (Часто слышимая жалоба на IPv6 заключается в том, что взаимодействие с IPv4 можно было бы легче поддерживать, если бы 4,3 миллиарда адресов IPv6 были зарезервированы как репрезентативные для существующих адресов IPv4, но это уже другая история.)
4-байтовый ASN между 0 а 65535 называется отображаемым ASN, потому что он может быть представлен всего в 2 байтах; первые 16 битов в каждом случае являются нулями.
Исходя из опасений, что 32-битные ASN могут быть трудными для написания и управления, существует три способа представления 4-байтовых ASN:
· asplain — это простое десятичное представление ASN от 0 до 4294967295.
· asdot + разбивает число на младшие и старшие 16-битные значения, разделенные точкой. Все старые 2-байтовые ASN могут быть представлены в младшем значении, при этом старшее значение установлено на 0. Так, например, 65535 равно 0.65535. Еще одно, 65536, находится за пределами значения, которое может быть представлено только в нижнем диапазоне, и поэтому представлено как 1.0. 65537 будет 1,1, 65680 — 1,144 и т. Д. Вы можете вычислить значения младшего и высокого порядка, вычитая кратные 65 536 из asplain представления ASN, причем старшее значение представляет кратные 65536. Таким образом, ASN 327700 составляет 5,20: пять умноженных на 65536 плюс еще 20. Самый большой ASN, 4294967295, равен 65535.65535: 65 535 умножить на 65535 плюс еще 65535.
· asdot представляет собой смесь asplain и asdot +. Любой ASN в 2-байтовом диапазоне от 0 до 65535 записывается asplain (поэтому 65535 записывается как «65535»), а любой ASN выше этого диапазона записывается как asdot + (таким образом, 65536 записывается как «1.0»).
Asplain, очевидно, является наиболее простым методом понимания новых ASN, хотя большие числа могут стать неудобными для написания и, следовательно, подвержены типографским ошибкам в письменной документации или конфигурациях маршрутизаторов.
Asdot + намного проще написать, но сложнее вычислить по его простому десятичному эквиваленту. Если вы регулярно работаете в этом формате, вероятно, стоит потратить время на написание простого скрипта, который выполняет преобразования за вас, чтобы предотвратить ошибки в расчетах.
Может показаться, что полезность Асдота ограничена. В конце концов, написать «0,3657» не сложнее, чем «3657», и необходимость в некоторых вычислениях возникает, когда вы превысите 65535; asdot ничего не делает, чтобы помочь вам в этом.Однако в этом есть тонкость. Региональные органы по присвоению номеров — региональные интернет-регистры или RIR — различают 16-битный номер, который является более старым 2-байтовым ASN, и отображаемым 4-байтовым ASN (опять же, набор 32-битных ASN, в которых первые 16 все биты равны 0). Таким образом, «3657» — это 2-байтовый ASN, а «0.3657» — 4-байтовый ASN.
Это, конечно же, заставляет нас вкратце взглянуть на то, каковы политики RIR для назначения 4-байтовых ASN.
Политики распределения ASN
Все пять RIR (AfriNIC, APNIC, ARIN, LACNIC и RIPE NCC) имеют одинаковые политики назначения для 4-байтовых ASN:
· 4-байтовые ASN доступны с 1 Январь 2007 г.Назначение по умолчанию, если вы запрашиваете ASN, заключается в предоставлении вам 2-байтового ASN и назначении 4-байтового ASN только в том случае, если вы его специально запрашиваете.
· Начиная с 1 января 2009 г. (да, примерно через месяц!) Эта политика меняется на противоположную: по умолчанию будет использоваться 4-байтовый ASN. Вы все еще можете получить 2-байтовый ASN, но только если вы его специально запросите.
· Год спустя, 1 января 2010 г., все назначения ASN будут 4-байтовыми. Полученный вами ASN может иметь форму 0.XX (где все старшие 16 бит равны 0, а младшие 16 бит — нет), но RIR не будут делать различия между этими числами и любыми другими 4-байтовыми ASN.И хотя это никоим образом не повлияет на вашу сеть, 16-битный ASN, который у вас был, возможно, в течение многих лет, в глазах RIR будет отображаемым 32-битным ASN. Например, AS3356 для Level3 Communications становится в глазах RIR в начале 2010 г. 0,3356.
Эти политики вызывают несколько вопросов:
· Если вы планируете запросить новое назначение ASN, начиная с 2009 года, что вам нужно сделать, чтобы подготовиться к этому?
· Как новые 4-байтовые ASN взаимодействуют со старыми автономными системами, использующими 2-байтовые ASN?
· Если у вас есть 2-байтовый ASN, что-нибудь изменится?
Роль ASN в BGP
Краткий обзор того, как BGP использует номера автономных систем, поможет понять, как новый формат может повлиять на сети BGP.Большинство из вас уже знакомы с основами BGP; если вы это сделаете, не стесняйтесь пропустить вперед.
Назначение BGP, в отличие от любого IGP (OSPF, IS-IS, EIGRP и RIP), заключается в маршрутизации между доменами, находящимися под отдельным административным контролем, то есть системами, которые автономны друг от друга. Если вы собираетесь выполнять маршрутизацию между этими автономными доменами маршрутизации (и между ними), вам понадобится способ идентификации отдельных AS. Этот идентификатор является номером автономной системы.
ASN выполняет две основные функции в BGP:
Во-первых, он помогает BGP определять кратчайший путь к месту назначения.Когда BGP объявляет маршрут к соседу в сообщении обновления, он присоединяет к маршруту несколько атрибутов пути . Когда маршрутизатор изучает более одного маршрута BGP к одному и тому же месту назначения, процесс принятия решения BGP оценивает атрибуты пути маршрутов в приоритетном порядке, чтобы решить, какой из маршрутов является наиболее предпочтительным. (Атрибуты пути BGP могут быть добавлены, удалены или изменены всевозможными способами, чтобы повлиять на процесс принятия решения BGP. Это основа для политик маршрутизации BGP.) Один из этих атрибутов, прикрепленных к каждому маршруту BGP, называется AS_PATH.Когда маршрутизатор объявляет пункт назначения в своей собственной AS соседу в другой AS, он помещает свой локальный ASN в AS_PATH. Поскольку маршрут объявляется последующим автономным системам, каждый граничный маршрутизатор AS добавляет свой собственный ASN к атрибуту. Таким образом, AS_PATH становится списком ASN, описывающим обратный путь к месту назначения. Маршрутизатор может выбрать кратчайший путь, выбрав маршрут с наименьшим количеством ASN, перечисленных в его AS_PATH.
Вторая функция ASN — очень простой механизм предотвращения петель.Поскольку маршрутизатор добавляет свой ASN к AS_PATH перед объявлением маршрута соседу в другой AS, маршрут, который зацикливается, то есть выходит из AS и впоследствии объявляется обратно в ту же AS, легко обнаруживается путем изучения AS_PATH. Если маршрутизатор видит свой собственный ASN, указанный в AS_PATH маршрута, объявленного ему соседом, он отбрасывает маршрут.
ASN также появляется в атрибуте пути, называемом AGGREGATOR. Когда несколько маршрутов суммируются (агрегируются), детали маршрута могут быть потеряны.Атрибут AGGREGATOR может быть добавлен к агрегированному маршруту для указания идентификатора маршрутизатора и ASN маршрутизатора, выполняющего агрегирование. Этот атрибут не влияет на процесс принятия решения BGP, но может быть полезен для отслеживания проблем с агрегированными маршрутами.
Третий атрибут, использующий ASN, — это СООБЩЕСТВА. Этот необязательный атрибут помогает управлять политиками маршрутизации, когда они применяются к большому количеству маршрутов; Используя ряд методов, вы можете назначить префиксам один или несколько атрибутов COMMUNITIES, а затем применить политику маршрутизации к сообществу, а не к отдельным маршрутам.Например, вы можете определить атрибут COMMUNITES с именем Cust_Routes, а затем добавить этот атрибут ко всем маршрутам, объявленным в вашу AS всеми вашими клиентами. Затем в любом месте вашей сети, где вам нужно применить политику ко всем вашим маршрутам клиентов, вы можете применить политику к маршрутам, имеющим атрибут Customer_Routes, вместо того, чтобы идентифицировать каждый префикс (и, возможно, изменить все свои списки префиксов в любое время, когда маршрут клиента добавляется или удаляется).
Атрибут COMMUNITES — это 32-битное значение, в котором первые 16 битов являются ASN, а последние 16 битов произвольно назначаются вами, чтобы иметь любое значение, которое вы хотите.
Однако здесь важны не столько функции AGGREGATOR или COMMUNITES, сколько то, что они, как и AS_PATH, отформатированы для передачи 2-байтовых ASN; поэтому форматы этих атрибутов должны быть адаптированы для переноса более крупных 32-битных ASN.
В дополнение к этим трем атрибутам пути сообщение BGP Open также ссылается на ASN в 16-битном поле My Autonomous System. BGP работает поверх сеанса TCP между соседями; после установления сеанса TCP соседи используют сообщения Open для согласования сеанса BGP.Каждый сосед указывает свой идентификатор маршрутизатора, ASN, версию BGP, на которой он работает (всегда версия 4 в современных сетях), время своего удержания (время, которое он ожидает дождаться Keepalive от соседа перед закрытием сеанса) и, возможно, некоторые дополнительные параметры. .
BGP — это намного больше, чем описано здесь. Для этого обсуждения важно то, что существует четыре объекта данных BGP, которые несут ASN:
· Атрибут AS_PATH;
· Атрибут АГРЕГАТОР;
· Атрибут COMUNITES; и
• Открытое сообщение
Каждому из этих объектов необходимо уделить внимание не только с точки зрения их адаптации к 4-байтовым ASN, но и обеспечения взаимодействия этих адаптаций со старыми реализациями BGP, которые понимают только 2-байтовые ASN.
Взаимодействие соседей
Для простоты мы будем называть реализации BGP, поддерживающие 4-байтовые ASN, New_BGP, а унаследованные реализации BGP, которые поддерживают только 2-байтовые ASN, Old_BGP.
Первое требование для реализации New_BGP — определить, является ли соседом New_BGP или Old_BGP. Это делается с помощью объявления возможностей BGP при открытии сеанса BGP. Помимо рекламы самого себя как New_BGP, он включает свой 4-байтовый ASN в объявление о возможностях.
Если сосед отвечает, что он также является узлом NEW_BGP, сосед включает свой 4-байтовый ASN в свое собственное объявление о возможностях. Таким образом, два соседа New_BGP могут информировать друг друга о своих 4-байтовых ASN без использования 2-байтового поля My Autonomous System в сообщении Open. (Если соседи — NEW_BGP, но имеют 2-байтовые ASN или отображаемые 4-байтовые ASN, они все равно могут поместить ASN в поле My Autonomous System в дополнение к объявлению о возможностях.)
Если соседом является Old-BGP, он либо отвечает, что не поддерживает возможность 4-байтового ASN, либо вообще не отвечает на объявление о возможностях.В этом случае сосед New_BGP все еще может инициировать сеанс с соседом Old-BGP, но не может анонсировать свой 4-байтовый ASN. Сосед этого не поймет. Вместо этого New_BGP использует зарезервированный 2-байтовый ASN, 23456, который называется AS_TRANS (AS_TRANS легко запоминается из-за его последовательности 2-3-4-5-6). Этот номер AS добавляется в поле «Моя автономная система» открытого сообщения. Поскольку AS_TRANS зарезервирован, никакой узел Old_BGP не может использовать его как свой собственный ASN; его могут использовать только динамики New_BGP.
Таким образом, совместимость пиринга достигается, потому что узел New_BGP «знает», что его сосед является узлом Old_BGP, и адаптируется к нему; узел Old-BGP просто продолжает использовать устаревшие правила BGP.
Взаимодействие атрибутов пути
Поскольку узел New_BGP знает, является ли его сосед New_BGP или Old_BGP, он знает, каким правилам следует следовать, объявляя маршруты к соседу.
8-битные и 16-битные изображения
Термин бит используется в любых цифровых носителях. Что касается цифровых изображений, битовая глубина имеет много названий, таких как глубина пикселей или глубина цвета. В цифровой фотографии споры о 8-битных и 16-битных файлах ведутся не меньше, чем Nikon и Canon.Эта статья призвана дать вам лучшее понимание того, что такое битовая глубина. Вы также узнаете, нужны ли нам 16-битные изображения или нет, и если да, то когда они нам нужны.
Что такое битовая глубина?
Большинство из нас знает, что пиксели являются основными элементами любого изображения. В частности, любой цвет в цифровом изображении представлен комбинацией красного, зеленого и синего оттенков. Для каждого пикселя используется одна такая комбинация, и миллионы пикселей составляют изображение. По этой причине битовая глубина также известна как глубина цвета.Например, чистый красный цвет представлен числами «255, 0, 0». Чистый зеленый цвет равен 0, 255, 0, а чистый синий — 0, 0, 255. В цифровой фотографии каждый основной цвет (красный, зеленый или синий) представлен целым числом от 0 до 255. Представлены любые неосновные цвета. комбинацией основных цветов, например «255, 100, 150» для определенного оттенка розового.
Давайте рассмотрим наибольшее число, представляющее красный цвет, а именно 255. Когда я конвертирую 255 в двоичное, я получаю 11111111, что составляет восемь цифр.8) заданного основного цвета.
Битовая глубина и цветовой охват
Некоторые фотографы путают глубину цвета с цветовым охватом. Цветовая гамма — это диапазон цветов, обычно используемый в контексте того, какой диапазон цветов может отображать данное устройство или выводить принтер. Электронные устройства и принтеры не могут отображать столько цветов, сколько может видеть человеческий глаз. Диапазон цветов, которые они могут отображать, обычно ограничен цветовой гаммой, такой как sRGB или AdobeRGB, или определенной гаммой в зависимости от используемого принтера / чернил / бумаги.Вы можете узнать больше о цветовой гамме в статье Спенсера о sRGB, Adobe RGB и ProPhoto RGB.
Битовая глубина, с другой стороны, может быть визуализирована как расстояние между цветами в пределах гаммы. Другими словами, у вас может быть два изображения радуги, которые переходят от красного к фиолетовому, то есть с одинаковой гаммой. Но первая радуга может быть мягким градиентом с множеством тысяч отдельных цветов, если вы увеличиваете пиксели, тогда как вторая радуга может состоять всего из семи или восьми цветов и выглядеть намного более блочно.1 = 2, здесь доступны только два значения: 0 и 1 — AKA черный и белый.
1-битное изображение, в котором есть только чистый черный и чистый белыйВзгляните на изображение ниже для аналогичного примера. Левая часть изображения 8-битная, а правая — 1-битная.
8 бит против 1 битПравая часть изображения содержит только черный и белый цвета. Некоторые области 1-битного изображения могут казаться серыми, но после увеличения до пиксельного пика разница становится очевидной, как показано ниже. 8-битное изображение может содержать 256 оттенков серого, тогда как изображение справа может содержать только черный или белый цвет.
8-битные изображения допускают до 256 тонов, тогда как 1-битные изображения могут иметь только двабит по сравнению с битами на канал
В приведенном выше разделе мы видели, что 8-битное изображение может содержать только 256 различных оттенков серого в общее. Но я упоминал в начале этой статьи, что 8-битные цветные изображения на самом деле имеют 256 оттенков на основной цвет . Итак, стандартное цветное изображение, которое мы обычно называем «8-битным», на самом деле хорошо подходит для более чем 256 оттенков. Точнее называть его 8-битным изображением на канал .24). Вот почему вы можете иногда слышать, что изображение с 8-битной разверткой на канал называется 24-битным изображением, хотя это не самый распространенный термин для этого.
Все еще не понятно? Позвольте мне воспользоваться помощью Photoshop, чтобы прояснить это. Взгляните на иллюстративное изображение ниже.
Изображение имеет три канала, каждый из которых имеет разрядность 8 бит.На вкладке «Каналы», отмеченной красным на изображении выше, вы можете видеть, что, хотя это изображение в оттенках серого, оно имеет четыре канала: по одному каналу для красного, зеленого и синего цветов и канал RGB для всего изображения.Невозможно узнать, смогу ли я восстановить цветное изображение в этом случае (насколько нам известно, я применил корректирующий слой B&W и сгладил изображение). Но, по крайней мере, в той или иной форме здесь остается три основных цветовых канала, каждый из которых содержит восемь бит информации.
Таким образом, все изображение здесь технически все еще 24-битное. Однако я мог удалить всю информацию о цвете, перейдя в верхнее меню и выбрав «Изображение»> «Режим»> «Оттенки серого». Как только я это сделаю, вы увидите, что сейчас существует только один канал, как показано на рисунке ниже:
После преобразования изображения в изображение в оттенках серого оно больше не будет содержать 4 канала, а будет содержать только один.16 оттенков на канал, или 65536. Если у вас есть изображение RGB, в котором каждый из красного, зеленого и синего имеет 16 бит, вы должны умножить 65536 × 65536 × 65536, чтобы увидеть, что изображение может содержать в общей сложности до 281 триллиона цветов.Хотя теоретически предполагается, что 16-битная битовая глубина на канал содержит 281 триллион цветов, 16-битная версия Photoshop не выдерживает этого. 15) + 1 = 32769.Поэтому, когда вы работаете с Photoshop в 16-битном режиме, пиксель может содержать любой из 35,2 триллиона цветов вместо 281 триллиона.
Действительно ли можно использовать 16 бит на канал?
Несмотря на то, что 16-битные изображения Photoshop на канал могут содержать только 12,5% от теоретического максимального значения, 35,2 триллиона цветов — это все еще много. Теперь возникает вопрос на миллион долларов: может ли человеческий глаз различать столько цветов? Ответ — нет. Исследования показали, что человеческий глаз может различать максимум 10 миллионов цветов.Взгляните на изображение ниже.
Тона 8-битного красногоВидите ли вы видимую разницу между тремя скругленными квадратами? Большинство из вас могут заметить тональную разницу между средним и правым. Но я точно не могу найти видимой разницы между левым и средним.
Крайний левый квадрат равен 255, 0, 0, а средний квадрат — 254, 0, 0. Это одна ступень разницы в 8-битном изображении, и даже близко к 16-битным изображениям Photoshop! Если бы приведенное выше изображение было 16-битным изображением на канал в Photoshop, вы могли бы разместить более 32 000 тонов между левым и центральным изображениями.
Поскольку 16-битные изображения на канал содержат исключительно большое количество цветов, очевидно, что они занимают много места. Например, программное обеспечение Nikon NX выводит файлы TIFF размером 130 МБ, когда я выбираю экспорт в 16-битном формате, тогда как размер файла уменьшается примерно до 70 МБ, когда я выбираю 8-битное изображение для одного из моих изображений.
Кроме того, очень немногие устройства вывода — мониторы, распечатки и т. Д. — в любом случае могут отображать более 8 бит на канал. Но это не значит, что более высокая битовая глубина не важна.
Какое значение имеет значение 16 бит на канал?
Из приведенного выше раздела может сложиться впечатление, что никому никогда не понадобится более 8 бит на канал.Тем не менее, у 16-битных изображений есть свои применения. Давайте рассмотрим изображение ниже.
Я открыл изображение и преобразовал его в 8-битное, выбрав пункт меню «Изображение»> «Режим»> «8 бит / канал». Теперь я применяю два корректирующих слоя кривых к открытому изображению. В кривых 1 я выбираю вход 255 и изменяю выход на 23. Проще говоря, я недоэкспонировал изображение. Используя Кривые 2, я выбрал вход 23 и изменил выход на 255. Это возвращает экспозицию туда, где она была до ее недоэкспонирования — но за счет «хруста» большого количества цветов.Это приводит к эффекту полос, который вы можете видеть в небе и облаках на изображении выше.
Когда я так же редактирую 16-битное изображение, на небе нет видимых полос. Вы можете видеть это в приведенном ниже сравнении, где я подверг оба изображения одинаковым настройкам:
8-битное изображение на канал показывает заметные полосы, которых почти избежать в 16-битном. Именно здесь 16-битные изображения находят свое применение. Чем резче вы редактируете, тем полезнее будет иметь как можно больше оттенков цвета.
Вы все еще можете избежать полос на 8-битных изображениях с помощью тщательной обработки — например, не выполняя настройки экстремальных кривых, которые я сделал выше, — но 16-битные изображения дают больше места для ошибок. Вот почему, если вы редактируете в таком программном обеспечении, как Photoshop, рекомендуется работать с 16-битными изображениями. Только после завершения редактирования рекомендуется преобразовать его в 8-битное изображение для вывода. (Хотя все же лучше сохранить 16-битный TIFF или PSD в своем архиве, на случай, если вы решите продолжить редактирование позже.)
Итак, в общем, полезный объем 16-битных изображений на канал начинается и заканчивается постобработкой.
Заключение
Я надеюсь, что эта статья дала нашим читателям базовое понимание того, что такое битовая глубина и разница между 8-битными и 16-битными изображениями на канал. Несмотря на то, что 16 бит может показаться излишним, мы видели здесь, что он находит свое применение при постобработке изображений. Но 8-битные изображения на канал занимают гораздо меньше файлового пространства, поэтому для экономии места стоит экспортировать изображения, особенно для Интернета, с 8-битными изображениями на канал.
Пожалуйста, дайте мне знать в разделе комментариев, если у вас есть вопросы или дополнения, чтобы другие читатели могли извлечь из этого пользу.
Фиксированная точка (целые числа)
Представление с фиксированной точкой используется для хранения целых чисел , положительных и отрицательных целые числа:… -3, -2, -1, 0, 1, 2, 3,…. Программы высокого уровня, такие как C и BASIC, обычно выделяют 16 бит для хранения каждого целого числа. В простейшем случае 2 16 = 65 536 возможных битовых комбинаций присваиваются номерам от 0 до 65 535.Это называется беззнаковым целочисленным форматом, и упрощенный пример показан на рис. 4-1. (используя только 4 бита на число). Преобразование между битовой комбинацией и представляемое число — это не что иное, как изменение между основанием 2 (двоичный) и основание 10 (десятичное). Недостаток беззнакового целого числа в том, что отрицательные числа не могут быть представлены.
Двоичное смещение аналогично целому числу без знака, за исключением десятичных значений. сместился на , чтобы учесть отрицательные числа.В 4-битном примере на рис. 4-1 десятичные числа смещены на семь , в результате получаются 16-битные шаблоны соответствующие целым числам от -7 до 8. Таким же образом, 16 битовое представление будет использовать 32 767 в качестве смещения, что приведет к диапазону между -32 767 и 32 768. Смещение двоичного файла не является стандартизированным форматом, и вы найти другие используемые смещения, например 32 768. Наиболее важное использование двоичного смещения находится в АЦП и ЦАП. Например, диапазон входного напряжения от -5 В до 5 В может быть сопоставлены с цифровыми числами от 0 до 4095 для 12-битного преобразования.
Знак и величина — еще один простой способ представления отрицательных целых чисел. Крайний левый бит называется битом знака, и для положительных чисел ему задается ноль , и , для отрицательных чисел. Остальные биты являются стандартными двоичными представление абсолютного значения числа. Это приводит к потере одного битовый шаблон, поскольку есть два представления для нуля, 0000 (положительный ноль) и 1000 (отрицательный ноль). Эта схема кодирования приводит к 16-битным числам, имеющим диапазон от -32 767 до 32 767.
Эти первые три представления концептуально просты, но их трудно понять. реализовать аппаратно. Помните, когда A = B + C вводится в компьютер программе, какому-то аппаратному инженеру пришлось придумать, как сделать битовую комбинацию представляющий B, объединить с битовой комбинацией, представляющей C, чтобы сформировать бит узор, представляющий A.
Два дополнения — это формат, который любят инженеры по аппаратному обеспечению, и именно так целые числа обычно представлены в компьютерах.Чтобы понять кодировку сначала посмотрите на десятичное число ноль на рис. 4-1, которое соответствует двоичный ноль, 0000. Когда мы считаем вверх, десятичное число — это просто двоичный эквивалент (0 = 0000, 1 = 0001, 2 = 0010, 3 = 0011 и т. д.). Сейчас, помните, что эти четыре бита хранятся в регистре, состоящем из 4 триггеров. Если мы снова начнем с 0000 и начнем вычитание, цифровое оборудование автоматически считается с дополнением до двух: 0 = 0000, -1 = 1111, -2 = 1110, -3 = 1101 и т. Д.Это аналог одометра в новом автомобиле. Если гонят вперед он меняется: 00000, 00001, 00002, 00003 и так далее. Когда везут назад, одометр меняется: 00000, 99999, 99998, 99997 и т.д.
Используя 16 бит, дополнение до двух может представлять числа от -32 768 до 32 767. Самый левый бит — 0, если число положительное или ноль, и 1, если число отрицательный. Следовательно, самый левый бит называется битом знака, как и в знаке & представление величины.Преобразование десятичной дроби в двойку дополнение является простым для положительных чисел, от простого десятичного до двоичного конверсия. Для отрицательных чисел часто используется следующий алгоритм: (1) взять абсолютное значение десятичного числа, (2) преобразовать его в двоичное, (3) дополнить все биты (единицы становятся нулями, а нули становятся единицами), (4) добавить 1 в двоичное число. Например: -5 → 5 → 0101 → 1010 → 1011. Двойки Дополнение сложно для людей, но легко для цифровой электроники.
Введение в математику 6502: зависимость, вычитание и многое другое
Числа могут быть забавными, и разговор о математике процессора 6502 — это просто еще один способ взглянуть на темы, которые мы уже знаем из простой математики. На самом деле в 6502 математических процедурах не задействованы никакие высшие математические науки. Тем не менее, нам время от времени приходится немного адаптировать наш разум.Известно, что микропроцессоры 6502/6510 имеют только инструкции сложения и вычитания. На самом деле у них есть дополнительный бонус, заключающийся в том, что они способны выполнять умножение на два на оборудовании.Также возможно целочисленное деление на два.
Начиная с того, что у нас есть, мы можем реализовать на программном уровне недостающие инструкции (общие инструкции умножения и деления).
Как мы все знаем, 6502 — это 8-битный микропроцессор. Это означает, что в данной ячейке памяти могут храниться только числа от 0 до 255. Однако есть способ связать вместе больше 8-битных чисел, чтобы мы могли производить вычисления с 16-битными или 32-битными числами. Или даже больше. Ключом к объединению чисел является флаг переноса .Мы увидим это через мгновение.
Дополнение
Сложение выполняется инструкцией ADC . Это означает: «ДОБАВИТЬ с переносом». Перенос всегда добавляется во время расчета. Итак, перед сложением двух чисел мы должны очистить перенос с помощью инструкции CLC (CLear Carry).
8-битное сложение может быть закодировано следующим образом:
clc lda num1 adc num2 sta результат rts
Итак, если num1 содержит 10, а num2 25, результат будет содержать значение 35.Довольно просто.
Но, если мы попробуем сложить значения 20 и 240? Все мы знаем результат (260), но он превышает 8-битный предел (255). Если вы попытаетесь запустить этот фрагмент кода с num1 = 20 и num2 = 240, вы увидите, что результат будет содержать значение 4. Фактически, результат превышает значение 255 на 5 единиц. Когда вы добавляете 1 к 255, результат становится равным 0. Вот почему в результате получается 4 единицы. Вот что происходит:
255 + 1 = 0 + 1 = 1 + 1 = 2 + 1 = 3 + 1 = 4
Но когда единица прибавляется к 255, что-то происходит.Флаг переноса установлен в 1. Мы можем использовать эту информацию для получения 16-битного результата. Взгляните на следующий код:
clc lda num1 adc num2 sta result_low lda result_high adc # $ 00 sta result_high rtsПоскольку АЦП всегда добавляет перенос, если младший байт результата ( result_low) переходит в 0, перенос будет установлен в 1, а очевидно бесполезная инструкция adc # $ 00 фактически добавит 1 к старший байт результата ( старший результат ).Конечно, мы предполагаем, что ячейка result_high инициализируется нулем перед запуском вышеуказанного кода.
Итак, результат разделяется в двух местах: result_high и result_low . Если мы сложим вместе 240 и 20, старший байт будет равен 1, а младший байт будет равен 4.
Старший байт превращается в 1, как только младший байт возвращается к 0 из 255. Таким образом, цифра 1 в старшем байте просто означает: 256 .
Итак, если у нас есть результат сложения «240 + 20» в форме старшего / младшего байта, мы можем получить результат в виде целого числа, выполнив следующие действия:
256 * старший_байт + младший_байт = 256 * 1 + 4 = 260 (240 + 20 = 260)
Так как 240 + 20 = 60, это верно.
Теперь, чтобы сложить два 16-битных числа вместе, мы можем поступить следующим образом:
clc lda num1_low adc num2_low sta result_low lda num1_high adc num2_high sta result_high rtsСлагаемые оба даны в виде старшего и младшего байта. Мы добавляем младшие байты слагаемых, затем старшие байты.
Обратите внимание, что CLC не выполняется перед добавлением двух старших байтов слагаемых! Это важно, поскольку мы должны учитывать перенос, который может возникнуть в результате добавления младших байтов.Это способ объединения 8-битных чисел для образования более крупных чисел.
На этом этапе могут быть полезны еще несколько пояснений по «разбиению» чисел. Предположим, нам нужно сложить 100 и 300 вместе. 100 нужен только 1 байт, поэтому мы установим num1_high в 0 и num1_low в 100.
Для300 требуется два байта. Поскольку каждая «единица» в старшем байте означает «256», старшее значение получается в результате следующего целочисленного деления:
число2_высокое = ЦЕЛОЕ (300/256) = 1
Младший байт затем вычисляется следующим образом:
num2_low = 300 - num2_high * 256 = 300 - 256 = 44
Если вместо этого у нас num2 = 1000, его можно выразить в виде старшего / младшего байта, используя следующие вычисления:
число2_высокое = ЦЕЛОЕ (1000/256) = 3 num2_low = 1000 - num2_high * 256 = 232 Доказательство: num2_high * 256 + num2_low = 3 * 256 + 232 = 1000
Еще один способ разбить число в форме старшего / младшего байта — использовать шестнадцатеричную нотацию.
1000 в десятичной системе счисления равняется 3E8 долларам в шестнадцатеричной системе. Берем пары чисел, начиная справа. Итак, у нас есть $ E8 и $ 03. Первая пара — это младший байт, вторая пара — старший байт. Итак:
1000 (младший байт) = $ e8 = 232 1000 (старший байт) = $ 03 = 3
Вычитание
Вычитание выполняется с помощью инструкции SBC (SuBtract with Carry). В ЦП 6502 нет «флага заимствования». Флаг переноса также не является заимствованием, но он действует как обратное заимствование .Итак, перед выполнением вычитания мы должны очистить заимствование или, как это делается на практике, мы должны УСТАНОВИТЬ перенос.
Все может быть настроено очень аналогично дополнительному коду. Итак, чтобы выполнить 16-битное вычитание, мы можем кодировать следующим образом:
с lda num1_low sbc num2_low sta result_low lda num1_high sbc num2_high sta result_high rtsОбратите внимание, что после вычитания младших байтов перенос НЕ очищается.Опять же, это необходимо для сохранения информации о переносе для старших байтов.
Умножение и деление на два
Хотя умножение или деление двух общих чисел не предусмотрено аппаратными средствами, оно дает нам возможность выполнять умножение или деление на два.
8-битное умножение на два выполняется инструкцией ASL .
Если вы хотите умножить число на десять, вы просто добавляете 0 справа от него, сдвигая число влево.
10 * 10 = 100 10 10 [] <- добавить 0 100
Поскольку ЦП работает с числами с основанием 2, добавление 0 справа от числа, таким образом, сдвиг его влево означает просто умножение на два.
Если у нас есть число 15, сдвигая его влево один раз, мы получим 30.
15 в десятичной системе счисления = 00001111 00001111 сдвиг влево ... [0] 0001111 [] <- добавить сюда 0 / \ / \ || || "отбросьте" это число (посмотрим, куда оно денется...) 00011110 00011110 = 30 десятичных
Итак, если число для умножения на два хранится в ячейке num1 , мы можем использовать код:
ASL число 1
Здесь ASL сдвигает содержимое ячейки num1 . Итак, num 1 будет содержать результат. Если мы не хотим изменять num1 и сохраняем результат в ячейке result , мы можем закодировать:
LDA номер1 ASL STA счет
Теперь ASL сдвигает содержимое аккумулятора.Итак, инструкция ASL бывает двух видов.
Предположим, мы хотим умножить десятичное число 255:
на два.LDA # $ ff ASL STA счет
Давайте использовать двоичные числа для сдвига:
$ ff = 11111111 основание 2 C <--- [1] 1111111 [] <--- 0 C = 1 11111110 с основанием 2 = 254 в десятичной системе счисления
Итак, мы получаем 254 десятичное значение в ячейке , результат . При этом первая левая цифра числа, на которое нужно умножить, была выброшена.Но на самом деле это не потеряно. ЦП сохраняет его во флаге переноса. Опять же, флаг переноса сохраняет недостающую информацию, и мы можем использовать его для построения 16-битного результата. Имея это в виду, вот код:
LDA номер1 ASL STA result_low Конец BCC INC результат_высокий конец RTSКод просто говорит следующее: когда произведено умножение числа num1 на два, если флаг переноса снят, ничего не делать. Если он установлен, поставьте 1 на result_high (или, что то же самое, увеличьте его на единицу).Конечно, мы предполагаем, что result_high инициализируется нулем перед запуском вышеуказанного кода.
Но мы можем использовать другой подход. Мы можем использовать два байта для хранения num1, а затем сдвинуть все 16-битное число. При смещении младшего байта мы просто его ASL. Теперь мы не можем продолжить, выполняя ASL для старшего байта: мы просто вводим старший байт с 0 справа. Вместо этого нам нужно войти в него с переносом, чтобы сохранить информацию с первой смены. Мы выполняем это с помощью инструкции ROL (повернуть влево).Смотреть:
0000000011111111 (16-битное число, умноженное на два, 255 десятичное) [0] 0000000111111110 (сдвиг целого числа) На каждый байт: LOW BYTE (ASL, вводим с 0 ): С <- 11111111 <- 0 Получаем: C = 1, 11111110 HIGH BYTE (ROL, мы входим с , переносим ) С <- 00000000 <- С = 1 Получаем: C = 0, 00000001 Объединение старшего байта и младшего байта вместе: 0000000111111110 (510 десятичное, правильно) ******** ######## * = старшая байтовая цифра, # = младшая байтовая цифра
Итак, если num1 - это 16-битное число, которое нужно умножить на два, мы можем использовать следующий код:
ASL num1_low ROL num1_high
Опять же, если мы не хотим изменять num1 и сохранять результат в желаемом месте:
LDA num1_low ASL STA result_low LDA num1_high ROL STA result_high
Division работает очень похоже, но мы должны использовать инструкции LSR (логический сдвиг вправо) и ROR (поворот вправо).Как вы, возможно, догадались, LSR аналогичен ASL, а ROR аналогичен ROL: оба вводятся с 0 или переносом соответственно, но сдвиг теперь выполняется вправо.
Тем не менее, это целочисленное деление, поэтому у нас может быть остаток. Но сейчас мы не будем об этом беспокоиться.
Деление 8-битного числа num1 на два выполняется кодом:
ЛСР номер1
или:
LDA номер1 ЛСР STA счет
Предположим, что num1 равно 128, мы можем увидеть, что происходит, используя двоичные числа:
128 в десятичной системе счисления = 10000000 по основанию 2 ЛСР 128 0 -> 10000000 -> С 01000000 -> C = 0Довольно легко увидеть, что результат равен 64.Поскольку 128 - четное число, остаток не создается. Флаг переноса содержит ноль в конце.
Давайте попробуем разделить 129 десятичных знаков на два:
129 в десятичной системе = 10000001 с основанием 2 ЛСР 129 0 -> 10000001 -> С 01000000 -> C = 1Теперь перенос держит 1 в конце. Это остальное.
Еще раз, мы можем использовать перенос, чтобы «связать» восьмибитовые числа вместе, тем самым выполняя операции с числами, превышающими 8 бит. Итак, следующий код умножит 16-битное число на два:
LSR num1_high ROR num1_low
Обратите внимание, что на этот раз мы начинаем со старшего байта .Поскольку мы выполняем сдвиг / поворот вправо, мы должны ввести целое число с 0 слева. Итак, именно поэтому мы сначала выполняем LSR старшего байта.
Если num1 является 16-битным числом и равно 256 десятичным, давайте еще раз посмотрим, что происходит при использовании двоичных чисел:
число1 = 256 в десятичной системе счисления = 0000000100000000 с основанием 2 LSR num1_high: 0 -> 00000001 -> С 00000000 -> C = 1 ROR num1_low: С -> 00000000 -> С 1 -> 00000000 -> С 10000000 -> C = 0 Конечный результат: 0000000010000000 = 128 десятичных чисел (256/2 = 128, правильно).******** ######## * = старшая байтовая цифра, # = младшая байтовая цифраКак видите, первый перенос, который мы получаем с LSR, используется как ссылка для хранения информации для второй операции (ROR).
16 разрядное число: 16 бит hex в 14 бит со знаком int python?Пролистать наверх


 ..
>>> g('1FFE')
8190
>>> g('E002')
-8190
..
>>> g('1FFE')
8190
>>> g('E002')
-8190
 signbit) — signbit if __name__ == ‘__main__’:
print(‘sext(0xe002, 14) =’, sext(0xe002, 14))
print(‘sext(0x1ffe, 14) =’, sext(0x1ffe, 14))
signbit) — signbit if __name__ == ‘__main__’:
print(‘sext(0xe002, 14) =’, sext(0xe002, 14))
print(‘sext(0x1ffe, 14) =’, sext(0x1ffe, 14))  Я уточняю, что каждый цветовой компонент этого изображения хранится на 14 или 16…
Я уточняю, что каждый цветовой компонент этого изображения хранится на 14 или 16…  ..
..



 Для того, чтобы сбросить настройки протокола, проделайте следующее:
Для того, чтобы сбросить настройки протокола, проделайте следующее:

 pack('<H',0xABCD)) # ary = array('B', [205, 171]) print("0x%X" % ary[0]) # 0xCD
pack('<H',0xABCD)) # ary = array('B', [205, 171]) print("0x%X" % ary[0]) # 0xCD Переполнение при вычислениях с фиксированной точкой не
вызывает
прерывания работы процессора. Машина продолжает считать, но результаты могут
оказаться неправильными.
Переполнение при вычислениях с фиксированной точкой не
вызывает
прерывания работы процессора. Машина продолжает считать, но результаты могут
оказаться неправильными. Здесь
m=0.25324 — мантисса, n=2 — порядок. Порядок указывает, на какое количество
позиций и в
каком направлении должна «переплыть», т.е. сместиться десятичная точка в
мантиссе. Отсюда название «плавающая точка».
Здесь
m=0.25324 — мантисса, n=2 — порядок. Порядок указывает, на какое количество
позиций и в
каком направлении должна «переплыть», т.е. сместиться десятичная точка в
мантиссе. Отсюда название «плавающая точка». Пусть в памяти компьютера вещественное число представляется в форме с плавающей
точкой в двоичной системе счисления (р=2) и занимает ячейку размером 4 байта. В
ячейке должна содержаться следующая информация о числе: знак числа, порядок и
значащие цифры мантиссы. Вот как эта информация располагается в ячейке:
Пусть в памяти компьютера вещественное число представляется в форме с плавающей
точкой в двоичной системе счисления (р=2) и занимает ячейку размером 4 байта. В
ячейке должна содержаться следующая информация о числе: знак числа, порядок и
значащие цифры мантиссы. Вот как эта информация располагается в ячейке: В
следующих
трех байтах хранятся значащие цифры мантиссы.
В
следующих
трех байтах хранятся значащие цифры мантиссы.

 Следовательно, максимальное и минимальное числа равны между
собой по модулю: Rmax = |Rmin|. Наименьшее по абсолютной величине число равно
нулю. Чему же равно Rmax? Это число с самой большой мантиссой и самым большим
порядком:
Следовательно, максимальное и минимальное числа равны между
собой по модулю: Rmax = |Rmin|. Наименьшее по абсолютной величине число равно
нулю. Чему же равно Rmax? Это число с самой большой мантиссой и самым большим
порядком: Множество же вещественных чисел, представимых в памяти ЭВМ в форме с
плавающей точкой, является ограниченным и дискретным. Каждое следующее значение
получается прибавлением к мантиссе предыдущего единицы в последнем (24-м)
разряде. Количество вещественных чисел, точно представимых в па-мяти машины,
вычисляется по формуле:
Множество же вещественных чисел, представимых в памяти ЭВМ в форме с
плавающей точкой, является ограниченным и дискретным. Каждое следующее значение
получается прибавлением к мантиссе предыдущего единицы в последнем (24-м)
разряде. Количество вещественных чисел, точно представимых в па-мяти машины,
вычисляется по формуле:


 Прямой код целого числа (J = n — 1, причем знаковым является крайний левый разряд) формируется как сумма 10 n-1 + | X |.
Прямой код целого числа (J = n — 1, причем знаковым является крайний левый разряд) формируется как сумма 10 n-1 + | X |. Действительно, при алгебраическом сложении чисел в прямом коде требуется выполнить четыре действия:
Действительно, при алгебраическом сложении чисел в прямом коде требуется выполнить четыре действия: Поскольку инверсия меньше дополнения на единицу младшего разряда, то для получения правильной разности необходимо производить соответствующую коррекцию суммы вспомогательных чисел.
Поскольку инверсия меньше дополнения на единицу младшего разряда, то для получения правильной разности необходимо производить соответствующую коррекцию суммы вспомогательных чисел.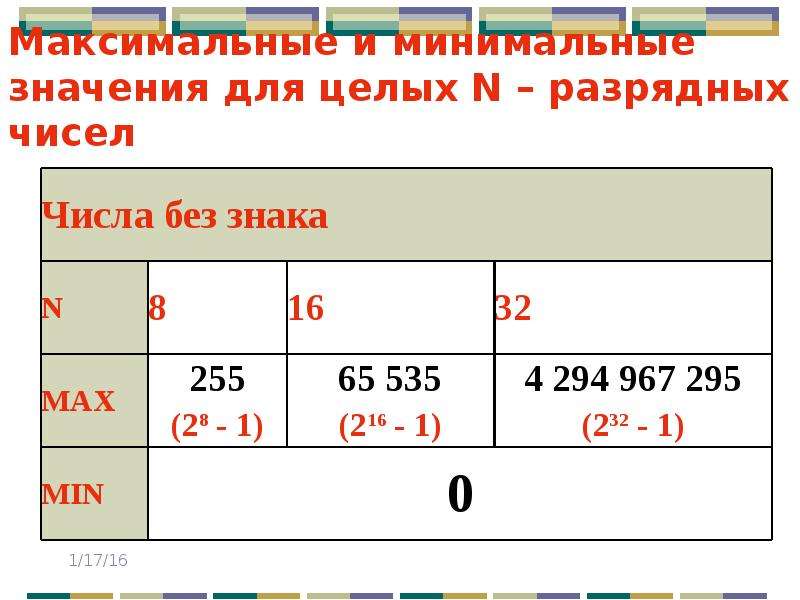 1100112 и X2 = -0.1100112 будут иметь вид [X1]обр = 0.110011; [X2]обр = 1.001100. Используя 8-разрядную сетку (J = 7) в дополнительном коде целые числа X1 = +1100112 и X2 = -1100112 будут иметь вид [X1]обр = 00110011; [X2]обр = 11001100.
1100112 и X2 = -0.1100112 будут иметь вид [X1]обр = 0.110011; [X2]обр = 1.001100. Используя 8-разрядную сетку (J = 7) в дополнительном коде целые числа X1 = +1100112 и X2 = -1100112 будут иметь вид [X1]обр = 00110011; [X2]обр = 11001100. Граничное число определяется как Xгр = 99 + 1 = 100 = 102 . Далее требуется алгебраически сложить числа Х1 = 84 и Х2 = -63. В соответствии с вышеизложенным, второе слагаемое поскольку оно отрицательно, заменится дополнением до Хгр = 102, т. е. положительным числом [X2]доп = 37. Далее выполняется арифметическое сложение чисел Х1 и [X2]доп:
Граничное число определяется как Xгр = 99 + 1 = 100 = 102 . Далее требуется алгебраически сложить числа Х1 = 84 и Х2 = -63. В соответствии с вышеизложенным, второе слагаемое поскольку оно отрицательно, заменится дополнением до Хгр = 102, т. е. положительным числом [X2]доп = 37. Далее выполняется арифметическое сложение чисел Х1 и [X2]доп:
 Оказывается, что сумма любой из этих пар равна старшей цифре системы счисления. Поскольку такие пары образуются при записи всех цифр сначала в прямом, а затем в обратном порядке, будем называть цифры, дающие в сумме старшую цифру, взаимно обратными. Замена в некотором отрицательном числе всех цифр на взаимно обратные равносильна сложению исходного числа с |Xmax|. Используя понятие взаимно обратных цифр, можно дать правило нахождения дополнения отрицательных чисел без использования вычитания: для получения дополнения отрицательного числа следует все цифры исходного числа заменить на взаимно обратные и к полученному таким образом «обратному» числу (инверсному изображению) добавить единицу младшего разряда.
Оказывается, что сумма любой из этих пар равна старшей цифре системы счисления. Поскольку такие пары образуются при записи всех цифр сначала в прямом, а затем в обратном порядке, будем называть цифры, дающие в сумме старшую цифру, взаимно обратными. Замена в некотором отрицательном числе всех цифр на взаимно обратные равносильна сложению исходного числа с |Xmax|. Используя понятие взаимно обратных цифр, можно дать правило нахождения дополнения отрицательных чисел без использования вычитания: для получения дополнения отрицательного числа следует все цифры исходного числа заменить на взаимно обратные и к полученному таким образом «обратному» числу (инверсному изображению) добавить единицу младшего разряда.

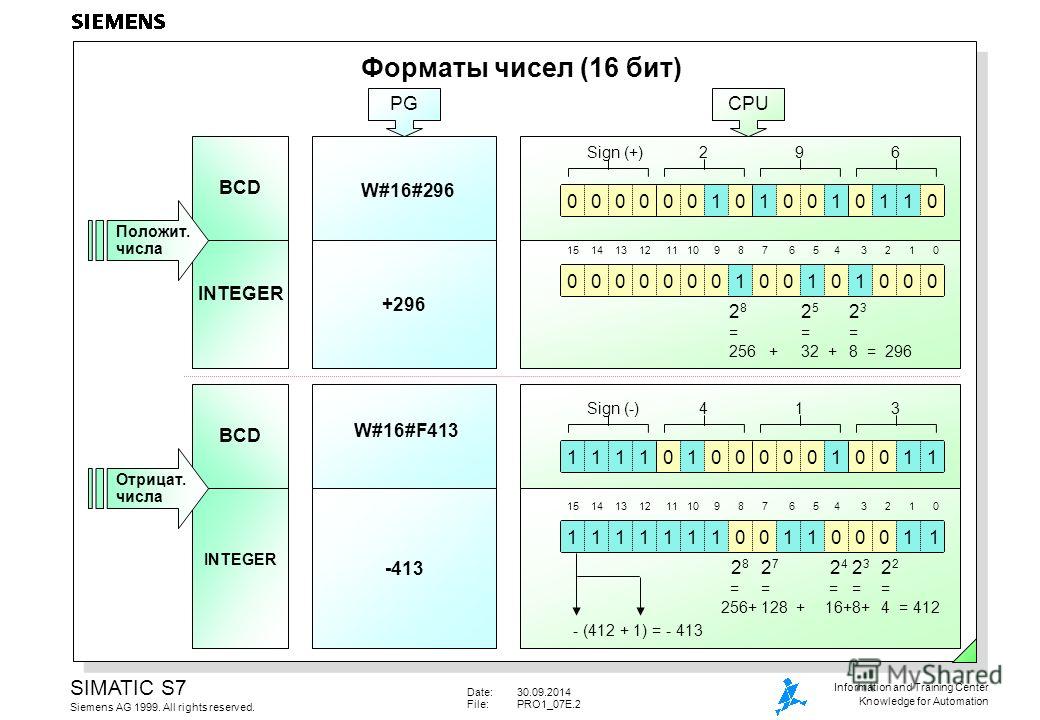 Однако практически производить такой переход легче по другому правилу: вначале заменить все цифры, за исключением знаковой, на взаимно обратные, после чего добавить единицу к младшему разряду.
Однако практически производить такой переход легче по другому правилу: вначале заменить все цифры, за исключением знаковой, на взаимно обратные, после чего добавить единицу к младшему разряду.

 32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
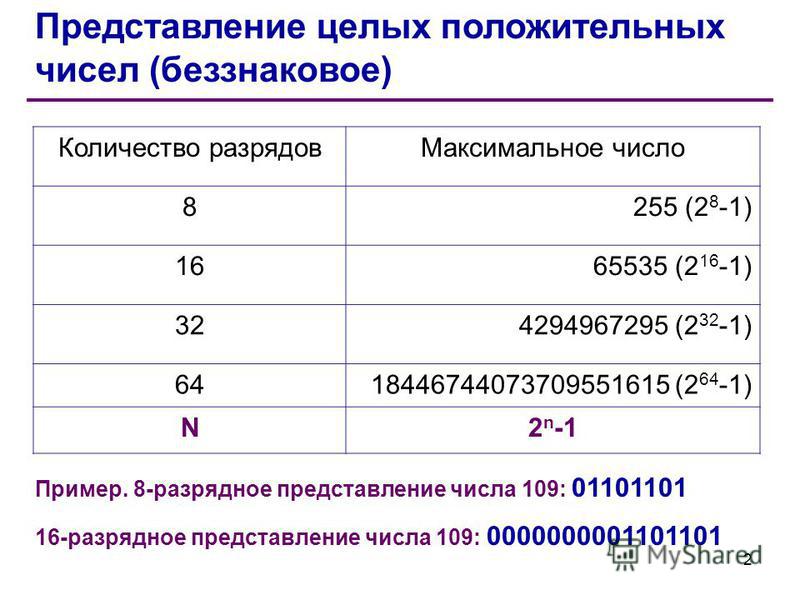

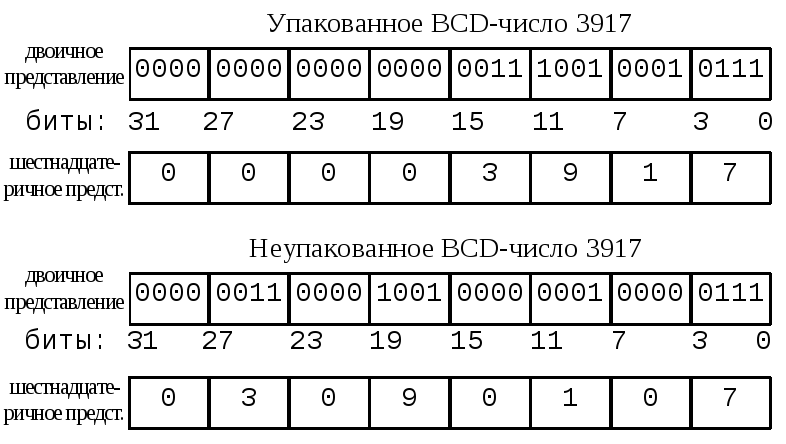
 5 = 30/32). Значение байта при этом будет 100.11110b или 0x9E.
5 = 30/32). Значение байта при этом будет 100.11110b или 0x9E.