Лучшая метрика для оценки точности классификационных моделей
Оценка качества классификационных моделей — сложная и трудоемкая задача. Сперва аналитик оценивает робастность классификационной модели с помощью таких средств, как AIC-BIC, площадь под ROC-кривой, критерий согласия Колмогорова-Смирнова и др. Следующим логическим шагом является оценка точности модели. Чтобы понять, почему эта задача является достаточно сложной, давайте рассмотрим базовые концепции.
Выход модели
В большинстве случаев классификационные модели, например, логистическая регрессия (logistic regression), дают на выходе вероятности в интервале от 0 до 1 вместо значений целевой переменой, таких как Да/Нет и т.п. Чтобы оценить точность модели, полученные вероятности необходимо преобразовать в значения целевой переменной. Давайте рассмотрим этот процесс на примере, представленном ниже.
Цель. Создать классификационную модель, идентифицирующую мошеннические операции.
Результат. Разбиение операций на 2 класса: мошеннические и добросовестные.
Разбиение операций на 2 класса: мошеннические и добросовестные.
Оценивание модели. Сравнение результатов классификации с фактическими данными.
Набор данных. Количество операций: 1000000. Количество мошеннических операций: 100. Количество добросовестных операций: 999900.
Мошеннические операции составляют всего 0.01% от всех операций. Таким образом, данная задача является типичным примером задачи с
Предположим, мы создали модель, которая классифицировала 95% операций как добросовестные, и все эти операции действительно оказались добросовестными. Звучит неплохо, однако мы не должны слишком радоваться по этому поводу, поскольку мошеннические операции составляют всего 0.01% операций, в то время как наша модель отнесла к классу мошеннических 5% операций.
Сравнив прогнозы модели с фактическими данными, мы получим 4 группы прогнозов:
- Истинноположительные (ИП). Мошеннические операции, классифицированные, как мошеннические.
- Истинноотрицательные (ИО). Добросовестные операции, классифицированные, как добросовестные.
- Ложноположительные (ЛП). Добросовестные операции, классифицированные, как мошеннические.
- Ложноотрицательные (ЛО). Мошеннические операции, классифицированные, как добросовестные.
Популярным способом представления этой информации является таблица сопряженности:
| Количество истинноположительных | Количество ложноотрицательных |
| Количество ложноположительных | Количество истинноотрицательных |
Как мы уже говорили, обычно классификационные модели дают на выходе вероятности. Ниже представлены первые 5 строк набора данных и прогнозы модели:
| Операция | Фактический класс операции | Прогноз |
| 1 | Добросовестная | 0.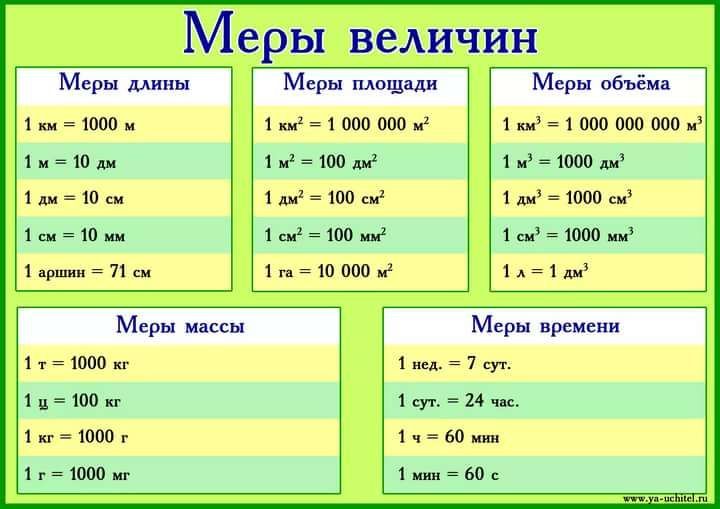 |
| 2 | Добросовестная | 0.10 |
| 3 | Мошенническая | 0.67 |
| 4 | Добросовестная | 0.60 |
| 5 | Добросовестная | 0.11 |
Предположим, что в качестве пороговой вероятности мы выбрали значение 0.5. То есть, если предсказанная моделью вероятность больше или равна 0.5, мы считаем операцию мошеннической, если меньше 0.5 – добросовестной. Соответственно, представленная выше таблица примет следующий вид:
| Операция | Фактический класс операции | Прогноз |
| 1 | Добросовестная | Добросовестная |
| 2 | Добросовестная | Добросовестная |
| 3 | Мошенническая | Мошенническая |
| 4 | Добросовестная | Мошенническая |
| 5 | Добросовестная | Добросовестная |
Обобщим прогнозы модели для полного набора данных с помощью таблицы сопряженности:
| ИП = 90 | ЛО = 10 |
| ЛП = 10 | ИО = 999890 |
Мы видим, что в таблице сопряженности нет ячеек с нулевыми значениями. Так насколько же хорош этот результат? Стремимся ли мы к тому, чтобы ЛП = 0 и ЛО = 0? Это зависит от цели прогноза.
Так насколько же хорош этот результат? Стремимся ли мы к тому, чтобы ЛП = 0 и ЛО = 0? Это зависит от цели прогноза.
Рассмотрим сценарий, где мы, как маркетинговые аналитики, хотели бы идентифицировать пользователей, которые склонны совершить покупку, но еще не совершили ее. Эти пользователи по своим характеристикам очень близки к пользователям, уже совершившим покупку. Таким образом, модель предскажет, что данные пользователи совершат покупку, хотя на самом деле это не произойдет. То есть, эти прогнозы будут ложноположительными. Следовательно, ненулевое значение ЛП также может быть полезно для нас. Как видите, вывод о качестве модели зависит от цели прогнозирования.
Основные метрики
Поскольку мы уже разобрались, как интерпретировать таблицу сопряженности, теперь давайте рассмотрим распространенные метрики, применяемые для оценивания качества классификационных моделей.
- Чувствительность (полнота)
Чувствительность (sensitivity), также известная, как полнота (recall), вычисляется по следующей формуле:
Чувствительность = ИП / (ИП + ЛО)
Поскольку формула не учитывает ЛП и ИО, чувствительность может дать нам смещенную оценку, особенно в случае несбалансированных классов. В задаче выявления мошенничества чувствительность представляет собой процент правильно классифицированных мошеннических операций от общего фактического количества мошеннических операций.
В задаче выявления мошенничества чувствительность представляет собой процент правильно классифицированных мошеннических операций от общего фактического количества мошеннических операций.
Чувствительность = 90 / (90 + 10) = 0.90
- Специфичность
Специфичность (specificity) вычисляется по следующей формуле:
Специфичность = ИО / (ИО + ЛП)
Поскольку формула не учитывает ЛО и ИП, специфичность может дать нам смещенную оценку, особенно в случае несбалансированных классов. В задаче выявления мошенничества специфичность представляет собой процент правильно классифицированных добросовестных операций от общего фактического количества добросовестных операций.
Специфичность = 999890 / (999890 + 10) = 1
- Точность
Точность (precision) вычисляется по следующей формуле:
Точность = ИП / (ИП + ЛП)
Поскольку формула не учитывает ЛО и ИО, точность, как и предыдущие метрики, может дать нам смещенную оценку, особенно в случае несбалансированных классов.
Точность = 90 / (90 + 10) = 0.90
- F-мера
F-мера (F1 score) представляет собой совместную оценку точности и полноты. Данная метрика вычисляется по следующей формуле:
F-мера = 2 * Точность * Полнота / (Точность + Полнота)
F-мера позволяет получить более сбалансированную характеристику модели, чем три метрики, рассмотренные выше. Однако, поскольку F-мера не учитывает ИО, эта метрика также может дать смещенную оценку в случае сценария, рассмотренного ниже.
F-мера = 2 * 0.90 * 0.90 / (0.90 + 0.90) = 0.90
- Коэффициент корреляции Мэтьюса
В отличие от остальных метрик, рассмотренных выше, коэффициент корреляции Мэтьюса (ККМ, Matthews сorrelation сoefficient) учитывает значения из всех ячеек матрицы сопряженности и вычисляется по следующей формуле:
ККМ может принимать значения из интервала от -1 до +1. Модель, получившая оценку +1, является идеальной. Модель, получившая оценку -1, является очень слабой. Одним из ключевых свойств ККМ является легкость интерпретации.
Модель, получившая оценку +1, является идеальной. Модель, получившая оценку -1, является очень слабой. Одним из ключевых свойств ККМ является легкость интерпретации.
Сравнение метрик
Далее мы оценим классификационную модель с помощью описанных выше метрик при различных пороговых вероятностях и сравним результаты.
Сценарий A. Пороговая вероятность 0.5.
Таблица сопряженности:
| ИП = 90 | ЛО = 10 |
| ЛП = 10 | ИО = 999890 |
Оценки модели, полученные с помощью различных метрик:
| Чувствительность | Специфичность | Точность | F-мера | ККМ |
| 0.90 | 1.00 | 0.90 | 0.90 | 0.90 |
Сценарий B. Пороговая вероятность 0.4.
Таблица сопряженности:
| ИП = 90 | ЛО = 10 |
| ЛП = 1910 | ИО = 997990 |
Мы видим, что при сценарии B существенно возросло значение ЛП по сравнению со сценарием A. Следовательно, мы должны наблюдать ухудшение оценок.
Следовательно, мы должны наблюдать ухудшение оценок.
Оценки модели, полученные с помощью различных метрик:
| Чувствительность | Специфичность | Точность | F-мера | ККМ |
| 0.90 | 1.00 | 0.05 | 0.09 | 0.20 |
Следует отметить, что значения чувствительности и специфичности не изменились.
Сценарий C. Пороговая вероятность 0.6.
Таблица сопряженности:
| ИП = 90 | ЛО = 1910 |
| ЛП = 10 | ИО = 997990 |
Мы видим, что при сценарии C существенно возросло значение ЛО по сравнению со сценарием A. Следовательно, мы должны наблюдать ухудшение оценок.
Оценки модели, полученные с помощью различных метрик:
| Чувствительность | Специфичность | Точность | F-мера | ККМ |
| 0.05 | 1.00 | 0.90 | 0. 09 09 |
0.20 |
Отметим, что значения специфичности и точности не изменились.
Основываясь на нашем сравнительном анализе, можно сделать вывод о том, что предпочтительными метриками являются F-мера и ККМ. Однако необходимо рассмотреть еще один сценарий.
В рассмотренных выше сценариях наша модель предсказывала вероятность того, что данная операция является мошеннической. Если модель будет предсказывать вероятность того, что данная операция является добросовестной, мы получим сценарий D.
Сценарий D. Пороговая вероятность 0.5.
Таблица сопряженности:
| ИП = 999890 | ЛО = 10 |
| ЛП = 10 | ИО = 90 |
Данная таблица аналогична таблице из сценария A, за исключением того, что значения для положительных и отрицательных прогнозов поменялись местами. В идеале оценки должны быть одинаковы для сценариев A и D.
Оценки модели, полученные с помощью различных метрик:
| Чувствительность | Специфичность | Точность | F-мера | ККМ |
| 1 | 0. 90 90 |
1 | 1 | 0.90 |
Как видим, все оценки, кроме ККМ, изменились по сравнению со сценарием A.
Итоговая таблица для всех сценариев:
| Сценарий | Чувствительность | Специфичность | Точность | F-мера | ККМ |
| A | 0.90 | 1.00 | 0.90 | 0.90 | 0.90 |
| B | 0.90 | 1.00 | 0.05 | 0.09 | 0.20 |
| C | 0.05 | 1.00 | 0.90 | 0.09 | 0.20 |
| D | 1 | 0.90 | 1 | 1 | 0.90 |
Заключение
Если вы, как аналитик, ищите метрику, чтобы оценить и максимизировать общее качество классификационной модели, оптимальным вариантом будет коэффициент корреляции Мэтьюса. Данная метрика не только легко интерпретируется, но также является устойчивой по отношению к смене класса, вероятность которого предсказывает модель.
Источник
Перевод Станислава Петренко
Метрики в задачах машинного обучения / Хабр
Привет, Хабр!
В задачах машинного обучения для оценки качества моделей и сравнения различных алгоритмов используются метрики, а их выбор и анализ — непременная часть работы датасатаниста.
В этой статье мы рассмотрим некоторые критерии качества в задачах классификации, обсудим, что является важным при выборе метрики и что может пойти не так.
Для демонстрации полезных функций sklearn и наглядного представления метрик мы будем использовать датасет по оттоку клиентов телеком-оператора.
Загрузим необходимые библиотеки и посмотрим на данные
import pandas as pd import matplotlib.pyplot as plt from matplotlib.pylab import rc, plot import seaborn as sns from sklearn.preprocessing import LabelEncoder, OneHotEncoder from sklearn.model_selection import cross_val_score from sklearn.linear_model import LogisticRegression from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier from sklearn.metrics import precision_recall_curve, classification_report from sklearn.model_selection import train_test_split df = pd.read_csv('../../data/telecom_churn.csv')
df.head(5)
Предобработка данных
# Сделаем маппинг бинарных колонок
# и закодируем dummy-кодированием штат (для простоты, лучше не делать так для деревянных моделей)
d = {'Yes' : 1, 'No' : 0}
df['International plan'] = df['International plan'].map(d)
df['Voice mail plan'] = df['Voice mail plan'].map(d)
df['Churn'] = df['Churn'].astype('int64')
le = LabelEncoder()
df['State'] = le.fit_transform(df['State'])
ohe = OneHotEncoder(sparse=False)
encoded_state = ohe.fit_transform(df['State'].values.reshape(-1, 1))
tmp = pd.DataFrame(encoded_state,
columns=['state ' + str(i) for i in range(encoded_state.shape[1])])
df = pd. concat([df, tmp], axis=1)
concat([df, tmp], axis=1)Accuracy, precision и recall
Перед переходом к самим метрикам необходимо ввести важную концепцию для описания этих метрик в терминах ошибок классификации — confusion matrix (матрица ошибок).
Допустим, что у нас есть два класса и алгоритм, предсказывающий принадлежность каждого объекта одному из классов, тогда матрица ошибок классификации будет выглядеть следующим образом:
| True Positive (TP) | False Positive (FP) | |
| False Negative (FN) | True Negative (TN) |
Здесь — это ответ алгоритма на объекте, а — истинная метка класса на этом объекте.
Таким образом, ошибки классификации бывают двух видов: False Negative (FN) и False Positive (FP).
Обучение алгоритма и построение матрицы ошибок
X = df.drop('Churn', axis=1) y = df['Churn'] # Делим выборку на train и test, все метрики будем оценивать на тестовом датасете X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y, test_size=0.33, random_state=42) # Обучаем ставшую родной логистическую регрессию lr = LogisticRegression(random_state=42) lr.fit(X_train, y_train) # Воспользуемся функцией построения матрицы ошибок из документации sklearn def plot_confusion_matrix(cm, classes, normalize=False, title='Confusion matrix', cmap=plt.cm.Blues): """ This function prints and plots the confusion matrix. Normalization can be applied by setting `normalize=True`. """ plt.imshow(cm, interpolation='nearest', cmap=cmap) plt.title(title) plt.colorbar() tick_marks = np.arange(len(classes)) plt.xticks(tick_marks, classes, rotation=45) plt.yticks(tick_marks, classes) if normalize: cm = cm.astype('float') / cm.
sum(axis=1)[:, np.newaxis] print("Normalized confusion matrix") else: print('Confusion matrix, without normalization') print(cm) thresh = cm.max() / 2. for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])): plt.text(j, i, cm[i, j], horizontalalignment="center", color="white" if cm[i, j] > thresh else "black") plt.tight_layout() plt.ylabel('True label') plt.xlabel('Predicted label') font = {'size' : 15} plt.rc('font', **font) cnf_matrix = confusion_matrix(y_test, lr.predict(X_test)) plt.figure(figsize=(10, 8)) plot_confusion_matrix(cnf_matrix, classes=['Non-churned', 'Churned'], title='Confusion matrix') plt.savefig("conf_matrix.png") plt.show()
Accuracy
Интуитивно понятной, очевидной и почти неиспользуемой метрикой является accuracy — доля правильных ответов алгоритма:
Эта метрика бесполезна в задачах с неравными классами, и это легко показать на примере.
Допустим, мы хотим оценить работу спам-фильтра почты. У нас есть 100 не-спам писем, 90 из которых наш классификатор определил верно (True Negative = 90, False Positive = 10), и 10 спам-писем, 5 из которых классификатор также определил верно (True Positive = 5, False Negative = 5).
Тогда accuracy:
Однако если мы просто будем предсказывать все письма как не-спам, то получим более высокую accuracy:
При этом, наша модель совершенно не обладает никакой предсказательной силой, так как изначально мы хотели определять письма со спамом. Преодолеть это нам поможет переход с общей для всех классов метрики к отдельным показателям качества классов.
Precision, recall и F-мера
Для оценки качества работы алгоритма на каждом из классов по отдельности введем метрики precision (точность) и recall (полнота).
Precision можно интерпретировать как долю объектов, названных классификатором положительными и при этом действительно являющимися положительными, а recall показывает, какую долю объектов положительного класса из всех объектов положительного класса нашел алгоритм.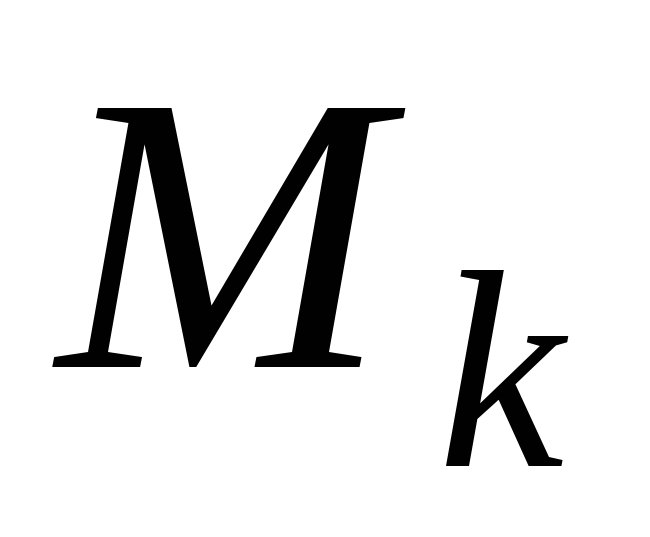
Именно введение precision не позволяет нам записывать все объекты в один класс, так как в этом случае мы получаем рост уровня False Positive. Recall демонстрирует способность алгоритма обнаруживать данный класс вообще, а precision — способность отличать этот класс от других классов.
Как мы отмечали ранее, ошибки классификации бывают двух видов: False Positive и False Negative. В статистике первый вид ошибок называют ошибкой I-го рода, а второй — ошибкой II-го рода. В нашей задаче по определению оттока абонентов, ошибкой первого рода будет принятие лояльного абонента за уходящего, так как наша нулевая гипотеза состоит в том, что никто из абонентов не уходит, а мы эту гипотезу отвергаем. Соответственно, ошибкой второго рода будет являться «пропуск» уходящего абонента и ошибочное принятие нулевой гипотезы.
Precision и recall не зависят, в отличие от accuracy, от соотношения классов и потому применимы в условиях несбалансированных выборок.
Часто в реальной практике стоит задача найти оптимальный (для заказчика) баланс между этими двумя метриками. Классическим примером является задача определения оттока клиентов.
Классическим примером является задача определения оттока клиентов.
Очевидно, что мы не можем находить всех уходящих в отток клиентов и только их. Но, определив стратегию и ресурс для удержания клиентов, мы можем подобрать нужные пороги по precision и recall. Например, можно сосредоточиться на удержании только высокодоходных клиентов или тех, кто уйдет с большей вероятностью, так как мы ограничены в ресурсах колл-центра.
Обычно при оптимизации гиперпараметров алгоритма (например, в случае перебора по сетке GridSearchCV ) используется одна метрика, улучшение которой мы и ожидаем увидеть на тестовой выборке.
Существует несколько различных способов объединить precision и recall в агрегированный критерий качества. F-мера (в общем случае ) — среднее гармоническое precision и recall :
в данном случае определяет вес точности в метрике, и при это среднее гармоническое (с множителем 2, чтобы в случае precision = 1 и recall = 1 иметь )
F-мера достигает максимума при полноте и точности, равными единице, и близка к нулю, если один из аргументов близок к нулю.
В sklearn есть удобная функция _metrics.classificationreport, возвращающая recall, precision и F-меру для каждого из классов, а также количество экземпляров каждого класса.
report = classification_report(y_test, lr.predict(X_test), target_names=['Non-churned', 'Churned']) print(report)
| class | precision | recall | f1-score | support |
|---|---|---|---|---|
| Non-churned | 0.88 | 0.97 | 0.93 | 941 |
| Churned | 0.60 | 0.25 | 0.35 | 159 |
| avg / total | 0.84 | 0.87 | 0.84 | 1100 |
Здесь необходимо отметить, что в случае задач с несбалансированными классами, которые превалируют в реальной практике, часто приходится прибегать к техникам искусственной модификации датасета для выравнивания соотношения классов. Их существует много, и мы не будем их касаться, здесь можно посмотреть некоторые методы и выбрать подходящий для вашей задачи.
Их существует много, и мы не будем их касаться, здесь можно посмотреть некоторые методы и выбрать подходящий для вашей задачи.
AUC-ROC и AUC-PR
При конвертации вещественного ответа алгоритма (как правило, вероятности принадлежности к классу, отдельно см. SVM) в бинарную метку, мы должны выбрать какой-либо порог, при котором 0 становится 1. Естественным и близким кажется порог, равный 0.5, но он не всегда оказывается оптимальным, например, при вышеупомянутом отсутствии баланса классов.
Одним из способов оценить модель в целом, не привязываясь к конкретному порогу, является AUC-ROC (или ROC AUC) — площадь (Area Under Curve) под кривой ошибок (Receiver Operating Characteristic curve ). Данная кривая представляет из себя линию от (0,0) до (1,1) в координатах True Positive Rate (TPR) и False Positive Rate (FPR):
TPR нам уже известна, это полнота, а FPR показывает, какую долю из объектов negative класса алгоритм предсказал неверно. В идеальном случае, когда классификатор не делает ошибок (FPR = 0, TPR = 1) мы получим площадь под кривой, равную единице; в противном случае, когда классификатор случайно выдает вероятности классов, AUC-ROC будет стремиться к 0.5, так как классификатор будет выдавать одинаковое количество TP и FP.
В идеальном случае, когда классификатор не делает ошибок (FPR = 0, TPR = 1) мы получим площадь под кривой, равную единице; в противном случае, когда классификатор случайно выдает вероятности классов, AUC-ROC будет стремиться к 0.5, так как классификатор будет выдавать одинаковое количество TP и FP.
Каждая точка на графике соответствует выбору некоторого порога. Площадь под кривой в данном случае показывает качество алгоритма (больше — лучше), кроме этого, важной является крутизна самой кривой — мы хотим максимизировать TPR, минимизируя FPR, а значит, наша кривая в идеале должна стремиться к точке (0,1).
Код отрисовки ROC-кривой
sns.set(font_scale=1.5)
sns.set_color_codes("muted")
plt.figure(figsize=(10, 8))
fpr, tpr, thresholds = roc_curve(y_test, lr.predict_proba(X_test)[:,1], pos_label=1)
lw = 2
plt.plot(fpr, tpr, lw=lw, label='ROC curve ')
plt.plot([0, 1], [0, 1])
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt. ylabel('True Positive Rate')
plt.title('ROC curve')
plt.savefig("ROC.png")
plt.show()
ylabel('True Positive Rate')
plt.title('ROC curve')
plt.savefig("ROC.png")
plt.show()
Критерий AUC-ROC устойчив к несбалансированным классам (спойлер: увы, не всё так однозначно) и может быть интерпретирован как вероятность того, что случайно выбранный positive объект будет проранжирован классификатором выше (будет иметь более высокую вероятность быть positive), чем случайно выбранный negative объект.
Рассмотрим следующую задачу: нам необходимо выбрать 100 релевантных документов из 1 миллиона документов. Мы намашинлернили два алгоритма:
- Алгоритм 1 возвращает 100 документов, 90 из которых релевантны. Таким образом,
- Алгоритм 2 возвращает 2000 документов, 90 из которых релевантны. Таким образом,
Скорее всего, мы бы выбрали первый алгоритм, который выдает очень мало False Positive на фоне своего конкурента. Но разница в False Positive Rate между этими двумя алгоритмами крайне мала — всего 0. 0019. Это является следствием того, что AUC-ROC измеряет долю False Positive относительно True Negative и в задачах, где нам не так важен второй (больший) класс, может давать не совсем адекватную картину при сравнении алгоритмов.
0019. Это является следствием того, что AUC-ROC измеряет долю False Positive относительно True Negative и в задачах, где нам не так важен второй (больший) класс, может давать не совсем адекватную картину при сравнении алгоритмов.
Для того чтобы поправить положение, вернемся к полноте и точности :
- Алгоритм 1
- Алгоритм 2
Здесь уже заметна существенная разница между двумя алгоритмами — 0.855 в точности!
Precision и recall также используют для построения кривой и, аналогично AUC-ROC, находят площадь под ней.
Здесь можно отметить, что на маленьких датасетах площадь под PR-кривой может быть чересчур оптимистична, потому как вычисляется по методу трапеций, но обычно в таких задачах данных достаточно. За подробностями о взаимоотношениях AUC-ROC и AUC-PR можно обратиться сюда.
Logistic Loss
Особняком стоит логистическая функция потерь, определяемая как:
здесь — это ответ алгоритма на -ом объекте, — истинная метка класса на -ом объекте, а размер выборки.
Подробно про математическую интерпретацию логистической функции потерь уже написано в рамках поста про линейные модели.
Данная метрика нечасто выступает в бизнес-требованиях, но часто — в задачах на kaggle.
Интуитивно можно представить минимизацию logloss как задачу максимизации accuracy путем штрафа за неверные предсказания. Однако необходимо отметить, что logloss крайне сильно штрафует за уверенность классификатора в неверном ответе.
Рассмотрим пример:
def logloss_crutch(y_true, y_pred, eps=1e-15):
return - (y_true * np.log(y_pred) + (1 - y_true) * np.log(1 - y_pred))
print('Logloss при неуверенной классификации %f' % logloss_crutch(1, 0.5))
>> Logloss при неуверенной классификации 0.693147
print('Logloss при уверенной классификации и верном ответе %f' % logloss_crutch(1, 0.9))
>> Logloss при уверенной классификации и верном ответе 0.105361
print('Logloss при уверенной классификации и НЕверном ответе %f' % logloss_crutch(1, 0.1))
>> Logloss при уверенной классификации и НЕверном ответе 2. 302585
302585Отметим, как драматически выросла logloss при неверном ответе и уверенной классификации!
Следовательно, ошибка на одном объекте может дать существенное ухудшение общей ошибки на выборке. Такие объекты часто бывают выбросами, которые нужно не забывать фильтровать или рассматривать отдельно.
Всё становится на свои места, если нарисовать график logloss:
Видно, что чем ближе к нулю ответ алгоритма при ground truth = 1, тем выше значение ошибки и круче растёт кривая.
Подытожим:
- В случае многоклассовой классификации нужно внимательно следить за метриками каждого из классов и следовать логике решения задачи, а не оптимизации метрики
- В случае неравных классов нужно подбирать баланс классов для обучения и метрику, которая будет корректно отражать качество классификации
- Выбор метрики нужно делать с фокусом на предметную область, предварительно обрабатывая данные и, возможно, сегментируя (как в случае с делением на богатых и бедных клиентов)
Полезные ссылки
- Курс Евгения Соколова: Семинар по выбору моделей (там есть информация по метрикам задач регрессии)
- Задачки на AUC-ROC от А.
 Г. Дьяконова
Г. Дьяконова - Дополнительно о других метриках можно почитать на kaggle. К описанию каждой метрики добавлена ссылка на соревнования, где она использовалась
- Презентация Богдана Мельника aka ld86 про обучение на несбалансированных выборках
Благодарности
Спасибо mephistopheies и madrugado за помощь в подготовке статьи.
Определение F-оценки | Глубокий ИИ
Что такое F-оценка?
F-оценка, также называемая F1-оценкой, является мерой точности модели в наборе данных. Он используется для оценки систем бинарной классификации, которые классифицируют примеры на «положительные» или «отрицательные».
F-оценка — это способ объединения точности и полноты модели, и он определяется как среднее гармоническое точности и полноты модели.
F-оценка обычно используется для оценки систем поиска информации, таких как поисковые системы, а также для многих видов моделей машинного обучения, в частности, для обработки естественного языка.
Можно настроить F-оценку, чтобы придать большее значение точности, чем отзыву, или наоборот. Обычными скорректированными F-оценками являются F0,5-оценка и F2-оценка, а также стандартная F1-оценка.
Формула F-оценки
Формула для стандартной оценки F1 представляет собой среднее гармоническое точности и полноты. Совершенная модель имеет F-оценку 1.
Математическое определение F-оценки
Объяснение символов формулы F-оценки
| точность | Точность — это доля истинно положительных примеров среди примеров, которые модель классифицировала как положительные. Другими словами, количество истинных срабатываний, деленное на количество ложных срабатываний плюс истинные срабатывания. |
| отзыв | отзыв, также известный как чувствительность, представляет собой долю примеров, классифицированных как положительные, среди общего числа положительных примеров. Другими словами, количество истинных положительных результатов, деленное на количество истинных положительных результатов плюс ложноотрицательные результаты. |
| | Количество истинных положительных результатов, классифицированных моделью. |
| | Количество ложноотрицательных результатов, классифицированных моделью. |
| | Количество ложных срабатываний, классифицированных моделью. |
Обобщенный F
β -оценка ФормулаСкорректированная F-оценка позволяет нам более высоко взвешивать точность или полноту, если это более важно для нашего варианта использования. Его формула немного отличается:
Математическое определение F β -SCORE
F
β -Score Символы, как это| |
| |
| |
Расчет F-показателя
Пример расчета F-показателя №1: Базовый F-показатель
Представим, что у нас есть дерево с десятью яблоками на нем. Семь созрели, а три еще не созрели, но мы не знаем, какой из них какой. У нас есть ИИ, который обучен распознавать, какие яблоки созрели для сбора, и выбирать все спелые яблоки, а не незрелые яблоки. Мы хотели бы рассчитать F-оценку, и мы считаем, что и точность, и полнота одинаково важны, поэтому мы установим β на 1 и используйте оценку F1.
ИИ выбирает пять спелых яблок, но также выбирает одно незрелое яблоко.
Мы можем представить истинные и ложные положительные и отрицательные результаты в матрице путаницы следующим образом:
Точность модели — это количество правильно собранных спелых яблок, деленное на все яблоки, собранные моделью.
Отзыв – это количество правильно собранных спелых яблок, деленное на общее количество спелых яблок.
Теперь мы можем рассчитать F-показатель
Напомним, что F-показатель представляет собой среднее геометрическое точности и полноты. Как и среднее арифметическое, F-оценка как среднее геометрическое находится между точностью и полнотой.
Пример расчета F-показателя №2: F2-показателя
Давайте представим, что теперь мы считаем, что отзыв в нашей модели в два раза важнее точности. Мы рассматриваем сверточную нейронную сеть в области медицины, которая оценивает маммограммы и обнаруживает опухоли. Мы считаем, что гораздо хуже пропустить опухоль, чем подать ложную тревогу по поводу несуществующей опухоли.
Используя те же цифры из последнего примера, давайте представим, что мы запускаем модель на десяти маммограммах. Модель выявляет опухоль на шести маммограммах и дает «все ясно» на четырех маммограммах.
Позже мы обнаруживаем, что из шести обнаруженных опухолей одна была ложной тревогой, другими словами, ложным срабатыванием. Из четырех четких маммограмм две действительно содержали опухоль и были ложноотрицательными.
Числа tp, fp, tn и fn такие же, как и в последнем примере, а значит, такие же точность и полнота. Поскольку мы придаем весу полноту в два раза большую важность, чем точность, мы должны использовать формулу для оценки F2. Полагая β = 2, получаем:
Поскольку мы взвесили полноту более высоко, а модель имеет хорошую точность, но плохую полноту, наш F-показатель снизился с 0,77 до 0,74 по сравнению с примером сборщика яблок, где точность и полнота были взвешены одинаково. Это показывает, как можно использовать оценку F2, когда стоимость ложноположительного результата не равна стоимости ложноотрицательного результата. Это распространенный сценарий при использовании ИИ в здравоохранении.
Пример расчета F-оценки №3: F2-оценка
Предположим, мы настроили классификатор маммографии. Мы снова проверяем это на другом наборе из десяти маммограмм.
Мы обнаруживаем, что теперь имеется два ложноположительных результата и только один ложноотрицательный результат, в то время как количество истинно положительных и истинно отрицательных результатов осталось прежним.
Снова подставив значения из матрицы путаницы в формулы точности и полноты, мы получим:
Полнота нашей модели улучшилась по сравнению с предыдущим примером, а точность снизилась.
Снова вычисляем оценку F2:
Запоминание улучшилось за счет точности, и это привело к улучшению оценки F2. Это связано с тем, что, используя оценку F2, мы отдаем предпочтение отзыву, а не точности.
Здесь полезно отметить, что показатель F2 улучшился, но точность модели (доля правильно классифицированных примеров) осталась прежней, поскольку модель по-прежнему правильно классифицировала семь примеров.
F-показатель и точность
Существует ряд показателей, которые можно использовать для оценки модели бинарной классификации, и точность является одной из самых простых для понимания. Точность определяется просто как количество правильно классифицированных примеров, деленное на общее количество примеров. Точность может быть полезной, но она не принимает во внимание тонкости дисбаланса классов или разную стоимость ложноотрицательных и ложноположительных результатов.
Оценка F1 полезна:
• при различной стоимости ложноположительных или ложноотрицательных результатов, например, в маммографии
• при наличии большого дисбаланса классов, например, если 10% яблок на деревьях, как правило, незрелые. В этом случае точность может ввести в заблуждение, поскольку классификатор, который классифицирует все яблоки как спелые, автоматически получит точность 90%, но будет бесполезен для реальных приложений.
Преимущество точности состоит в том, что ее очень легко интерпретировать, но недостатком является то, что она ненадежна, когда данные распределены неравномерно или когда существует более высокая стоимость, связанная с определенным типом ошибки.
Расчет F-показателя в зависимости от точности
Во всех трех приведенных выше примерах классификатор правильно классифицировал семь из десяти примеров (яблоки или маммограммы) и неправильно классифицировал три примера.
Точность определяется как отношение правильно классифицированных примеров ко всем примерам, поэтому для всех трех случаев мы имеем:
потому что оценка F2 придает большее значение запоминанию, чем точности.
Для модели с более низкой полнотой и более высокой точностью F2 составил:
А для модели с более высокой полнотой F2 составил:
менее надежен и неспособен уловить нюансы различных типов ошибок.
Расчет F-показателя и точности с учетом дисбаланса классов
Представим дерево со 100 яблоками, 90 из которых спелые, а 10 незрелые.
У нас есть ИИ, который очень доволен триггерами, классифицирует все 100 как созревшие и выбирает все. Ясно, что модель, классифицирующая все примеры как положительные, не очень полезна.
В этом случае наша матрица путаницы будет выглядеть следующим образом:
Точность будет следующей:
Мы можем видеть, что наша модель достигла точности 90% без принятия каких-либо полезных решений.
Вычисляя точность и полноту, получаем
Подставляя их в формулу для F 1 , мы получаем:
Принимая во внимание дисбаланс классов, если бы мы заранее подозревали, что наша модель страдает низкой точностью, мы могли бы выбрать скорректированный F-показатель. с β = 0,5 для приоритета точности:
с β = 0,5 для приоритета точности:
Из этого примера видно, что точность гораздо менее надежна, когда существует большой дисбаланс классов, и F-оценка может быть скорректирована, чтобы учесть, учитываем ли мы точность или полноту быть более важным для данной задачи.
Применение F-оценки
Существует ряд областей ИИ, где F-оценка является широко используемой метрикой для оценки производительности модели.
F-оценка в поиске информации
Приложения для поиска информации, такие как поисковые системы, часто оцениваются с помощью F-оценки.
Поисковая система должна индексировать потенциально миллиарды документов и возвращать пользователю небольшое количество релевантных результатов за очень короткое время. Обычно первая страница результатов, возвращаемых пользователю, содержит не более десяти документов. Большинство пользователей не переходят на вторую страницу результатов, поэтому очень важно, чтобы первые десять результатов содержали релевантные страницы.
Первоначально оценка F 1 в основном использовалась для оценки поисковых систем, но в настоящее время обычно предпочтительнее откалиброванная оценка F β , поскольку она обеспечивает более точный контроль и позволяет нам отдавать предпочтение точности или отзыву. В идеале поисковая система не должна пропускать ни одного релевантного документа по запросу, но и не должна выдавать большое количество нерелевантных документов на первой странице.
F-оценка является мерой, основанной на множестве, что означает, что если вычисляется F-оценка первых десяти результатов, то F-оценка не учитывает относительное ранжирование этих документов. По этой причине F-оценка часто используется в сочетании с другими показателями, такими как средняя точность или 11-точечная интерполированная средняя точность, чтобы получить хорошее представление о производительности поисковой системы.
F-оценка в обработке естественного языка
Существует множество приложений для обработки естественного языка, которые легче всего оценить с помощью F-оценки. Например, при распознавании именованных объектов модель машинного обучения анализирует документ и должна идентифицировать любые личные имена и адреса в тексте.
Например, при распознавании именованных объектов модель машинного обучения анализирует документ и должна идентифицировать любые личные имена и адреса в тексте.
В биомедицинских науках модели распознавания именованных объектов часто используются для распознавания названий белков в документах, поскольку они часто похожи на повседневные английские слова или аббревиатуры и программному обеспечению очень трудно их точно идентифицировать. Пример предложения:
Сшивание CD 40 на В-клетках быстро активирует…
Модель должна определить, что «CD 40» — это название белка.
Модель обучается на данных, где отдельные слова были аннотированы как начало белка или внутри него:
Когда модель запущена, можно сравнить список истинных белков (основные истины) белкам, распознаваемым моделью (прогнозируемые значения).
Сравнивая списки, можно рассчитать точность и полноту, а затем F 1 , F 2 , F 0,5 или другой F β -оценка может быть выбрана для соответствующей оценки модели.
История F-оценки
Считается, что F-оценка впервые была определена голландским профессором компьютерных наук Корнелисом Йоостом ван Рейсбергеном, который считается одним из отцов-основателей области поиска информации. В своей книге 1979 года «Поиск информации» он определил функцию, очень похожую на F-оценку, признав неадекватность точности в качестве показателя для систем поиска информации.
В своей книге он назвал свою метрику функцией эффективности и присвоил ей букву E , потому что она «измеряет эффективность поиска по отношению к пользователю, который придает в β раз большее значение припоминанию, чем точности». . Неизвестно, почему F-оценке сегодня присваивается буква F .
Ссылки
Van Rijsbergen, CJ (1979). Информационный поиск (2-е изд.). Баттерворт-Хайнеманн.
Ю. Сасаки, Правда о F-мере (2007 г.), https://www.cs.odu.edu/~mukka/cs795sum09dm/Lecturenotes/Day3/F-measure-YS-26Oct07.pdf
Как рассчитать точность, полноту и F-меру для несбалансированной классификации
Последнее обновление: 2 августа 2020 г.
Точность классификации — это общее количество правильных прогнозов, деленное на общее количество прогнозов, сделанных для набора данных.
В качестве меры производительности точность не подходит для задач несбалансированной классификации.
Основная причина заключается в том, что подавляющее количество примеров из класса (или классов) большинства превысит количество примеров из класса меньшинства, а это означает, что даже неумелые модели могут достичь показателей точности 90 или 99 процентов, в зависимости от того, как серьезный дисбаланс классов случается.
Альтернативой использованию точности классификации является использование показателей точности и полноты.
В этом уроке вы узнаете, как рассчитывать и развивать интуицию для точности и отзыва для несбалансированной классификации.
После прохождения этого урока вы будете знать:
- Точность количественно определяет количество предсказаний положительного класса, которые фактически относятся к положительному классу.

- Отзыв определяет количество положительных прогнозов класса, сделанных из всех положительных примеров в наборе данных.
- F-Measure обеспечивает единую оценку, которая уравновешивает как точность, так и полноту в одном числе.
Начните свой проект с моей новой книги «Несбалансированная классификация с помощью Python», включающей пошаговые руководства и файлы исходного кода Python для всех примеров.
Давайте начнем.
- Обновление, январь 2020 г. : улучшены формулировки о цели точности и отзыва. Исправлены опечатки в отношении того, какие точность и полнота стремятся свести к минимуму (спасибо за комментарии!).
- Обновление, февраль 2020 г. : исправлена опечатка в имени переменной для отзыва и f1.
Как рассчитать точность, полноту и F-меру для несбалансированной классификации
Фото Вальдемара Мергера, некоторые права защищены.
Обзор учебника
Это руководство разделено на пять частей. они:
- Матрица путаницы для несбалансированной классификации
- Точность для несбалансированной классификации
- Отзыв из-за несбалансированной классификации
- Сравнение точности и полноты для несбалансированной классификации
- F-мера для несбалансированной классификации
Матрица путаницы для несбалансированной классификации
Прежде чем мы углубимся в точность и отзыв, важно просмотреть матрицу путаницы.
Для несбалансированных задач классификации класс большинства обычно называют отрицательным результатом (например, « без изменений » или « отрицательный результат теста »), а класс меньшинства обычно называют положительным результатом ( например, «изменение» или «положительный результат теста»).
Матрица путаницы дает больше информации не только о производительности прогностической модели, но и о том, какие классы предсказываются правильно, какие неправильно и какие ошибки совершаются.
Простейшая матрица путаницы предназначена для задачи классификации с двумя классами, с отрицательным (класс 0) и положительным (класс 1) классами.
В этом типе матрицы путаницы каждая ячейка в таблице имеет конкретное и понятное имя, резюмированное следующим образом:
| Положительный прогноз | Отрицательный прогноз Положительный класс | Истинный положительный результат (TP) | Ложноотрицательный (ЛН) Отрицательный класс | Ложноположительный результат (FP) | Истинно отрицательный (TN)
| | Положительный прогноз | Отрицательный прогноз Положительный класс | Истинный положительный результат (TP) | Ложноотрицательный (FN) Отрицательный класс | Ложноположительный результат (FP) | Истинный отрицательный результат (TN) |
Метрики точности и полноты определяются с точки зрения ячеек в матрице путаницы, в частности таких терминов, как истинно положительные и ложноотрицательные результаты.
Теперь, когда мы освежили матрицу путаницы, давайте более подробно рассмотрим показатель точности.
Точность для несбалансированной классификации
Точность — это показатель, который количественно определяет количество сделанных правильных положительных прогнозов.
Точность, таким образом, вычисляет точность для класса меньшинства.
Рассчитывается как отношение правильно предсказанных положительных примеров к общему количеству предсказанных положительных примеров.
Точность оценивает долю правильно классифицированных экземпляров среди тех, которые классифицированы как положительные …
— Страница 52, Изучение несбалансированных наборов данных, 2018.
Точность для двоичной классификации
В задаче несбалансированной классификации с двумя классами точность рассчитывается как количество истинных срабатываний, деленное на общее количество истинных срабатываний и ложных срабатываний.
- Точность = TruePositives / (TruePositives + FalsePositives)
Результатом является значение от 0,0 для отсутствия точности до 1,0 для полной или идеальной точности.
Давайте конкретизируем этот расчет на нескольких примерах.
Рассмотрим набор данных с отношением меньшинства к большинству 1:100, со 100 примерами меньшинства и 10 000 примеров классов большинства.
Модель делает предсказания и предсказывает 120 примеров как принадлежащих к классу меньшинства, 90 из которых верны, а 30 неверны.
Точность для этой модели рассчитывается как:
- Точность = TruePositives / (TruePositives + FalsePositives)
- Точность = 90 / (90 + 30)
- Точность = 90/120
- Точность = 0,75
Результатом является точность 0,75, что является разумным значением, но не выдающимся.
Как видите, точность — это просто отношение правильных положительных прогнозов ко всем сделанным положительным прогнозам или точность прогнозов меньшинства.
Рассмотрим тот же набор данных, где модель предсказывает 50 примеров, принадлежащих классу меньшинства, 45 из которых являются истинно положительными, а пять — ложноположительными. Мы можем рассчитать точность для этой модели следующим образом:
- Точность = TruePositives / (TruePositives + FalsePositives)
- Точность = 45 / (45 + 5)
- Точность = 45/50
- Точность = 0,90
В этом случае, несмотря на то, что модель предсказала гораздо меньшее количество примеров, принадлежащих к классу меньшинства, соотношение правильных положительных примеров намного лучше.
Это подчеркивает, что, хотя точность и полезна, она не раскрывает всей истории. Он не комментирует, сколько примеров реального положительного класса было предсказано как принадлежащее к отрицательному классу, так называемые ложноотрицательные результаты.
Хотите начать работу с классификацией дисбаланса?
Пройдите мой бесплатный 7-дневный экспресс-курс по электронной почте прямо сейчас (с образцом кода).
Нажмите, чтобы зарегистрироваться, а также получить бесплатную электронную версию курса в формате PDF.
Точность для многоклассовой классификации
Точность не ограничивается задачами бинарной классификации.
В задаче несбалансированной классификации с более чем двумя классами точность рассчитывается как сумма истинных срабатываний по всем классам, деленная на сумму истинных срабатываний и ложных срабатываний по всем классам.
- Точность = Сумма c в C TruePositives_c / Сумма c в C (TruePositives_c + FalsePositives_c)
Например, у нас может возникнуть проблема несбалансированной мультиклассовой классификации, в которой класс большинства является отрицательным классом, но есть два положительных класса меньшинства: класс 1 и класс 2. Точность может количественно определить соотношение правильных прогнозов для обоих положительных классов.
Рассмотрим набор данных с соотношением классов меньшинства и большинства 1:1:100, то есть соотношением 1:1 для каждого положительного класса и соотношением 1:100 для классов меньшинства к классу большинства, и у нас есть 100 примеров в каждом класс меньшинства и 10 000 примеров в классе большинства.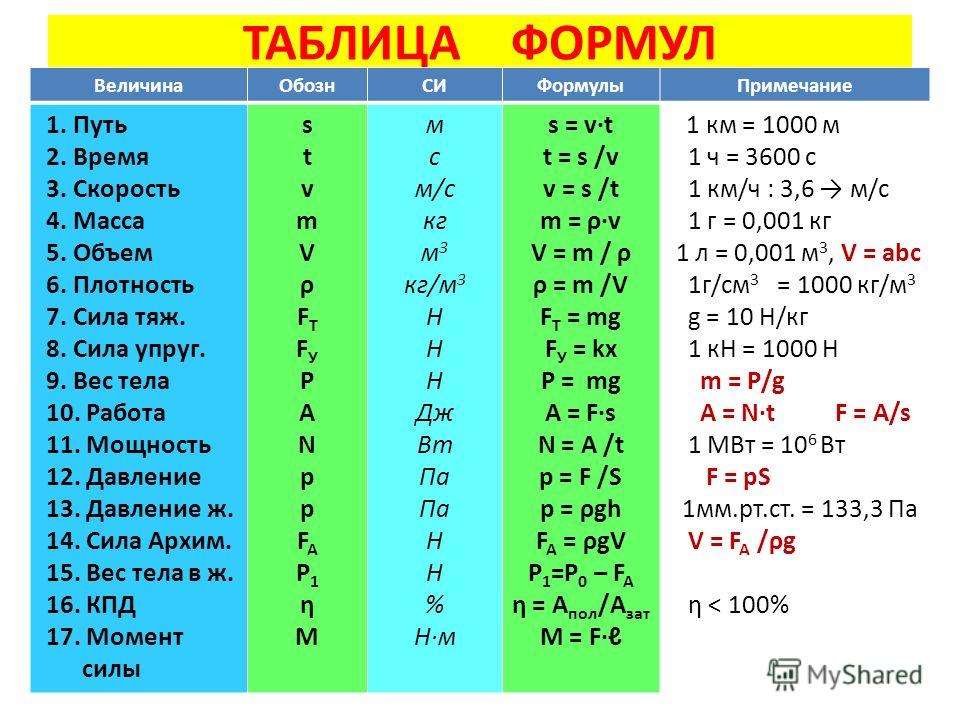
Модель делает предсказания и предсказывает 70 примеров для первого класса меньшинства, где 50 правильных и 20 неправильных. Он предсказывает 150 для второго класса с 99 правильными и 51 неправильным. Точность можно рассчитать для этой модели следующим образом:
- Точность = (TruePositives_1 + TruePositives_2) / ((TruePositives_1 + TruePositives_2) + (FalsePositives_1 + FalsePositives_2))
- Точность = (50 + 99) / ((50 + 99) + (20 + 51))
- Точность = 149/ (149 + 71)
- Точность = 149/220
- Точность = 0,677
Мы видим, что вычисление метрики точности масштабируется по мере увеличения числа миноритарных классов.
Расчет точности с помощью Scikit-Learn
Показатель точности можно рассчитать с помощью функции scikit-learn precision_score().
Например, мы можем использовать эту функцию для вычисления точности для сценариев из предыдущего раздела.
Во-первых, случай, когда имеется от 100 положительных до 10 000 отрицательных примеров, а модель предсказывает 90 истинных срабатываний и 30 ложных срабатываний. Полный пример приведен ниже.
Полный пример приведен ниже.
# вычисляет точность для набора данных 1:100 с 90 tp и 30 fp из sklearn.metrics импортировать precision_score # определить фактический act_pos = [1 для _ в диапазоне (100)] act_neg = [0 для _ в диапазоне (10000)] y_true = акт_поз + акт_отрицательный # определяем прогнозы pred_pos = [0 для _ в диапазоне (10)] + [1 для _ в диапазоне (90)] pred_neg = [1 для _ в диапазоне (30)] + [0 для _ в диапазоне (9970)] y_pred = пред_поз + пред_отрицательный # рассчитать прогноз точность = точность_оценка (y_true, y_pred, среднее = ‘двоичный’) print(‘Точность: %.3f’ % точности)
|
1 2 3 4 5 6 7 8
10 110005 12 13 |
# вычисляет точность для набора данных масштаба 1:100 с 90 tp и 30 fp из sklearn.metrics _ в диапазоне(10000)] y_true = act_pos + act_neg # определить прогнозы pred_pos = [0 для _ в диапазоне (10)] + [1 для _ в диапазоне (90)] pred_neg = [1 для _ в диапазоне (30) ] + [0 for _ in range(9970)] y_pred = pred_pos + pred_neg # расчет прогноза точность = точность_оценки(y_true, y_pred, medium=’binary’) print(‘Точность: %. |
При выполнении примера вычисляется точность, соответствующая нашему ручному расчету.
Точность: 0,750
| Точность: 0,750 |
Затем мы можем использовать ту же функцию для вычисления точности для задачи мультикласса с 1:1:100, со 100 примерами в каждом классе меньшинства и 10 000 в классе большинства. Модель предсказывает 50 истинных срабатываний и 20 ложных срабатываний для класса 1 и 99 истинных срабатываний и 51 ложноположительный результат для класса 2.
При использовании precision_score() для мультиклассовой классификации важно указать миноритарные классы с помощью аргумента « labels » и установить для аргумента « среднее » значение « микро », чтобы гарантировать, что расчет выполняется так, как мы ожидаем.
Полный пример приведен ниже.
# вычисляет точность для набора данных 1:1:100 с 50tp, 20fp, 99tp, 51fp
из sklearn.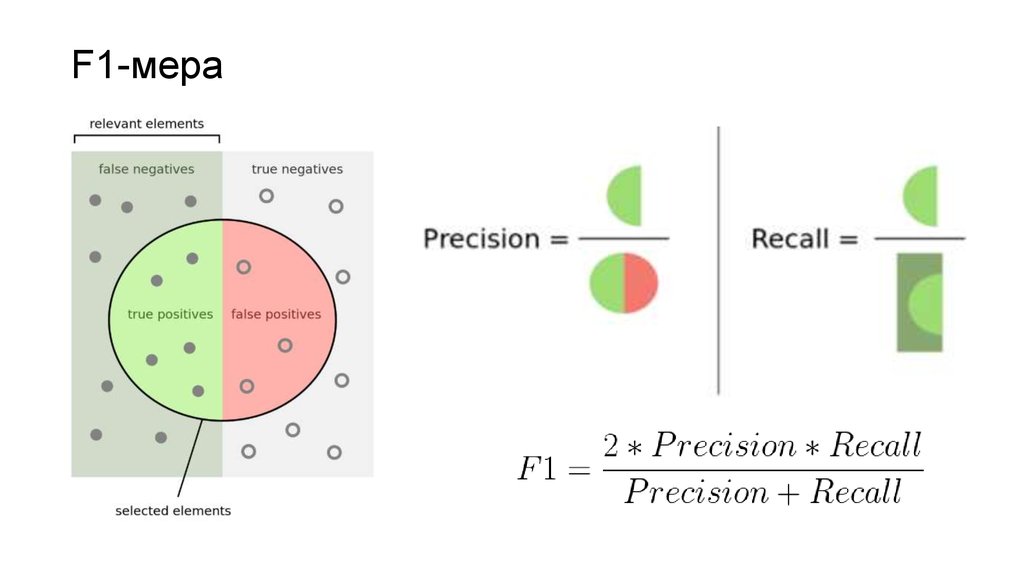 metrics импортировать precision_score
# определить фактический
act_pos1 = [1 для _ в диапазоне (100)]
act_pos2 = [2 для _ в диапазоне (100)]
act_neg = [0 для _ в диапазоне (10000)]
y_true = акт_поз1 + акт_поз2 + акт_отрицательный
# определяем прогнозы
pred_pos1 = [0 для _ в диапазоне (50)] + [1 для _ в диапазоне (50)]
pred_pos2 = [0 для _ в диапазоне (1)] + [2 для _ в диапазоне (9)9)]
pred_neg = [1 для _ в диапазоне (20)] + [2 для _ в диапазоне (51)] + [0 для _ в диапазоне (9929)]
y_pred = пред_поз1 + пред_поз2 + пред_отрицательный
# рассчитать прогноз
точность = точность_оценка (y_true, y_pred, labels=[1,2], среднее=’микро’)
print(‘Точность: %.3f’ % точности)
metrics импортировать precision_score
# определить фактический
act_pos1 = [1 для _ в диапазоне (100)]
act_pos2 = [2 для _ в диапазоне (100)]
act_neg = [0 для _ в диапазоне (10000)]
y_true = акт_поз1 + акт_поз2 + акт_отрицательный
# определяем прогнозы
pred_pos1 = [0 для _ в диапазоне (50)] + [1 для _ в диапазоне (50)]
pred_pos2 = [0 для _ в диапазоне (1)] + [2 для _ в диапазоне (9)9)]
pred_neg = [1 для _ в диапазоне (20)] + [2 для _ в диапазоне (51)] + [0 для _ в диапазоне (9929)]
y_pred = пред_поз1 + пред_поз2 + пред_отрицательный
# рассчитать прогноз
точность = точность_оценка (y_true, y_pred, labels=[1,2], среднее=’микро’)
print(‘Точность: %.3f’ % точности)
|
1 2 3 4 5 6 7 8
10 11 12 13 14 15 |
# вычисляет точность для набора данных 1:1:100 с 50tp, 20fp, 99tp, 51fp из sklearn. act_neg = [0 for _ in range(10000)] y_true = act_pos1 + act_pos2 + act_neg # определение прогнозов pred_pos1 = [0 for _ in range( 50)] + [1 для _ в диапазоне (50)] pred_pos2 = [0 для _ в диапазоне (1)] + [2 для _ в диапазоне (99)] pred_neg = [1 для _ в диапазоне (20)] + [2 для _ в диапазоне (51)] + [0 for _ in range(9929)] y_pred = pred_pos1 + pred_pos2 + pred_neg # расчет прогноза точность = точность_оценки (y_true, y_pred, labels=[1,2], medium=’micro’) print(‘Точность: %.3f’ % точности) |
Опять же, выполнение примера вычисляет точность для примера с несколькими классами, соответствующего нашему ручному вычислению.
Точность: 0,677
| Точность: 0,677 |
Отзыв из-за несбалансированной классификации
Отзыв — это показатель, который количественно определяет количество правильных положительных прогнозов, сделанных из всех положительных прогнозов, которые могли быть сделаны.
В отличие от точности, которая комментирует только правильные положительные прогнозы из всех положительных прогнозов, отзыв указывает на пропущенные положительные прогнозы.
Таким образом, отзыв дает некоторое представление о покрытии положительного класса.
При несбалансированном обучении отзыв обычно используется для измерения охвата класса меньшинства.
— стр. 27, Несбалансированное обучение: основы, алгоритмы и приложения, 2013.
Отзыв для двоичной классификации
В задаче несбалансированной классификации с двумя классами полнота вычисляется как количество истинных положительных результатов, деленное на общее количество истинных положительных и ложных отрицательных результатов.
- Отзыв = TruePositives / (TruePositives + FalseNegatives)
Результатом является значение от 0,0 для отсутствия отзыва до 1,0 для полного или идеального отзыва.
Давайте конкретизируем этот расчет на нескольких примерах.
Как и в предыдущем разделе, рассмотрим набор данных с отношением меньшинства к большинству 1:100, со 100 примерами меньшинства и 10 000 примеров классов большинства.
Модель делает прогнозы и предсказывает 90 прогнозов положительного класса правильно и 10 неправильно. Мы можем рассчитать отзыв для этой модели следующим образом:
- Отзыв = TruePositives / (TruePositives + FalseNegatives)
- Отзыв = 90 / (90 + 10)
- Отзыв = 90/100
- Отзыв = 0,9
Эта модель имеет хороший отзыв.
Отзыв для многоклассовой классификации
Отзыв не ограничивается задачами бинарной классификации.
В задаче несбалансированной классификации с более чем двумя классами полнота вычисляется как сумма истинных положительных результатов по всем классам, деленная на сумму истинных положительных и ложных отрицательных результатов по всем классам.
- Отзыв = Сумма c в C TruePositives_c / Сумма c в C (TruePositives_c + FalseNegatives_c)
Как и в предыдущем разделе, рассмотрим набор данных с отношением класса меньшинства к классу большинства 1:1:100, то есть соотношением 1:1 для каждого положительного класса и соотношением 1:100 для классов меньшинства к классу большинства, и у нас есть 100 примеров в каждом классе меньшинства и 10 000 примеров в классе большинства.
Модель предсказывает 77 примеров правильно и 23 неправильно для класса 1 и 95 правильно и 5 неправильно для класса 2. Мы можем рассчитать отзыв для этой модели следующим образом:
- Отзыв = (TruePositives_1 + TruePositives_2) / ((TruePositives_1 + TruePositives_2) + (FalseNegatives_1 + FalseNegatives_2))
- Отзыв = (77 + 95) / ((77 + 95) + (23 + 5))
- Отзыв = 172 / (172 + 28)
- Отзыв = 172/200
- отзыв = 0,86
Рассчитать отзыв с помощью Scikit-Learn
Оценка отзыва может быть рассчитана с помощью функции scikit-learn Recall_score().
Например, мы можем использовать эту функцию для расчета отзыва для описанных выше сценариев.
Во-первых, мы можем рассмотреть случай дисбаланса 1:100 с 100 и 10 000 примеров соответственно, и модель предсказывает 90 истинных положительных результатов и 10 ложных отрицательных результатов.
Полный пример приведен ниже.
# вычисляет полноту для набора данных 1:100 с 90 tp и 10 fn
из sklearn. metrics импортировать Recall_score
# определить фактический
act_pos = [1 для _ в диапазоне (100)]
act_neg = [0 для _ в диапазоне (10000)]
y_true = акт_поз + акт_отрицательный
# определяем прогнозы
pred_pos = [0 для _ в диапазоне (10)] + [1 для _ в диапазоне (9)0)]
pred_neg = [0 для _ в диапазоне (10000)]
y_pred = пред_поз + пред_отрицательный
# рассчитать отзыв
отзыв = отзыв_оценка (y_true, y_pred, среднее = ‘двоичный’)
print(‘Отзыв: %.3f’ % отзыва)
metrics импортировать Recall_score
# определить фактический
act_pos = [1 для _ в диапазоне (100)]
act_neg = [0 для _ в диапазоне (10000)]
y_true = акт_поз + акт_отрицательный
# определяем прогнозы
pred_pos = [0 для _ в диапазоне (10)] + [1 для _ в диапазоне (9)0)]
pred_neg = [0 для _ в диапазоне (10000)]
y_pred = пред_поз + пред_отрицательный
# рассчитать отзыв
отзыв = отзыв_оценка (y_true, y_pred, среднее = ‘двоичный’)
print(‘Отзыв: %.3f’ % отзыва)
|
1 2 3 4 5 6 7 8
10 110005 12 13 |
# вычисляет полноту для набора данных 1:100 с 90 tp и 10 fn из sklearn.metrics import Recall_score # определить фактический act_pos = [1 for _ in range(100)] act_neg = [0 for _ in range(10000)] y_true act_pos + act_neg # определить прогнозы pred_pos = [0 для _ в диапазоне (10)] + [1 для _ в диапазоне (90)] pred_neg = [0 для _ в диапазоне (10000)] y_pred = pred_pos + pred_neg # вычислить отзыв отзыв = отзыв_оценка(y_true, y_pred, Average=’binary’) print(‘Отзыв: %. |
Запустив пример, мы видим, что оценка соответствует ручному расчету выше.
Напомним: 0,900
| Отзыв: 0,900 |
Мы также можем использовать Recall_score() для задач несбалансированной мультиклассовой классификации.
В этом случае набор данных имеет дисбаланс 1:1:100, по 100 в каждом меньшинстве и 10 000 в большинстве классов. Модель предсказывает 77 истинных положительных результатов и 23 ложных отрицательных результата для классов 1 и 9.5 истинных положительных результатов и 5 ложноотрицательных результатов для класса 2.
Полный пример приведен ниже.
# вычисляет полноту для набора данных 1:1:100 с 77tp,23fn и 95tp,5fn
из sklearn.metrics импортировать Recall_score
# определить фактический
act_pos1 = [1 для _ в диапазоне (100)]
act_pos2 = [2 для _ в диапазоне (100)]
act_neg = [0 для _ в диапазоне (10000)]
y_true = акт_поз1 + акт_поз2 + акт_отрицательный
# определяем прогнозы
pred_pos1 = [0 для _ в диапазоне (23)] + [1 для _ в диапазоне (77)]
pred_pos2 = [0 для _ в диапазоне (5)] + [2 для _ в диапазоне (9)5)]
pred_neg = [0 для _ в диапазоне (10000)]
y_pred = пред_поз1 + пред_поз2 + пред_отрицательный
# рассчитать отзыв
отзыв = отзыв_оценка (y_true, y_pred, labels=[1,2], среднее=’микро’)
print(‘Отзыв: %. 3f’ % отзыва)
3f’ % отзыва)
|
1 2 3 4 5 6 7 8
10 110005 12 13 14 2009 15
|
# вычисляет полноту для набора данных 1:1:100 с 77tp,23fn и 95tp,5fn из sklearn.metrics = [2 for _ in range(100)] act_neg = [0 for _ in range(10000)] y_true = act_pos1 + act_pos2 + act_neg # определение прогнозов pred_pos1 = [0 for _ in range( 23)] + [1 для _ в диапазоне (77)] pred_pos2 = [0 для _ в диапазоне (5)] + [2 для _ в диапазоне (9)5)] pred_neg = [0 for _ in range(10000)] y_pred = pred_pos1 + pred_pos2 + pred_neg # вычисление отзыва =’микро’) print(‘Отзыв: %.3f’ % отзыва) |
Опять же, выполнение примера вычисляет отзыв для примера с несколькими классами, соответствующего нашему ручному вычислению.
Напомним: 0,860
| Повторный вызов: 0,860 |
Точность и полнота для несбалансированной классификации
Вы можете решить использовать точность или отзыв в своей несбалансированной задаче классификации.
Максимальная точность сведет к минимуму количество ложных срабатываний, тогда как максимальная полнота сведет к минимуму количество ложных отрицательных результатов.
- Точность : Подходит, когда сводит к минимуму ложные срабатывания .
- Отзыв : Подходит, когда сводит к минимуму ложноотрицательные результаты .
Иногда нам нужны отличные прогнозы положительного класса. Нам нужна высокая точность и высокая полнота.
Это может быть сложной задачей, так как часто увеличение отзыва происходит за счет снижения точности.
В несбалансированных наборах данных цель состоит в том, чтобы улучшить полноту без ущерба для точности. Эти цели, однако, часто противоречат друг другу, поскольку для увеличения TP для класса меньшинства также часто увеличивается количество FP, что приводит к снижению точности.
— стр. 55, Несбалансированное обучение: основы, алгоритмы и приложения, 2013.
Тем не менее, вместо того, чтобы выбирать тот или иной показатель, мы можем выбрать новый показатель, который сочетает точность и полноту в одном показателе.
F-мера для несбалансированной классификации
Точность классификации широко используется, поскольку это единственная мера, используемая для обобщения производительности модели.
F-Measure позволяет объединить точность и полноту в единую меру, которая охватывает оба свойства.
Сами по себе, ни точность, ни отзыв не могут рассказать всю историю. Мы можем иметь превосходную точность с ужасной памятью или, наоборот, ужасную точность с отличной памятью. F-мера позволяет выразить обе проблемы с помощью одной оценки.
После расчета точности и полноты для задачи бинарной или мультиклассовой классификации эти два показателя можно объединить для расчета F-меры.
Традиционная мера F рассчитывается следующим образом:
- F-мера = (2 * точность * полнота) / (точность + полнота)
Это среднее гармоническое двух дробей. Это иногда называют F-оценкой или F1-оценкой, и она может быть наиболее распространенной метрикой, используемой в задачах несбалансированной классификации.
Это иногда называют F-оценкой или F1-оценкой, и она может быть наиболее распространенной метрикой, используемой в задачах несбалансированной классификации.
… мера F1, которая одинаково взвешивает точность и полноту, чаще всего используется при обучении на несбалансированных данных.
— стр. 27, Несбалансированное обучение: основы, алгоритмы и приложения, 2013 г.
Как и точность и полнота, плохая оценка F-меры равна 0,0, а лучшая или идеальная оценка F-меры равна 1,0
Например, идеальная оценка точности и отзыва приведет к идеальной оценке F-меры:
- F-мера = (2 * точность * полнота) / (точность + полнота)
- F-мера = (2 * 1,0 * 1,0) / (1,0 + 1,0)
- F-мера = (2 * 1,0) / 2,0
- F-мера = 1,0
Давайте конкретизируем этот расчет на рабочем примере.
Рассмотрим набор данных бинарной классификации с отношением меньшинства к большинству 1:100, со 100 примерами меньшинства и 10 000 примерами классов большинства.
Рассмотрим модель, которая предсказывает 150 примеров для положительного класса, 95 правильных (истинно положительных), что означает, что пять были пропущены (ложноотрицательные) и 55 неверных (ложноположительные).
Точность можно рассчитать следующим образом:
- Точность = TruePositives / (TruePositives + FalsePositives)
- Точность = 95 / (95 + 55)
- Точность = 0,633
Мы можем рассчитать отзыв следующим образом:
- Отзыв = TruePositives / (TruePositives + FalseNegatives)
- Отзыв = 95 / (95 + 5)
- Отзыв = 0,95
Это показывает, что модель имеет низкую точность, но отличный отзыв.
Наконец, мы можем рассчитать F-меру следующим образом:
- F-мера = (2 * точность * полнота) / (точность + полнота)
- F-мера = (2 * 0,633 * 0,95) / (0,633 + 0,95)
- F-мера = (2 * 0,601) / 1,583
- F-мера = 1,202 / 1,583
- F-мера = 0,759
Мы видим, что хороший отзыв нивелирует плохую точность, давая хороший или приемлемый F-показатель.
Расчет F-меры с помощью Scikit-Learn
Оценку F-меры можно рассчитать с помощью функции scikit-learn f1_score().
Например, мы используем эту функцию для расчета F-меры для описанного выше сценария.
Это случай дисбаланса 1:100 со 100 и 10 000 примеров соответственно, и модель предсказывает 95 истинных положительных результатов, пять ложноотрицательных результатов и 55 ложноположительных результатов.
Полный пример приведен ниже.
# вычисляет f1 для набора данных 1:100 с 95tp, 5fn, 55fp
из sklearn.metrics импортировать f1_score
# определить фактический
act_pos = [1 для _ в диапазоне (100)]
act_neg = [0 для _ в диапазоне (10000)]
y_true = акт_поз + акт_отрицательный
# определяем прогнозы
pred_pos = [0 для _ в диапазоне (5)] + [1 для _ в диапазоне (9)5)]
pred_neg = [1 для _ в диапазоне (55)] + [0 для _ в диапазоне (9945)]
y_pred = пред_поз + пред_отрицательный
# рассчитать балл
оценка = f1_score (y_true, y_pred, среднее = ‘двоичный’)
print(‘F-мера: %. 3f’ % оценка)
3f’ % оценка)
|
1 2 3 4 5 6 7 8
10 110005 12 13 |
# вычисляет f1 для набора данных 1:100 с 95tp, 5fn, 55fp из sklearn.metrics import f1_score # определить фактическое значение act_pos + act_neg # определить прогнозы pred_pos = [0 для _ в диапазоне (5)] + [1 для _ в диапазоне (95)] pred_neg = [1 для _ в диапазоне (55)] + [0 for _ in range(9945)] y_pred = pred_pos + pred_neg # вычислить счет score = f1_score(y_true, y_pred, medium=’binary’) print(‘F-Measure: %.3f’ % оценка) |
При выполнении примера вычисляется F-мера, соответствующая нашему ручному расчету, с небольшими ошибками округления.
F-мера: 0,760
| Размер F: 0,760 |
Дополнительное чтение
В этом разделе содержится больше ресурсов по теме, если вы хотите углубиться.
Учебники
- Как рассчитать точность, полноту, F1 и другие параметры для моделей глубокого обучения
- Как использовать кривые ROC и кривые Precision-Recall для классификации в Python
Бумаги
- Систематический анализ показателей эффективности для задач классификации, 2009 г.
Книги
- Несбалансированное обучение: основы, алгоритмы и приложения, 2013 г.
- Изучение несбалансированных наборов данных, 2018 г.
API
- sklearn.metrics.precision_score API.
- sklearn.metrics.recall_score API.
- sklearn.metrics.f1_score API.
Артикул
- Матрица путаницы, Википедия.
- Точность и полнота, Википедия.
- Счет F1, Википедия.
Сводка
В этом уроке вы узнали, как вычислять и развивать интуицию для точности и отзыва для несбалансированной классификации.
В частности, вы узнали:
- Точность количественно определяет количество предсказаний положительного класса, которые фактически относятся к положительному классу.

- Отзыв определяет количество положительных прогнозов класса, сделанных из всех положительных примеров в наборе данных.
- F-Measure обеспечивает единую оценку, которая уравновешивает как точность, так и полноту в одном числе.
Есть вопросы?
Задавайте свои вопросы в комментариях ниже, и я постараюсь ответить.
Разберитесь с несбалансированной классификацией!
Разработка несбалансированных моделей обучения за считанные минуты
…с помощью всего нескольких строк кода Python
Узнайте, как это сделать, в моей новой электронной книге:
Несбалансированная классификация с помощью Python -конец проектов on:
Показатели производительности , Методы недостаточной выборки , SMOTE , Перемещение порога , Калибровка вероятности , Экономичные алгоритмы
и многое другое…
Использование несбалансированных методов классификации в ваших проектах по машинному обучению
Узнайте, что внутри
О Джейсоне Браунли
Джейсон Браунли, доктор философии, специалист по машинному обучению, который обучает разработчиков тому, как получать результаты с помощью современных методов машинного обучения с помощью практических руководств.

 Стандартный F-показатель эквивалентен установке β равным единице.
Стандартный F-показатель эквивалентен установке β равным единице.  3f ‘ % точности)
3f ‘ % точности) 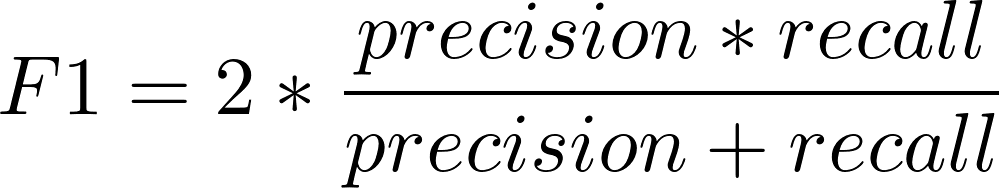 metrics = [2 for _ in range(100)]
metrics = [2 for _ in range(100)]  3f’ % отзыва)
3f’ % отзыва)