соединяем точки так, чтобы было красиво / Хабр
Как построить график по
nточкам? Самое простое — отметить их маркерами на координатной сетке. Однако для наглядности их хочется соединить, чтобы получить легко читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается довольно тяжело: взгляд цепляется за углы, а не скользит вдоль линии. Да и выглядят изломы не очень красиво. Получается, что кроме ломаных нужно уметь строить и кривые. Однако тут нужно быть осторожным, чтобы не получилось вот такого:
Немного матчасти
Восстановление промежуточных значений функции, которая в данном случае задана таблично в виде точек
P1 … 
Pn, называется интерполяцией. Есть множество способов интерполяции, но все они могут быть сведены к тому, что надо найти
n – 1 функцию для расчёта промежуточных точек на соответствующих сегментах. При этом заданные точки обязательно должны быть вычислимы через соответствующие функции. На основе этого и может быть построен график:
На основе этого и может быть построен график:
Функции fi могут быть самыми разными, но чаще всего используют полиномы некоторой степени. В этом случае итоговая интерполирующая функция (кусочно заданная на промежутках, ограниченных точками Pi) называется сплайном.
В разных инструментах для построения графиков — редакторах и библиотеках — задача «красивой интерполяции» решена по-разному. В конце статьи будет небольшой обзор существующих вариантов. Почему в конце? Чтобы после ряда приведённых выкладок и размышлений можно было поугадывать, кто из «серьёзных ребят» какие методы использует.
Ставим опыты
Самый простой пример — линейная интерполяция, в которой используются полиномы первой степени, а в итоге получается ломаная, соединяющая заданные точки.
Давайте добавим немного конкретики. Вот набор точек (взяты
почтис потолка):
0 0
20 0
45 -47
53 335
57 26
62 387
74 104
89 0
95 100
100 0
Результат линейной интерполяции этих точек выглядит так:
Однако, как отмечалось выше, иногда хочется получить в итоге гладкую кривую.
Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При этом в математике гладкость имеет порядок, равный номеру последней непрерывной производной, и область, на которой эта непрерывность сохраняется. То есть, если функция имеет гладкость порядка 1 на отрезке [
a; b], это означает, что на [a; b] она имеет непрерывную первую производную, а вот вторая производная уже терпит разрыв в каких-то точках.
У сплайна в контексте гладкости есть понятие дефекта. Дефект сплайна — это разность между его степенью и его гладкостью. Степень сплайна — это максимальная степень использованных в нём полиномов.
Важно отметить, что «опасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз Pi, то есть точки сочленения сегментов, в которых происходит переход от одного полинома к другому. Все остальные точки «безопасны», ведь у полинома на области его определения нет проблем с непрерывностью производных.
Чтобы добиться гладкой интерполяции, нужно повысить степень полиномов и подобрать их коэффициенты так, чтобы в граничных точках сохранялась непрерывность производных.
Традиционно для решения такой задачи используют полиномы третьей степени и добиваются непрерывности первой и второй производной. То, что получается, называют кубическим сплайном дефекта 1. Вот как он выглядит для наших данных:
Кривая, действительно, гладкая. Но если предположить, что это график некоторого процесса или явления, который нужно показать заинтересованному лицу, то такой метод, скорее всего, не подходит. Проблема в ложных экстремумах. Появились они из-за слишком сильного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совсем не кстати, ведь он оказывается обманут относительно пиковых значений функции. А ради наглядной визуализации этих значений, собственно, всё и затевалось.
Так что надо искать другие решения.
Другое традиционное решение, кроме кубических сплайнов дефекта 1 — полиномы Лагранжа.
Но вот что получается:
Гладкость, конечно, присутствует, но наглядность пострадала так сильно, что… пожалуй, стоит поискать другие методы. На некоторых наборах данных результат выходит нормальный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, ложные экстремумы) может получаться слишком большой — из-за того, что тут всего один полином на все сегменты.
В компьютерной графике очень широко применяются кривые Безье, представленные полиномами k-й степени.
Они не являются интерполирующими, так как из k + 1 точек, участвующих в построении, итоговая кривая проходит лишь через первую и последнюю. Остальные

Вот пример кубической кривой Безье:
Как это можно использовать для интерполяции? На основе этих кривых тоже можно построить сплайн. То есть на каждом сегменте сплайна будет своя кривая Безье k-й степени (кстати, k = 1 даёт линейную интерполяцию). И вопрос только в том, какое k взять и как найти k – 1 промежуточную точку.
Здесь бесконечно много вариантов (поскольку k ничем не ограничено), однако мы рассмотрим классический: k = 3.
Чтобы итоговая кривая была гладкой, нужно добиться дефекта 1 для составляемого сплайна, то есть сохранения непрерывности первой и второй производных в точках сочленения сегментов (
Pi), как это делается в классическом варианте кубического сплайна.
Решение этой задачи подробно (с исходным кодом) рассмотрено здесь.
Вот что получится на нашем тестовом наборе:
Стало лучше: ложные экстремумы всё ещё есть, но хотя бы не так сильно отличаются от реальных.
Думаем и экспериментируем
Можно попробовать ослабить условие гладкости: потребовать дефект 2, а не 1, то есть сохранить непрерывность одной только первой производной.
Достаточное условие достижения дефекта 2 в том, что промежуточные контрольные точки кубической кривой Безье, смежные с заданной точкой интерполируемой последовательности, лежат с этой точкой на одной прямой и на одинаковом расстоянии:
В качестве прямых, на которых лежат точки Ci – 1(2), Pi и Ci
Методом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежуточной контрольной получилась такой:
Первая и последняя промежуточные контрольные точки равны первой и последней точке графика соответственно (точки
C1(1)и
Cn – 1(2)совпадают с точками
P1и
Pn соответственно).
В этом случае получается вот такая кривая:
Как видно, ложных экстремумов уже нет. Однако если сравнивать с линейной интерполяцией, местами ошибка очень большая. Можно сделать её ещё меньше, но тут в ход пойдут ещё более хитрые эвристики.
К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно сделать это ещё раз: пусть сплайн будет иметь дефект 3. По факту, тем самым формально функция не будет гладкой вообще: даже первая производная может терпеть разрывы. Но если рвать её аккуратно, визуально ничего страшного не произойдёт.
Отказываемся от требования равенства расстояний от точки Pi до точек Ci – 1(2) и Ci(1), но при этом сохраняем их все лежащими на одной прямой:
Эвристика для вычисления расстояний будет такой:
Расчёт l1 и l2 такой же, как в «эвристике 1».
При этом, однако, стоит ещё проверять, не совпали ли точки Pi и P Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).
Это защитит от «вспухания» графика на плоских отрезках (что тоже немаловажно с точки зрения правдивого отображения данных).
Результат получается такой:
В результате на шестом сегменте ошибка уменьшилась, а на седьмом — увеличилась: кривизна у Безье на нём оказалась больше, чем хотелось бы. Исправить ситуацию можно, принудительно уменьшив кривизну и тем самым «прижав» Безье ближе к отрезку прямой, которая соединяет граничные точки сегмента. Для этого используется следующая эвристика:
Если абсцисса точки пересечения касательных в точках Pi(xi, yi) и Pi + 1(xi + 1
, yi + 1) лежит в отрезке [xi; xi + 1], то l1 либо l2 полагаем равным нулю. В том случае, если касательная в точке Pi направлена вверх, нулю полагаем максимальное из l1 и l2, если вниз — минимальное.
Результат следующий:
На этом было принято решение признать цель достигнутой.
Может быть, кому-то пригодится код.
А как люди-то делают?
Обещанный обзор. Конечно, перед решением задачи мы посмотрели, кто чем может похвастаться, а уже потом начали разбираться, как сделать самим и по возможности лучше. Но вот как только сделали, не без удовольствия ещё раз прошлись по доступным инструментам и сравнили их результаты с плодами наших экспериментов. Итак, поехали.
MS Excel
Это очень похоже на рассмотренный выше сплайн дефекта 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, тут всего два ложных экстремума — первый и второй сегменты (у нас было четыре). Видимо, к классическому поиску промежуточных контрольных точек тут добавляются ещё какие-то эвристики. Но ото всех ложных экстремумов они не спасли.
LibreOffice Calc
В настройках это названо кубическим сплайном. Очевидно, он тоже основан на Безье, и вот тут уже точная копия нашего результата: все четыре ложных экстремума на месте.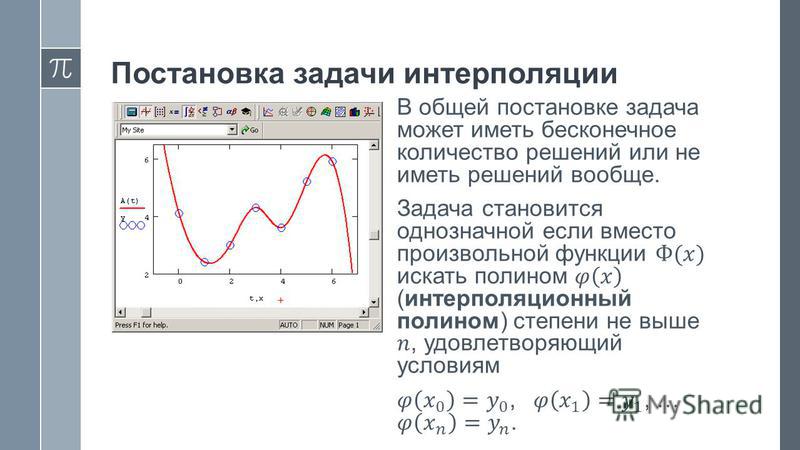
Есть там ещё один тип интерполяции, который мы тут не рассматривали: B-сплайн. Но для нашей задачи он явно не подходит, так как даёт вот такой результат 🙂
Highcharts, одна из самых популярных JS-библиотек для построения диаграмм
Тут налицо «метод касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежуточных контрольных. Ложных экстремумов нет, зато есть сравнительно большая ошибка относительно линейной интерполяции (седьмой сегмент).
amCharts, ещё одна популярная JS-библиотека
Картина очень похожа на экселевскую, те же два ложных экстремума в тех же местах.
Coreplot, самая популярная библиотека построения графиков для iOS и OS X
Есть ложные экстремумы и видно, что используется сплайн дефекта 1 на основе Безье.
Библиотека открытая, так что можно посмотреть в код и убедиться в этом.
aChartEngine, вроде как самая популярная библиотека построения графиков для Android
Больше всего похоже на кривую Безье степени n – 1, хотя в самой библиотеке график называется «cubic line». Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.
Странно! Как бы то ни было, тут не только присутствуют ложные экстремумы, но и в принципе не выполняются условия интерполяции.
Вместо заключения
В конечном счёте получается, что из «больших ребят» лучше всех проблему решили Highcharts. Но метод, описанный в этой статье, обеспечивает ещё меньшую ошибку относительно линейной интерполяции.
Вообще, заняться этим пришлось по просьбе покупателей, которые зарепортили нам «острые углы» в качестве бага в нашем
движке диаграмм. Будем рады, если описанный опыт кому-то пригодится.
Интерполировать точки—Portal for ArcGIS | Документация для ArcGIS Enterprise
В этом разделе
Инструмент Интерполировать точки позволяет прогнозировать значения в новых местоположениях на основе измерений, полученных в наборе точек.
Схема рабочего процесса
Примеры
Количество осадков измеряется на определенных метеорологических станциях. Интерполировать точки может использоваться для создания непрерывного слоя прогнозируемых дождевых осадков по всему региону.
Интерполировать точки может использоваться для создания непрерывного слоя прогнозируемых дождевых осадков по всему региону.
Примечания по использованию
В качестве входных данных используется слой точек. Входной слой должен иметь числовое поле, которое будет служить основой интерполирования. Интерполировать точки предназначен для работы с постепенно и плавно изменяющимися данными над ландшафтом, например – температура и уровень загрязнения окружающей среды. Он не подходит для таких данных, как численность населения или средний доход, которые меняются очень резко за короткий отрезок времени.
Инструмент Интерполировать точки можно настроить для оптимизации скорости или точности, или средней позиции. Более точные прогнозы требуют больше времени и наоборот.
Чтобы создать слой стандартных ошибок, необходимо установить метку в окне Ошибки выходных прогнозов. Рассчитать 95-процентный доверительный интервал для интерполированного слоя можно путем добавления к значению интерполяции двух стандартных ошибок для верхнего предела и вычитания двух стандартных ошибок от нижнего предела.
| Опция | Описание | По умолчанию |
|---|---|---|
Вырезать результат по | Для указания области интереса может использоваться область из слоя или инструмент Рисовать. Будет выполнена интерполяция, которая будет обрезана по границам области. | Нет |
Классифицировать по | Схема классификации используется для отображения полученного слоя плотности. Предусмотрены опции Геометрические интервалы, Равные интервалы, Равные площади и Вручную. При выборе опции Вручную необходимо указать свои собственные граничные значения для классов, при этом параметр Число классов применяться не будет. | Геометрические интервалы |
Число классов | Число классов, которые будут использоваться в полученном слое. | 10 |
Интерполяция в этих местоположениях | Точки наносятся из слоя, что позволяет делать прогнозы в определенных местоположениях, представляющих интерес. Прогнозы будут записываться в выходном слое точек. | Нет |
Если отмечен экстент Использовать текущую карту, то интерполироваться будут только объекты входного слоя точек в пределах экстента карты. Если отметку снять, то буду интерполированы все объекты входного слоя точек, даже если они находятся вне текущего экстента карты.
Ограничения
Инструмент Интерполировать точки может использоваться только на точечных объектах.
Как работает инструмент Интерполировать точки
Интерполировать точки использует инструмент геообработки Эмпирический байесовский кригинг для выполнения интерполяции. Параметры, которые указываются для инструмента Эмпирический байесовский кригинг, контролируются параметром Оптимизировать для. Эти параметры приведены ниже.
Параметры, которые указываются для инструмента Эмпирический байесовский кригинг, контролируются параметром Оптимизировать для. Эти параметры приведены ниже.
| Параметр | Скорость | По умолчанию | Точность |
|---|---|---|---|
Тип преобразования данных | NONE | NONE | EMPIRICAL |
Тип модели вариограммы | POWER | POWER | K_BESSEL |
Максимальное число точек в каждой локальной модели | 50 | 75 | 200 |
Коэффициент перекрытия областей локальной модели | 1 | 1. | 3 |
Число моделируемых вариограмм | 30 | 100 | 200 |
Минимальное число соседей | 8 | 10 | 15 |
Максимальное число соседей | 8 | 10 | 15 |
Похожие инструменты
Используйте Интерполировать точки для прогнозирования значений на основе точечных измерений. Другие инструменты могут оказаться полезными для решения похожих, но немного отличающихся проблем.
Другие инструменты могут оказаться полезными для решения похожих, но немного отличающихся проблем.
Инструменты анализа вьюера карт
Если для создания карты плотности вы используете точечные или линейные измерения, используйте инструмент Вычисление плотности.
Инструменты анализа ArcGIS Desktop
Интерполировать точки использует Эмпирический байесовский кригинг для выполнения интерполяции, которая доступна в группе инструментов Интерполяция набора инструментов дополнительного модуля Geostatistical Analyst.
Интерполировать точки также доступен в ArcGIS Pro. Для запуска инструмента из ArcGIS Pro версия активного портала проекта Portal for ArcGIS должна быть не ниже 10.5. Кроме того, вход на портал необходимо выполнить под учетной записью, имеющей права доступа для выполнения стандартного анализа объектов на данном портале.
Отзыв по этому разделу?
Что значит интерполяция 13 мегапикселей.
 Что такое интерполяция камеры в телефоне и для чего она нужна? Пример изменения размера изображения
Что такое интерполяция камеры в телефоне и для чего она нужна? Пример изменения размера изображения
Рынок мобильных телефонов заполнен моделями с камерами с огромными разрешениями. Встречаются даже относительно недорогие смартфоны с сенсорами разрешением 16-20 Мп. Незнающий покупатель гонится за «крутой» камерой и отдает предпочтение тому телефону, у которого разрешение камеры выше. Он даже и не догадывается, что попадается на удочку маркетологов и продавцов.
Что такое разрешение?
Разрешение камеры — это параметр, который указывает на конечный размер изображения. Он определяет только то, насколько полученное изображение будет большим, то есть его ширину и высоту в пикселях. Важно: качество картинки при этом не изменяется. Фотография может получиться некачественной, но большой из-за разрешения.
Разрешение не влияет на качество. Нельзя было не упомянуть об этом в контексте интерполяции камеры смартфона. Теперь можно переходить непосредственно к сути.
Что такое интерполяция камеры в телефоне?
Интерполяция камеры — это искусственное увеличение разрешения изображения. Именно изображения, а не То есть это специальное программное обеспечение, благодаря которому снимок с разрешением 8 Мп интерполируется до 13 Мп или больше (или меньше).
Именно изображения, а не То есть это специальное программное обеспечение, благодаря которому снимок с разрешением 8 Мп интерполируется до 13 Мп или больше (или меньше).
Если проводить аналогию, то интерполяция камеры подобна или биноклю. Эти устройства увеличивают изображение, но не делают его более качественным или детализированным. Так что если в характеристиках к телефону указана интерполяция, то фактическое разрешение камеры может быть ниже заявленного. Это не плохо и не хорошо, это просто есть.
Для чего это нужно?
Интерполяцию придумали для увеличения размера изображения, не более того. Сейчас это уловка маркетологов и производителей, которые пытаются продать продукт. Они большими цифрами указывают на рекламном постере разрешение камеры телефона и позиционируют это как преимущество или нечто хорошее. Мало того, что само по себе разрешение не оказывает влияния на качество фотографий, так оно еще может быть интерполировано.
Буквально 3-4 года тому назад многие производители гнались за количеством мегапикселей и разными способами пытались впихнуть их в свои смартфоны сенсоры с как можно большим числом. Так появлялись смартфоны с камерами с разрешением 5, 8, 12, 15, 21 Мп. Фотографировать они при этом могли как самые дешевые мыльницы, но покупатели, увидев наклейку «Камера на 18 Мп», сразу хотели купить такой телефон. С появлением интерполяции продавать такие смартфоны стало проще из-за возможности искусственно добавить мегапикселей камере. Конечно, качество фото со временем начало расти, но точно не из-за разрешения или интерполяции, а из-за естественного прогресса в плане разработки сенсоров и программного обеспечения.
Так появлялись смартфоны с камерами с разрешением 5, 8, 12, 15, 21 Мп. Фотографировать они при этом могли как самые дешевые мыльницы, но покупатели, увидев наклейку «Камера на 18 Мп», сразу хотели купить такой телефон. С появлением интерполяции продавать такие смартфоны стало проще из-за возможности искусственно добавить мегапикселей камере. Конечно, качество фото со временем начало расти, но точно не из-за разрешения или интерполяции, а из-за естественного прогресса в плане разработки сенсоров и программного обеспечения.
Техническая сторона
Что такое интерполяция камеры в телефоне технически, ведь весь текст выше описывал только основную идею?
С помощью специального программного обеспечения на изображении «рисуются» новые пиксели. Например, для увеличения изображения в 2 раза после каждой строки пикселей картинки добавляется новая строка. Каждый пиксель в этой новой строке заполняется цветом. Цвет заливки высчитывается специальным алгоритмом. Самый первый способ — залить новую строку цветами, которыми обладают ближайшие пиксели. Результат такой обработки будет ужасным, но зато подобный способ требует минимум вычислительных операций.
Результат такой обработки будет ужасным, но зато подобный способ требует минимум вычислительных операций.
Чаще всего используется другой метод. То есть на исходное изображение добавляются новые строки пикселей. Каждый пиксель заливается цветом, который, в свою очередь, вычисляется как среднее значение соседних пикселей. Этот способ дает лучшие результаты, но требует больше вычислительных операций.
Благо, современные мобильные процессоры быстры, и на практике пользователь не замечает, как программа редактирует изображение, пытаясь искусственно увеличить его размер.
Есть много продвинутых способов и алгоритмов интерполяции, которые совершенствуются постоянно: улучшаются границы перехода между цветами, линии становятся более точными и четкими. Неважно, как построены все эти алгоритмы. Сама идея интерполяции камеры банальна и вряд ли приживется в ближайшем будущем. С помощью интерполяции невозможно сделать изображение более детализированным, добавить новые детали или улучшить его каким-либо еще образом. Только в фильмах маленькая размытая картинка после наложения пары фильтров становится четкой. На практике такого быть не может.
Только в фильмах маленькая размытая картинка после наложения пары фильтров становится четкой. На практике такого быть не может.
Нужна ли вам интерполяция?
Многие пользователи по своему незнанию задают на разных форумах вопросы, как сделать интерполяцию камеры, полагая, что это улучшит качество изображений. На самом деле интерполяция не только не улучшит качество картинки, но даже может сделать хуже, ведь к фотографиям будут добавляться новые пиксели, и из-за не всегда точного вычисления цветов для заливки на фото могут быть недетализированные участки, зернистость. В результате качество падает.
Так что интерполяция в телефоне — это маркетинговая уловка, которая совершенно не нужна. Она может увеличивать не только разрешение фото, но и стоимость самого смартфона. Не попадайтесь на уловки продавцов и производителей.
Сенсоры — это устройства, определяющие лишь градации серого (градации интенсивности света — от полностью белого до полностью черного). Чтобы камера могла различать цвета, на кремний с помощью процесса фотолитографии накладывается массив цветных фильтров.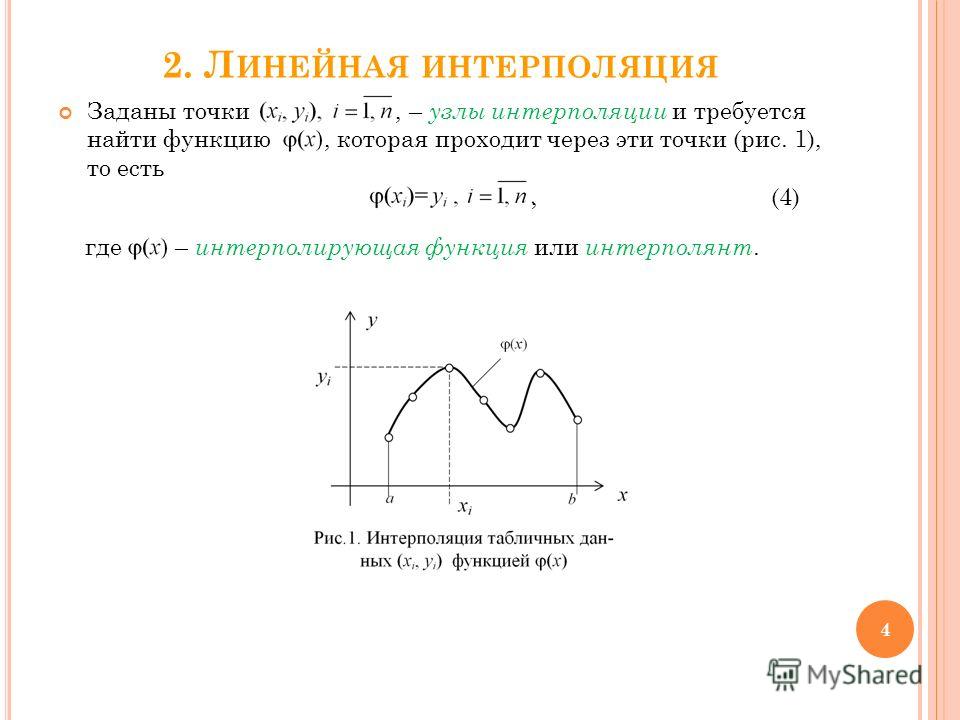 В тех сенсорах, где используются микролинзы, фильтры помещаются между линзами и фотоприемником. В сканерах, где используются трилинейные ПЗС (рядом расположенные три ПЗС, реагирующие соответственно на красный, синий и зеленый цвета), или в high-end цифровых камерах, где также используются три сенсора, на каждый сенсор фильтруется свет своего определенного цвета. (Заметим, что в некоторых камерах с несколькими сенсорами используются комбинации нескольких цветов в фильтрах, а не три стандартных). Но для устройств с одним сенсором, каковыми является большинство потребительских цифровых фотоаппаратов, для обработки различных цветов используются массивы цветных фильтров (color filter arrays, CFA).
В тех сенсорах, где используются микролинзы, фильтры помещаются между линзами и фотоприемником. В сканерах, где используются трилинейные ПЗС (рядом расположенные три ПЗС, реагирующие соответственно на красный, синий и зеленый цвета), или в high-end цифровых камерах, где также используются три сенсора, на каждый сенсор фильтруется свет своего определенного цвета. (Заметим, что в некоторых камерах с несколькими сенсорами используются комбинации нескольких цветов в фильтрах, а не три стандартных). Но для устройств с одним сенсором, каковыми является большинство потребительских цифровых фотоаппаратов, для обработки различных цветов используются массивы цветных фильтров (color filter arrays, CFA).
Для того чтобы каждому пикселю соответствовал свой основной цвет, над ним помещается фильтр соответствующего цвета. Фотоны, прежде чем попасть на пиксель, сначала проходят через фильтр, который пропускает только волны своего цвета. Света другой длины будет просто поглощаться фильтром. Ученые определили, что любой цвет в спектре можно получить смешением всего нескольких основных цветов. В модели RGB таких цвета три.
В модели RGB таких цвета три.
Для каждого применения разрабатываются свои массивы цветных фильтров. Но в большинстве сенсоров цифровых камер наиболее популярными являются массивы фильтров цветовой модели Байера (Bayer pattern). Эта технология была изобретена в 70-х компанией Kodak, когда проводились исследования в области пространственного разделения. В этой системе фильтры расположены вперемежку, в шахматном порядке, а количество зеленых фильтров в два раза больше, чем красных или синих. Порядок расположения таков, что красные и синие фильтры расположены между зелеными.
Такое количественное соотношение объясняется строением человеческого глаза — он более чувствителен к зеленому свету. А шахматный порядок обеспечивает одинаковые по цвету изображения независимо от того, как вы держите камеру (вертикально или горизонтально). При чтении информации с такого сенсора, цвета записываются последовательно в строчках. Первая строчка должна быть BGBGBG, следующая — GRGRGR и т.д. Такая технология называется последовательной RGB (sequential RGB).
В ПЗС камерах совмещение всех трех сигналов воедино происходит не на сенсоре, а в устройстве формирования изображения, уже после того, как сигнал преобразован из аналогового вида в цифровой. В КМОП сенсорах это совмещение может происходить непосредственно на чипе. В любом случае, первичные цвета каждого фильтра математически интерполируются с учетом цветов соседних фильтров. Заметим, что в любом изображении большинство точек — это смешение основных цветов, и лишь немногие действительно представляют чистый красный, синий или зеленый цвет.
Например, чтобы определить, влияние соседних пикселей на цвет центрального при линейной интерполяции будет обрабатываться матрица пикселей размером 3х3. Возьмем, к примеру, простейший случай — три пикселя — с синим, красным и синим фильтрами, расположены в одной строчке (BRB). Предположим, вы пытаетесь получить результирующее значение цвета красного пикселя. Если все цвета равноправны, то цвет центрального пикселя вычисляется математически как две части синего к одной части красного.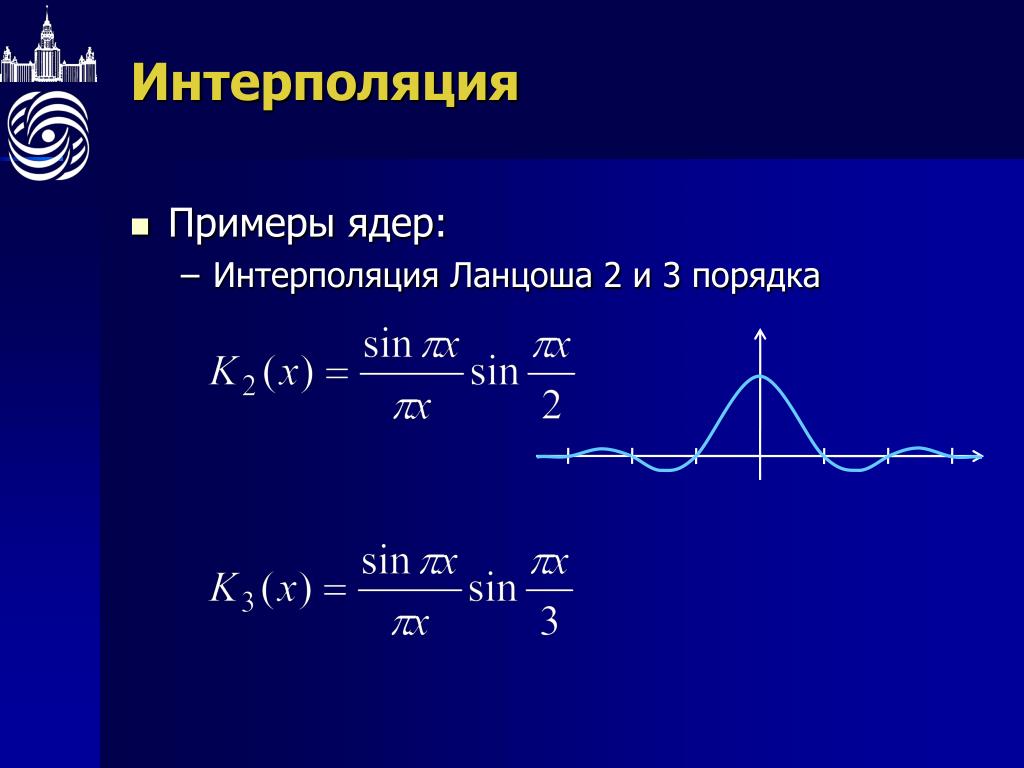 На самом же деле, алгоритмы даже простой линейной интерполяции намного более сложны, они учитывают значения всех окружающих пикселей. Если интерполяция происходит плохо, то получаются зубцы на границах смены цветов (или появляются цветовые артефакты).
На самом же деле, алгоритмы даже простой линейной интерполяции намного более сложны, они учитывают значения всех окружающих пикселей. Если интерполяция происходит плохо, то получаются зубцы на границах смены цветов (или появляются цветовые артефакты).
Отметим, что слово «разрешение» в области цифровой графики употребляется некорректно. Пуристы (или педанты — кому как больше нравится), знакомые с фотографией и оптикой, знают, что разрешение — это мера способности человеческого глаза или прибора различать отдельные линии на сетке разрешений, например, на сетке ISO, показанной ниже. Но в компьютерной индустрии принято разрешением называть количество пикселей, и раз уж так повелось, мы также последуем этой конвенции. Ведь даже разработчики называют разрешением количество пикселей в сенсоре.
Посчитаем?
Размер файла изображения зависит от количества пикселей (разрешения). Чем больше пикселей, тем больше файл. Например, изображение сенсоров стандарта VGA (640х480 или 307200 активных пикселей) будет занимать в несжатом виде около 900 килобайт. (307200 пикселей по 3 байта (R-G-B) = 921600 байт, что примерно равно 900 килобайтам) Изображение 16 MP сенсора будет занимать около 48 мегабайт.
(307200 пикселей по 3 байта (R-G-B) = 921600 байт, что примерно равно 900 килобайтам) Изображение 16 MP сенсора будет занимать около 48 мегабайт.
Казалось бы, что такого — сосчитать количество пикселей в сенсоре, чтобы определить размер получающегося изображения. Тем не менее, производители камер представляют кучу разных цифр, и каждый раз утверждают, что это и есть истинное разрешение камеры.
В общее число пикселей входят все пиксели, физически существующие в сенсоре. Но активными считаются только те, которые участвуют в получении изображения. Около пяти процентов всех пикселей не будут участвовать в получении изображения. Это либо дефектные пиксели, либо пиксели, использующиеся камерой по другому назначению. Например, могут существовать маски для определения уровня темнового тока или для определения формата кадра.
Формат кадра — соотношения между шириной и высотой сенсора. В некоторых сенсорах, например, с разрешением 640х480, это соотношение равно 1,34:1, что соответствует формату кадра большинства компьютерных мониторов.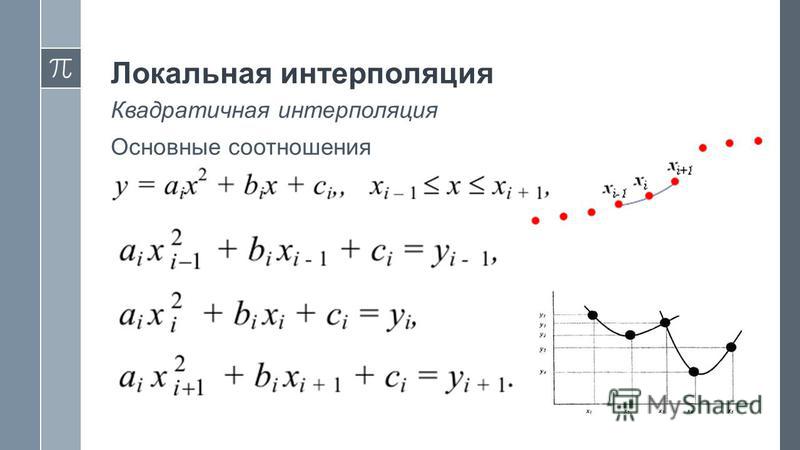 Это означает, что изображения, созданные такими сенсорами, будут точно укладываться в экран монитора, без предварительного кадрирования. Во многих аппаратах формат кадра соответствует формату традиционной 35-милиметровой пленки, где соотношение равно 1:1,5. Это позволяет делать снимки стандартного размера и формы.
Это означает, что изображения, созданные такими сенсорами, будут точно укладываться в экран монитора, без предварительного кадрирования. Во многих аппаратах формат кадра соответствует формату традиционной 35-милиметровой пленки, где соотношение равно 1:1,5. Это позволяет делать снимки стандартного размера и формы.
Интерполяция разрешения
Кроме оптического разрешения (реальная способность пикселей реагировать на фотоны), существует также разрешение, увеличенное программно-аппаратным комплексом, с помощью интерполирующих алгоритмов. Как и в интерполяции цветов, в интерполяции разрешения математически анализируются данные соседних пикселей. При этом в результате интерполяции создаются промежуточные значения. Такое «внедрение» новых данных может производиться довольно гладко, при этом интерполированные данные будут чем-то средними, между реальными оптическими данными. Но иногда при такой операции могут возникать различные помехи, артефакты, появляться искажения, в результате которых качество изображения лишь ухудшится. Поэтому многие пессимисты считают, что интерполяция разрешения — это вовсе не способ улучшения качества изображений, а лишь метод увеличения файлов. При выборе устройства обращайте внимание, какое разрешение указано. Не стоит сильно радоваться высокому интерполированному разрешению. (Оно помечается как interpolated или enhanced).
Поэтому многие пессимисты считают, что интерполяция разрешения — это вовсе не способ улучшения качества изображений, а лишь метод увеличения файлов. При выборе устройства обращайте внимание, какое разрешение указано. Не стоит сильно радоваться высокому интерполированному разрешению. (Оно помечается как interpolated или enhanced).
Ещё один процесс обработки изображения на программном уровне — это субдискретизация (Sub-sampling). По сути, это процесс, обратный интерполяции. Этот процесс производится на стадии обработки изображения, уже после того, как данные преобразованы из аналогового цифровой вид. При этом удаляются данные различных пикселей. В КМОП сенсорах эту операцию можно провести на самом чипе, временно отключив считывание определенных строчек пикселей, или считывая данные лишь с избранных пикселей.
Субдискретизация выполняет две функции. Во-первых, для уплотнения данных — чтобы хранить больше снимков в памяти определенного размера. Чем меньше количество пикселей, тем меньше получается размер файла, и тем больше снимков вы сможете уместить на карточке памяти или во внутренней памяти устройства и тем реже вам придется скачивать фотографии на компьютер или менять карточки памяти.
Вторая функция этого процесса — создание изображений определенного размера для определенных целей. Камеры с 2MP сенсором вполне по зубам сделать снимок стандартной фотографии размером 8х10 дюймов. Но если вы попытаетесь переслать такую фотографию по почте, то это заметно увеличит размер письма. Субдискретизация позволяет обработать изображение так, чтобы оно нормально смотрелось на мониторах ваших друзей (если не ставить целью детализацию) и при этом отправлялось достаточно быстро даже на машинах с медленным соединением.
Теперь, когда мы ознакомились с принципами работы сенсоров, знаем, как получается изображение, давайте заглянем несколько глубже и затронем более сложные ситуации, возникающие при цифровой фотографии.
Интерполяция камеры, зачем и что это такое?
- Типа 8 Мп матрица, а 13 Mp сам снимок
- Это чтоб не крутить лишних проволок к матрице, мегапуксели раздувают прямо в проце.
- Это когда пиксель дробят на несколько, чтоб при увеличении изображение не было в квадратики.
 Реального разрешения не прибавляет. Размазывает рисунок.
Реального разрешения не прибавляет. Размазывает рисунок. - интерполяция — это нахождение неизвестного значения по известным значениям.
качество интерполяции в фотографии (приближение к оригиналу) будет зависеть от грамотно составленного программного обеспечения - Сенсор камеры 8мп, а изображение растянули до 13мп. Отключай однозначно. Фото будут 13мп, но по качеству как 8мп (цифровой шум больше будет).
- Реальное разрешение там в линиях на мм без замыливания в любом случае на 2мп.
- Ну просто раздутые пикселы
Например многие web камеры, написано что 720 и т. д. смотришь настройки а там 240х320 - Интерполяция — в общем смысле — использование при вычислении менее сложной функции с целью достижения результата, максимально приближнного к абсолютному, достижимому только с помошью наиболее точных и правильных действий.
В данном варианте — попросту говоря, программисты хвалят себя тем, что снимки телефоном незначительно отличаются от сделанных более сложными устройствами — фотокамерами.
- Загрузка… какие матрицы лучше Live MOS или CMOS ??? «Live MOS матрица торговое название разновидности светочувствительных матриц, разрабатываемых Panasonic и применяемых также в изделиях Leica…
- Загрузка… что такое линза Френеля Копировать статьи из Википедии без указания источника — нехорошо. 1. Линза Френеля2. Обычная линза Основным преимуществом линзы Френеля является е…
- Загрузка… Скажите, а фотоаппарат Fujifilm FinePix S4300, 26-х ЗУМ, является полупрофессональным? Является продвинутой мыльницей мыльница, супурзум. для фотосессий непригодная. смотрите тут http://torg.mail.ru/digitalphoto/all/?param280=1712,1711amp;price=22000,100000 Блин, этими большими…
- Загрузка… Чем отличается зеркальный видоискатель от оптического? что лучше? Зеркальный видоискатель — визирование происходит с помощи системы зеркал, свет проходит через непосредственно сам объектив и…
- Загрузка… В чём разница CMOS-датчиков и CCD-датчиков пзс у видеокамер? КМОП-матрица (CMOS) — цифровое устройство, поэтому может монтироваться на одном чипе со всеми остальными кишками.
 ..
..
В смартфоне камера 8 MPix. Что означает интерполяция до 13 MPix?
-
Интерполяция — это способ нахождения промежуточных значений
Если это все перевести на более человеческий язык, применимо к вашему вопросу, то получится следующее:
- программное обеспечение может обрабатывать(увеличивать, растягивать)) файлы до 13 MPIX.

- программное обеспечение может обрабатывать(увеличивать, растягивать)) файлы до 13 MPIX.
Доброго времени суток.
Это обозначает, что ваш смартфон растягивает фотографию/изображение, отснятую на камеру 8 MPix, до 13 MPix. А делается это посредством того, что реальные пиксели раздвигаются и вставляются дополнит — ые.
Но, если сравнить качество изображения/фотографии, сделанную на 13 МП и 8 МП с интерполяцией до 13, то качество второго будет заметно хуже.
Если по простецки пояснить,то к активным пикселям матрицы процессор смарта при создании фото добавляет еще свои пиксели,как бы просчитывает картинку и дорисовывает ее до размера 13 ти мП..На выходе имеем матрицу на 8 а фото по разрешению как с 13 ти Мп.Качество от этого улучшается не особо.
Это значит что камера может сделать снимок до 8 MPIX, но программно она может увеличивать снимки до 12 MPIX. Значит она программно увеличивает, но при этом изображение не становится качественней, изображение все ровно будет на 8 MPIX. Это чисто уловка производителя и стоят такие смартфоны дороже.
Это чисто уловка производителя и стоят такие смартфоны дороже.
Такое понятие предполагает то, что камера вашего устройства так и будет делать фото на 8 MPIX, но вот уже программно есть возможность увеличение до 13 MPIX. При этом качество лучшим не становится. Просто пространство между пикселями забивается вот и вс.
Это означает, что в вашей камере, как было 8 MPIX их так и остается — не больше и не меньше, а все остальное — маркетинговый ход, научное одурачивание народа, чтобы продать товар по-дороже и не более. Данная функция никчемная, при интерполяции качество фото теряется.
На китайских смартфонах это сейчас используется постоянно, просто сенсор камеры на 13мп стоит гораздо дороже, чем на 8мп, вот поэтому и ставят на 8мп, но приложение камеры растягивает полученное изображение, в итоге качество у этих 13мп будет заметно хуже, если посмотреть в оригинальном разрешении.
На мой взгляд эта функция вообще ни к чему, поскольку и 8мп вполне достаточно для смартфона, мне в принципе и 3мп хватает, главное, чтобы сама камера была качественной.
Интерполяция камеры, это уловка производителя, так искусственно завышают цену смартфону.
Если у вас камера 8 MPIX, то и снимок она может делать соответствующий, интерполяция не улучшает качества фото снимка, она просто увеличивает размер фото снимка до 13 мегапикселей.
Дело в том, что реальная камера в таких телефонах это 8 мегапикселей. Но с помощью внутренних программ изображения растягивается до 13 мегапикселей. По сути, оно не доходит до реальных 13 мегапикселей.
Интерполяция мегапикселей — это такое программное размазывание картинки. Раздвигаются реальные пиксели, и вставляются между ними дополнительные, с цветом среднего значения от цветов раздвинутых. Ерунда, никому не нужный самообман. Качество не улучшает.
До 13 MPix — это может быть 8 MPix реальных, как у Вас. Или 5 MPix реальных. Программное обеспечение камеры интерполирует графический продукт камеры до 13 MPix, не улучшая изображения, а электронно увеличивая его. Просто говоря, как увеличительное стекло или бинокль. Качество не меняется.
Интерполяция камеры — это искусственное увеличение разрешения изображения. Именно изображения, а не размера матрицы. То есть это специальное программное обеспечение, благодаря которому снимок с разрешением 8 Мп интерполируется до 13 Мп или больше (или меньше). Если проводить аналогию, то интерполяция камеры подобна увеличительному стеклу или биноклю. Эти устройства увеличивают изображение, но не делают его более качественным или детализированным. Так что если в характеристиках к телефону указана интерполяция, то фактическое разрешение камеры может быть ниже заявленного. Это не плохо и не хорошо, это просто есть.
Интерполяцию придумали для увеличения размера изображения, не более того. Сейчас это уловка маркетологов и производителей, которые пытаются продать продукт. Они большими цифрами указывают на рекламном постере разрешение камеры телефона и позиционируют это как преимущество или нечто хорошее. Мало того, что само по себе разрешение не оказывает влияния на качество фотографий, так оно еще может быть интерполировано.
Сейчас это уловка маркетологов и производителей, которые пытаются продать продукт. Они большими цифрами указывают на рекламном постере разрешение камеры телефона и позиционируют это как преимущество или нечто хорошее. Мало того, что само по себе разрешение не оказывает влияния на качество фотографий, так оно еще может быть интерполировано.
Буквально 3-4 года тому назад многие производители гнались за количеством мегапикселей и разными способами пытались впихнуть их в свои смартфоны сенсоры с как можно большим числом. Так появлялись смартфоны с камерами с разрешением 5, 8, 12, 15, 21 Мп. Фотографировать они при этом могли как самые дешевые мыльницы, но покупатели, увидев наклейку «Камера на 18 Мп», сразу хотели купить такой телефон. С появлением интерполяции продавать такие смартфоны стало проще из-за возможности искусственно добавить мегапикселей камере. Конечно, качество фото со временем начало расти, но точно не из-за разрешения или интерполяции, а из-за естественного прогресса в плане разработки сенсоров и программного обеспечения.
Что такое интерполяция камеры в телефоне технически, ведь весь текст выше описывал только основную идею?
С помощью специального программного обеспечения на изображении «рисуются» новые пиксели. Например, для увеличения изображения в 2 раза после каждой строки пикселей картинки добавляется новая строка. Каждый пиксель в этой новой строке заполняется цветом. Цвет заливки высчитывается специальным алгоритмом. Самый первый способ — залить новую строку цветами, которыми обладают ближайшие пиксели. Результат такой обработки будет ужасным, но зато подобный способ требует минимум вычислительных операций.
Чаще всего используется другой метод. То есть на исходное изображение добавляются новые строки пикселей. Каждый пиксель заливается цветом, который, в свою очередь, вычисляется как среднее значение соседних пикселей. Этот способ дает лучшие результаты, но требует больше вычислительных операций. Благо, современные мобильные процессоры быстры, и на практике пользователь не замечает, как программа редактирует изображение, пытаясь искусственно увеличить его размер. интерполяция камеры смартфона Есть много продвинутых способов и алгоритмов интерполяции, которые совершенствуются постоянно: улучшаются границы перехода между цветами, линии становятся более точными и четкими. Неважно, как построены все эти алгоритмы. Сама идея интерполяции камеры банальна и вряд ли приживется в ближайшем будущем. С помощью интерполяции невозможно сделать изображение более детализированным, добавить новые детали или улучшить его каким-либо еще образом. Только в фильмах маленькая размытая картинка после наложения пары фильтров становится четкой. На практике такого быть не может.
интерполяция камеры смартфона Есть много продвинутых способов и алгоритмов интерполяции, которые совершенствуются постоянно: улучшаются границы перехода между цветами, линии становятся более точными и четкими. Неважно, как построены все эти алгоритмы. Сама идея интерполяции камеры банальна и вряд ли приживется в ближайшем будущем. С помощью интерполяции невозможно сделать изображение более детализированным, добавить новые детали или улучшить его каким-либо еще образом. Только в фильмах маленькая размытая картинка после наложения пары фильтров становится четкой. На практике такого быть не может.
.html
Что делать, если я хочу, чтобы 3D сплайн / гладкая интерполяция случайных неструктурированных данных?
Я был вдохновлен этим ответом @James, чтобы посмотреть, как можно использовать griddata и map_coordinates . В приведенных ниже примерах я показываю 2D-данные, но мой интерес к 3D. Я заметил, что griddata предоставляет только сплайны для 1D и 2D и ограничивается линейной интерполяцией для 3D и выше (вероятно, по очень веским причинам). Однако map_coordinates кажется прекрасным с 3D, используя более высокую последовательность (более гладкую, чем кусочно-линейную) интерполяцию.
Однако map_coordinates кажется прекрасным с 3D, используя более высокую последовательность (более гладкую, чем кусочно-линейную) интерполяцию.
Мой основной вопрос: если у меня есть случайные, неструктурированные данные (где я не могу использовать map_coordinates) в 3D, есть ли какой-то способ добиться более плавной, чем кусочно-линейная интерполяция внутри вселенной NumPy SciPy или, по крайней мере, поблизости?
Мой второстепенный вопрос: сплайн для 3D недоступен в griddata потому что это сложно или утомительно для реализации или есть фундаментальная трудность?
Изображения и ужасный питон ниже показывают мое нынешнее понимание того, как griddata и map_coordinates могут или не могут быть использованы. Интерполяция выполняется по густой черной линии.
СТРУКТУРИРОВАННЫЕ ДАННЫЕ:
СТРУКТУРИРОВАННЫЕ ДАННЫЕ ООН :
Ужасный питон:
import numpy as np import matplotlib. pyplot as plt def g(x, y): return np.exp(-((x-1.0)**2 + (y-1.0)**2)) def findit(x, X): # or could use some 1D interpolation fraction = (x - X[0]) / (X[-1]-X[0]) return fraction * float(X.shape[0]-1) nth, nr = 12, 11 theta_min, theta_max = 0.2, 1.3 r_min, r_max = 0.7, 2.0 theta = np.linspace(theta_min, theta_max, nth) r = np.linspace(r_min, r_max, nr) R, TH = np.meshgrid(r, theta) Xp, Yp = R*np.cos(TH), R*np.sin(TH) array = g(Xp, Yp) x, y = np.linspace(0.0, 2.0, 200), np.linspace(0.0, 2.0, 200) X, Y = np.meshgrid(x, y) blob = g(X, Y) xtest = np.linspace(0.25, 1.75, 40) ytest = np.zeros_like(xtest) + 0.75 rtest = np.sqrt(xtest**2 + ytest**2) thetatest = np.arctan2(xtest, ytest) ir = findit(rtest, r) it = findit(thetatest, theta) plt.figure() plt.subplot(2,1,1) plt.scatter(100.0*Xp.flatten(), 100.0*Yp.flatten()) plt.plot(100.0*xtest, 100.0*ytest, '-k', linewidth=3) plt.hold plt.imshow(blob, origin='lower', cmap='gray') plt.text(5, 5, "don't use jet!", color='white') exact = g(xtest, ytest) import scipy.
pyplot as plt def g(x, y): return np.exp(-((x-1.0)**2 + (y-1.0)**2)) def findit(x, X): # or could use some 1D interpolation fraction = (x - X[0]) / (X[-1]-X[0]) return fraction * float(X.shape[0]-1) nth, nr = 12, 11 theta_min, theta_max = 0.2, 1.3 r_min, r_max = 0.7, 2.0 theta = np.linspace(theta_min, theta_max, nth) r = np.linspace(r_min, r_max, nr) R, TH = np.meshgrid(r, theta) Xp, Yp = R*np.cos(TH), R*np.sin(TH) array = g(Xp, Yp) x, y = np.linspace(0.0, 2.0, 200), np.linspace(0.0, 2.0, 200) X, Y = np.meshgrid(x, y) blob = g(X, Y) xtest = np.linspace(0.25, 1.75, 40) ytest = np.zeros_like(xtest) + 0.75 rtest = np.sqrt(xtest**2 + ytest**2) thetatest = np.arctan2(xtest, ytest) ir = findit(rtest, r) it = findit(thetatest, theta) plt.figure() plt.subplot(2,1,1) plt.scatter(100.0*Xp.flatten(), 100.0*Yp.flatten()) plt.plot(100.0*xtest, 100.0*ytest, '-k', linewidth=3) plt.hold plt.imshow(blob, origin='lower', cmap='gray') plt.text(5, 5, "don't use jet!", color='white') exact = g(xtest, ytest) import scipy. ndimage.interpolation as spndint ndint0 = spndint.map_coordinates(array, [it, ir], order=0) ndint1 = spndint.map_coordinates(array, [it, ir], order=1) ndint2 = spndint.map_coordinates(array, [it, ir], order=2) import scipy.interpolate as spint points = np.vstack((Xp.flatten(), Yp.flatten())).T # could use np.array(zip(...)) grid_x = xtest grid_y = np.array([0.75]) g0 = spint.griddata(points, array.flatten(), (grid_x, grid_y), method='nearest') g1 = spint.griddata(points, array.flatten(), (grid_x, grid_y), method='linear') g2 = spint.griddata(points, array.flatten(), (grid_x, grid_y), method='cubic') plt.subplot(4,2,5) plt.plot(exact, 'or') #plt.plot(ndint0) plt.plot(ndint1) plt.plot(ndint2) plt.title("map_coordinates") plt.subplot(4,2,6) plt.plot(exact, 'or') #plt.plot(g0) plt.plot(g1) plt.plot(g2) plt.title("griddata") plt.subplot(4,2,7) #plt.plot(ndint0 - exact) plt.plot(ndint1 - exact) plt.plot(ndint2 - exact) plt.title("error map_coordinates") plt.subplot(4,2,8) #plt.plot(g0 - exact) plt.
ndimage.interpolation as spndint ndint0 = spndint.map_coordinates(array, [it, ir], order=0) ndint1 = spndint.map_coordinates(array, [it, ir], order=1) ndint2 = spndint.map_coordinates(array, [it, ir], order=2) import scipy.interpolate as spint points = np.vstack((Xp.flatten(), Yp.flatten())).T # could use np.array(zip(...)) grid_x = xtest grid_y = np.array([0.75]) g0 = spint.griddata(points, array.flatten(), (grid_x, grid_y), method='nearest') g1 = spint.griddata(points, array.flatten(), (grid_x, grid_y), method='linear') g2 = spint.griddata(points, array.flatten(), (grid_x, grid_y), method='cubic') plt.subplot(4,2,5) plt.plot(exact, 'or') #plt.plot(ndint0) plt.plot(ndint1) plt.plot(ndint2) plt.title("map_coordinates") plt.subplot(4,2,6) plt.plot(exact, 'or') #plt.plot(g0) plt.plot(g1) plt.plot(g2) plt.title("griddata") plt.subplot(4,2,7) #plt.plot(ndint0 - exact) plt.plot(ndint1 - exact) plt.plot(ndint2 - exact) plt.title("error map_coordinates") plt.subplot(4,2,8) #plt.plot(g0 - exact) plt. plot(g1 - exact) plt.plot(g2 - exact) plt.title("error griddata") plt.show() seed_points_rand = 2.0 * np.random.random((400, 2)) rr = np.sqrt((seed_points_rand**2).sum(axis=-1)) thth = np.arctan2(seed_points_rand[...,1], seed_points_rand[...,0]) isinside = (rr>r_min) * (rr<r_max) * (thth>theta_min) * (thth<theta_max) points_rand = seed_points_rand[isinside] Xprand, Yprand = points_rand.T # unpack array_rand = g(Xprand, Yprand) grid_x = xtest grid_y = np.array([0.75]) plt.figure() plt.subplot(2,1,1) plt.scatter(100.0*Xprand.flatten(), 100.0*Yprand.flatten()) plt.plot(100.0*xtest, 100.0*ytest, '-k', linewidth=3) plt.hold plt.imshow(blob, origin='lower', cmap='gray') plt.text(5, 5, "don't use jet!", color='white') g0rand = spint.griddata(points_rand, array_rand.flatten(), (grid_x, grid_y), method='nearest') g1rand = spint.griddata(points_rand, array_rand.flatten(), (grid_x, grid_y), method='linear') g2rand = spint.griddata(points_rand, array_rand.flatten(), (grid_x, grid_y), method='cubic') plt.
plot(g1 - exact) plt.plot(g2 - exact) plt.title("error griddata") plt.show() seed_points_rand = 2.0 * np.random.random((400, 2)) rr = np.sqrt((seed_points_rand**2).sum(axis=-1)) thth = np.arctan2(seed_points_rand[...,1], seed_points_rand[...,0]) isinside = (rr>r_min) * (rr<r_max) * (thth>theta_min) * (thth<theta_max) points_rand = seed_points_rand[isinside] Xprand, Yprand = points_rand.T # unpack array_rand = g(Xprand, Yprand) grid_x = xtest grid_y = np.array([0.75]) plt.figure() plt.subplot(2,1,1) plt.scatter(100.0*Xprand.flatten(), 100.0*Yprand.flatten()) plt.plot(100.0*xtest, 100.0*ytest, '-k', linewidth=3) plt.hold plt.imshow(blob, origin='lower', cmap='gray') plt.text(5, 5, "don't use jet!", color='white') g0rand = spint.griddata(points_rand, array_rand.flatten(), (grid_x, grid_y), method='nearest') g1rand = spint.griddata(points_rand, array_rand.flatten(), (grid_x, grid_y), method='linear') g2rand = spint.griddata(points_rand, array_rand.flatten(), (grid_x, grid_y), method='cubic') plt. subplot(4,2,6) plt.plot(exact, 'or') #plt.plot(g0rand) plt.plot(g1rand) plt.plot(g2rand) plt.title("griddata") plt.subplot(4,2,8) #plt.plot(g0rand - exact) plt.plot(g1rand - exact) plt.plot(g2rand - exact) plt.title("error griddata") plt.show()
subplot(4,2,6) plt.plot(exact, 'or') #plt.plot(g0rand) plt.plot(g1rand) plt.plot(g2rand) plt.title("griddata") plt.subplot(4,2,8) #plt.plot(g0rand - exact) plt.plot(g1rand - exact) plt.plot(g2rand - exact) plt.title("error griddata") plt.show()
Хороший вопрос! (и приятные сюжеты!)
Для неструктурированных данных вы хотите переключиться на функции, предназначенные для неструктурированных данных. griddata – один из вариантов, но между ними используется триангуляция с линейной интерполяцией. Это приводит к «жестким» краям на границах треугольника.
Сплайны являются радиальными базисными функциями. В scipy терминах вы хотите scipy.interpolate.Rbf . Я бы рекомендовал использовать function="linear" или function="thin_plate" над кубическими сплайнами, но куб также доступен. (Кубические сплайны будут усугублять проблемы с «перерегулированием» по сравнению с линейными или тонкопленочными сплайнами. )
)
Одно из предостережений заключается в том, что эта конкретная реализация радиальных базисных функций всегда будет использовать все точки в вашем наборе данных. Это самый точный и плавный подход, но он плохо масштабируется по мере увеличения количества точек наблюдения. Есть несколько способов обойти это, но все будет усложняться. Я оставлю это по другому вопросу.
Во всяком случае, вот упрощенный пример. Мы будем генерировать случайные данные и затем интерполировать их в точках, которые находятся на регулярной сетке. (Обратите внимание, что вход не находится на регулярной сетке, и интерполированные точки также не должны быть.)
import numpy as np import scipy.interpolate import matplotlib.pyplot as plt np.random.seed(1977) x, y, z = np.random.random((3, 10)) interp = scipy.interpolate.Rbf(x, y, z, function='thin_plate') yi, xi = np.mgrid[0:1:100j, 0:1:100j] zi = interp(xi, yi) plt.plot(x, y, 'ko') plt.imshow(zi, extent=[0, 1, 1, 0], cmap='gist_earth') plt. colorbar() plt.show()
colorbar() plt.show()
Выбор типа сплайна
Я выбрал "thin_plate" как тип сплайна. Наши входные точки наблюдений варьируются от 0 до 1 (они создаются np.random.random ). Обратите внимание, что наши интерполированные значения немного превышают 1 и значительно ниже нуля. Это «перерегулирование».
Линейные сплайны полностью избегают перерегулирования, но вы получите «бычьи» паттерны (нигде не столь строгие, как при использовании методов IDW). Например, вот те же самые данные, интерполированные с линейной радиальной базисной функцией. Обратите внимание, что наши интерполированные значения никогда не превышают 1 или ниже 0:
Сплавы более высокого порядка будут делать тенденции в данных более непрерывными, но будут превышать больше. По умолчанию "multiquadric" довольно похож на сплайн с тонкой пластинкой, но сделает вещи немного более непрерывными и превысит немного хуже:
Однако, когда вы переходите к сплайнам более высокого порядка, таким как "cubic" (третий порядок):
и "quintic" (пятый порядок)
Вы действительно можете получить необоснованные результаты, как только будете двигаться немного за пределы ваших входных данных.
Во всяком случае, вот простой пример для сравнения различных радиальных базисных функций на случайных данных:
import numpy as np import scipy.interpolate import matplotlib.pyplot as plt np.random.seed(1977) x, y, z = np.random.random((3, 10)) yi, xi = np.mgrid[0:1:100j, 0:1:100j] interp_types = ['multiquadric', 'inverse', 'gaussian', 'linear', 'cubic', 'quintic', 'thin_plate'] for kind in interp_types: interp = scipy.interpolate.Rbf(x, y, z, function=kind) zi = interp(xi, yi) fig, ax = plt.subplots() ax.plot(x, y, 'ko') im = ax.imshow(zi, extent=[0, 1, 1, 0], cmap='gist_earth') fig.colorbar(im) ax.set(title=kind) fig.savefig(kind + '.png', dpi=80) plt.show()
Интерполяция кусочно-постоянная — Энциклопедия по машиностроению XXL
Из рисунка видно, что при N при квадратичной аппроксимации точность решения несколько выше, чем при кусочно-постоянной. Однако при квадратичной аппроксимации количество узлов интерполяции в два раза больше, чем при кусочно-постоянной. При одинаковом количестве узлов интерполяции кусочно-постоянная аппроксимация дает более точные результаты.
[c.169]
При одинаковом количестве узлов интерполяции кусочно-постоянная аппроксимация дает более точные результаты.
[c.169]При использовании интерполяции кусочно-постоянного типа, описанной выше, не всегда удобно делать равными погрешности площади областей, лежащих над графиком функции возмущающей силы и под ним. Более грубым подходом является выбор ординат кривой, относящихся к началу (или концу) интервала времени, в качестве значения импульса прямоугольной формы (или ступенчатой функции). При этом для сохранения заданной точности решения может потребоваться большее число шагов по времени, и при вычислении может стать значительной ошибка округления. Для того чтобы избежать указанных трудностей, можно воспользоваться интерполирующими функциями более высокого порядка. На рис. 1.57 показан логически вытекающий из сказанного способ представления импульсного возмущения с помощью наклонных линий и вертикальных полос. Для этой интерполяции кусочно-линейного типа переме-
[c.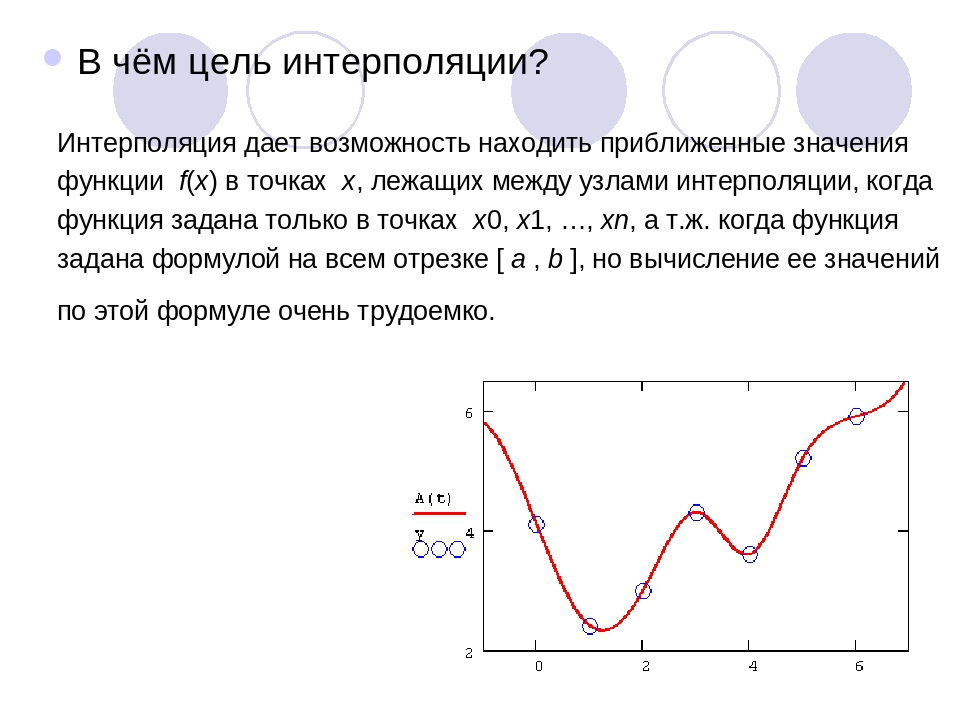 121]
121]
Рассмотрим вначале интерполяцию кусочно-постоянного типа, описанную в п. 1.15 (см. рис. 1.56). Не теряя общности, здесь будем использовать только кусочно-постоянного вида функцию возмущающей силы /п (Aij-), кусочно-постоянная форма вектора сил имеет вид [c.315]
Показатель степени шага h в оценке погрешности называют порядком точности квадратурной формулы. Квадратурные формулы прямоугольников и трапеций имеют второй порядок точности для функций, имеющих вторую производную, т. е. R = О (Л ). Заметим, что порядок точности обеих формул одинаков, хотя в одной использована интерполяция линейными функциями, а в другой — кусочно-постоянными. [c.62]
Параметры капель на границах ячеек также определялись из решения задачи о нестационарном одномерном течении газа частиц с кусочно-постоянным начальным распределением в предположении об отсутствии межфазного взаимодействия. В силу принятых допущений газ частиц не обладает собственным давлением, поэтому все возмущения переносятся в такой среде со скоростью частиц (семейство характеристик вырождено), а разрыв в начальном распределении скоростей приводит к возникновению либо зоны вакуума , либо зоны взаимопроникающего движения двух потоков частиц. Если нормальные к границе ячейки составляющие скорости капель направлены в одну сторону ( i 2>0), то на границу приходят/ характеристики только из одной ячейки и значения параметров принимаются равными значениями в той ячейке, из которой газ частиц вытекает. Если нормальные составляющие скорости имеют разные знаки ( i 2 0), то граница ячейки попадает в область, где характеристики отсутствуют ( вакуум ) или пересекаются (зона взаимопроникающего движения). В этих случаях решение в обычном смысле найдено быть не может и возникает необходимость дополнить решение. В расчетах были опробованы несколько вариантов аппроксимации параметров частиц на границах ячеек при условии i 2варианте схемы скорость капель определялась с помощью линейной интерполяции, а значения плотности р2 и энергии сносились из той ячейки, из которой газ частиц вытекает.
В силу принятых допущений газ частиц не обладает собственным давлением, поэтому все возмущения переносятся в такой среде со скоростью частиц (семейство характеристик вырождено), а разрыв в начальном распределении скоростей приводит к возникновению либо зоны вакуума , либо зоны взаимопроникающего движения двух потоков частиц. Если нормальные к границе ячейки составляющие скорости капель направлены в одну сторону ( i 2>0), то на границу приходят/ характеристики только из одной ячейки и значения параметров принимаются равными значениями в той ячейке, из которой газ частиц вытекает. Если нормальные составляющие скорости имеют разные знаки ( i 2 0), то граница ячейки попадает в область, где характеристики отсутствуют ( вакуум ) или пересекаются (зона взаимопроникающего движения). В этих случаях решение в обычном смысле найдено быть не может и возникает необходимость дополнить решение. В расчетах были опробованы несколько вариантов аппроксимации параметров частиц на границах ячеек при условии i 2варианте схемы скорость капель определялась с помощью линейной интерполяции, а значения плотности р2 и энергии сносились из той ячейки, из которой газ частиц вытекает. Такой способ определения параметров капель на границах ячеек обеспечивает устойчивость вычислительного процесса и гладкость профилей параметров капель.
[c.132]
Такой способ определения параметров капель на границах ячеек обеспечивает устойчивость вычислительного процесса и гладкость профилей параметров капель.
[c.132]
| Рис. 7, Графики кусочно-постоянной интерполяции и ошибки интерполяции непрерывного процесса |
Нами рассматривались варианты метода граничных элементов с полиномами нулевой и второй степеней, т. е. кусочно-постоянная и квадратичная аппроксимации на каждом граничном элементе. При квадратичной аппроксимации уравнения метода граничных элементов и особенно их коэффициенты более сложные, чем соответствующие уравнения для кусочно-постоянной аппроксимации. Точность получаемых результатов, как будет показано, с увеличением степени интерполяционного полинома растет незначительно. Поэтому при решении поставленных задач использовалась кусочно-постоянная аппроксимация.
 При этом уравнения (7.18) упрощаются исчезает суммирование по д, а узлы интерполяции, которые располагаются на серединах граничных эЗ ементов, можно нумеровать теми же индексами, что и элементы. Тогда система уравнений метода граничных элементов запишется в виде
[c.165]
При этом уравнения (7.18) упрощаются исчезает суммирование по д, а узлы интерполяции, которые располагаются на серединах граничных эЗ ементов, можно нумеровать теми же индексами, что и элементы. Тогда система уравнений метода граничных элементов запишется в виде
[c.165]Используя показанный на рис. 1.56 метод кусочно-постоянной интерполяции, определить и построить график для перемещения в системе с одной степенью свободы и без демпфирования, на которую действует возмуп ающая сила, представляемая функцией в задаче 1.12.7. Использовать постоянный по времени шаг Д/г — и рассмотреть отрезок времени О 1. Начальные условия суть Хо = Хо = О, величины к равны единице. Сравнить полученные результаты с точным решением этой задачи, считая, что = т/2. [c.129]
Постоянная 1/8 неулучшаема, и не только для ошибки линейной интерполяции, но и для произвольной кусочно линейной аппроксимации. Вторая производная и» от функции, где аппроксимация хуже всех, меняется от +1 до —1 на соседних интервалах (рис.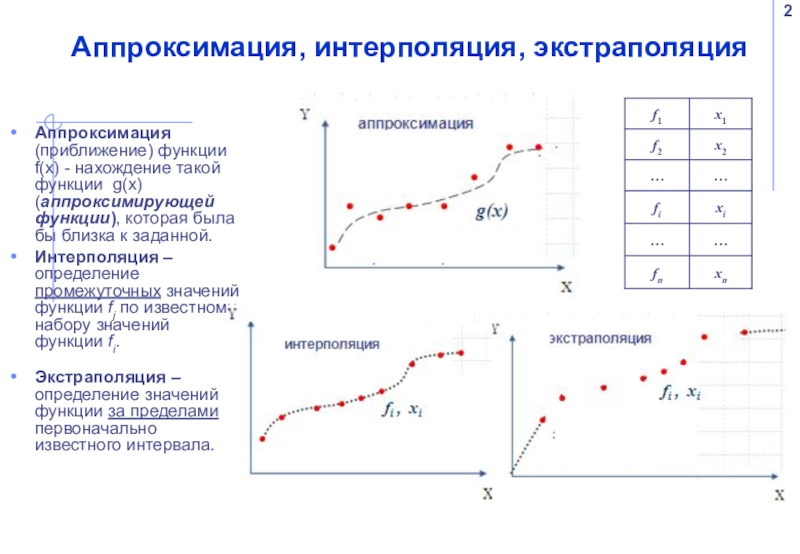 1.5). Наилучшая кусочно линейная аппроксимация в этом экстремальном случае — тождественный нуль, и ошибка составляет h jb.
[c.59]
1.5). Наилучшая кусочно линейная аппроксимация в этом экстремальном случае — тождественный нуль, и ошибка составляет h jb.
[c.59]
Интерполяция строк | Python
Все хорошо знают об операторе форматирования в языке Python. В этой заметке приводятся малоизвестные приемы его использования.
В самом простом способе применения оператора форматирования его поведение аналогично функций *printf в C:
>>> print 'Длина удава: %d попугаев и %d попугайское крылышко' % (38, 1) Длина удава: 38 попугаев и 1 попугайское крылышко
При использовании ‘%s’ или ‘%r’ объекты любого типа автоматически преобразуются к строке, как если бы к ним применялась функция str или repr соответственно:
>>> print 'Длина удава: %s попугаев и %s попугайское крылышко' % (38, 1) Длина удава: 38 попугаев и 1 попугайское крылышко
Для длинных строк с большим количеством параметров удобнее ссылаться на значения по имени. Это позволит менять порядок следования значений в строке не меняя правый аргумент оператора форматирования:
>>> args = {'parrots': 38, 'wings': 1}
>>> print '%(parrots)s попугаев и %(wings)s попугайское крылышко' % args
38 попугаев и 1 попугайское крылышко
>>> print '%(wings)s крылышко в добавок к %(parrots)s попугаям' % args
1 крылышко в добавок к 38 попугаям
>>> print '%(wings)s крылышко не в счет' % args
1 крылышко не в счетМожно не составлять словарь самостоятельно, а использовать функцию globals, locals или vars:
>>> print '%(parrots)s попугаев и %(wings)s попугайское крылышко' % vars() 38 попугаев и 1 попугайское крылышко
Однако и это не все, что можно делать с оператором форматирования. Тем, кто знаком с языком perl, обычно сильно не достает интерполяции строк с выражениями, записанными непосредственно в строке-шаблоне. Аналогичный эффект можно получить и в языке Python с помощью простого классом, имитирующего поведение словаря:
Тем, кто знаком с языком perl, обычно сильно не достает интерполяции строк с выражениями, записанными непосредственно в строке-шаблоне. Аналогичный эффект можно получить и в языке Python с помощью простого классом, имитирующего поведение словаря:
class EvalDict:
def __getitem__(self, key):
return eval(key)Использовать класс EvalDict можно аналогично функции vars:
>>> nums = [38, 1] >>> print '%(nums[0])s попугаев и %(nums[1])s крылышко' % EvalDict() 38 попугаев и 1 крылышко
Приведенный класс EvalDict обладает двумя недостатками. Во-первых, он ищет значения переменных только в глобальном пространстве имен модуля, в котором он определен. Во-вторых, он не будет обрабатывать вложенные выражения. Исправим эти недостатки.
import sys
class EvalDict:
def __init__(self, globals=None, locals=None):
if globals is None:
globals = sys._getframe(1).f_globals
self.globals = globals
if locals is None:
locals = sys. _getframe(1).f_locals
self.locals = locals
def __getitem__(self, key):
key = key % self
return eval(key, self.globals, self.locals)
_getframe(1).f_locals
self.locals = locals
def __getitem__(self, key):
key = key % self
return eval(key, self.globals, self.locals)Теперь определение класса можно спокойно вынести в отдельный модуль и использовать вложенные выражения:
>>> nums = [38, 1] >>> units = ['попугаев', 'крылышко'] >>> index = 0 >>> print '%(nums[index])d %(units[index])s' % EvalDict() 38 попугаев >>> index = 1 >>> print '%(nums[index])d %(units[index))s' % EvalDict() 1 крылышко
PHP. Линейная интерполяция или если по-русски красивое сглаживание графиков
Закончил почти 9 часовое сражение с невообразомой херней, так как херня была крайне не стандартная, то решил поделиться с миром.Вообще, вначале хотел пост обозвать «Линейная интерполяция или Интерполяционный многочлен Лагранжа», но я сам толком не понимаю что это значит.
Работаю в данный момент над одним крупным проектом аналитической системы, как и в любой системе, здесь дофига графиков. Ниже пример.
Ниже пример.
Ну график как график, куча значений и все такое, но вот прибило заказчику, хочу говорит, сглаженный график как в Экселе и все тут. И подкинул он мне мило ссылочку на википедию Интерполяционный_многочлен_Лагранжа Как бы я тоже слегка прибалдел, когда прочитал что от меня хотят. Ну думаю, ладно, фик с вами в интернете явно что-то есть готовое… Я искал долго, очень долго и самое забавное нифига не нашел, было пара решений на Си, но там использовались встроенные библиотеки. Долго думал что делать, потом подсказали, что на странице википедии, как бы есть код на Си, который можно легко переписать на PHP. Код мелкий, 24 строки всего, быстренько переделал и получилось вот что…
Обрадовался, показываю заказчику, на что мне выдается ответ, а чего по бокам прыжки огромные? Ну думаю жопа. Все вроде бы по формуле, что делать не особо понятно. Ладно, будем копать дальше. Вначале был найден эксельный файл, который тоже умеет это делать, но как оттуда выцепить алгоритм непонятно, да и вообще мне кажется, что в экселе это какие-то встроенные функции. Дальше наткнулся на очень прикольный проект на яваскрипте JSXGraph Надо будеть взять на заметку и попользовать его функционал в будущем. Тут я тоже нашел рабоющий пример интерполяции и решил переписать метод отсюда, в результате кстати получилось почти тоже самое что и на графике выше. Совсем я погрустнел, и пересмотрел множество запасных решений, нашел пару модулей для Perl, пытался найти консольную утилиту через которую можно было бы тоже данные подцепить, но ничего не получилось.. После долгих экспериментов выяснилось что если клонировать первичное и конечное значение в массиве координат, то крайние пики очень сильно сглаживаются. На выходе у меня получился вот такой вот график.
Дальше наткнулся на очень прикольный проект на яваскрипте JSXGraph Надо будеть взять на заметку и попользовать его функционал в будущем. Тут я тоже нашел рабоющий пример интерполяции и решил переписать метод отсюда, в результате кстати получилось почти тоже самое что и на графике выше. Совсем я погрустнел, и пересмотрел множество запасных решений, нашел пару модулей для Perl, пытался найти консольную утилиту через которую можно было бы тоже данные подцепить, но ничего не получилось.. После долгих экспериментов выяснилось что если клонировать первичное и конечное значение в массиве координат, то крайние пики очень сильно сглаживаются. На выходе у меня получился вот такой вот график.
Как видите пиков нет, все плавненько. Степень скругления можно задавать в параметре функции.. Код прилагаю снизу, в принципе все понятно. Пишу на случай, вдруг кому пригодится, чтобы не мучился как я..
/* значит так, входящие параметры это координаты Y и X для которого получаем Yз.ы. Сервис для подсветки PHP код я искал дольше чем писал эту заметку, но все таки нашел http://highlight.hohli.com/ всем советую, отличный сервис!
* массив координат x строится автоматом так как он у меня всегда массив [0 - кол-во значений Y]
* smooth - степень скругления, иначе на концах графика у нас огромные скачки...
*/ function lagrange_polynomial($y, $argx, $smooth = 10 ) { $num = 0; $denom = 0; $x = range( -1*$smooth, count($y) + $smooth + 1 ); $last = $y[count($y)-1]; for( $i=1;$i<=$smooth;$i++) { $y[] = $y[0]; array_unshift( $y, $last); } $len = count($y); for ($i=0;$i<$len;$i++) { $w[$i] = 1.0; $xi = $x[$i]; for ($k=0;$k<$len;$k++) if ($k!=$i) { $w[$i] *= ($xi-$x[$k]); } $w[$i] = 1/$w[$i]; } for ($i=0;$i<$len;$i++) { $xi = $x[$i]; if ( $argx==$xi ) { return $y[$i]; } else { $s = $w[$i]/( $argx-$xi ); $denom += $s; $num += $s*$y[$i]; } } return $num/$denom; }
Интерполяция в статистике: определение, формула и пример — видео и стенограмма урока
Пример интерполяции
Вот пример, который иллюстрирует концепцию интерполяции. Садовник посадил помидор, и она измеряла и отслеживала его рост через день. Этот садовник — любопытный человек, и она хотела бы оценить, насколько высоким было ее растение на четвертый день.
Этот садовник — любопытный человек, и она хотела бы оценить, насколько высоким было ее растение на четвертый день.
Ее таблица наблюдений выглядела так:
Исходя из диаграммы, нетрудно догадаться, что высота растения на четвертый день была, вероятно, 6 мм.Это потому, что это дисциплинированное растение томата росло линейно; была линейная зависимость между количеством измеренных дней и ростом растения. Линейный узор означает, что точки образуют прямую линию. Мы могли даже оценить, нанеся данные на график.
А что, если растение росло не по удобной линейной схеме? Что, если бы его рост выглядел примерно так?
Что бы сделал садовник, чтобы сделать оценку на основе приведенной выше кривой? Что ж, вот здесь и пригодится формула интерполяции.
Формула интерполяции
Формула интерполяции выглядит следующим образом:
Теперь давайте рассмотрим, как использовать эту формулу. Два набора точек, между которыми можно найти оценку:
Два набора точек, между которыми можно найти оценку:
Возвращаясь к примеру с томатом, первый набор значений для третьего дня равен (3,4), второй набор значений для пятого дня (5,8), а значение для x равно 4, так как мы хотим найти высоту y на четвертый день.Подставив эти значения в формулу, рассчитайте предполагаемую высоту растения на четвертый день.
Исходя из расчетов, расчетная высота растения на четвертые сутки составляет 6 мм.
Интерполяция с помощью графика
С помощью интерполяции иногда можно провести прямую линию через две точки на кривой. Затем эту линию можно использовать для аппроксимации значения в других точках кривой.Например, если у томатов не было линейной модели роста, можно построить линию от точек данных за день 3 до точек данных за день 5. На основе этой линии можно спроектировать высоту растения. На графике это иллюстрируется зелеными пунктирными линиями, которые показывают, что высота на четвертый день будет 4 мм.
На основе этой линии можно спроектировать высоту растения. На графике это иллюстрируется зелеными пунктирными линиями, которые показывают, что высота на четвертый день будет 4 мм.
Сводка урока
Интерполяция — это способ найти значения между парой точек данных.Формулу интерполяции можно использовать для поиска пропущенного значения. Однако, проведя прямую линию через две точки на кривой, можно приблизительно определить значение в других точках кривой. В формуле для интерполяции x-sub1 и y-sub1 представляют первый набор точек данных наблюдаемых значений. X-sub2 и y-sub2 представляют второй набор точек данных. Неизвестные значения находятся между этими двумя наборами точек.
Ключевые термины
Интерполяция — процесс нахождения значения между двумя точками на линии или кривой
Линейный образец — образец, в котором нанесенные на график точки образуют прямую линию
Результаты обучения
Накопление знаний о статистической интерполяции из этого урока, а затем попытайтесь:
- Дайте определения для интерполяции и линейного массива
- Вычислить значения между парой точек данных с помощью формулы интерполяции
Формула линейной интерполяции — Образование
Формула интерполяции: Метод поиска новых значений для любой функции, использующей набор значений, выполняется путем интерполяции. Неизвестное значение точки определяется по этой формуле. Если речь идет о формуле линейной интерполяции, то ее следует использовать для нахождения нового значения из двух заданных точек. По сравнению с формулой интерполяции Лагранжа, должен быть доступен набор чисел «n», и для нахождения нового значения следует использовать метод Лагранжа.
Неизвестное значение точки определяется по этой формуле. Если речь идет о формуле линейной интерполяции, то ее следует использовать для нахождения нового значения из двух заданных точек. По сравнению с формулой интерполяции Лагранжа, должен быть доступен набор чисел «n», и для нахождения нового значения следует использовать метод Лагранжа.
Читайте также: 5 советов по сдаче онлайн-тестов по математике
Интерполяция — это процесс нахождения значения между двумя точками на линии или кривой. Чтобы помочь нам запомнить, что это означает, мы должны думать о первой части слова «интер» как о значении «вводить», что напоминает нам о том, чтобы заглянуть «внутрь» данных, которые у нас были изначально.Этот инструмент, интерполяция, полезен не только в статистике, но также полезен в науке, бизнесе или в любое время, когда необходимо предсказать значения, которые попадают в две существующие точки данных.
Формула линейной интерполяцииФормула линейной интерполяции
Если две известные точки заданы координатами {\ displaystyle (x_ {0}, y_ {0})} и {\ displaystyle (x_ {1}, y_ {1})}, линейный интерполянт является прямая линия между этими точками. Для значения x в интервале {\ displaystyle (x_ {0}, x_ {1})} значение y вдоль прямой линии определяется из уравнения уклонов
Для значения x в интервале {\ displaystyle (x_ {0}, x_ {1})} значение y вдоль прямой линии определяется из уравнения уклонов
- {\ displaystyle {\ frac {y-y_ {0}} {x-x_ {0}}} = {\ frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}) }},}
, который геометрически может быть получен из рисунка справа.Это частный случай полиномиальной интерполяции с n = 1.
Решение этого уравнения для y , которое является неизвестным значением при x , дает
- {\ displaystyle y = y_ {0} + (x-x_ {0}) {\ frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}}} = {\ frac {y_ {0} (x_ {1} -x) + y_ {1} (x-x_ {0})} {x_ {1} -x_ {0}}},}
— формула линейной интерполяции в интервале {\ displaystyle (x_ {0}, x_ {1})}. За пределами этого интервала формула идентична линейной экстраполяции.
Эту формулу также можно понимать как средневзвешенное значение. Веса обратно пропорциональны расстоянию от конечных точек до неизвестной точки; более близкая точка имеет большее влияние, чем более удаленная. Таким образом, веса равны {\ textstyle {\ frac {x-x_ {0}} {x_ {1} -x_ {0}}}} и {\ textstyle {\ frac {x_ {1} -x} {x_ { 1} -x_ {0}}}}, которые представляют собой нормализованные расстояния между неизвестной точкой и каждой из конечных точек. Потому что эти суммы равны 1
Таким образом, веса равны {\ textstyle {\ frac {x-x_ {0}} {x_ {1} -x_ {0}}}} и {\ textstyle {\ frac {x_ {1} -x} {x_ { 1} -x_ {0}}}}, которые представляют собой нормализованные расстояния между неизвестной точкой и каждой из конечных точек. Потому что эти суммы равны 1
- {\ displaystyle y = y_ {0} \ left (1 — {\ frac {x-x_ {0}} {x_ {1} -x_ {0}}} \ right) + y_ {1} \ left ( 1 — {\ frac {x_ {1} -x} {x_ {1} -x_ {0}}} \ right) = y_ {0} \ left (1 — {\ frac {x-x_ {0}} { x_ {1} -x_ {0}}} \ right) + y_ {1} \ left ({\ frac {x-x_ {0}} {x_ {1} -x_ {0}}} \ right),}
Калькулятор формул интерполяции
Решенные примеры
Вопрос 1: Используя формулу интерполяции, найти значение y при x = 8 для некоторого набора значений (2, 6), (5, 9)?Решение:
Известные значения: x0 = 8, x1 = 2, x2 = 5, y1 = 6, y2 = 9y = y1 + (x − x1) (x2 − x1) × (y2 − y1)
.у = 6 + ((8-2) (5-2) × (9-6)
г = 6 + 6
г = 12
Что такое метод линейной интерполяции?
Линейная интерполяция — это простейший метод получения значений в положениях между точками данных. Точки просто соединяются отрезками прямых линий.
Точки просто соединяются отрезками прямых линий.
Как найти интерполяцию между двумя числами?
Знать формулу для процесса линейной интерполяции . Формула : y = y1 + ((x — x1) / (x2 — x1)) * (y2 — y1), где x — известное значение, y — неизвестное значение, x1 и y1 — координаты, которые ниже известного значения x, а x2 и y2 — координаты выше значения x.
Что такое метод интерполяции?
В математической области численного анализа, интерполяция — это метод построения новых точек данных в диапазоне дискретного набора известных точек данных.… Несколько точек данных исходной функции можно интерполировать на , чтобы получить более простую функцию, которая все еще довольно близка к исходной.
Формула интерполяции Excel
Формула интерполяции ExcelВот пример, иллюстрирующий концепцию интерполяции. Садовник посадил помидор, и она измеряла и отслеживала его рост через день. Этот садовник — любопытный человек, и она хотела бы оценить, насколько высоким было ее растение на четвертый день.
Читайте также: Средняя и мгновенная скорость изменения
Ее таблица наблюдений выглядела так:
Исходя из диаграммы, нетрудно понять, что на четвертый день растение было, вероятно, 6 мм высотой. Это потому, что это дисциплинированное растение томата росло линейно; была линейная зависимость между количеством измеренных дней и ростом растения. Линейный образец означает, что точки образуют прямую линию.Мы могли даже оценить, нанеся данные на график.
А что, если растение росло не по удобной линейной схеме? Что, если бы его рост выглядел примерно так?
Что бы сделал садовник, чтобы сделать оценку на основе приведенной выше кривой? Что ж, вот здесь и пригодится формула интерполяции.
Формула интерполяции Thermo
Линейная интерполяция использовалась с древних времен для заполнения пробелов в таблицах.Предположим, у вас есть таблица, в которой перечислено население какой-либо страны в 1970, 1980, 1990 и 2000 годах, и вы хотите оценить численность населения в 1994 году. Линейная интерполяция — простой способ сделать это. Считалось, что метод использования линейной интерполяции для составления таблиц использовался вавилонскими астрономами и математиками в Месопотамии Селевкидов (последние три века до нашей эры), а также греческим астрономом и математиком Гиппархом (2 век до нашей эры). Описание линейной интерполяции можно найти в Альмагесте (2 век нашей эры) Птолемея.
Основная операция линейной интерполяции между двумя значениями обычно используется в компьютерной графике. На жаргоне этой области его иногда называют lerp . Термин может использоваться как глагол или существительное для операции. например «Алгоритм Брезенхема постепенно перемещается между двумя конечными точками линии».
Lerp-операций встроены в аппаратную часть всех современных графических процессоров. Их часто используют в качестве строительных блоков для более сложных операций: например, билинейную интерполяцию можно выполнить за три лерпа.Поскольку эта операция стоит недорого, это также хороший способ реализовать точные таблицы поиска с быстрым поиском плавных функций без слишком большого количества записей в таблице.
Читайте также: Что такое буквенно-цифровые символы?
Формула интерполяции
Допустим, у нас есть две известные точки x1, y1x1, y1 и x2, y2x2, y2.
Теперь мы хотим оценить, какое значение yy мы получили бы для некоторого значения xx, которое находится между x1x1 и x2x2. Назовите это значение yy оценкой — , интерполированное значение .
На ум приходят два простых метода выбора yy. Во-первых, нужно посмотреть, ближе ли xx к x1x1 или к x2x2. Если xx ближе к x1x1, тогда мы используем y1y1 в качестве оценки, в противном случае мы используем y2y2. Это называется интерполяцией ближайшего соседа .
Это называется интерполяцией ближайшего соседа .
Второй — провести прямую линию между x1, y1x1, y1 и x2, y2x2, y2. Мы смотрим, чтобы увидеть значение yy в строке для нашего выбранного xx. Это линейная интерполяция .
Можно показать, что формула линии между x1, y1x1, y1 и x2, y2x2, y2:
y = y1 + (x − x1) y2 − y1x2 − x1y = y1 + (x − x1) y2 − y1x2 − x1
Формула двойной интерполяции
Чтобы выполнить линейную интерполяцию в Excel, мы будем использовать приведенное ниже уравнение, где x — независимая переменная, а y — значение, которое мы хотим найти:
Линейная интерполяция
Линейная интерполяция Up: Возврат
Линейная интерполяция — это способ заполнить « дыры » в таблицах.В качестве
Например, если вы хотите найти давление насыщения воды при
температуры 40C вы можете посмотреть в Таблице B.1.1, (стр.674),
40C в первом столбце. Соответствующее желаемое давление
тогда находится в следующем столбце; в данном случае 7,384 кПа. Но что, если ты
хотите найти давление насыщения при 38 ° C вместо
40C?
Но что, если ты
хотите найти давление насыщения при 38 ° C вместо
40C?
Температура 38C отсутствует в таблице. Вы, конечно, могли бы просто игнорируйте разницу между 38C и 40C, и по-прежнему принимать давление насыщения равным 7.384 кПа. Но это не так приемлемо в этом классе; это слишком неточно. Чтобы получить точный значение, необходимо использовать линейную интерполяцию. (Хотя выбирая ближайший значение 40C, конечно, лучше, чем ничего, если вы забыл, как делать линейную интерполяцию во время экзамена.)
Введем несколько символов. Пусть г будет вашим заданным значением,
38C в этом примере. Пусть g 1 и g 2 будут двумя ближайшими
приближения от до г в таблице.Взглянув на Таблицу B.1.1, можно увидеть
что два ближайших значения, которые вы можете найти в таблице, — 35C
и 40C, поэтому в нашем примере g 1 = 35C и
г 2 = 40 ° С. (Желаемое значение находится между этими двумя, следовательно,
« in » в « интерполяции ». )
)
Кроме того, пусть d будет нашим желаемым значением, в нашем примере насыщенный давление. Пусть d 1 и d 2 будут приблизительными желаемыми значениями. соответствует г 1 и г 2 .В нашем примере таблица B.1.1 дает давление насыщения при г 1 = 35 ° C должно быть d 1 = 5,628 кПа и давление насыщения при г 2 = 40 ° C должно быть d 2 = 7,384 кПа. И d 1 и d 2 являются приближенными к нашему желаемому давлению, но ни то, ни другое не является достаточно точным.
Формула линейной интерполяции:
Итак, в нашем примере желаемое давление насыщения d при 38C является:
Вам нужны две переменные, чтобы считать сжатую жидкость или
таблицы перегретого пара.В следующем примере мы найдем
удельный объем пара при заданной температуре 100 ° C и
заданное давление 20 кПа.
Пар (перегретый водяной пар) приведен в таблице B.1.3. У нас нет трудно найти данные 100C в этой таблице, но мы не можем найти заданное давление 20 кПа. Ближайшие давления в таблице составляют 10 кПа и 50 кПа.
Итак, в формуле линейной интерполяции из предыдущего раздела
заданное значение г устанавливаем равным 20 кПа, а ближайшую таблицу значения г 1 и г 2 до 10 кПа и 50 кПа.
Требуемое количество d теперь является удельным объемом при 100 ° C. и 20 кПа. Устанавливаем значение d 1 на удельный объем г 1 = 10 кПа (и 100C,), поэтому d 1 = 17,19561 м 3 / кг согласно таблица и d 2 к удельному объему при г 2 = 50 кПа (и 100C,) так что d 2 = 3,41833 м 3 / кг.
Наша формула дает удельный объем при 20 кПа и 100 ° C. в качестве:
в качестве:
Вы можете спросить, что происходит с последним примером, если ни один из указанных давление и заданная температура не указаны в таблице.Например, чтобы найти удельный объем при 20 кПа и 110 ° C, ни при 20 кПа ни 110C не указаны в таблице B.1.4. Я не думаю, что мы сделаем это вам во время экзамена. Но ответ был бы сделать три линейных интерполяции: сначала интерполируйте удельный объем при 110C и 10 кПа (заполните « дырку » 110C в данных 10 кПа), затем интерполируйте удельный объем при 110 ° C и 50 кПа (введите « дыра » 110C в данных 50 кПа), и, наконец, линейная интерполировать эти значения 110C так же, как мы делали для 100C в предыдущем разделе.
Другая проблема возникает, если вы пытаетесь интерполировать удельный объем
пара при 11 кПа и 50 ° C. Вы можете использовать запись B.1.3 для
50C и г 1 = 10 кПа, что дает d 1 = 14,86920 м 3 / кг. Но
к сожалению, данные для 50 кПа начинаются с 81,33 ° C; нет 50C
существует пар при 50 кПа. Ключ, чтобы найти вторую запись в таблице, чтобы дать
г 2 и d 2 , заключается в том, чтобы признать, что перегретый пар заканчивается в
насыщенность, которая находится в таблице Б.1.1. Вы можете найти желаемую секунду
запись в таблице; в частности, B.1.1 при 50C дает секунду
давление г 2 = 12,350 и удельный объем г 2 = 12,0318. Что значит
что формула
Ключ, чтобы найти вторую запись в таблице, чтобы дать
г 2 и d 2 , заключается в том, чтобы признать, что перегретый пар заканчивается в
насыщенность, которая находится в таблице Б.1.1. Вы можете найти желаемую секунду
запись в таблице; в частности, B.1.1 при 50C дает секунду
давление г 2 = 12,350 и удельный объем г 2 = 12,0318. Что значит
что формула
дает удельный объем пара при 11 кПа и 50 ° C как:
Вверх: Возврат
Interpolate with Excel — Excel Off The Grid
Интерполяция — это процесс оценки точек данных в существующем наборе данных.Поскольку это блог об Excel, очевидно, что мы хотим ответить на следующий вопрос: можем ли мы выполнять интерполяцию с помощью Excel. Это частый вопрос. Фактически, это был следующий вопрос от читателя, который первым заставил меня изучить эту тему:
«У меня есть вопрос Excel — есть ли способ интерполировать значение из таблицы? У меня есть X и Y, которых нет в таблице, но есть коррелированные данные, поэтому я хочу вычислить интерполированное значение ».
В качестве простого примера, если бы потребовалось 15 минут, чтобы пройти 1 милю в понедельник и 1 час, чтобы пройти 4 мили во вторник, мы могли бы разумно оценить, что на то, чтобы пройти 2 мили, потребуется 30 минут.
Не следует путать с экстраполяцией, которая оценивает значения вне набора данных. Оценка того, что пройти 8 миль займет 2 часа, будет экстраполяцией, поскольку оценка выходит за рамки известных значений.
Excel — отличный инструмент для интерполяции, так как в конечном итоге это большой визуальный калькулятор.
Загрузите файл примера
Я рекомендую вам загрузить файл примера для этого поста. Тогда вы сможете работать с примерами и увидеть решение в действии, а файл будет полезен для дальнейшего использования.
Загрузите файл: 0020 Interpolate with Excel.xlsx
Посмотрите видео
Посмотрите видео на YouTube.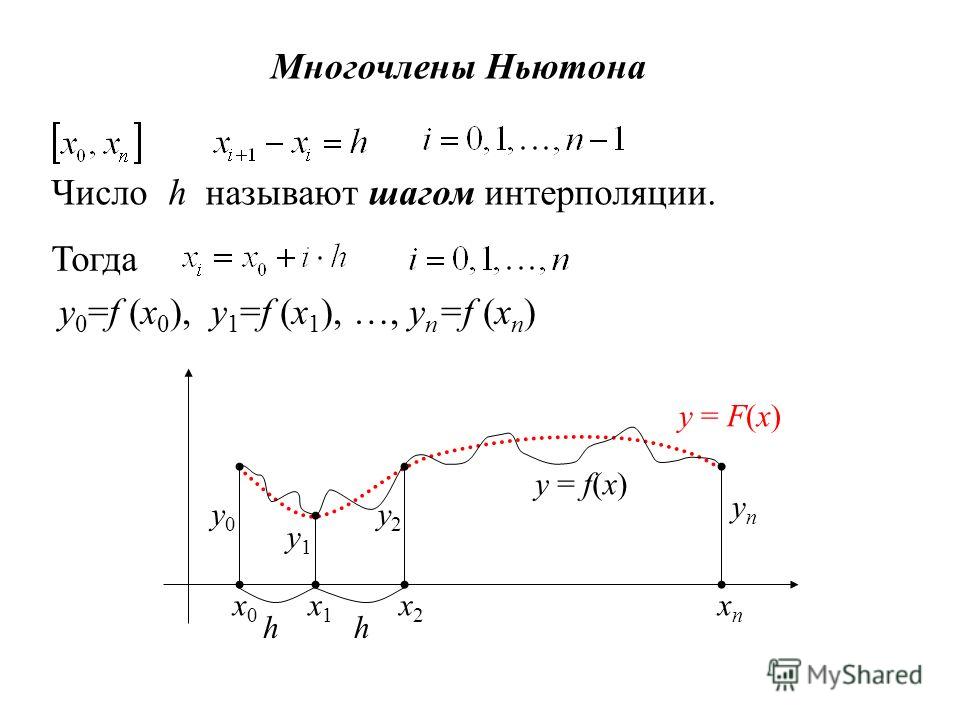
Варианты интерполяции в Excel
С точки зрения ответа на вопрос, есть несколько сценариев, которые могут привести к различным решениям.
Во-первых, мы могли использовать простую математику. Это сработало бы, если бы результаты были абсолютно линейными (т.е. значения X и Y перемещались синхронно друг с другом).Но в противном случае мы могли бы получить немного искаженный результат.
В качестве альтернативы мы могли бы использовать функцию ПРОГНОЗ в Excel (или ПРОГНОЗ.ЛИНЕЙНЫЙ в Excel 2016 и последующих версиях). Судя по названию, функция ПРОГНОЗ выглядит странным выбором. Казалось бы, это функция специально для экстраполяции; однако это также один из лучших вариантов линейной интерполяции в Excel. ПРОГНОЗ использует все значения в наборе данных для оценки результата; поэтому он отлично подходит для линейных отношений, даже если они не полностью коррелированы.
Тогда еще одна мысль, а что, если отношения X и Y вообще не линейны? Как мы могли интерполировать значение, когда данные экспоненциальны?
Давайте посмотрим на все эти сценарии.
Интерполяция с использованием простой математики
Простая математика хорошо работает, когда есть только две пары чисел или когда отношения между X и Y совершенно линейны.
Вот базовый пример (посмотрите на вкладку Пример 1 в вспомогательном файле загрузки):
Формула в ячейке E4:
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
Некоторым это может показаться немного сложным, поэтому вот краткий обзор формулы.
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
В последнем разделе (выделенном зеленым цветом выше) вычисляется, насколько изменяется значение Y при изменении значения X на 1. В в нашем примере Y перемещается на 1,67 на каждый 1 из X.
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
Во втором разделе (зеленом выше) вычисляется, насколько далеко интерполированный X находится далеко от первого X, затем умножается на значение, вычисленное выше. В нашем примере результат равен 17.5 (ячейка E2) минус 10 (ячейка A2), результат умножается на 1,67. Все это равно 12,5.
= B2 + (E2-A2) * (B3-B2) / (A3-A2)
Наконец, мы переходим к первой части формулы (выделенной зеленым цветом выше), которая складывает первое значение Y. В нашем примере это дает окончательный результат 77,5 (65 + 12,5). Для тех, кто помнит математику в средней школе, формула будет следующей:
Вот результат, наложенный на диаграмму.
Даже если вы не помните линейную интерполяцию в школе, хорошая новость заключается в том, что Excel предоставил нам более простой вариант — функцию ПРОГНОЗ.
Formula Magic с динамическими массивами
Из всех функций, доступных в Excel, динамические массивы обеспечивают максимальную мощность при минимальных затратах времени. Однако большинство пользователей Excel даже не знают, что они собой представляют.
Вы когда-нибудь сталкивались с подобными сценариями работы с электронными таблицами?
- Как я могу использовать ВПР для возврата всех совпадающих элементов , а не только первого?
- Как я могу отсортировать мою информацию с помощью формулы , чтобы мне не приходилось нажимать кнопку сортировки постоянно?
- Как я могу быстро создать уникальные списки элементов для использования с моим вычислением СУММЕСЛИМН?
- Как я могу, , прекратить копирование формул каждый раз при изменении исходных данных.
- Как я могу создать отчет, похожий на сводную таблицу , но с использованием формул , чтобы мне больше не приходилось нажимать кнопку «Обновить».
Что ж, я здесь, чтобы сообщить вам хорошие новости. с динамическими массивами все это может быть легко достигнуто 🙂
Интерполяция с помощью функции ПРОГНОЗ
В версии Excel 2016 было добавлено множество новых статистических функций. Чтобы освободить место для этих новых функций, ПРОГНОЗ был заменен на ПРОГНОЗ.Линейная функция. Хотя ПРОГНОЗ остается на данный момент с целью обратной совместимости с Excel 2013 и ранее.
Поскольку FORECAST и FORECAST.LINEAR фактически одно и то же, мы будем использовать эти термины как синонимы.
Интерполяция при идеальной линейности
Теперь давайте воспользуемся ПРОГНОЗОМ для интерполяции результата.
Используя те же числа из приведенного выше примера, формула в ячейке E6:
= ПРОГНОЗ (E2, B2: B3, A2: A3)
Функция ПРОГНОЗ имеет следующий синтаксис:
= ПРОГНОЗ (x, известные_y, известные_x)
Три аргумента функции:
- x — точка данных, для которой мы хотим спрогнозировать значение
- известное_y — диапазон ячеек или массив значений содержащие известные значения Y
- известные_x — диапазон ячеек или массив значений, содержащий известные значения X
При использовании функции ПРОГНОЗ результат ячейки E6 также равен 77.5 (как и в математическом подходе).
Для полноты картины файл примера также содержит использование функции FORECAST.LINEAR. Как и следовало ожидать, результат идентичен устаревшей функции ПРОГНОЗ.
Интерполяция, когда приблизительно линейна
Но … что, если наши данные не совсем линейны? Посмотрите на диаграмму ниже, данные явно имеют линейную зависимость, но она не идеальна. Посмотрите на вкладку Пример 2 во вспомогательном файле.
В этих обстоятельствах функция ПРОГНОЗ даже более полезна, поскольку она не просто интерполирует между первым и последним значениями.Вот данные, использованные в диаграмме.
Функция ПРОГНОЗ в ячейке E4 интерполирует значение Y на основе значения X, равного 17,5.
= ПРОГНОЗ (E2, B2: B11, A2: A11)
В этом сценарии ПРОГНОЗ оценивает значение на основе всех доступных точек данных, а не только начала и конца. Результат функции ПРОГНОЗ в ячейке E4 равен 77,3 (округлено до 1 десятичного знака), что в большинстве случаев будет более точным, чем простая линейная интерполяция, применяемая в математическом подходе.
Помните, что для оценки значений используется интерполяция. 77.3 может быть неточным результатом, но это разумная оценка, основанная на имеющейся у нас информации.
И снова FORECAST.LINEAR вычисляет тот же результат.
Интерполяция, когда данные не линейны
Но вот более сложный вопрос: что, если данные вообще не линейны? И что?
Посмотрите на вкладку Пример 3 во вспомогательном файле. Вот наш новый сценарий графика:
Если бы мы использовали простой линейный подход, это дало бы нам значение 77.5, который, как вы можете видеть ниже, довольно далеко от кривой. Использование функции ПРОГНОЗ даст результат 70,8, что лучше, но также далеко от кривой.
Есть еще два варианта для получения более точной оценки (1) интерполяция экспоненциальных данных с помощью функции РОСТА (2) вычисление внутренней линейной интерполяции
Интерполировать экспоненциальные данные
Функция РОСТА аналогична ПРОГНОЗУ, но может применяться к данным с экспоненциальным ростом.
Результат функции РОСТ в ячейке E10 равен 70,4. Опять же, это ближе к черте, но все же немного дальше.
Формула в ячейке E10:
= РОСТ (B2: B11, A2: A11, E2)
Функция РОСТ имеет следующий синтаксис:
= РОСТ (известные_y, [известные_x], [новые_x] , [const])
Четыре аргумента в функции РОСТ (только имейте в виду, что аргументы не в том же порядке, что и функция ПРОГНОЗ).
- known_y’s — диапазон ячеек или массив значений, содержащих известные значения Y
- [known_x’s] — диапазон ячеек или массив значений, содержащих известные значения X
- [new_x’s] — точка данных, для которой мы хотим спрогнозировать значение
- [Const] — мера истина / ложь, указывающая, как должна вычисляться формула. В нашем сценарии мы можем оставить этот последний аргумент.
Квадратные скобки указывают, какие аргументы являются необязательными для функции для вычисления результата.Нам нужны значения known_y, , known_x, и new_x, , но мы проигнорировали аргумент const .
Хотя результат 70,4 является более близким приближением, мы не должны слепо использовать функцию РОСТ. Проверьте свои интерполяции, чтобы убедиться, что они разумны.
Внутренняя линейная интерполяция
Разумным вариантом может быть найти результат выше и ниже нового значения X, а затем применить линейную интерполяцию между этими двумя точками.Это было бы довольно близко.
В нашем примере значения по обе стороны от X, равного 17,5:
- X: 16 и 18
- Y: 66,3 и 68
Используя эти значения, теперь мы можем выполнить стандартную линейную интерполяцию. .
Быстрый одноразовый метод
Если бы это было разовое действие, мы могли бы сделать это быстро, включив в формулу только основные ячейки.
= ПРОГНОЗ (E2, B6: B7, A6: A7)
Однако, как только мы изменим интерполированное значение, ПРОГНОЗ может вычислить неточный результат.Итак, давайте перейдем к рассмотрению гибкого метода.
Гибкий подход
Для создания гибкого подхода мы будем использовать функции ИНДЕКС, ПОИСКПОЗ и ПРОГНОЗ вместе. Это может показаться сложным, но не волнуйтесь, мы рассмотрим это медленно. В конечном итоге мы пытаемся достичь того же результата, что и описанный выше одноразовый метод, но автоматически корректируем диапазоны в зависимости от интерполируемого значения.
ПРИМЕЧАНИЕ. Для работы этого метода требуется, чтобы диапазон известных X был указан в порядке возрастания.
Функция ПОИСКПОЗ
Во-первых, мы используем функцию ПОИСКПОЗ, чтобы получить позицию значения ниже 17,5.
= ПОИСКПОЗ (E2, A2: A11,1)
Эта формула говорит, что найдите значение в ячейке E2 из диапазона ячеек A2-A11. 1 в конце формулы сообщает функции ПОИСКПОЗ, что мы хотим использовать приблизительное совпадение (т. Е. Ближайшее значение ниже искомого значения). 16 — ближайшее значение ниже 17,5. Поскольку 16 — это 5-й элемент в ячейках A2-A11, ПОИСКПОЗ возвращает значение 5.
Функция ИНДЕКС
Определив на предыдущем этапе, что пятая позиция содержит значение ниже, мы можем использовать функцию ИНДЕКС, чтобы определить ссылку на ячейку для этого значения.
ИНДЕКС (A2: A11, MATCH (E2, A2: A11,1))
Это вернет ссылку на ячейку A6.
Чтобы найти указанное выше значение, мы можем использовать ту же функцию, но добавить 1 к функции ПОИСКПОЗ.
ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1) +1 )
Приведенная выше формула вернет ссылку на ячейку A7.
Динамический диапазон
Теперь все становится интереснее. Мы можем объединить эти функции с двоеточием (:) в середине, чтобы создать диапазон для двух значений X.
ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1)): ИНДЕКС (A2: A11, ПОИСКПОЗ (E2, A2: A11,1) +1)
Первая функция ИНДЕКС возвращает ссылку в ячейку A6 (результат выделенного зеленым цветом раздела). Вторая функция ИНДЕКС возвращает ссылку на ячейку A7 (результат выделенного фиолетовым цветом раздела).Они разделены двоеточием (:) (выделено красным), чтобы создать диапазон — A6: A7
Мы можем сделать то же самое, чтобы создать диапазон для двух значений Y. Единственная разница в том, что функции ИНДЕКС будут смотреть на ячейки B2-B11.
ИНДЕКС (B2: B11, ПОИСКПОЗ (E2, A2: A11,1)): ИНДЕКС (B2: B11, ПОИСКПОЗ (E2, A2: A11,1) +1)
Используя ячейки B2-B11 в ИНДЕКСЕ функция, она вычислит диапазон B6: B7.
ИНДЕКС СООТВЕТСТВИЕ И ПРОГНОЗ
Теперь у нас есть два диапазона; значения X A6: A7 и значения Y B6: B7.Давайте объединим все это в функции ПРОГНОЗ.
= ПРОГНОЗ (E2, ИНДЕКС (B2: B11; ПОИСКПОЗ (E2; A2: A11,1)): ИНДЕКС (B2: B11; ПОИСКПОЗ (E2; A2: A11,1) +1), ИНДЕКС (A2: A11, MATCH (E2, A2: A11,1)): INDEX (A2: A11, MATCH (E2, A2: A11,1) +1))
Это довольно большая формула, верно. Но, надеюсь, мне удалось объяснить это так, что это не слишком страшно.
Результат внутренней линейной интерполяции с использованием функции ПРОГНОЗ составляет 67,6 (с точностью до 1 десятичного разряда, как показано в ячейке E14). Взгляните на график еще раз; вы увидите, что 67.6 — разумная оценка, основанная на имеющихся данных.
ПРЕДУПРЕЖДЕНИЕ. В конечном счете, это все еще вычисление линейной интерполяции, основанное на двух значениях по обе стороны от значения X. Расстояние между значениями выше и ниже будет иметь прямое влияние на точность интерполяции.
Заключение
Первоначально то, что казалось простым вопросом, привело нас к множеству потенциальных решений для трех различных сценариев. Ключевым моментом является то, что вам необходимо знать свои данные, чтобы выбрать метод, обеспечивающий наиболее точные результаты.
В процессе мы рассмотрели функции FORECAST и FORECAST.LINEAR и убедились, что они полезны как для интерполяции, так и для экстраполяции.
Кроме того, в этом посте мы использовали ИНДЕКС и ПОИСКПОЗ для создания динамических диапазонов, что является очень мощным методом для сложных формул в Excel.
Если вам нужна дополнительная информация о методах прогнозирования в Excel, загляните в Engineer Excel (https://engineerexcel.com/blog). Хотя вы, возможно, не работаете в инженерном контексте, методы применимы во многих других обстоятельствах.
Получите нашу БЕСПЛАТНУЮ электронную книгу на VBA с 30 наиболее полезными макросами Excel VBA.
Автоматизируйте Excel, чтобы сэкономить время и перестать выполнять ту работу, которую могла бы выполнять обученная обезьяна.
Вводя свой адрес электронной почты, вы соглашаетесь получать электронные письма от Excel Off The Grid. Мы будем уважать вашу конфиденциальность, и вы можете отказаться от подписки в любое время.
Не забывайте:
Если вы нашли этот пост полезным или у вас есть лучший подход, оставьте комментарий ниже.
Вам нужна помощь в адаптации этого к вашим потребностям?
Я полагаю, что примеры в этом посте не совсем соответствуют вашей ситуации. Все мы используем Excel по-разному, поэтому невозможно написать сообщение, которое удовлетворит потребности всех. Потратив время на то, чтобы понять методы и принципы, изложенные в этом посте (и в других местах на этом сайте), вы сможете адаптировать их к своим потребностям.
Но, если вы все еще боретесь, вам следует:
- Прочитать другие блоги или посмотреть видео на YouTube на ту же тему.Вы получите гораздо больше пользы, открыв свои собственные решения.
- Спросите «Excel Ninja» в своем офисе. Удивительно то, что знают другие люди.
- Задайте вопрос на форуме, например в Mr Excel, или в сообществе ответов Microsoft. Помните, что люди на этих форумах обычно проводят свое время бесплатно. Так что постарайтесь сформулировать свой вопрос, сделайте его ясным и кратким. Составьте список всего, что вы пробовали, и предоставьте снимки экрана, фрагменты кода и примеры книг.
- Воспользуйтесь Excel Rescue, которые являются моим партнером-консультантом.Они помогают, предлагая решения небольших проблем с Excel.
Что дальше?
Не уходите, об Excel Off The Grid можно узнать еще много. Проверьте последние сообщения:
Интерполяция | математика | Britannica
Интерполяция , в математике определение или оценка значения f ( x ) или функции x , исходя из определенных известных значений функции. Если x 0 <… < x n и y 0 = f ( x 0 ),…, y n =
f ( x n ) известны, и если x 0 < x < x n , то оценочное значение f ( x ) называется интерполяцией.Если x < x 0 или x > x n , оценочное значение f ( x ) считается экстраполяцией.
Если даны x 0 ,…, x n , а также соответствующие значения y 0 ,…, y n (см. Рисунок), интерполяцию можно рассматривать как определение функции y = f ( x ), график которой проходит через n + 1 точек, ( x i , y i ) для i = 0, 1,…, n .Таких функций бесконечно много, но самая простая — это функция полиномиальной интерполяции y = p ( x ) = a 0 + a 1 x +… + a n x n с константой a i такие, что p ( x i ) =
y для i = 0,…, n .Существует ровно один такой интерполирующий полином степени n или меньше. Если x i расположены на одинаковом расстоянии, скажем, с некоторым коэффициентом h , то следующая формула Исаака Ньютона дает полиномиальную функцию, которая соответствует данным: f ( x ) = a 0 + a 1 ( x — x 0 ) / h + a ( x — x 0 ) ( x — x 1 ) / 2! h 2 +… + a n ( x — x 0 ) ⋯ ( x — x 90/) — n ! h nПолиномиальное приближение полезно, даже если фактическая функция f ( x ) не является полиномом, для полинома p ( x ) часто дает хорошие оценки для других значения f ( x ).
Линейная интерполяция в Python — одна строка кода | Дэвид С. Фулфорд
Получение практических алгоритмов
Использование
numpy для упрощения техники, которая должна быть в наборе инструментов каждого Интерполированные лог-линейные и обратные (линейно-логарифмические) значения Линейная интерполяция создает непрерывную функцию из дискретных данных . Это фундаментальный строительный блок для алгоритма градиентного спуска, который используется при обучении практически всем методам машинного обучения.Глубокое обучение, при всей его сложности, не могло бы работать без него. Здесь мы рассмотрим теоретические основы построения алгоритма линейной интерполяции, а затем реализуем практический алгоритм и применим его к конкретному примеру.
Если вы предпочитаете пропустить вывод, прокрутите вниз до раздела под названием The One-liner для изюминки. В противном случае продолжайте читать! Это не займет так много времени…
В предыдущей статье мы обсуждали основы линейной регрессии с использованием некоторой линейной алгебры.В частности, у нас был этот результат для определения коэффициентов регрессии:
И у нас также было это уравнение для прогнозирования с этими коэффициентами:
Если мы подставим первое уравнение во второе, мы получим прямую оценку предсказанных значений:
И все эти X термины образуют нечто, называемое матрицей проекции, также называемой матрицей шляпы:
Матрица проекции преобразует (или проецирует ) наблюдаемые значения Y в прогнозируемые значения Ŷ .Для этого он должен содержать всю информацию, необходимую для прогнозирования любого произвольного значения Y .
Итак, кажется, что если мы знаем H , мы знаем, как предсказать любое значение! Чтобы проиллюстрировать это, давайте создадим игрушечный пример и посмотрим, как выглядит матрица шляп. Мы будем использовать две точки данных, которые лежат в координатах (0, 1) и (5, 2).
Давайте продемонстрируем на Python:
import numpy as np
np.set_printoptions (suppress = True) # нет научного форматирования # np.r_ и np.c_ - это короткие руки для конкатенации массивов
# np.r_ выполняет по первой оси (строкам)
# np.c_ выполняет по второй - axis (columns) # наши значения x
x = np.c_ [1., 1.,], [0., 5.]] # наши значения y
y = np.r_ [1., 2.] print (x)
array ([[1., 0.],
[1., 5.]])
Пока все довольно просто. Мы можем найти коэффициенты регрессии, используя первое уравнение:
# @ - оператор numpy для умножения матриц
c = np.linalg.inv (x.T @ x) @ x.T @ Yprint (c)
array ([1., 0.2])
И мы видим наклон 1/5 и точку пересечения 1, как и ожидалось. Следующая матрица проекции:
# @ - оператор числового числа для умножения матриц
h = x @ np.linalg.inv (xT @ x) @ x.Tprint (h)
array ([[1., 0. ],
[0., 1.]])
Напомним, что когда мы умножаем H на Y , мы получаем прогнозы Ŷ . Поскольку у нас есть единицы на диагонали и нули в других местах, в этом случае H фактически является единичной матрицей, поэтому мы просто возвращаем прогнозы (1, 2) для фактических значений y (1, 2).Это не тот случай, когда наши точки не образуют прямую линию, как почти в любой задаче линейной регрессии. Однако для интерполяции мы всегда можем сделать это предположение, поскольку есть только две точки, ограничивающие желаемую точку, в которой мы хотим выполнить интерполяцию!
А как насчет фактической интерполяции? Если мы вспомним второе уравнение, мы можем предоставить любые значения для X , чтобы создать прогноз для значений. Давайте перепишем нашу матрицу проекции, используя этот факт, с X₀ , представляющими наши фактические значения, и X₁ , представляющими значение, по которому мы хотим интерполировать.Мы будем использовать W , чтобы представить это как матрицу весов, по причинам, которые мы вскоре увидим:
Что произойдет, если мы попробуем различные значения X₀ между значениями X₁ , которые равны 0 и 5?
для i в np.linspace (0, 5, 6):
w = np.c_ [1., I] @ np.linalg.inv (xT @ x) @ xT
y_hat = w @ y
print ( f'x0 = {i: .1f}, w = {w}, y_hat = {y_hat} ') x0 = 0.0, w = [[1.0 0.0]], y_hat = [1.0]
x0 = 1.0, w = [ [0.8 0,2]], y_hat = [1,2]
x0 = 2,0, w = [[0,6 0,4]], y_hat = [1,4]
x0 = 3,0, w = [[0,4 0,6]], y_hat = [1,6]
x0 = 4.0, w = [[0.2 0.8]], y_hat = [1.8]
x0 = 5.0, w = [[0.0 1.0]], y_hat = [2.0]
Происходит что-то интересное! В каждом случае сумма весовой матрицы равна единице. Когда мы умножаем эту весовую матрицу на значения Y , мы получаем средневзвешенное значение двух значений. Первый вес пропорционален расстоянию X₀ между двумя значениями X₁ , а второй вес является просто дополнением к первому весу.Другими словами:
Это дает нам линейную интерполяцию в одну строку:
new_y = np.c_ [1., New_x] @ np.linalg.inv (xT @ x) @ xT @ y
Конечно, это немного бесполезен. Мы должны точно знать два значения в исходном массиве значений x, между которыми находится наше новое интерполированное значение x. Нам нужна функция для определения индексов этих двух значений. К счастью, numpy содержит именно такую функцию: np.searchsorted . Давайте воспользуемся им, чтобы превратить линейную алгебру в векторизованную функцию.Вместо того, чтобы вычислять матрицу весов для каждого интерполированного значения, мы просто собираемся сохранить соответствующую информацию: сам вес и индексы значений X (которые также будут по индексам Y значения при вычислении интерполированных значений).
от ввода import NamedTupleclass Coefficient (NamedTuple):
lo: np.ndarray # int
hi: np.ndarray # int
w: np.ndarray # floatdef interp_coef ( x0: np.ndarray, x : np.ndarray) -> Coefficient:
# найти индексы в исходном массиве
hi = np.minimum (len (x0) - 1, np.searchsorted (x0, x, 'right'))
lo = np.maximum (0, hi - 1)# вычислить расстояние в диапазоне
# веса являются пропорциональное расстояние
d_left = x - x0 [lo]
d_right = x0 [hi] - x
d_total = d_left + d_right
w = d_right / d_total # коррекция, если мы вне диапазона массива
w [np.isinf (w)] = 0.0 # вернуть информацию, содержащуюся в матрицах проекции
return Coefficient (lo, hi , w) def interp_with ( y0 : np.ndarray, coef : Coefficient) -> np.ndarray:
return coef.w * y0 [coef.lo] + (1 - coef.w) * y0 [coef.hi]
Что делает этот алгоритм удобным в том, что нам нужно вычислить наши веса только один раз. С помощью весов мы можем затем интерполировать любой вектор значений y, который совпадает с нашим вектором значений x.
В инженерных задачах моделируемые физические процессы часто являются экспоненциальными или степенными функциями. Когда мы собираем данные для этих процессов, мы можем делать это через равные промежутки времени, разнесенные по времени.Многие методы интерпретации предназначены для работы с четными интервалами времени, разнесенными на логарифм. Однако некоторые численные методы более удобны для работы даже с линейно разнесенными значениями. Поэтому возможность трансформировать туда-сюда удобна. Линейная интерполяция — один из инструментов для выполнения этого преобразования.
Фактически, мы не ограничены линейной интерполяцией. Мы можем сначала линеаризовать наши значения, а затем выполнить интерполяцию. Давайте посмотрим на пример расхода, q , и давления, p , в радиальной системе.Эти данные были созданы синтетически с равномерно разнесенными по логарифмической шкале выборками, и когда мы наносим их на логарифмический график, мы видим отчетливое степенное поведение для большинства данных. В более поздние времена скорость потока переходит в экспоненциальное снижение, но это не должно сильно влиять на нашу интерполяцию.
Данные о давлении и расходе для системы с радиальным потокомДавайте выполним интерполяцию, используя массив равномерно распределенных значений. Мы собираемся принять степенную функцию в качестве основы для нашей интерполяции, сначала применив логарифмическое преобразование к нашим значениям.Мы также обратим интерполяцию, чтобы убедиться, что она выполнена правильно:
# построить линейный временной рядИнтерполированные лог-линейные и обратные (linear-log) значения
tDi = np.linspace (1e-3, 1e4, 100_001) # интерполировать от логарифма к линейному
coef = interp_coef (np. log (время), np.log (time_interp))
pi = np.exp (interp_with (np.log (давление), coef))
qi = np.exp (interp_with (np.log (скорость), coef)) # обратный от линейного к логарифмическому
coef_i = interp_coef (np.log (time_interp), np.log (time))
pr = np.exp (interp_with (np.log (pi), coef_i))
qr = np.exp (interp_with (np.log (qi), coef_i))
Линейные методы являются важным инструментом для манипулирования данными. Преобразование переменных, например, с помощью np.log , как показано в примере, позволяет нам применять эти методы в ситуациях, когда мы не ожидаем, что данные будут линейными.
Хотя мы разработали и реализовали наш собственный алгоритм, стандартный алгоритм все же существует: scipy.interpolated.interp1d . Однако для использования в некоторых пакетах, например при использовании pymc3 , может потребоваться реализовать что-то подобное для себя.
Существуют также более общие методы интерполяции. Один из них — B-сплайны, которые мы обсудим в следующей статье этой серии. B-сплайны также могут выполнять линейную интерполяцию, а также квадратичную, кубическую и т. Д. B-сплайны работают, расширяя концепции, которые мы здесь разработали. А именно, весовой вектор расширяется до матрицы весов . Вместо того, чтобы писать функцию для поиска индексов для каждого интерполированного значения, мы можем просто вычислить интерполированные значения y с матричным умножением коэффициентов и новых значений x.
Что делать, если данные отсутствуют?
AKA magics, чтобы заткнуть дыры в вашем наборе данных
и не с лисенок;)
Это перевод сообщения на португальский 🙂
Мы можем примерно разделить любые данные на две категории: временные и вневременные. Неустаревающие данные довольно часто встречаются в наиболее часто используемых наборах данных в учебных пособиях по науке о данных: например, характеристики выживших на Титанике, размеры лепестков цветов или характеристики опухолей.Данные могут иметь временные данные, например, момент, когда пользователь определил определенную позицию, но время является второстепенным признаком данных, а не его сущностью.
С другой стороны, при работе с временными данными чрезвычайно важен момент (время), когда эти данные были созданы. Классические примеры — это дневная стоимость или количество пользователей веб-сайта в час.
Когда во вневременных данных отсутствуют данные, нас обычно учат, что самый простой способ — удалить эту строку данных из нашего набора данных.Лучше всего удалить данные, потому что многие алгоритмы не могут выполнять анализ с отсутствующими данными, и в большинстве случаев данных достаточно, чтобы практически не повлиять на удаление нескольких строк.
Когда мы говорим о временных данных, их удаление может вызвать большие затруднения. Этот тип данных требует шаблона, особенно если мы должны проводить частотный анализ. Итак, какие у нас есть альтернативы? Этот текст именно для того, чтобы о них рассказать 🙂
Вся графика и код доступны на этом ноутбуке.
Наши временные данные
Мы будем использовать следующие данные для анализа. У нас есть довольно простые данные, имеющие сеноидальную форму. Прежде всего мы знаем, что эти данные не имеют резких изменений и что они должны поступать через регулярные промежутки времени. Таким образом, мы можем видеть, что девятый элемент был потерян, и это данные, которые мы сосредоточим на полном заполнении.
Исходные данные выделены красным:
Заполнить средним значением
Одна из возможностей — заполнить недостающие данные средним значением всей серии.Результат представлен ниже:
Кажется странным, правда? И это! Поскольку мы знаем общий шаблон данных, эта альтернатива действительно не подходит. Однако этот метод может быть весьма полезным в зависимости от того, что у вас есть, поскольку среднее значение всех данных остается неизменным.
Однако не дайте себя обмануть! Среднее значение не изменится, но другие статистические характеристики могут (и, вероятно, будут) изменяться. Поскольку мы добавляем другие данные, более близкие к среднему, стандартное отклонение обычно меньше.См .:
Интерполяция
Интерполяция — это математический метод, который подстраивает функцию под ваши данные и использует эту функцию для экстраполяции недостающих данных. Самый простой тип интерполяции — это линейная интерполяция, которая вычисляет среднее значение между значениями перед отсутствующими данными и значением после них.
Поскольку наши данные представляют собой кривую, а не линию, у нас есть разница между реальной исходной точкой и интерполированной точкой. Однако, поскольку у нас есть хорошее представление о том, как должны вести себя наши данные, это довольно хорошее приближение, которое решает нашу проблему.
Конечно, здесь может быть довольно сложный паттерн, и линейной интерполяции может быть недостаточно. Хотя я показываю только один тип, у нас есть несколько разных типов интерполяции, по одному для каждой реальности, с которой вы можете столкнуться. Просто в Pandas у нас есть следующие варианты: «линейный», «время», «индекс», «значения», «ближайший», «ноль», «линейный», «квадратичный», «кубический», «барицентрический», « krogh ‘,’ полином ‘,’ сплайн ‘,’ кусочно_полином ‘,’ from_derivatives ‘,’ pchip ‘,’ akima ‘.
Интерполяция при неизвестном шаблоне данных
Важно сказать, что не все временные сигналы имеют четкую структуру, подобную той, которую мы только что видели.Итак, давайте взглянем на второй временной ряд.
В данном случае мы не знаем закономерности, не можем с уверенностью предсказать, какие данные были потеряны, и не можем предсказать, какое низкое значение они имели на самом деле. Таким образом, линейная интерполяция может быть не лучшим выбором:
В этом случае имеет смысл заполнить пропущенное значение средним значением ряда! Поскольку никакие данные не могут фактически предсказать пропущенное значение, значение среднего будет поддерживать данные в соответствии с их общим поведением, и вы вернете свою непрерывность.В зависимости от того, какой вид анализа вы хотите провести, это может быть именно то, что вам нужно.
В нашем случае недостающие данные и среднее значение имеют очень близкие значения, но это не всегда так. Представьте, что недостающая точка была указателем в начале данных?
Заполнение другими данными
Другой вариант — заменить отсутствующие данные данными, которые их окружают. Мы можем, например, заменить предыдущие данные.

 Использовались со схемой классификации в опции Классифицировать по.
Использовались со схемой классификации в опции Классифицировать по. 5
5