Размер матрицы и что такое кроп фактор — 100dorog.org
Немного истории.
Совсем недавно были времена, когда в фотоаппаратах и видеокамерах использовали фотопленку, а не светочувствительную матрицу или сенсор. И большинство специалистов говорили, что по качеству никогда не сможет электронный чип заменить пленку. В те времена большинство фотографов использовали фотопленки с форматом кадра 36х24 мм. Стали появляться все больше фотоаппаратов и видеокамер с электронным сенсором внутри и постепенно они вытеснили пленочное оборудование и в любительской и в профессиональной сфере. Сначала такие сенсоры были больших размеров и с малым количеством мегапикселей. Потом количество мегапикселей стало стремительно увеличиваться. Размеры матриц при этом уменьшались. Дошло до того, что матрицы начали помещаться на спичечной головке и при этом иметь больше 10 мегапикселей. Понятно, что качество картинки при этом нельзя назвать удовлетворительным. Матрицы и оптика к ним стали настолько малыми по размеру, что их уже спокойно можно было ставить даже в мобильные телефоны. Мобильные телефоны стали конкурировать с любительскими видеокамерами и на сегодняшний момент практически вытеснили их с рынка. И только благодаря тому, что фотоаппараты имели большие по физическому размеру сенсоры и при этом они тоже могли снимать видео, они не только сохранились на рынке, но и заняли свое достойное место в профессиональном и любительском фото и видео деле.
Размеры сенсора.
Иногда приходится видеть в интернете картинки, на которых изображены сравнительные размеры разных матриц. Эти картинки никак не отражают настоящие физические размеры матриц и имеют только относительные размеры. Покупатели начинают думать, что они покупают камеру с большим сенсором, а на самом деле сенсор там стоит «микроскопических» размеров. И как бы ни старались производители, какие бы мощные процессоры они не «запихивали» в камеру, улучшить качество уже не получится. Неминуемо будут возникать шумы, хроматические аберрации, засветка соседних пикселей и другие явления, отрицательно влияющие на качество картинки. Например Panasonic в своих последних любительских видеокамерах ставил не одну, а сразу три матрицы, каждая из которых принимала свой цвет: красный, синий или зеленый. Потом картинки объединялась в одну, и на изображении не было заметно смещения по цвету. Но физические размеры матрицы в камере Panasonic TM900 всего 3х2 мм каждая, и качество все равно уступает качеству изображения с одноматричных камер, но с большим физическим размером сенсора.

Размеры матриц на картинке изображены с большим увеличением и не соответствуют их реальным размерам.
Видимо, чтобы окончательно запутать пользователей и чтобы они не понимали ситуацию, производители стали обозначать размеры светочувствительных сенсоров в дюймах. Только эти дюймы не имеют никакого отношения к настоящим дюймам, которыми измеряют длину. Например, ставшие сейчас популярными матрицы в
Реальные размеры наиболее популярных сенсоров представлены на следующей картинке:
Кроп фактор — Crop Factor
Для того, чтобы фотографам как можно более «безболезненно» перейти с пленки на цифровой сенсор, производители стали делать самый крупный сенсор такого же размера как и кадр фотопленки – 24х36 мм. Такой сенсор принято считать полнокадровым или фулл фрейм (Full Frame). Соответственно кроп фактор для него приравняли к единице. Кстати, из-за этого многие ошибочно считают, что раз кроп фактор равен «1», то такую матрицу нужно принимать за эталон качества.
Чем меньше матрица, тем выше будет кроп фактор. Измеряется он в относительных размерах матрицы к размеру 36х24мм. Таким образом, если мы возьмем следующий популярный размер матриц – примерно 25х16 мм, обозначаемый как APS-sensor (APS-C, APS-H или DX), то кроп фактор для таких матриц будет примерно равен 1,5. Значит физический размер такой матрицы в полтора раза меньше полнокадрового. Сенсоры такого размера ставятся во многие зеркальные и беззеркальные камеры таких производителей как Canon, Nikon и Sony.
Дальше идет уже упоминавшийся выше размер матрицы 1″ — кроп-фактор равен 2.7
Сенсор 2/3″ – кроп фактор = 4
1/1.8″ — кроп фактор примерно равен 5. Сейчас это редкий размер сенсора и тут важно его не перепутать с 1/8. (Сенсор размером 1/8″ — это размер просто «микроскопических» матриц, которые ставят на самые дешевые видеокамеры и в мобильные телефоны).
1/1.7″ (примерно 7,5 х 5,5 мм) = 4,6 crop factor (Canon S100, Olympus XZ-1, Panasonic LX-5)
1/2,3″ соответствует 6,17 x 4,55 мм (1/2,33″ — 6,1 x 4,6 мм) — кроп фактор примерно 6
1/3″
матрица — кроп фактор = 7.21/6″ – кроп фактор = 14,7
Важно заметить, что к размерам сенсора никаким образом не имеют отношения мегапиксели «втиснутые» в эту матрицу. Чем больше мегапикселей в матрице одинакового размера, тем значит меньше каждый отдельный светоприёмный пиксель. Высокое разрешение иногда достигается методом интерполяции – информацию с одного реального пикселя расписывают на несколько несуществующих и таким способом фиктивно увеличивают мегапиксели матрицы. На мой взгляд, последний способ является прямым обманом покупателей.
Пример: возьмем и сравним новый полноразмерный full frame сенсор Nikon D800 с 36,3 мегапикселей и Sony NEX-5N с APS-C сенсором (23,4×15,6 мм) с 16 мегапикселями. Получаем 16Х1,5 (кроп фактор) = 24 мегапикселя. Значит, если бы мы разместили точно такие же пиксели как в NEX-5N на полноразмерном сенсоре, то они получились бы больше по своему размеру, чем у нового Nikon D800. Слава Богу, последнее время производители одумались и «гонка мегапикселей» уже в прошлом.
Очень важно:
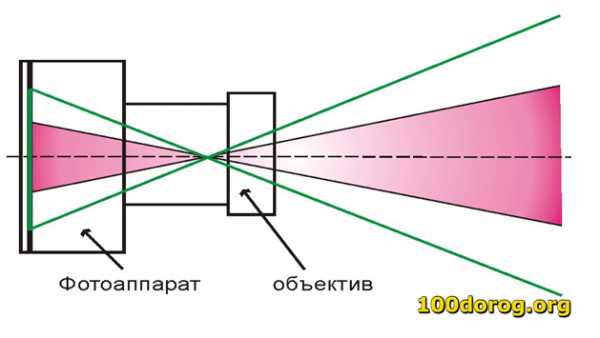
Если взять две камеры с объективами с одинаковым фокусным расстоянием и при этом с разными физическими размерами матриц, то мы получим изображение с разными фокусными расстояниями. Чтобы избежать путаницы, принято значение фокусного расстояния приводить к тому, какое оно было бы для полноразмерной матрицы, тоесть умножать его на кроп фактор данной конкретной матрицы.
Например, мы имеем аппарат с сенсором APS-C (кроп 1,5) и объектив 18-55 мм. Значит в реальности мы получим снимки как если бы мы снимали на полноматричную (full frame) камеру с объективом 24-82 мм. Получается, что при одинаковых объективах, наиболее широкоугольную картинку мы можем получить только с самой крупной по размеру матрицы.
Если Вам понравилась статья, расскажите о ней друзьям в социальных сетях (кнопки ниже) — 269350
Похожие статьи:
Фото-видео камеры → Светосила объектива
Фото-видео камеры → Panasonic GF3 в сравнении с Sony NEX-5
Фото-видео камеры → ГРИП и что такое диафрагма и как она влияет на глубину резкости
Фото-видео камеры → Какие бывают объективы — широкоугольные и длиннофокусные
Фото-видео камеры → Фотоаппарат для путешествий
100dorog.org
Что такое размер матрицы фотоаппарата, видеокамеры? Как определить размер матрицы?
Продавцы и производители фотоаппаратов стараются обращать внимание покупателей на количество мегапикселей и умалчивать о таком важном параметре, как физический размер матрицы. Конечно, это нечестно, однако маркетинг никто не отменял, и он успешно диктует свои условия, поэтому производители и продавцы просто вынуждены давать пользователям то, чего они хотят.
Почему так важен размер матрицы?
Количество мегапикселей вообще не влияет на качество. Оно только определяет, насколько большим будет изображение. Картинка может быть просто огромной, но плохой. А чтобы она была хорошего качества, необходим большой размер матрицы. Эта информация не нова, но про нее намеренно забывают даже в магазинах.

Между тем хороший размер матрицы фотоаппарата (не максимальный, а просто хороший) важнее разрешения, ведь именно от него зависит качество картинки и то, насколько много света попадет на сам сенсор. Разрешение играет роль только тогда, когда планируется печать фотографий на большом носителе. Например, для печати фото на формате A1 необходимо большое разрешение, но даже здесь 4 Мп будет достаточно. Но для печати на обычной фотобумаге размером 10 х 15 см подойдет разрешение 2 Мп, не более. А вообще, большинство пользователей загружают фото в социальные сети, где они проходят предварительное сжатие.
Это соотношение фактического размера матрицы фотоаппарата к стандартному размеру пленки, который равен 35 мм. Поясним: современные камеры имеют кропнутые (обрезанные) матрицы, поэтому их размер чаще всего не равен и половине стандартного. Однако он всегда указывается в дробной величине (например, 1/3.2″), и покупатель при этом запутывается окончательно.

Часто люди видят большое значение и думают, что это хорошо, но на самом деле большое значение в знаменателе — это плохо. Ведь чем оно будет больше, тем размер матрицы видеокамеры или фотоаппарата будет меньше, а значит, и качество снимков будет хуже.
Типовые размеры
В зависимости от того, насколько дорогой или хороший фотоаппарат, размер матрицы может быть малым, средним или большим. Ниже представим типовые размеры, которые встречаются чаще всего.
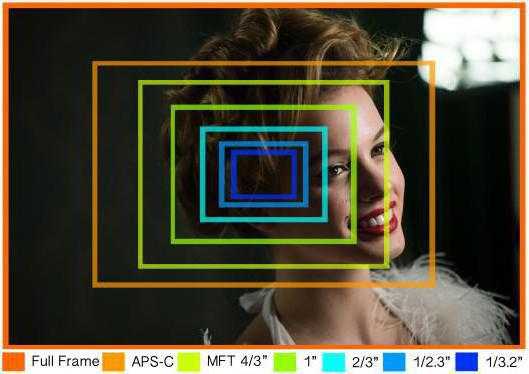
Начнем с самых маленьких матриц:
- 1/3.2″ — матрицы с таким размером являются самыми маленькими. Хуже ничего на рынке быть не может. Видя такой параметр в характеристиках фотоаппарата, покупать его не стоит. Физический размер здесь равен 3,4 х 4,5 квадратных миллиметра, и ни один более-менее достойный фотоаппарат не будет оснащаться столь маленькой матрицей.
- 1/2.7″ — этот размер также мал (4 х 5,4 квадратных миллиметра) и встречается только в дешевых камерах.
- 1/2.5″ — физический размер матрицы с таким соотношением равен 4,3 х 5,8 кв. мм. Большинство современных «мыльниц» среднего ценового диапазона оснащаются такими сенсорами. Можно сказать, что это стандарт даже для современных беззеркальных и дешевых зеркальных фотоаппаратов.
- 1/1.8″ — геометрический размер сенсора равен 5,3 х 7,2 кв. мм. Отсюда начинается категория более-менее достойных фотоаппаратов. Дорогие зеркальные камеры среднего уровня могут оснащаться сенсором с такими геометрическими параметрами. Также и простые небольшие мыльницы могут иметь такие матрицы.
- 2/3″ — соотношение, при котором физический размер будет равен 6,6 х 8,8 квадратным миллиметрам. Сенсоры с таким параметром используются в дорогих зеркальных и компактных фотоаппаратах со сменной или несменной оптикой.
- 4/3″ — матрицы с таким соотношением применяются исключительно в дорогих камерах. Здесь размер равен 18 х 13,5 кв. мм.
- DX, APS-C. Редко размер указывается буквами. Если вы видите такой параметр, то это значит, что матрица в фотоаппарате больше предыдущего формата, и ее размер составляет 24 х 18 мм. Он соответствует полукадру 35 мм. Эти матрицы довольно популярны и часто их можно увидеть в полупрофессиональных фотоаппаратах. Они дешевые в изготовлении, а размер пикселя при этом в них остается большим даже при разрешении 11-12 Мп.
- Полнокадровые матрицы. По размеру они соответствуют классическому кадру 35 мм, и их размер составляет 36 х 24 кв. мм. На рынке существует мало фотоаппаратов с такими матрицами. Это профессиональные модели, которые очень дорого стоят. Сами матрицы сложны в производстве, чем и объясняется высокая стоимость фотоаппаратов, созданных на базе этих сенсоров.
Как определить размер матрицы?
Сделать это несложно. Он всегда указывается в технических характеристиках к любой камере. Но это можно даже сделать визуально. Например, цифровые фотоаппараты с матрицами размером 1/2.7″ будут небольшими, легкими. А вот камера с матрицей 1/1.8″ при прочих равных характеристиках будет немного больше и тяжелее.

Размер оказывает влияние на вес и объем камеры, ведь размеры оптики тесно связаны с геометрическими параметрами сенсоров. Профессиональные фотографы могут «на глаз» определить, какой размер матрицы используется в том или ином фотоаппарате.
Шумы
Зернистость на фото — это один из самых распространенных дефектов, который может быть на фото. Если камера имеет небольшую матрицу, то количество света на нее попадает тоже небольшое. Из-за этого при ограниченном свете (например, в помещении) такие камеры делают фотографии с зернистостью (шумами). При равных условиях фотоаппарат с матрицей размером 1/1.8″ сделает фото с меньшим количеством шумов по сравнению с моделью с матрицей 1/2.3″. Конечно, в появлении шумов имеют место также внутренние электрические процессы, дефекты или нагрев матрицы, но это уже не относится к нашей теме.

Заключение
Помните, что фотоаппарат с разрешением 20 Мп и размером матрицы 1/2.3″ сделает фото по качеству хуже, чем камера с разрешение 8 Мп, но матрицей с размером 1/1.8″. Так что дело здесь совсем не в разрешении, которое влияет только на размер изображения. Он то вообще в нынешних условиях не играет роли, ведь в основном люди «заливают» свои фото в социальные сети, где никто не будет открывать их оригинальный размер.
Помните: размером матрицы называется физический реальный размер используемого сенсора, который оказывает наибольшее влияние на качество изображения. Выбирая камеру, в первую очередь обращайте внимание именно на геометрические размеры сенсора, которые всегда указываются в характеристиках. И только затем смотрите на остальные параметры, включая разрешение.
fb.ru
О видиконовских дюймах
© 2015 Vasili-photo.com
Одной из существеннейших характеристик цифрового фотоаппарата является физический размер светочувствительной матрицы, иными словами – её формат. Вместо того чтобы всегда указывать точные размеры сенсора в миллиметрах, например, 36 x 24 мм или 24 x 16 мм, производители фотооборудования предпочитают для краткости использовать устоявшиеся названия, например, FX или DX, предполагая, что пользователь достаточно компетентен, чтобы не смущаться подобными обозначениями. Действительно, редкий фотолюбитель не знает, что FX или Full-frame – это полный кадр, а DX или APS-C – умеренный кроп. Однако когда речь заходит о сенсорах компактных камер, использование тривиальных обозначений может привести к некоторой путанице.
Вы могли заметить, что размер компактных матриц принято указывать в дюймах, например, 1/2.3″, 1/1.7″, 1″, 4/3″ и т.д. Что означают эти цифры? Что за величина здесь измеряется и почему именно в дюймах? Давайте возьмём один из компактных форматов, скажем, 1″, и рассмотрим его поподробнее.
Увидев название «1″» неподготовленный человек, скорее всего, поймёт это именно как «один дюйм», и решит, что, вероятно, либо длина, либо ширина, либо, на худой конец, диагональ сенсора составляет один дюйм, т.е. 25,4 мм. В любом случае, такой сенсор кажется достаточно крупным. Однако из технической характеристики любой фотокамеры формата 1″ следует, что её матрица имеет весьма скромные размеры 12,8 x 9,6 мм. Здесь и не пахнет дюймом. Попробуем вычислить диагональ и получим 16 мм. Это тоже далеко не дюйм. Точнее, это не тот старый добрый имперский дюйм, к которому мы все привыкли.
Всё дело в том, что длину диагонали сенсора компактных камер измеряют в т.н. видиконовских дюймах. Один видиконовский дюйм составляет 2/3 полноразмерного имперского дюйма и равен 17 мм. Таким образом, сенсор формата 1″ с диагональю 16 мм, строго говоря, не дотягивает даже до видиконовского дюйма, но это уже не столь важно. Важно то, что из-за использования «дюймовых» размеров для обозначения форматов компактных матриц, создаётся обманчивое впечатление, будто матрицы эти в полтора раза больше, чем они суть на самом деле.
Откуда же взялись ущербные видиконовские дюймы, и на каком основании производители фототехники используют вводящую в заблуждение номенклатуру? Ответ на этот вопрос неочевиден.
До распространения полупроводниковых светочувствительных матриц, т.е. до начала 90-х гг. XX в. в теле- и видеокамерах использовались передающие телевизионные трубки, преобразующие изображение в видеосигнал. Наиболее известным типом передающей трубки был видикон. Светочувствительным элементом видикона являлась фотопроводящая мишень, располагавшаяся внутри собственно вакуумной трубки. Важнейшей характеристикой видикона являлся внешний диметр трубки, выраженный в дюймах. При этом диагональ рабочей области светочувствительной мишени была в 2/3 раза меньше диаметра трубки. Так, например, наиболее популярными были видиконы размера 1”. Это означает, что внешний диаметр трубки был равен 1 дюйму, т.е. 25,4 мм, в то время как диагональ мишени – 2/3 дюйма, т.е. примерно 17 мм. Это и есть злополучный видиконовский дюйм.
Инерция традиции была столь велика, что даже когда на смену видиконам пришли матрицы на основе ПЗС или КМОП, их размеры по-прежнему продолжали исчислять в видиконовских дюймах, несмотря на то, что никаких вакуумных трубок в современных теле- и видеокамерах нет, и ни о каком диаметре трубки речи уже быть не может. Отсюда видиконовская зараза перекинулась и на цифровые фотоаппараты, даром, что традиционные плёночные фотоаппараты никогда не имели к видиконам ни малейшего отношения. И если сегодня размер матрицы цифровой фотокамеры указан в дюймах, то это говорит нам не столько об истинном размере сенсора, сколько о том, каков был бы внешний диаметр вакуумной трубки, если бы вместо матрицы камера была снабжена видиконом со светочувствительной мишенью соответствующего размера. Сложно представить себе что-нибудь более нелепое, но именно таковы истоки дюймовой номенклатуры фотографических матриц.
В наши дни никто уже не помнит о видиконовских дюймах, и их использование компаниями, производящими малоформатную фотоаппаратуру, можно объяснить только не вполне чистоплотным стремлением скрыть от потребителя истинные размеры компактных матриц.
Спешу заметить, что критика моя относится не к самим матрицам дюймовых форматов, а лишь к вздорной традиции измерять их видиконовскими дюймами, которые достаточно легко спутать с дюймами настоящими. Тем не менее, маленькие матрицы вполне имеют право на существование, коль скоро габариты или ценовая ниша устройства не позволяют снабдить его полнокадровой или хотя бы APS-С матрицей. Форматы 1” и 4/3” (кроп-фактор 2,7 и 2 соответственно) с успехом используются в беззеркальных фотокамерах и зачастую представляют собой разумный компромисс, позволяющий совместить относительно компактные размеры камеры и вполне приемлемое качество изображения.
Спасибо за внимание!
Василий А.
Post scriptum
Если статья оказалась для вас полезной и познавательной, вы можете любезно поддержать проект, внеся вклад в его развитие. Если же статья вам не понравилась, но у вас есть мысли о том, как сделать её лучше, ваша критика будет принята с не меньшей благодарностью.
Не забывайте о том, что данная статья является объектом авторского права. Перепечатка и цитирование допустимы при наличии действующей ссылки на первоисточник, причём используемый текст не должен ни коим образом искажаться или модифицироваться.
Желаю удачи!
| Дата публикации: 29.06.2015 |
Вернуться к разделу «Матчасть»
Перейти к полному списку статей
vasili-photo.com
Матрица (франшиза) — Википедия
Материал из Википедии — свободной энциклопедии
У этого термина существуют и другие значения, см. Матрица.«Ма́трица» (англ. Matrix trilogy) — американская научно-фантастическая медиафраншиза в жанре киберпанк. Началась с фильма «Матрица», снятого в 1999 году братьями Эндрю и Ларри Вачовски. Позднее, в 2003 году, вышло два продолжения: «Матрица: Перезагрузка» и «Матрица: Революция». В том же 2003 году был выпущен аниме-сериал «Аниматрица». Также по мотивам фильмов были выпущены сборники веб-комиксов и несколько компьютерных игр.
Вачовски неоднократно заявляли о том, что намеревались воспроизвести стиль аниме-киберпанка в кинокартине[1], и на создание медиафраншизы, в числе прочего, повлияло аниме «Призрак в доспехах»[2].
20 августа 2019 года был анонсирован выход четвёртого фильма в серии с участием Киану Ривза и Керри-Энн Мосс[3]. Сценаристом и режиссёром выступит Лана Вачовски.
«Матрица»[править | править код]
Программист одной американской компании Томас Андерсон, также известный в неофициальных кругах как хакер Нео, узнаёт, что наш мир, всё, что есть вокруг, это всего лишь порождение компьютерной программы — Матрицы. На самом же деле на Земле уже давно правят машины, которые выращивают людей на специальных плантациях и используют в качестве источников энергии. Но есть и люди, которые противостоят Машинам, они живут в единственном городе людей, до которого Машины ещё не смогли добраться, и периодически входят в Матрицу. Нео узнаёт, что он «избранный», и именно ему предстоит разрушить Матрицу, чтобы освободить людей от власти Машин.
«Матрица: Перезагрузка»[править | править код]
Чтобы выполнить свою миссию избранного, Нео необходимо встретиться с Архитектором Матрицы, но найти к нему путь очень непросто. Тем временем Агент Смит нашёл возможность самопроизвольного копирования, и теперь он готов сразиться с Нео не в одиночку — с каждым днём Смит пополняет ряды своих репликантов. К тому же Машины начали рыть землю, устремившись к Зиону — последнему оплоту человечества. Нео остаётся последней надеждой человечества на свободу от гнёта Машин.
«Матрица: Революция»[править | править код]
Машины начинают штурм единственного города людей — Зиона. Сил защитников города не хватит на то, чтобы отразить этот натиск, им остаётся только умереть, защищая свой город. Нео решает отправиться в город Машин (01), чтобы не допустить падения Зиона и выполнить предначертанное ему. Тем временем Смит сумел подчинить себе Матрицу и вывести её из-под контроля Машин. Если Нео сможет противостоять Смиту, то у людей появится шанс уцелеть и жить в мире с Машинами. Если же Нео не справится — наступит крушение Матрицы и человечество погибнет.
Затраты на фильмы и кассовые сборы[править | править код]
| Фильм | Дата выхода на экраны | Кассовые сборы (долл.) | Бюджет (долл.) | Примечание | ||
|---|---|---|---|---|---|---|
| США | Другие страны | Во всём мире | ||||
| «Матрица» | 31 марта 1999 | 171 479 930 | 292 037 453 | 463 517 383 | 63 000 000 | [4] |
| «Матрица: Перезагрузка» | 15 мая 2003 | 281 576 461 | 460 552 000 | 742 128 461 | 150 000 000 | [5] |
| «Матрица: Революция» | 5 ноября 2003 | 139 313 948 | 288 029 350 | 427 343 298 | 150 000 000 | [6] |
| Итого | 592 370 339 | 1 040 618 803 | 1 632 989 142 | 363 000 000 | ||
Актёры и персонажи[править | править код]
Съёмочная группа[править | править код]
Гонорары[править | править код]
Гонорары режиссёров и основных актёров (в долларах США)[7].
- «Матрица» (1999)
- Киану Ривз (Нео) — 10 млн +10 % от сборов (17 млн), а также бонус в размере 8 млн[8][неавторитетный источник?]. Киану Ривз вложил собственные 38 млн в производство спецэффектов для двух сиквелов.
- Лоуренс Фишборн (Морфеус) — 500 тыс.
- Керри-Энн Мосс (Тринити) — 500 тыс.
- Хьюго Уивинг (агент Смит) — 500 тыс.
- «Матрица
- Перезагрузка» (2003)
- Эндрю и Ларри Вачовски (режиссёры) — 4 млн (+ % от сборов, составивший 6 млн) каждому
- Киану Ривз (Нео) — 15 млн (+15 % от сборов, составившие 42 млн). Киану Ривз отказался от причитающейся ему доли от продажи билетов, равной примерно 40 млн, после того как продюсеры засомневались, что картина окупит затраты на спецэффекты.
- Лоуренс Фишборн (Морфеус) — 1 млн
- Керри-Энн Мосс (Тринити) — 1 млн
- Хьюго Уивинг (агент Смит) — 1 млн
- Дэвид Килд (агент Джексон) — 500 тыс. (в неделю)
- «Матрица
- Революция» (2003)
- Эндрю и Ларри Вачовски (режиссёры) — 4 млн (+ % от сборов, составивший 6 млн) каждому
- Киану Ривз (Нео) — 15 млн (+15 % от сборов, составившие 21 млн)
- Лоуренс Фишборн (Морфеус) — 1 млн
- Керри-Энн Мосс (Тринити) — 1 млн
- Хьюго Уивинг (агент Смит) — 1 млн
В 2003 году по мотивам вселенной «Матрицы» был выпущен сборник коротких аниме-OVA, связанных между собой общей тематикой и сеттингом. Название является комбинацией двух слов — «аниме» (англ. anime) и «матрица» (англ. matrix). По словам Вачовски, у них изначально были планы создать аниме по мотивам своего нашумевшего фильма, так как японские анимационные фильмы во многом послужили для них вдохновением.[9] Вачовски являются авторами сценария только первого эпизода «Аниматрицы» («Последний полёт „Осириса“»). Для остальных эпизодов лично Вачовски были приглашены другие режиссёры (за исключением эпизода «Мировой рекорд»), которые сами написали сценарии своих работ.
В период с 1999 по 2004 год по мотивам вселенной «Матрицы» была выпущена коллекция историй, первоначально выходивших как веб-комиксы на официальном веб-сайте трилогии[10]. Большинство историй было опубликовано в двух томах (в 2003 и 2004 годах соответственно), изданных компанией[11], основанной братьями Вачовски. Редактором комиксов является Спенсер Лэмм. Братья Вачовски, создатели трилогии фильмов «Матрица», написали один из сценариев комиксов, «Bits and Pieces of Information», некоторые части которого были позже включены в один из коротких анимационных фильмов «Аниматрицы», «The Second Renaissance». Комиксы «Неверный номер»[12] и «Бабочка»[13] были экранизированы в 2006 и 2011 годах соответственно[значимость факта?].
ru.wikipedia.org
Физический размер матрицы фотоаппарата
Так как матрица (фотосенсор) состоит из множества пикселей, то физический размер матрицы фотоаппарата зависит от размеров самого пикселя и их количества, то-есть от разрешения матрицы. А вот размер пикселя зависит от того, какую чувствительность от него требуют. Ведь чем больше размер пикселя, тем больше света он соберет и тем больше будет его светочувствительность и отношение сигнал-шум. Получается, что на больших по размеру фотосенсорах меньше шума и больше светочувствительность, поэтому и такая разница в цене.
Влияние на кроп-фактор и ГРИП
Разные размеры фотосенсора определяют и значение кроп-фактора. Числовое значение кроп фактора получается из отношения диагонали кадра 35 миллиметровой пленки к диагонали матрицы. Чем меньше матрица, тем меньше её диагональ и значит кроп-фактор больше. Значение кроп-фактора влияет на эквивалентное фокусное расстояние, а ЭФК в свою очередь влияет на ГРИП.
Вляние физической величины матрицы на ГРИП происходит по законам оптики. При проведении опыта брали три фотоаппарата и делали снимки при полностью одинаковых настройках, но с тремя разными по размеру фотосенсорами.
И в итоге ГРИП (резкость предметов на разном удалении от фотокамеры) был больше у фотоаппарата с наименьшей матрицей, то есть все предметы были в резкости. А у фотоаппарата с большими матрицами ГРИП был меньше.
Это важно когда вы делаете снимки с размытым фоном. Если на вашей фотокамере фотоэлемент с маленькой диагональю, то будет тяжело получить размытый фон на снимке.
Обозначение матриц
Обозначают размер фотосенсора обычно как дробь дюйма. Например, 1/1.8 дюйма. Такое значение больше реальной диагонали матрицы, для которой это обозначение применяется.
Это обозначение прижилось еще в 50-х годах прошлого века. Тогда это значение применялось для обозначения размера передающей трубки (круглой), которая называлась «видикон». С тех пор и называются эти дюймы — «видиконовские». Тогда было установлено, что полезное изображение по диагонали примерно равно 2/3 диаметра трубки. Потому что прямоугольное изображение помещалось в кругу передающей трубки.
Внешний вид видикона и определение диагонали
Так до сих пор и считается, что реальный размер диагонали матрицы примерно равен 2/3 от значения типоразмера выраженного в дроби дюймов (видиконовских).
Применяются таблицы соответствия значения в дюймах и соотношения сторон фотосенсора в миллиметрах.
| Размер в «видиконовых дюймах» | Диагональ в мм. | Ширина в мм. | Высота в мм. | Площадь матрицы мм2 |
| 1/6″ | 2.67 | 1.97 | 1.47 | 2.90 |
| 1/4″ | 4.00 | 2.95 | 2.21 | 6.53 |
| 1/3.6″ | 4.44 | 3.28 | 2.46 | 8.06 |
| 1/3.2″ | 5.00 | 3.69 | 2.77 | 10.20 |
| 1/3″ | 5.33 | 3.93 | 2.95 | 11.60 |
| 1/2.7″ | 5.93 | 4.37 | 3.28 | 14.32 |
| 1/2″ | 8.00 | 5.90 | 4.42 | 26.10 |
| 1/1.8″ | 8.89 | 6.55 | 4.92 | 32.22 |
| 1/1.7″ | 9.41 | 6.94 | 5.21 | 36.13 |
| 2/3″ | 10.67 | 7.87 | 5.90 | 46.40 |
| 1″ | 16.00 | 11.80 | 8.85 | 104.40 |
| 4/3″ | 21.33 | 15.73 | 11.80 | 185.60 |
Размеры матрицы могут быть указаны в спецификации как диагональ в дюймах, или можно воспользоваться значением кроп-фактора для определения диагонали, а для нахождения кроп-фактора используйте значение фокусного расстояния.
Узнать величину фотосенсора можно по коэффициенту (кроп-фактор), который показывает во сколько раз диагональ матрицы меньше диагонали кадра пленки в 35 мм. А вот для вычисления этого коэффициента можно использовать значения фокусного расстояния и эквивалентного фокусного расстояния (ЭФР). Обычно они обозначаются как две пары чисел (фокусное расстояние должно быть написано на объективе), например, F=18-55 мм. Эквивалентное фокусное расстояние так же обозначается парой чисел Feq=28-84 мм. Теперь берем соответствующие числа и делим, например, 28/18 или 84/55. В результате получим коэффициент, который мы и искали (кроп-фактор), равным 1,53. И можно воспользоваться таблицей для определения физического размера фотоэлемента. Получим, что на фотокамере используется матрица APS 23х15 мм.
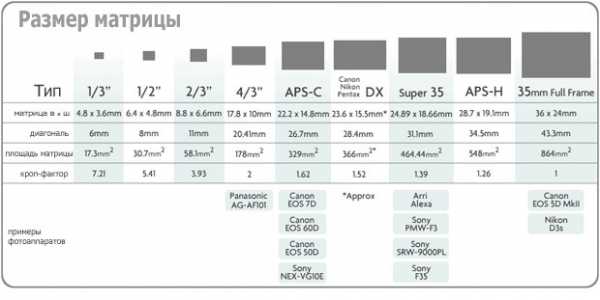
Эти отношения площади различных по размеру фотосенсоров (смотрите рисунок) могут примерно показать вам, насколько реальная чувствительность будет различаться у разных фотокамер, какие будут шумы, где и почему большие габариты фотоаппарата.
Чем больше размер сенсора, тем должна быть и больше оптика для обслуживания такой матрицы, поэтому фотоаппараты с большим фотосенсором и сами по размеру больше.
Откуда берутся шумы на снимках и как их уменьшить.

Как можно почистить фотосенсор в зеркальном фотоаппарате.
Строение матрицы фотокамеры и её характеристики.
vybrat-tekhniku.ru
Единичная матрица — Википедия
Материал из Википедии — свободной энциклопедии
Едини́чная ма́трица — квадратная матрица, элементы главной диагонали которой равны единице поля, а остальные равны нулю.
Квадратная матрица En=(eij){\displaystyle E_{n}=(e_{ij})} размера (порядка) n{\displaystyle n}, где eii=1{\displaystyle e_{ii}=1} для всякого i∈1,n¯{\displaystyle i\in {\overline {1,n}}}, и eij=0{\displaystyle e_{ij}=0} для всяких i≠j{\displaystyle i\neq j}, называется единичной матрицей порядка n{\displaystyle n}.
Единичную матрицу можно определить как матрицу (eij){\displaystyle (e_{ij})}, у которой eij=δij{\displaystyle e_{ij}=\delta _{ij}}, где δij{\displaystyle \delta _{ij}} — символ Кронекера.
Единичная матрица является частным случаем скалярной матрицы.
Единичная матрица размера n×n{\displaystyle n\times n} обычно обозначается En{\displaystyle E_{n}} и имеет вид:
- En=[10⋯001⋯0⋯⋯⋯⋯00⋯1],{\displaystyle E_{n}={\begin{bmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\cdots &\cdots &\cdots &\cdots \\0&0&\cdots &1\end{bmatrix}},}
Так же используется и другое обозначение: In{\displaystyle I_{n}}.
Если из контекста ясно, какого размера матрица, то нижний индекс (указывающий порядок) опускается: E{\displaystyle E}, I{\displaystyle I}.
- Произведение любой матрицы и единичной матрицы подходящего размера равно самой матрице:
- AE=EA=A{\displaystyle AE=EA=A}
- A0=E{\displaystyle A^{0}=E}
- При умножении матрицы на обратную ей тоже получается единичная матрица:
- AA−1=E{\displaystyle AA^{-1}=E}
- AAT=E{\displaystyle AA^{T}=E}
- detE=1{\displaystyle \mathrm {det} \,E=1}.
Единичные матрицы первых порядков имеют вид
- E1=(1), E2=(1001), E3=(100010001){\displaystyle E_{1}={\begin{pmatrix}1\end{pmatrix}},\ E_{2}={\begin{pmatrix}1&0\\0&1\end{pmatrix}},\ E_{3}={\begin{pmatrix}1&0&0\\0&1&0\\0&0&1\end{pmatrix}}}
ru.wikipedia.org
Определитель матрицы.
Навигация по странице:
Определитель матрицы или детерминант матрицы — это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.Определение.
Определителем матрицы n×n будет число:| det(A) = | Σ | (-1)N(α1,α2,…,αn)·aα11·aα22·…·aαnn |
| (α1,α2,…,αn) |
Обозначение
Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).Свойства определителя матрицы
Определитель матрицы с двумя равными строками (столбцами) равен нулю.
Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
- При транспонировании значение определителя матрицы не меняется:
det(A) = det(AT)
- Определитель обратной матрицы:
det(A-1) = det(A)-1
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
- Общий множитель в строке (столбце) можно выносить за знак определителя:
a11a12…a1na21a22…a2n….k·ai1k·ai2…k·ain….an1an2…ann = k·a11a12…a1na21a22…a2n….ai1ai2…ain….an1an2…ann
- Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени:
B = k·A => det(B) = kn·det(A)
где A матрица n×n, k — число. - Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:
a11a12…a1na21a22…a2n….bi1 + ci1bi2 + ci2…bin + cin….an1an2…ann = a11a12…a1na21a22…a2n….bi1bi2…bin….an1an2…ann + a11a12…a1na21a22…a2n….ci1ci2…cin….an1an2…ann
Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
- Определитель произведения матриц равен произведению определителей этих матриц:
det(A·B) = det(A)·det(B)
Методы вычисления определителя матрицы
Вычисление определителя матрицы 1×1
Правило:
Для матрицы первого порядка значение определителя равно значению элемента этой матрицы:∆ = |a11| = a11
Вычисление определителя матрицы 2×2
Правило:
Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:| ∆ = | = a11·a22 — a12·a21 |
Пример 1.
Найти определитель матрицы A| A = |
|
Решение:
| det(A) = | = 5·1 — 7·(-4) = 5 + 28 = 33 |
Вычисление определителя матрицы 3×3
Правило треугольника для вычисления определителя матрицы 3-тего порядка
Правило:
Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.| + | – |
| ∆ = |
|
= |
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 — a13·a22·a31 — a11·a23·a32 — a12·a21·a33
Правило Саррюса для вычисления определителя матрицы 3-тего порядка
Правило:
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:| ∆ = |
|
= |
= a11·a22·a33 + a12·a23·a31 + a13·a21·a32 — a13·a22·a31 — a11·a23·a32 - a12·a21·a33
Пример 2.
Найти определитель матрицы A = 571-410203Решение:
det(A) = 571-410203 = 5·1·3 + 7·0·2 + 1·(-4)·0 — 1·1·2 — 5·0·0 — 7·(-4)·3 = 15 + 0 + 0 — 2 — 0 + 84 = 97Вычисление определителя матрицы произвольного размера
Разложение определителя по строке или столбцу
Правило:
Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:| n | |||
| det(A) = | Σ | aij·Aij | — разложение по i-той строке |
| j = 1 |
Правило:
Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:| n | |||
| det(A) = | Σ | aij·Aij | — разложение по j-тому столбцу |
| i = 1 |
При разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.
Пример 3.
Найти определитель матрицы A| A = |
|
Решение: Вычислим определитель матрицы разложив его по первому столбцу:
= 2·(-1)1+1· 2111 + 0·(-1)2+1· 4111 + 2·(-1)3+1· 4121 == 2·(2·1 — 1·1) + 2·(4·1 — 2·1) = 2·(2 — 1) + 2·(4 — 2) = 2·1 + 2·2 = 2 + 4 = 6
Пример 4.
Найти определитель матрицы AA = 2411020021134023
Решение: Вычислим определитель матрицы, разложив его по второй строке (в ней больше всего нулей):
det(A) = 2411020021134023 = — 0· 411113023 + 2· 211213423 — 0· 241213403 + 0· 241211402 == 2·(2·1·3 + 1·3·4 + 1·2·2 — 1·1·4 — 2·3·2 — 1·2·3) = 2·(6 +12 + 4 — 4 — 12 — 6) = 2·0 = 0
Приведение определителя к треугольному виду
Правило:
Используя свойства определителя для элементарных преобразований над строками и столбцами 8 — 11, определитель приводится к треугольному виду, и тогда его значение будет равно произведению элементов стоящих на главной диагонали.Пример 5.
Найти определитель матрицы A приведением его к треугольному видуA = 2411021021134023
Решение:
det(A) = 2411021021134023
Сначала получим нули в первом столбце под главной диагональю. Для этого отнимем от 3-тей строки 1-ую строку, а от 4-той строки 1-ую строку, умноженную на 2:
det(A) = 241102102 — 21 — 41 — 13 — 14 — 2·20 — 4·22 — 1·23 — 1·2 = 241102100-3020-801
Получим нули во втором столбце под главной диагональю. Для этого поменяем местами 2-ой и 3-тий столбцы (при этом детерминант сменит знак на противоположный):
det(A) = — 2141012000-3200-81
Получим нули в третьем столбце под главной диагональю. Для этого к 3-ему столбцу добавим 4-тий столбец, умноженный на 8:
det(A) = — 214 + 1·81012 + 0·8000-3 + 2·8200-8 + 1·81 = — 211210120001320001 = -2·1·13·1 = -26
Теорема Лапласа
Теорема:
Пусть ∆ — определитель n-ого порядка. Выберем в нем произвольные k строк (столбцов), причем k < n. Тогда сумма произведений всех миноров k-ого порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.Присоединяйтесь
© 2011-2019 Довжик МихаилКопирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне [email protected]
ru.onlinemschool.com
