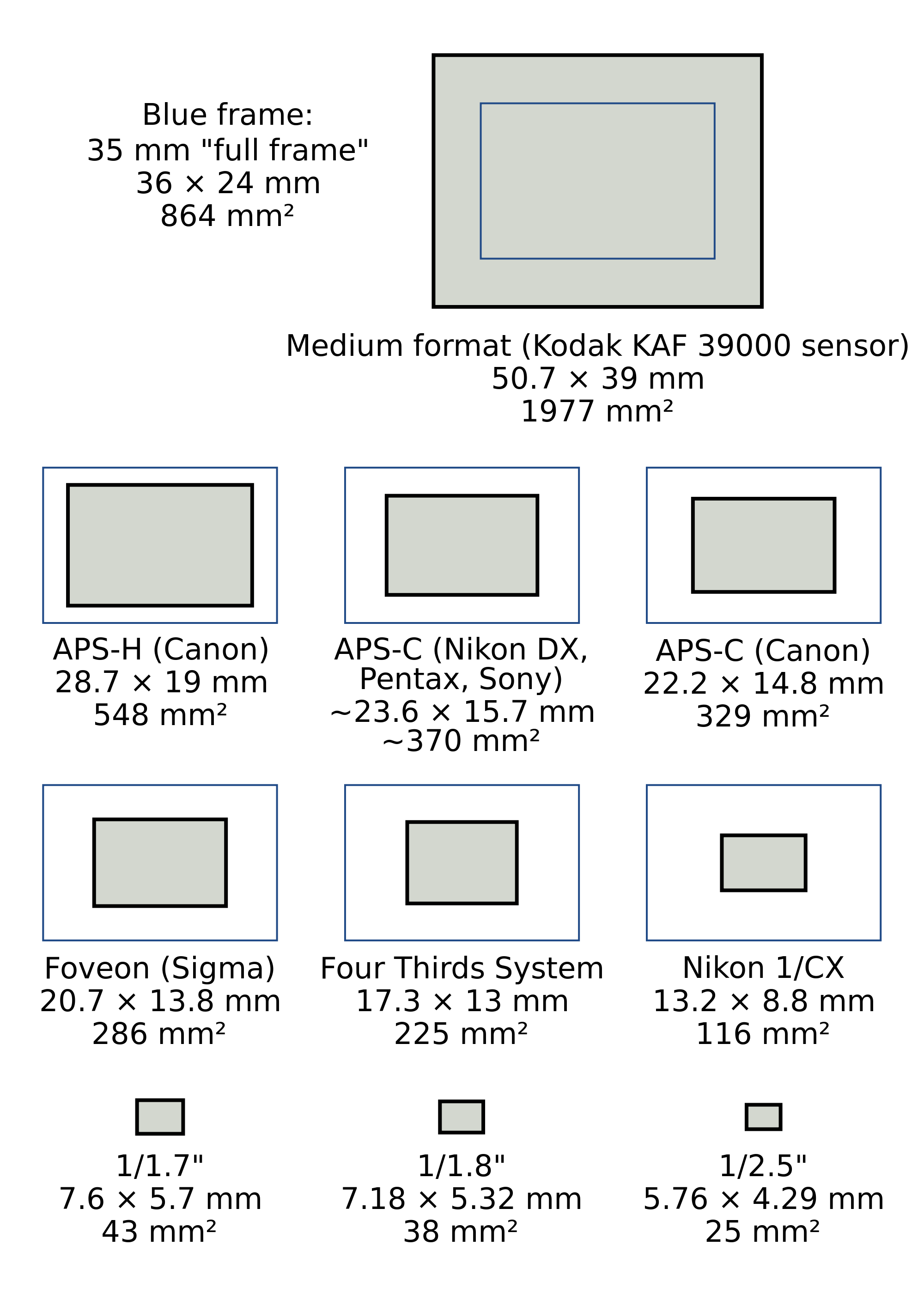
Формат матрицы у камер и пересчет ее размеров
При выборе камеры размер матрицы является важным параметром, поскольку чувствительность камеры напрямую зависит от размера пикселя на матрице. Однако, размеры сенсоров не соответствуют написанным цифрам, так 1-дюймовый сенсор действительно больше, чем 1/2-дюймовый сенсор, но его размеры не равны 1 дюйму, даже если замерить его диагональ.
Условные обозначения размеров матриц остались еще из тех времен, когда в камерах использовались электронные лампы. Так для матрицы диаметром 1″ вакуумная трубка устанавливалась в отклоняющую катушку диаметром 1″, поэтому датчик диаметром 1″ фактически был меньше дюйма. Соотношение между диаметром катушки и форматом изображения трубки составляло примерно 63%.
На таблице показаны некоторые матрицы распространенных форматов с указанием размеров сенсоров и их эквивалентных размеров в миллиметрах. Эти размеры могут варьироваться от матрицы к матрице. Для определения точных размеров матрицы стоит обратиться к документации на камеру либо на ее матрицу, если последняя серийно изготовляемая.
В зависимости от размера матрицы очень важно подобрать для камеры подходящий объектив. Линейки объективов у многих производителей разделены по разрешающей способности объектива и размера матрицы камеры. В выборе объектива важно учитывать оба фактора, если разрешение камеры будет больше разрешения объектива — изображения будут смазанные.
Бюджетные объективы для камер видеонаблюдения рассчитаны на невысокие разрешения и малый размер матрицы. Они подходят лишь немногим камерам машинного зрения, имеющим размер матрицы до 1/3″. Для камер высокоскоростной съемки, с матрицами 1″ и более (1,1″, 4/3) они не подходят.
От максимального размера сенсора для выбранного объектива будет зависеть увидит ли матрица камеры все поле зрения объектива или на краях изображения будут темные участки. Если матрица камеры будет больше (например 1″) допустимого размера у объектива (2/3″), то полученное изображение с камеры будет обрезано — оно будет круглым, как показано на изображении:
Если использовать объектив, рассчитанный на большую матрицу, чем установлена в вашей камере — вы можете выиграть в качестве получаемого изображения, так как оптические искажения объектива (дисторсия) проявляется ближе к краям изображения, а в центре изображение наилучшего качества.
Также объективы имеют ряд других параметров, которые нужно учитывать при выборе (байонеты, переходники, фокусное расстояние, диафрагма, ИК и УФ коррекции и т.д.). Мы готовы оказать вам профессиональную консультацию в выборе оптики для вашей камеры — свяжитесь с нами.
Типы и размеры матриц камер видеонаблюдения
Светочувствительная матрица — важнейший элемент видеокамеры, который обеспечивает качество изображения на 90%. Представляет собой интегральную микросхему, состоящую из фотодиодов. Сенсор генерирует видеопоток, преобразуя проецируемое в него оптическое изображение в аналоговые электрические импульсы. В сетевых видеокамерах эти импульсы сразу преобразовываются в цифровой поток данных за счет наличия в системе АЦП, сразу обрабатывающего сигнал.
Сенсоры имеют ряд характеристик, важнейшие из которых — вид, разрешение и размер матрицы камеры видеонаблюдения. От этих параметров зависит быстродействие устройства, уровень его энергозатратности, а также конечное качество воспроизводимого камерой видео.
Типы матриц, которые используют в современных камерах видеонаблюдения
- CCD (ПЗС). Характеризуются лучшей светочувствительностью, обеспечивают хорошую цветопередачу и низкий уровень шума на изображении. Это достигается за счет последовательного считывания зарядов в каждой ячейке сенсора. Однако принцип действия таких матриц слишком медленный и не удовлетворяет современное видеонаблюдение с большими разрешениями и высокой кадровой частотой. Кроме того, такие сенсоры энергозатратны, дороже в производстве и сложнее в эксплуатации. В современных цифровых камерах важно какая матрица используется. Поэтому, чтобы не тормозить процесс передачи видеопотока, технологию CCD практически не применяют;
- Live-MOS. Разработка компании Panasonic. Применяется для трансляций «живого» изображения за счет технологии, которая позволяет упрощенно организовать передачу сигналов управления и преобразование света в электрические импульсы.
 Для технологии характерно меньшее напряжение электропитания, перегрев и уровень шумовых помех;
Для технологии характерно меньшее напряжение электропитания, перегрев и уровень шумовых помех; - CMOS (КМОП). Главное достоинство — более низкое энергопотребление. Ячейки в сенсоре считываются в произвольном порядке, что позволяет избежать размытия изображения при съемке движущихся объектов. Камерой с типом матрицы CMOS гораздо проще управлять, поскольку большая часть электроники расположена на ячейке. Однако такая конструкция сенсора уменьшает светочувствительную площадь.
Для современного видеонаблюдения в соотношении быстродействия, энергопотребления и цены КМОП матрицы предпочтительнее. Поэтому крупнейшие производители камер сосредоточились на закупке или производстве собственных CMOS сенсоров. Например, компании Hikvision и Dahua разрабатывают собственные светочувствительные элементы, которые использует при производстве оборудования. В топовых видеокамерах Dahua DH-SD50430I-HC-S2 или HIKVISION DS-2CD2942F используются именно КМОП матрицы.
Размеры матриц видеокамер наблюдения
Физические размеры матриц выражаются условной длиной, приведенной к диагонали видикона.
Видикон — родоначальник современной фото- и видеотехники. Его диаметр равнялся 1 условному дюйму при рабочей диагонали 16 мм. «Видиконовый дюйм» принят стандартом для определения типоразмера матрицы. Таким образом, если указано, что сенсор имеет размер 1/2”, это значит, что его диагональ равна 8 мм.
Современные видеокамеры чаще всего используют следующие типоразмеры: 1/2”; 1/3”; 1/4”; 1/6” и реже 1/10”.
На что влияет размер матрицы в камере?
От диагонали сенсора напрямую зависит качество изображения.
Какой размер матрицы лучше для видеокамеры
Это зависит от конкретных задач, стоящих перед видеонаблюдением. Важно помнить, что при выборе устройства характеристики нужно рассматривать комплексно. Например, хорошее разрешение при маленьком размере сенсора дадут плохое изображение. Кроме того, чем больше матрица, тем она дороже. Поэтому при выборе видеокамеры необходимо рассматривать вариант, в котором будут учитываться оптимальное соотношение трех показателей, удовлетворяющих потребности видеонаблюдения — это цена, разрешение и типоразмер.
О матрицах простым языком, Гл. 1, Или опять про мегапиксели
Для начала, дадим определение матрице.
Наверное не одну сотню раз вы слышали, что чем больше в матрице мегапикселей, тем качественней и детализированней будут снимки. Это самое большое заблуждение. Не количество мегапикселей в матрице влияет на картинку, а ее физический размер.
И раз уж обещал обо все рассказывать простым языком и, что у нас на сайте не будет рутинной теории, то расскажу пожалуй на “пальцах”.
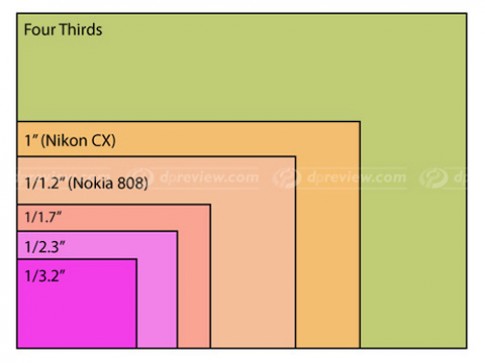
Взгляните на эту картинку, здесь схематично представлены матрицы, вернее их физические размеры, каждому цвету соответствует определенный размер матрицы. А ниже будут приведены модели фотокамер с сопоставлением физического размера ИХ матрицы и количеством мегапикселей “затолканным” в нее.
На этой картинке видно, как разительно отличаются матрицы по своему размеру. (между прочим прошу обратить ваше внимание на то, что масштаб здесь увеличен).
1) Начнем как полагается с цифры 1. Красным цветом выделена матрица «стандартной» цифровой компактной камеры, ее диагональ измеряется в дюймах и равна 1/2,3″. Такой матрицей снабжено огромное кол-во компакт камер. Для примера я взял популярные на данный момент цифрокомпакты от Canon, а теперь посмотрите на физический размер их матриц и на кол-во «впиханных» в них мегапикселей…. Есть над чем поразмыслить?
|
СANON Digital IXUS 100 IS Размер матрицы — 1/2,3″ Число Мпикселей — 12,1
|
||
|
СANON Digital IXUS 990 IS Размер матрицы — 1/2,3″ Число Мпикселей — 12,1 |
||
|
СANON Digital IXUS 85 IS Размер матрицы — 1/2,3″ Число Мпикселей — 10 |
||
|
СANON PowerShot SX1 IS Размер матрицы — 1/2,3″ Число Мпикселей — 12,1 |
||
|
СANON PowerShot A480 Размер матрицы — 1/2,3″ Число Мпикселей — 10 |
||
|
СANON PowerShot SX200 IS Размер матрицы — 1/2,3″ Число Мпикселей — 12 |
||
|
Olympus -SP-565 UZ |
2) Под цифрой 2 показана матрица размером 4/3 дюйма. В основном матрицы такого размера ставит на свои камеры компания Olympus.
В основном матрицы такого размера ставит на свои камеры компания Olympus.
Ниже представлены яркие представители семейства Olympus обладающими такими матрицами
|
Olympus — E-410 Размер матрицы — 4/3″ Число Мпикселей — 10
|
||
|
Olympus -E-P1 Размер матрицы — 4/3″ Число Мпикселей — 13.1
|
||
|
||||
3) Под цифрой 3 показана матрица формата APS-C, матрицы этого размера можно встретить на всех популярных моделях цифровых зеркальных фотокамерах начального уровня (т.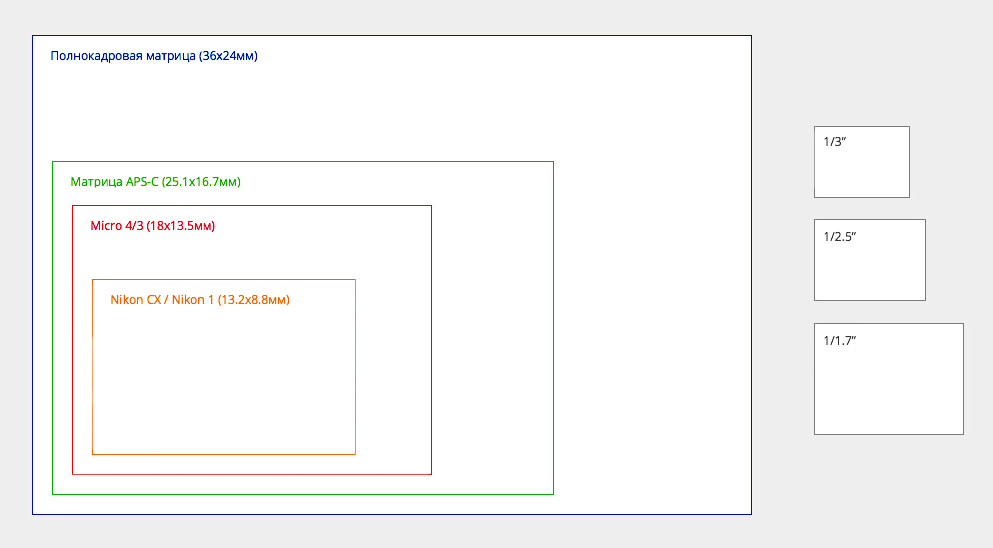 е. любительских) от Canon и Nikon. Давайте немного углубимся в терминологию. Наверняка вы не раз встречали аббривеатуру DSLR (в интернет или бумажных обзорах по зеркальным фотокамерам). DSLR — (Digital single-lens reflex camera), что означает — Цифровая однообъективная зеркальная камера (однообективная — вовсе не означает, что камера может использует всего один объектив, а означает это что камера не может использовать более одного объектива одновременно; т.е за раз более одного объектива не нацепить)
е. любительских) от Canon и Nikon. Давайте немного углубимся в терминологию. Наверняка вы не раз встречали аббривеатуру DSLR (в интернет или бумажных обзорах по зеркальным фотокамерам). DSLR — (Digital single-lens reflex camera), что означает — Цифровая однообъективная зеркальная камера (однообективная — вовсе не означает, что камера может использует всего один объектив, а означает это что камера не может использовать более одного объектива одновременно; т.е за раз более одного объектива не нацепить)
|
Canon — EOS 1000D Формат матрицы — APS-C Размер матрицы — 22,2 x 14,8 мм Число Мегапикселей — 10,1
|
||
|
Canon — EOS 500D Формат матрицы — APS-C Размер матрицы — 22,3 x 14,9 мм Число Мегапикселей — 15 |
||
|
Canon — EOS 50D Формат матрицы — APS-C Размер матрицы — 22,3 x 14,9 мм Число Мегапикселей — 15,1 |
||
|
Nikon — D60 Формат матрицы — APS-C Размер матрицы — 23,6×15,8 мм Число Мегапикселей — 10,1 |
||
|
Nikon — D5000 Формат матрицы — APS-C Размер матрицы — 23,6×15,8 мм Число Мегапикселей — 12,9 |
||
|
Sony — A700P Формат матрицы — APS-C Размер матрицы — 23,5×15,6 мм Число Мегапикселей — 12,2 |
||
|
Sony — A350K Формат матрицы — APS-C Размер матрицы — 23,5 x 15,7 мм Число Мегапикселей — 14,2 |
||
|
Pentax K-x Формат матрицы — APS-C Размер матрицы — 23,6 х 15,8 мм Число Мегапикселей — 12,4 |
||
|
Pentax K7 Формат матрицы — APS-C Размер матрицы — 23,4 х 15,6 мм Число Мегапикселей — 14,6 |
Если вы внимательно рассмотрели таблицу, то у вас наверняка появились вопросы: почему формат один (APS-C), а размеры в миллиметрах разные, да и что это вообще за формат? Отвечаю: размеры данного формата могут варьироваться от 20. 7?13.8 мм до 25,1?16,7 мм. APS-C — Advanced Photo System type-C, что означает Усовершенственная фотосистема классического типа.
7?13.8 мм до 25,1?16,7 мм. APS-C — Advanced Photo System type-C, что означает Усовершенственная фотосистема классического типа.
4) И наконец перейдем к цифре 4. Эта матрица имеет размер 36х24 мм, и равняется по размеру с кадром 35 мм пленки, да, да той пленки на которую вы когда то снимали своими мыльницами от Kodak или Minolta. Матрицу такого размера имеют профессиональные DSLR камеры (это я вас потихоньку приучаю вас привыкать к аббревиатурам), их еще называют полнокадровые или фул фрейм (от full frame) матрицы. Давайте посмотрим на некоторых «монстров», которые имеют их.
|
Canon — EOS 5D Размер матрицы — 36 x 24 мм Число Мегапикселей — 12,8
|
||
|
Canon — EOS 5D Mark II Размер матрицы — 36 x 24 мм Число Мегапикселей — 21,1 |
||
|
Canon — EOS-1Ds Mark III Размер матрицы — 36 x 24 мм Число Мегапикселей — 21,1 |
||
|
Nikon — D700 Размер матрицы — 36 x 24 мм Число Мегапикселей — 12,1 |
||
|
Nikon — D3X Размер матрицы — 36 x 24 мм Число Мегапикселей — 24,5 |
||
|
Sony — A900 Размер матрицы — 36 x 24 мм Число Мегапикселей — 24,6 |
Выводы: Увеличение количества пикселей на матрицах маленького размера происходит за счет уменьшения размера этого самого пикселя. А это черевато возникновением таких проблем как «шумы». Если сравнить матрицы фотокамер СANON Digital IXUS 990 IS и скажем Nikon — D700, то вы уведите, что число мегапикселей у них равно, но вот если сравнить размеры их матриц в миллиметрах…., то сразу видно, кто кому даст фору, так что уважаемые читатели не ведитесь на количество пикселей при покупке фотоаппарата, приглядитесь к размеру матрицы и качеству объектива.
А это черевато возникновением таких проблем как «шумы». Если сравнить матрицы фотокамер СANON Digital IXUS 990 IS и скажем Nikon — D700, то вы уведите, что число мегапикселей у них равно, но вот если сравнить размеры их матриц в миллиметрах…., то сразу видно, кто кому даст фору, так что уважаемые читатели не ведитесь на количество пикселей при покупке фотоаппарата, приглядитесь к размеру матрицы и качеству объектива.
Матрица цифровой камеры. Типы и размер матриц
Выбирая цифровую камеру для микроскопа или телескопа, часто обращают внимание лишь на разрешение матрицы, т.е. количество мегапикселей. Однако это не единственный важный параметр цифровой камеры, определяющий качество полученных фотоснимков и видеороликов. По каким же признакам следует выбирать цифровую камеру, и чем они могут отличаться одна от другой?
Главным элементом цифровой камеры является ее матрица, которая, собственно, и фиксирует изображение в цифровой камере. Отметим, что также в техническом описании цифровых камер часто употребляется и термин сенсор, обозначающий то же, что и матрица. Матрица состоит из массива светочувствительных ячеек, и именно от нее зависит качество изображения, полученного с помощью цифровой камеры.
Отметим, что также в техническом описании цифровых камер часто употребляется и термин сенсор, обозначающий то же, что и матрица. Матрица состоит из массива светочувствительных ячеек, и именно от нее зависит качество изображения, полученного с помощью цифровой камеры.
Существует два основных типа матриц: CCD (ПЗС матрицы) и CMOS (КМОП матрицы), отличающиеся по применяемой технологии. И если на рынке фотоаппаратов наиболее распространены цифровые камеры с ПЗС матрицей, то большинство моделей цифровых камер для телескопов и микроскопов имеют именно КМОП матрицу.
Чем же отличается ПЗС матрица от КМОП матрицы? Основным их отличием является то, что в ПЗС матрицах информация из ячеек считывается последовательно, в то время как в КМОП матрицах информация считывается индивидуально из каждой отдельной ячейки. По этой причине в ПЗС матрицах Вы не можете сделать следующий снимок до тех пор, пока не будет целиком сформирован предыдущий. Что же касается КМОП матриц, то благодаря применяемой технологии их можно использовать не только для фотосъемки, но и для экспонометрии и работы автофокуса. Помимо этого, КМОП матрицы гораздо дешевле в производстве, и поэтому доступнее для многих пользователей. Еще одно немаловажное преимущество КМОП матриц над ПЗС матрицами – потребление меньшего количества энергии.
Помимо этого, КМОП матрицы гораздо дешевле в производстве, и поэтому доступнее для многих пользователей. Еще одно немаловажное преимущество КМОП матриц над ПЗС матрицами – потребление меньшего количества энергии.
Первым делом при выборе цифровой камеры мы рекомендуем Вам обратить внимание на размер матрицы. Физическим размером матрицы называется ее геометрический размер, т.е. длина и ширина матрицы, выраженные в мм. Физический размер матрицы определяет ее качество. Узнать значение этого параметра можно из ее технического описания, хотя, как правило, размеры фотосенсоров производители указывают не в мм, а введя специальное обозначение типа матрицы в виде дробных частей дюйма, например: 1/4″, 1/3″, 1/2.5″, 1/2″ и пр. Сравнивая различные цифровые камеры, Вы должны понимать, что размер матрицы больше у той цифровой камеры, у которой знаменатель в указанной дроби будет меньше, т.е. сенсор 1/2″ будет больше сенсора 1/3″.
Какая же связь между физическим размером матрицы, указанным в мм и типом матрицы, выраженном в 1/дюйм? Отметим, что введенное обозначение типа матрицы выражает не размер ее диагонали, а внешний размер колбы передающей трубки. Обратите внимание на то, что не существует конкретной математической формулы, четко выражающей взаимосвязь между устоявшимся обозначением типа матрицы, выраженного в 1/дюйм, и самим физическим размером диагонали матрицы в мм. Тем не менее, в грубом приближении принято считать, что диагональ сенсора равна двум третям его типоразмера.
Обратите внимание на то, что не существует конкретной математической формулы, четко выражающей взаимосвязь между устоявшимся обозначением типа матрицы, выраженного в 1/дюйм, и самим физическим размером диагонали матрицы в мм. Тем не менее, в грубом приближении принято считать, что диагональ сенсора равна двум третям его типоразмера.
Размеры в мм | Тип матрицы |
4.5х3.4 | 1/3.2″ |
5.4х4.0 | 1/2.7″ |
5.8×4.3 | 1/2.5″ |
6.2×4.6 | 1/2.3″ |
7.2×5.3 | 1/1.8″ |
Вполне целесообразно задать вопрос, а на что же влияет размер матрицы? Прежде всего, сколь иронично это бы не звучало, размер матрицы цифровой камеры влияет на ее стоимость и вес.
Помимо этого, как мы уже отмечали ранее, размер сенсора влияет на качество полученных фотоснимков и видеороликов. Во-первых, от размера сенсора зависит количество цифрового шума, который передается на светочувствительные элементы матрицы вместе с основным сигналом.
Из-за цифрового шума полученные снимки получают неестественный вид, в связи с чем возникает такое ощущение, что сверху на снимок наложена маска из точек различного цвета и яркости.
Причинами возникновения шумов могут быть дефекты в структуре сенсора, токи утечки (заряд может пробивать изоляцию и переходить с одного пикселя на другой), нагрева матрицы (так называемый тепловой шум, когда при повышении температуры на 6-8 градусов шум увеличивается в 2 раза) и пр.
Конечно же, нужно понимать, что абсолютно бессмысленно рассматривать показатель шума отдельно – важно соотношение сигнал / шум.
Итак, на количество шумов главным образом влияет физический размер матрицы, а также размер пикселя.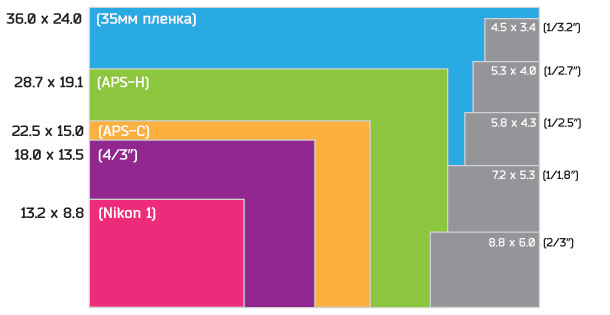 Чем больше физический размер сенсора цифровой камеры, тем больше его площадь и, соответственно тем больше света попадает на него. А, следовательно, полезный сигнал матрицы будет сильнее и, значит, мы получим лучшее соотношение сигнал / шум, что обеспечит более яркое и качественное изображение с более правильной и естественной цветопередачей.
Чем больше физический размер сенсора цифровой камеры, тем больше его площадь и, соответственно тем больше света попадает на него. А, следовательно, полезный сигнал матрицы будет сильнее и, значит, мы получим лучшее соотношение сигнал / шум, что обеспечит более яркое и качественное изображение с более правильной и естественной цветопередачей.
Помимо этого, отметим, что слой изоляции, разделяющий пиксели друг от друга, будет толще для пикселей большого размера. Разумеется, что чем толще слой изоляции, тем меньше зарядов смогут пробить ее. Следовательно, токов утечки будет тоже меньше, что соответственно приведет и к уменьшению шумов.
В качестве примера предлагаем Вам представить матрицу определенного размера. Предположим, что на одной такой матрице 3000 пикселей (3 Мпикс), а на второй такой же матрице расположено 5000 (5 Мпикс). А теперь представьте толщину изоляции пикселей для первого и для второго случая!
Еще раз отметим, что чем меньше матрица, тем меньшее количество света на нее попадает. В таком случае Вы получаете слабый полезный сигнал, который приходится усиливать. А с усилением полезного сигнала естественно усиливаются и становятся более заметными шумы.
В таком случае Вы получаете слабый полезный сигнал, который приходится усиливать. А с усилением полезного сигнала естественно усиливаются и становятся более заметными шумы.
В заключение еще раз повторим, что чем больше физический размер матрицы, тем большее количество света на нее попадает, а значит, тем более качественно изображение Вы получите.
Автор статьи: Галина Цехмистро
Матрицы в видеорегистраторах. Что это?
В этой статье, мы подробно расскажем вам, за что отвечает матрица в видеорегистраторе и какие её параметры влияют на качество записываемого видео.
Матрица, также известная как видеосенсор, это безусловно один из важнейших элементов абсолютно любого видеорегистратора. Вместе с объективом, они образуют тандем, который отвечает за качество видеозаписи. Естественно, что многих автомобилистов интересует именно получаемое изображение, его четкость и детализация, однако многие не совсем понимают, на какие характеристики стоит обратить свое внимание.
Итак, для матрицы существуют два главных параметра, это её размер и количество пикселей.
Физический размер матрицы, определяет расположение и размер пикселя. В свою очередь площадь пикселя определяет светочувствительность и улучшает динамический диапазон, а также снижает количество видео-шумов в кадре.
Иными словами, физический размер матрицы определяет общее качество изображения, ведь чем больше матрица, тем больше размер пикселя, а чем больше пиксель, тем он чувствительнее. Матрицы с маленькой площадью неизбежно «шумят» во время ночной съемки. На первый взгляд, может показаться, что размер матрицы и количество пикселей, для улучшения качества записи, должно стремиться к увеличению, это так, но во всем необходимо знать меру.
Если переводить все в конкретные значения, то выходит следующее. Матрица 1/1,6 больше матрицы 1/2,5 по площади примерно в 2,44 раза. Теоретически туда можно поместить и 15-17 мегапикселей. Реклама говорит нам, что, чем больше мегапикселей, тем лучше. Но это не совсем так. Да, чем их больше, тем детальнее картинка. Но не в ущерб размерам каждого отдельного пикселя. Матрица 1/1,6 с 15-17 мегапикселями «на борту» по качеству то же самое, что и матрица 1/2,5 с 6-7 Мп. А вот если в первом случае оставить «всего» 10 Мп, то картинка окажется уже значительно лучше.
Реклама говорит нам, что, чем больше мегапикселей, тем лучше. Но это не совсем так. Да, чем их больше, тем детальнее картинка. Но не в ущерб размерам каждого отдельного пикселя. Матрица 1/1,6 с 15-17 мегапикселями «на борту» по качеству то же самое, что и матрица 1/2,5 с 6-7 Мп. А вот если в первом случае оставить «всего» 10 Мп, то картинка окажется уже значительно лучше.
Из этого следует, что чем матрица больше, тем качественнее будет картинка в условиях плохой освещенности. Но увеличение матрицы – это увеличение и самого прибора, и его стоимости. А так как видеорегистратор должен быть компактен и незаметен, приходится искать «золотую середину». Сейчас у всех регистраторов матрицы примерно одного размера. Качество теперь заключается в нюансах настроек и параметров.
Полнокадровая технология — Sony Pro
Два стандартных параметра ISO
Для эффективной работы цифрового датчика изображения необходимо использовать базовое значение ISO. Благодаря ему вы обеспечите максимально низкий уровень шума, оптимальное соотношение «сигнал — шум» и наиболее расширенный динамический диапазон. Это возможно, так как при использовании базовых настроек ISO на сигнал, исходящий от матрицы, не действует коэффициент усиления напряжения. Довольно часто при повышении этого коэффициента, например чтобы увеличить значение ISO или сделать изображение ярче, на картинке появляются шумы и снижается динамический диапазон. Ваше изображение действительно будет в два раза ярче, но при этом так же увеличится соотношение «сигнал — шум», а качество снимка значительно снизится. Если зернистый кадр, снятый на аналоговую пленку, например ASA 400, может выглядеть интересно и уникально, то шум на цифровом изображении свидетельствует о его низком качестве.
Это возможно, так как при использовании базовых настроек ISO на сигнал, исходящий от матрицы, не действует коэффициент усиления напряжения. Довольно часто при повышении этого коэффициента, например чтобы увеличить значение ISO или сделать изображение ярче, на картинке появляются шумы и снижается динамический диапазон. Ваше изображение действительно будет в два раза ярче, но при этом так же увеличится соотношение «сигнал — шум», а качество снимка значительно снизится. Если зернистый кадр, снятый на аналоговую пленку, например ASA 400, может выглядеть интересно и уникально, то шум на цифровом изображении свидетельствует о его низком качестве.
Поэтому в настройках полнокадровой матрицы, встроенной в камеры VENICE и FX9, доступны два базовых значения ISO, с помощью которых можно отрегулировать показатели чувствительности датчика изображения. Они имеют лишь небольшую разницу в качестве изображения. Цветопередача и динамический диапазон остаются практически идентичными, что можно сказать и об уровне шумов.
В камере VENICE используется базовое значение ISO 500, что обеспечивает оптимальный баланс динамического диапазона при стандартном освещении на съемочной площадке. Вспомогательное высокое базовое значение ISO равняется 2500 и отлично подходит для съемки в расширенном динамическом диапазоне в условиях низкой освещенности. Камера FX9 с чувствительностью ISO 800 обеспечивает оптимальный динамический диапазон для съемки как на улице, так и в ярко освещенных помещениях. Вспомогательное высокое базовое значение чувствительности ISO равняется 4000 и отлично подходит для работы в условиях низкой освещенности. Вы можете подобрать базовое значение ISO под свой уровень освещенности и менять его, не снижая качество изображения и не прерывая рабочий процесс.
Физический размер матрицы. Цифровая фотография. Трюки и эффекты
Читайте также
3.2.1 Физический уровень
3. 2.1 Физический уровень
Физический уровень (physical layer) имеет дело с физическими носителями, разъемами и сигналами для представления логических нулей и единиц. Например, адаптеры сетевого интерфейса Ethernet и Token-Ring и соединяющие их кабели реализуют функции физического
2.1 Физический уровень
Физический уровень (physical layer) имеет дело с физическими носителями, разъемами и сигналами для представления логических нулей и единиц. Например, адаптеры сетевого интерфейса Ethernet и Token-Ring и соединяющие их кабели реализуют функции физического
8.1.8. Реализация разреженной матрицы
8.1.8. Реализация разреженной матрицы Иногда бывает нужен массив, в котором определена лишь небольшая часть элементов, а остальные не определены вовсе или (даже чаще) равны 0. Подобная разреженная матрица потребляет так много памяти зря, что были найдены способы более
9.4.1. Реализация графа в виде матрицы смежности
9.4.1. Реализация графа в виде матрицы смежности
Нижеприведенный пример основан на двух предыдущих. В листинге 9.3 неориентированный граф реализован в виде матрицы смежности с помощью класса ZArray (см. раздел 8.1.26). Это нужно для того, чтобы новые элементы по умолчанию получали
В листинге 9.3 неориентированный граф реализован в виде матрицы смежности с помощью класса ZArray (см. раздел 8.1.26). Это нужно для того, чтобы новые элементы по умолчанию получали
11.14. Реализация динамической матрицы
11.14. Реализация динамической матрицы ПроблемаТребуется реализовать числовые матрицы, размерности которых (количество строк и столбцов) неизвестны на этапе компиляции.РешениеВ примере 11.28 показана универсальная и эффективная реализация класса динамической матрицы,
11.15. Реализация статической матрицы
11.15. Реализация статической матрицы
ПроблемаТребуется эффективно реализовать матрицу, когда ее размерность (т.е. количество строк и столбцов) постоянна и известна на этапе компиляции. РешениеКогда размерность матрицы известна на этапе компиляции, компилятор может легко
РешениеКогда размерность матрицы известна на этапе компиляции, компилятор может легко
Физический размер изображения
Физический размер изображения Физический размер изображения – это количество пикселов в изображении по ширине и по высоте. Таким образом, мы получаем размеры изображения в пикселах.Чем больше пикселов в изображении и чем больше его физический размер, тем выше может
Размер страницы и размер кэша по умолчанию
Размер страницы и размер кэша по умолчанию При восстановлении вы можете изменить размер страницы, включив в команду переключатель -р[age_size], за которым следует целое число, задающее размер в байтах. Допустимые размеры страниц см. в табл. 38.2.В этом примере gbak восстанавливает
Числогрызы ткнулись в физический предел полупроводников.
 Куда дальше? Евгений Золотов
Куда дальше? Евгений Золотов
Числогрызы ткнулись в физический предел полупроводников. Куда дальше? Евгений Золотов Опубликовано 27 ноября 2013 Суперкомпьютеры всегда представлялись особенным классом вычислительной техники. Поскольку строят такие машины для решения задач
Разрешение матрицы
Разрешение матрицы Мы знаем, что матрица состоит из мельчайших светочувствительных элементов. Количество таких элементов в матрице – это и есть ее разрешение. Разрешение матрицы получают умножением количества элементов по горизонтали и вертикали. Самые
Динамический диапазон матрицы
Динамический диапазон матрицы
Динамический диапазон светочувствительной матрицы – это ее способность воспринимать градации каждого из цветов. Говоря проще, динамический диапазон определяет, сколько ступеней разности контраста может увидеть и зафиксировать матрица.
Говоря проще, динамический диапазон определяет, сколько ступеней разности контраста может увидеть и зафиксировать матрица.
Физический уровень
Физический уровень Хотя физический доступ и не рассматривается как реальная угроза сегодняшнего дня, очевидно, что нарушение физической безопасности может привести к нарушению информационной безопасности. Для обеспечения высокой степени доверия к защите физического
Чистка матрицы зеркальной камеры
Чистка матрицы зеркальной камеры У владельцев зеркальных камер к радости от возможности смены объективов прибавляется забота о чистоте матрицы. Что делать, если вы заметили на снимках ровной светлой поверхности соринки и пятна? В некоторых моделях зеркальных камер
Чистка матрицы зеркальной камеры
Чистка матрицы зеркальной камеры
В зеркальной камере, в отличие от компактной, приходится чистить матрицу. Хотите вы или нет, но рано или поздно на матрицу попадает пыль, мелкие соринки. Насколько скоро это произойдет, зависит от частоты смены объективов, условий
Хотите вы или нет, но рано или поздно на матрицу попадает пыль, мелкие соринки. Насколько скоро это произойдет, зависит от частоты смены объективов, условий
Размер головного мозга и размер социального окружения
Размер головного мозга и размер социального окружения Дискуссии по поводу взаимосвязи между размером головного мозга какого-либо организма и размером группы, к которой этот организм принадлежит, ведутся нейробиологами уже давно. При этом взаимосвязь с социальной
ТЕМА НОМЕРА: Реформирование матрицы
ТЕМА НОМЕРА: Реформирование матрицы Автор: Леонид Левкович-МаслюкГде-то в конце 1980-х или начале 1990-х я читал в «Независимой газете» обзор событий в мире книг. Автор отмечал, что на прилавках появилось оригинальнейшее сочинение по истории древнего мира, которое написал
Введение в матрицы / Размер матрицы
Введение
в Матрицы / Размер матрицы (стр. 1 из 3)
1 из 3)
Разделы: Дополненные и коэффициенты матрицы / Размер матрицы, Обозначение матрицы и типы, Матрица равенства
Дополненный матрицы
Матрицы невероятно полезные вещи, которые возникают во многих различных прикладных областях.А пока вы наверное, только простейшие манипуляции с матрицами, а потом вы перейдете к следующей теме. Но не стоит удивляться, встретив матрицы опять же, скажем, в физике или технике. (Множественное число «матрицы» произносится как «MAY-truh-seez».)
Матрицы изначально были на основе систем линейных уравнений.
- Учитывая следующее систему уравнений, напишите соответствующую расширенную матрицу.
Запишите коэффициенты.
и значения ответов, включая все знаки «минус». Если там
— коэффициент «нет», тогда коэффициент равен «1».
То есть, учитывая систему (линейных) уравнений, вы можете связать с ним матрицу (сетку чисел внутри скобок), который содержит только коэффициенты линейного система. Это называется «расширенной матрицей»: сетка, содержащая коэффициенты из левой части каждого уравнения были «дополнены» с ответами из правой части каждого уравнения.
Записи (то есть значения в) матрице соответствуют x -, л — и z -значения в исходной системе, если исходная система устроена правильно на первом месте. Иногда вам нужно переставить термины или вставить нули в качестве заполнителей в вашей матрице.
- Учитывая следующее систему уравнений, напишите соответствующую расширенную матрицу.
Мне сначала нужно переставить система как:
Тогда я могу написать
связанная матрица как:
При формировании дополненной
матрица, используйте ноль для любой записи, где соответствующее место в системе
линейных уравнений пусто.
Коэффициент матрицы
Если сформировать матрицу только по значениям коэффициентов матрица будет выглядеть так:
Это называется » матрица коэффициентов «.авторское право Элизабет Стапель 2003-2011 Все права защищены
Выше мы пошли от линейного систему в расширенную матрицу. Вы можете пойти и другим путем.
- Учитывая следующее дополненную матрицу, напишите связанную линейную систему.
Помните, что матрицы требуют, чтобы все переменные были выстроены аккуратно и аккуратно. И это обычно, когда у вас есть три переменные, использовать x , л , г. и z , в этой последовательности.Таким образом, соответствующая линейная система должна быть:
Размер матрицы
Матрицы часто упоминаются
по их размерам. Размер матрицы задается в виде измерения,
примерно так же, как комнату можно назвать «комнатой десять на двенадцать».
Размеры матрицы — это строки и столбцы, а не размер
ширина и длина. Например, рассмотрим следующую матрицу A :
Размер матрицы задается в виде измерения,
примерно так же, как комнату можно назвать «комнатой десять на двенадцать».
Размеры матрицы — это строки и столбцы, а не размер
ширина и длина. Например, рассмотрим следующую матрицу A :
Начиная с A имеет три ряда и четыре столбца , размер А это 3 4 (произносится как «три на четыре»).
Ряды идут бок о бок; колонны идут вверх и вниз. «Строка» и «столбец» — это технические термины и не являются взаимозаменяемыми. Размеры матрицы всегда задается сначала количеством строк, а затем количеством столбцов. Следуя этому соглашению, следующая матрица B :
… это 2 3. Если матрица имеет такое же количество строк, что и столбцы, матрица называется «квадратной». матрица.Например, матрица коэффициентов сверху:
. .. это 3
3 квадратная матрица.
.. это 3
3 квадратная матрица.
Верх | 1 | 2 | 3 | Вернуться к указателю Далее >>
Цитируйте эту статью как: | Стапель, Елизавета.
«Введение в матрицы / размер матрицы.« Purplemath .
Доступно по номеру |
Обозначение матрицы и размер матрицы
Матрицы используются во множестве различных математических задач, от алгебры и линейной алгебры до конечной математики. Конечно, чтобы иметь возможность работать с матрицами, вам необходимо понимать используемые обозначения и простые (но важные) идеи, такие как размер матрицы.
объявление
Элементы матрицы
Матрица — это способ организации чисел в строки и столбцы. Он может представлять собой систему уравнений, реальную ситуацию или просто представлять собой интересующую нас матрицу. Матрицы обычно обозначаются заглавными буквами, например A , B или C . Ниже вы можете увидеть матрицу, которую мы будем называть «матрица A ».
Числа в матрице называются элементами.Один из способов рассказать о конкретном элементе — использовать строчную букву и пометить ее строкой и столбцом элемента.
Обратите внимание, что вы также можете сказать «5 — это запись (1,2)» и «8 — это запись (2,3)».
Размер матрицы
Общая тема с матрицами — «думайте о строках-столбцах», и это справедливо даже при обсуждении размера или размерности матрицы. Если матрица имеет 4 строки и 6 столбцов, мы говорим, что это матрица 4 x 6 (читай: четыре на шесть).
Сводка
Изучая матрицы, помните следующие идеи:
- Элементы упоминаются по их расположению в строке, затем в столбце.

- Размер матрицы: (количество строк) x (количество столбцов). Для матрицы 2 x 3 вы бы сказали «размер матрицы 2 на 3».
Продолжить изучение матриц
Теперь, когда вы ознакомились с важными обозначениями и идеями, такими как размер матрицы, вы готовы изучить, как складывать, вычитать и умножать матрицы.
Операций с матрицами:
Подпишитесь на нашу рассылку новостей!
Мы всегда публикуем новые бесплатные уроки и добавляем новые учебные пособия, руководства по калькуляторам и пакеты задач.
Подпишитесь, чтобы получать электронные письма (раз в пару или три недели) с информацией о новинках!
Связанные Размер(функции MATLAB) Размер
(функции MATLAB)| Справочник по функциям MATLAB |
Размеры массива
Синтаксис
d = размер (X) [m, n] = размер (X) m = размер (
X, размер) [d1, d2, d3 ,. .., dn] = размер (X)
.., dn] = размер (X)
Описание
d = размер (X) возвращает размеры каждого измерения массива X в векторе d с элементами ndims (X) . Если X является скаляром, который MATLAB рассматривает как массив 1 на 1, size (X) возвращает вектор [1 1] .
[m, n] = размер (X) возвращает размер матрицы X в отдельных переменных m и n .
м = размер (X, тусклый) возвращает размер измерения X , заданный скаляром dim .
[d1, d2, d3, ..., dn] = размер (X), для n > 1, возвращает размеры размеров массива X в переменных d1, d2, d3, …, dn, при условии, что количество выходных аргументов n равно ndims (X) . Если n не равно ndims (X) , выполняются следующие исключения:
n | |
n> ndims (X) | size возвращает единицы в «дополнительных» переменных, то есть те, которые соответствуют ndims (X) +1 от до n . |
Примечание Для массива Java size возвращает длину массива Java как количество строк. Количество столбцов всегда равно 1. Для массива массивов Java результат описывает только массив верхнего уровня. |
Примеры
Пример 1. Размер второго измерения rand (2,3,4) равен 3.
м = размер (ранд (2,3,4), 2) m = 3
Здесь размер выводится как один вектор.
Здесь размер каждого измерения присваивается отдельной переменной.
[m, n, p] = размер (rand (2,3,4)) m = 2 п = 3 p = 4
Пример 2. Если X = единицы (3,4,5), то
Если X = единицы (3,4,5), то
Но когда количество выходных переменных меньше ndims (X):
«Дополнительные» измерения свернуты в единый продукт.
Если n> ndims (X), все "дополнительные" переменные представляют одноэлементные измерения:
[d1, d2, d3, d4, d5, d6] = размер (X) d1 = d2 = d3 = 3 4 5 d4 = d5 = d6 = 1 1 1
См. Также
exist , длина , numel , whos
| sinh | срез |
© 1994-2005 The MathWorks, Inc.
Размер
(функции MATLAB) Размер
(функции MATLAB)| Справочник функций MATLAB |
Размеры массива
Синтаксис
d = размер (X) [m, n] = размер (X) m = размер (
X, размер) [d1, d2, d3, ..., dn] = размер (X)
Описание
d = размер (X) возвращает размеры каждого измерения массива X в векторе d с элементами ndims (X) .
[m, n] = размер (X) возвращает размер матрицы X в отдельных переменных m и n .
м = размер (X, тусклый) возвращает размер измерения X , заданный скаляром dim .
[d1, d2, d3, ..., dn] = размер (X) возвращает размеры первых n измерений массива X в отдельных переменных.
Если количество выходных аргументов n не равно ndims (X) , то для:
n> ndims (X) | size возвращает единицы в «дополнительных» переменных, т.е.е., выводит ndims (X) +1 - n . |
n | dn содержит произведение размеров остальных размеров X, , то есть размеров от n + 1 до ndims (X) . |
Примечание Для массива Java size возвращает длину массива Java как количество строк. Количество столбцов всегда равно 1.Для массива массивов Java результат описывает только массив верхнего уровня. |
Примеры
Пример 1. Размер второго измерения rand (2,3,4) равен 3.
м = размер (ранд (2,3,4), 2) m = 3
Здесь размер выводится как один вектор.
Здесь размер каждого измерения присваивается отдельной переменной.
[m, n, p] = размер (rand (2,3,4)) m = 2 п = 3 p = 4
Пример 2. Если X = единицы (3,4,5), то
Но когда количество выходных переменных меньше ndims (X):
«Дополнительные» измерения свернуты в единый продукт.
Если n> ndims (X), все "дополнительные" переменные представляют одноэлементные измерения:
[d1, d2, d3, d4, d5, d6] = размер (X) d1 = d2 = d3 = 3 4 5 d4 = d5 = d6 = 1 1 1
См. Также
есть , длина , whos
| sinh | размер (серийный) |
Что такое матрица?
Этот урок знакомит с матрицей - прямоугольным массивом, лежащим в основе матричная алгебра.Матричная алгебра довольно часто используется в расширенной статистике, в основном потому что он дает два преимущества.
- Эффективные методы манипулирования наборами данных и решения наборов уравнения.
Определение матрицы
Матрица представляет собой прямоугольный массив чисел, расположенных в строки и столбцы. Приведенный ниже массив чисел является примером матрицы.
Количество строк и столбцов, которое имеет матрица, называется ее размер или его порядка .Условно, строки указываются первыми; и столбцы, вторые. Таким образом, можно сказать, что размер (или порядок) вышеуказанной матрицы составляет 3 x 4, что означает, что она имеет 3 ряда и 4 столбика.
Числа, которые появляются в строках и столбцах матрицы, называются элементов матрицы. В приведенной выше матрице элемент в первом столбце первой строки 21; элемент во втором столбец первой строки - 62; и так далее.
Матричная нотация
Статистики используют символы для обозначения матричных элементов и матриц.
Матричные элементы. Рассмотрим матрицу ниже, в котором элементы матрицы полностью представлены символами.
По соглашению первый нижний индекс относится к номер строки; а второй индекс - к номеру столбца. Таким образом, первый элемент в первой строке представлен А 1 1 . Второй элемент в первой строке - представлен A 1 2 . И так далее, пока мы не дойдем до четвертого элемента во второй строке, которая представлена А 2 4 .Матрицы. Есть несколько способов изобразить матрица символически. Простейший - использовать жирный шрифт, например A , B , или C . Таким образом, A может представлять собой Матрица 2 x 4, как показано ниже.
Другой подход для представления матрицы A :
A = [ A i j ], где i = 1, 2 и j = 1, 2, 3, 4
Это обозначение означает, что A - это матрица с 2 строками и 4 столбца.Фактические элементы массива не отображаются; они есть представлен символом A i j .
При необходимости будут введены другие матричные обозначения. Для описания всех матричных обозначений, используемых в этом руководстве, увидеть Матричные обозначения Приложение.
Равенство матриц
Чтобы понять алгебру матриц, нам нужно понять матрицу равенство. Две матрицы равны, если все три из следующих условий выполнены:
- Каждая матрица имеет одинаковое количество строк.
- Каждая матрица имеет одинаковое количество столбцов.
- Соответствующие элементы в каждой матрице равны.
Рассмотрим три матрицы, показанные ниже.
Если A = B , мы знаем, что x = 222 и у = 333; поскольку соответствующие элементы равных матриц также равны. А мы знаем, что матрица C не равно A или B , потому что C имеет больше столбцов, чем A или В .
Проверьте свое понимание
Задача 1
Приведенные ниже обозначения описывают две матрицы - матрицу A, и матрица B .
A = [ A i j ]
, где i = 1, 2, 3 и j = 1, 2
Какие из следующих утверждений о A и B верны?
I. Матрица A состоит из 5 элементов.
II. Размер матрицы B составляет 4 x 2.
III. В матрице B элемент B 2 1 является
равно 222.
(A) Только I
(B) Только II
(C) Только III
(D) Все вышеперечисленное
(E) Ничего из вышеперечисленного
Решение
Правильный ответ (E).
- Матрица A имеет 3 строки и 2 столбца; это, 3 ряда по 2 элемента в каждом. Это в сумме составляет 6 элементов, всего - нет 5.
- Размер матрицы B равно 2 х 4, а не 4 х 2.То есть матрица B имеет 2 строки и 4 столбца, а не 4 строки и 2 столбца.
- И, наконец, элемент B 2 1 относится к первый элемент в вторая строка матрицы B , которая равна 555, а не 222.
Оптимальный размер матрицы рентгенограмм грудной клетки для компьютерного обнаружения узелков или новообразований в легких с глубоким обучением
Schalekamp S, van Ginneken B , Koedam E et al (2014) Компьютерное обнаружение улучшает обнаружение легочных узелков на рентгенограммах грудной клетки, помимо поддержки изображений с подавлением костей.Радиология 272: 252–261
Статья Google Scholar
van Ginneken B, Hogeweg L, Prokop M (2009) Компьютерная диагностика при рентгенографии грудной клетки: за пределами узелков. Eur J Radiol 72: 226–230
Статья Google Scholar
Nam JG, Park S, Hwang EJ et al (2018) Разработка и проверка основанного на глубоком обучении алгоритма автоматического обнаружения злокачественных узелков в легких на рентгенограммах грудной клетки.Радиология 290: 218–228
Статья Google Scholar
Закиров А., Кулеев Р., Тимошенко А., Владимиров А. (2015) Современные подходы к компьютерному выявлению заболеваний грудной клетки на рентгенограммах грудной клетки. Appl Math Sci 9: 4361–4369
Google Scholar
Horváth G, Orbán G, Horváth Á et al (2009) CAD-система для скрининга рентгенографии грудной клетки. Всемирный конгресс по медицинской физике и биомедицинской инженерии, 7-12 сентября 2009 г., Мюнхен, Германия.Springer, pp 210–213
Lodwick GS, Keats TE, Dorst JP (1963) Кодирование рентгеновских изображений для компьютерного анализа применительно к раку легких. Радиология 81: 185–200
CAS Статья Google Scholar
Leibstein JM, Nel AL (2006) Выявление туберкулеза на рентгенограммах грудной клетки с использованием методов обработки изображений. Университет Йоханнесбурга
Carrillo-de-Gea JM, García-Mateos G (2010) Выявление нормальности / патологии на рентгенограммах грудной клетки с использованием LBP.Int Conf BioInformatics, 20-23 января 2010 г., Валенсия, Испания, стр. 167-172
Chan YH, Zeng YZ, Wu HC, Wu MC, Sun HM (2018) Эффективное обнаружение пневмоторакса при рентгенографии грудной клетки изображения с использованием локального двоичного шаблона и машины векторов поддержки. J Healthc Eng 2018: 1-12
Dunnmon JA, Yi D, Langlotz CP, Ré C, Rubin DL, Lungren MP (2018) Оценка сверточных нейронных сетей для автоматической классификации рентгенограмм грудной клетки. Радиология 290 (2): 537-544
Chaya Devi S, Satya Savithri T (2018) Обзор: О сегментации узелков на рентгенограммах заднего и переднего отделов грудной клетки. Int J Biomed Imaging 2018: 1-11
Pesce E, Withey SJ, Ypsilantis P-P, Bakewell R, Goh V, Montana G (2019) Обучение обнаружению рентгенограмм грудной клетки, содержащих поражения легких, с использованием сетей визуального внимания. Med Image Anal 53: 26–38
Статья Google Scholar
Annarumma M, Withey SJ, Bakewell RJ, Pesce E, Goh V, Montana G (2019) Автоматическая сортировка рентгенограмм грудной клетки взрослых с помощью глубоких искусственных нейронных сетей.Радиология 291: 196-202
Герас К.Дж., Вольфсон С., Шен Й, Ким С., Мой Л., Чо К. (2017) Скрининг рака молочной железы с высоким разрешением с помощью глубоких сверточных нейронных сетей с несколькими проекциями. Препринт arXiv arXiv: 170307047
Ван Дж, Ян Х, Цай Х, Тан В., Джин С., Ли Л. (2016) Дискриминация рака груди с помощью микрокальцификатов на маммографии с помощью глубокого обучения. Научный представитель 6: 27327
CAS Статья Google Scholar
Park S, Lee SM, Lee KH et al (2020) Система обнаружения мультиклассовых поражений на рентгенограммах грудной клетки, основанная на глубоком обучении: сравнение с показаниями наблюдателя. Eur Radiol 30: 1359–1368
Статья Google Scholar
Irvin J, Rajpurkar P, Ko M et al (2019) Chexpert: большой набор данных рентгенограммы грудной клетки с метками неопределенности и экспертным сравнением. препринт arXiv arXiv: 1
031
He K, Gkioxari G, Dollár P, Girshick R (2017) Mask R-CNN.IEEE Int Conf. Компьютерное зрение, 22-29 октября 2017 г., Венеция, Италия. pp 2961-2969
Lin T-Y, Goyal P, Girshick R, He K, Dollár P (2017) Потеря фокуса для обнаружения плотных объектов. IEEE Trans Pattern Anal Mach Intell 42 (2): 318-327
Szegedy C, Vanhoucke V, Ioffe S, Shlens J, Wojna Z (2016) Переосмысление начальной архитектуры компьютерного зрения. IEEE Int Conf. Компьютерное зрение и распознавание образов, 26–1 июня 2016 г., Лас-Вегас, Невада, США. С. 2818-2826
Szegedy C, Liu W, Jia Y et al (2015) Углубляясь в извилины. IEEE Int Conf Computer Vision and Pattern Recognition, 7-12 июня 2015 г., Бостон, Массачусетс, США. pp 1-9
Матрицы и матричная алгебра - Статистика Как сделать
Матрицы и содержание матричной алгебры (щелкните, чтобы перейти к этому разделу):
- Матричная алгебра: введение
- Добавление матрицы: другие примеры
- Умножение матриц
- Определение сингулярной матрицы
- Матрица идентичности
- Что такое обратная матрица?
- Собственные значения и собственные векторы
- Расширенные матрицы
- Определитель матрицы
- Диагональная матрица
- Что такое симметричная и кососимметричная матрицы?
- Что такое матрица транспонирования?
- Что такое матрица дисперсии-ковариации?
- Корреляционные матрицы
- Идемпотентная матрица.
Матрица представляет собой прямоугольный массив чисел, упорядоченных по столбцам и строкам (как в электронной таблице). Матричная алгебра используется в статистике для выражения наборов данных. Например, ниже представлен рабочий лист Excel со списком оценок за экзамены:
Преобразование в матричную алгебру в основном просто включает удаление идентификаторов столбцов и строк. Добавляется идентификатор функции (в данном случае «G» для оценок):
Числа, которые появляются в матрице, называются элементами матрицы .
: Обозначение
Почему странная нотация?
Мы используем другую нотацию (в отличие от хранения данных в формате электронной таблицы) по простой причине: соглашение. Соблюдение соглашений упрощает соблюдение правил матричной математики (таких как сложение и вычитание). Например, в элементарной алгебре, если у вас есть список вроде этого: 2 яблока, 3 банана, 5 виноградин, вы должны изменить его на 2a + 3b + 5g, чтобы соблюсти соглашение.
Некоторые из наиболее распространенных терминов, с которыми вы встретитесь при работе с матрицами:
- Размер (также называемый порядком): сколько строк и столбцов имеет матрица.Сначала перечислены строки, за ними следуют столбцы. Например, матрица 2 x 3 означает 2 строки и 3 столбца.
- Элементы : числа, которые появляются внутри матрицы.
- Матрица идентичности (I): Диагональная матрица с нулями в качестве элементов, за исключением диагонали, у которой есть единицы.
- Скаляр : любое действительное число.
- Матрица Функция: скаляр, умноженный на матрицу, для получения другой матрицы.
Матрицы идентичности. Изображение: Википедия.com.
Матричная алгебра: сложение и вычитание
Размер матрицы (т.е. 2 x 2) также называется размером матрицы , размером или порядком матрицы. Если вы хотите сложить (или вычесть) две матрицы, их размеры должны быть равны точно так же, как . Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одно и то же место (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).
Примечание к обозначениям: рабочий лист (например, в Excel) использует буквы столбцов (ABCD) и номера строк (123), чтобы указать местоположение ячейки, например A1 или D2. Для матриц типично использование обозначений типа g ij , что означает i-ю строку и j-й столбец матрицы G.
Вычитание матриц работает точно так же.
К началу
Матричное дополнение - это всего лишь серия дополнений. Для матрицы 2 × 2:
- Сложите верхние левые числа вместе и запишите сумму в новую матрицу в верхнем левом положении.
- Сложите верхние правые числа и запишите сумму в верхнем правом углу.
- Сложите нижние левые числа вместе и запишите сумму в нижнем левом углу.
- Сложите нижние правые числа вместе и запишите сумму в правом нижнем углу:
Используйте ту же процедуру для матрицы 2 × 3:
Фактически, вы можете использовать этот базовый метод для добавления любых матриц, если ваши матрицы имеют одинаковые размеры (одинаковое количество столбцов и строк).Другими словами, , если матрицы одинакового размера, вы можете их добавить. Если они разного размера, вы не можете их добавить.
- Матрица с 4 строками и 2 столбцами может быть добавлена к матрице с 4 строками и 2 столбцами.
- Матрица с 4 строками и 2 столбцами не может быть добавлена к матрице с 5 строками и 2 столбцами.
Вышеупомянутый метод иногда называют «начальным суммированием», так как вы просто складываете элементы и фиксируете результат.
Другой способ подумать об этом…
Подумайте, что представляет собой матрица. Эта очень простая матрица [5 2 5] может представлять 5x + 2y + 5z. И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
5x + 2y + 5z + 2x + y + 6z = 7x + 3y + 11z.
Это тот же результат, что и при сложении записей в матрицах.
Дополнение матрицы для неравных размеров
Если у вас неравные размеры, вы все равно можете сложить матрицы вместе, но вам придется использовать другой (гораздо более продвинутый) метод.Один из таких приемов - прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q является матрицей размера (m + p) × (n + q):
Например:
Вернуться к началу
Относительно легко умножить на одно число (так называемое «скалярное умножение»), например 2:
Просто умножьте каждое число в матрице на 2, и вы получите новую матрицу. На изображении выше:
2 * 9 = 18
2 * 3 = 6
2 * 5 = 10
2 * 7 = 14
Результат четырех умножений дает числа в новой матрице справа.
Умножение матриц: две матрицы
Когда вы хотите перемножить две матрицы, процесс становится немного сложнее. Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.
Если все это звучит немного сложно, это (очень короткое) видео показывает, как это делается:
Не можете посмотреть видео? Кликните сюда.
Вы можете выполнить матричное умножение для двух матриц, только если количество столбцов в первой матрице равно количеству строк во второй матрице. Например, вы можете умножить матрицу 2 x 3 (две строки и три столбца) на матрицу 3 x 4 (три строки и четыре столбца).
Очевидно, что это может стать очень сложным (и утомительным) процессом. Тем не менее, вы можете найти множество достойных инструментов для умножения матриц в Интернете. Мне нравится этот от Матрицы Решиш. После расчета вы можете умножить результат на другую матрицу и другую, что означает, что вы можете перемножить несколько матриц вместе.
Microsoft Excel также может выполнять матричное умножение с использованием функций «массива». Вы можете найти инструкции здесь, на сайте Стэнфорда. Прокрутите вниз до места, где написано Матричные операции в Excel.
Наверх
Быстрый взгляд на матрицу может сказать вам, является ли она сингулярной матрицей. Если матрица квадратная и имеет одну строку или столбец с нулями или , два равных столбца или две равные строки, то это особая матрица. Например, следующие десять матриц являются единственными (изображение: Wolfram):
Существуют и другие типы сингулярных матриц, некоторые из которых не так-то легко обнаружить.Следовательно, необходимо более формальное определение.
Следующие три свойства определяют сингулярную матрицу:
- Матрица квадратная и
- Не имеет инверсии.
- Имеет определитель 0.
1. Квадратная матрица
Квадратная матрица имеет (как следует из названия) равное количество строк и столбцов. Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Особая матрица - это квадратная матрица, но не все квадратные матрицы сингулярны.
Необратимые матрицы
Если квадратная матрица не имеет обратной, то это особая матрица.
Обратная матрица - это то же самое, что и обратная величина числа. Если умножить матрицу на обратную, вы получите единичную матрицу , , матричный эквивалент 1. Идентификационная матрица в основном представляет собой последовательность единиц и нулей.Идентификационная матрица различается в зависимости от размера матрицы.
Матрицы идентичности. Изображение: Wikipedia.com.
Определитель нуля
Определитель - это просто специальное число, которое используется для описания матриц и поиска решений систем линейных уравнений. Формула для вычисления определителя различается в зависимости от размера матрицы. Например, матрица 2 × 2, формула ad-bc.
Эта простая матрица 2 × 2 сингулярна, потому что ее определитель равен нулю:
К началу
Единичная матрица - это квадратная матрица с единицами в качестве элементов на главной диагонали сверху слева направо снизу и нулями в остальных местах.Когда вы умножаете квадратную матрицу на единичную матрицу, исходная квадратная матрица остается неизменной. Например:
По идее аналогичен айдентике. В базовой математике элемент идентичности оставляет число неизменным. Например, кроме того, тождественный элемент равен 0, потому что 1 + 0 = 1, 2 + 0 = 2 и т. Д., А при умножении тождественный элемент равен 1, потому что любое число, умноженное на 1, равно этому числу (т. Е. 10 * 1 = 10 ). Говоря более формально, если x - действительное число, то число 1 называется мультипликативным тождеством , потому что 1 * x = x и x * 1 = x.По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .
В матричной алгебре единичный элемент различается в зависимости от размера матрицы, с которой вы работаете; в отличие от сингулярной единицы для мультипликативной идентичности и 0 для аддитивной идентичности, не существует единой единичной матрицы для всех матриц. Для любой матрицы n * n существует единичная матрица I n * n .На главной диагонали всегда будут единицы, а оставшиеся пробелы - нули. На следующем изображении показаны матрицы идентичности для матрицы 2 x 2 и матрицы 5 x 5:
Матрица аддитивной идентичности
Когда люди говорят о «матрице идентичности», они обычно имеют в виду мультипликативную матрицу идентичности. Однако есть и другой тип: аддитивная единичная матрица. Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах - нули.Поэтому их иногда называют нулевой матрицей .
Аддитивная единичная матрица для матрицы 3 * 3.
Вернуться к началу
Обзор поиска инверсий смотрите в этом коротком видео:
Не можете посмотреть видео? Кликните сюда.
Обратные матрицы - это то же самое, что и обратные. В элементарной алгебре (а может быть, и раньше) вы столкнулись с идеей обратного: одно число, умноженное на другое, может равняться 1.
Изображение предоставлено LTU
Если вы умножите одну матрицу на обратную, вы получите матричный эквивалент 1: Identity Matrix , которая в основном представляет собой матрицу с единицами и нулями.
Шаг 1: Найдите адъюгат матрицы. Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой:
Чтобы найти сопряжение матрицы 2 × 2, поменяйте местами диагонали a и d, а затем поменяйте местами знаки c и d.
Шаг 2: Найдите определитель матрицы. Для матрицы
A B C D (см. Изображение выше) определитель равен (a * d) - (b * c).
Шаг 3: Умножить 1 / определитель * адъюгат. .
Проверка ответа
Вы можете проверить свой ответ с помощью умножения матриц.Умножьте свою матрицу ответов на исходную матрицу, и вы получите единичную матрицу. Вы также можете воспользоваться онлайн-калькулятором здесь.
К началу
Собственное значение (λ) - это специальный скаляр, используемый при матричном умножении и имеющий особое значение в нескольких областях физики, включая анализ устойчивости и небольшие колебания колеблющихся систем. Когда вы умножаете матрицу на вектор и получаете тот же вектор в качестве ответа вместе с новым скаляром, скаляр называется собственным значением . Основное уравнение:
A x = λ x ; мы говорим, что λ является собственным значением A.
Все приведенное выше уравнение говорит о том, что , если вы возьмете матрицу A и умножите ее на вектор x , вы получите то же самое, как если бы вы взяли собственное значение и умножили его на вектор x .
Пример собственных значений
В следующем примере 5 - собственное значение A, а (1,2) - собственный вектор:
Давайте рассмотрим это по шагам, чтобы наглядно продемонстрировать, что такое собственное значение.В обычном умножении, если вы умножаете матрицу n x n на вектор n x 1, в результате вы получаете новый вектор n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):
Что, если бы вместо новой матрицы nx 1 можно было получить ответ с помощью вектора , который вы умножили на вместе с новым скаляром?
Когда это возможно, вектор умножения (то есть тот, который также есть в ответе) называется собственным вектором, а соответствующий скаляр - собственным значением.Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в так называемом разложении по собственным значениям . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.
Расчет
Найдите собственные значения для следующей матрицы:
Шаг 1: Умножьте единичную матрицу на λ.Единичная матрица для любой матрицы 2 × 2 равна [1 0; 0 1], поэтому:
Шаг 2: Вычтите ответ из шага 1 из матрицы A, используя вычитание матрицы:
Шаг 3: Найдите определитель матрицы, вычисленной на шаге 2:
det = (5- λ) (- 1-λ) - (3) (3)
Упрощая, получаем:
-5 - 5λ + λ + λ 2 - 9
= λ 2 - 4λ - 14
Шаг 4: Установите уравнение, которое вы нашли на шаге 3, равным нулю и решите для λ:
0 = λ 2 - 4λ - 14 = 2
Мне нравится использовать свой TI-83, чтобы найти корни, но вы можете также воспользуйтесь алгеброй или этим онлайн-калькулятором.Находя корни (нули), получаем x = 2 + 3√2, 2 - 3√2
Ответ : 2 + 3√2 и 2-3√2
Математика для больших матриц такая же, но вычисления могут быть очень сложными. Для матриц 3 × 3 используйте калькулятор внизу этого раздела; для больших матриц попробуйте этот онлайн-калькулятор.
Наверх
На изображении выше показана расширенная матрица (A | B) внизу. Расширенные матрицы обычно используются для решения систем линейных уравнений, и именно поэтому они были впервые разработаны.Три столбца слева от полосы представляют коэффициенты (по одному столбцу для каждой переменной). Эта область называется матрицей коэффициентов . Последний столбец справа от полосы представляет собой набор констант (т. Е. Значений справа от знака равенства в наборе уравнений). Она называется расширенной матрицей , потому что матрица коэффициентов была «дополнена» значениями после знака равенства.
Например, следующая система линейных уравнений:
x + 2y + 3z = 0
3x + 4y + 7z = 2
6x + 5y + 9z = 11
Может быть помещен в следующую расширенную матрицу:
После того, как вы поместили свою систему в расширенную матрицу, вы можете выполнять операции со строками для решения системы.
У вас нет , у вас нет , чтобы использовать вертикальную черту в расширенной матрице. Обычно матрицы вообще не имеют линий. Полоса просто упрощает отслеживание ваших коэффициентов и ваших констант справа от знака равенства. Если вы вообще используете вертикальную полосу, зависит от учебника, который вы используете, и от предпочтений вашего преподавателя.
Написание системы уравнений
Вы также можете работать в обратном направлении, чтобы написать систему линейных уравнений, заданную расширенной матрицей.
Пример вопроса: Напишите систему линейных уравнений для следующей матрицы.
Шаг 1: Запишите коэффициенты для первого столбца, за которым следует «x». Обязательно запишите положительные или отрицательные числа:
-1x
2x
6x
Шаг 2: Напишите коэффициенты для второго столбца, а затем укажите «y». Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y
2x + 4y
6x + 2y
Шаг 3: Напишите коэффициенты для второго столбца, а затем укажите «z.«Сложите, если это положительное число, и вычтите, если оно отрицательное:
-1x + 7y + 3
2x + 4y - 7
6x + 2y + 9
Шаг 3. Запишите константы в третьем столбце, поставив перед знаком равенства.
-1x + 7y + 3 = 0
2x + 4y - 7 = 2
6x + 2y + 9 = 7
Примечание : если на этом шаге стоит знак минус, просто сделайте константу отрицательным числом.
К началу
Определитель матрицы - это просто специальное число, которое используется для описания матриц для нахождения решений систем линейных уравнений, нахождения обратных матриц и для различных приложений в исчислении.Определить на простом английском языке невозможно; обычно его определяют в математических терминах или в терминах того, что он может вам помочь. Определитель матрицы имеет несколько свойств:
- Это действительное число. Сюда входят отрицательные числа.
- Определители существуют только для квадратных матриц.
- Обратная матрица существует только для матриц с ненулевыми определителями.
Символ для определителя матрицы A - | A |, который также является тем же самым символом, который используется для абсолютного значения, хотя эти два символа не имеют ничего общего друг с другом.
Формула для вычисления определителя матрицы различается в зависимости от размера матрицы.
Определитель матрицы 2 × 2
Формула определителя матрицы 2 × 2 - ad-bc. Другими словами, умножьте верхний левый элемент на нижний правый, затем вычтите произведение верхнего правого и нижнего левого.
Определитель матрицы 3 × 3
Определитель матрицы 3 × 3 находится по следующей формуле:
| A | = a (ei - fh) - b (di - fg) + c (dh - eg)
Это может показаться сложным, но если вы пометили элементы с помощью a, b, c в верхнем ряду, d, e, f во второй строке и g, h, i в последней, становится основной арифметикой.
Пример :
Найдите определитель следующей матрицы 3 × 3:
= 3 (6 × 2-7 × 3) –5 (2 × 2-7 × 4) +4 (2 × 3-6 × 4)
= -219
По сути, здесь происходит умножение a, b и d на детерминанты меньших 2x2 в матрице 3x3. Этот шаблон продолжается для поиска определителей матриц более высокого порядка.
Определитель матрицы 4 × 4
Чтобы найти определитель матрицы 4 × 4, вам сначала нужно найти определители четырех матриц 3 × 3, которые находятся в матрице 4 × 4.В виде формулы:
Вернуться к началу
Диагональная матрица - это симметричная матрица со всеми нулями, кроме ведущей диагонали, которая проходит от верхнего левого угла до нижнего правого.
Записи на самой диагонали также могут быть нулями; любую квадратную матрицу со всеми нулями еще можно назвать диагональной матрицей.
Единичная матрица, которая содержит все 1s по диагонали, также является диагональной матрицей. Любая матрица с равными элементами по диагонали (т. Е. 2,2,2 или 9,9,9) является скалярным кратным единичной матрице и также может быть классифицирована как диагональная.
Диагональная матрица имеет максимум n чисел, которые не равны нулю, где n - порядок матрицы. Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Обозначение
Обозначение, обычно используемое для описания диагональной матрицы: diag (a, b, c) , где abc представляет числа в первой диагонали. Для приведенной выше матрицы это обозначение будет diag (3,2,4)..
Верхние и нижние треугольные матрицы
Диагональ матрицы всегда относится к ведущей диагонали. Ведущая диагональ в матрице помогает определить два других типа матриц: нижнетреугольные матрицы и верхние треугольные матрицы. В нижнетреугольной матрице числа под диагональю; верхнетреугольная матрица имеет числа над диагональю.
Диагональная матрица - это матрица с нижней диагональю и матрица с нижней диагональю.
Прямоугольные диагональные матрицы
Для наиболее распространенного использования диагональная матрица представляет собой квадратную матрицу с порядком (размером) n .Существуют и другие формы, которые обычно не используются, например, прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.
К началу
Транспонирование матрицы (или транспонирование матрицы) - это как раз то место, где вы переключаете все строки матрицы в столбцы. Матрицы транспонирования полезны при комплексном умножении.
Альтернативный способ описания транспонированной матрицы состоит в том, что элемент в строке «r» и столбце «c» транспонируется в строку «c» и столбец «r».Например, элемент в строке 2, столбце 3 будет транспонирован в столбец 2, строку 3. Размер матрицы также изменится. Например, если у вас есть матрица 4 x 5, вы бы транспонировали ее в матрицу 5 x 4.
Симметричная матрица - это частный случай транспонированной матрицы; он равен своей транспонированной матрице.
Говоря более формально, A = A T .
Символы для транспонированной матрицы
Обычный символ для транспонированной матрицы - A T Однако Wolfram Mathworld утверждает, что также используются два других символа: A ‘ и.
Свойства матриц транспонирования
Свойства транспонированных матриц аналогичны основным числовым свойствам, с которыми вы столкнулись в базовой алгебре (например, ассоциативным и коммутативным). Основные свойства матриц:
- (A T ) T = A: транспонированная матрица транспонирования является исходной матрицей.
- (A + B) T = A T + B T : Транспонирование двух сложенных вместе матриц такое же, как транспонирование каждой отдельной матрицы, сложенной вместе.
- (rA) T = rA T : когда матрица умножается на скалярный элемент, не имеет значения, в каком порядке вы транспонируете (примечание: скалярный элемент - это величина, которая может умножать матрицу).
- (AB) T = B T A T : транспонирование двух матриц, умноженных вместе, совпадает с произведением их матриц транспонирования в обратном порядке.
- (A -1 ) T = (A T ) -1 : транспонирование и инверсия матрицы могут выполняться в любом порядке.
Наверх
Симметричная матрица - это квадратная матрица, имеющая симметрию относительно ведущей диагонали, сверху слева направо. Представьте себе складку в матрице по диагонали (не включайте числа в действительную диагональ). Верхняя правая половина матрицы и нижняя левая половина являются зеркальными отображениями относительно диагонали:
Если вы можете сопоставить числа друг с другом вдоль линии симметрии ( всегда - ведущая диагональ), как в примере справа , у вас симметричная матрица.
Альтернативное определение
Другой способ определить симметричную матрицу состоит в том, что симметричная матрица равна ее транспонированной. При транспонировании матрицы первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
Если вы возьмете симметричную матрицу и транспонируете ее, матрица будет выглядеть точно так же, отсюда и альтернативное определение, что симметричная матрица равна ее транспонированию.С математической точки зрения, M = M T , где M T - матрица транспонирования.
Максимальное количество номеров
Поскольку большинство чисел в симметричной матрице дублируются, существует ограничение на количество различных чисел, которые она может содержать. Уравнение для максимального количества чисел в матрице порядка n: n (n + 1) / 2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, имеется максимум 4 (4 + 1) / 2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ - это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6.
Диагональные матрицы
Диагональная матрица - это частный случай симметричной матрицы. Диагональная матрица имеет все нули, кроме ведущей диагонали.
Что такое асимметричная матрица?
Кососимметричная матрица, иногда называемая антисимметричной матрицей , представляет собой квадратную матрицу, симметричную относительно обеих диагоналей. Например, следующая матрица является асимметричной:
Математически асимметричная матрица удовлетворяет условию a ij = -a ji .Например, возьмите запись в строке 3, столбце 2, которая равна 4. Его симметричным аналогом является -4 в строке 2, столбце 3. Это условие также можно записать в терминах его транспонированной матрицы: A T = - А. Другими словами, матрица является кососимметричной, только если A T = -A, где A T - это транспонированная матрица.
Все старшие диагональные элементы в кососимметричной матрице должны быть нулевыми. Это потому, что i, i = −a i, i влечет i, i = 0.
Еще одним интересным свойством этого типа матрицы является то, что если у вас есть две кососимметричные матрицы A и B одинакового размера, вы также получите кососимметричную матрицу, если сложите их вместе:
Добавление двух кососимметричных матриц все вместе.
Этот факт может помочь вам доказать, что две матрицы кососимметричны. Первый шаг - убедиться, что все элементы на главной диагонали равны нулю (то, что невозможно «доказать» математически!).Второй шаг - сложение матриц. Если результатом является третья матрица, которая является кососимметричной, то вы доказали, что a ij = - a ji .
Косоэрмитский
Косоэрмитова матрица по сути такая же, как кососимметричная матрица, за исключением того, что косоэрмитова матрица может содержать комплексные числа.
Косоэрмитова матрица, показывающая комплексные числа.
Фактически, кососимметричный и кососимметричный эквивалентны для вещественных матриц (матрицы, которая почти полностью состоит из действительных чисел).Старшая диагональ косоэрмитовой матрицы должна содержать чисто мнимые числа; в мнимой сфере ноль считается мнимым числом.
Вернуться к началу
Матрица ковариации и дисперсии (также называемая матрицей ковариации или матрицей дисперсии) - это квадратная матрица, которая отображает дисперсию и ковариацию двух наборов двумерных данных вместе. Дисперсия - это мера того, насколько разбросаны данные. Ковариация - это мера того, насколько две случайные величины перемещаются вместе в одном направлении.
Дисперсии отображаются в диагональных элементах, а ковариации между парами переменных отображаются в недиагональных элементах. Дисперсии находятся в диагоналях ковариантной матрицы, потому что в основном эти дисперсии являются ковариатами каждой отдельной переменной с самой собой.
Следующая матрица показывает дисперсию для A (2,00), B (3,20) и C (0,21) в диагональных элементах.
Ковариации для каждой пары показаны в других ячейках.Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете посмотреть столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.
Создание матрицы дисперсии-ковариации
Многие статистические пакеты, включая Microsoft Excel и SPSS, могут создавать ковариативно-вариативные матрицы. Обратите внимание, что Excel вычисляет ковариацию для генеральной совокупности (знаменатель n), а не для выборки (n-1).Это может привести к немного неправильным вычислениям для матрицы дисперсии-ковариации. Чтобы исправить это, вам нужно умножить каждую ячейку на n / n-1.
Если вы хотите сделать один вручную:
Шаг 1: Вставьте отклонения для ваших данных в диагонали матрицы.
Шаг 2: Вычислите ковариацию для каждой пары и введите их в соответствующую ячейку. Например, ковариация для A / B в приведенном выше примере появляется в двух местах (A B и B A).

 Для технологии характерно меньшее напряжение электропитания, перегрев и уровень шумовых помех;
Для технологии характерно меньшее напряжение электропитания, перегрев и уровень шумовых помех;
 .., dn] = размер (X)
.., dn] = размер (X)