Угол рисунок: Что такое угол? Определение, виды, как обозначают, примеры

Что такое угол? Определение, виды, как обозначают, примеры

Определение угла

Угол — это простая геометрическая фигура. Определение угла напрямую связано с понятием луча.

Луч — прямая линия, у которой есть начало, но нет конца, и продолжается она только в одну сторону.

Если нам дана прямая a на плоскости, и на ней есть некоторая точка O — выходит, что прямая разделена точкой на две части, каждая из которых является лучом с началом в точке O.

Луч можно обозначить одной строчной буквой латинского алфавита или двумя прописными. Например, вот так:

Угол — часть плоскости между двумя линиями, исходящими из одной точки. Каждая сторона угла является лучом, а вершина — общим началом сторон.

Что такое вершина и стороны угла

В математике существует специальный символ для обозначения угла, вот он: ∠.

Если стороны угла названы малыми латинскими буквами, то их записывают после символа. Например, так: ∠ab или ∠ba.

Если стороны угла названы большими буквами, то обозначение угла будет состоять из символа и трех букв, при этом вершина всегда записывается в центре. При сторонах угла OA и OB название угла запишем так: ∠AOB и ∠BOA. Также можно назвать угол одной большой буквой, которая указывает на его вершину, например: ∠O.

Иногда встречается обозначение в виде цифр — так тоже можно.

Для наглядности — все способы обозначения углов:

Так как угол делит плоскость на две части, одна будет внутренней областью угла, а другая — внешней областью угла. Вот так:

Единица измерения углов — градусы.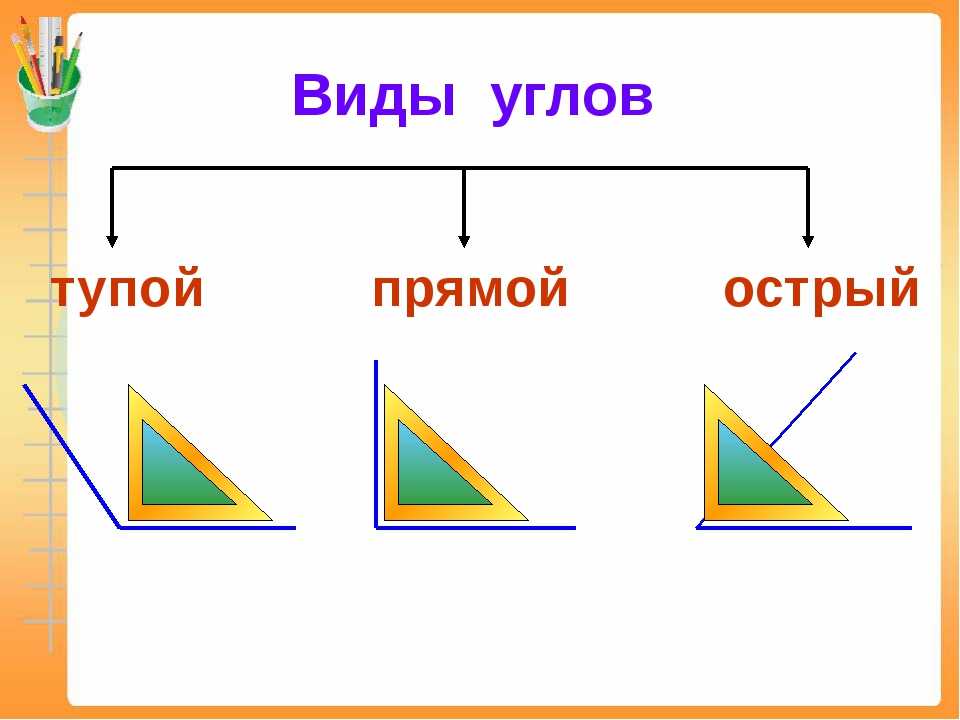 Символ для обозначения градуса угла: °.

Демо урок по математике

Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.

Виды углов

Есть разные типы углов и у каждого своё название:

• острый
• прямой
• тупой
• развернутый
• выпуклый
• полный

Различать виды углов в геометрии важно. Определять можно на глаз или с помощью линейки.

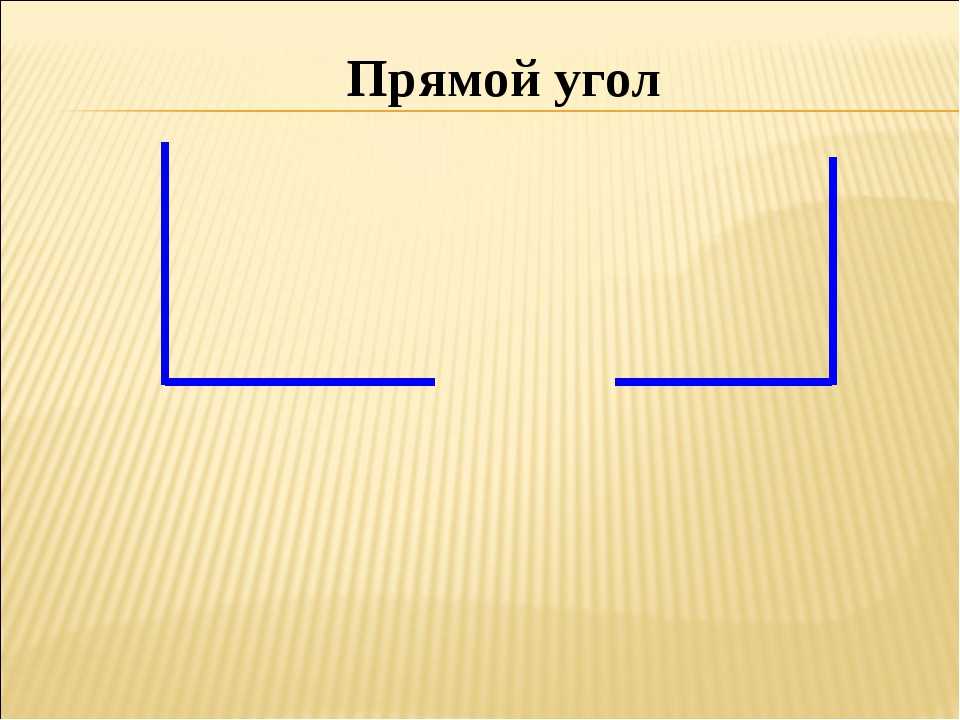
Прямой угол — это угол, стороны которого перпендикулярны друг другу. Прямой угол всегда равен 90°.

Если два смежных угла равны между собой, то каждый из них является прямым. Для удобства прямой угол обозначается уголком. Вот так:

На картинке изображены два прямых угла ∠AOC и ∠COB. Общая сторона OC перпендикулярна прямой AB, а точка O — основание перпендикуляра.

Острый угол — это угол, который меньше прямого угла, то есть < 90°.

Развернутый угол — это открытый угол, который образован двумя лучами и равен сумме двух прямых углов. Развернутый угол равен 180°. Как выглядит развернутый угол, показано на первой картинке.

При разделении развернутым углом на плоскости любая из его частей считается внутренней областью развернутого угла.

Неразвернутый угол — это любой угол, который не является развернутым, то есть не равен 180°.

Тупой угол — это угол, который больше прямого угла, но меньше развернутого:
90° < тупой угол < 180°.

Выпуклый угол — это угол, который больше развернутого угла, но меньше полного:
180° < выпуклый угол < 360°.

Полный угол — это угол, обе стороны которого совпадают с одним лучом. Он равен сумме четырех прямых углов, то есть = 360°.

Прилежащие углы — это пара углов с общей вершиной и стороной, другие стороны при этом лежат по разные стороны от общей стороны.

На картинке мы видим два прилежащих угла ∠AOB и ∠BOC, общую вершину O и общую сторону OB.

Можно сформулировать определение по-другому: если из вершины любого угла провести луч, разделяющий угол на два, то образованные углы будут прилежащими.

Чтобы найти угол, который разделен лучом, нужно сложить полученные углы: ∠AOB = ∠AOC + ∠COB. Из этого можно выделить следующие верные разности:

• ∠AOC = ∠AOB − ∠COB,
• ∠COB = ∠AOB − ∠AOC.

Запоминаем!

Угол называется прямым, если он равен 90°, острым, если он меньше 90°, тупым, если он больше 90°, но меньше 180°. Развернутый угол равен 180°.

Онлайн-школа Skysmart приглашает детей и подростков на курсы по математике — за интересными задачами, новыми прикладными знаниями и хорошими оценками!

Сравнение углов

Для сравнения углов можно использовать самый простой способ из программы 4 класса — метод наложения. Для этого нужно совместить две вершины и сторону одного угла со стороной другого. Если стороны заданных углов совпадут, значит углы равные. Если нет, то угол, который лежит внутри другого, будет меньшим. Здесь два наглядных примера с равными и неравными углами:

При этом развернутые углы всегда являются равными.

Совмещение углов ∠𝐴𝐵𝐶 и ∠𝑀𝑁𝐾 происходит следующим образом:

 

1. Вершину 𝐵 одного угла совмещаем с вершиной 𝑁 другого угла.


2. Сторону 𝐵𝐴 одного угла накладываем на сторону 𝑁𝑀 другого угла так, чтобы стороны 𝐵𝐶 и 𝑁𝐾 располагались в одном направлении.

Если совпадут и другие стороны, то углы равны: ∠𝐴𝐵𝐶 = ∠𝑀𝑁𝐾.

Если нет, то один угол — меньше другого: ∠𝐴𝐵𝐶<∠𝑀𝑁𝐾.

Сравнить углы можно также, измерив их величины. Для этого понадобится специальный инструмент для построения и измерения углов — транспортир. Вот как он выглядит:

Как правильно измерять углы

Измерение углов похоже на измерение отрезков: нужно сравнить их с углом, принятым за единицу измерения. В геометрии обычно за единицу измерения принимают

градус — угол, равный 1/180 части развернутого угла. Он обозначается так: °.

Градусная мера угла — положительное число, которое показывает, сколько раз градус и его части укладываются в данном углу.

Есть еще две возможные меры угла: минуты и секунды. Они позволяют выполнять более точные расчеты, особенно, когда величина не является целым обозначением градуса.

Минута — 1/60 часть градуса. Обозначается ´.

Секунда — 1/60 часть минуты. Обозначается ´´.

Градус состоит из 3600 секунд, то есть: 1° = 60´ = 3600´´.

Как происходит измерение угла: сначала измеряют стороны угла, а после — его внутреннюю область. Всегда нужно считать количество уложенных углов, так как они предопределяют меру измеряемого угла.

Когда луч делит угол на два или более углов, градусная мера всего угла равна сумме градусных мер этих углов.

На рисунке изображен угол АОВ, он состоит из углов АОС, СОD и DОВ. Можно записать так: ∠AOB = ∠AOC + ∠COD + ∠DOB = 45° + 30° + 60° = 135 °.

Равные углы имеют равную градусную меру.

Обозначение углов на чертеже

Чертеж помогает решать задачки по геометрии в разы быстрее. Чтобы наглядно изображать углы и прочие фигуры, придумали даже отдельное направление — геометрический чертеж.

Задачи с углами могут быть разными, и не всегда есть возможность правильно изобразить и отметить угол. Вот что важно запомнить при обозначении лучей и углов:

• Равные углы обозначают одинаковым количеством дуг.
• Неравные углы обозначают разным количеством дуг, чтобы они отличались между собой.

На чертеже отмечены три неравных угла:

Для обозначения на чертеже более трех углов используем разные виды дуг: волнистые, зубчатые.

Обозначать углы можно разными цветами. Главное, чтобы было просто и броско. При этом не обязательно отмечать все-все углы — достаточно только тех, которые нам нужны для решения задачки.

Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Планиметрия

Справочник по математике

Геометрия (Планиметрия)

Углы

      Углом называют часть плоскости, ограниченную двумя лучами, выходящими из одной точки. Лучи,ограничивающие угол, называют сторонами угла. Точку, из которой выходят лучи, называют вершиной угла.

      Схему обозначения углов рассмотрим на примере угла, изображенного на рисунке 1.

Рис.1

      Изображенный на рисунке 1 угол можно обозначить тремя способами:

      Углы называют равными углами, если их можно совместить.

      Если при пересечении двух прямых образуются четыре равных угла, то такие углы называют прямыми углами (рис.2). Пересекающиеся прямые линии, образующие прямые углы, называют перпендикулярными прямыми.

Рис.2

      Если через точку A, не лежащую на прямой l, проведена прямая, перпендикулярная к прямой l и пересекающая прямую l точке B, то говорят, что из точки B опущен перпендикупяр AB на прямую l (рис.3). Точку B называют основанием перпендикуляра AB.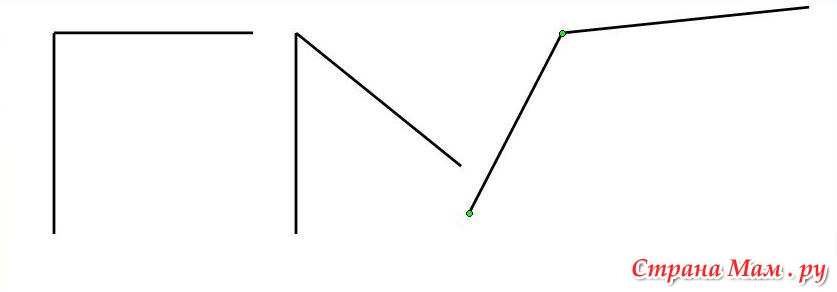

Рис.3

      Замечание. Длину отрезка AB называют расстоянием от точки A до прямой l.

      Углом в 1° (один градус) называют угол, составляющий одну девяностую часть прямого угла.

      Угол, в k раз больший угла в 1°, называют углом в k° ( k градусов).

      Углы измеряют также и в радианах. О радианах можно прочитать в разделе нашего справочника «Измерение углов. Градусы и радианы».

Таблица 1 – Типы углов в зависимости от величины в градусах

Рисунок	Типы углов	Свойства углов
	Прямой угол	Прямой угол равен 90°
	Острый угол	Острый угол меньше 90°
	Тупой угол	Тупой угол больше 90°, но меньше 180°
	Развернутый угол	Развернутый угол равен 180°
	Угол больший, чем развернутый	Такой угол больше 180°, но меньше 360°
	Полный угол	Полный угол равен 360°
	Угол, равный нулю	Такой угол равен 0°

Прямой угол

Свойство: Прямой угол равен 90°

Острый угол

Свойство: Острый угол меньше 90°

Тупой угол

Свойство: Тупой угол больше 90°, но меньше 180°

Развернутый угол

Свойство: Развернутый угол равен 180°

Угол больший, чем развернутый

Свойство: Такой угол больше 180°, но меньше 360°

Полный угол

Свойство: Полный угол равен 360°

Угол, равный нулю

Свойство: Такой угол равен 0°

Таблица 2 – Типы углов в зависимости расположения сторон

Рисунок	Типы углов	Свойства углов
	Вертикальные углы	Вертикальные углы равны
	Смежные углы	Сумма смежных углов равна 180°
	Углы с соответственно параллельными сторонами	Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми
		Сумма  углов с соответственно параллельными сторонами равна 180°, если один из них острый, а другой тупой
	Углы с соответственно перпендикулярными сторонами	Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми
		Сумма углов с соответственно перпендикулярными сторонами равна 180°, если один из них острый, а другой тупой

Вертикальные углы

Свойство вертикальных углов: Вертикальные углы равны

Смежные углы

Свойство смежных углов: Сумма смежных углов равна 180°

Углы с соответственно параллельными сторонами

Свойство углов с соответственно параллельными сторонами: Углы с соответственно параллельными сторонами равны, если оба являются острыми или оба являются тупыми

Свойство углов с соответственно параллельными сторонами: Сумма  углов с соответственно параллельными сторонами равна 180°, если один из них острый, а другой тупой

Углы с соответственно перпендикулярными сторонами

Свойство углов с соответственно перпендикулярными сторонами: Углы с соответственно перпендикулярными сторонами равны, если оба являются острыми или оба являются тупыми

Свойство углов с соответственно перпендикулярными сторонами: Сумма углов с соответственно перпендикулярными сторонами равна 180°, если один из них острый, а другой тупой

      Определение. Биссектрисой угла называют луч, делящий угол пополам.

      Задача. Доказать, что биссектрисы смежных углов перпендикулярны.

      Решение. Рассмотрим рисунок 4.

Рис.4

      На этом рисунке углы AOB и BOC – смежные, а лучи OE и OD – биссектрисы этих углов. Поскольку

2α + 2β = 180°.

то

α + β = 90°,

что и требовалось доказать.

   На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Онлайн транспортир и угловая машина | интерактивный угловой визуализатор

Интернет-угломер и угломер | интерактивный визуализатор углов | виснос

Эта деятельность позволяет манипулировать и исследовать различные виды углов. Онлайн-инструмент транспортир можно использовать для тренировки измерения углов. Его можно использовать в различных классах уровни.

В основном для обучения типам углов, острым, тупой или рефлекторный. Для более продвинутого использования для создания угловых задач в которые должны быть найдены недостающие значения угла буквы. Вы можете щелкнуть и перетащить ручки для изменения углов, и значения будут обновлены.

Органы управления

• Управление режимом используется для выбора типа угловой задачи.
• Рядом с этим указано количество строк. Но обратите внимание, что этот элемент управления отключен для режимов «один» и «пересечение».
• случайная кнопка устанавливает каждый угол на случайное значение
• кнопка равенства сделать все углы равными.
• кнопка Транспортир при нажатии покажет или скроет транспортир
• Бумага может выбирать пятна, квадраты или нет для фона.
• Используйте дисплей углов, чтобы выбрать, следует ли показать или скрыть углы

Например, во всех режимах можно показать или скрыть отдельные ракурсы. нажмите на угол (а). Обратите внимание, когда значение скрыто значение угла рядом с дугой угла заменяется на соответствующее письмо.

Ручки в конце каждой строки можно щелкнуть и перетащить изменить угол.

Режим ‘один’ Идентификация типов углов.

Исходный режим уникален тем, что есть только один угол. Этот режим отлично подходит для определения различных типов углов. Нажмите клавишу Ctrl, чтобы показать или скрыть угол. тип. Так что теперь вы можете изменить угол, перетащив ручку или щелкнув кости для случайного значения. Угол определения типов перечислены в глоссарии ниже.

Режим дополнительных углов

В этом режиме отображается дополнительный угол, дополнительный сумма углов составляет 90° Первоначально 90° разделены только одной линией но это можно изменить, выбрав другое количество строк. Стандартная школьная проблема состоит в том, чтобы иметь один недостающий угол, который необходимо рассчитать. Вы можете производить бесконечные такие проблемы, выбрав расчет из дисплея углов, теперь нажмите кости для нового проблема.

Режим дополнительных углов

Дополнительные углы — это углы, сумма которых составляет 180°. Этот режим ведет себя точно так же, как и предыдущий.

Углы в точечном режиме

Углы в точке в сумме составляют 360°. В этом режиме нажмите = кнопку, чтобы сделать все углы равными. Это может быть хорошим способом начать Проблема с последующей небольшой корректировкой линий путем перетаскивания.

Углы в режиме пересечения линий

Последний режим имеет дело с углами, полученными при пересечении двух линий. Если вы выбрали рассчитать вы будете обратите внимание, что задан только один угол, а все остальные 3 можно вычислить. используя вертикально противоположное правило или определяя дополнительные углы.

Глоссарий углов

Острый угол

Любой угол меньше 90°

Прямоугольный

Угол, равный 90°

Тупой угол

Угол больше 90°, но меньше 180°

Прямоугольный

Угол 180°, образующий прямую линию

Угол рефлекса

Угол больше 180°

Родственная деятельность

Упражнение с интерактивными часами также можно использовать для объяснения углов.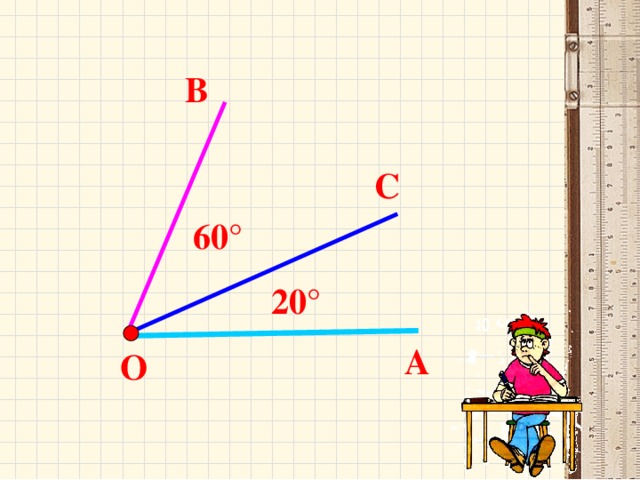

Выберите режим, каждая опция представляет собой другой тип угла.

Измените этот номер, чтобы добавить или удалить линии/углы к текущей задаче

Переключите, чтобы показать/скрыть тип отображаемого угла.

Щелкните, чтобы задать для всех значений случайные значения.

=

Нажмите, чтобы автоматически установить равные углы.

Переключить отображение транспортира.

Выберите стиль фона бумаги

Нажмите случайную кнопку, и это начальное состояние отображения углов

Рисование углов менее 180 с транспортиром

Интерактивная математика для 7 класса — второе издание Рисование углов менее 180 с транспортиром Чтобы нарисовать угол с помощью транспортира, выполните следующие действия: Начертите прямую линию (т. е. плечо угла). Поставьте точку на одном конце руки. Эта точка представляет вершина угла. Поместите центр транспортира в точку вершины и базовую линию транспортира по плечу угла. Найдите нужный угол на шкале и отметьте маленькую точку на край транспортира. Присоедините маленькую точку к вершине с помощью линейки, чтобы сформировать второе плечо. угла. Обозначьте угол заглавными буквами. Пример 1 Решение: Проведите прямую линию AB . Поставьте точку на B . Эта точка представляет собой вершину угол. Поместите центр транспортира на B и базовый уровень транспортир по плечу ВА . Найдите 60 на шкале и отметьте маленькую точку на краю шкалы. транспортир. Соедините вершину B с маленькой точкой с помощью линейки, чтобы сформировать второе плечо, до н.э. , угла. Отметьте угол небольшой дугой, как показано ниже.   Рисование рефлекторных углов Чтобы нарисовать угол рефлекса (т.е. угол больше 180 и меньше 360), действуйте следующим образом: Вычтите угол рефлекса из 360.  Затем начертите полученное угол, как описано выше. Требуемый угол выходит за пределы нарисованного. Отметьте угол небольшой дугой. Обозначьте угол. Пример 2 Решение: Проведите прямую линию PQ . Поставьте точку на Q . Эта точка представляет собой вершину угол. Переверните транспортир вверх дном и поместите центр транспортира в точке Q и базовой линии транспортира вдоль плеча PQ . Используйте внешнюю шкалу, чтобы найти 120 и отметить маленькую точку на краю транспортир. Затем удалите транспортир и соедините вершину Q с маленькой точку с линейкой, чтобы сформировать второе плечо, QR , угла. Отметьте угол небольшой дугой, как показано ниже. Деятельность 1

---

| Домашняя страница | Заказать программное обеспечение по математике | О сериале | Учебники по математическому программному обеспечению |
| Программное обеспечение по математике для 7 класса | Программное обеспечение по математике для 8 класса | 9 годПрограммное обеспечение по математике | Программное обеспечение по математике для 10 класса |
| Программное обеспечение для домашних заданий | Программное обеспечение для репетиторов | Математическая программная платформа | Пробное математическое программное обеспечение |
| Обратная связь | О mathsteacher.